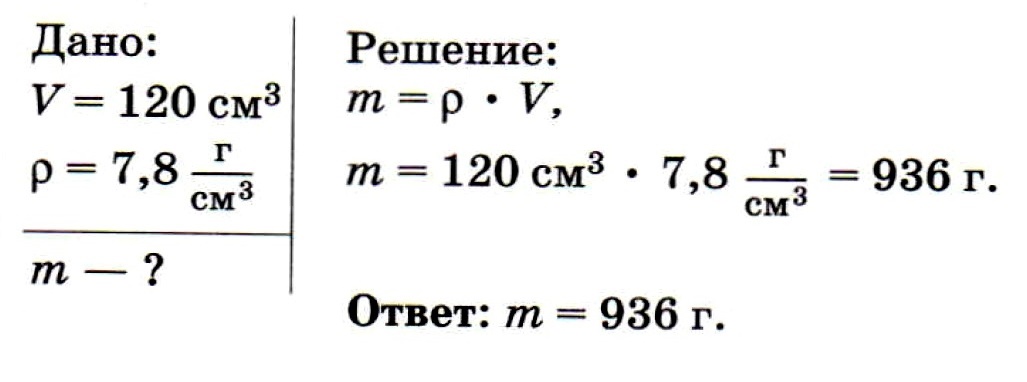Задачи на плотность, массу и объем с решением
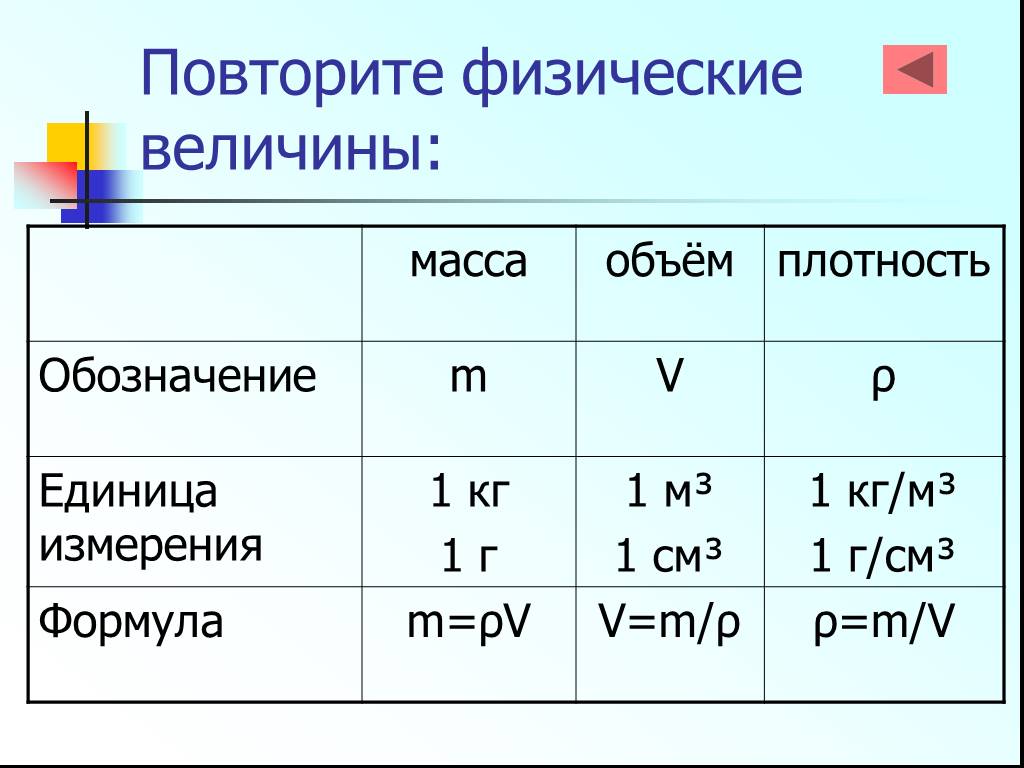
Формулы, используемые по теме «Задачи на плотность, массу и объем с решением»
Название величины |
Обозначение |
Единицы измерения |
Формула |
Масса |
m |
кг |
m = ρ * V |
Объем |
V |
м3 |
V = m / ρ |
Плотность |
ρ |
г/см3,
|
ρ = m / V |
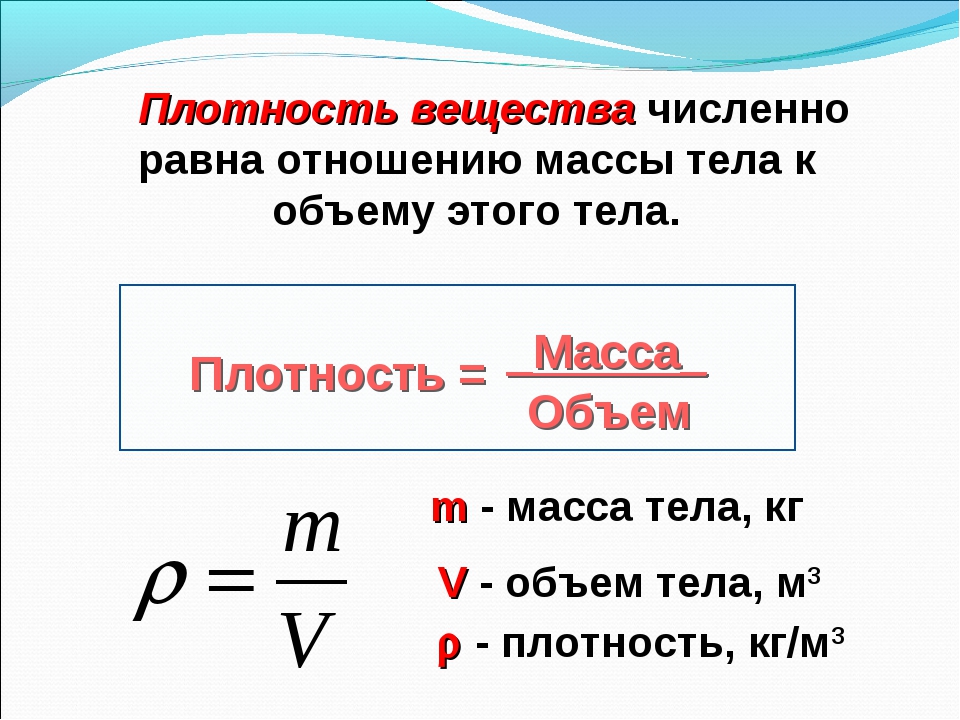
Плотность равна отношению массы тела к его объёму. Плотность обозначают греческой буквой ρ (ро).
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Найдите плотность молока, если 206 г молока занимают объем 200 см3?
Задача № 2.
Определите объем кирпича, если его масса 5 кг?
Задача № 3.
Определите массу стальной детали объёмом 120 см3
Задача № 4.
Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?
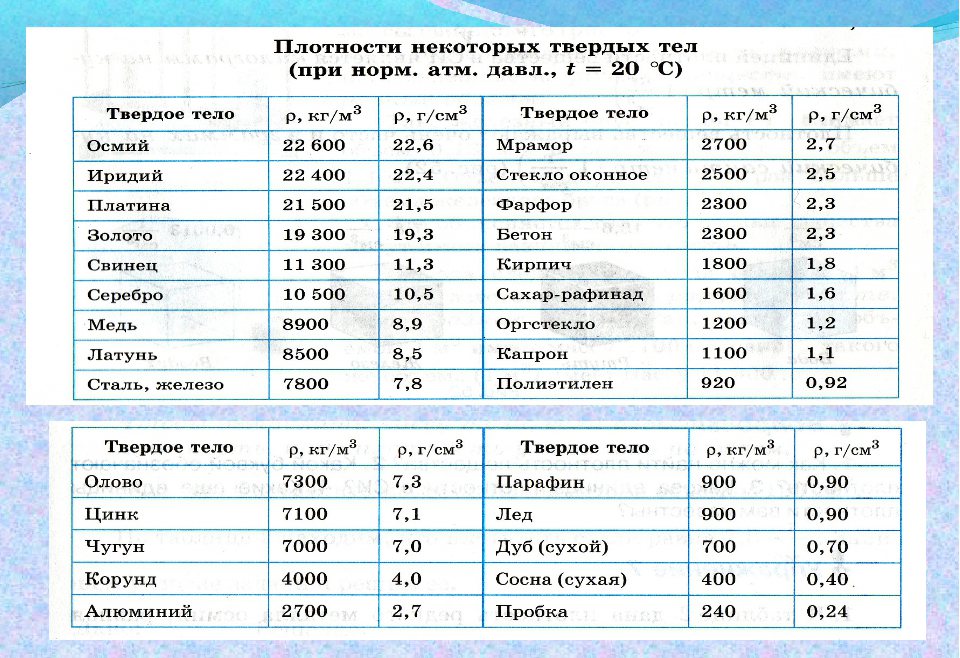
Решение: Из таблицы плотности веществ (см. в конце страницы) определим, что плотность чугуна (ρ2 = 7000 кг/м3) меньше плотности стали (ρ1 = 7800 кг/м3). Следовательно, в единице объема чугуна содержится меньшая масса, чем в единице объема стали, так как чем меньше плотность вещества, тем меньше его масса, если объемы тел одинаковы.
Задача № 5.
Определите плотность мела, если масса его куска объемом 20 см3 равна 48 г. Выразите эту плотность в кг/м3 и в г/см3.
Ответ: Плотность мела 2,4 г/см3, или 2400 кг/м3.
Задача № 6.
Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м2 ?
ОТВЕТ: 160 кг.
Указания к решению. Из формулы для плотности получаем m = p • V. С учетом того, что объем балки V = S • l , получаем: m = p • S • l.
Вычисляем: m = 800 кг/м3 • 0,04 м2 • 5 м = 160 кг.
Задача № 7.
Брусок, масса которого 21,6 г, имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.
ОТВЕТ: Брусок сделан из алюминия.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задача № 8 (повышенной сложности).
Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?
ОТВЕТ: 5 мм.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задача № 9 (олимпиадный уровень).
Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.
ОТВЕТ: 8000 кг/м3
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Задачи на плотность,
массу и объем с решением
Справочный материал для
«Задачи на плотность, массу и объем«
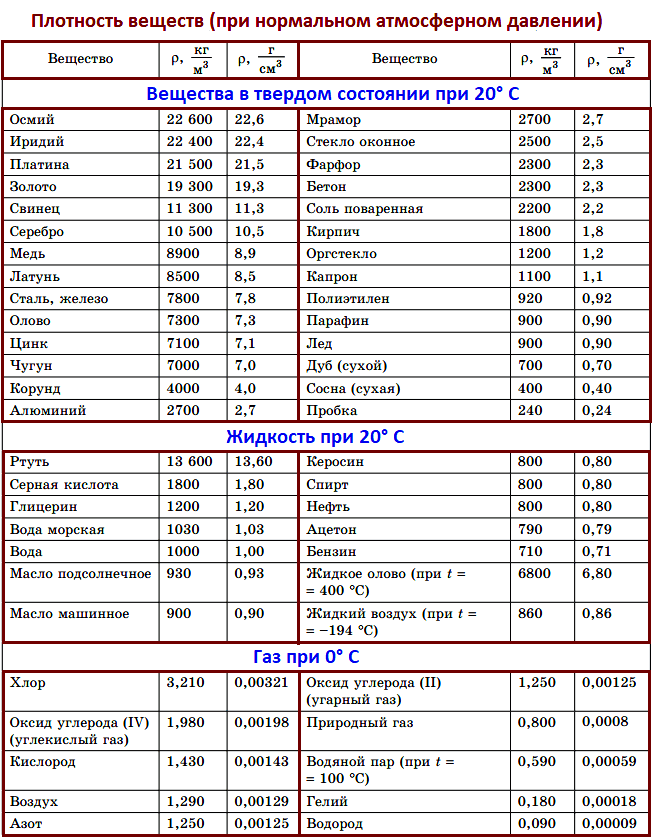
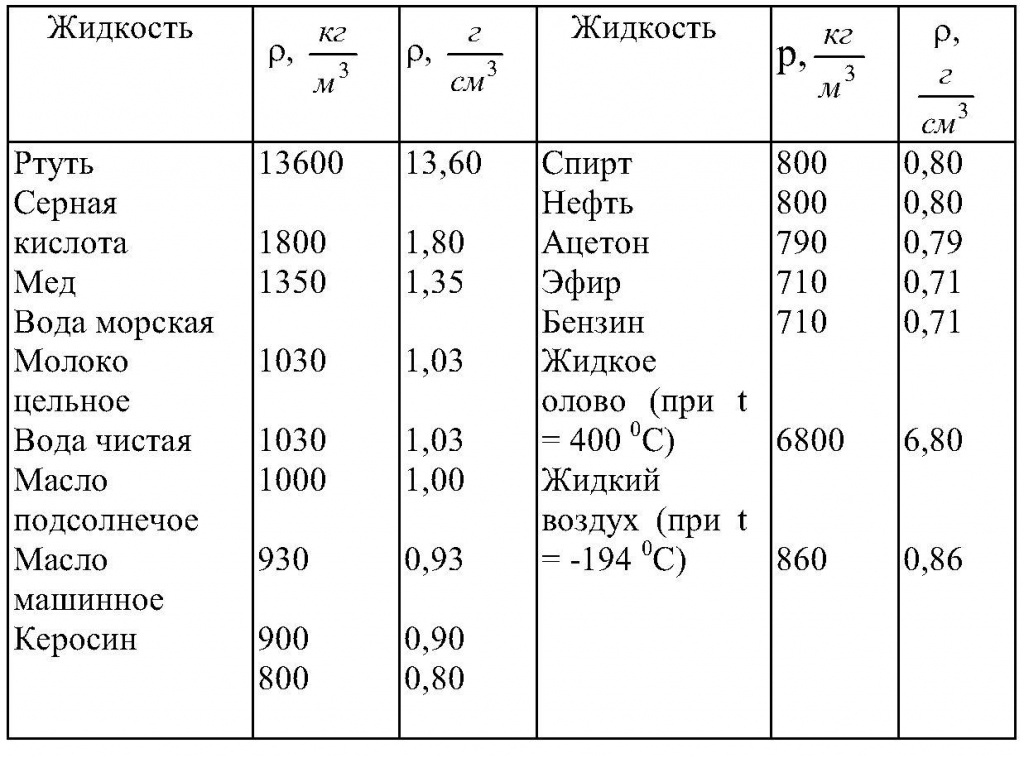
Таблица плотности веществ.
Как, зная только массу, рассчитать плотность?
- Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
- Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
- Если жидкость занимает не всю емкость или емкость нестандартная, то перелейте ее в другую тару, объем которой известен.Если подходящей емкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки). В процессе вычерпывания жидкости просто посчитайте количество таких кружек и умножьте на объем мерной тары.
- Если тело имеет простую форму, то вычислите его объем, используя соответствующие геометрические формулы. Так, например, если тело имеет форму прямоугольного параллелепипеда, то его объем будет равен произведению длин его ребер. То есть: Vпар. = a • b • c, где Vпар. – объем прямоугольного параллелепипеда, а a, b, c — значения его длины, ширины и высоты (толщины), соответственно.
- Если тело имеет сложную геометрическую форму, то попробуйте (условно!) разбить его на несколько простых частей, найти объем каждой из них отдельно и затем сложить полученные значения.
- Если тело невозможно разделить на более простые фигуры (например, статуэтку), то воспользуйтесь методикой Архимеда. Опустите тело в воду и измерьте объем вытесненной жидкости. Если тело не тонет, то «утопите» его с помощью тонкой палочки (проволоки).
- Если объем вытесненной телом воды посчитать проблематично, то взвесьте вылившуюся воду, или найдите разность между начальной и оставшейся массой воды. При этом, количество килограммов воды будет равняться количеству литров, количество граммов – количеству миллилитров, а количество тонн – количеству кубометров.
Задачи на плотность,
массу и объем с решением
ВОПРОСЫ ОТ ПОЛЬЗОВАТЕЛЕЙ САЙТА
Публикуем популярные вопросы от наших пользователей, оставленные в поле Комментариев. Прежде чем написать свой вопрос, проверьте: нет ли похожей задачи в начале статьи в разделе «Примеры решения задач» или среди вопросов в данном разделе!
Вопрос № 1. Длина стального листа 120 см, ширина 60 см, толщина 10 мм. Определить массу одного листа.
ОТВЕТ:≈ 56 кг.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Вопрос № 2. Какова масса платинового стержня, объём которого равен 21 дм3 ?
ОТВЕТ: 451,5 кг.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Вопрос № 3. Определить плотность бензина, если бак с бензином ёмкостью 20 литров имеет массу 14,2 кг?
Ответ: 710 кг/м3
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Вопрос № 4. Масса бетонного блока, имеющего форму параллелепипеда, равна 12 кг. Какой станет масса блока, если одну его сторону увеличить в 2 раза, вторую – в 2,5 раза, а третью оставить без изменения?
ОТВЕТ: 60 кг.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Вопрос № 5. Сколько рейсов должен сделать самосвал грузоподъемностью 5 т, чтобы перевезти 100 м3 гранита? Плотность гранита 2600 кг/м3.
ОТВЕТ: 52 рейса.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Вопрос № 6. Плотность некоторого раствора 1300 кг/м3. После того как в этот раствор добавили 10 л воды (деминерализованной) плотность этого раствора стала 1290 кг/м3. Сколько литров раствора было с исходной плотностью?
ОТВЕТ: 290 литров.
Нажмите на спойлер, чтобы увидеть РЕШЕНИЕ
Конспект урока по физике в 7 классе «Задачи на плотность, массу и объем с решением». Выберите дальнейшие действия:
- Перейти к теме: «ЗАДАЧИ на силу тяжести и вес тела».
- Вернуться к Списку конспектов по физике для 7-11 классов
- Найти конспект через Кодификатор ОГЭ по физике
- Найти конспект через Кодификатор ЕГЭ по физике
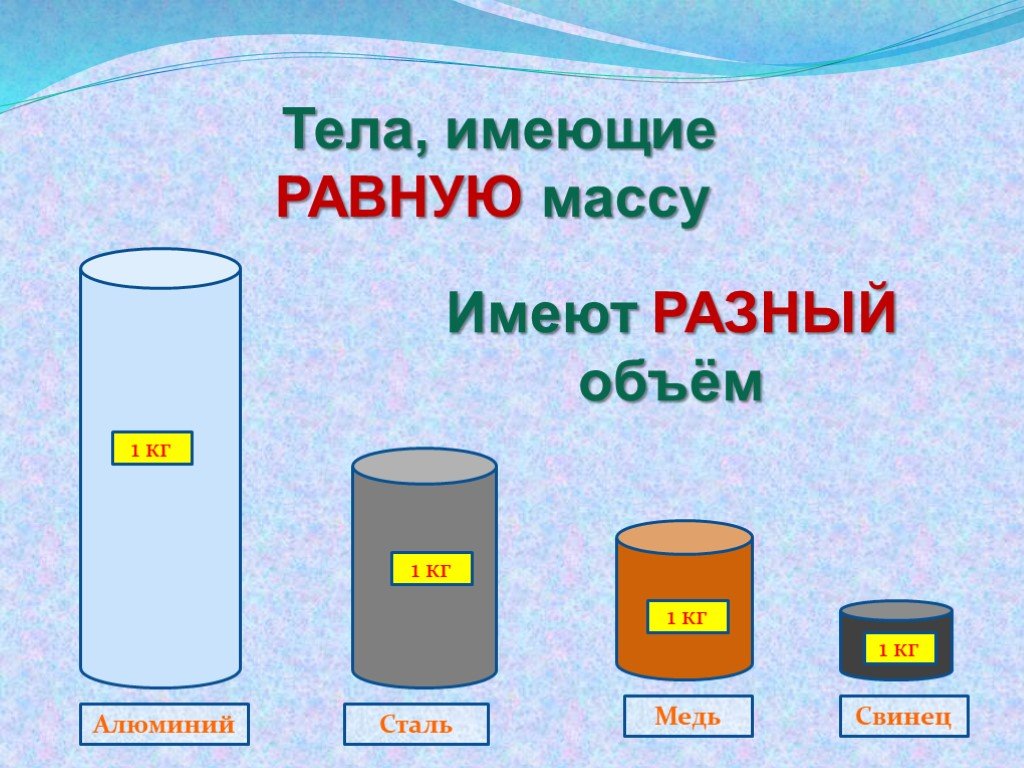
Тела, состоящие из различных веществ, при одинаковой массе будут иметь различные объемы, а при одинаковых объемах — различные массы. Происходит это из-за того, что каждое вещество имеет определенную плотность, которая описывается формулой $rho = frac{m}{V}$.
На данном уроке мы рассмотрим задачи на нахождение массы, объема или плотности по другим известным параметрам тел и их подробные решения. Вам понадобятся табличные значения плотностей различных веществ, из которых состоят тела, — их вы можете найти здесь.
Задача №1
Определите массу бензина, спирта, меда объемом $10 space л$.
Дано:
$V = 10 space л$
$rho_б = 710 frac{кг}{м^3}$
$rho_c = 800 frac{кг}{м^3}$
$rho_м = 1350 frac{кг}{м^3}$
СИ:
$V = 0.01 space м^3$
$m_б, m_с, m_м — ?$
Показать решение и ответ
Скрыть
Решение:
При известных плотности и объеме мы можем рассчитать массу по формуле $m = rho V$.
Перед вычислениями не забывайте переводить единицы измерения величин в СИ!
Рассчитаем массу бензина:
$m_б = rho_б V$,
$m_б = 710 frac{кг}{м^3} cdot 0.01 space м^3 = 7.1 space кг$.
Рассчитаем массу спирта:
$m_с = rho_с V$,
$m_с = 800 frac{кг}{м^3} cdot 0.01 space м^3 = 8 space кг$.
Рассчитаем массу меда:
$m_м = rho_м V$,
$m_м = 1350 frac{кг}{м^3} cdot 0.01 space м^3 = 13.5 space кг$.
Ответ: $m_б = 7.1 space кг$, $m_с = 8 space кг$, $m_м = 13.5 space кг$.
Задача №2
Медная кастрюля имеет массу $0.5 space кг$. Если кастрюлю такого же размера изготовить из стали, какая у нее будет масса?
Дано:
$m_1 = 0.5 space кг$
$rho_1 = 8900 frac{кг}{м^3}$
$rho_2 = 7800 frac{кг}{м^3}$
$V_1 = V_2 = V$
$m_2 — ?$
Показать решение и ответ
Скрыть
Решение:
Обратите внимание, что, когда в задаче говорится о размерах тела, речь идет о его объеме.
Рассчитаем объем медной кастрюли:
$V = frac{m_1}{rho_1}$,
$V = frac{0.5 space кг}{8900 frac{кг}{м^3}} approx 5.6 cdot 10^{-5} space м^3$.
Теперь рассчитаем массу такой же кастрюли из стали:
$m_2 = rho_2 V$,
$m_2 = 7800 frac{кг}{м^3} cdot 5.6 cdot 10^{-5} space м^3 approx 0.4 space кг$.
Ответ: $m_2 approx 0.4 space кг$.
Задача №3
Металлический кусок имеет объем $200 space см^3$ и массу $540 space г$. Из какого металла этот кусок? Какова его плотность?
Дано:
$V = 200 space см^3$
$m = 540 space г$
$rho — ?$
Показать решение и ответ
Скрыть
Решение:
Плотность часто измеряют в $frac{г}{см^3}$, а также у нас есть табличные значения плотностей в этих единицах. Поэтому мы не стали переводить единицы измерения массы и объема в $кг$ и $м^3$.
Найдем плотность металла:
$rho = frac{m}{V}$,
$rho = frac{540 space г}{200 space см^3} = 2.7 frac{г}{см^3}$.
Пользуясь таблицей, найдем металл с такой плотностью — это алюминий.
Ответ: алюминий, $rho = 2.7 frac{г}{см^3}$.
Задача №4
Вычислите массу чугунного бруска с внутренней выемкой (рисунок 1).
Дано:
$a = 5 space см$
$b = 3 space см$
$c = 2 space см$
$a_1 = 2 space см$
$b_1 = 1 space см$
$rho = 7 frac{г}{см^3}$
Показать решение и ответ
Скрыть
Решение:
Используя длину $a$, высоту $b$ и ширину $c$ бруска мы можем рассчитать его объем вместе с выемкой. Потом мы вычтем объем этой выемки и получим реальный объем этой детали.
Объем бруска вместе с объемом выемки:
$V_2 = a cdot b cdot c$,
$V_2 = 5 space см cdot 3 space см cdot 2 space см = 30 space см^3$.
Теперь вычислим объем выемки:
$V_1 = a_1 cdot b_1 cdot c$,
$V_2 = 2 space см cdot 1 space см cdot 2 space см = 4 space см^3$.
Рассчитаем действительный объем бруска:
$V = V_2 — V_1$,
$V = 30 space см^3 — 4 space см^3 = 26 space см^3$.
Зная объем бруска и плотность, найдем его массу:
$m = rho V$,
$m = 7 frac{г}{см^3} cdot 26 space см^3 = 182 space г$.
Ответ: $m = 182 space г$.
Задача №5
Емкость бадьи для бетона $1.5 space м^3$. Такая емкость выбрана для того, чтобы ее масса с бетоном не превышала грузоподъемности подъемного крана, которая равна $5 space т$. Определите плотность бетона, если вес самой бадьи $1.7 space т$.
Дано:
$m = 5 space т$
$m_1 = 1.7 space т$
$V = 1.5 space м^3$
СИ:
$m = 5 cdot 10^3 space кг$
$m_1 = 1.7 cdot 10^3 space кг$
$rho — ?$
Показать решение и ответ
Скрыть
Решение:
Бадья с бетоном не должна весить больше $5 cdot 10^3 space кг$. Тогда максимальная масса бетона будет равна:
$m_2 = m — m_1$,
$m_2 = 5 cdot 10^3 space кг — 1.7 cdot 10^3 space кг = 3.3 cdot 10^3 space кг$.
Рассчитаем плотность бетона, если бадья будет полностью заполнена:
$rho = frac{m_2}{V}$,
$rho = frac{3.3 cdot 10^3 space кг}{1.5 space м^3} = 2.2 cdot 10^3 frac{кг}{м^3} = 2.2 frac{г}{см^3}$.
Ответ: $rho = 2.2 frac{г}{см^3}$.
Задача №6
Мензурка, до краев наполненная спиртом, имеет массу $500 space г$. Та же мензурка без спирта имеет массу $100 space г$. Какой объем вмещает мензурка?
Дано:
$m = 500 space г$
$m_1 = 100 space г$
$rho = 0.8 frac{г}{см^3}$
$V — ?$
Показать решение и ответ
Скрыть
Решение:
Масса спирта будет равна разности масс наполненной мензурки и пустой мензурки:
$m_2 = m — m_1$,
$m_2 = 500 space г — 100 space г = 400 space г$.
Так как мензурку заполняли спиртом до краев, объем спирта будет равен объему мензурки:
$V = frac{m_2}{rho}$,
$V = frac{400 space г}{0.8 frac{г}{см^3}} = 500 space см^3$.
Ответ: $V = 500 space см^3$.
Один из самых легких металлов — магний — является главной составной частью сплава, которая называется “электрон-металл”, имеющего применение в авиастроении. Плотность этого сплава $1.8 frac{г}{см^3}$. Во сколько раз предмет, изготовленный из электрон-металла, будет легче такого же размера изделия из стали?
Дано:
$rho = 1.8 frac{г}{см^3}$
$rho_с = 7.8 frac{г}{см^3}$
$frac{m_с}{m} — ?$
Показать решение и ответ
Скрыть
Решение:
Масса предмета, изготовленного из электрон-металла, рассчитывается по формуле:
$m = rho V$.
Масса предмета, изготовленного из стали, рассчитывается по формуле:
$m_с = rho_с V$.
Объем у нас остается тем же, ведь мы говорим об одном и том же предмете, но выполненном из разных материалов:
$V = frac{m}{rho} = frac{m_с}{rho_с}$.
Отсюда сравним массы таких предметов:
$frac{m_с}{m} = frac{rho_с}{rho}$,
$frac{m_с}{m} = frac{7.8 frac{г}{см^3}}{1.8 frac{г}{см^3}} approx 4.3$.
Значит, предмет, изготовленный из электрон-металла, будет в 4.3 раза легче такого же размера изделия из стали.
Ответ: в 4.3 раза.
Задача №8
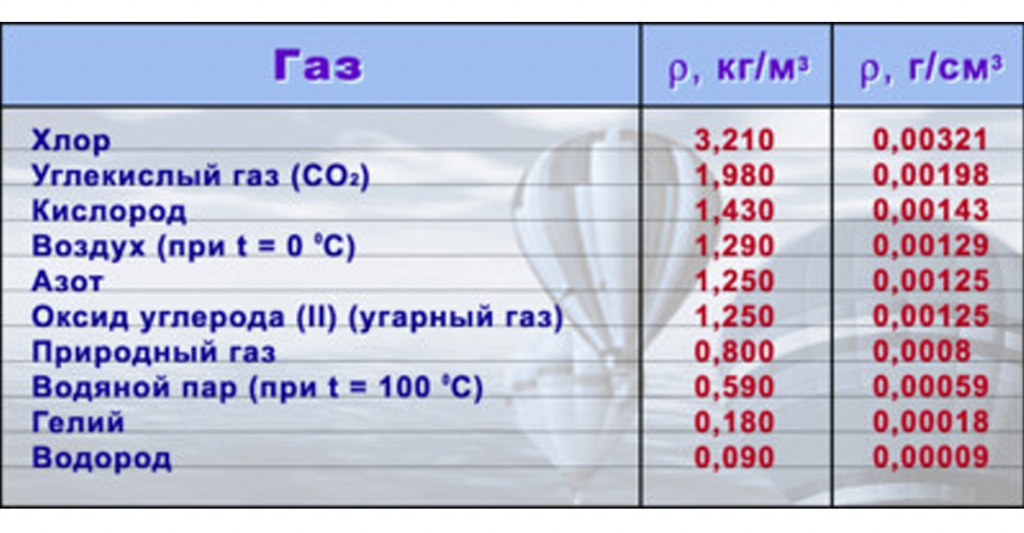
Газовый баллон имеет объем $30 space дм^3$. Его наполняют газом, обращенным в жидкое состояние. Рассчитайте, сколько в баллоне помещается килограммов жидкого хлора, плотность которого $1.2 frac{г}{см^3}$. Сколько получится при выпуске литров газообразного хлора, плотность которого $0.0032 frac{г}{см^3}$?
Дано:
$V_1 = 30 space дм^3 = 30 cdot 10^3 space см^3$
$rho_1 = 1.2 frac{г}{см^3}$
$rho_2 = 0.0032 frac{г}{см^3}$
$m — ?$
$V_2 — ?$
Показать решение и ответ
Скрыть
Решение:
В жидком состоянии хлор имеет определенную плотность $rho_1$ и занимает определенный объем $V_1$. В газообразном же состоянии хлор будет иметь другую плотность $rho_2$ и другой объем $V_2$. При этом масса хлора остается постоянной: что в жидком, что в газообразном виде.
Рассчитаем массу хлора, используя данные для его жидкого состояния:
$m = rho_1 V_1$,
$m = 1.2 frac{г}{см^3} cdot 30 cdot 10^3 space см^3 = 36 cdot 10^3 space г = 36 space кг$.
Теперь вычислим объем газообразного хлора и выразим его в литрах:
$V_2 = frac{m}{rho_2}$,
$V_2 = frac{36 cdot 10^3 space г}{0.0032 frac{г}{см^3}} = 11 space 250 space 000 space см^3 = 11 space 250 space л$.
Ответ: $m = 36 space кг$, $V_2 = 11 space 250 space л$.
Задача №9
Ртуть и нефть одинаковой массы налили в разные емкости. Во сколько раз объем, занимаемой ртутью, меньше объема, занимаемого нефтью?
Дано:
$m_1 = m_2 = m$
$rho_1 = 13.6 frac{г}{см^3}$
$rho_2 = 0.8 frac{г}{см^3}$
$frac{V_2}{V_1} — ?$
Показать решение и ответ
Скрыть
Решение:
Так как масса ртути и масса нефти равны друг другу, мы можем записать:
$m = rho_1 V_1 = rho_2 V_2$.
Выразим отсюда отношение объемов:
$frac{V_2}{V_1} = frac{rho_1}{rho_2}$.
Рассчитаем:
$frac{V_2}{V_1} = frac{13.6 frac{г}{см^3}}{0.8 frac{г}{см^3}} = 17$.
Значит, объем, занимаемой ртутью, в 17 раз меньше объема, занимаемого нефтью.
Ответ: в 17 раз.
Задача №10
На одну чашу весов положили мраморный шарик, на другую — шарик из латуни, втрое меньший по объему. Останутся ли весы в равновесии?
Дано:
$V_2 = frac{V_1}{3}$
$rho_1 = 2700 frac{кг}{м^3}$
$rho_2 = 8500 frac{кг}{м^3}$
$frac{m_2}{m_1} — ?$
Показать решение и ответ
Скрыть
Решение:
Весы останутся в равновесии в том случае, если массы шариков будут равны, т. е. $frac{m_2}{m_1} = 1$.
Выразим массу каждого шарика через его объем и плотность:
$frac{m_2}{m_1} = frac{rho_2 V_2}{rho_1 V_1} = frac{rho_2 V_1}{3 rho_1 V_1} = frac{rho_2}{3 rho_1}$.
Рассчитаем это отношение масс:
$frac{m_2}{m_1} = frac{8500 frac{кг}{м^3}}{3 cdot 2700 frac{кг}{м^3}} approx 1.05$.
Это означает, что весы не останутся в равновесии. Масса шарика из латуни больше массы шарика из мрамора.
Ответ: нет.
Задача 1
Определить плотность серной кислоты, если бидон емкостью 35 литров вмещает 63 кг кислоты
Задача 2
Металлическая деталь массой 949 г. имеет объем 130 куб. дм. Какой это металл?
Задача 3
Чугунный шар имеет массу 70 кг, а объем 10 дм.3 Определить, сплошной этот шар или полый (с пустотами).
Задача 4
Масса чугунной плиты — 64 кг. Определить массу мраморной плиты таких же размеров.
Задача 5
Найдите плотность молока, если 206 г молока занимают объем 200 см3?
Задача 6
Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?
Задача 7
Определите плотность мела, если масса его куска объемом 20 см3 равна 48 г. Выразите эту плотность в кг/м3 и в г/см3.
Задача 8
Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м2 ?
Задача 9
Брусок, масса которого 21,6 г. имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.
Задача 10
Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?
Задача 11
Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.
Задача 12
Картофелина массой 59 г. имеет объем 50 см.3. Определите плотность картофеля и выразите ее в килограммах на кубический метр.
Задача 13
Подсолнечное масло объемом 1 литр имеет массу 920 грамм. Определите плотность масла. Выразите ее в килограммах на кубический метр.
Задача 14
Точильный брусок, масса которого 300 грамм, имеет размер 15*5*2 см. Определите плотность вещества из которого он сделан.
Задача 15
Какая из двух ложек одинаковой массы — стальная или серебряная — имеет большие размеры?
Задача 16
Из какого металла может быть изготовлен деталь, если ее масс 3,9 кг., а объем 500 см.3?
Задача 17
Сплав состоит из олова массой 2,92 кг. и свинца массой 1,13 кг. Какова плотность сплава, если считать, что объем сплава равен сумме объемов его составных частей?
Задача 18
Какова плотность бензина, если 12 литров имеют массу 8,52 кг.?
Задача 19
В пол литровую бутылку налито 465 грамм подсолнечного масла. Какова плотность масла?
Задача 20
Тщательным совместным растиранием смешали по 100 г парафина, буры и воска. Какова средняя плотность получившейся смеси, если плотность этих веществ равна соответственно 0,9 г/см3, 1,7 г/см 3, 1 г/см3 ?
Задача 21
Определите плотность стекла из которого сделан куб массой 857,5 г, если площадь всей поверхности куба равна 294 см2.
Задача 22
В сообщающиеся сосуды налита ртуть. В один сосуд добавили воду, высота столба которого 4 см. Какой высоты должен быть столб некоторой жидкости в другом сосуде, чтобы уровень ртути в обоих сосудах был одинаков, если плотность жидкости в 1,25 раза меньше плотности воды?
Задача 23
Вес тела в воде в 2 раза меньше, чем в воздухе. Какова плотность вещества тела?
Задача 24
Тело весит в воздухе 3 Н, в воде 1,8 Н и в жидкости неизвестной плотности 2,04 Н. Какова плотность этой неизвестной жидкости?
Задача 25
В заброшенном парке дети откопали слиток. На нем было выгравировано старинными буквами, что слиток состоит из двух частей золота и трех частей серебра, и его объем составляет V=357 см3 . Какова масса слитка?
Задача 26
В цирке клоун одной левой поднимает огромную гирю, на которой написано 500 кг. На самом деле масса гири в сто раз меньше. Объем этой гири 0,2 м3. Вычисли плотность цирковой гири.
Задача 27
Печальный дядя Боря хотел сам сварить себе суп, и у него получилось пол кастрюли зеленой гадости. Объем этой гадости, которую дядя Боря не отважился попробовать, 0,001 м3.
Масса этого кубического дециметра гадости 1 кг 300 г. Вычисли плотность дяди Бориной гадости.
Задача 28
Ученый с мировым именем Иннокентий решил плотно пообедать и с аппетитом съел комплексный обед из трех блюд. Масса первого блюда — 550 граммов, объем — 0,0005 м3. Масса второго — 150 грамм, объем — 0,0002 м3.
Задача 29
Масса компота — 1 кг 100 грамм, объем — 0,0011 м3. Как вычислить среднюю плотность плотного обеда, который ученый с мировым именем съел без хлеба?
Задача 30
После того как трое мышей на дне рождения мышки Мушки угостились одним крупным куском хозяйственного мыла, их общая масса увеличилась на 540 г. Мыло до того, как мыши его съели, имело размеры 10 см, 12 см, 3 см. Определите плотность уже не существующего мыла.
Задача 31
Стакан, заполненный до краев водой, имеет массу m1 = 214,6 г. Когда в этот стакан с водой поместили небольшой камень массой 29,8 г и часть воды вылилась наружу, масса стакана с содержимым оказалась равной m2 = 232 г. Определить плотность вещества камня.
Задача 32
В сосуд, заполненный водой, бросают кусок алюминиевого сплава. После того, как часть воды вылилась из сосуда, масса его с оставшейся водой и куском сплава увеличилась на 25 г. Когда вместо воды использовали жидкое масло плотностью 0,9 г/см.3 и повторили измерения, то масса сосуда с маслом и куском сплава увеличилась на 26 г. Определите плотность сплава.
Задача 33
Какая жидкость налита в емкость объемом 125 л, если ее масса оказалась равной 88 кг 750 г.?
Задача 34Котелок ёмкостью 3 литра плотно набили снегом и повесили над костром. Когда снег растаял, котелок оказался на 1/4 своего объёма наполнен водой. Какова была плотность снега в котелке, если плотность воды составляет ρ = 1000 кг/м3? Ответ выразить в кг/м3.
Задача 35
Скульптор изваял три фигуры одинаковой массы из мрамора, сухого дуба и льда. Определите, из какого вещества сделана каждая фигура.
Задача 36
Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м2 ?
Задача 37
Определить объем оловянного бруска массой 146 г.
Задача 38
Вычислите массу тела по его плотности и объему.
| Вещество |
Плотность вещества p, г/см3 |
Объем тела V, см3 |
Масса тела m, г |
| Полученная экспериментально | Вычисленная по формуле | ||
| картофель | 0,67 | 48 |
Задача 39
Вычислите объем тела по его плотности и массе.
| Вещество |
Плотность вещества p, г/см3 |
Объем тела V, см3 |
Масса тела m, г |
|
| Получено экспериментально | Вычислено по формуле | |||
| пластилин | 1,4 | 16,2 |
Задача 40
Определите объем кирпича, если его масса 5 кг?
Задача 41
Определите массу стальной детали объёмом 120 см3
Задача 42
Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?
Задача 43
Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?
Задача 44
В куске кварца содержится небольшой самородок золота. Масса куска равна 100 г, а его средняя плотность
г/см
. Определите массу золота, содержащегося в куске кварца, если плотность кварца 2,65 г/см
, а плотность золота 19,4 г/см3.
Задача 45
Для накачивания керосина в бак используется насос производимостью 20 кг в минуту. Определите время, необходимое для наполнения бака,если его длина 2 м, ширина 150 см, высота 1800 мм.
Задача 46
Золото можно расплющить до толщины 0,0001 мм. Какую площадь поверхности металла (или дерева) можно покрыть такими пластинками, изготовленными из золота массой 2,316 г. Плотность золота 19,3 г/см
Задача 47
В чистой воде растворена кислота. Масса раствора 240 г, его плотность 1,2 г/см3. Определите массу кислоты, содержащейся в растворе, если плотность кислоты 1,8 г/см3. Принять объем раствора равным сумме объема его составных частей. Плотность воды 1 г/см3.
Задача 48
В воздушный шарик накачали порцию воздуха. При этом масса возросла в 4 раза, а объём – вдвое. Во сколько раз возросла плотность воздуха в шарике?
Задача 49
Подсчитайте, во сколько раз отличаются плотности воды и спирта.
Задача 50
Найдите ошибку в рассуждении: плотность 1 м3 керосина 800 кг/м3. Тогда плотность 2 м3 керосина будет 1600 кг/м3.
Задача 51
Для измерения плотности пластилина взяли его кусок массой 100 г. Как изменятся результаты измерений, если будет взят кусок массой 200 г
Задача 52
Чтобы отлить бетонный фундамент, вырыли траншею объёмом 2 м3. Для её заполнения влили 4800 кг бетона. Вычислите плотность бетона.
Задача 53
Объём одной комнаты в квартире равен 40 м3. Какую массу имеет воздух, находящийся в комнате?
Задача 54
Чтобы заполнить банку доверху, потребовалось 4,1 кг меда. Вычислите объём банки.
Задача 55
Масса шара объёмом 1,5 м3 составляет более 3 т. Верно ли, что плотность вещества шара более 2 т/м3?
Задача 56
Объём куба массой 80 кг составляет более 10 дм3. Правда ли, что металл, из которого сделан куб, имеет плотность более 80 кг/дм3?
Задача 57
Плотность золота 19 г/см3. Верно ли, что золотой кубик с объёмом более 10 см3 будет иметь массу более 100 г?
Задача 58
Плотность мёда 1,35 г/см3. Правда ли, что порция мёда при объёме более 100 см3 будет иметь массу более 200 г?
Задача 59
Верно ли, что объём воздуха массой 13 кг более 10 м3?
Задача 60
Верно ли, что водород массой менее 1 кг имеет объём более 10 м3?
Задача 61
Плотность вещества картофеля составляет 1,2 г/см3. Выразите это значение в кг/м3. Почему это значение намного больше табличного?
Задача 62
В кастрюлю объёмом 7,3 л положили 5,7 кг картофеля и доверху залили водой. Ее понадобилось 2,3 л. Найдите плотность картофелины.
Задача 63
Имеются ли пустоты в чугунной отливке (литой детали) массой 34 кг, если объём формы для литья был 5 дм3?
Задача 64
После рейса в бензобаке автобуса осталось более 50 кг бензина. Что можно сказать про объём бензобака?
Задача 65
Масса канистры, заполненной машинным маслом, равна 19,5 кг. Масса пустой канистры 1,5 кг. Каков её объём?
Задача 66
Трёхлитровую стеклянную банку наполовину заполнили мёдом. На сколько увеличилась масса банки?
Задача 67
Площадь пола овощехранилища равна 40 м2, а высота слоя картофеля не должна превышать 60 см. Какая масса картофеля может находиться в таком овощехранилище?
Задача 68
Вычислите, поместится ли в большой 120-литровой алюминиевой бочке 110 кг спирта?
Задача 69
Сколько воды выльется из полного стеклянного сосуда при всыпании в него 340 г свинцовой дроби?
Задача 70
В кружку с 50 г мёда долили ещё 200 мл молока. На сколько возросла масса кружки?
Задача 71
В банку опустили свинцовый шар объёмом 20 см3 и долили 100 мл керосина. На сколько возросла масса банки?
Задача 72
Изготовили ящик объемом 3 м3. Насыпав в него песка, обнаружили, что ящик заполнен на четверть. На сколько увеличилась масса ящика?
Задача 73
В мензурку, где находится 150 мл воды, опускают стальной кубик массой 10 г. На сколько увеличится объём содержимого мензурки?
Задача 74
В мензурку, где находится 150 мл воды, опускают стальной кубик массой 10 г. До какой отметки поднимется уровень воды в мензурке?
Задача 75
На какой отметке будет уровень воды в мензурке при вливании туда 100 г воды и 100 г подсолнечного масла?
Задача 76
На какой отметке установится уровень воды в мензурке при вливании туда 100 г воды и 100 мл ртути?
- Подробности
- Обновлено 02.09.2018 16:03
- Просмотров: 1704
Задачи по физике — это просто!
Вспомним формулы, которые связывают плотность, массу и объем:

Не забываем, что решать задачи надо всегда в системе СИ!
Поэтому потренируемся в достаточно сложном переводе единиц измерения:
1 куб. см — это одна миллионная доля метра кубического,
поэтому
1 куб. дм — это тысячная доля метра кубического,
поэтому
Существует единица объема — 1 литр.
Эта единица не входит в систему СИ!
Переводим литры в метры кубические:
И не забудем о массе:
Не забывайте:
Килограмм- это единица массы,
буквенное обозначение массы
— m
Метр кубический — это единица объема,
буквенное обозначение объема — V
А теперь к задачам!
Элементарные задачи из курса школьной физики
Задача 1
Определить плотность серной кислоты, если бидон емкостью 35 литров вмещает 63 кг кислоты.
Задача 2
Определить объем оловянного бруска массой 146 г.
Задача 3
Какую массу имеет стеклянная пластина объемом 15 куб. дм ?
Задача 4
Металлическая деталь массой 949 г имеет объем 130 куб. дм. Какой это металл?
Чтобы ответить на вопрос задачи, необходимо рассчитать плотность металла, а затем по справочной таблице плотностей (она есть в учебнике) определить, для какого металла характерна вычисленная плотность.
Задача 5
Чугунный шар имеет массу 70 кг, а объем 10 куб. дм. Определить, спошной этот шар или полый (с пустотами).
Сплошной шар, т.е. целиком из чугуна, должен иметь плотность, равную плотности чугуна (посмотреть в таблице).
Если у шара внутри есть пустоты, то такой шар называется полым. В этом случае средняя плотность шара должна быть меньше табличной плотности чугуна. Ведь пустоты заполнены воздухом, а он очень легкий.
Рассчитаем по формуле плотность шара и сравним с расчетной!
Задача 6
Масса чугунной плиты — 64 кг. Определить массу мраморной плиты таких же размеров.
Если читать условия задачи внимательно, то ясно, что объем чугунной плиты равен объему мраморной плиты:
Vч = Vм
Задача 7
Бутыль с керосином имеет массу 4 кг. Масса бутыли без керосина составляет 400 г.
Какая масса воды поместится в эту бутыль?
Обратите внимание:
объем бутыли = объему керосина, заполняющего бутыль = объему воды, заполняющей бутыль
Достаточно знать любой из этих объемов!
Задача 8
Емкость цистерны молоковоза составляет 10 куб. м
Сколько рейсов должен сделать молоковоз, чтобы перевезти 30 тонн молока?
Задача 9
На стройку самосвалом перевезли 400 куб. м песка. Определить грузоподъемность самосвала, если для перевозки всего песка самосвалу понадобилось сделать 50 рейсов.
Задача 10
Сосновые доски нагружены на платформу и имеют массу 12 тонн. Размер одной доски составляет 500 х 20 х 10 (куб. см). Сколько досок на платформе?
Решение
задач на нахождение плотности смесей и сплавов,
средней
плотности неоднородных тел (7 класс)
Ларионов Вадим Сергеевич,
учитель физики МБОУ Лицея №
15 г.Сарова, larionvadim@yandex.ru
Ларионова Наталья Валентиновна,
к.п.н., учитель физики МБОУ Лицея № 15
г.Сарова, nvlarionova@yandex.ru
В статье сформулированы методические рекомендации по
организации факультативного занятия по решению задач на нахождение плотности
смесей, сплавов и неоднородных тел. Представлены учебные материалы по теме,
структурированные по уровню сложности.
Задачи на
нахождение плотности смеси или сплава, средней плотности неоднородного
(«составного») тела являются базовыми при изучении темы «Плотность» и
достаточно часто встречаются в олимпиадах по физике в 7-8-х классах. Именно
поэтому целесообразно данному типу задач посвятить отдельное факультативное занятие,
структура которого соответствует принципу «от простого к сложному» и содержит последовательные
блоки задач: ключевые, олимпиадные и задачи для самостоятельного решения (см.
приложение).
Средняя плотность
неоднородного («составного») тела, плотность смеси или сплава рассчитывается по
формуле
где m1, m2, m3… -массы отдельных частей тела
(компонентов смеси или сплава), а V1, V2, V3 … — их объёмы.
Для решения задач
по данной теме, необходимо составить систему уравнений, в основе которой лежат
следующие положения:
1. Определительная формула
плотности
2. Свойство аддитивности массы
(масса смеси или сплава равна сумме масс его составных частей)
m=m1+ m2+ m3+…
3. Как правило, в таких задачах
полагают, что объём сплава (смеси) равен сумме объёмов его составных частей
V=V1+V2+V3 …
В задачах, предложенных ниже,
исключением является задача № 6 из блока олимпиадных задач (задача о смешивании
спирта и воды).
Ключевые задачи,
представленные в занятии, в зависимости от подготовки учащихся могут быть
решены непосредственно на уроке при изучении темы «Плотность». В этом случае на
факультативном занятии рассматриваются олимпиадные задачи. Далее ученикам
предлагаются задачи для самостоятельного решения, которые, как правило,
составляют домашнее задание. В этом случае удобно дифференцировать домашнее
задание учеников, предложив не более трёх обязательных задач в зависимости от
уровня подготовленности учеников. Учитель может дополнить списки олимпиадных
задач и задач для самостоятельного решения, используя материалы последних
олимпиад.
Приложение
Плотность смесей, сплавов, «составных» тел
Цель: Научиться решать задачи
на нахождение плотности смесей и сплавов, а также средней плотности
неоднородных тел («составных») тел.
Ключевые задачи
1. Какова плотность сплава из
300г олова и 100г свинца? (8г/см3)
2.
Сплав
изготовлен из меди объёмом 0,4 м3 и цинка массой 710 кг. Какова
плотность сплава? (8540 кг/м3)
3. Для приготовления вишнёвого
сиропа в кастрюлю вылили 1 л вишнёвого варенья и 2 л воды и хорошо перемешали.
Какова плотность сиропа, если плотность варенья 1300 кг/м3? (1100
кг/м3)
4. Какова плотность смеси из
глицерина и спирта, если объём спирта составляет половину объёма смеси? Как
изменится ответ, если масса спирта составляет половину массы смеси? (1030 кг/м3, 980 кг/м3)
Олимпиадные задачи
1. Масса первого изделия в 2
раза больше массы второго изделия, а их объёмы находятся в отношении V1:V2=1:3. Плотность первого изделия ρ1=4г/см3.
Какова будет средняя плотность «составного» тела, если два изделия склеить?
Массой и объёмом клея пренебречь. (1,5 г/см3)
2. Изделие, склеенное из трёх
различных частей, имеет объём V=600см3.
Объёмы частей находятся в соотношении V1:V2:V3=2:3:5, а их плотности – в соотношении ρ1:ρ2:ρ3=4:3:1.
Чему равна масса изделия, если плотность первой части ρ1=2000кг/м3?
(660 г)
3. Ученик измерил плотность
деревянного бруска, покрытого краской, и она оказалась равной ρ=600 кг/м3. Но на
самом деле брусок состоит из двух частей, равных по массе, плотность одной из
которых в два раза больше плотности другой. Найдите плотности обеих частей
бруска. Массой краски можно пренебречь. (450 кг/м3, 900 кг/м3)
4. В дистиллированную воду
аккуратно вливают серную кислоту. Получившийся раствор имеет плотность ρр=1200
кг/м3 и массу m=120г. Объём раствора равен
сумме объёмов воды и кислоты. Плотность воды ρв=1000 кг/м3,
плотность кислоты ρк=1800 кг/м3. Какова масса кислоты,
влитой в воду? (45 г)
5. 
a и плотностью ρ поместили внутрь куска глины с плотностью 4ρ, которому придали
форму куба со стороной 2a. Получившийся куб облепили пластилином плотностью 2ρ,
в результате чего получился куб со стороной 3a (см. рисунок). Определите
среднюю плотность получившейся системы. (67ρ/27≈2,5ρ)
6. Плотностью вещества называют
отношение массы тела из этого вещества к его объёму. Например, масса 1 см3
воды составляет 1 г, поэтому плотность воды 1 г/см3. Представим, что
смешали 100 литров воды и 100 литров спирта плотностью 0,8 г/см3, и
при смешении оказалось, что суммарный объём уменьшился на 5 процентов. Какова
плотность полученного раствора? (ρ=18/19 г/cм3≈0,95г/cм3)
Задачи
для самостоятельного решения
1. Какую плотность имеет сплав
из 270г алюминия и 445г меди? (≈4,77
г/cм3)
2. Сплав золота и серебра массой
400 г имеет плотность 1,4·104 кг/м3. Полагая объём сплава
равным сумме объёмов его составных частей, определите массу золота в сплаве? (220
г)
3. Масса первого изделия в 3
раза меньше массы второго изделия, а их объёмы находятся в соотношении V1:V2=2:1. Плотность первого тела ρ1=1,8 г/см3.
Какова будет средняя плотность «составного» тела, если два изделия склеить? Массой
и объёмом клея пренебречь. (4,8 г/см3)
4. Изделие, склеенное из трёх
различных частей, имеет объём V=900см3.
Объёмы частей находятся в соотношении V1:V2:V3=5:3:1, а их плотности – в соотношении ρ1:ρ2:ρ3=1:2:5.
Чему равна масса изделия, если плотность первой части ρ1=500кг/м3?
(800 г)
5. Кубик с ребром a=20см сделан из материала с
плотностью ρ=3000кг/м3. Однако внутри кубика имеется воздушная
полость, поэтому его средняя плотность ρср=1200кг/м3.
Определите объём этой воздушной полости. Во сколько раз изменится средняя
плотность кубика, если полость целиком заполнить водой? Массой воздуха внутри
полости можно пренебречь. (4800 см3, 1,5)
Литература к занятию
1. Генденштейн Л.Э., Кирик Л.А.,
Гельгафт И.М. Задачи по физике с примерами решений. 7-9 классы. Под ред. В.А.Орлова.
– М.: Илекса, 2009. – 416 с.
2. Бажанский И.И., Гой В.А.,
Чубов Ю.Б. Приморские олимпиады школьников по физике (2003-2007 гг). Учебное
пособие. – Владивосток: Изд-во Дальневост. ун-та, 2008. – 200с.
3. Олимпиады 2008-2009. Физика.
Задачи Московских олимпиад школьников. Под ред. М.В.Семёнова, А.А.Якуты. – М.:
МЦНМО, 2009. – 70 с.
4. 400 физических этюдов.
Избранные задачи физических олимпиад Санкт-Петербурга. – СПб, 2006. –284 с.
5.
Борисов
С.Н. Учебное пособие по физике для учащихся 7-го класса. – М.: МИФИ, 2009. –
100 с.