Учебник
Геометрия, 11 класс
Ромб: Свойства, Формулы. Задачи
Ромб — это параллелограмм, у которого все стороны равны.
- «Чтоб Выучить, распознать нечто стоящее — узнать его в движении, при изменениях»
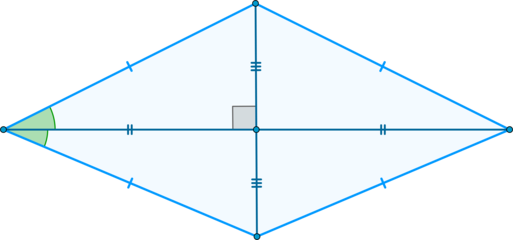
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей — ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали — новый ромб совпадет с прежним. Симметрия.
Замечание: Если «зряче видим» центральную и осевые симметрии ромба, то все его свойства у нас «в кармане».
Свойства ромба:
- Ромб симметричен относительно точки O — пересечения диагоналей. O — центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ — ось симметрии.
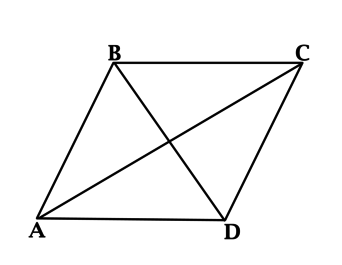
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
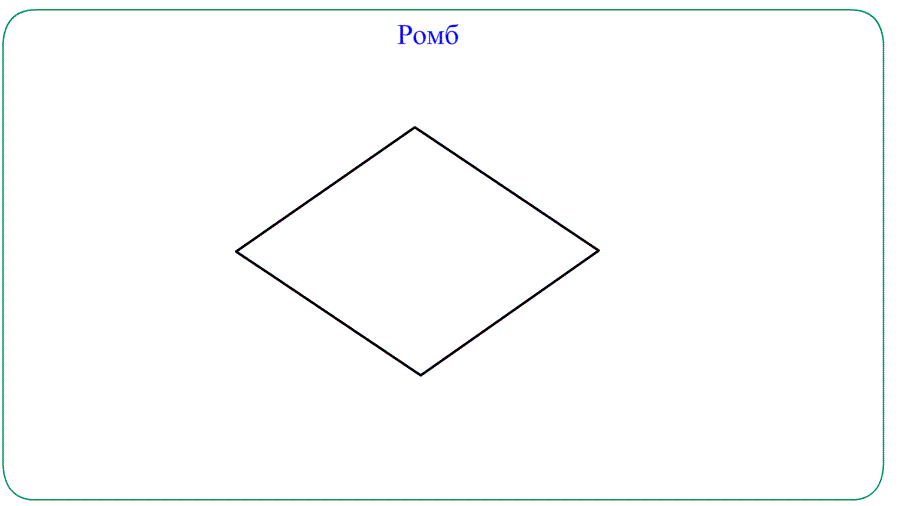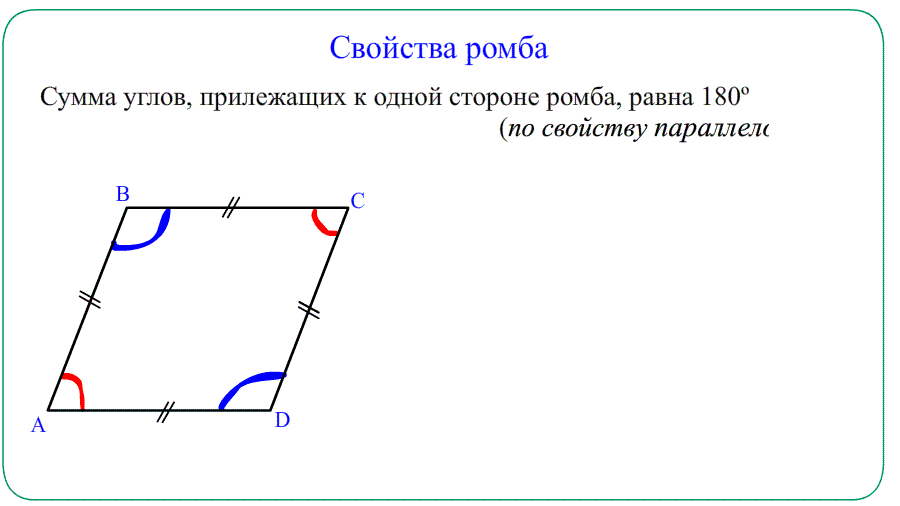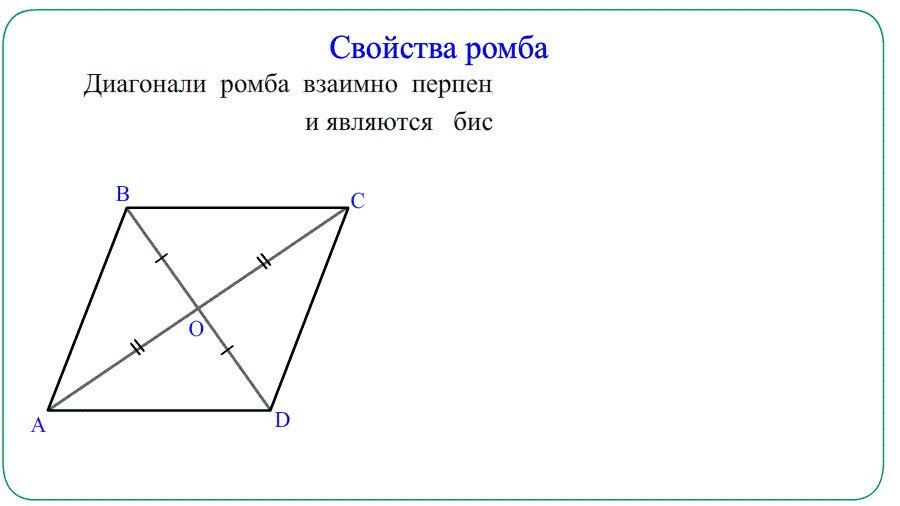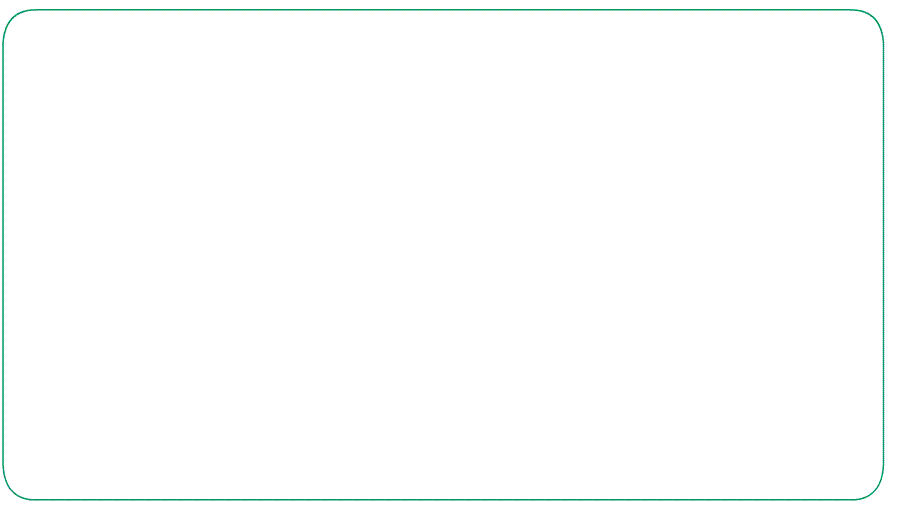
- Противолежащие углы равны $angle A=angle C$ , $angle B=angle D$ . Прилежащие $angle A+angle B=180^o$ , $angle A+angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=frac{AC}{2}$ и $BO=OD=frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов — делят углы пополам.
- Диагонали ромба со сторонами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.
- Меньшая диагональ $AC^2=a^2+b^2-2cdot acdot bcdotcos D$ , большая — $BD^2=a^2+b^2+2cdot acdot bcdotcos D$ .
- Сумма {Цвет:Red квадратов диагоналей ромба равна $AC^2+BD^2=4cdot a^2$ четырежды квадрат стороны.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.

Формулы Площади ромба:
- Площадь ромба равна произведению основания на высоту $S_{ABCD}=ADcdot CH$ , $S=acdot h$ ;
- Площадь ромба равна через синус угла: $S=a^2cdotsin A$ , квадрат стороны на синус .
- Площадь ромба через диагонали: $S=frac{ACcdot BD}{2}$ . — половина произведения диагоналей
Вписанная окружность в ромб:
- В четырехугольник можно вписать окружность только если … суммы противоположных сторон равны.
- Вписать окружность можно в ромб и квадрат, ;
- Если вписывается, то площадь $S=pcdot r$, $p=2cdot a$ $S=2cdot a cdot r$.
- Центр Вписанной окружности находится на пересечении диагоналей. Диагонали — суть биссектрисы углов.
Задача 1: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: «Односторонние углы»: В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30’$ , $67^o30’$


Задача 2: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Решение: Проведем высоту из той же вершины, из которой проведена меньшая диагональ.
- Получили прямоугольный треугольник $BED$ . Он подобен тем треугольникам, на которые ромб делится диагоналями:
- $bigtriangleup BED sim bigtriangleup AOD=bigtriangleup AOB=bigtriangleup COB=bigtriangleup COD$ . Все прямоугольные и есть равные углы.
- например $alpha$. Для нахождения площади нам нужно найти или сторону ромба, или его вторую диагональ.
- Для угла $alpha$ в $bigtriangleup EBD$ мы знаем гипотенузу и противолежащий катет $Rightarrow$ $sinalpha=frac{BE}{BD}=frac{12}{13}$
- Перейдем к $bigtriangleup OCD$ : в нем прилежащий катет $OD=frac{1}{2}BD=6,5$. Чтобы найти второй катет, нам нужен тангенс,
- а чтобы найти гипотенузу, т. е. сторону ромба, – косинус. Найдем их через основное тригонометрическое тождество :
- $sin^2alpha+cos^2alpha=1$ . Тогда косинус: $cosalpha=pmsqrt{1-sin^2alpha}=pmsqrt{1-frac{144}{169}}=pmsqrt{frac{25}{169}}=pmfrac{5}{13}$
- Угол $alpha$ острый, так как он входит в прямоугольный треугольник, т. е. принадлежит первой четверти.
- Следовательно, косинус положительный и мы останавливаемся на одном значении: $cosalpha = frac{5}{13}$
- Тогда: $frac{DO}{DC}=frac{6,5}{DC}=cosalpha=frac{5}{13}$ $Rightarrow$ $DC=frac{6,5cdot13}{5}=frac{13cdot13}{10}=16,9$
- Площадь ромба равна произведению основания на высоту: Ответ: $S=16,9cdot12=202,8$
Задача 3: В Ромбе $ABCD$ точка $K$ делит сторону $CD$ в соотношении $2:7$, а $M$ делит $1:3$ сторону $BC$. $MN$ параллельна $AB$, $O$ — пересечение $MN$ и $BK$. Найти площадь трапеции $ABON$, если площадь $ABCD=420$.
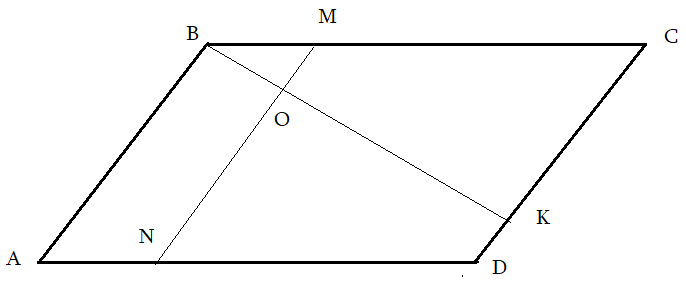
Решение: пробa Анализ рисунка:
- $AB$, $MN$, $CD$ — параллельные. Какие углы равные?
- Треугольники $BMO$ и $BKC$ подобные. Коэффициент подобия $1:3$.
- Отношение площадей $BMO$ и $BKC$ равен $1:9$ — квадрату коэффициента подобия.
- (по формулам) Площади $BKC$ и $BCD$ относятся как $CK$ и $CD$, т.е. $5:7$.
- Площадь $BCD$ равен половине площади $ABCD$, т.е. $S_{BCD}=210$.
- $S_{ABMN}:S_{ABCD}=1:3$ $Rightarrow$ $S_{ABMN}=140$ .
- Из складываемости площадей: площадь $ABON$ = разности площадей $ABMN$ и $BOM$.
Упражнения:
Ромб — это параллелограмм, у которого все стороны равны.
- «Чтоб Выучить, распознать нечто стоящее — узнать его в движении, при изменениях»
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей — ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали — новый ромб совпадет с прежним. Симметрия.
- Отразим ромб зеркально по другой диагонали — ромб совпадает с самим собой. Симметрия.
Замечание: Если «зряче видим» центральную и осевые симметрии ромба, то все его свойства у нас «в кармане».
Свойства ромба:
- Ромб симметричен относительно точки O — пересечения диагоналей. O — центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ — ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
- Противолежащие углы равны $angle A=angle C$ , $angle B=angle D$ . Прилежащие $angle A+angle B=180^o$ , $angle A+angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=frac{AC}{2}$ и $BO=OD=frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов — делят углы пополам.
- Диагонали ромба со сторанами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.
- Меньшая диагональ $AC^2=a^2+b^2-2cdot acdot bcdotcos D$ , большая — $BD^2=a^2+b^2+2cdot acdot bcdotcos D$ .
- Сумма {Цвет:Red квадратов диагоналей ромба равна $AC^2+BD^2=4cdot a^2$ четырежды квадрат стороны.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.

Формулы Площади ромба:
- Площадь ромба равна произведению основания на высоту $S_{ABCD}=ADcdot CH$ , $S=acdot h$ ;
- Площадь ромба равна через синус угла: $S=a^2cdotsin A$ , квадрат стороны на синус .
- Площадь ромба через диагонали: $S=frac{ACcdot BD}{2}$ . — половина произведения диагоналей
Вписанная окружность в ромб:
- В четырехугольник можно вписать окружность только если … суммы противоположных сторон равны.
- Вписать окружность можно в ромб и квадрат, ;
- Если вписывается, то площадь $S=pcdot r$, $p=2cdot a$ $S=2cdot a cdot r$.
- Центр Вписанной окружности находится на пересечении диагоналей. Диагонали — суть биссектрисы углов.
Задача 1: Найти периметр ромба $ABCD$, в котором $angle C=60^o$ , а меньшая диагональ равна $10,5$ см.
- Решение: Рассмотрим $bigtriangleup BCD$. Что в нём равного? $Rightarrow$ каков данный треугольник?
- По условию, угол $bigtriangleup BCD$ у вершине $angle B=60^o$ , тогда как два других угла?
- Каков все-таки этот треугольник? Чему равны стороны ромба. А сумма сторон? Ответ: $p=42$ см.
Задача 2: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: «Односторонние углы»: В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30’$ , $67^o30’$


Задача 3: Найти площадь ромба $ABCD$, если его высота $EB=12$ , а меньшая диагональ $BD=13$.
- Решение: Проведем высоту из той же вершины, из которой проведена меньшая диагональ.
- Получили прямоугольный треугольник $BED$ . Он подобен тем треугольникам, на которые ромб делится диагоналями:
- $bigtriangleup BED sim bigtriangleup AOD=bigtriangleup AOB=bigtriangleup COB=bigtriangleup COD$ . Все прямоугольные и есть равные углы.
- например $alpha$. Для нахождения площади нам нужно найти или сторону ромба, или его вторую диагональ.
- Для угла $alpha$ в $bigtriangleup EBD$ мы знаем гипотенузу и противолежащий катет $Rightarrow$ $sinalpha=frac{BE}{BD}=frac{12}{13}$
- Перейдем к $bigtriangleup OCD$ : в нем прилежащий катет $OD=frac{1}{2}BD=6,5$. Чтобы найти второй катет, нам нужен тангенс,
- а чтобы найти гипотенузу, т. е. сторону ромба, – косинус. Найдем их через основное тригонометрическое тождество :
- $sin^2alpha+cos^2alpha=1$ . Тогда косинус: $cosalpha=pmsqrt{1-sin^2alpha}=pmsqrt{1-frac{144}{169}}=pmsqrt{frac{25}{169}}=pmfrac{5}{13}$
- Угол $alpha$ острый, так как он входит в прямоугольный треугольник, т. е. принадлежит первой четверти.
- Следовательно, косинус положительный и мы останавливаемся на одном значении: $cosalpha = frac{5}{13}$
- Тогда: $frac{DO}{DC}=frac{6,5}{DC}=cosalpha=frac{5}{13}$ $Rightarrow$ $DC=frac{6,5cdot13}{5}=frac{13cdot13}{10}=16,9$
- Площадь ромба равна произведению основания на высоту: Ответ: $S=16,9cdot12=202,8$
Задача 4: В Ромбе $ABCD$ точка $K$ делит сторону $CD$ в соотношении $2:7$, а $M$ делит $1:3$ сторону $BC$. $MN$ параллельна $AB$, $O$ — пересечение $MN$ и $BK$. Найти площадь трапеции $ABON$, если площадь $ABCD=420$.

Решение: пробa Анализ рисунка:
- $AB$, $MN$, $CD$ — параллельные. Какие углы равные?
- Треугольники $BMO$ и $BKC$ подобные. Коэффициент подобия $1:3$.
- Отношение площадей $BMO$ и $BKC$ равен $1:9$ — квадрату коэффициента подобия.
- (по формулам) Площади $BKC$ и $BCD$ относятся как $CK$ и $CD$, т.е. $5:7$.
- Площадь $BCD$ равен половине площади $ABCD$, т.е. $S_{BCD}=210$.
- $S_{ABMN}:S_{ABCD}=1:3$ $Rightarrow$ $S_{ABMN}=140$ .
- Из складываемости площадей: площадь $ABON$ = разности площадей $ABMN$ и $BOM$.
Упражнения:
Ромб — это параллелограмм, у которого все стороны равны.
- «Чтоб Выучить, распознать нечто неподвижное — узнать его в движении, при изменениях»
- Ромб провернем на 180 градусов вокруг точки пересечения диагоналей — ромб совместится с самим собой. Симметрия.
- Отразим ромб зеркально по диагонали — новый ромб совпадет с прежним. Симметрия.
- Отразим ромб зеркально по другой диагонали — ромб совпадает с самим собой. Симметрия.
Замечание: Если «зряче видим» центральную и осевые симметрии ромба, то все его свойства у нас «в кармане».
Свойства ромба:
- Ромб симметричен относительно точки O — пересечения диагоналей. O — центр симметрии.
- Ромб симметричен относительно любой из диагоналей. Диагональ — ось симметрии.
- У ромба, по определению, Стороны равны $AB=BC=CD=DA=a$.
- Противолежащие углы равны $angle A=angle C$ , $angle B=angle D$ . Прилежащие $angle A+angle B=180^o$ , $angle A+angle D=180^o$.
- Диагонали ромба пересекаются и точкой пересечения делятся пополам $AO=OC=frac{AC}{2}$ и $BO=OD=frac{BD}{2}$.
- Диагонали ромба взаимно перпендикулярны и образуют прямоугольные $bigtriangleup$ треугольники.
- Диагонали ромба со сторонами ромба образуют равнобедренные $bigtriangleup$ треугольники.
- Диагонали ромба являются биссектрисами углов — делят углы пополам.
- Диагонали ромба со сторонами образуют равные накрест лежащие углы.
- Угол между высотами ромба, проведенными из вершины тупого угла, равен острому углу ромба.

Квадрат — одновременно прямоугольник, ромб, параллелограмм. Диагонали квадрата равны между собой и делятся пополам.
Задача 1: Найти периметр ромба $ABCD$, в котором $angle C=60^o$ , а меньшая диагональ равна $10,5$ см.
- Решение: Рассмотрим $bigtriangleup BCD$. Что в нём равного? $Rightarrow$ каков данный треугольник?
- По условию, угол $bigtriangleup BCD$ у вершины $angle B=60^o$ , тогда как два других угла?
- Каков все-таки этот треугольник? Чему равны стороны ромба. А сумма сторон? Ответ: $p=42$ см.
Задача 2: Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен $45^o$.
- Решение: «Односторонние углы»: В параллелограмме сумма углов, прилежащих к одной стороне, равна $180^o$ .
- Противоположные стороны ромба параллельны, их пересекает диагональ (секущая). Какие накрест лежащие углы равны?
- Как найти все углы ромба. Кем является Диагональ в ромбе для угла? Ответ: $22^o30’$ , $67^o30’$


- Полезные напоминания: «В равностороннем треугольнике все углы равны 60 градусов.
- Если в равнобренном треугольнике один из углов 60, то это равносторонный треугольник — стороны равны, углы тоже.
- В прямоугольном треугольнике катет напротив угла 30 градусов равен половине гипотенузы.
Упражнения:
Задачи из сайта https://resh.edu.ru :
Задача 11: В ромбе АВСD ∠А = 140°, диагонали пересекаются в точке O. Найдите угол CBO.
Задача 12: В ромбе ABCD ∠С = 50°. Точка O – точка пересечения диагоналей ромба. Найдите угол OBC.
Задача 13: Одна из диагоналей ромба образует с его стороной угол 65°. Найдите больший угол ромба.
Задача 14: ???? В любом ромбе равны… Противолежащие углы равны, сумма соседних углов равна 180 градусов:(?) Ромб, у которого все углы равны, это… (?) Диагонали пересекаются и точкой пересечения делятся пополам. (?) Диагонали взаимно перпендикулярны. (?)
Задача 15: Отрезки AB и CD пересекаются в их общей середине. В образовавшемся четырёхугольнике ∠CAD = ∠ADB. Найдите ∠BCA.
Задача 16: На диагонали квадрата как на стороне построен новый квадрат. Чему равна его диагональ, если сторона исходного квадрата равна 6 см?
Задача 17: Одна из диагоналей ромба образует с его стороной угол 65°. Найдите больший угол ромба.
Найти углы ромба, зная только его сторону, нельзя: существуют ромбы, имеющие разные углы, но одинаковые стороны. На пальцах: сделайте ромб из проволоки, «сплющите» его — он останется ромбом, стороны будут те же, углы изменятся.
Значит, чтобы найти углы ромба нужно знать что-то ещё (или что-то другое). Например, зная сторону и диагональ, найти угол можно по теореме косинусов: если x — сторона, d — диагональ, a — угол напротив диагонали, то условие теоремы косинуов — d^2 = x^2 + x^2 — 2 * x^2 * cos(a), из него следует a = arccos((2x^2 — d^2)/2x^2). (Я говорю «найти угол», а не «найти углы», потому что если мы знаем один угол, остальные находятся тривиально: если один угол равен а градусов, то угол напротив него тоже а, остальные два — по 180-а).
Есть и другие варианты: через сторону и площадь (пользуясь тем, что площадь — это квадрат стороны умножить на синус угла), через две диагонали (мы знаем, что диагонали в ромбе пересекаются под прямым углом и делятся точкой пересечения пополам — отсюда следует, что тангенс половины угла ромба равен отношению диагоналей, просто по определнию тангенса; зная сторону и диагональ, кстати, тоже можно искать угол примерно таким способом, вместо теоремы косинусов) и так далее.
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Ромб и его свойства
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства ромба:
(blacktriangleright) Те же, что и у параллелограмма:
(sim) Противоположные стороны попарно равны;
(sim) Диагонали точкой пересечения делятся пополам;
(sim) Противоположные углы попарно равны, а сумма соседних равна (180^circ);
(blacktriangleright) Диагонали взаимно перпендикулярны и являются биссектрисами углов ромба.
Признаки ромба.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – ромб:
(blacktriangleright) все стороны равны;
(blacktriangleright) диагонали взаимно перпендикулярны и он является параллелограммом;
(blacktriangleright) диагонали являются биссектрисами углов и он является параллелограммом.
Площадь ромба
1. Т.к. ромб является параллелограммом, то для него верна та же формула площади. Таким образом, площадь ромба равна произведению высоты на основание, к которому эта высота проведена.
2. Площадь ромба равна половине произведения его диагоналей.
Задание
1
#2716
Уровень задания: Легче ЕГЭ
В ромбе (ABCD): (angle ACD = 26^{circ}). Найдите (angle ABD). Ответ дайте в градусах.
В ромбе диагонали перпендикулярны, тогда (angle CDB = 90^{circ} — angle ACD = 64^{circ}).
(BC = CD), тогда (angle CBD = angle CDB = 64^{circ}).
Так как диагонали ромба делят его углы пополам, то (angle ABD = angle CBD = 64^{circ}).
Ответ: 64
Задание
2
#2717
Уровень задания: Равен ЕГЭ
Найдите большую диагональ ромба (ABCD), если (AB = 2sqrt{3}), а острый угол равен половине тупого.
Так как сумма односторонних углов при параллельных прямых и секущей равна (180^{circ}), то сумма острого и тупого углов ромба равна (180^{circ}).
Так как в данном ромбе острый угол равен половине тупого, то острый угол ромба (ABCD) равен (60^{circ}).
Треугольник (ABD) – равнобедренный, один из углов которого равен (60^{circ}), тогда треугольник (ABD) – равносторонний и (BD = 2sqrt{3}).
Пусть (O) – точка пересечения диагоналей ромба, тогда (OD = 0,5 BD = sqrt{3}), следовательно, по теореме Пифагора находим: (AO^2 + OD^2 = AD^2), тогда (AO^2 + 3 = 12), откуда находим (AO = 3). В ромбе, как и в любом другом параллелограмме, диагонали точкой пересечения делятся пополам, значит, (AC = 6).
Ответ: 6
Задание
3
#2715
Уровень задания: Равен ЕГЭ
Острый угол ромба (ABCD) равен (60^{circ}), одна из его сторон равна 10. Найдите меньшую из диагоналей этого ромба.
Пусть (angle A = 60^{circ}). В ромбе все стороны равны, тогда треугольник (ABD) – равнобедренный, у которого один из углов равен (60^{circ}), следовательно, треугольник (ABD) – равносторонний и (BD = 10).
Треугольник (ABC) – тупоугольный. В треугольнике против большего угла лежит большая сторона, тогда (AC > AB = BD), значит, (BD) – меньшая из диагоналей.
Ответ: 10
Задание
4
#1794
Уровень задания: Равен ЕГЭ
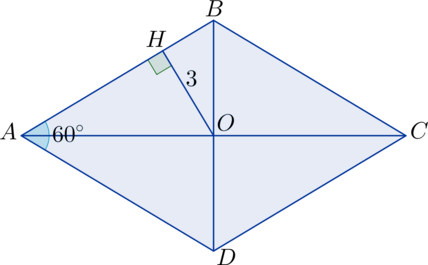
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно (3), а острый угол ромба равен (60^circ). Найдите большую диагональ ромба.
Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), (angle DAB = 60^circ), тогда (angle
OAB = 30^circ). Получаем, что (OH) – катет лежащий напротив угла в (30^circ), значит (AO = 2cdot OH = 6). Т.к. (AC) и есть большая диагональ, то (AC = 2cdot AO = 12).
Ответ: 12
Задание
5
#1757
Уровень задания: Равен ЕГЭ
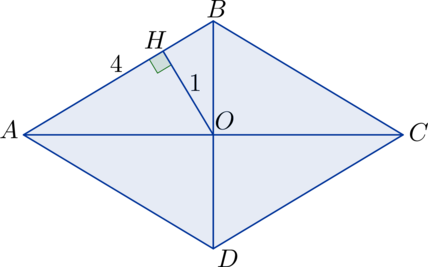
Сторона ромба равна (4). Расстояние от точки пересечения его диагоналей до одной из сторон равно (1). Найдите площадь ромба.
Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), тогда (S_{triangle ABO} = frac{1}{2}cdot 1 cdot 4 = 2). Диагонали ромба делят его на (4) равных прямоугольных треугольника (Rightarrow) (S_{ABCD} = 4cdot 2 = 
Ответ: 8
Задание
6
#2718
Уровень задания: Равен ЕГЭ
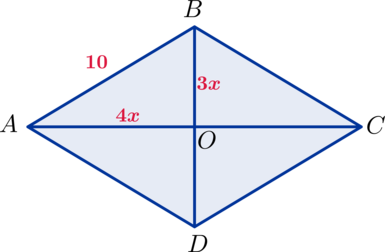
Периметр ромба равен (40), а диагонали относятся, как (3:4). Найдите площадь ромба.
Половины диагоналей находятся в таком же отношении, как и диагонали, то есть в отношении (3:4). Зная периметр, найдем сторону ромба: (40
: 4 = 10). Сторона и половинки диагоналей образуют прямоугольный треугольник (AOB).
Пусть (AO=4x), (BO=3x).
Тогда по теореме Пифагора: ((3x)^2 + (4x)^2 = 10^2) (Rightarrow) (25x^2 = 100) (Rightarrow) (x^2 = 4) (Rightarrow) (x = 2). Диагонали равны (BD=2BO=12) и (AC=2AO=16) (Rightarrow) (S_{ABCD} =
frac{1}{2}cdot12cdot16 = 96).
Ответ: 96
Задание
7
#2719
Уровень задания: Равен ЕГЭ
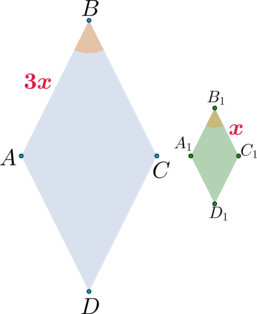
Во сколько раз отличаются площади ромбов, имеющие по равному углу, у которых стороны относятся как (3:1)?
Пусть (angle B) и (angle B_1) – равные углы ромбов. Так как стороны ромбов относятся как (3:1), то можно обозначить их за (3x) и (x) соответственно.
Тогда и (angle D=angle D_1) (так как у ромба противоположные углы равны). Следовательно, (triangle ABCsim triangle A_1B_1C_1) и (triangle ADCsimtriangle A_1D_1C_1) по двум пропорциональным сторонам и углу между ними, причем коэффициент подобия этих треугольников равен (3). Следовательно, их площади относятся как (9:1). А так как (S_{ABC}+S_{ADC}=S_{ABCD}) и (S_{A_1B_1C_1}+S_{A_1D_1C_1}=S_{A_1B_1C_1D_1}), то (S_1:S_2=9:1).
Ответ: 9
Геометрические задачи на тему «Свойства ромба» в обязательном порядке включаются в ЕГЭ по математике. Причем, в зависимости от условия задания, учащийся может давать как краткий, так и развернутый ответ. Именно поэтому на этапе подготовки к сдаче ЕГЭ школьникам непременно стоит понять принцип решения задач на применение свойств и признаков ромба.
Еще раз повторить данную тему и восполнить пробелы в знаниях вам поможет образовательный проект «Школково». С помощью нашего сайта можно легко и эффективно подготовиться к ЕГЭ по математике.
Чтобы успешно справляться с геометрическими заданиями, учащимся старших классов стоит повторить базовые понятия и определения: свойства углов ромба и других четырехугольников, признаки этой фигуры, а также формулу для нахождения ее площади. Данный материал представлен в разделе «Теоретическая справка» на сайте «Школково». Информация, которую подготовили наши специалисты, изложена в максимально доступной форме.
Повторив основные свойства диагоналей ромба, а также его углов и биссектрис, учащиеся могут попрактиковаться в выполнении упражнений. Большая подборка заданий по данной теме, а также по решению нестандартных задач по математике представлена в разделе «Каталог». Найти правильный ответ выпускники смогут, предварительно освежив в памяти свойства биссектрис ромба, в также углов и диагоналей этой фигуры. Подробный алгоритм решения каждой задачи прописан нашими специалистами.
Выполнять простые и более сложные задания по теме «Ромб и его свойства», а также на нахождение площади квадрата на этапе подготовки к ЕГЭ по математике школьники из Москвы и других городов могут в режиме онлайн. При необходимости любое упражнение можно сохранить в разделе «Избранное». Это позволит в дальнейшем быстро найти это задание и, к примеру, обсудить алгоритм его решения со школьным преподавателем.

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Содержание:
- Определение ромба
- Свойства ромба
- Признаки ромба
- Примеры решения задач
Определение ромба
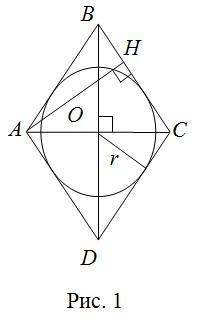
На рисунке 1 $ABCD$ — ромб, $A B=B C=C D=A D$. Так как ромб — это
параллелограмм,
то он обладает всеми свойствами параллелограмма, но так же есть свойства присущие только ромбу.
В любой ромб можно вписать окружность. Центр окружности, вписанной в ромб, является точкой пересечения его диагоналей.
Радиус окружности равен половине высоты ромба $r=frac{A H}{2}$ (рис.1)
Свойства ромба
- Диагонали ромба перпендикулярны;
- Диагонали ромба являются биссектрисами его углов.
Признаки ромба
- Параллелограмм, диагонали которого пересекаются под прямым углом, есть ромб;
- Параллелограмм, диагонали которого являются биссектрисами его углов, есть ромб.
Примеры решения задач
Пример
Задание. Диагонали ромба
$ABCD$ равны 6 и 8 см. Найти сторону ромба.
Решение. Сделаем рисунок (рис. 1). Пусть для определенности, $A C=6$ см, $B D=8$ см.
По свойству ромба его диагонали
пересекаются под прямым углом. В точке пересечения диагонали делятся пополам (свойство параллелограмма, а ромб является
частным случаем параллелограмма).
Рассмотрим треугольник $A O B$. Он
прямоугольный ( $angle O=90^{circ}$),
$A O=frac{A C}{2}=frac{6}{2}=3$ см, $B O=frac{B D}{2}=frac{8}{2}=4$ см.
Запишем для этого треугольника
теорему Пифагора:
$$A B^{2}=A O^{2}+B O^{2}$$
подставим найденные значения $AO$ и $BO$,
$A B^{2}=3^{2}+4^{2}$
$A B^{2}=9+16$
$A B^{2}=25$
$A B=sqrt{25}$
$A B=5$ (см)
Ответ. Сторона ромба равна 5 см.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
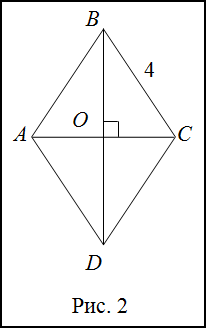
Задание. В ромбе со стороной 4 дм, один из углов равен $60^{circ}$. Найти диагонали ромба.
Решение. Сделаем рисунок (рис. 2).
Пусть для определенности $angle B=60^{circ}$. Тогда, по свойству ромба, диагональ $BD$ является биссектрисой угла $B$,
$angle A B O=angle O B C=frac{angle B}{2}=30^{circ}$. Рассмотрим
$Delta O B C$, он прямоугольный (
$angle B O C=90^{circ}$), потому что диагонали ромба пересекаются под
прямым углом. Так как
$angle O B C=30^{circ}, O C=frac{B C}{2}=2$ дм — катет лежащий против угла в
$30^{circ}$. По теореме Пифагора найдем
$B O$:
$$B O=sqrt{B C^{2}-O C^{2}}$$
$$B O=sqrt{4^{2}-2^{2}}$$
$$B O=sqrt{12}$$
$$B O=2 sqrt{3}$$
Диагонали ромба в точке пересечения делятся пополам, поэтому
$B D=2 cdot B O=2 cdot 2 sqrt{3}=4 sqrt{3}$ (дм)
$A C=2 cdot O C=2 cdot 2=4$ (дм)
Ответ. $B D=4 sqrt{3}$ дм, $A C=4$ дм
Пример
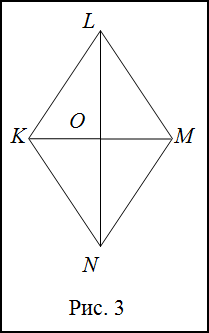
Задание. В ромбе угол образованный одной из диагоналей и стороной ромба равен $27^{circ}$. Найти углы ромба.
Решение. Сделаем рисунок (рис. 3)
Для определенности
$angle K L O=27^{circ}$. Диагонали в ромбе являются биссектрисами его углов, поэтому
$angle L=2 cdot angle K L O=2 cdot 27^{circ}=54^{circ}$. Так как ромб является параллелограммом, на него
распространяются следующие свойства: сумма прилегающих к одной стороне углов равна
$180^{circ}$ и противолежащие углы равны. Поэтому,
$angle M=angle K=180^{circ}-angle L=180^{circ}-54^{circ}=126^{circ}$
$angle N=angle L=54^{circ}$
Ответ. $angle N=angle L=54^{circ}$
$angle M=angle K=126^{circ}$
Читать дальше: что такое круг.
Всего: 46 1–20 | 21–40 | 41–46
Добавить в вариант
На каждой из двух окружностей с радиусами 3 и 4 лежат по три вершины ромба. Найдите его сторону.
Источник: ГИА-2012. Математика. Тренировочная работа № 2(1 вар)
Сторона ромба равна 24, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Перечислите эти длины в ответе без пробелов в порядке неубывания.
Источник: Банк заданий ФИПИ
Периметр ромба равен 116, а один из углов равен 30°. Найдите площадь ромба.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 14, а одна из диагоналей ромба равна 56. Найдите углы ромба.
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 28.
Точка O — центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR — ромб. Найдите угол ORQ. Ответ дайте в градусах.
Точка O — центр окружности, на которой лежат точки S, T и V таким образом, что OSTV — ромб. Найдите угол STV. Ответ дайте в градусах.
Высота AH ромба ABCD делит сторону CD на отрезки DH = 12 и CH = 3. Найдите высоту ромба.
Высота AH ромба ABCD делит сторону CD на отрезки DH = 15 и CH = 2. Найдите высоту ромба.
Высота AH ромба ABCD делит сторону CD на отрезки DH = 24 и CH = 6. Найдите высоту ромба.
Точка O — центр окружности, на которой лежат точки A, B и C таким образом, что OABC — ромб. Найдите угол OCB. Ответ дайте в градусах.
Точка O — центр окружности, на которой лежат точки A, B и C таким образом, что OABC — ромб. Найдите угол OAB. Ответ дайте в градусах.
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 56.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 15, а одна из диагоналей ромба равна 60. Найдите углы ромба.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 12, а одна из диагоналей ромба равна 48. Найдите углы ромба.
Один из углов ромба равен 43°. Найдите больший угол этого ромба. Ответ дайте в градусах.
Источник: Банк заданий ФИПИ
В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.
Источник: Банк заданий ФИПИ
Сторона ромба равна 4, а один из углов этого ромба равен 150°. Найдите высоту этого ромба.
Источник: Банк заданий ФИПИ
Периметр ромба равен 24, а один из углов равен 30°. Найдите площадь ромба.
Всего: 46 1–20 | 21–40 | 41–46