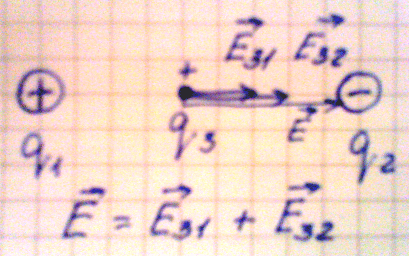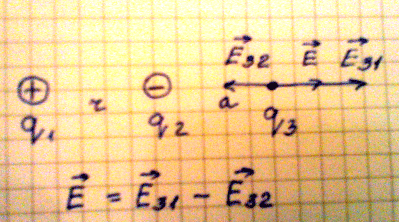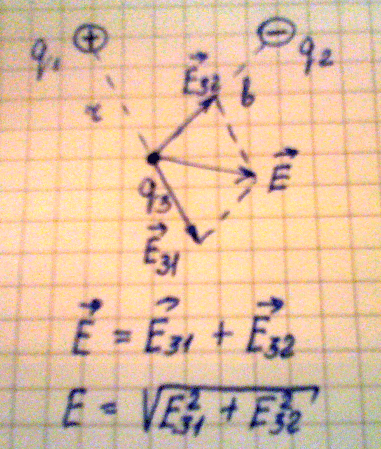Электрическое поле. ЗАДАЧИ с решениями
Формулы, используемые на уроках по теме «Электрическое поле. ЗАДАЧИ» в 10-11 классах при подготовке к ЕГЭ.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Электрон движется без начальной скорости вдоль силовой линии однородного электрического поля напряженностью Е = 2 • 104 Н/Кл. Какой путь S он пролетит прежде, чем его скорость станет v = 100 км/с ? Среда — воздух. Модуль заряда электрона е = 1,6 • 10–19 Кл, его масса me = 9,1 • 10–31 кг.
Задача № 2.
Пылинка с зарядом q = 1 нКл неподвижно висит в однородном электрическом поле напряженностью Е = 2 • 104 Н/Кл, вектор напряженности которого направлен вверх (рис. 2-9). Найти массу пылинки т. Сколько избыточных электронов N содержит пылинка?
Смотреть решение и ответ
Задача № 3.
Заряженный шар диаметром D находится в равновесии в жидком диэлектрике плотностью р1 с диэлектрической проницаемостью ε (рис. 2-10). Найти поверхностную плотность зарядов на шаре σ, если плотность вещества шара р2. Напряженность электрического поля в диэлектрике Е, вектор напряженности направлен вверх.
Смотреть решение и ответ

Задача № 4.
На каком расстоянии г2 от точечного заряда напряженность электрического поля этого заряда в жидком диэлектрике с диэлектрической проницаемостью ε2 = 81 (вода) такая же, как на расстоянии r1 = 9 см от этого заряда в воздухе?
Смотреть решение и ответ

Задача № 5.
Электрон влетает в однородное электрическое поле со скоростью v0, направленной перпендикулярно вектору напряженности Е (рис. 2-11). Под каким углом φ к линиям вектора напряженности будет направлен вектор его скорости через время t полета в поле? Чему будет равна работа сил поля А за это время? Чему будет равна кинетическая энергия электрона Wк через время t ? Напряженность поля Е. Масса электрона те и его заряд е известны.
Задача № 6.
Тонкая металлическая пластинка массой m падает вертикально вниз равноускоренно так, что ее плоскость остается горизонтальной. Падению пластинки противодействует сила сопротивления среды Fсоnp. Найти напряженность электрического поля Е, возникающего внутри пластинки вследствие инерции свободных электронов. Масса электрона me, его заряд е.
Задача № 7.
К бесконечной, вертикальной, равномерно заряженной плоскости прикреплена одним кондом невесомая нить, на другом конце которой находится одноименно с нитью заряженный шарик радиусом R = 0,5 см, несущий заряд q = 1 • 10–10 Кл. Плотность вещества шарика р = 2 • 103 кг/м3. Натяжение нити Fн = 4,9 • 10–2 Н. Какой угол а образует с плоскостью нить, на которой висит шарик (рис. 2-12)? Среда – воздух. Чему равна поверхностная плотность σ зарядов на плоскости?
Задача № 8.
Сфера радиусом R = 1 см равномерно заряжена. Поверхностная плотность зарядов на сфере σ = 10 нКл/см2. Найти напряженность Е1 электрического поля на расстоянии r1 = 10 см от центра сферы (рис. 2-13). Построить график зависимости напряженности Е от расстояния r в пределах от r0 = 0 до r1 = 10 см. Среда — воздух.
Задача № 9.
Заряды q1 = 20 нКл и q2 = 10 нКл расположены на расстоянии r = 10 см друг от друга. Найти напряженность электрического поля Е1, созданного этими зарядами в точке 1, расположенной на расстоянии r1 = 4 см от заряда q1 и напряженность Е2 в точке 2, расположенной на расстоянии г2 = 2 см от заряда q2 (рис. 2-15). Среда — вакуум.
Задача № 10.
Два одноименных точечных заряда q и 4q расположены на расстоянии r друг от друга. На каком расстоянии r1 от заряда q находится точка М, в которой напряженность поля этих зарядов Е = 0? На каком расстоянии r2 от заряда q находится такая точка, если эти заряды разноименные?
Задача № 11.
На расстоянии г = 3 см от поверхности шара радиусом R = 2 см находится точечный отрицательный заряд q = –2 нКл. Шар заряжен положительно с поверхностной плотностью зарядов σ = 2 нКл/м2. Найти напряженность поля Е, созданного заряженным шаром и точечным зарядом, в точке, расположенной на расстоянии r1 = 4 см от центра шара, и г2 = 3 см от заряда q. Среда — воздух.
Задача № 12.
В вершинах равностороннего треугольника со стороной а находятся заряды q, –q и q. Найти напряженность поля Е, созданного этими зарядами в центре треугольника. Среда — воздух.
(с) В учебных целях использованы цитаты из учебного пособия «Новый репетитор по физике для подготовки к ЕГЭ : задачи и методы их решения / И.Л. Касаткина; под ред. Т.В. Шкиль. — Ростов н /Д : Феникс».
Это конспект по теме «Электрическое поле. ЗАДАЧИ с решениями». Выберите дальнейшие действия:
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.
Напряженность поля .
Напряженностью поля называют отношение силы, действующей на пробный электрический заряд
к величине этого заряда.
(E=dfrac {F}{q} )
Задача 1.
Найти напряженность электрического поля, если сила, действующая на заряд (q=0,001 Кл )
равна (F=0,01 Н )
Показать ответ
Показать решение
Видеорешение
Задача 2.
Найти силу, действующую на точечный заряд (q=100 мкКл) , помещенный в однородное электрическое
поле напряженностью (E=1000 В/м )
Показать ответ
Показать решение
Видеорешение
Задача 4.
Найти величину электрического заряда (q) , если в поле напряженностью (E=1000 В/м )
на него действует сила (F=0,005 Н )
Дать ответ в микрокулонах
Показать ответ
Показать решение
Видеорешение
Задача 5.
Найти напряженность однородного электрического поля, если
протон массой (m=1,67 cdot 10^{-27} кг ) и зарядом (q=1,6 cdot 10^{-19} Кл ) движется в нем
с ускорением (a=160000 м/с^2 )
Показать ответ
Показать решение
Видеорешение
Задача 6.
С каким ускорением будет двигаться шарик, находящийся в космосе вдали от небесных тел в однородном электрическом поле
напряженностью ( E=1000 В/м ? )
Заряд шарика (q=70 мкКл)
Масса шарика (m=5 г )
Показать ответ
Показать решение
Видеорешение
Задача 7.
Найти ускорение пылинки массой (m=0,001 г ) и зарядом (q=625 нКл ), находящейся в однородном электрическом поле
напряженностью ( E=500 В/м ? )
Силой тяжести пренебречь.
Показать ответ
Показать решение
Видеорешение
Задача 8.
С каким ускорением движется электрон в однородном электрическом поле напряженностью ( E=90 В/м ),
если заряд электрона (e=1,6 cdot 10^{-19} Кл ), а его масса (m=9 cdot 10^{-31} кг ?)
Показать ответ
Показать решение
Видеорешение
С электрическим полем человек сталкивается не только на уроках физики в школе или институте, но и в повседневной жизни. Изучение такого явления способствует техническому прогрессу. Важно уметь пользоваться основными формулами для расчета характеристик электрического поля, что поможет понять природу взаимодействия заряженных тел и решать задачи любой сложности.
Электрическое поле: решение задач
Электрическое поле является одной из пары компонент электромагнитного поля и представляет собой векторное поле, которое образовано вблизи объектов или частиц, заряженных положительно и отрицательно.
Электромагнитное поле возникает в процессе изменений магнитного поля, к примеру, в волнах электромагнитного характера. В физике можно встретить множество задач по теме электрического поля. Для того чтобы рассчитать характеристики данного явления, необходимо знать фундаментальные законы и основные формулы.
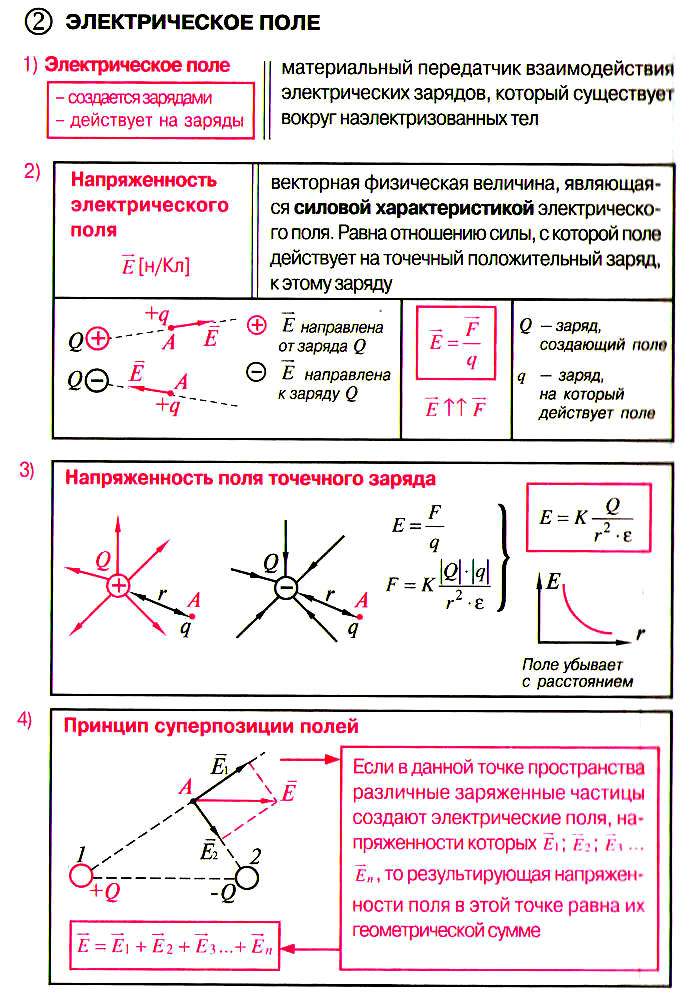
Электрическое поле выступает в роли материального передатчика взаимодействия заряженных частиц, который формируется вокруг наэлектризованных тел. Свойства такого физического явления:
- образуется зарядами;
- воздействует на заряженные частицы.
Напряженностью электрического поля является векторная величина в виде силовой характеристики электрического поля. Данный параметр определяется отношением силы воздействия поля на точечный положительный заряд и этого заряда. Обозначается напряженность таким образом: (vec{E}) (Н/Кл)
Формула для расчета напряженности электрического поля выглядит следующим образом:
(vec{E}=frac{vec{F}}{q})
где q является зарядом, на который действует поле.
Напряженность поля точечного заряда определяется, согласно формулам:
(E=frac{F}{q})
(F=Kfrac{left|Q right|times left|q right|}{r^{2}times varepsilon })
Таким образом:
(E=Kfrac{Q}{r^{2}times varepsilon })
Можно сделать вывод, что поле уменьшается при увеличении расстояния.
Принцип суперпозиции полей заключается в том, что при нахождении в точке пространства различных заряженных частиц, создающих электрические поля с напряженностью:
(vec{E_{1}}), (vec{E_{2}}), (vec{E_{3}}), (vec{E_{n}})
Результирующая напряженности поля в указанной точке будет равна геометрической сумме этих напряженностей:
(vec{E}=vec{E_{1}}+vec{E_{2}}+vec{E_{3}}…+vec{E_{n}})
Задача №1. Закон Кулона
Шар, обладающий зарядом, соприкасается с аналогичным незаряженным шаром. Если расстояние между этими объектами составляет r=15 см, то они отталкивают друг друга с силой F=1 мН. Требуется рассчитать первоначальный заряд заряженного шара.
Решение
Соприкасаясь, одинаковые объекты делят пополам первоначальный заряд. С помощью данной силы взаимодействия можно рассчитать заряды шаров, которыми они стали обладать после соприкосновения. Перед этим необходимо перевести все величины в единицы СИ:
(F=10^{-3}) H
(r = 0,15) м
Затем необходимо записать основные формулы:
(F=frac{kq^{2}}{r^{2}})
(q^{2}=frac{Fr^{2}}{k})
(k=frac{1}{4pi varepsilon _{0}}=9times 10^{9})
Подставив значения, получим уравнение:
(q=sqrt{frac{Fr^{2}}{k}}=sqrt{frac{10^{-3}times (0.15)^{2}}{9times 10^{9}}}=5times 10^{-8})
Известно, что первоначальный заряд был в два раза больше:
(q=2times 5times 10^{-8}=10^{-7})
Ответ: первоначальный заряд составлял (10^{-7}) Кл или 10 мкКл.
Задача №2. Электрическое поле
Необходимо определить силу взаимодействия двух заряженных частиц, которые обладают зарядами по 10 нКл и удалены друг от друга на 3 см. Данные заряды можно считать точечными и находящимися в вакуумной среде.
Решение
Требуется записать значение величин в стандартном виде:
(q_{1}=q_{2}=10) нКл или (10^{-8}) Кл
(r=3) см или (r=3*10^{-2}) м
Далее необходимо записать формулу для F:
(F=kfrac{left|q_{1} right|times left|q_{2} right|}{r^{2}})
Подставив числовые значения, получим:
(F=9times 10^{-9}frac{10^{-8}times 10^{-8}}{left(3times 10^{-2} right)^{2}}=10^{-3}) Н или 1 мН
Ответ: заряды взаимодействуют с силой в 1мН.
Задача №3. Конденсатор
Разность потенциалов между точками А и В составляет U=9 В. Значения емкости конденсаторов равны соответственно (C_{1}=3) мкФ и (C_{2}=6) мкФ. Требуется определить заряды (Q_{1}) и (Q_{2}) и разности потенциалов (U_{1}) и (U_{2}) для обкладок первого и второго конденсаторов.
Решение
Общая емкость такого соединения составит:
(frac{1}{C_{Sigma }}=frac{1}{C_{1}}+frac{1}{C_{2}})
(C_{Sigma }=frac{C_{1}times C_{2}}{C_{1}+C_{2}}=frac{3times 6}{3+6}=2) мкФ
Емкость рассчитана в микрофарадах для того, чтобы не прибегать к расписыванию степени десятки.
Величину заряда можно определить по формуле:
(q_{Sigma }=C_{Sigma }times U=2times 9=18) мкКл
Если соединение пластин конденсатора выполнено последовательно, то заряды будут обладать одинаковыми значениями. Таким образом, можно записать справедливые равенства:
(q_{1}=q_{Sigma }=C_{1}times U_{1})
(q_{2}=q_{Sigma }=C_{2}times U_{2})
Формула для определения напряжения на конденсаторах будет записана таким образом:
(U_{1}=frac{q_{1}}{C_{1}}=frac{18times 10^{-6}}{3times 10^{-6}}=6) В
(U_{2}=frac{q_{2}}{C_{2}}=frac{18times 10^{-6}}{6times 10^{-6}}=3) В
Ответ: разность потенциалов составляет 18 мкКл, напряжения соответственно равны 6 В и 3В.
Задача №4. Энергия конденсатора
Диэлектрическая проницаемость диэлектрика, которым заполнили плоский конденсатор, равна 2. Если конденсатор не имеет диэлектрика, то его энергия составляет 20 мкДж. Требуется рассчитать энергию конденсатора, отключенного от питания и заполненного диэлектрическим веществом.
Решение
Энергию конденсатора в незаполненном состоянии можно рассчитать по формуле:
(W_{0}=frac{q_{0}}{2C_{0}}=frac{C_{0}U_{0}^{2}}{2})
Когда конденсатор заполнили диэлектриком, его емкость изменится таким образом:
(C_{1}=varepsilon C_{0})
Исходя из этого утверждения, энергию конденсатора можно определить так:
(W_{1}=frac{varepsilon C_{0}U_{0}^{2}}{2}=varepsilon W_{0}=2times 20=40) мкФ
Ответ: энергия конденсатора после заполнения диэлектрика составит 40 мкФ.
Задача №5. Потенциал поля
Два точечных зарядов величиной 100 нКл и 10 нКл удалены друг от друга на расстояние r = 10 см. Требуется определить потенциальную энергию системы этих зарядов.
Решение
Формула для расчета точечного заряда имеет вид:
(phi =frac{q}{4pi varepsilon _{0}r})
Таким образом, потенциальную энергию зарядов можно рассчитать по формуле:
(E=frac{q_{1}q_{2}}{4pi varepsilon _{0}r})
Подставив числовые значения, получим:
(E=frac{10^{-7}times 10^{-8}}{4pi times 8.85times 10^{-12}times 0.1}=9times 10^{-5}) Дж
Ответ: потенциальная энергия системы зарядов равна (9times 10^{-5}) Дж
Вопросы на тему «Электрическое поле»
- Как переводится слово electron с греческого языка? Ответ: Янтарь.
- Название величины, которая характеризует свойство объектов участвовать в электромагнитных взаимодействиях. Ответ: Электрический заряд.
- Каким образом обозначают электрический заряд в физике. Ответ: с помощью букв q или Q.
- Единица заряда в международной системе СИ. Ответ: кулон.
- Прибор для определения заряженных частиц. Ответ: электрометр.
- Что такое точечный заряд? Ответ: точечным зарядом является заряженное тело с размерами, которые существенно меньше, чем расстояние между этим телом, точкой наблюдения или другими заряженными телами.
- Пример положительно заряженных тел. Ответ: стекло, наэлектризованное путем трения о шелковую ткань.
- Пример отрицательно заряженных тел. Ответ: эбонитовая палочка, наэлектризованная путем трения о шерстяную ткань.
- Описать взаимодействие заряженных тел. Ответ: одинаковые заряды отталкиваются, а разноименные – притягиваются.
- Объяснить понятие дискретности электрического заряда. Ответ: Дискретность заряда означает существование некоторого наименьшего, универсального, далее не делимого элементарного заряда.
- Какова величина элементарного заряда? Ответ: (e=1,6times 10^{-19}) Кл.
- Дать определение протона и электрона. Ответ: Частицу, которая обладает элементарным положительным зарядом, называется протоном. Частица, для которой характерен элементарный отрицательный заряд, является электроном.
- Объяснить положительный и отрицательный заряд тела. Ответ: Тело будет заряжено положительно, если в нем преобладает количество протонов по сравнению с числом электронов. При избытке электронов тело будет заряжено отрицательно.
- Закон сохранения электрического заряда. Ответ: в условиях замкнутой системы алгебраическая сумма электрических зарядов сохраняет постоянное значение при любых взаимодействиях внутри этой системы.
- Что такое изолированная или замкнутая система? Ответ: изолированной или замкнутой системой тел является такая система, в которую не добавляют и не выводят из нее электрические заряды.
- Способы электризации тел. Ответ: трением, воздействием различных излучений, с помощью электрической индукции.
- Когда открыт закон Кулона? Ответ: в 1785 году.
- Какой прибор Кулон использовал в опытах? Ответ: крутильные весы.
- Запись закона Кулона. Ответ: (F=kfrac{left|q_{1} right|times left|q_{2} right|}{r^{2}})
- Что называют точечным зарядом? Ответ: точечным зарядом называют заряженное тело с размерами, которые можно не учитывать в решении данной задачи.
- Единица заряда. Ответ: кулон (кл).
- Представить запись электрической постоянной. Ответ: (varepsilon _{0}=8,85times 10^{-12}) Кл2/Н*м2.
- Назвать источник и ключевое свойство электрического поля. Ответ: электрическое поле создается любым заряженным телом, его главным свойством является действие на электрические заряды с какой-то силой.
- Определение напряженности. Ответ: напряженностью называют силовую характеристику электрического поля.
- Что такое электростатическое поле. Ответ это электрическое поле зарядов, которые не двигаются и не меняются в течение времени.
- Зачем нужны силовые линии? Ответ: с помощью силовых линий наглядно представляют электрическое поле.
- Чему равна работа сил электростатического поля, если заряд перемещается по какой-то замкнутой траектории. Ответ: нулю.
- Дать определение потенциала электрического поля. Ответ: физическая величина, которая равна отношению потенциальной энергии электрического заряда в электрическом поле к величине этого заряда.
- Единицы измерения потенциала в СИ. Ответ: вольт.
Зная методику решения распространенных задач по теме электрического поля, можно без труда выполнять расчеты основных его показателей. Такие навыки и умения пригодятся для более углубленного изучения электромагнетизма и сопутствующих тем. При возникновении каких-либо трудностей в процессе освоения материала можно обратиться за помощью к ресурсу Фенинкс.Хелп.
Цель урока: дать понятие напряжённости электрического поля и ее
определения в любой точке поля.
Задачи урока:
- формирование понятия напряжённости электрического поля; дать понятие о
линиях напряжённости и графическое представление электрического поля; - научить учащихся применять формулу E=kq/r2 в решении
несложных задач на расчёт напряжённости.
Электрическое поле – это особая форма материи, о существовании которой можно
судить только по ее действию. Экспериментально доказано, что существуют два рода
зарядов, вокруг которых существуют электрические поля, характеризующиеся
силовыми линиями.
Графически изображая поле, следует помнить, что линии напряженности
электрического поля:
- нигде не пересекаются друг с другом;
- имеют начало на положительном заряде (или в бесконечности) и конец на
отрицательном (или в бесконечности), т. е. являются незамкнутыми линиями; - между зарядами нигде не прерываются.
Рис.1
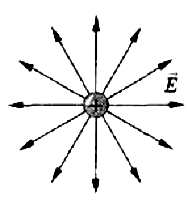
Силовые линии положительного заряда:
Рис.2
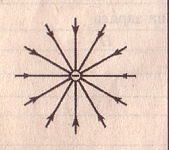
Силовые линии отрицательного заряда:
Рис.3
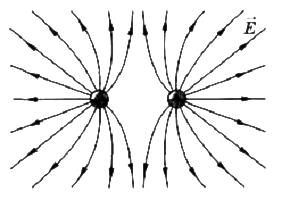
Силовые линии одноименных взаимодействующих зарядов:
Рис.4
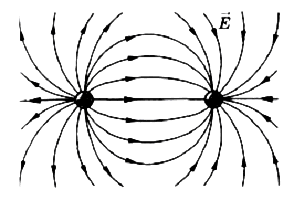
Силовые линии разноименных взаимодействующих зарядов:
Рис.5
Силовой характеристикой электрического поля является напряженность, которая
обозначается буквой Е и имеет единицы измерения
или
.
Напряженность является векторной величиной, так как определяется отношением силы
Кулона к величине единичного положительного заряда
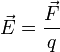
В результате преобразования формулы закона Кулона и формулы напряженности
имеем зависимость напряженности поля от расстояния, на котором она определяется
относительно данного заряда
где: k – коэффициент пропорциональности, значение которого зависит от
выбора единиц электрического заряда.
В системе СИ
Н·м2/Кл2,
где ε0 – электрическая
постоянная, равная 8,85·10-12 Кл2/Н·м2;
q – электрический заряд (Кл);
r – расстояние от заряда до точки в которой определяется напряженность.
Направление вектора напряженности совпадает с направлением силы Кулона.
Электрическое поле, напряженность которого одинакова во всех точках
пространства, называется однородным. В ограниченной области пространства
электрическое поле можно считать приблизительно однородным, если напряженность
поля внутри этой области меняется незначительно.
Общая напряженность поля нескольких взаимодействующих зарядов будет равна
геометрической сумме векторов напряженности, в чем и заключается принцип
суперпозиции полей:
Рассмотрим несколько случаев определения напряженности.
1. Пусть взаимодействуют два разноименных заряда. Поместим точечный
положительный заряд между ними, тогда в данной точке будут действовать два
вектора напряженности, направленные в одну сторону:
Е31 – напряженность точечного заряда 3 со стороны заряда 1;
Е32 – напряженность точечного заряда 3 со стороны заряда 2.
Согласно принципу суперпозиции полей общая напряженность поля в данной точке
равна геометрической сумме векторов напряженности Е31 и Е32.
Напряженность в данной точке определяется по формуле:
Е = kq1/x2 + kq2/(r – x)2
где: r – расстояние между первым и вторым зарядом;
х – расстояние между первым и точечным зарядом.
Рис.6
2. Рассмотрим случай, когда необходимо найти напряженность в точке удаленной
на расстояние а от второго заряда. Если учесть, что поле первого заряда больше,
чем поле второго заряда, то напряженность в данной точке поля равна
геометрической разности напряженности Е31 и Е32.
Формула напряженности в данной точке равна:
Е = kq1/(r + a)2 – kq2/a2
Где: r – расстояние между взаимодействующими зарядами;
а – расстояние между вторым и точечным зарядом.
Рис.7
3. Рассмотрим пример, когда необходимо определить напряженность поля в
некоторой удаленности и от первого и от второго заряда, в данном случае на
расстоянии r от первого и на расстоянии bот второго заряда. Так как одноименные
заряды отталкиваются , а разноименные притягиваются, имеем два вектора
напряженности исходящие из одной точки, то для их сложения можно применить метод
противоположному углу параллелограмма будет являться суммарным вектором
напряженности. Алгебраическую сумму векторов находим из теоремы Пифагора:
Е = (Е312 +Е322)1/2
Следовательно:
Е = ((kq1/r2 )2 + (kq2/b2)2)1/2
Рис.8
Исходя из данной работы, следует, что напряженность в любой точке поля можно
определить, зная величины взаимодействующих зарядов, расстояние от каждого
заряда до данной точки и электрическую постоянную.
4. Закрепление темы.
Проверочная работа.
Вариант № 1.
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: электрическое поле – это ….
3. Как направлены силовые линии напряженности данного заряда?
4. Определить знаки зарядов:
5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
Вариант № 2.
1. Продолжить фразу: “электростатика – это …
2. Продолжить фразу: напряженностью называется …
3. Как направлены силовые линии напряженности данного заряда?
4. Определить заряды.
5. Указать вектор напряженности.
6. Определить напряженность в точке В исходя из суперпозиции полей.
| Своя оценка работы | Оценка работы другим учеником |
Задачи на дом:
1. Два заряда q1 = +3·10-7 Кл и q2 = −2·10-7
Кл находятся в вакууме на расстоянии 0,2 м друг от друга. Определите
напряженность поля в точке С, расположенной на линии, соединяющей заряды, на
расстоянии 0,05 м вправо от заряда q2.
2. В некоторой точке поля на заряд 5·10-9 Кл действует сила 3·10-4
Н. Найти напряженность поля в этой точке и определите величину заряда,
создающего поле, если точка удалена от него на 0,1 м.
Задачи по электростатике с решениями
Закон Кулона
6.1.1 В парафине на расстоянии 20 см помещены два точечных заряда. На каком
6.1.2 Два электрических заряда притягиваются друг к другу в керосине с силой 7,8 Н
6.1.3 Два шарика, расположенные на расстоянии 10 см друг от друга, имеют одинаковые
6.1.4 С какой силой ядро атома железа (Fe) притягивает электрон, находящийся
6.1.5 На двух одинаковых капельках воды находится по одному лишнему электрону
6.1.6 Два заряженных шара одинакового радиуса, массой 0,3 кг каждый, расположены
6.1.7 По теории Бора электрон в атоме водорода вращается вокруг ядра
6.1.8 В атоме водорода электрон движется вокруг протона с угловой скоростью
6.1.9 Два одинаковых шара, массы которых 600 г и радиусы – 20 см, имеют
6.1.10 Какое первоначальное ускорение получит капелька жидкости массой 1,6×10^(-5) г
6.1.11 Два точечных заряда 5 и 15 нКл находятся на расстоянии 4 см друг от друга
6.1.12 Два одинаковых металлических шарика с зарядами -15 и 25 мкКл, вследствие притяжения
6.1.13 Два одинаковых маленьких металлических шарика с зарядами 120 и 80 нКл
6.1.14 Во сколько раз изменится сила кулоновского притяжения двух маленьких шариков
6.1.15 Каждый из двух маленьких шариков положительно заряжен так, что их общий заряд
6.1.16 Два одинаковых шарика, заряженные одноименными зарядами и помещенные
6.1.17 Два маленьких одинаковых шарика находятся на расстоянии 0,2 м и притягиваются
6.1.18 Вокруг отрицательного точечного заряда -5 нКл равномерно вращается
6.1.19 Два заряда по 25 нКл каждый, расположенные на расстоянии 0,24 м друг от друга
6.1.20 На нити подвешен заряженный шар массой 300 г. Когда к нему поднесли снизу
6.1.21 На нити подвешен маленький шарик массой 10 г, которому сообщили заряд 1 мкКл
6.1.22 Три одинаковых точечных заряда по -1,7 нКл каждый находятся в вершинах
6.1.23 Две частицы массой 10 г и зарядом 2 мкКл находятся в вершинах равностороннего
6.1.24 В вертикальной трубке, заполненной воздухом, закреплен точечный заряд 5 мкКл
6.1.25 Два одинаковых шарика подвешены на нитях в воздухе так, что их поверхности
6.1.26 Два шарика массой по 1 г подвешены на нитях длиной 0,5 м в одной точке. После
6.1.27 Два маленьких проводящих шарика подвешены на длинных непроводящих нитях
6.1.28 Два одинаковых шарика, имеющих одинаковые заряды 1,6 мкКл, подвешены на одной
6.1.29 Точечные положительные заряды q и 2q закреплены на расстоянии L друг от друга
6.1.30 Точечные положительные заряды q и 2q закреплены на расстоянии L друг
6.1.31 Два маленьких одинаковых металлических шарика заряжены положительным зарядом 5q
Напряженность электростатического поля
6.2.1 Указать размерность единицы напряженности электростатического поля
6.2.2 Определить напряженность электрического поля, если на точечный заряд 1 мкКл
6.2.3 С какой силой действует однородное поле, напряженность которого 2 кВ/м
6.2.4 В некоторой точке поля на заряд 0,1 мкКл действует сила 4 мН. Найти напряженность
6.2.5 Найти заряд, создающий электрическое поле, если на расстоянии 5 см от него
6.2.6 Точечный заряд удалили от точки A на расстояние, в три раза превышающее
6.2.7 Напряженность электрического поля на расстоянии 30 см от точечного заряда 0,1 мкКл
6.2.8 Поле в глицерине образовано точечным зарядом 70 нКл. Какова напряженность поля
6.2.9 Определить напряженность электрического поля на поверхности иона, считая его
6.2.10 Очень маленький заряженный шарик погрузили в керосин. На каком расстоянии
6.2.11 Шарик, несущий заряд 50 нКл, коснулся внутренней поверхности незаряженной
6.2.12 Проводящему шару радиусом 24 см сообщается заряд 6,26 нКл. Определить
6.2.13 Напряженность электрического поля на расстоянии 10 см от поверхности заряженной
6.2.14 Поверхностная плотность заряда на проводящем шаре равна 0,32 мкКл/м2. Определить
6.2.15 Заряд металлического шара, радиус которого 0,5 м, равен 30 мкКл. На сколько
6.2.16 Шар радиусом 5 см зарядили до потенциала 180 В и потом поместили в керосин
6.2.17 Точечные заряды 10 и -20 нКл закреплены на расстоянии 1 м друг от друга в воздухе
6.2.18 Два точечных заряда 4 и 2 нКл находятся друг от друга на расстоянии 50 см. Определить
6.2.19 Два точечных заряда 4 и -2 нКл находятся друг от друга на расстоянии 60 см. Определить
6.2.20 Найти напряженность поля, создаваемого двумя точечными зарядами 2 и -4 нКл
6.2.21 Определить расстояние между двумя точечными зарядами 16 и -6 нКл, если
6.2.22 В однородном электрическом поле напряженностью 40 кВ/м, направленным
6.2.23 Заряды по 0,1 мкКл расположены на расстоянии 6 см друг от друга. Найти
6.2.24 Одинаковые по модулю, но разные по знаку заряды 40 нКл расположены
6.2.25 В серединах всех сторон равностороннего треугольника расположены одинаковые
6.2.26 В двух противоположных вершинах квадрата со стороной 30 см находятся заряды
6.2.27 В трёх вершинах квадрата со стороной 30 см находятся точечные заряды
6.2.28 В трёх вершинах квадрата со стороной 1 м находятся положительные точечные заряды
6.2.29 Четыре одинаковых заряда 40 мкКл расположены в вершинах квадрата со стороной
6.2.30 Шарик массой 1 г подвешен вблизи земли на невесомой и непроводящей нити
6.2.31 На какой угол отклонится бузиновый шарик с зарядом 4,9 нКл и массой 0,40 г
6.2.32 В однородном электрическом поле напряженностью 1 МВ/м, направленном вверх
6.2.33 Поле равномерно заряженной плоскости действует в вакууме на заряд 0,2 нКл
6.2.34 Бесконечная, равномерно заряженная пластина имеет поверхностную плотность
6.2.35 Две бесконечные параллельные пластины равномерно заряжены поверхностной
6.2.36 Две плоские пластинки площадью 200 см2, расстояние между которыми очень мало
6.2.37 Две бесконечные плоскости, заряженные с поверхностной плотностью 2 и 0,6 мкКл/м2
6.2.38 Напряженность электрического поля вблизи земли перед разрядом молнии
6.2.39 Между горизонтальными пластинами заряженного конденсатора, напряженность
6.2.40 Свинцовый шарик радиусом 0,5 см помещён в глицерин. Определить заряд шарика
6.2.41 Капля массой 10^(-10) г, на которой находится заряд, равный 10 зарядам электрона
6.2.42 Капля массой 10^(-13) кг поднимается вертикально вверх с ускорением 2,2 м/с2
6.2.43 Положительно заряженный шарик массой 18 г и плотностью 1800 кг/м3 находится
6.2.44 Для ионизации нейтральной молекулы воздуха электрон должен обладать
6.2.45 Два заряженных шарика с зарядами 300 и 200 нКл, массы которых 0,2 и 0,8 г
6.2.46 Протон движется с ускорением 76 км/с2 в электрическом поле. Определить
6.2.47 Электрон влетает в плоский конденсатор параллельно его пластинам со скоростью
6.2.48 Электрон влетает в однородное электрическое поле напряженностью 200 В/м
6.2.49 Электрон, попадая в однородное электрическое поле, движется вдоль силовых линий
6.2.50 Поток электронов, направленный параллельно обкладкам плоского конденсатора
6.2.51 Электрон, обладающий скоростью 18 км/с, влетает в однородное электрическое поле
6.2.52 Три равных по величине и знаку заряда q расположены в вакууме вдоль одной прямой
6.2.53 Указать направление вектора напряженности электрического поля, созданного в точке
6.2.54 Точечный положительный заряд создаёт на расстоянии 10 см электрическое поле
6.2.55 На каком расстоянии от поверхности шара напряженность электрического поля
6.2.56 Равномерно заряженный проводящий шар радиуса 5 см создаёт на расстоянии 10 см
6.2.57 Проводящий шар радиуса R заряжен зарядом q. Найти напряженность поля в точке
6.2.58 Точечный отрицательный заряд создаёт на расстоянии 10 см поле, напряженность
Потенциал. Разность потенциалов. Работа сил электрического поля
6.3.1 Указать размерность единицы потенциала электростатического поля
6.3.2 Определить электрический потенциал на поверхности сферы радиусом 5 см
6.3.3 При сообщении металлической сфере радиусом 10 см некоторого заряда
6.3.4 Определить напряженность электрического поля в точке, находящейся на расстоянии
6.3.5 На расстоянии 10 м от центра заряженного металлического шара радиусом 3 м
6.3.6 Определить потенциал шара радиусом 10 см, находящегося в вакууме
6.3.7 Металлический шар диаметром 30 см заряжен до потенциала 5400 В. Чему равен
6.3.8 На расстоянии 1 м от центра заряженного металлического шара радиусом 3 м
6.3.9 Найти потенциал электрического поля в точке, лежащей посредине между двумя
6.3.10 Сколько электронов следует передать металлическому шарику радиусом 7,2 см
6.3.11 Определить разность потенциалов (по модулю) между точками, отстоящими
6.3.12 Расстояние между точечными зарядами 10 и -1 нКл равно 1,1 м. Найти
6.3.13 В двух вершинах равностороннего треугольника со стороной 0,5 м находятся
6.3.14 Капля росы в виде шара получилась в результате слияния 216 одинаковых капелек
6.3.15 Электрический пробой воздуха наступает при напряженности поля 3 МВ/м
6.3.16 Два одинаковых точечных заряда по 5 мкКл взаимодействуют с силой 10 Н
6.3.17 Два металлических шара, радиусы которых 5 и 15 см, расположенные далеко друг
6.3.18 Энергия 10^(-17) Дж, выраженная в эВ, составляет
6.3.19 Модуль напряженности однородного электрического поля равен 150 В/м. Какую
6.3.20 На какое расстояние вдоль силовой линии перемещен заряд 1 нКл, если
6.3.21 При лечении статическим душем к электродам электрической машины приложена
6.3.22 Электрическое поле в глицерине образовано точечным зарядом 9 нКл. Какую работу
6.3.23 Два шарика с зарядами 0,8 и 0,5 мкКл находятся на расстоянии 0,4 м. До какого
6.3.24 Какая совершается работа при перенесении точечного заряда 20 нКл из бесконечности
6.3.25 Потенциал заряженного металлического шара 45 В. Какой минимальной скоростью
6.3.26 Две равномерно заряженные проводящие пластины образовали однородное поле
6.3.27 Напряженность поля внутри конденсатора равна E. Найти работу перемещения заряда
6.3.28 На сколько изменится потенциальная энергия взаимодействия зарядов 25 и -4 нКл
6.3.29 Два одинаковых маленьких шарика, имеющих одинаковые заряды 2 мкКл, соединены
6.3.30 На расстоянии 90 см от поверхности шара радиусом 10 см, несущего положительный
6.3.31 Электрон переместился из точки с потенциалом 200 В в точку с потенциалом 300 В
6.3.32 Электрон вылетает из точки, потенциал которой 600 В, со скоростью 12 Мм/с
6.3.33 Электрон с начальной скоростью 2000 км/с, двигаясь в поле плоского конденсатора
6.3.34 В поле неподвижного точечного заряда 1 мкКл по направлению к нему движется
6.3.35 Электрическое поле в вакууме образовано точечным зарядом 1,5 нКл. На каком
6.3.36 Электрическое поле в глицерине образовано точечным зарядом 20 нКл. На каком
6.3.37 Между двумя горизонтально расположенными пластинами, заряженными до 10 кВ
6.3.38 Заряженная частица, пройдя ускоряющую разность потенциалов 600 кВ, приобрела
6.3.39 Электрическое поле образовано двумя параллельными пластинами, находящимися
6.3.40 Пылинка массой 4×10^(-12) кг и зарядом 10^(-16) Кл попадает в поле заряженного
6.3.41 Пылинка массой 10 нг покоится в однородном электростатическом поле между
6.3.42 Электрон с некоторой скоростью влетает в плоский конденсатор параллельно
6.3.43 Какую разность потенциалов должен пройти первоначально покоящийся электрон
6.3.44 Какую скорость может сообщить электрону, находящемуся в состоянии покоя
6.3.45 Заряд 5 нКл находится на расстоянии 0,45 м от поверхности шара диаметром 0,1 м
6.3.46 Два электрона движутся под действием сил электростатического отталкивания
6.3.47 Между катодом и анодом двухэлектродной лампы приложена разность потенциалов
6.3.48 Энергия 100 эВ в системе СИ равна
6.3.49 Найти скорость, которую приобретает электрон, пролетевший в электрическом поле
6.3.50 В углах квадрата со стороной 4 см поместили 4 электрона. Под действием электрических
6.3.51 Электрон, ускоренный разностью потенциалов 5 кВ, влетает в середину зазора между
6.3.52 Маленький металлический шарик массой 1 г и зарядом 100 нКл брошен издалека
6.3.53 В электронно-лучевой трубке поток электронов с кинетической энергией 8 кэВ
6.3.54 В закрепленной металлической сфере радиусом 1 см, имеющей заряд -10 нКл
6.3.55 В зазор между пластинами плоского конденсатора влетает электрон, пройдя перед
6.3.56 Неподвижно закрепленный шарик, заряженный положительно, находится над шариком
6.3.57 Заряды q1=2 мкКл и q2=5 мкКл расположены на расстоянии AB=40 см друг от друга
6.3.58 Шарик массой 10 г с зарядом 100 мкКл подвешен на тонкой нити длиной 50 см
6.3.59 Внутри шарового металлического слоя, внутренний и внешний радиусы которого
6.3.60 По тонкому проволочному кольцу радиуса 3 см равномерно распределен заряд 10^(-9) Кл
6.3.61 Какую работу необходимо совершить, чтобы три одинаковых точечных положительных
6.3.62 В центре закрепленной полусферы радиуса R, заряженной равномерно с поверхностной
6.3.63 В центре закрепленной полусферы радиуса R, заряженной равномерно
6.3.64 На тонком закрепленном кольце радиуса R равномерно распределен заряд q. Какова
Электроемкость. Плоский конденсатор. Соединение конденсаторов. Энергия электростатического поля
6.4.1 Указать размерность единицы электроемкости
6.4.2 Проводник электроемкостью 10 пФ имеет заряд 600 нКл, а проводник электроемкостью
6.4.3 Два металлических шара радиусами 6 и 3 см соединены тонкой проволокой. Шары
6.4.4 Шар радиусом 0,3 м, заряженный до потенциала 1000 В, соединяют проводником
6.4.5 Проводники, заряженные одинаковым зарядом, имеют потенциалы 40 и 60 В
6.4.6 Тысяча одинаковых шарообразных капелек ртути заряжены до одинакового потенциала
6.4.7 Шар радиусом 15 см, заряженный до потенциала 300 В, соединяют проволокой
6.4.8 Шарообразная капля, имеющая потенциал 2,5 В, получена в результате слияния двух
6.4.9 Плоский воздушный конденсатор состоит из двух пластин площадью 100 см2 каждая
6.4.10 Определить площадь пластин плоского воздушного конденсатора электроемкостью 1 мкФ
6.4.11 Плоский конденсатор составлен из двух круглых пластин диаметром 0,54 м каждая
6.4.12 Плоский воздушный конденсатор погрузили в керосин. Во сколько раз изменилась
6.4.13 Плоский конденсатор состоит из двух пластин площадью 50 см2 каждая. Между
6.4.14 Во сколько раз изменится электроемкость плоского конденсатора при уменьшении
6.4.15 Плоский конденсатор, площадь пластин которого 25×25 см2 и расстоянием между ними
6.4.16 Плоский воздушный конденсатор погрузили в воду так, что над водой находится девятая
6.4.17 Между пластинами плоского конденсатора по всей площади проложили слюду (диэлектрик)
6.4.18 Плоский воздушный конденсатор зарядили до 50 В и отключили от источника тока
6.4.19 Плоский воздушный конденсатор, заряженный до напряжения 200 В, отключили
6.4.20 Воздушный конденсатор емкостью 4 мкФ подключен к источнику 10 В. Какой заряд
6.4.21 Какой заряд пройдет по проводам, соединяющим пластины плоского воздушного конденсатора
6.4.22 Во сколько раз увеличится электроемкость плоского конденсатора, пластины которого
6.4.23 Две пластины конденсатора площадью 2 дм2 находятся в керосине на расстоянии 4 мм
6.4.24 Напряжение на батарее из двух последовательно включенных конденсаторов
6.4.25 Батарея из двух последовательно соединенных конденсаторов электроемкостью
6.4.26 Два последовательно соединенных конденсатора с электроемкостью 1 и 3 мкФ подключены
6.4.27 Два плоских конденсатора электроемкостью по 2 мкФ каждый, соединенные последовательно
6.4.28 Два конденсатора электроемкостью 4 и 1 мкФ соединены последовательно и подключены
6.4.29 Два одинаковых плоских воздушных конденсатора соединены последовательно и подключены
6.4.30 Два одинаковых конденсатора соединены последовательно и подключены к источнику
6.4.31 Бумага пробивается при напряженности поля 18 кВ/см. Два плоских конденсатора с изолятором
6.4.32 Три конденсатора электроемкостью 0,1, 0,125 и 0,5 мкФ соединены последовательно
6.4.33 Три воздушных конденсатора емкостью 1 мкФ каждый соединены последовательно
6.4.34 Батарея из 5 последовательно соединенных конденсаторов емкостью 4 мкФ каждый
6.4.35 Определить электроемкость одного конденсатора, если для зарядки батареи, составленной
6.4.36 Конденсаторы электроемкостью 1 и 2 мкФ заряжены до разности потенциалов 20 и 50 В
6.4.37 Незаряженный конденсатор электроемкостью 5 мкФ соединяют параллельно с конденсатором
6.4.38 Плоский заряженный конденсатор соединили параллельно с незаряженным плоским
6.4.39 Шесть конденсаторов электроемкостью 5 нФ каждый соединили параллельно и зарядили
6.4.40 На батарею из трех параллельно соединенных конденсаторов электроемкостью
6.4.41 Конденсатор, заряженный до разности потенциалов 20 В, соединили параллельно разноименными
6.4.42 Найти общую электроемкость соединенных по схеме конденсаторов, если
6.4.43 Определить электроемкость батареи конденсаторов, изображенной на рисунке
6.4.44 Батарея из четырех одинаковых конденсаторов включена один раз по схеме A, другой раз по схеме B
6.4.45 Какое количество теплоты выделяется при замыкании пластин конденсатора электроемкостью
6.4.46 Какое количество теплоты выделяется при заземлении заряженного до потенциала 3000 В
6.4.47 Шар радиусом 25 см заряжен до потенциала 600 В. Какое количество тепла выделится
6.4.48 Плоский воздушный конденсатор после зарядки отключают от источника напряжения
6.4.49 Площадь пластины слюдяного конденсатора 36 см2, толщина слоя диэлектрика 0,14 см
6.4.50 На корпусе конденсатора написано 100 мкФ, 200 В. Какую максимальную энергию можно
6.4.51 При сообщении конденсатору заряда 5 мкКл его энергия оказалось равной 0,01 Дж
6.4.52 Два удаленных друг от друга одинаковых шара емкостью 4,7 мкФ каждый, заряжены
6.4.53 В импульсной фотовспышке лампа питается от конденсатора емкостью 800 мкФ, заряженного
6.4.54 Напряженность электрического поля конденсатора электроемкостью 0,8 мкФ равна 1 кВ/м
6.4.55 Определить работу, которую необходимо совершить, чтобы увеличить расстояние между пластинами
6.4.56 Парафиновая пластинка заполняет все пространство между обкладками плоского конденсатора
6.4.57 Определить количество электрической энергии, перешедшей в тепло при соединении одноименно
6.4.58 Три воздушных конденсатора электроемкостью 1 мкФ каждый соединены параллельно
6.4.59 Плоский конденсатор имеет в качестве изолирующего слоя пластинку из слюды толщиной
6.4.60 Два одинаковых плоских конденсатора электроемкостью 1 мкФ соединены параллельно
6.4.61 Конденсаторы соединены в батарею, причем C1=C2=2 мкФ, C3=C4=C5=6 мкФ
6.4.62 Принимая протон и электрон, из которых состоит атом водорода, за точечные заряды
6.4.63 Плоский воздушный конденсатор, площадь пластин которого равна S, заряжен
6.4.64 Два одинаковых плоских воздушных конденсатора соединены последовательно и подключены
6.4.65 Три одинаковых конденсатора соединены, как показано на рисунке. При разности
6.4.66 Три одинаковых конденсатора соединены, как показано на рисунке. При
6.4.67 Три одинаковых конденсатора соединены, как показано на рисунке. При разности потенциалов
6.4.68 Площадь каждой пластины плоского вакуумного конденсатора S. Конденсатор заряжен
( 42 оценки, среднее 4.55 из 5 )