В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить объем сегмента шара, а также разберем пример решения задачи для закрепления теоретического материала.
- Определение сегмента шара
-
Формулы для нахождения объема шарового сегмента
- Через радиус шара и высоту сегмента
- Через радиус основания сегмента и его высоту
-
Пример задачи
Определение сегмента шара
Сегмент шара (или шаровый сегмент) – это часть шара, отсеченная плоскостью. На чертеже ниже закрашен зеленым цветом.
- R – радиус шара;
- r – радиус основания сегмента;
- h – высота сегмента; это длина перпендикуляра от центра его основания (точка O2) до точки на поверхности шара.
Формулы для нахождения объема шарового сегмента
Пояснения:
- В формулах ниже используется радиус шара (R) или радиус основания сегмента (r). Поэтому, если изначально дан их диаметр (d), то чтобы найти требуемый радиус, нужно соответствующий диаметр разделить на два.
- Число π округленно равняется до 3,14.
Через радиус шара и высоту сегмента
Чтобы найти объем (V) сегмента шара, необходимо знать радиус шара и высоту сегмента.
Через радиус основания сегмента и его высоту
Вычислить объем (V) шарового сегмента можно, зная его высоту и радиус основания (круга).
Данная формула получена следующим образом:
Радиус шара можно выразить через радиус основания сегмента и его высоту:
Таким образом, заменив R в первой формуле для расчета объема на выражение выше, получаем:
Пример задачи
Найдите объем сегмента шара, если известно, что его высота равняется 4 см, а радиус шара – 9 см.
Решение
В данном случае с учетом известных значений нам подходит первая формула:
Шаровым сегментом называется часть шара, отсекаемая от него плоскостью.
Рисуется большой круг.
|
|
|
Круг с центром (A) — основание шарового сегмента. (AC = r) — радиус основания шарового сегмента,
(AB = H) — высота шарового сегмента,
(OC = R) — радиус шара.
Площадь сферического сегмента вычисляется по формуле
Объём шарового сегмента вычисляется по формуле
(V(сегм.) =)
πH2
·(R
−H3)
, где (R) — радиус шара, (H) — высота шарового сегмента.
В формулах для сегмента не используется радиус основания сегмента, а используется радиус шара.
Источники:
Рисунки © Якласс
Как найти объем шарового сегмента?
Шаровой сектор — это часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью, основанием которой служит основание сегмента, а вершиной — центр шара. Формула объема шарового сектора: V = (2/3)*πR²*h, где h — высота сегмента.
Что такое шаровой сегмент?
Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Рисуется большой круг. Круг с центром A — основание шарового сегмента.
Как вычислить объем шара формула?
Формула для вычисления объема шара Объем шара равен четырем третим от его радиуса в кубе помноженого на число пи. где V — объем шара, R — радиус шара, π = 3.
Как найти высоту сегмента шара?
S=πR(2h+r), где h − высота соответствующего шарового сегмента, r − радиус основания шарового сегмента (или конуса), R − радиус шара.
Как найти хорду в окружности?
Формула длины хорды окружности
- α = градус
- α = радиан
- α = x / радиан
Как найти сегмент круга?
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой. P=s+a, где s − длина дуги, a − длина хорды.
Как вычислить площадь сегмента круга?
Площадь сегмента круга
- α = градус
- α = радиан
- α = x / радиан
Как вычислить окружность круга?
Диаметр круга рассчитывается по следующим формулам:
- Если нам известна длина: Формула для расчета диаметра круга через его длину: D=P/π
- Если нам известна площадь: Формула для расчета диаметр круга через площадь: D=2√S/π
- Если нам известен диаметр: Формула для расчета диаметр круга через радиус: D=2R.
Что такое круговой сегмент как можно вычислить его площадь?
Можно воспользоваться приближенной формулой вычисления площади кругового сегмента: S=2/3*(a*h), где a – основание треугольника или длина хорды, h – высота сегмента, которая является результатом разности между радиусом круга и высотой равнобедренного треугольника. … Как правило, за основу берется треугольник.
Как найти площадь сегмента формула?
Площадь сегмента можно найти как разность площадей сектора круга и этого равнобедренного треугольника.
Что такое круговой сегмент?
Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
Что такое сегмент в математике?
Сегмент — (от лат. segmentum отрезок, полоса, от seco режу, рассекаю) часть чего либо. В математике Сегмент, или отрезок множество точек прямой, включающее свои концы.
Что такое сегмент в биологии?
Сегмент (биология) — части тела, похожие по строению и расположенные последовательно вдоль продольной оси тела.
Что такое сегмент по анатомии?
segmentum — «отрезок») — анатомический комплекс, состоящий из двух смежных позвонков с соответствующими суставами и мышечно-связочным аппаратом на этом уровне, и одного межпозвонкового диска между этими позвонками. травматологии, мануальной терапии, рентгенологии и др. специальностях медицины.
Что означает слово сегмент?
Сегмент, или отрезок — множество точек прямой, включающее свои концы. Сегмент (геометрия) — плоская фигура, заключённая между кривой и её хордой. Сегмент (стереометрия) — часть тела, ограниченная плоскостью и отсекаемой ею частью поверхности. Как частный случай: шаровой сегмент.
Что такое сегментация целевой аудитории?
Сегментирование целевой аудитории – это разделение аудитории на группы, где они объединены по признаку схожих потребностей (запросов).
Что такое сегмент в бизнесе?
Область рынка, в которой компания имеет возможность занять лидирующие позиции. Бизнес—сегмент — область деятельности, направление специализации компании, в котором она получает и наращивает конкурентные преимущества.
Что такое сектор и сегмент?
Определение. Сектор (◔) — часть круга, которая ограничена двумя радиусами и дугой между этими радиусами. Определение. Сегмент — часть круга, которая ограничена дугой и хордой, что соединяет ее концы.
Что называется сектором?
Сектор круга — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Что такое сектор в информатике?
Се́ктор диска — минимальная адресуемая единица хранения информации на дисковых запоминающих устройствах (НЖМД, дискета, CD). Является частью дорожки диска. Первоначально у большинства устройств размер сектора составляет 512 байт (например, у жестких и гибких дисков), либо 2048 байт (например, у оптических дисков).
Что такое кластер на компьютере?
Кластер (англ. cluster) — в некоторых типах файловых систем — логическая единица хранения данных в таблице размещения файлов, объединяющая группу секторов. … Как правило, это наименьшее место на диске, которое может быть выделено для хранения файла.
Что такое сектор дорожка и кластер магнитного диска?
Сектор диска — минимальная адресуемая единица хранения информации на дисковых запоминающих устройствах (НЖМД, дискета, CD). Является частью дорожки диска. В случае FAT16 для диска объемом 512 Мб кластер будет составлять 8 Кб, до 1 Гб — 16 Кб, до 2 Гб — 32 Кб и так далее. …
Что такое кластер по литературе?
Кластер — это графическая форма организации информации, когда выделяются основные смысловые единицы, которые фиксируются в виде схемы с обозначением всех связей между ними. Он представляет собой изображение, способствующее систематизации и обобщению учебного материала.
Что такое цилиндр на жестком диске?
Цили́ндр у дискового накопителя — совокупность всех дорожек в заданном положении привода. В каждой позиции привода жёсткого диска каждая из головок может считывать свою дорожку (участок поверхности пластины в виде кольца).
Что такое дисковый накопитель?
Накопи́тель на жёстких магни́тных ди́сках, или НЖМД (англ. hard (magnetic) disk drive, HDD, HMDD), жёсткий диск, разг. винчестер — запоминающее устройство (устройство хранения информации, накопитель) произвольного доступа, основанное на принципе магнитной записи.
Сколько секторов в одной дорожке в адресации CHS?
Затем контроллеры стали сообщать, будто в дорожке 63 сектора, а на одной поверхности диска 255 дорожек (максимально допустимые значения), число же головок подбирается сообразно объёму.
Как определяется физический адрес сектора?
Информация на магнитных дисках размещается и передается блоками, которые называются секторами. … Физический адрес сектора на диске определяется триадой [c-h-s], где c — номер цилиндра (cylinder), h — номер рабочей поверхности диска (магнитной головки, head), s — номер сектора на дорожке (sector).
Объем шарового сегмента, формула
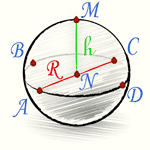
Часть шара, [шар, сфера] осекаемая от него какой-нибудь плоскостью, называется шаровым или сферическим сегментом. Основанием шарового сегмента называется круг ABCD. Высотой шарового сегмента называется отрезок NM, т.е. длина перпендикуляра, восстановленного из центра N основания до пересечения с поверхностью шара. Точка M называется вершиной шарового сегмента.
Объем шарового сегмента выражается формулой:
[ V = pi h^2 ( R — frac{1}{3} h ) ]
(R — радиус большого круга шара, h — высота шарового сегмента)
Формулы шара, сферы
Вычислить, найти объем шарового сегмента по формуле (1)
Объем шарового сегмента |
стр. 344 |
|---|
Поскольку шаровой сегмент представляет собой часть сферы, сечение которой находится под прямым углом к оси вращения, следовательно, становится возможным найти объем шарового сегмента, площадь поверхности, периметр сечения сферы и его диаметр, зная радиус и высоту шарового сегмента.
Диаметр шарового сегмента, также как и диаметр сферы, равен удвоенному радиусу тела.
d=2r
Периметр сечения сферы, образующего шаровой сегмент, является длиной окружности с заданным радиусом, и равен удвоенному произведению радиуса на число π.
P=2πr
Чтобы вычислить объем шарового сегмента через радиус и высоту, нужно найти треть произведения числа π и квадрата радиуса на разность утроенного радиуса и высоты.
V=(πh^2 (3R-h))/3
Найти площадь поверхности шарового сегмента, зная радиус и высоту, можно, умножив длину окружности, являющуюся периметром сечения сферы, на высоту шарового сегмента. Так как периметр сечения равен удвоенному произведению числа π и радиуса шарового сегмента, то формула площади поверхности шарового сегмента выглядит следующим образом:
S=2πrh