|
Найдите 2 высоту параллелограмма, если одна из его высот и сторон соответственно равны 10 и 5 см? Задача неопределенная, вторая высота может принимать любые значения в промежутке от 0 до 5. Начертите прямоугольник высотой 10 и шириной 5 см. Теперь Через вехнюю сторону (5 см) проведите бесконечную прямую. Теперь переместите эту сторону (5 см) по этой прямой вправо или влево на любое расстояние. Получите бесконечное число параллелограммов с самыми разными длинами боковых сторон и расстояний между ними, площадью 50 см^2. Знаете ответ? |
Как найти длину второй высоты параллелограмма, зная его площадь и одну высоту?
Параллелограмм — это четырехугольник, у которого противоположные стороны параллельны.
Для нахождения длины второй высоты параллелограмма, зная его площадь и одну высоту, нужно использовать формулу:
h2 = (2 * S) / b,
где h2 — искомая вторая высота, S — площадь параллелограмма, b — длина стороны параллелограмма, на которую опущена известная высота.
Пример:
Пусть дан параллелограмм с площадью 24 и известной высотой, опущенной на сторону длиной 6.
Тогда, подставляя значения в формулу, получим:
h2 = (2 * 24) / 6 = 8
Таким образом, длина второй высоты параллелограмма равна 8.
Используя данную формулу, можно легко находить длину второй высоты параллелограмма, зная его площадь и одну из высот.
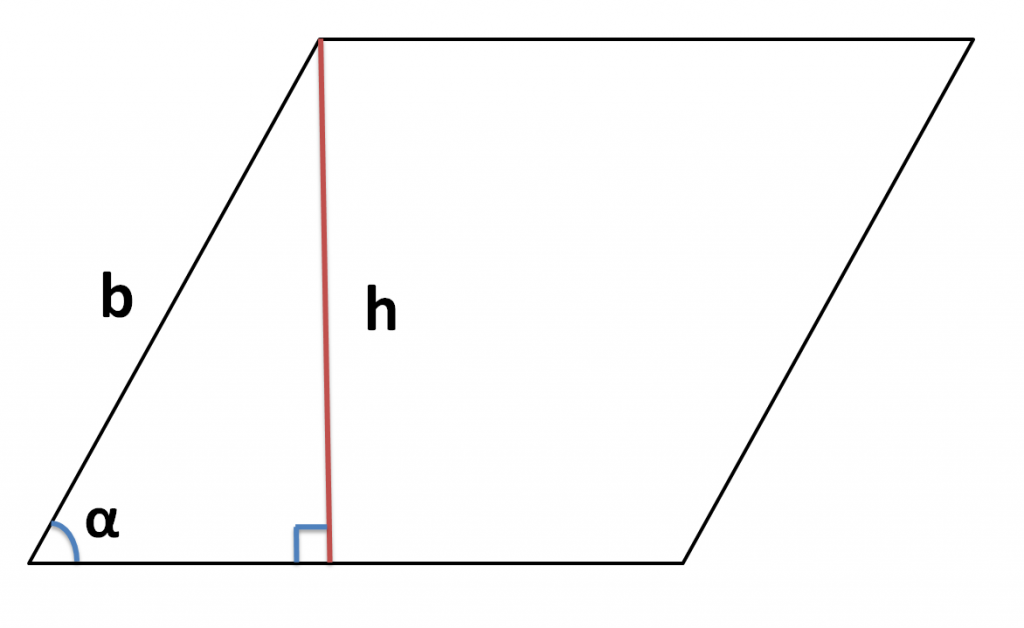
В параллелограмме могут быть проведены две высоты. Одна из них опускается из верхнего угла на противоположную, длинную сторону, разделяя параллелограмм на прямоугольный треугольник и прямоугольную трапецию. Вторая высота опускается на короткую сторону параллелограмма.
Образованный прямоугольный треугольник внутри параллелограмма дает возможность найти высоту через известную сторону параллелограмма и острый угол, находящийся напротив высоты. Если известен тупой угол, то рассчитать острый можно, отняв известный угол из 180°. Высота будет равна синусу противолежащего угла, умноженному на сторону параллелограмма:
h=a sinα
Формулировка задачи: Стороны параллелограмма равны M и N. Высота, опущенная на меньшую сторону, равна K. Найдите длину высоты, опущенной на большую сторону параллелограмма.
Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 15 (Задачи по планиметрии).
Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.
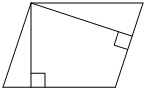
Пример задачи:
Стороны параллелограмма равны 10 и 12. Высота, опущенная на меньшую сторону, равна 6. Найдите длину высоты, опущенной на большую сторону параллелограмма.
Решение:
По условию задачи даны 2 стороны параллелограмма и одна из его высот. С помощью этих данных можно получить площадь параллелограмма:
S = 10 ⋅ 6 = 60
По второй стороне параллелограмма и площади можно получить искомую высоту:
H = 60 / 12 = 5
Ответ: 5
В общем виде решение данной задачи по планиметрии выглядит следующим образом:
S = a ⋅ h – площадь параллелограмма
H = S / b = a ⋅ h / b
где a – меньшая сторона, b – большая сторона, h – высота, опущенная на меньшую сторону, H – искомая высота.
Остается лишь подставить конкретные значения и подсчитать результат.
Поделитесь статьей с одноклассниками «Найдите длину высоты, опущенной на большую сторону параллелограмма – как решать».
При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.
Четырёхугольник, у которого стороны, находящиеся напротив друг друга параллельны и равны друг другу,
называется параллелограммом. Отрезок перпендикулярной прямой, проходящей от любой точки прямой, на
которой лежит одна из сторон параллелограмма через прямую, на которой расположена противоположная
сторона данной фигуры, является высотой параллелограмма. Высот параллелограмма можно провести
бесконечное множество через разные точки, но они неизменно будут перпендикулярны двум сторонам
фигуры.
- Высота параллелограмма через площадь и основание
- Высота параллелограмма через боковую сторону и острый угол
при основании - Высота параллелограмма через длину отрезка, образованного
на основании и боковую сторону - Высота параллелограмма через длину отрезка, образованного
на основании и диагональ
Через площадь и основание
Высота параллелограмма равна отношению площади к основанию.
h = S / a
где h – длина высоты параллелограмма, S – площадь, a – длина основания.
Цифр после
запятой:
Результат в:
Пример. На рисунке представлены пара абсолютно одинаковых параллелограммов. На левом
обозначена длина стороны (основания) в 6 единиц и проходящие через нее в разных точках высоты в 4
единицы.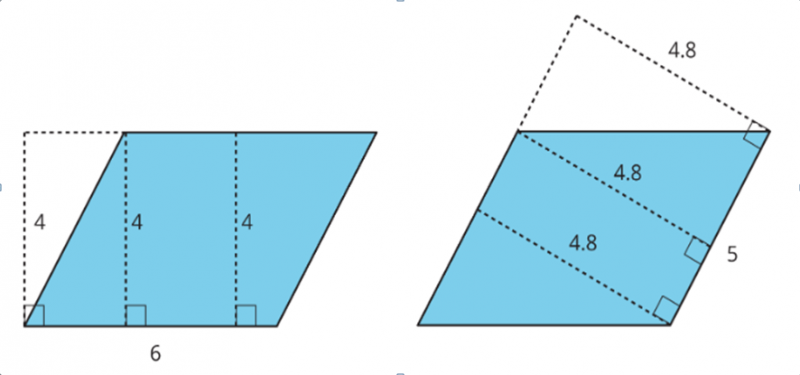
правом обозначена длина стороны (основания) в 5 единиц и проходящие через нее в разных точках высоты
в 4,8 единиц. Площадь параллелограмма можно вычислить умножением длины высоты на длину той стороны
(основания), которой эта высота перпендикулярна. Результат умножения будет одинаков для любой 2 двух
пар высота-основание. В рассматриваемом случае: 4 × 6 = 24; 4,8 × 5 = 24.
Можно визуально убедиться в этом, если разрезать фигуру и переставив части так, как показано на
рисунке.
Исходя из полученного, путем обратного подсчета можно вывести правило для определения высоты из
заданной площади и основания. В приведенном примере расчет будет выглядеть следующим образом: 24 / 6 = 4; 24 / 5 = 4,8.
Через длину отрезка, образованного на основании и диагональ
Вычисление высоты параллелограмма при известных длине отрезка образованного на основании и диагонали
производится также с использованием теоремы Пифагора. Высота в этом случае будет равна квадратному
корню из разницы диагонали и отрезка на основании.
h = √(d² — A2²)
где d — диагональ, A2 — отрезок образованный на основании.
Цифр после
запятой:
Результат в:
Пример. Пусть боковая сторона равна 47 см, отрезок образованный на основании равен
34 см, тогда получим h = √(b² — A1²) = √(47² — 34²) = 32,4 см.
Через боковую сторону и острый угол при основании
Если от тупого угла параллелограмма провести к основанию высоту, то образуется прямоугольный
треугольник, как показано на рисунке ниже. Если нам известна величина острого угла и длина боковой
стороны, то можно вычислить высоту через формулу синуса, который определяется как отношение катета к
гипотенузе. Роль катета здесь играет высота, а боковая сторона является гипотенузой. Соответственно
высота здесь будет равна произведению длины боковой стороны на синус острого угла.
h = b * sinα
где b — боковая сторона, sin α — острый угол при основании.
Цифр после
запятой:
Результат в:
Если известна величина тупого угла параллелограмма, то величину острого можно получить, отняв
величину тупого угла от 180 градусов.
Пример. Пусть боковая сторона b равна 115 см, острый угол при основании α равен 65º,
тогда получим h = b * sinα = 115 * sin 65 = 104 см.
Через длину отрезка, образованного на основании и боковую сторону
Вычисление высоты параллелограмма при известных длине отрезка образованного на основании и боковой
стороне производится с использованием теоремы Пифагора. Высота будет равна квадратному корню из
разницы квадратов боковой стороны и диагонали.
h = √(b² — A1²)
где b — боковая сторона, A1 — отрезок образованный на основании.
Цифр после
запятой:
Результат в:
Пример. Пусть боковая сторона равна 39 см, отрезок образованный на основании равен
16 см, тогда получим h = √(b² — A1²) = √(39² — 16²) = 35,6 см.
Пирамида определяется как трехмерная структура – многогранник, в основе которой лежит многоугольник.
В основании пирамиды находится многоугольник. Углы многоугольника соединены линиями – боковыми
ребрами с одной точкой, которая в пирамиде именуется как вершина. Треугольники, образованные парами
соседних боковых ребер и стороной основания называются боковыми гранями.
В основании правильной пирамиды лежит правильный многоугольник (тот у которого все стороны равны
между собой). У правильной пирамиды длина боковых ребер одинаковая. Соответственно правильная
пирамида образована боковыми гранями, являющимися равными равнобедренными треугольниками,
соединенными с основанием.
Апофемами в пирамиде называют отрезки прямых, проведенных от вершины перпендикулярно к основаниям.
Также, одновременно апофемы являются высотами треугольников – боковых граней.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на
апофему грани.
Установлено, что умение вычислять длину апофемы, было востребовано с древнейших времен для
строительства сооружений. Предположительно, перед возведением подобных сооружений предварительные
размеры могли быть отрегулированы древними инженерами с помощью натянутых шнуров. Расшифровка
древнеегипетских иероглифов дает перевод значения понятия землемера как «натяжителя веревок».
Умение вычислять высоту параллелограммов, было востребовано с древнейших времен для проверки
правильности измерений земельных участков. Множество древних народов тысячи лет назад воздвигали
пирамиды и курганы для различных целей. Современные измерения позволяют утверждать, что некоторые их
них точно ориентированы – как по сторонам света, так и в трехмерном измерении по созвездиям.
Вероятно, часть из этих сооружений использовалась для определения орбиты Земли относительно звезд.
Эти сведения использовались для определения времени начала различных сельскохозяйственных работ. От
этого зависела урожайность, а значит вопрос выживания народов. Таким образом, вычисление апофемы
позволяло точно ориентировать пирамиду в пространстве и спасало жизни людей.