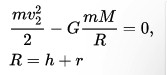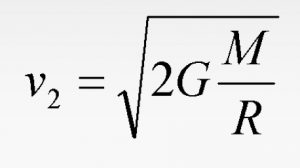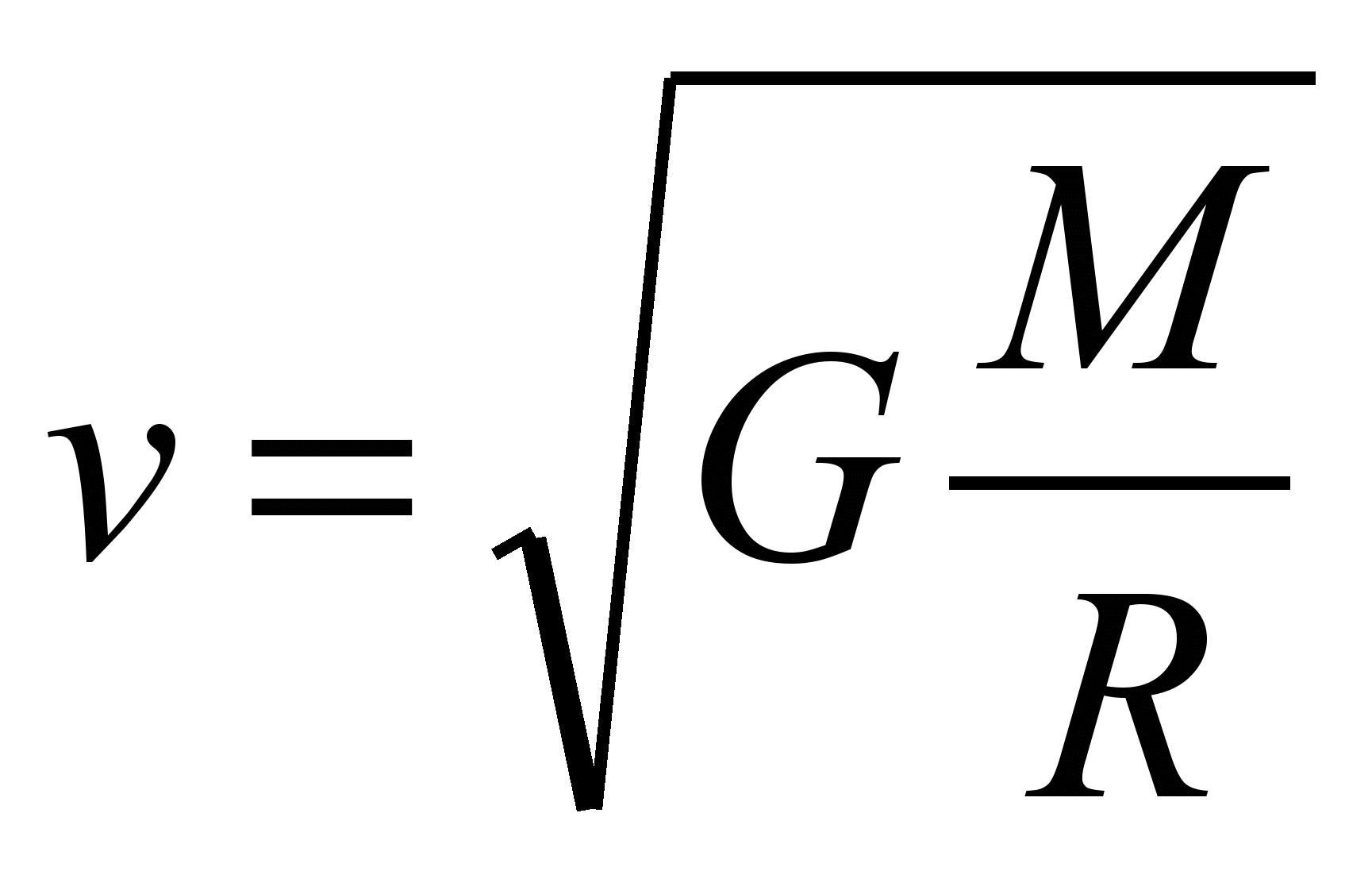Вторая космическая скорость юпитера как найти

Из школьного курса физики мы помним, что первая космическая скорость Земли – это показатель, которого необходимо достичь, чтобы объект мог выйти на эллиптическую орбиту вращения вокруг планеты. Это же, собственно, касается и любого массивного космического тела. В свою очередь, вторая космическая скорость – это предел, необходимый для того, чтобы полностью покинуть гравитационное поле планеты.

Вторая космическая скорость зависит от ряда параметров и для каждого космического объекта – отличается. Давайте рассмотрим, по какому принципу она вычисляется, и разберем примеры для крупных планет Солнечной Системы, Солнца и Луны. 

Как рассчитать вторую космическую скорость

Вторая космическая скорость зависит от массы и радиуса небесного тела. Условно можно себе представить, что для ее расчета можно пойти от обратного решения задачи. То есть, вычислить скорость с какой объект будет падать на планету из космоса. По модулю это и будет вторая космическая скорость.

Итак, учитывая закон сохранение кинетической и потенциальной энергий при движении тел, можно вывести такую формулу в падающем объекте на небесное тело:

Где m – масса стартующего объекта, М – масса небесного тела, R – сумма радиуса планеты и высоты расположение объекта над поверхностью, G – гравитационная постоянная, V – искомая вторая космическая скорость. Таким образом, из формулы можно вычислить V:

 Это и будет решение нашей задачи со знанием всего двух параметров – радиуса небесного тела и его массы.

Вторая скорость для разных небесных тел

Итак, попробуем на основании выведенной формулы рассчитать вторую космическую скорость для разных небесных тел Солнечной Системы, учитывая что их радиус и массу мы знаем.

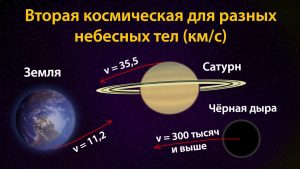
Начнем с самого простого – Земли. Радиус нашей планеты равен 6,37 тысяч километров, а масса – 5,97 х 10²³ кг. Подставляем в нашу формулу и получаем – вторая космическая скорость Земли равна 11,2 километра в секунду. Именно до таких цифр нужно разогнать гипотетический объект, чтобы он покинул зону гравитационного притяжения нашей планеты.

Теперь можно перейти к нашей звезде и посчитать вторую космическую скорость для Солнца. Радиус его равен 696 тысяч километров, а масса 1,989 х 10³⁰ кг. Расчеты по формуле дают результат в 617,7 километров в секунду! До такой скорости нужно разогнать предмет, чтобы он смог покинуть нашу Солнечную Систему и попасть в межзвездное пространство.

Теперь попробуем вычислить показатель для остальных планет системы. Итак, радиус и масса Меркурия составляют соответственно 2,438 тысяч километров и 330 х 10²¹ кг. Подставив в формулу цифры, получаем вторую космическую скорость Меркурия 4,3 км/с. 

Идем далее и получаем такие цифры – вторая космическая скорость Венеры – 11,2 километров в секунду, Марса – 5,0 км/с, Юпитера – 61 км/с, Сатурна – 36 км/с, Нептуна – 24 км/с, Урана – 22 км/с, Луна – 2,4 км/с.

Таким образом, мы видим, что преимущественно чем массивнее планета (а вернее, чем плотнее, потому что радиус тоже важен) – тем больше нужна скорость, чтобы объект мог вырваться за пределы гравитационного влияния.

Показательными и интересными также являются примеры третей и четвертой космических скоростей. Что это за параметры? Если говорить грубо – то третья космическая скорость, это вторая космическая для Солнца, но высчитываемая вблизи Земли. Простыми словами – какую скорость нужно развить с Земли, чтобы покинуть Солнечную Систему? Посчитав по формуле, получим 16,65 километров в секунду.

Четвертая космическая скорость показывает, до какой цифры нужно разогнаться чтобы покинуть галактику из заданной точки. Для Млечного пути этот показатель будет разным в зависимости от выбранной координаты. Ближе к центральной сверхмассивной черной дыре он будет гигантским, ближе к периферии галактики – меньше. Примерно в области нашей Солнечной Системы четвертая космическая скорость равна 550 километрам в секунду!

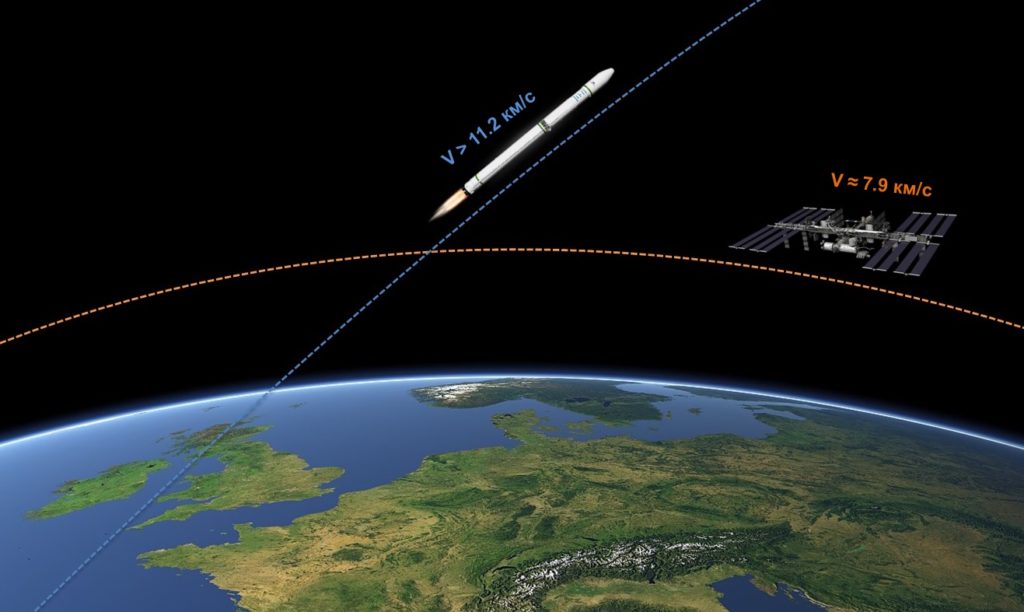
Если мы подбросим камень в воздух – он упадет на Землю. Если у самолета на высоте 10 километром отключаться двигатели – он тоже упадет на Землю. Но спутники и космические корабли, что мы запускаем в космос, не падают. Почему?

Все дело в том, с какой скоростью тот или иной объект удаляется от планеты. Хватит ли этому объекту энергии преодолеть притяжение планеты.

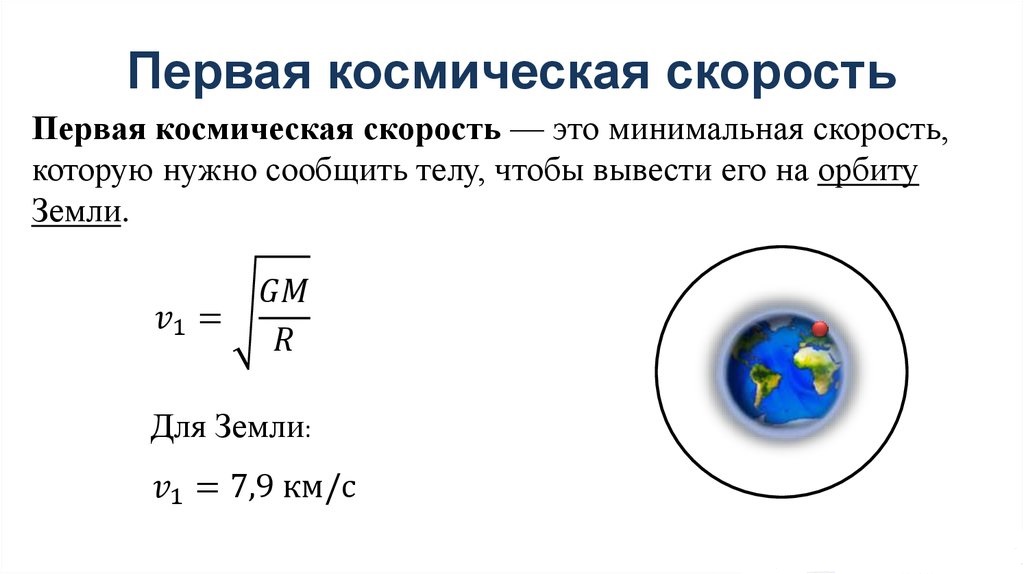
Первая космическая скорость

Это та самая минимальная скорость для выхода корабля или спутника на круговую орбиту, равную радиуса планеты, без учета вращения планеты и сопротивления ее атмосферы.

Если скорость будет превышать первую, но не достигнет второй космической скорости, то траектория тела из круговой начнет переходить в эллиптическую.

Впервые такую скорость смог достичь первый искусственный спутник Земли «Спутник-1» СССР 4 октября 1957 года.

Расчет

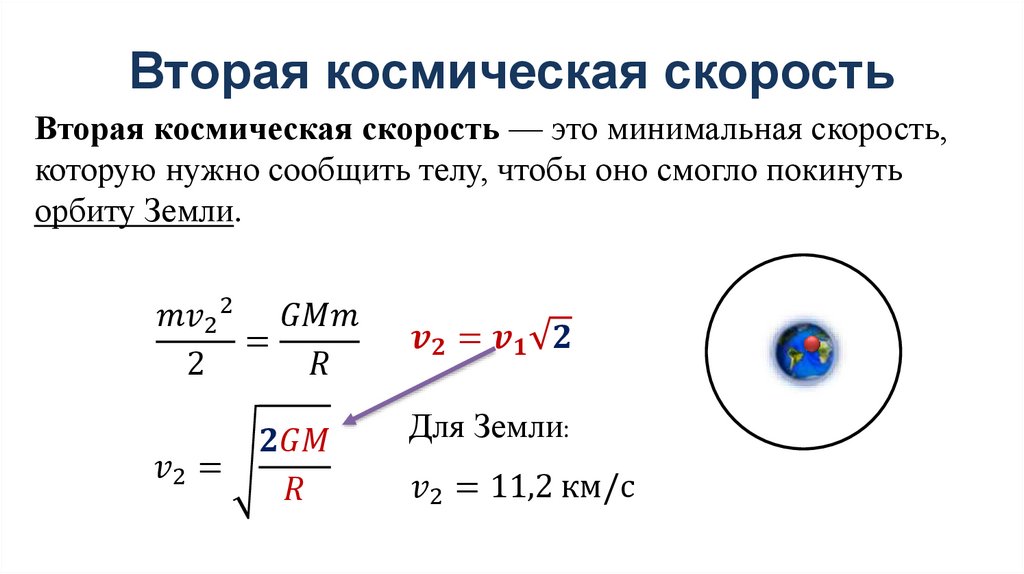
Вторая космическая скорость

Это минимальная скорость, которую следует придать телу для того, чтобы оно покинуло замкнутую орбиту и смогло улететь от небесного тела за пределы его гравитационного поля.

Иными словами, для Земли, это та скорость, с которой должны двигаться космические аппараты (КА) для полетов к другим объектам Солнечной системы: Луны, Марса и т.д.

Движение тела на второй космической скорости происходит по параболической траектории.

Впервые такую скорость развил Советский космический аппарат Луна-1 2 января 1959 года, чтобы преодолеть расстояние от Земли до Луны и изучить наш естественный спутник.

Расчет

Третья космическая скорость

Такую скорость необходимо придать телу, чтобы оно смогло покинуть Солнечную систему. Так как 99,8% массы Солнечной системы приходится на Солнце, то можно сказать, что КА надо преодолеть гравитационное притяжение Солнца.

Расчет

Для Солнечной системы это величина равна 16,650 км/с.

Самое выгодное расположение космодрома для подобного запуска – максимально близко к экватору, так как на экваторе самая большая скорость собственного вращения Земли вокруг своей оси и направление движения в сторону вращения Земли и в сторону орбитального движения Земли по орбите.

КА «Новые горизонты» покинул атмосферу Земли со скоростью близкой к третьей космической – 16,26 км /с. Относительно Солнца он имел скорость 45 км/с. Такой скорости недостаточно, чтобы покинуть Солнечную систему. Но благодаря гравитационному маневру у Юпитера, «Новые горизонты» добавил еще 4 км/с, что позволило ему покинуть Солнечную системы, предварительно показав нам карликовую планету Плутон.

Четвертая космическая скорость

Эта та скорость, которая позволит покинуть галактику в данной точке.

Четвертая космическая в основном не зависит от месторасположения Земли в Млечном пути. Она зависит от расположения и плотности звездного вещества в окрестностях Солнечной системы. А эти данные пока мало изучены.
Для нашей части галактики четвертая космическая скорость примерно равна 550 км/с.

Пятая космическая скорость

Эта скорость редко применима и является больше «фантазией», так как такую скорость необходимо развить для путешествия на другую планету в другую звездную систему, независимо от их взаимного расположения, с траекторией перпендикулярно плоскости эклиптики.

Для Земли эта скорость будет равна 43,6 км/с.

Почему спутники не падают на Землю

Этот вопрос поднимался в самом начале статьи. Теперь давайте на него ответим.

На спутник на орбите действует сила тяжести со стороны Земли. И под действием этой силы спутнику логичнее упасть.
Но, он летит вокруг Земли с первой космической скоростью – 7,9 км/с. Вспомните, чем больше скорость – тем сложнее затормозить. Вот и здесь, спутник и хотел бы упасть, но он не может затормозить и просто пролетает мимо Земли по инерции, тем самым продолжая бесконечное падение.

То есть, спутники падают, но промахиваются и не попадают в Землю.

Еще больше космоса и интересных фактов в телеграмм-канале.

Задания

Версия для печати и копирования в MS Word

В астрономии и динамике космических полётов используются понятия трёх космических скоростей. 

Первой космической скоростью (или круговой скоростью) называется наименьшая начальная скорость, которую нужно сообщить телу, чтобы оно стало искусственным спутником Земли (ИСЗ).

Второй космической называется скорость, обладая которой, космический аппарат(КА) может преодолеть притяжение Земли.

Третьей космической является скорость преодоления притяжения Солнца, то есть скорость, с которой космический аппарат может покинуть пределы Солнечной системы.

ИСЗ выводятся на орбиту с помощью многоступенчатых ракет. Последняя ступень ракеты сообщает спутнику определённую скорость на заданной высоте h от поверхности Земли. Тело станет ИСЗ, если его скорость будет достаточной.

Если скорость запуска точно равна круговой скорости на данной высоте h, то тело будет двигаться по круговой орбите. Если скорость превышает круговую, то тело будет двигаться по эллиптической траектории, причём перигей эллипса окажется в точке выхода на орбиту.

Macca спутника очень мала по сравнению с массой Земли (m << M). Круговая скорость спутника на высоте h будет определяться относительно расстояния от центра Земли г = R + h ( где R — это средний радиус Земли, при чем h << R), тогда первая космическая скорость может быть вычислена исходя из формул Второго закона Ньютона

и Закона всемирного тяготения

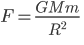
отсюда

Так как нормальное ускорение определяется по формуле

тогда

сократив на m и R, получим

тогда

где G — гравитационная постоянная 6,67 х 10^-11(м³/кг с² ) М — масса Земли 6 х 10²⁴кг, R- её радиус 6,37 х 10⁶ м.

Это формула справедлива для вычисления первой космической скорости и для других планет.

Траектория космического аппарата состоит из двух основных участков: активного и пассивного. Движение на активном участке определяется тягой реактивных двигателей и притяжением Земли. Пассивный участок начинается с момента выключения двигателя последней ступени. На пассивном участке космический аппарат движется под действие притяжения Земли и других тел Солнечной системы.

Для того, чтобы космический аппарат преодолел притяжение Земли и ушёл в космическое пространство, необходимо в начале пассивного участка сообщить ему вторую космическую скорость. Вторая космическая скорость вычисляется на основания закона сохранения энергии

где Еk — кинетическая энергия, а Ер — потенциальная энергия, отсюда

Для того, чтобы космический аппарат, преодолев притяжение Земли и войдя в сферу действия Солнца, не упал на его поверхность, он должен иметь в этот момент скорость относительно Солнца, отличную от нуля.

Минимальная скорость v₃ = 16,6 км/с называется третьей космической скоростью относительно Земли. Скорость, при которой запущенный с Земли космический аппарат может уйти за пределы Солнечной системы, сильно зависит от направления выхода аппарата из сферы действия Земли по отношению к направлению орбитального движения Земли.

Гипотетически можно определить ещё и четвёртую космическую скорость выхода за пределы галактики Млечный путь.

Космическая эра

Первый искусственный спутник

Первым искусственным спутником  Земли стал выведенный на орбиту 4 октября 1957 года советский Спутник-1. Первый шарообразный спутник вышел на орбиту, передав обратно сигнал об успешном старте. Единственной целью его запуска была проверка теорий. Устройство представляло собой две сваренные полусферы из магниевого сплава и четыре стабилизатора, параллельно играющие роль передающих антенн. Общая масса устройства не превышала 88.5 кг.

Первый запуск космического аппарата

Первым  космическим аппаратом, вышедшим на орбиту, стал также советский Спутник-5. В нём летели специально обученные собаки Белка и Стрелка. Они благополучно вернулись на землю 19 августа 1960 года.

Человек в космосе

12 апреля 1961 года корабль Восток-1 успешно вывел на орбиту Земли первого в мире человека. Космический аппарат сделал виток вокруг Земли и благополучно приземлился с находящимся в нём гражданином Советского Союза Юрием Алексеевичем Гагариным.

Первая высадка на Луну

В 1969 году NASA запустили миссию Апполон-11, совершившую высадку на Луну. Первым человеком, ступившим на поверхность спутника, стал Нил Армстронг. Пребывание в этих условиях длилось 2.5 часа, после чего был осуществлён возврат на Землю.

Основоположники космонавтики

Константин Эдуардович Циолковский

изобретатель, философ, учёный, разрабатывавший теоретические вопросы космонавтики, мыслитель, занимавшийся философскими проблемами освоения космоса. Циолковского называют отцом русской космонавтики. Стоял у истоков зарождения теоретической космонавтики, первым нашел обоснование для применения ракет в космических полетах, доказал необходимость использования так называемых «ракетных поездов», которые были прототипом современных многоступенчатых ракет.

Он рассчитал и доказал достижение ракетой космической скорости. Циолковский задумался о создании искусственного спутника Земли. Роль Циолковского в космонавтике, и в астрономии в целом, огромная.

Сергей Павлович Королев

Советский конструктор, разработчик ракетно-космических комплексов. Внес огромный вклад в отечественное ракетостроение и покорение космоса.Имя выдающегося конструктора Сергея Королева известно во всем мире. В историю он вошел, как талантливый ученый, положивший начало развитию отечественной космонавтики. Результаты изысканий Сергея Павловича по сей день применяются в ракетостроении и ряде смежных областей.

В конце 1929-го изобретатель познакомился с Константином Циолковским, и это стало самым знаковым событием в биографии молодого конструктора. Ученый подарил коллеге книгу «Космические ракетные поезда» и посоветовал ему заняться изучением космических полетов.
Королев вел активную деятельность по разработке многоступенчатых ракет межконтинентальной серии. Конструктор разработал баллистическую ракету Р-7 дальностью 8000 км., а позже и ее модернизированный вариант – Р-7А, способную преодолевать расстояние до 12000 км.
Сергей Павлович занимался конструированием космических летательных аппаратов. В октябре 1957 года под его руководством был запущен первый в истории человечества искусственный спутник Земли. В 1960 году на орбиту вывели КА с собаками на борту.

12 апреля 1961 года Королев и его команда отправили в космос Юрия Гагарина.
При жизни конструктор поучаствовал в еще семи запусках пилотируемых космических аппаратов. Помимо этого, в космос были отправлены десятки спутников, позволивших собрать бесценные научные данные. В конце трудовой биографии Сергей Павлович разрабатывал программы по покорению Марса и Луны.

Межпланетные полёты

Для полётов космических аппаратов к другим планетам и телам Солнечной системы необходимо производить очень точные расчёты траекторий с использованием законов небесной механики. При их запуске исходят из трёх основных соображений. Во-первых, геоцентрическая скорость космического аппарата при выходе на орбиту относительно Земли должна превышать вторую космическую скорость. Во-вторых, после преодоления притяжения Земли гелиоцентрическая орбита аппарата должна пересекаться с орбитой данной планеты (или другого небесного тела). А также необходимо подобрать такой момент запуска, чтобы орбита аппарата была наиболее оптимальной с точки зрения сроков полёта, затрат топлива и ряда других требований.

Одним из классов межпланетных траекторий являются энергетически оптимальные орбиты, которые соответствуют наименьшей геоцентрической скорости космических аппаратов в момент достижения границы сферы действия Земли.

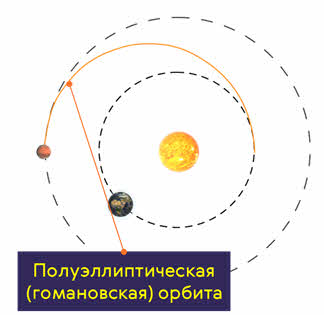
Рассмотрим одну такую орбиту на примере Марса. Для простоты будем считать, что орбиты Марса и Земли являются круговыми. Для оптимального запуска нужно выбрать такой момент, когда орбитальная скорость Земли и скорость космического аппарата будут сонаправлены. При этом запускаемый аппарат и Марс, двигаясь по своим орбитам, должны одновременно достигнуть точки встречи.

Полученная нами орбита называется полуэллиптической или гомановской, в честь немецкого астронома Вальтера Гомана, занимавшегося теорией межпланетных полётов.

Теперь давайте рассчитаем время полёта Марса по этой полуэллиптической орбите, если его большая полуось равна 1,52 а. е.

Конструкция и оборудование современных космических аппаратов обеспечивают возможность совершения межпланетных перелетов с выходом на орбиту спутника планеты, посадкой на планету и передвижение по её поверхности.

Задачи:

1. Определите первую космическую скорость для Марса, при чём масса планеты 6,42 10²³ кг, радиус 3390 км
2. Определите вторую космическую скорость для Юпитера, если масса Юпитера 1,898 10²⁷ кг, радиус 71 492 км
3. Рассчитайте время полёта по полуэллиптической траектории до Сатурна.

Контрольные вопросы:

1. Первая космическая скорость. Определение, формула, значение.
2. Вторая космическая скорость. Определение, формула, значение.
3. Третья космическая скорость. Определение, формула, значение.
4. Четвертая космическая скорость. Определение, формула, значение.
5. Этапы развития космонавтики.
6. Основоположники космонавтики.
7. Межпланетные перелёты.
8. Расчёт траектории и времени полёта до Марса.

Видео: Открытый космос.