Производные
Для расчета производных используется функция D:
| In[1]:= |
|
| Out[1]= |
Или штрих в традиционной нотации:
| In[2]:= |
|
| Out[2]= |
Дифференцирование работает также для пользовательских функций:
| In[1]:= |
⨯ f[x_] := x^2 + 2 x + 1; f'[x] |
| Out[1]= |
Производные можно использовать в явном виде для построения графиков:
| In[2]:= |
⨯ Plot[{f[x], f'[x]}, {x, -3, 3}]
|
| Out[2]= | 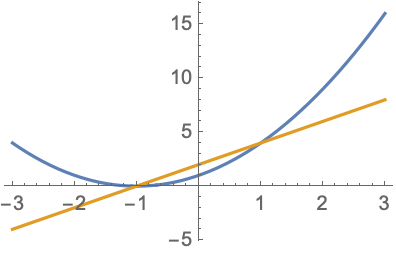 |
Рассчитаем производную более высокого порядка с использованием функции:
| In[1]:= |
|
| Out[1]= |
Или несколько раз запишем символ штриха:
| In[2]:= |
|
| Out[2]= |
Solve derivatives with Wolfram|Alpha
More than just an online derivative solver
Wolfram|Alpha is a great calculator for first, second and third derivatives; derivatives at a point; and partial derivatives. Learn what derivatives are and how Wolfram|Alpha calculates them.
Learn more about:
- Derivatives »
Tips for entering queries
Enter your queries using plain English. To avoid ambiguous queries, make sure to use parentheses where necessary. Here are some examples illustrating how to ask for a derivative.
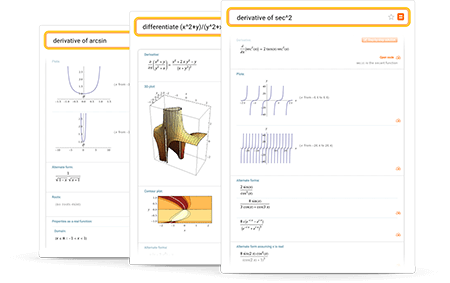
- derivative of arcsin
- derivative of lnx
- derivative of sec^2
- second derivative of sin^2
- derivative of arctanx at x=0
- differentiate (x^2 y)/(y^2 x) wrt x
- View more examples »
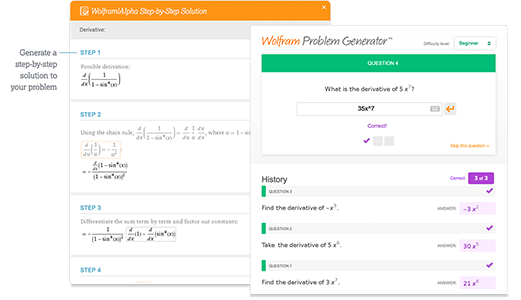
Access instant learning tools
Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator
Learn more about:
- Step-by-step solutions »
- Wolfram Problem Generator »
What are derivatives?
The derivative is an important tool in calculus that represents an infinitesimal change in a function with respect to one of its variables.
Given a function , there are many ways to denote the derivative of with respect to . The most common ways are and . When a derivative is taken times, the notation or is used. These are called higher-order derivatives. Note for second-order derivatives, the notation is often used.
At a point , the derivative is defined to be . This limit is not guaranteed to exist, but if it does, is said to be differentiable at . Geometrically speaking, is the slope of the tangent line of at .
As an example, if , then and then we can compute : . The derivative is a powerful tool with many applications. For example, it is used to find local/global extrema, find inflection points, solve optimization problems and describe the motion of objects.
How Wolfram|Alpha calculates derivatives
Wolfram|Alpha calls Wolfram Languages’s D function, which uses a table of identities much larger than one would find in a standard calculus textbook. It uses well-known rules such as the linearity of the derivative, product rule, power rule, chain rule and so on. Additionally, D uses lesser-known rules to calculate the derivative of a wide array of special functions. For higher-order derivatives, certain rules, like the general Leibniz product rule, can speed up calculations.
Wolfram|Alpha — база знаний и набор вычислительных алгоритмов (англ. computational knowledge engine), вопросно-ответная система. Запущена 15 мая 2009 года. Не является поисковой системой.
Основные операции[править]
- Примеры
- 314+278; 314—278; 314*278; 314^278;
- (a^2+b^2)+(a^2-b^2); (a^2+b^2)/(a^2-b^2); (a+b)^(2+2/3).
Знаки сравнения[править]
Логические символы[править]
Основные константы[править]
Основные функции[править]

Решение уравнений[править]
Чтобы получить решение уравнения вида 
- Примеры
- Solve [Cos[x]+Cos[2x]+Sin[4x]=0,x]или Cos[x]+Cos[2x]+Sin[4x]=0;
- Solve[x^5+x^4+x+1=0,x] или x^5+x^4+x+1=0;
- Solve[Log[3,x²+x+1]-Log[9,x²]=0,x] или Log[3,x²+x+1]-Log[9,x²]=0.
Если Ваше уравнение содержит несколько переменных, то запись: f[x, y,…,z]=0 даст весьма разнообразный набор сведений, таких как решение в целых числах, частные производные функции 


- Примеры
- Cos[x+y]=0 или Solve[Cos[x+y]=0,x] или Solve[Cos[x+y]=0,y];
- x²+y²-5=0 или Solve[x²+y²-5=0,x] или Solve[x²+y²-5=0,y];
- x+y+z+t+p+q=9.
Решение неравенств[править]
Решение в Wolfram Alpha неравенств типа 


Нужно написать в строке WolframAlpha: f[x]>0 или f[x]>=0 или Solve[f[x]>0, x] или Solve[f[x]>=0,x].
- Примеры
- Cos[10x]-1/2>0 или Solve[Cos[10x]-1/2>0,x];
- x^2+5x+10>=0 или Solve[x^2+5x+10>=0,x].
Если Ваше неравенство содержит несколько переменных, то запись: f[x, y,…,z]>0 или f[x, y,…,z]>=0 даст весьма разнообразный набор сведений, как и в случае соответствующих уравнений. Чтобы получить решение такого неравенства по какой-либо одной из переменных нужно написать в строке: Solve[f[x, y,…,z]>0,j] или Solve[f[x, y,…,z]>=0,j], где 
- Примеры
- Cos[x+y]>0 или Solve[Cos[x+y]>0,x] или Solve[Cos[x+y]>0,y];
- x^2+y^3-5<0 или Solve[x^2+y^3-5<0,x] или Solve[x^2+y^3-5<0,y];
- x+y+z+t+p+q>=9.
Решение различных систем неравенств и уравнений[править]
Решение систем различного вида в Wolfram Alpha крайне просто. Достаточно набрать уравнения и неравенства Вашей системы, точно так, как это описано выше в пунктах 7. и 8., соединяя их союзом «И», который в Wolfram Alpha имеет вид &&.
- Примеры
- x^3+y^3==9&&x+y=1;
- x+y+z+p==1&&x+y-2z+3p=2&&x+y-p=-3;
- Sin[x+y]+Cos[x+y]==Sqrt[3]/4&&x+y²=1;
- Log[x+5]=0&&x+y+z<1.
Построение графиков функций[править]
Сервис Wolfram Alpha поддерживает возможность построения графиков функций как вида 

Для того, чтобы построить график функции 
![{displaystyle xin left[{a,b}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/79750ae6a53caebc756bd2794ecdd70a74cd3639)

![{displaystyle yin left[{c,d}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e531b452bceac0edbcc03670a1dc130afe7bea0)
- Примеры
- Plot[x^2+x+2, {x,-1,1}];
- Plot[x^2+x+2, {x,-1,1},{y,-1,5}];
- Plot[Sin[x]^x, {x,-Pi,E}];
- Plot[Sin[x]^x, {x,-Pi,E},{y,0,1}].
Если Вам требуется построить сразу несколько графиков на одном рисунке, то перечислите их, используя союз «И»:Plot[f[x]&&g[x]&&h[x]&&…&&t[x],{x, a, b}].
- Примеры
- Plot[x&&x^2&&x^3, {x,-1,1},{y,-1,1}];
- Plot[Sin[x]&&Sin[5x]&&Sin[10x]&&Sin[15x], {x,-5,5}].
Для того, чтобы построить график функции 
![{displaystyle xin left[{a,b}right],yin left[{c,d}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ca93f92ae72e121c2531aba3844b750186bb0d7)


- Примеры
- Plot[Sin[x^2+y^2],{x,-1,-0.5},{y,-2,2}];
- Plot[xy,{x,-4,4},{y,-4,4}].
Математический анализ[править]
Wolfram Alpha способен находить пределы функций, последовательностей, различные производные, определенные и неопределенные интегралы, решать дифференциальные уравнения и их системы и многое многое другое.
Пределы[править]
Для того, чтобы найти предел последовательности 
- Примеры
- Limit[n^3/(n^4 + 2*n), n -> Infinity];
- Limit[(1+1/n)^n, n -> Infinity].
Найти предел функции 

- Примеры
- Limit[Sin[x]/x, x -> 0];
- Limit[(1-x)/(1+x), x -> −1].
Производные[править]
Для того, чтобы найти производную функции 



Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение производной при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.
- Примеры
- D[x*E^x, x];
- D[x^3*E^x, {x,17}];
- D[x^3*y^2*Sin[x+y], x];
- D[x^3*y^2*Sin[x+y], y],
- D[x/(x+y^4), {x,6}].
Интегралы[править]
Для того, чтобы найти неопределенный интеграл от функции 

Важно подчеркнуть, что Wolfram Alpha выдает пошаговое нахождение интеграла при нажатии на «Show Steps» в правом верхнем углу выдаваемого ей ответа.
- Примеры
- Integrate[Sin[x]/x², x].
- Integrate[x^10*ArcSin[x], x].
- Integrate[(x+Sin[x])/x, {x,1,100}].
- Integrate[Log[x^3+1]/x^5, {x,1,Infinity}].
Дифференциальные уравнения и их системы[править]
Чтобы найти общее решение дифференциального уравнения 
Если Вам требуется решить задачу Коши, то впишите: F[x, y, y’,y»,…], y[s]==A,y'[s]==B, …. Если нужно получить решение краевой задачи, что краевые условия, так же перечисляются через запятую, причем они должны иметь вид y[s]==S.
Решение систем дифференциальных уравнений также просто, достаточно вписать: {f_1,f_2,…,f_n}, где f_1, f_2, …, f_n — дифференциальные уравнения, входящие в систему.
К сожалению, решение задач Коши и краевых задач для систем дифференциальных уравнений пока что не поддерживается.
- Примеры
- y»’+y»+y=Sin[x];
- y»+y’+y=ArcSin[x];
- y»+y+y^2=0;
- y»=y, y[0]=0, y'[0]=4;
- y+x*y’=x, y[6]=2;
- y»'[x]+2y»[x]-3y'[x]+y=x, y[0]=1, y[1]=2, y'[1]=2;
- {x’+y’=2, x’-2y’=4}.
Ошибки при работе с системой[править]
Система может допускать некоторые ошибки при решении сложных задач[1]. К примеру, если попытаться решить неравенство 

Примечания[править]
- ↑ Ошибки при работе с системой Wolfram|Alpha
Ссылки[править]
- Wolfram Alpha(англ.)
- Examples
WolframAlpha по-русски
Математика с WolframAlpha ® . Объяснения с примерами.
Дифференцирование функций в Wolfram|Alpha
Как найти производную функции в Wolfram|Alpha?
Wolfram|Alpha использует для дифференцирования функций несколько различных запросов. Проще всего найти обычную производную функции f(x) в Wolfram|Alpha можно с помощью запроса-префикса d/dx.
Вот, как это выглядит на практике
Чтобы получить пошаговое решение с пояснениями каждого шага, достаточно нажать «Show steps».
Для вычисления производных второго порядка служит запрос d^2/dx^2:
Аналогично вычисляются производные высших порядков. Например, так вычисляется производная третьего порядка:
Wolfram|Alpha может находить сразу производные нескольких порядков. Как, например, это может понадобиться при отыскании коэффициентов ряда Тейлора. Для этого используется запрос на табуляцию функции с указанием наименьшего, наибольшего порядка производной, а также шага между ними. Чтобы не загромождать изложение, рассмотрим простой пример на вычисление производных функции cos(x) до 5-го порядка включительно:
Тот же результат (табулирование производной) получим по запросу вида
Для вычисления значения производной в заданной точке, нужно указать значение аргумента:
Частные производные вычисляются аналогично:
Естественно, с помощью Wolfram|Alpha можно визуально сравнить функцию и ее производную:
Конечно, навряд ли можно научиться дифференцировать функции, используя исключительно Wolfram|Alpha. Однако, система Wolfram|Alpha вполне подходит, чтобы проверить свои знания, освежить их, например, перед экзаменом, и убедиться, что вы к нему вполне готовы.
Преподавателям Wolfram|Alpha поможет оценить сложность и время на выполнение заданий на производные, которые предлагаются студентам.
Вольфрам альфа уравнение в частных производных
1. Решение рациональных, дробно-рациональных уравнений любой степени, показательных, логарифмических, тригонометрических уравнений.
Пример 1 . Чтобы решить уравнение x 2 + 3 x — 4 = 0, нужно ввести solve x^2+3x-4=0
Пример 2. Чтобы решить уравнение log32x = 2 , нужно ввести solve log(3, 2x)=2
Пример 3. Чтобы решить уравнение 25 x-1 = 0.2 , нужно ввести solve 25^(x-1)=0.2
Пример 4. Чтобы решить уравнение sin x = 0.5 , нужно ввести solve sin(x)=0.5
2. Решение систем уравнений.
Пример . Чтобы решить систему уравнений
нужно ввести solve x+y=5 && x-y=1
Знаки && в данном случае обозначает логическое «И».
3. Решение рациональных неравенств любой степени.
Пример . Чтобы решить неравенство x 2 + 3 x — 4 solve x^2+3x-4
4. Решение систем рациональных неравенств.
Пример. Чтобы решить систему неравенств
нужно ввести solve x^2+3x-4 && 2х^2 — x + 8 > 0
Знаки && в данном случае обозначает логическое «И».
5. Раскрытие скобок + приведение подобных в выражении.
Пример . Чтобы раскрыть скобки в выражении (c+d) 2 (a-c) и привести подобные, нужно
ввести expand (c+d)^2*(a-c) .
6. Разложение выражения на множители.
Пример . Чтобы разложить на множители выражение x 2 + 3 x — 4, нужно ввести factor x^2 + 3x — 4 .
7. Вычисление суммы n первых членов последовательности (в том числе арифметической и геометрической прогрессий).
Пример . Чтобы вычислить сумму 20 первых членов последовательности, заданной формулой an = n 3 +n, нужно ввести sum n^3+n, n=1..20
Если нужно вычислить сумму первых 10 членов арифметической прогрессии, у которой первый член a 1 = 3, разность d = 5, то можно, как вариант, ввести a1=3, d=5, sum a1 + d(n-1), n=1..10
Если нужно вычислить сумму первых 7 членов геометрической прогрессии, у которой первый член b 1 = 3, разность q = 5, то можно, как вариант, ввести b1=3, q=5, sum b1*q^(n-1), n=1..7
8. Нахожд ение производной.
Пример . Чтобы найти производную функции f(x) = x 2 + 3 x — 4, нужно ввести derivative x^2 + 3x — 4
9. Нахожд ение неопределенного интеграла.
Пример . Чтобы найти первообразную функции f(x) = x 2 + 3 x — 4, нужно ввести integrate x^2 + 3x — 4
10. Вычисление определенного интеграла.
Пример . Чтобы вычислить интеграл функции f(x) = x 2 + 3 x — 4 на отрезке [5, 7],
нужно ввести integrate x^2 + 3x — 4, x=5..7
11. Вычисление пределов.
Пример . Чтобы убедиться, что
введите lim (x -> 0) (sin x)/x и посмотрите ответ. Если нужно вычислить какой-то предел при x, стремящемся к бесконечности, следует вводить x -> inf .
12. Исследование функции и построение графика .
Пример . Чтобы исследовать функцию x 3 — 3 x 2 и построить ее график, просто введите x^3-3x^2 . Вы получите корни (точки пересечения с осью ОХ), производную, график, неопределенный интеграл, экстремумы.
13. Нахождение наибольшего и наименьшего значений функции на отрезке .
Пример . Чтобы найти минимальное значение функции x 3 — 3 x 2 на отрезке [0.5, 2],
нужно ввести minimize (x^3-x^2),
Чтобы найти максимальное значение функции x 3 — 3 x 2 на отрезке [0.5, 2],
нужно ввести maximize (x^3-x^2),
Рубрика «уравнения в частных производных»
Обзор новых возможностей Mathematica 11 и языка Wolfram Language
Перевод поста Стивен Вольфрам (Stephen Wolfram) «Today We Launch Version 11!».
Выражаю огромную благодарность Полине Сологуб за помощь в переводе и подготовке публикации
Содержание
Я рад объявить о выходе новой версии системы Mathematica и 11-й версии языка Wolfram Language, доступной как для Desktop-компьютеров, так и в облачном виде. В течение последних двух лет сотни человек упорно трудились над ее созданием, а несколько тысяч часов и я лично. Я очень взволнован; это важный шаг вперед, имеющий важное значение для многих крупнейших технологических областей.
Прошло больше 28 лет с тех пор, как вышла 1-я версия, — и почти 30 лет с тех пор, как я занялся ее разработкой. И все это время я продолжал воплощать дерзкую мечту — строить все больший и больший стек технологий. Большая часть программного обеспечения спустя несколько лет и несколько версий, за исключением мелких доработок, практически не меняется. С системой Mathematica и Wolfram Language сложилась совсем другая история: в течение трех десятилетий мы c каждой новой версией продвигались вперед, завоевывая постепенно огромное количество новых областей.
Читать полностью »
Новое в Wolfram Language | Аналитическое решение уравнений в частных производных
Перевод поста Devendra Kapadia «New in the Wolfram Language: Symbolic PDEs».
Код, приведенный в статье, можно скачать здесь.
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе и подготовке публикации.
Уравнения в частных производных (УрЧП) играют очень важную роль в математике и ее приложениях. Их можно использовать для моделирования реальных явлений, таких как колебания натянутой струны, распространения потока тепла в стержне, в финансовых областях. Цель этой статьи — приоткрыть завесу в мир УрЧП (тем кто еще с ним не знаком) и ознакомить читателя с тем, как можно эффективно решать УрЧП в Wolfram Language, используя новый функционал для решения краевых задач в DSolve, а так же новую функцию DEigensystem, которая появилась в версии 10.3.
История УрЧП восходит к работам известных математиков восемнадцатого века — Эйлера, Даламбера, Лапласа, однако развитие этой области в последние три столетия так и не остановилось. И потому в статье я приведу как классические, так и современные примеры УрЧП, что позволит рассмотреть эту область знаний под разными углами.
Давайте начнем с рассмотрения колебаний натянутой струны с длиной π, закрепленной на обоих концах. Колебания струны можно смоделировать с помощью одномерного волнового уравнения, приведённого ниже. Здесь u(x,t) — вертикальное смещение точки струны с координатой х в момент времени t:
Читать полностью »
http://gghelp.ru/index/wolfram_alpha/0-43
http://www.pvsm.ru/cat/uravneniya-v-chastny-h-proizvodny-h
In case you have any problems, I recommend using the Derivative operator instead of D, since the latter works on expressions, while the former one can work on pure functions.
{Derivative[1, 0][f][x, y], Derivative[0, 1][f][x, y]} // TraditionalForm
The subtlety here is that one cannot use it to find partial derivatives of f at {0,0}, e.g.
Derivative[0, 1][f][0, 0]
Power::infy: Infinite expression 1/0 encountered. >> Infinity::indet: Indeterminate expression E^ComplexInfinity encountered. >> Power::infy: Infinite expression 1/0^2 encountered. >> Indeterminate
however, you can use Limit instead of Derivative:
Limit[ #, h -> 0] & /@ {( f[0 + h, 0] - f[0, 0] )/ h, ( f[0, 0 + h] - f[0, 0] )/ h}
{0, 0}
In general, it works as we would like:
Limit[ #, h -> 0] & /@ { (f[x + h, y] - f[x, y])/ h, (f[x, y + h] - f[x, y])/ h} ==
{ Derivative[1, 0][f][x, y], Derivative[0, 1][f][x, y] }
True
One can also take advantage of FoldList to follow computing several limits, e.g. :
FoldList[ Limit, (f[x + h, y] - f[x, y])/h, {h -> 0, y -> 0, x -> 0}] // TraditionalForm
We have shown that the partial derivative with respect to x is continuous at {0,0}.
We can show much more; namely, that any derivative of any order vanishes at {0,0}. We find here the few first terms of a Taylor series expansion near {0,0} :
Limit[ Limit[ Normal @ Series[ f[x, y], {y, y0, 7}, {x, x0, 7}], x0 -> 0], y0 -> 0]
0
i.e. this function is not analytic at {0,0}, since the Taylor series expansion is identically 0, while the function f itself is not.