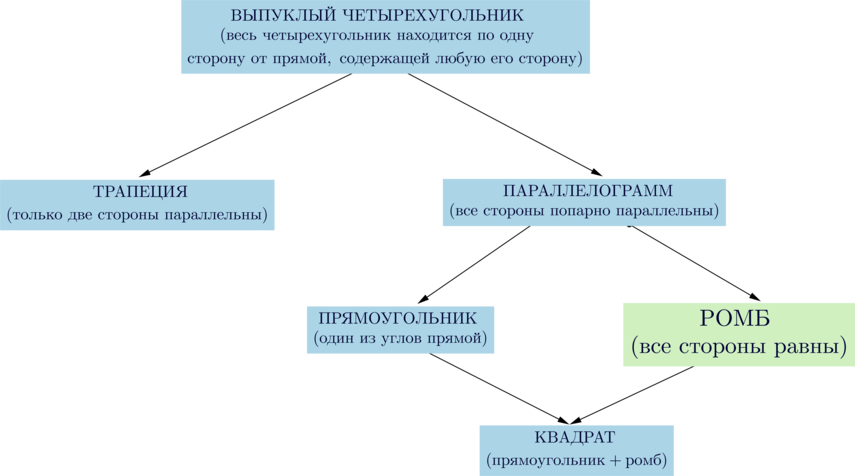
Найти углы ромба, зная только его сторону, нельзя: существуют ромбы, имеющие разные углы, но одинаковые стороны. На пальцах: сделайте ромб из проволоки, «сплющите» его — он останется ромбом, стороны будут те же, углы изменятся.
Значит, чтобы найти углы ромба нужно знать что-то ещё (или что-то другое). Например, зная сторону и диагональ, найти угол можно по теореме косинусов: если x — сторона, d — диагональ, a — угол напротив диагонали, то условие теоремы косинуов — d^2 = x^2 + x^2 — 2 * x^2 * cos(a), из него следует a = arccos((2x^2 — d^2)/2x^2). (Я говорю «найти угол», а не «найти углы», потому что если мы знаем один угол, остальные находятся тривиально: если один угол равен а градусов, то угол напротив него тоже а, остальные два — по 180-а).
Есть и другие варианты: через сторону и площадь (пользуясь тем, что площадь — это квадрат стороны умножить на синус угла), через две диагонали (мы знаем, что диагонали в ромбе пересекаются под прямым углом и делятся точкой пересечения пополам — отсюда следует, что тангенс половины угла ромба равен отношению диагоналей, просто по определнию тангенса; зная сторону и диагональ, кстати, тоже можно искать угол примерно таким способом, вместо теоремы косинусов) и так далее.
Геометрические фигуры. Ромб. Углы ромба. Как найти угол ромба.
Углы ромба, нахождение:
1. Сумма 4-х внутренних углов ромба равняется 360°, точно так же как и у всякого четырехугольника. Противоположные углы ромба имеют одинаковую величину, причем, всегда в 1-ой паре равных углов — углы острые, во второй — тупые. 2 угла, которые прилегают к 1-ной стороне в сумме составляют развернутый угол.
Ромбы с равным размером стороны могут внешне довольно сильно отличаться друг от друга. Это разница объясняется различной величиной внутренних углов. То есть, для определения угла ромба не хватит знать лишь длину его стороны.
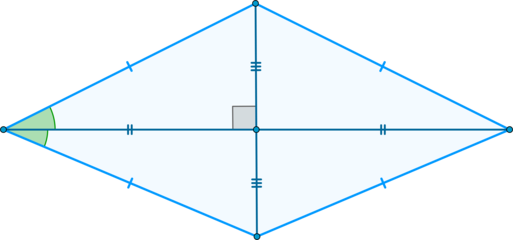
2. Для вычисления величины углов ромба хватит знать длины диагоналей ромба. После построения диагоналей ромб разбивается на 4 треугольника. Диагонали ромба располагаются под прямым углом, то есть, треугольники, которые образовались, оказываются прямоугольными.
Ромб — симметричная фигура, его диагонали есть в одно время и осями симметрии, вот почему каждый внутренний треугольник равен остальным. Острые углы треугольников, которые образованы диагоналями ромба, равняются ½ искомых углов ромба.
3. Тангенс острого угла прямоугольного треугольника соответствует отношению противолежащего катета к прилежащему. ½ любой из диагоналей ромба оказывается катетом прямоугольного треугольника.
Обозначим большую и малую диагонали ромба как d₁ и d₂, а углы ромба — А (острый) и В (тупой), теперь из соотношения сторон в прямоугольных треугольниках внутри ромба находим:
4. Из формулы двойного угла tg (2α) = 2/(сtg α — tg α) находим тангенсы углов ромба:
По тригонометрическим таблицам находят углы, которые соответствуют полученным значениям тангенсов.
Острый угол ромба равен 60 градусам.
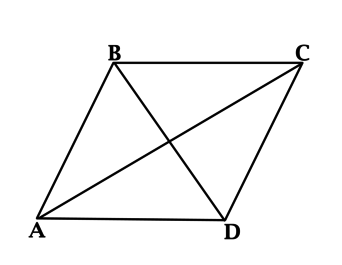
Когда острый угол ромба = 60°, значит, диагональ равняется стороне ромба и делит его на 2 одинаковых равносторонних треугольника.
∆ ABD и ∆ BCD — равносторонние,
1) Изучим треугольник ABD.
Т.к. AB=AD (так как являются сторонами ромба), значит, ∆ ABD является равнобедренным треугольником с основанием BD.
Углы при основании равнобедренного треугольника:
Так как каждый угол треугольника ABD равен 60 градусов, значит, ∆ ABD является равносторонним треугольником. Значит, BD=AB.
2) Треугольники ABD и BCD одинаковы по трем сторонам (AB=BC=CD=AD (как стороны ромба), BD=AB (из доказанного)).
То есть, ∆ BCD оказывается равносторонним треугольником.
Что и требовалось доказать.
Т.к. сумма углов ромба, которые прилежат к одной стороне, равна 180º, когда острый угол ромба равен 60º, его тупой угол равен 120º. Таким образом:
Когда тупой угол ромба равен 120 градусам, значит диагональ равняется стороне ромба и делит его на 2 равных равносторонних треугольника.
Ромб с прямыми углами называется квадратом.
Найти углы ромба
1. Ромб — частный случай параллелограмма
2. Противоположные стороны — параллельны
3. Все четыре стороны — равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
β — тупой угол
Формулы косинуса углов через диагональ и сторону:
Формулы синуса углов через диагонали :
Формулы синуса углов через площадь S и сторону :
Формулы тангенса половинных углов через диагонали
Формулы соотношения острого и тупого углов:
Для определения величины угла в градусах или радианах, используем функции arccos или arcsin или arctg
Углы ромба онлайн
С помощю этого онлайн калькулятора ромба можно найти углы ромба по известным элементам. Для нахождения углов ромба введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
Открыть онлайн калькулятор
1. Углы ромба через сторону и высоту
Пусть известны сторона и высота ромба (Рис.1).
Покажем, что углы ромба через сторону и высоту вычисляются по формулам
| ( small alpha= mathrmfrac<large h> <large a>) | (1) |
| ( small beta= 180°-alpha ) | (2) |
| (small frac<large h><large sin alpha>=frac<large a><large sin 90°>.) | (3) |
| (small sin alpha=frac<large h><large a>) | (4) |
| (small alpha=mathrmfrac<large h><large a>) | (5) |
Поскольку сумма соседних углов ромба равна 180° (свойство 4 статьи Ромб), то угол β вычисляется из формулы (2).
2. Углы ромба ромба через площадь и высоту
Рассмотрим ромб с высотой h и площадью S (Рис.2).
Покажем, что углы ромба через площадь и высоту вычисляются по формулам:
| ( small alpha= mathrmfrac<large h^2><large S>, ) | (6) |
| ( small beta= 180°-alpha . ) | (7) |
Площадь ромба через сторону и высоту вычисляется из формулы:
| ( small S=a cdot h. ) | (8) |
Найдем a из формулы (8) и подставим в (1):
| ( small alpha= mathrmfrac<large h><large a>=mathrmfrac<large h><large frac |
(9) |
Как отметили в параграфе 1, соседний угол β вычисляется по формуле (7).
3. Углы ромба через площадь и сторону
Пусть известны площадь и сторона ромба (Рис.3).
Чтобы найти формулу углов ромба через площадь и сторону, из формулы (8) найдем h и подставим в (1):
Следовательно угол α ромба через площадь и сторону вычисляется из формулы:
| ( small alpha =mathrmfrac<large S><large a^2>. ) | (10) |
Как отметили выше, соседний угол β вычисляется по формуле (7).
4. Углы ромба через диагонали
Пусть известны диагонали d1 и d2 ромба (Рис.4). Выведем формулу вычисления углов α и β ромба.
| (small h=frac<large d_1d_2><large sqrt>.) | (11) |
| (small a=frac<large sqrt><large 2>.) | (12) |
Подставляя (11) и (12) в (4), получим:
| (small sin alpha=frac<large h><large a>) ( small =frac<frac<large d_1d_2><large sqrt>><frac<large sqrt><large 2>> ) ( small =frac<large 2d_1d_2> <large d_1^2+d_2^2>.) | (13) |
| (small alpha=mathrm frac<large 2d_1d_2> <large d_1^2+d_2^2>.) | (14) |
Как отметили выше, соседний угол β вычисляется по формуле (7).
5. Углы ромба через сторону и диагональ
Пусть известны сторона a=AB ромба и диагональ d=AC (Рис.5).
Найдем углы ромба. Учитывая свойства 5, 6 и 7 ромба, получаем, что треугольник AOB прямоугольный и ( small angle ABO =frac<alpha> <2>.) Тогда для треугольника AOB имеют места следующие равненства:
(small frac<large AO><large a>=sin frac<alpha><2>,)
(small frac<large AO><large a>=cos frac<beta><2>)
| (small sin frac<alpha><2>=frac<large d><large 2a>) | (15) |
| (small cos frac<beta><2>=frac<large d><large 2a >.) | (16) |
Формулы половинного угла для синуса и косинуса имеют следующий вид:
| (small sin frac<alpha><2>=±sqrt<frac<large 1-cos alpha><large 2 >>,) | (17) |
| (small cosfrac<beta><2>=±sqrt<frac<large 1+cos beta><large 2 >>.) | (18) |
Найдем из формул (17),(18) ( small cos alpha ) и ( small cos beta: )
| (small cos alpha=1-2cdot sin^2 frac<alpha><2>,) | (19) |
| (small cos beta=2cdot sin^2 frac<beta><2>-1,) | (20) |
Подставляя (15),(16) в (19),(20), получим формулы углов ромба через сторону и диагональ:
| (small cos alpha=1- frac<large d^2><large 2a^2>,) | (21) |
| (small cos beta=frac<large d^2><large 2a^2>-1.) | (22) |
| (small alpha=mathrm left(1- frac<large d^2> <large 2a^2>right),) | (23) |
| (small beta=mathrm left( frac<large d^2><large 2a^2>-1 right).) | (24) |
Отметим, что полученный угол α находится напротив диагонали d, а угол β делится диагональю d на две равные части.
6. Углы ромба через сторону и радиус вписанной окружности
Пусть известны сторона ромба и радиус вписанной окружности (Рис.6). Найдем углы ромба.
В статье Высота ромба мы вывели формулу высоты ромба через радиус вписанной октужности:
| (small h=2 cdot r.) | (25) |
Подставляя (25) в (4) и (5) параграфа 1 данной статьи, получим:
| (small sin alpha=frac<large 2 cdot r><large a>) | (26) |
| (small alpha=mathrmfrac<large 2 cdot r><large a>) | (27) |
Как отметили выше, соседний угол β ромба вычисляется по формуле:
http://www-formula.ru/2011-11-26-01-41-07
http://matworld.ru/geometry/ugly-romba.php
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Ромб и его свойства
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства ромба:
(blacktriangleright) Те же, что и у параллелограмма:
(sim) Противоположные стороны попарно равны;
(sim) Диагонали точкой пересечения делятся пополам;
(sim) Противоположные углы попарно равны, а сумма соседних равна (180^circ);
(blacktriangleright) Диагонали взаимно перпендикулярны и являются биссектрисами углов ромба.
Признаки ромба.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – ромб:
(blacktriangleright) все стороны равны;
(blacktriangleright) диагонали взаимно перпендикулярны и он является параллелограммом;
(blacktriangleright) диагонали являются биссектрисами углов и он является параллелограммом.
Площадь ромба
1. Т.к. ромб является параллелограммом, то для него верна та же формула площади. Таким образом, площадь ромба равна произведению высоты на основание, к которому эта высота проведена.
2. Площадь ромба равна половине произведения его диагоналей.
Задание
1
#2716
Уровень задания: Легче ЕГЭ
В ромбе (ABCD): (angle ACD = 26^{circ}). Найдите (angle ABD). Ответ дайте в градусах.
В ромбе диагонали перпендикулярны, тогда (angle CDB = 90^{circ} — angle ACD = 64^{circ}).
(BC = CD), тогда (angle CBD = angle CDB = 64^{circ}).
Так как диагонали ромба делят его углы пополам, то (angle ABD = angle CBD = 64^{circ}).
Ответ: 64
Задание
2
#2717
Уровень задания: Равен ЕГЭ
Найдите большую диагональ ромба (ABCD), если (AB = 2sqrt{3}), а острый угол равен половине тупого.
Так как сумма односторонних углов при параллельных прямых и секущей равна (180^{circ}), то сумма острого и тупого углов ромба равна (180^{circ}).
Так как в данном ромбе острый угол равен половине тупого, то острый угол ромба (ABCD) равен (60^{circ}).
Треугольник (ABD) – равнобедренный, один из углов которого равен (60^{circ}), тогда треугольник (ABD) – равносторонний и (BD = 2sqrt{3}).
Пусть (O) – точка пересечения диагоналей ромба, тогда (OD = 0,5 BD = sqrt{3}), следовательно, по теореме Пифагора находим: (AO^2 + OD^2 = AD^2), тогда (AO^2 + 3 = 12), откуда находим (AO = 3). В ромбе, как и в любом другом параллелограмме, диагонали точкой пересечения делятся пополам, значит, (AC = 6).
Ответ: 6
Задание
3
#2715
Уровень задания: Равен ЕГЭ
Острый угол ромба (ABCD) равен (60^{circ}), одна из его сторон равна 10. Найдите меньшую из диагоналей этого ромба.
Пусть (angle A = 60^{circ}). В ромбе все стороны равны, тогда треугольник (ABD) – равнобедренный, у которого один из углов равен (60^{circ}), следовательно, треугольник (ABD) – равносторонний и (BD = 10).
Треугольник (ABC) – тупоугольный. В треугольнике против большего угла лежит большая сторона, тогда (AC > AB = BD), значит, (BD) – меньшая из диагоналей.
Ответ: 10
Задание
4
#1794
Уровень задания: Равен ЕГЭ
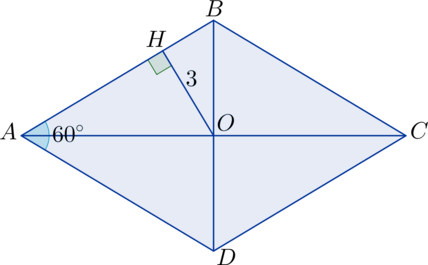
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно (3), а острый угол ромба равен (60^circ). Найдите большую диагональ ромба.
Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), (angle DAB = 60^circ), тогда (angle
OAB = 30^circ). Получаем, что (OH) – катет лежащий напротив угла в (30^circ), значит (AO = 2cdot OH = 6). Т.к. (AC) и есть большая диагональ, то (AC = 2cdot AO = 12).
Ответ: 12
Задание
5
#1757
Уровень задания: Равен ЕГЭ
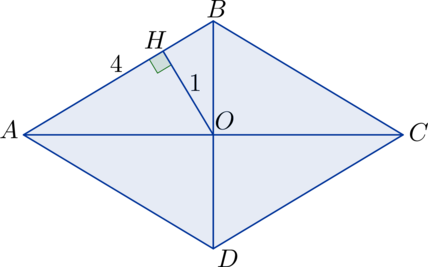
Сторона ромба равна (4). Расстояние от точки пересечения его диагоналей до одной из сторон равно (1). Найдите площадь ромба.
Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), тогда (S_{triangle ABO} = frac{1}{2}cdot 1 cdot 4 = 2). Диагонали ромба делят его на (4) равных прямоугольных треугольника (Rightarrow) (S_{ABCD} = 4cdot 2 = 
Ответ: 8
Задание
6
#2718
Уровень задания: Равен ЕГЭ
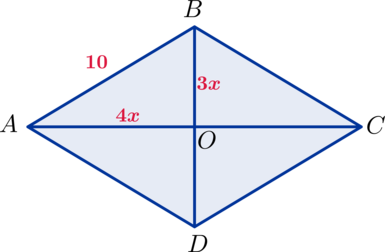
Периметр ромба равен (40), а диагонали относятся, как (3:4). Найдите площадь ромба.
Половины диагоналей находятся в таком же отношении, как и диагонали, то есть в отношении (3:4). Зная периметр, найдем сторону ромба: (40
: 4 = 10). Сторона и половинки диагоналей образуют прямоугольный треугольник (AOB).
Пусть (AO=4x), (BO=3x).
Тогда по теореме Пифагора: ((3x)^2 + (4x)^2 = 10^2) (Rightarrow) (25x^2 = 100) (Rightarrow) (x^2 = 4) (Rightarrow) (x = 2). Диагонали равны (BD=2BO=12) и (AC=2AO=16) (Rightarrow) (S_{ABCD} =
frac{1}{2}cdot12cdot16 = 96).
Ответ: 96
Задание
7
#2719
Уровень задания: Равен ЕГЭ
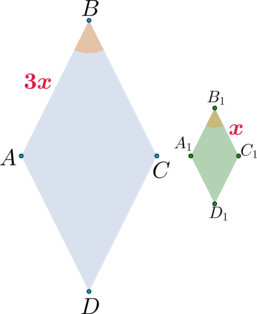
Во сколько раз отличаются площади ромбов, имеющие по равному углу, у которых стороны относятся как (3:1)?
Пусть (angle B) и (angle B_1) – равные углы ромбов. Так как стороны ромбов относятся как (3:1), то можно обозначить их за (3x) и (x) соответственно.
Тогда и (angle D=angle D_1) (так как у ромба противоположные углы равны). Следовательно, (triangle ABCsim triangle A_1B_1C_1) и (triangle ADCsimtriangle A_1D_1C_1) по двум пропорциональным сторонам и углу между ними, причем коэффициент подобия этих треугольников равен (3). Следовательно, их площади относятся как (9:1). А так как (S_{ABC}+S_{ADC}=S_{ABCD}) и (S_{A_1B_1C_1}+S_{A_1D_1C_1}=S_{A_1B_1C_1D_1}), то (S_1:S_2=9:1).
Ответ: 9
Геометрические задачи на тему «Свойства ромба» в обязательном порядке включаются в ЕГЭ по математике. Причем, в зависимости от условия задания, учащийся может давать как краткий, так и развернутый ответ. Именно поэтому на этапе подготовки к сдаче ЕГЭ школьникам непременно стоит понять принцип решения задач на применение свойств и признаков ромба.
Еще раз повторить данную тему и восполнить пробелы в знаниях вам поможет образовательный проект «Школково». С помощью нашего сайта можно легко и эффективно подготовиться к ЕГЭ по математике.
Чтобы успешно справляться с геометрическими заданиями, учащимся старших классов стоит повторить базовые понятия и определения: свойства углов ромба и других четырехугольников, признаки этой фигуры, а также формулу для нахождения ее площади. Данный материал представлен в разделе «Теоретическая справка» на сайте «Школково». Информация, которую подготовили наши специалисты, изложена в максимально доступной форме.
Повторив основные свойства диагоналей ромба, а также его углов и биссектрис, учащиеся могут попрактиковаться в выполнении упражнений. Большая подборка заданий по данной теме, а также по решению нестандартных задач по математике представлена в разделе «Каталог». Найти правильный ответ выпускники смогут, предварительно освежив в памяти свойства биссектрис ромба, в также углов и диагоналей этой фигуры. Подробный алгоритм решения каждой задачи прописан нашими специалистами.
Выполнять простые и более сложные задания по теме «Ромб и его свойства», а также на нахождение площади квадрата на этапе подготовки к ЕГЭ по математике школьники из Москвы и других городов могут в режиме онлайн. При необходимости любое упражнение можно сохранить в разделе «Избранное». Это позволит в дальнейшем быстро найти это задание и, к примеру, обсудить алгоритм его решения со школьным преподавателем.

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Ромб, свойства, признаки, формулы, площадь и периметр.
Ромб – это параллелограмм, у которого все стороны равны.
Ромб (определение и понятие)
Видеоурок “Ромб”
Свойства ромба
Признаки ромба
Формулы ромба. Площадь ромба. Периметр ромба
Ромб (определение и понятие):
Ромб (др.-греч. ῥόμβος, лат. rombus, в буквальном переводе – «бубен») – это параллелограмм, у которого все стороны равны.
Рис. 1. Ромб
Так как ромб является параллелограммом, то он обладает всеми свойствами параллелограмма.
Ромбы отличаются друг от друга размером углов и длиной стороны.
Если у ромба – прямые углы, то он называется квадратом.
@ https://youtu.be/AavypoP06_U
Свойства ромба:
1. Противолежащие стороны ромба равны, т. к. все стороны ромба равны.
Рис. 2. Ромб
AB = BC = CD = AD
2. Противолежащие стороны ромба попарно параллельны.

АВ || CD, AD || ВС
3. Соседние углы ромба дополняют друг друга до 180°. Иными словами, сумма углов, прилежащих к любой из сторон ромба, равна 180°.
Рис. 4. Ромб
∠CDA + ∠DAB = 180°
4. Диагонали ромба взаимно перпендикулярны.
Рис. 5. Ромб
AC ⊥ BD
5. Диагонали ромба точкой пересечения делятся пополам.
Рис. 6. Ромб
BO = OD, AO = OC
6. Диагонали ромба делят ромб на четыре прямоугольных треугольника.
Рис. 7. Ромб
7. Диагонали ромба являются биссектрисами его углов и делят углы пополам.
Рис. 8. Ромб
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
8. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре.
Рис. 9. Ромб
AC2 + BD2 = 4AB2
9. В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
Центром окружности вписанной в ромб будет точка пересечения его диагоналей. 
Рис. 10. Ромб
Признаки ромба:
Параллелограмм ABCD является ромбом тогда и только тогда, когда выполняется хотя бы одно из следующих условий:
– если две смежные стороны параллелограмма равны (отсюда следует, что все стороны равны), то он является ромбом.
AB = BC, то AB = BC = CD = AD;
– если диагонали параллелограмма пересекаются под прямым углом, то он является ромбом.
AC ⊥ BD;
– если одна из диагоналей параллелограмма делит содержащие её углы пополам, то он является ромбом.
∠BAC = ∠CAD или ∠ABD = ∠DBC или ∠BCA = ∠ACD или ∠ADB = ∠BDC;
– если в параллелограмм можно вписать круг, то он является ромбом;
– если диагонали делят параллелограмм на четыре равных прямоугольных треугольника, то он является ромбом.
Квадрат
Прямой угол
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Ромб
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Видео https://youtu.be/AavypoP06_U
Коэффициент востребованности
2 025
Как найти угол ромба
Ромб образуется из квадрата при растягивании фигуры за вершины, расположенные на одной диагонали. Два угла становятся меньше прямых. Два других угла увеличиваются, превращаясь в тупые.
Сумма четырех внутренних углов ромба равна 360°, как у любого четырехугольника. Противоположные углы ромба равны, при этом всегда в одной паре равных углов — углы острые, в другой — тупые.Два угла, прилегающие к одной стороне в сумме составляют развернутый угол. Ромбы с одинаковым размером стороны могут внешне очень сильно отличаться друг от друга.Это различие объясняется разной величиной внутренних углов. Следовательно, для нахождения угла ромба недостаточно знать только его сторону.
Достаточным для определения величины углов ромба является знание диагоналей фигуры.После проведения в ромбе обеих диагоналей ромб будет разбит на четыре треугольника. Диагонали ромба расположены под прямым углом, следовательно, полученныетреугольники являются прямоугольными. Ромб — симметричная фигура, его диагонали являются одновременно осями симметрии, поэтому все внутренние треугольникиравны. Острые углы треугольников, образованных диагоналями ромба, равны половине углов ромба, которые нужно найти.
Тангенс острого угла прямоугольного треугольника равен отношению катетов, противолежащего к прилежащему. Половина каждой диагонали ромба является катетом прямоугольного треугольника. Если большую и малую диагонали ромба обозначить d₁ и d₂соответственно, а углы ромба — А (острый) и В (тупой), то из соотношения сторон в прямоугольных треугольниках внутри ромба следует: tg (A/2)=(d₂/2)/(d₁/2)=d₂/d₁,tg(B/2)=(d₁/2)/(d₂/2)=d₁/d₂.
По формуле двойного углаtg (2α) = 2/(сtg α — tg α) найдитетангенсы углов ромба: tg A = 2/((d₁/d₂)-(d₂/d₁)) и tg B =2/((d₂/d₁)-(d₁/d₂)). По тригонометрическим таблицам найдите углы, соответствующие рассчитанным значениям их тангенсов.