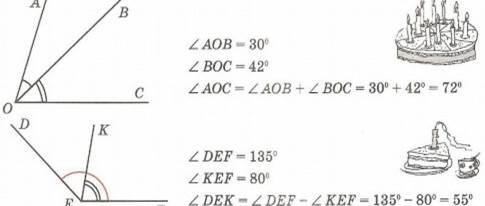На
предыдущем уроке вы познакомились с измерением отрезков. Измерение углов
аналогично измерению отрезков, т. е. нам нужно сравнить их с углом, принятым за
единицу измерения. Обычно за единицу измерения принимают градус. Градус
— это угол, равный части
развёрнутого угла.
А
вот положительное число, которое показывает, сколько раз градус и его части
укладываются в измеряемом угле, называется градусной мерой угла. Для
измерения градусной меры углов используется транспортир.
Рассмотрим
угол АОВ, градусная мера которого равна 60 градусов. Удостоверимся в этом с
помощью транспортира:
Действительно
верно.
Определённые
части градуса носят специальные названия. Так часть
градуса называют минутой и обозначают «’». А часть
минуты называют секундой и обозначают «”». Например
угол в 120 градусов 10 минут 22 секунды обозначают так:
Если
два угла равны, то градус и его части укладываются в этих углах одинаковое
число раз, т. е. равные углы имеют равные градусные меры.
А
если два угла неравны, то в меньшем из углов градус (или его части)
укладываются меньшее число раз, чем в большем. Следовательно, меньший угол
имеет меньшую градусную меру.
Выше
мы отметили, что градус составляет часть
развёрнутого угла. Т. е. развёрнутый угол равен 180 градусам.
Возьмём
угол АОВ, из вершины О проведём луч ОС, который делит
угол АОВ на два угла АОС и СОВ:
Измерим
эти углы:
Видим,
что угол АОС=50 градусам, угол СОВ=110 градусам, а угол АОВ=160 градусам.
Получили, что АОС+СОВ=АОВ.
Следовательно,
можем сказать, что когда луч делит угол на два угла, градусная мера всего угла
равна сумме градусных мер этих углов.
В
зависимости от величины выделяют прямой угол:
Острый
угол:
Тупой
угол:
С
прямыми углами мы сталкиваемся очень часто. Например:
Для
измерения градусной меры углов мы пользовались транспортиром. А вот измерять угол
на местности нужно с помощью специальных инструментов.
Один
из старейших инструментов имеет название «астролябия». Он состоит из диска,
разделённого на градусы, и вращающейся вокруг центра диска линейки или,
по-другому, алидады. На концах алидады есть окошечки, которые используются для
установки её в определённом направлении. Прибор используется для определения
широты и долготы.
Содержание:
- § 1 Сравнение углов
- § 2 Транспортир. Измерение углов
- § 3 Краткие итоги урока
§ 1 Сравнение углов
В этом уроке научимся сравнивать и измерять углы.
Вспомним, что угол — геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (которая называется вершиной угла).
Давайте сравним два угла с помощью наложения и выясним, равны углы или нет.
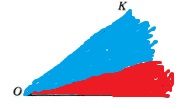
Возьмём два угла.
Один угол закрасим в синий цвет, а другой – в красный и наложим красный угол на синий.
На рисунке видно, что синий угол больше, чем красный, но мы не знаем на сколько больше. Чтобы сравнивать углы, надо научиться точно их измерять.
Измеряют величину угла так же, как и любую другую величину.
Для этого выбирают единицу измерения (мерку) и узнают, сколько раз она содержится в измеряемой величине.
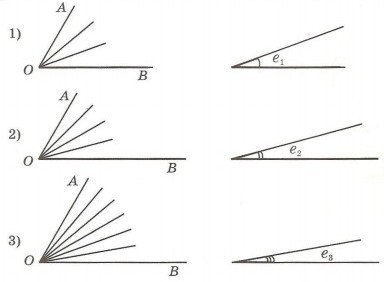
Представим себе такую ситуацию: Серёжа, Петя и Коля решили измерить угол, но мерку каждый решил сделать себе сам.
Что же получилось?
Оказалось, что один и тот же угол у Серёжи равен трём его меркам, у Пети – четырем меркам, а у Коли – шести меркам.
Кто из них прав?
Какой величины этот угол на самом деле?
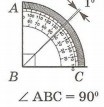
В геометрии существует общепринятая, единая для всех, мерка – это 1/90 часть прямого угла. Эту мерку называют градусом и обозначают: 1°.
Таким образом, прямой угол равен 90°, а развёрнутый – 180°.
Любой острый угол будет меньше 90°, а любой тупой будет больше 90°.
При сложении углов их градусные меры складываются, а при вычитании – вычитаются, например:
Надо также запомнить, что сумма смежных углов всегда равна 180°.
§ 2 Транспортир. Измерение углов
Давайте попробуем решить задачу, используя наши знания.
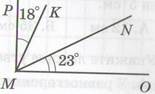
Дан угол ОМР – он прямой, т.е. 90°, два луча разделили его на три угла.
Как видно из рисунка, один угол – 18 градусов, а другой – 23 градуса.
Нам нужно вычислить, чему равен угол КМN?
Чтобы найти величину угла КМN, нужно из градусной меры угла ОМР вычесть градусные меры углов КМР и NМО:
∠КМN = ∠ОМР – ∠КМР – ∠NМО = 90° – 18° – 23° = 49°
Угол КМN равен 49°.
Решим ещё одну задачу.
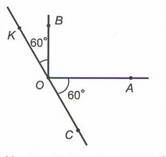
На рисунке мы видим, что ∠КОС – развёрнутый, значит, он равен 180°.
∠КОВ = 60° и ∠АОС = 60°.
Найдём величину ∠ВОА.
∠ВОА = ∠КОС – ∠КОВ – ∠АОС = 180° – 60° – 60° = 60°
∠ВОА = 60°
Чтобы измерить угол в градусах, необходимо знать, сколько раз в нем содержится мерка 1°. Для измерения углов в градусах используют специальный инструмент – транспортир.
Транспортир состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы), разделённого на градусы от 0 до 180. В некоторых моделях, например, круговой транспортир – от 0 до 360. Шкала транспортира располагается на полуокружности.
Центр этой полуокружности отмечен на транспортире черточкой, его называют центр транспортира.
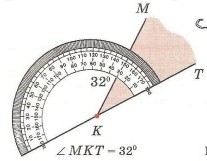
Давайте измерим ∠МКТ.
Для этого наложим транспортир так, чтобы центр транспортира совпал с точкой К — началом луча КТ, а сам луч КТ прошел через начало отсчета шкалы транспортира. Градусную меру угла покажет штрих на шкале транспортира, через который проходит другая сторона угла.
Итак, ∠МКТ равен 32°.
С помощью транспортира можно не только измерять, но и строить углы.
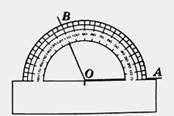
Давайте построим угол, равный 110°, одной стороной которого служит луч ОА.
Сначала проведем луч ОА.
Затем наложим транспортир на наш луч так, чтобы центр транспортира совпал с точкой О — началом луча ОА, а сам луч ОА прошел через начало отсчета шкалы транспортира.
Поставим точку В против штриха шкалы транспортира с отметкой 110° и проведем луч ОВ.
Получим ∠АОВ, содержащий 110°.
Для удобства отсчет градусов по шкале транспортира идет в двух направлениях, и, когда мы измеряем или строим угол, всегда нужно помнить, что острый угол меньше 90°, а тупой больше 90°.
§ 3 Краткие итоги урока
Подведем итоги нашего урока:
1. Углы измеряют при помощи транспортира.
2. Чтобы измерить угол транспортиром, нужно:
· приложить центр транспортира к вершине угла;
· расположить транспортир так, чтобы одна сторона угла прошла через начало отсчета шкалы транспортира деление 0;
· посмотреть, через какое деление этой шкалы пройдет другая сторона угла;
· при измерении нужно помнить, что острый угол меньше 90°, а тупой больше 90°.
3. Чтобы построить угол определенной величины, нужно:
· провести луч;
· наложить на этот луч транспортир так, чтобы центр транспортира совпал с началом луча, а сам луч прошел через начало отсчета шкалы транспортира деление 0;
· поставить точку против штриха шкалы транспортира с отметкой нужной нам величины и провести через эту точку второй луч от начала исходного луча.
4. Прямой угол равен 90°, острый угол — меньше 90°, а тупой угол — больше 90°, развернутый угол равен 180°.
5. При сложении углов их градусные меры складываются, а при вычитании – вычитаются.
6. Сумма смежных углов всегда равна 180°.
Список использованной литературы:
- Петерсон Л.Г. Математика. 4 класс. Часть 1. / Л.Г. Петерсон. – М.: Ювента, 2014. – 96 с.: ил.
- Математика. 4 класс. Методические рекомендации к учебнику математики «Учусь учиться» для 4 класса. / Л.Г. Петерсон. – М.: Ювента, 2014. – 280 с.: ил.
- Зак С.М. Все задания к учебнику математики для 4 класса Л.Г. Петерсон и комплекту самостоятельных и контрольных работ. ФГОС. – М.: ЮНВЕС, 2014.
Во время сегодняшнего урока мы изучим понятие смежных и вертикальных углов, свойства смежных и вертикальных углов. Также разберемся, в чем отличие аксиомы от теоремы.
Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.
Свойства смежных углов:
- Сумма смежных углов равна 1800.
- Если два угла равны, то и смежные с ними углы равны.
- Угол, смежный с прямым углом, есть прямой угол.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Свойство вертикальных углов: вертикальные углы равны.
Аксиома – положение, принимаемое без доказательств.
Развернутый угол — угoл, стороны которого лежат на одной прямой.
Прямой угoл — угoл, который равен половине развернутого угла.
Острый угол — угoл меньше прямого угла.
Тупой угoл — угoл больше прямого, но меньше развернутого.
Единицы измерения углов:
- Градус — величина (градусная мера) угла, равная части развернутого угла.
- Минута — часть градуса.
- Секунда — часть минуты.
Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Следовательно, два смежных угла составляют развернутый угол. Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны (только в том случае, когда смежные углы не равны).
Например, мы чертим прямую АС, в середину у нее точка В, из которой прочерчен луч ВD. В этом случае ∠ABD и ∠DBC — это смежные углы, AC — прямая, луч BD — общая сторона углов и наклонная к прямой AC, ∠ABC — развернутый угол, B — основание наклонной.
Чтобы построить угол, смежный с данным углом, нужно одну из сторон угла продлить за вершину.
Сумма смежных углов
Любые два смежных угла составляют в сумме развернутый угол. Развернутый угол равен двум прямым углам, поэтому можно сказать, что сумма двух смежных углов равна двум прямым углам.
Изобразим прямую MN, отметим на ней точку A. Получили развернутый угол MAN. Проведем произвольный луч АК с началом в точке А.
Луч АК разделил развернутый угол MAN на два угла: MAK и KAN. Эти два угла и являются смежными.
Смежными называются два угла, у которых одна сторона общая, а две другие являются дополнительными полупрямыми.
На рисунке сверху АК – общая сторона, АМ и AN – дополнительные полупрямые. (Напомню, что дополнительные полупрямые – это две полупрямые, лежащие на одной прямой, имеющие общее начало и направленные в разные стороны).
Поскольку смежные углы вместе составляют развернутый угол, то они обладают следующим свойством:
ТЕОРЕМА: Сумма смежных улов равна 180 о
Дано: угол AON и угол NOB – смежные.
Доказать: AON + NOB = 180 о.
Доказательство:
По определению смежных углов, луч ON является общей стороной углов AON и NOB, значит, он проходит между сторонами угла AOB. По аксиоме V (градусная мера угла равна сумме градусных мер углов, на которые он разбивается каким-нибудь лучом, проходящим между его сторонами) можем записать равенство:
угол AOB = угол AON + угол NOB
Опять-таки, по определению смежных углов, лучи ОА и ОВ — дополнительные, значит, образуют развернутый угол АОВ. А развёрнутый угол имеет градусную меру, равную 180о. Значит,
угол AON + угол NOB = 180о
Из этой теоремы выходят три следствия, которые предлагаются для самостоятельного доказательства.
Следствие 1. Если два угла равны, то смежные с ними углы тоже равны.
Следствие 2. Угол, смежный с прямым углом, есть прямой угол.
Следствие 3. Угол, смежный с острым углом, — тупой; угол, смежный с тупым углом, — острый.
Вертикальные углы
Вертикальные углы — это пара углов, у которых стороны одного угла являются продолжением сторон другого угла. Пересечение двух прямых линий образует две пары вертикальных углов.
Давайте проведем две прямые АВ и CD, пересекающиеся в точке О. Среди всех получившихся углов обратим внимание на те углы, стороны которых являются дополнительными полупрямыми.
Вертикальными называются два угла, у которых стороны одного угла являются дополнительными полупрямыми к сторонам другого угла.
На рисунке луч ОА является дополнительным к лучу ОВ, а луч ОС – дополнительным к лучу OD. Значит, угол АОС и угол BOD – вертикальные. Аналогично, угол AOD и угол BOC – тоже вертикальные.
То есть, при пересечении двух прямых получается две пары вертикальных углов. Визуально вы, наверное, уже успели заметить, что вертикальные углы равны. А теперь мы это докажем.
ТЕОРЕМА: Вертикальные углы равны
Дано: угол АОС и угол BOD – вертикальные, угол AOD и угол BOC – вертикальные.
Доказать: угол АОС = углу BOD и угол AOD = углу BOC.
Доказательство:
- развернутый, значит, . Луч проходит между его сторонами, т.е.
- развернутый, значит, . Луч проходит между его сторонами, т.е.
Рассмотрим последние равенства из пункта 1 и пункта 2:
Здесь мы использовали логическую связку: «Если в двух равенствах правые части равны, значит, равны и левые части».
Аналогично доказывается равенство углов .
Измерение углов
1) Каждый угол имеет определенную градусную меру больше нуля.
2) Развернутый угол равен 180о.
3) Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
4) Равные углы имеют равные градусные меры.
5) Если два угла имеют равные градусные меры, то они равны.
Сегодня мы говорили о смежных и вертикальных углах и об измерении углов. Мы смогли доказать теоремы. Сумели разобраться со свойствами смежных углов.