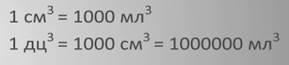Цели урока:
Образовательные цели: сформировать у учащихся представления о понятии объема. Выявить свойства объемов.
Развивающие цели: содействовать развитию пространственного мышления. Содействовать развитию умений обобщать и систематизировать полученные знания.
Воспитательные цели: привить интерес к геометрии. Воспитать ответственное отношение к учебному труду.
Тип урока: урок объяснения нового материала.
Ход урока:
1. Организационный момент.
- приветствие;
- проверка готовности учащихся к уроку;
- организация внимания учащихся.
2. Объяснение нового материала.
В повседневной жизни очень часто нам приходится сталкиваться с понятием объема. Например, нас интересует объем вместимость коробки или банки.
А в практической деятельности человеку необходимо уметь вычислять объем при изготовлении каких-либо деталей, или при строительстве различных сооружений. Ведь многие строительные объекты и детали конструкций имеют форму геометрических тел: параллелепипедов, призм, пирамид, шаров и т. д.
Итак, мы с вами продолжаем изучать стереометрию.
Давайте разберемся, что же мы будем понимать под понятием объема.
Проще всего измерить объем прямоугольного параллелепипеда.
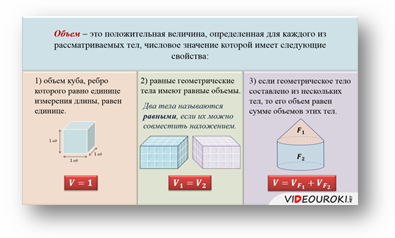
Итак, объем — это положительная величина, определенная для каждого из рассматриваемых тел, числовое значение которой имеет следующие свойства:
Давайте ответим на несколько несложных вопросов.
3. Обобщение и закрепление нового материала.
На этом уроке мы говорили об объеме, одной из важных величин, связанной с геометрическими телами.
Объем — это положительная величина, определенная для каждого из рассматриваемых тел, числовое значение которой имеет следующие свойства:
1) равные геометрические тела имеют равные объемы;
2) если геометрическое тело составлено из нескольких тел, то его объем равен сумме объемов этих тел;
3) объем куба, ребро которого равно единице измерения длины, равен единице.
4. Рефлексия.
Хотелось бы узнать, понравился ли вам урок? Что было не понятным на уроке? Что еще бы вы хотели узнать?
5. Домашнее задание.
Содержание:
- § 1 Расчет массы и объема вещества по его плотности
- § 2 Решение задач
- § 3 Важно запомнить
§ 1 Расчет массы и объема вещества по его плотности
В этом уроке мы изучим, как можно определить массу и объем тела, если известна плотность вещества.
Плотность – скалярная физическая величина, показывающая, чему равна масса вещества, взятого в объеме 1 м3, и равная отношению массы тела к его объему: p = m : v.
Из формулы плотности следует, что масса тела равна произведению плотности вещества на объем этого тела: m = ρ · V.
Чтобы вычислить объем тела, нужно массу тела разделить на его плотность: v = m : p.
Для правильного решения задач нужно уметь верно переводить единицы измерения величин в Международную систему единиц: 1 г = 0,001 кг, 1 л = 1 дм3 = 0,001 м3, 1 см3 = 0,000 001 м3, 1 г/см3 = 1000 кг/м3.
§ 2 Решение задач
Какова масса подсолнечного масла в бутылке объемом 3 л, если плотность масла равна 930 кг/м3?
Запишем условие задачи. Нам известны объем бутылки (обозначается буквой V) 3 л, и плотность подсолнечного масла (обозначается буквой ρ) 930 кг/м3. Выразим объем бутылки в Международной системе единиц. 1 л = 0,001 м3, следовательно, 3 л составляют 0,003 м3.
Решение: Чтобы найти массу тела, нужно плотность умножить на объем: m = ρ · V. Подставим числовые значения величин: 930 кг/м3 · 0,003 м3 = 2,79 кг.
Сколько штук строительного кирпича размером 250 мм х 120 мм х 65 мм допускается перевозить на автомашине грузоподъемностью 4 т? Плотность кирпича 1800 кг/м3.
Запишем условие задачи и выразим данные в Международной системе единиц. Известны размеры кирпича: длина а = 250 мм = 0,25 м, ширина b= 120 мм = 0,12 м, высота с = 60 мм = 0,06 м, плотность кирпича ρ = 1800 кг/м3, грузоподъемность – наибольшая масса груза, которую может перевезти автомобиль – m = 4 т = 4000 кг. Найти количество кирпичей – обозначим латинской буквой N.
Решение: Количество кирпичей можно найти, поделив общую массу всех кирпичей на массу одного кирпича: N = m/m1. Чтобы найти массу одного кирпича, нужно плотность умножить на его объем: m1 = ρ · V. Кирпич имеет форму прямоугольного параллелепипеда, следовательно, его объем равен произведению длины, ширины и высоты кирпича. Подставим числовые значения известных величин и вычислим. Объем кирпича равен 0,0018 м3. Масса одного кирпича m1 равна 1800 кг/м3 , умножим на 0,0018 м3 , равно 3,24 кг. Тогда число кирпичей равно N 4000 кг, разделим на 3,24 кг и получим 1234, 567 штук или число целых кирпичей 1234 штуки.
Медный шар имеет массу 840 г при объеме 120 см3. Сплошной этот шар или полый? Плотность меди 8900 кг/м3.
Запишем условие задачи. Известна масса шара m 840 г, что в системе СИ составляет 0,84 кг, объем шара V=120 см3, в СИ 0,00 012 м3, плотность меди ρ = 8900 кг/м3. Определить, сплошной шар или содержит внутри пустое пространство?
Решение. Представим, что на рычажных весах лежат два медных шара, один сплошной, второй содержит внутри пустое пространство, то есть полый шар. Если у них массы одинаковы, то объем полого шара должен быть больше, чем объем сплошного шара (рис 1).
Определим, каков объем шара, состоящего полностью из меди. Если объем окажется равным 120 см3, то шар сплошной и пустот не содержит. Если же вычисленный объем окажется меньше 120 см3, значит, внутри есть полость.
Чтобы найти объем сплошного медного шара, массу шара разделим на его плотность. Для упрощения проведем вычисления в граммах и кубических сантиметрах.
§ 3 Важно запомнить
Плотность – скалярная физическая величина, показывающая, чему равна масса вещества, взятого в объеме 1 м3, и равная отношению массы тела к его объему: p = m : v.
Масса тела равна произведению плотности вещества на объем этого тела: m = ρ · V.
Чтобы вычислить объем тела, нужно массу тела разделить на его плотность: V = m : p.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. — М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс — М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
Использованные изображения:
§ 1 Понятие объема и единицы измерения объема
В этом уроке Вы познакомитесь с таким понятием как объем, узнаете о единицах измерения объёма, а также научитесь находить объем прямоугольного параллелепипеда.
Объем – это количественная характеристика пространства, занимаемого телом. Объем тела или фигуры определяется его формой и размерами.
Единицами измерения объема являются:
кубический миллиметр,
кубический сантиметр,
кубический дециметр,
кубический метр,
кубический километр.
Кубический сантиметр – это объем куба с ребром 1 см, кубический метр – это объем куба с ребром 1 м, кубический дециметр – это объем куба с ребром 1 дм. Между прочим, кубический дециметр также называют литром. Т.е. 1 литр равен одному кубическому дециметру.
Единицы измерения объема связаны друг с другом.
Например,
1 кубический сантиметр = 1000 кубическим миллиметрам,
а 1 кубический дециметр – это 1000 кубических сантиметров или 1 000 000 кубических миллиметров.
§ 2 Объем прямоугольного параллелепипеда
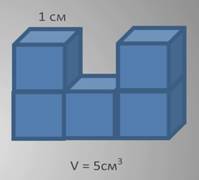
Рассмотрим фигуру, состоящую из 5 кубиков с ребром 1 см.
Так как объем каждого кубика составляет 1 кубический сантиметр, значит, объем всей фигуры равен 5 кубическим сантиметрам.
Т.е. можно сделать вывод, что объем всей фигуры равен сумме объемов ее частей.
Давайте выведем правило для вычисления объема прямоугольного параллелепипеда.
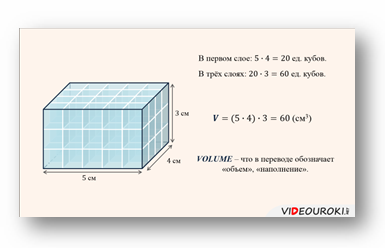
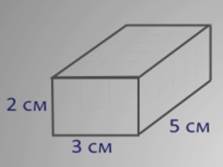
Пусть прямоугольный параллелепипед имеет длину 5 см, ширину 3 см и высоту 2 см.
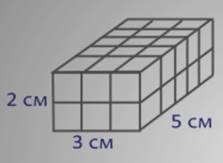
Разобьём его на два слоя толщиной 1 см каждый.
Т.е. первый слой состоит из 15 кубиков, так как в длину 5 кубиков и в ширину 3 кубика, а 5 умножить на 3, будет 15. Второй слой такой же.
Значит, чтобы найти объем всего параллелепипеда надо 15 умножить на 2.
Т.е. перемножили 5 и 3 – длину и ширину, а затем помножили на 2, т.е. на высоту.
Таким образом, получили правило:
Чтобы найти объем прямоугольного параллелепипеда, надо его длину умножить на ширину и на высоту.
В формулах для обозначения объёма используется заглавная латинская буква V, являющаяся сокращением от лат. Volume — «объём» или «наполнение».
Формула объема прямоугольного параллелепипеда имеет вид:
V = авс, где V – это объем, а, в, и с – измерения (т.е. длина, ширина, высота).
Давайте решим задачу, например, найти объем прямоугольного параллелепипеда, длина которого равна 10 см, ширина 4 см, высота 3 см.
Решение: чтобы найти объем прямоугольного параллелепипеда, нужно перемножить длину, ширину и высоту, т.е. 10 умножить на 4 и умножить на 3, получаем 120.
Ответ: объем равен 120 кубическим сантиметрам.
Таким образом, на этом уроке Вы познакомились с таким понятием как объем, узнали о единицах измерения объёма – кубические миллиметры, кубические сантиметры, кубические метры и так далее. А также получили правило для нахождения объема прямоугольного параллелепипеда: чтобы найти объем прямоугольного параллелепипеда, надо его длину умножить на ширину и на высоту.
Видеоурок: Объем и площадь поверхности многогранников
Лекция: Объём куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара
Для нахождения объема любого тела необходимо произведение трех параметров тела. Именно поэтому, чтобы проверить правильность решения, следует убедиться в том, что в выведенной Вами формуле оказалось в виде множителя три параметра тела.

Для нахождения объема куба следует перемножить три стороны. Так как в кубе все они равны, следует просто возвести значение стороны в куб: V = a3

Так как в данной фигуре все углы прямые, то её объем находится просто, как произведение всех сторон: V = abc

Как уже говорилось ранее, эти две фигуры очень похожи. Различие только в том, что у нее разные основания.
Объем пирамиды и конуса находится, как третья произведения площади основания на высоту: V = SocH/3
Для пирамиды данная формула изменяется в зависимости от многоугольника, который будет находится в основании.
У конуса же данная формула стандартна, поскольку в его основании лежит окружность: V = πR2H/3

Для нахождения объема цилиндра необходимо найти произведение площади основания на высоту. Так как в основании лежит окружность, получается следующая формула: V = πR2H
Не трудно заметить, что формула цилиндра очень похожа на формулу для нахождения объема конуса.

Как и в нескольких предыдущих случаях, объем призмы находится, как произведение основания на высоту. И не важно, прямая ли эта призма или нет.
Данная формула видоизменяется в зависимости от того, какой многоугольник лежит в основании. Формула очень похожа на формулу нахождения объема пирамиды: V = SocH

Для нахождения объема шара достаточно воспользоваться несложной формулой: V = 4/3*πR3