Как найти высоту в треугольной пирамиде
Треугольной называется пирамида, в основании которой лежит треугольник. Высотой такой пирамиды будет перпендикуляр, опущенный из вершины на плоскость ее основания. Для того, чтобы найти высоту правильной треугольной пирамиды, то есть такой пирамиды, все грани которой являются равносторонними треугольниками, необходимо знать длину ребра пирамиды (а).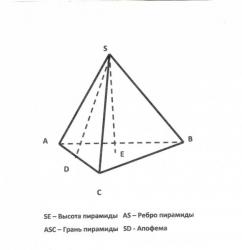
В данном случае ребрами пирамиды будут стороны этих равносторонних треугольников. Высотой правильной треугольной пирамиды будет длина ребра пирамиды, помноженная на корень из двух третей : h=а√2/3.
Для вычисления высоты любой другой треугольной пирамиды можно воспользоваться формулой объема: V = 1/3Sh, где V — это объем пирамиды, S — это площадь основания, а h — это высота. Из формулы объема выводим формулу высоты: чтобы найти высоту треугольной пирамиды, необходимо умножить объем пирамиды на 3 и поделить полученное значение на площадь основания: h=3V/S.
Поскольку основанием треугольной пирамиды служит треугольник, воспользуемся формулой расчета площади треугольника. Если известна длина одной стороны этого треугольника (а) и высота (h), опущенная на эту сторону, то рассчитываем площадь, умножив длину стороны на длину высоты и поделив полученное значение на 2: S=1/2ah. Если известны две стороны треугольника (a и b) и угол между ними (C), то пользуемся формулой: S=1/2absinC. Значение синуса угла можно посмотреть в таблице синусов, которую легко найти в Интернете.
Как правило, если в задаче требуется найти высоту треугольной пирамиды, объем этой пирамиды известен. Поэтому, после того, как найдена площадь основания пирамиды, остается только умножить объем на 3 и поделить на площадь основания, чтобы получить высоту треугольной пирамиды.
Правильная треугольная пирамида – это пирамида, у которой в основании лежит правильный, иными
словами, равносторонний треугольник и у которой боковые стороны – это равнобедренные треугольники.
Такая объемная фигура также именуется правильным тетраэдром. Высота – это отрезок перпендикуляра,
проведенного из вершины фигуры на основание или на продолжение основания. Обозначается латинской
буквой h и на чертеже отмечается квадратом. Высота треугольной пирамиды, проведенная из вершины,
попадает на основание в центр пересечения медиан фигуры.
- Высота правильной треугольной пирамиды через обьём и
площадь основания - Высота правильной треугольной пирамиды через обьём и ребро
основания
Через объём и площадь основания
Объем любой пирамиды находится по формуле: V = 1/3h * S, где h является высотой пирамиды, а S
является площадью основания пирамиды. Из этой формулы можно получить формулу для нахождения высоты
пирамиды:
h = (V * 3) / S
Цифр после
запятой:
Результат в:
Пример. По условию дана правильная треугольная пирамида, у которой площадь
основания равна S = 18 см², а объем равен V = 90 смᶾ, нужно найти высоту фигуру. Для этого нужно
подставить в формулу все известны переменные, тогда h = 90 * 3 / 18 = 15,
значит высота равна 15 см. Так можно находить высоту и правильной, и наклонной фигуры.
Через объём и ребро основания
Найти высоту правильной треугольной пирамиды можно также через объем и ребро основания в случае,
когда неизвестна площадь основания. Вычисления в данном случае надо производить по формуле:
H = √ (V * 4 * √3 / a²)
Цифр после
запятой:
Результат в:
Пример. Дана правильная треугольная пирамида с объемом V = 90 смᶾ и длиной ребра
основания a = 5 см, нужно найти высоту этой фигуры. Подставим значения в формулу и получим: H = √ (90 * 4 * √3 / 5²) = 5 см.
Найти высоту правильной треугольной пирамиды можно также через объем и ребро основания по-другому.
Итак, V = 1/3h * S, значит h = V * 3 / S.
Поскольку площадь основания нам не известна, но известно ребро, то площадь можно выразить по
формуле: S = 1/2 * a * b * sin α, где a и b равны между собой, поскольку
пирамида по условию задачи является правильной, а sin α = sin 60°, в
равностороннем треугольнике все углы раны 60°.
Подставив формулу площади основания пирамиды через стороны треугольника и синус в исходную формулу,
получим: h = (V * 3 * 2) / (a * b * sin α).
Пример. Дана правильная треугольная пирамида с объемом V = 90 смᶾ и длиной ребра
основания a = 5 см, нужно найти высоту этой фигуры. При решении задачи сначала необходимо выполнить
все преобразования, описанные выше, а затем уже переходить к подстановке числовых значений. Это
принцип соблюдения логики при решении математических задач. В ином случае вам не поставят полный
балл за задачу, поскольку конечной формулы нет в кодификаторе. Выполнив все преобразования можно
подставлять числа, получается: h = (90 * 3 * 2) / (5 * 5 * (√3 / 2)),
преобразовываем это выражение до h = (18 * 3 * 2 * 2) / (5 * √3),
получается h = (72 * 3 * √3) / (5 * 3) = (72 * √3) / 5.
Получается для того, чтобы вычислить высоту в правильной треугольной пирамиде (тетраэдре) прежде
всего так или иначе нужно отыскать площадь основания и объем фигуры. Чтобы определить площадь
достаточно иметь данные об одном из ребер основания фигуры. Вычисление высоты пирамиды может
пригодиться при нахождении объема фигуры.
Высота правильной треугольной пирамиды.
Основание правильной пирамиды представляет собой правильный многоугольник. Так как мы имеем дело с треугольной пирамидой, то её основанием будет равносторонний треугольник.
Чтобы найти высоту пирамиды SO, достаточно вспомнить, что:
1) AO = BO = CO = R = a√3 / 3. (св-во равностороннего треугольника).
2) SB = AB. (боковое ребро равно длине стороны основания).
По теореме Пифагора высота SO равна:
SO = √(SB² — OB²) = √(a² — a²/3) = √(a²(1 — 1/3)) = √(a² * (2/3) = a√(2/3).
Итак, высота правильной треугольной пирамиды (H) равна произведению длины ребра (a) на корень из 2/3:
Высоту пирамиды также можно найти из формулы объёма:
V = 1 / 3 Sосн * H.
Так как основание пирамиды — это равносторонний треугольник, то Sосн = a² * √3 / 4.
Отсюда V = a² * √3 * H / 12 = a² * H / 4√3.
Остаётся выразить высоту:
V * 4√3 = a² * H.
H = V * (4√3 / a²).
Высота правильной треугольной пирамиды (H) равна дроби — в числителе произведение объёма пирамиды (V) на 4√3, в знаменателе — квадрат ребра (a).
Если же в условии задачи уже известна площадь основания, то высоту найти ещё проще:
H = 3 * V / Sосн.
Пример
Сторона основания правильной треугольной пирамиды равна 4 см, объём равен 10√3.
Нужно найти высоту пирамиды.
Воспользуемся вышеприведённой формулой:
H = V * (4√3 / a²) = 10√3 * 4√3 / 16 = 120 / 16 = 7,5 см.
Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) – треугольники, имеющие общую вершину (вершину пирамиды) – точку пересечения отрезков (боковых ребер), соединяющих ее с вершинами основания.
Пирамида является многогранником.
Высотой пирамиды называется перпендикуляр, опущенный из ее вершины на плоскость основания.
В зависимости от многоугольника, являющегося основанием, пирамида может быть:
-
треугольной (тетраэдром, или четырехгранником),
-
четырехугольной,
-
пятиугольной,
-
шестиугольной и т.д., n-угольной.
Треугольная, четырехугольная и пятиугольная пирамида
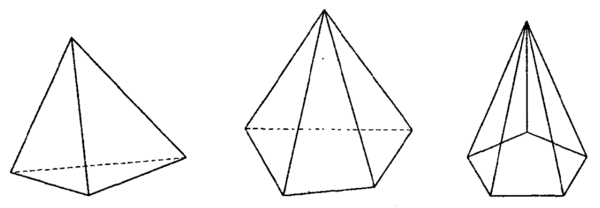
Рис.1
Пирамида называется правильной, если в основании лежит правильный многоугольник, а ее высота проходит через центр основания. Все боковые ребра правильной пирамиды равны; все боковые грани — равнобедренные треугольники.
Высота боковой грани правильной пирамиды называется апофемой. Тело, ограниченное сечением, проведенным в пирамиде параллельно основанию, основанием пирамиды, и заключенной между ними боковой поверхностью, называется усеченной пирамидой.
Усеченная пирамида
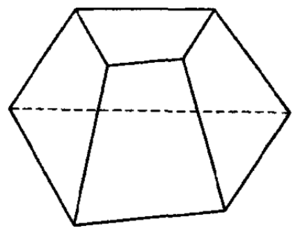
Рис.2
Пирамида – многогранник, в основании которого n − угольник, а остальные n граней – треугольники с общей вершиной.
Объем пирамиды V вычисляется по формуле : $V = frac{1}{3}SH$ , где S – площадь основания пирамиды, H – высота пирамиды.
Правильная пирамида – пирамида, основанием которой является правильный многоугольник, а высота пирамиды проходит через центр основания.
Свойства правильной пирамиды:
-
Боковые рёбра правильной пирамиды равны.
-
Боковые грани правильной пирамиды являются равными равнобедренными треугольниками.
Усеченная пирамида – это часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию.
Объем усеченной пирамиды вычисляется по формуле : $V = frac{1}{3} H( S_1 + S_2 + sqrt{S_1 cdot S_2} )$ , где H – высота усеченной пирамиды, S1 и S2 – площади ее оснований.
Вершина пирамиды – общая вершина всех боковых граней.
Боковые рёбра –стороны боковых граней, не лежащие в основании пирамиды.
Высота пирамиды – перпендикуляр, проведённый из вершины пирамиды к плоскости основания.
Площадь полной поверхности пирамиды – сумма площадей всех её граней.
Площадь боковой поверхности пирамиды – сумма площадей её боковых граней.
Пример №1

Пример №2

Пример №3: есть опечатка
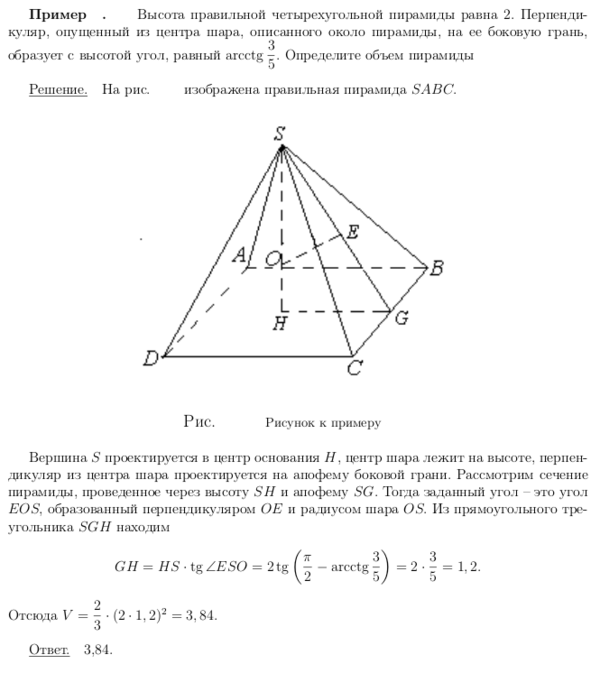

Формула для вычисления объёма пирамиды V=1/3Sh, S — площадь основания, h — высота пирамиды. Найди высоту, если V=75, S=30.




