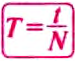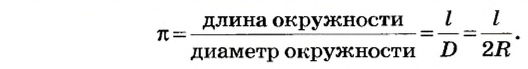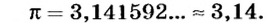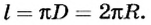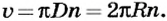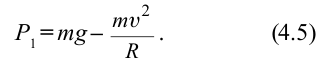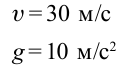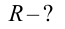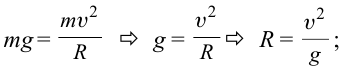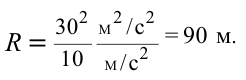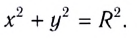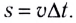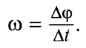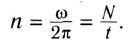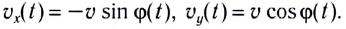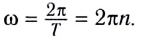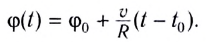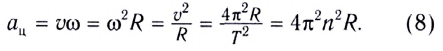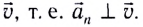Положение
частицы, движущейся по окружности, можно
задать углом
,
который образует радиус-вектор с
каким-либо неизменным направлением
.
Движения частицы по окружности
Характеризуется угловой скоростью и
угловым ускорением.
Угловой
скоростью называется производная угла
поворота радиус-вектора, определяющего
положение материальной точки, по времени
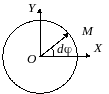
Рис.
1.9
.
При равномерном вращении угловую
скорость называют также угловой
частотой вращения. Она показывает,
на какой угол поворачивается радиус-вектор,
определяющий положение материальной
точки, за единицу времени. Величина
дает число оборотов в единицу времени
и называется частотой вращения.
Время, за которое частица совершает
полный оборот, называется периодом
вращения.

Рис.
1.10
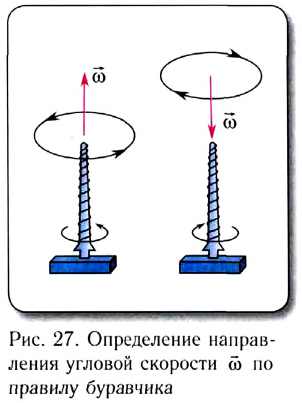
Вектор угловой скорости можно
записать через вектор углового
перемещения. Пусть за время
радиус-вектор, определяющий положение
материальной точки, поворачивается на
угол
.
Элементарное угловое перемещение
характеризуется не только своим
значением, но и плоскостью, в которой
оно происходит. Чтобы фиксировать эту
плоскость следует
рассматривать как вектор, перпендикулярный
этой плоскости. Его направление находится
по правилу правого винта: если винт
вращать в сторону увеличения
,
то направление движения винта должно
совпадать с вектором
.
Однако, чтобы иметь основание определенную
так величину
называть вектором, необходимо доказать,
что она обладает его свойствами.
Действительно,
путь, проходимый частицей при очень
малом повороте, можно считать прямолинейным.
Поэтому два совершаемых последовательно
очень малых поворота
и
обусловливают, как видно из рис. 1.10,
такое же перемещение
частицы
,
как и поворот
,
получаемый из
и
сложением по правилу параллелограмма.
Отсюда следует, что очень малые повороты
можно рассматривать как векторы. Тогда
вектор угловой скорости можно записать
следующим образом:
,
а
перемещение частицы
.
(1.1)
Вектор
угловой скорости
может изменяться как за счет изменения
скорости вращения тела, так и за счет
поворота оси в пространстве. Пусть за
время
вектор
получает приращение
.
Изменение вектора угловой скорости со
временем характеризуется величиной
,
которая
называется угловым ускорением.
Отдельные
точки вращающегося тела имеют различные
линейные скорости
,
скорость каждой из точек непрерывно
изменяет свое направление. Можно
показать, что модуль линейной скорости
зависит от угловой скорости и от
расстояния до оси вращения. Пусть за
малый промежуток времени
тело повернулось на угол
.
Точка, находящаяся на расстоянии
от оси вращения проходит при этом путь
.
Модуль линейной скорости точки равен
.
Таким
образом
.
(1.2)

Рис.
1.11
Соотношение (1.2) связывает модули
линейной и угловой скорости.
Найдем
выражение, связывающее векторы
и
.
Положение движущейся точки будем
определять радиус-вектором
,
проведенным из начала координат, лежащего
на оси вращения. Из рис. 1.11
видно, что векторное произведение
совпадает по направлению с вектором
и имеет модуль, равный
.
Следовательно,
.
Последнее выражение можно получить,
если поделить (1.1) на
.
Нормальное
и тангенциальное ускорения материальной
точки можно выразить через угловую
скорость. Нормальное ускорение можно
записать следующим образом:
.
Предположим,
что ось вращения не поворачивается в
пространстве. Тогда модуль тангенциального
ускорения
.
Воспользовавшись соотношением (1.2),
тангенциальное ускорение можно
представить следующим образом:
,
где
– модуль углового ускорения.
Таким
образом, нормальное и тангенциальное
ускорения растут линейно с увеличением
расстояния до оси вращения. Модуль
полного ускорения
,
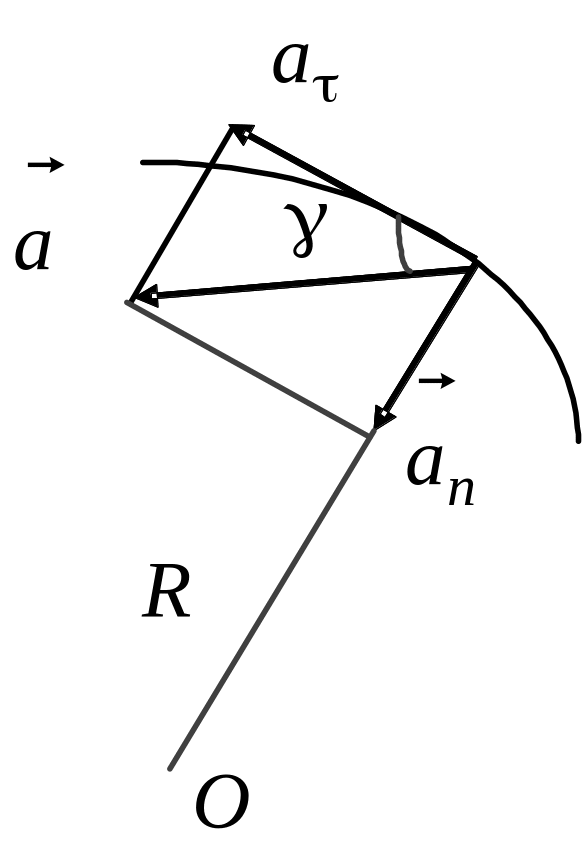
Рис.
1.12
а тангенс угла между направлениями
нормального и тангенциального ускорений
(рис.1.12)
.
Таким
образом, направление вектора
не зависит от
,
то есть одинаково для всех точек, лежащих
на одном радиусе.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
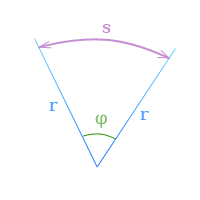
Угловое перемещение (угол поворота) — это угол, на который переместился радиус-вектор при перемещении тела из точки 1 в точку 2.
Δφ=φ-φ0
Угловое Δφ перемещения при движении тела по окружности.
Единица измерения угла поворота — 1 радиан [1 рад]. Радиан — это угол, опирающийся на дугу окружности, равную ее радиусу.
Длина дуги связана с углом поворота соотношением Δl = RΔφ.
Считая, что в начальный момент времени φ0=0, угловое перемещение (угол поворота) часто обозначают φ.
Зная угловую скорость и время, за которое был совершен поворот, можно определить угол поворота:
φ=ωt
Обозначения:
Δφ, φ— угловое перемещение (угол поворота)
Δl — длина дуги
R — радиус окружности
ω — угловая скорость
t — время, за которое был совершен поворот
Как вы знаете, в общем случае задача описания движения тел
является довольно сложной. Но кинематика позволяет нам «разложить» любое
сложное движение на три составляющих. Например, если у нас есть кусок
резинового шланга, то мы можем изогнуть его (то есть изменить его форму), можем
повернуть (то есть по-другому сориентировать в пространстве), а можем перенести
в другое место, не изменяя его формы и ориентации. Следовательно, и форма, и
ориентация в пространстве, и местоположение тела с течением времени могут
изменяться. И каждому из этих изменений соответствует один из трёх основных
видов механического движения — деформация, вращательное движение и
поступательное движение.
Во многих задачах по кинематике деформированием тела можно
пренебречь. В таких случаях для описания движения тела используют ещё одну
механическую модель — абсолютно твёрдое тело. Так принято называть тело,
расстояние между любыми двумя точками которого остаётся неизменным при его
движении.
Наиболее просто описывается поступательное движение
абсолютно твёрдого тела. При таком движении прямая, проходящая через любые две
точки тела, остаётся параллельной самой себе.
Представим себе некое абсолютно твёрдое тело, которое
движется поступательно. Выберем в нём две произвольные точки, например М
и К, и проведём через них вектор . Так
как тело абсолютно твёрдое, то длина этого вектора не изменяется в процессе
движения, как не изменяется и его направление (движение-то у нас
поступательное).
Следовательно, траектории точек М и К
одинаковы, так как они могут быть полностью совмещены параллельным переносом на
вектор .
Из полученного рисунка также видно, что перемещения
исследуемых точек одинаковы и совершаются за одно и то же время. Следовательно,
они имеют одинаковые скорости и ускорения. Любая другая точка нашего твёрдого
тела (пусть это будет точка N)
будет двигаться точно так же, как точки М и К: она опишет такую
же траекторию, совершит такое же перемещение с той же скоростью и с тем же
ускорением.
Тогда становится очевидным, что для описания
поступательного движения абсолютно твёрдого тела достаточно описать движение
какой-либо одной его точки. То есть мы можем использовать модель
материальной точки. А как описывается её движение, мы с вами уже знаем.
Примером почти поступательного движения может служить
движение выдвижного ящика письменного стола, поезда на прямолинейном участке
дороги. Даже движение педали велосипеда или кабины колеса обозрения также можно
считать поступательным.
Сложнее описывается вращательное движение абсолютно твёрдого
тела. Вращательное движение — это движение, при котором происходит изменение
ориентации тела в пространстве (проще говоря, его поворот).
В технике такой вид движения встречается очень часто:
например, вращение валов двигателей и генераторов, турбин и пропеллеров
самолётов.
Частным случаем вращательного движения является вращательное
движение вокруг неподвижной оси.
Вращательным движением абсолютно твёрдого тела вокруг
неподвижной оси называется такое его движение, при котором все точки
тела описывают окружности, центры которых находятся на одной прямой, называемой
осью вращения. При этом плоскости, которым принадлежат эти окружности,
перпендикулярны оси вращения.
Очевидно, что при вращательном движении разные точки тела
проходят за одно и то же время разные пути. Значит, и модули скоростей точек
будут отличаться друг от друга. Но вот радиус-векторы, определяющие положение
точек, за исследуемый промежуток времени поворачиваются на одинаковые углы. И
чем больше угол поворота радиус-вектора за определённый промежуток времени, тем
быстрее вращается тело. Для характеристики быстроты вращения была введена
скалярная физическая величина, называемая угловой скоростью. Она
численно равна отношению угла поворота радиус-вектора к промежутку времени, в
течение которого этот поворот произошёл:
Обозначать угловую скорость мы будем греческой буквой
(ω) «омега».
Если учесть, что в СИ угол поворота измеряется в радианах, а
время — в секундах, получим, что единицей измерения угловой скорости является
радиан в секунду (рад/с).
Давайте с вами вспомним, что радиан — это центральный
угол, опирающийся на дугу, длина которой равна радиусу окружности.
Например, полному обороту тела по окружности соответствует
угол:
Время, за которое тело совершает один полный оборот,
называется периодом вращения.
Тогда формулу для определения угловой скорости можно
переписать в таком виде:
Величина, обратная периоду, называется частотой вращения
тела. Она показывает, сколько оборотов тело совершает за единицу времени:
Обозначается частота вращения греческой буквой «Ню» (ν).
А единицей её измерения в СИ является оборот в секунду или секунда в минус
первой степени:
Таким образом, мы с вами можем получить ещё одну формулу, по
которой можно определить угловую скорость вращения тела:
Теперь давайте получим кинематическое уравнение движения тела
по окружности. Итак, пусть в начальный момент времени угловая координата
тела равна φ0,
а в некоторый момент времени t
— φ.
Тогда за промежуток времени Δt = t – t0 угол поворота
радиус-вектора Δφ
= φ – φ0. Подставим
эти данные в формулу для определения угловой скорости вращения:
И упростим её, приняв, что начальный момент времени равен
нулю.
Выразив из полученного равенства угол φ, мы и получим кинематическое
уравнение движения тела по окружности:
Оно позволяет определить положение любой точки тела в
произвольный момент времени.
Обратим внимание на то, что угловая скорость может принимать
как положительные, так и отрицательные значения. Давайте условимся брать её со
знаком «плюс», если угол между радиус-вектором, определяющим положение одной из
точек твёрдого тела, и осью ОХ увеличивается, а со знаком «минус» —
когда угол уменьшается.
Но вернёмся к нашему рисунку. Итак, очевидно, что за время
поворота радиус-вектора точка пройдёт некоторый путь, равный длине дуги
окружности. Тогда значение угла поворота радиус-вектора можно найти как
отношение длины этой дуги к радиусу окружности:
Подставим значение этого угла поворота в формулу для
определения угловой скорости тела:
Теперь вспомним, что отношение пути к промежутку времени, за
который этот путь пройдён, есть модуль скорости точки. Эту скорость мы с вами
будем называть линейной скоростью, дабы подчеркнуть её отличие от
угловой скорости. Направлена линейная скорость по касательной к окружности в
данной точке.
Тогда после небольших преобразований получим формулу,
связывающую линейную скорость с угловой:
Из этой формулы следует, что чем дальше расположена точка
тела от оси́ вращения, тем больше её линейная скорость. Но вот угловая
скорость вращения для всех точек тела одинакова.
Например, угловая скорость вращения Земли вокруг своей оси
примерно равна 7,3 ∙ 10–5 рад/с. И эта скорость будет
одинакова для любых точек нашей планеты. Но вот их линейная скорость будет
существенно отличаться. Так, например, линейная скорость вращения точки на
экваторе примерно равна 465 м/с. На широте 60о она почти в два раза
меньше (233 м/с). А на полюсах Земли — вообще равна нулю.
Мы уже с вами знаем, что при движении точки по окружности
направление вектора линейной скорости непрерывно изменяется. То есть точка
движется с ускорением, которое мы с вами назвали центростремительным. Напомним,
что его модуль прямо пропорционален квадрату линейной скорости и обратно
пропорционален радиусу окружности, по которой движется точка тела:
Учитывая это, а также связь между линейной и угловой
скоростью получим формулу, связывающую центростремительное ускорение точки тела
с угловой скоростью тела:
Предлагаем вам самостоятельно получить ещё две расчётные
формулы для центростремительного ускорения, используя связь между угловой
скоростью, периодом и частотой вращения.
Для закрепления материала решим с вами небольшую задачу.
Вертолёт начал вертикальное снижение с ускорением 0,2 м/с2.
Определите число оборотов лопасти винта за время снижения на 40 м, если её
длина равна 5 м, а частота вращения вокруг оси — 300 с–1.
Содержание:
Вращательное движение тела:
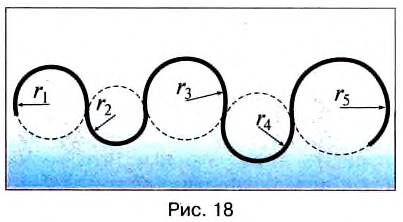
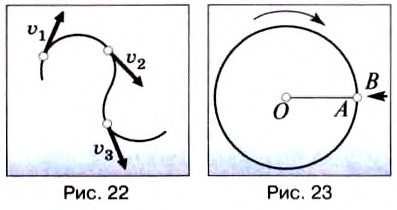
До сих пор мы изучали прямолинейное движение тел, хотя в природе и технике часто совершаются более сложные движения тел — криволинейные, когда траекторией тела является кривая линия. Любую кривую линию всегда можно представить как совокупность дуг окружностей разных радиусов (рис. 18).
Поэтому, изучив движение материальной точки по окружности, сможем в дальнейшем изучать и любые другие криволинейные движения. Кроме того, из всех возможных криволинейных движений в технике широко применяется вращательное движение деталей машин и механизмов, например вращение шестерён машин и станков, деталей, обрабатываемых на токарных станках, валов двигателей, колес машин, фрез, свёрл и т. п. Любая точка этих деталей движется по окружности. Эти две особенности и обусловили обязательное изучение движения по окружности, а именно — равномерное движение тела по окружности.
Движение материальной точки по круговой траектории с постоянной по значению, но изменяющейся по направлению скоростью, называют равномерным движением по окружности.
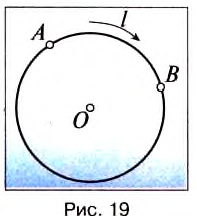
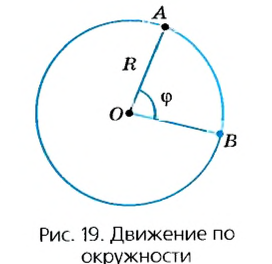
Предположим, что тело равномерно движется по окружности из точки А в точку В (рис. 19). Тогда пройденный им путь — это длина дуги
где 
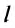
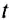
Направление скорости проще всего определить на опыте.
Опыт:
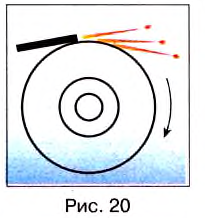
К вращающемуся точильному кругу, прикоснемся железным стержнем. Увидим, что искры из-под стержня летят по касательной к окружности этого круга (рис. 20).
Результат будет таким же в любой точке этого круга. Но каждая искра — это раскалённая частичка, оторвавшаяся от круга и летящая с такой же скоростью, какую она имела в последний момент движения вместе с кругом.
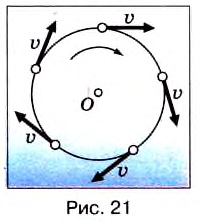
Итак, скорость материальной точки при движении по окружности направлена по касательной к ней в любой точке круга (рис. 21), а с учётом представления кривой на рисунке 18 этот вывод можно распространить на любые криволинейные движения (рис. 22).
Опыт:
Закрепим на горизонтальной оси О фанерный диск (рис. 23), на котором проведен радиус ОА. Напротив точки А поставим указатель В и будем медленно и равномерно вращать диск. Увидим, что точка А с каждым оборотом диска снова появляется напротив указателя В, т. е. совершает движение, повторяющееся через определенный интервал времени.
Движения, при которых определенные положения материальной точки повторяются через одинаковые интервалы времени, называют периодическими движениями.
Равномерное движение по окружности — это периодическое движение. Периодическое движение характеризуют такими величинами, как период обращения и частота обращения.
Период обращения — это интервал времени, в течение которого материальная точка совершает один оборот при равномерном движении по окружности.
Обозначается период обращения большой латинской буквой Т.
Если за время 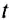
Единицей периода обращения в СИ является одна секунда (1 с).
Если период обращения равняется 1 с, то материальная точка при равномерном движении по окружности осуществляет один оборот за 1 с.
Частота обращения определяется числом оборотов, которое материальная точка совершает за единицу времени при равномерном движении по окружности
Обозначается частота обращения малой латинской буквой 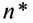
* В научной и учебной литературе частоту обращения еще обозначают малой греческой буквой 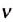
Если за время 
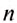

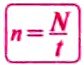


Из последней формулы видно, что частота обращения и период обращения связаны обратно пропорциональной зависимостью, а для определения единицы частоты обращения нужно единицу разделить на единицу периода обращения, т. е. на секунду.
Единицей частоты обращения в СИ является единица, разделённая на секунду 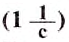
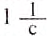
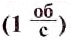
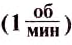
Движение точки по окружности
Движения, происходящие в природе и технике, могут отличаться по изменению значения скоростей и по изменению направления скоростей. Так, например, при движении точки вдоль прямой линии в одном направлении направление скорости не меняется, хотя ее значение может быть различным. В этом случае движение считается неравномерным.
Но движения могут быть и криволинейными, например, точки могут двигаться по окружностям. На рисунке 18 изображена траектория движения точек нити или ленты между круглыми барабанами. Такие траектории можно представить в виде отрезков прямых линий и окружностей разных размеров. Понятно, что такие движения могут быть и равномерными, каждая точка все время будет иметь одинаковую скорость по значению, хотя направление скорости от точки к точке траектории может меняться.
Рассмотрим движение материальной точки по окружности, когда это движение равномерно, т. е. значение скорости остается постоянным (рис. 19). Точка, двигаясь по окружности радиуса R, за определенное время 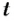

где 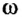

Угловое перемещение определяется в радианах (рад.). 1 радиан — это такое перемещение, когда траектория движения точки — длина дуги окружности АВ — равна длине радиуса R.
Единицей угловой скорости является радиан в секунду (рад/с).
1 рад/с равен угловой скорости такого равномерного движения по окружности, при котором за 1 с осуществляется угловое перемещение 1 рад.
При определении угловой скорости слово «рад» обычно не пишут, а просто обозначают 1/с (имеется в виду рад/с).
Движение точки по окружности (и вращение твердого тела) характеризуют также такие величины, как период и частота вращения.
Период вращения (Т) — это время, на протяжении которого точка (тело) совершает один полный оборот по окружности. Период вращения:
где t — время вращения, N — количество выполненных оборотов.
Период вращения Т измеряется в секундах. Период равен 1 с, если точка (тело) осуществляет один оборот в секунду. Частота вращения (вращательная частота):
где N — количество совершенных оборотов за время t .
Частота вращения измеряется в оборотах за секунду (об/с).
Частота вращения 
Еще Архимед установил, что для всех окружностей любого радиуса отношение длины окружности к его диаметру является величиной постоянной. это число обозначили греческой буквой 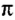
Таким образом, длина окружности
За один оборот материальная точка осуществляет угловое перемещение 2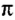
Движение по окружности характеризуется привычным для нас понятием скорости как пути, который проходит точка за единицу времени. В данном случае эта скорость называется линейной. Если учитывать, что за один оборот (время Т) точка проходит путь 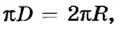
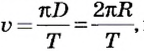
Вращение твердого тела
Твердые тела состоят из большого количества частичек. Абсолютно твердыми наукой считаются тела, расстояние между точками которых не изменяется во время явлений, которые с ними происходят. Однако следует иметь в виду, что абсолютно твердых тел в природе нет.
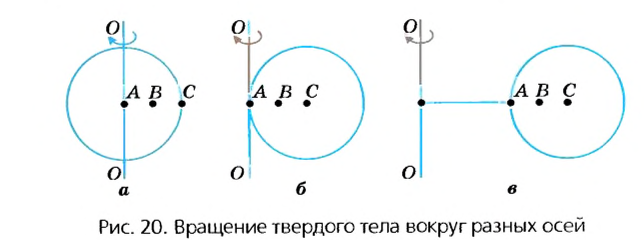
Как упоминалось в § 3, движения твердых тел бывают поступательные и вращательные. Твердые тела могут вращаться вокруг любых осей, в том числе и тех, которые проходят через их центры.
В случае а (рис. 20) ось вращения проходит через центр шара (например, вращаются колеса транспортных средств или Земля в своем суточном вращении вокруг оси). В случае в ось проходит через край шара. В случае в шар находится на определенном расстоянии от оси (например, Земля движется вокруг Солнца или Луна вокруг Земли). В некоторых случаях даже Землю и Луну можно считать материальными точками, а в некоторых случаях это сделать невозможно. Подумайте, в каких?
Что же является наиболее характерным для вращательного движения твердых тел? Очевидно, что при этом все точки этих тел в своем движении описывают окружности, центры которых находятся на осях вращения.
Понятно также, что разные точки тел за одно и то же время проходят по своим траекториям разные расстояния — чем дальше от оси вращения лежат точки, тем больше эти расстояния. Но за одно и то же время угловое перемещение 
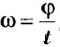
Для характеристики вращательного движения твердых тел используют такие же понятия, что и для движения точки по окружности: период вращения Т — время одного полного вращения; вращательная частота (частота вращения) 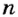
Период вращения Земли вокруг- Солнца равен в среднем 365 суток, а период вращения Луны вокруг Земли в среднем 28 суток. Изучая физику, астрономию, вы узнаете, что небесные тела, например планеты Солнечной системы, движутся не по окружностям, а по так называемым эллипсам.
Динамика вращательного движения
При просмотре фильмов-боевиков вы могли наблюдать, что при резком вращении руля автомобиля машина опрокидывается. В цирке мотоциклисты катаются по поверхности стен.
Проведем такой опыт. Нальем воду в ведро и раскрутим его в вертикальной плоскости. При определенной скорости вращения вода не выливается из ведра.
Из приведенных выше примеров можно сделать заключение, что существует сила, которая опрокинет машину при резком повороте, удержит мотоциклиста на стене и не даст вылиться воде из ведра при вращении.
Откуда появляется эта сила? От чего зависит ее величина?
Для этого вспомним о возникновении центростремительной силы в теле при равномерном вращательном движении:
По третьему закону Ньютона:
и при вращении появляется также центробежная сила.
Вот эта центробежная сила опрокинет резко разворачивающуюся машину, удержит воду в ведре при вращении и т.д.
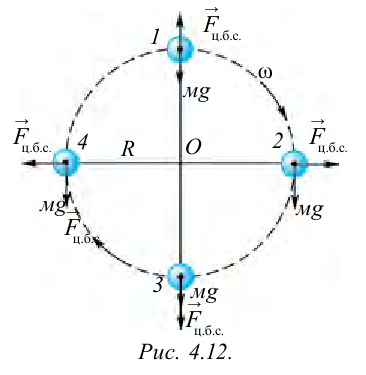
На рисунке 4.12 показаны силы, действующие на тело, которое совершает вращательные движения по кругу радиусом 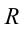
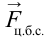
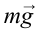
В точке 3 сила тяжести тела и центробежная сила направлены вниз, т.е. в одном направлении. В этом случае вес тела растет:
Центробежную силу нужно учитывать при вращении тела и в случаях поворота в ходе движения.
Кроме того, на поворотах дороги под воздействием центробежной силы наблюдается отклонение тела от вертикального положения. Чтобы это не приводило к авариям, велосипедисты или мотоциклисты должны двигаться с небольшим уклоном в сторону от центра вращения (рис. 4.13а).
Для уравновешивания этой силы специально для автомобилей на поворотах строят участки дороги с уклоном с одной стороны (рис. 4.13б). Для трамваев и поездов рельсы на поворотах дороги с внешней стороны круга делаются чуть выше.
- Заказать решение задач по физике
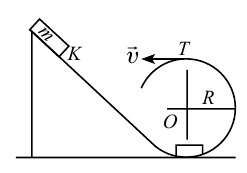
Пример
При движении по кругу тело опускается вниз. При каком радиусе круга тело не упадет с точки 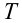
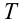
Дано:
Найти:
Решение:
Чтобы тело не упало из точки 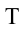
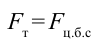
Ответ: 90 м.
Кинематика вращательного движения
При криволинейном движении материальной точки ее мгновенная скорость направлена по касательной к траектории в данной точке.
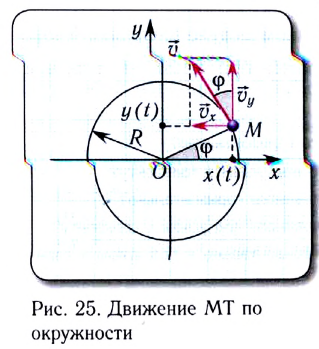
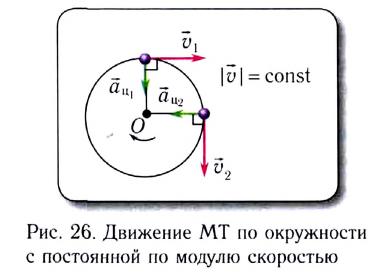
Движение тела (МТ) по окружности является частным случаем криволинейного движения по траектории, лежащей в одной плоскости.
Одним из простейших и широко распространенных видов такого движения является движение по окружности с постоянной по модулю скоростью. Это такое движение, при котором тело (МТ) за любые равные промежутки времени описывает одинаковые дуги. Подчеркнем, что при подобном движении скорость точки постоянно меняет свое направление.
Для описания движения по окружности используется ряд физических величин. Рассмотрим некоторые из них.
Удобным параметром для определения положения материальной точки М, совершающей движение по окружности радиусом R с центром в начале координат, является угол поворота 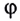
радиус-вектора точки М. Он отсчитывается от оси Ох против хода часовой стрелки и связан с декартовыми координатами соотношениями:
По теореме Пифагора можно найти, что координаты х и у материальной точки в декартовой системе координат удовлетворяют соотношению
Скорость 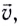
Проходимый точкой путь s (длина дуги окружности) равен, как и для всякого равномерного движения, произведению модуля скорости v и промежутка времени движения
Модуль угловой скорости 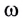
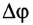
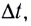
Угловая скорость 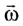
Единица угловой скорости в СИ — радиан в секунду
При движении по окружности с постоянной по модулю скоростью v угловая скорость 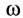
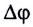
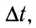
Здесь n — частота вращения — физическая величина, численно равная числу оборотов N материальной точки в единицу времени:
Единица частоты вращения в СИ — секунда в минус первой степени 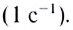
Следовательно,
В СИ период измеряется в секундах (1с).
При совершении полного оборота 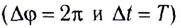
Модуль постоянной линейной скорости тела (МТ), движущегося по окружности, вычисляется по формуле
Проекции скорости 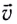
Модуль угловой скорости определяется соотношением
Следовательно, соотношение между модулями линейной и угловой скорости имеет вид
Поскольку 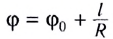
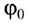
При движении МТ по окружности с постоянной по модулю скоростью ее направление непрерывно изменяется и, следовательно, движение МТ происходит с ускорением, которое называется центростремительным 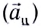
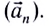
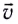
Нормальное ускорение 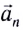
Как и при прямолинейном равноускоренном движении, ускорение 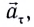
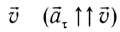
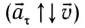
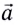
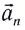
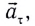
Полное ускорение 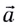
Модуль полного ускорения находится по теореме Пифагора:
где 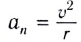
окружности радиусом r, заменяющей траекторию в окрестности рассматриваемой точки. Этот радиус r называют радиусом кривизны траектории.
- Равномерное движение материальной точки по окружности
- Колебательное движение
- Физический и математический маятники
- Пружинные и математические маятники
- Поступательное движение
- Равномерное и неравномерное движение
- Равномерное движение
- Неравномерное движение
Вращательное движение (Движение тела по окружности)
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:
Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α
Вращательное движение, характеристики
| Вращательное движение | Угловая скорость | Угловое ускорение |
|---|---|---|
| Равномерное | Постоянная | Равно нулю |
| Равномерно ускоренное | Изменяется равномерно | Постоянно |
| Неравномерно ускоренное | Изменяется неравномерно | Переменное |
Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).
Если
φ — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана
[
φ = frac{s}{r}
]
Соотношение между единицами угла
[ frac{φ_{рад}}{φ_{°}} = frac{π}{180°} ]
|
$ 1 enspace рад = 57.3° $ |
$ 1° = 17.45 enspace мрад $ |
$ 1´ = 291 enspace мкрад $ |
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.
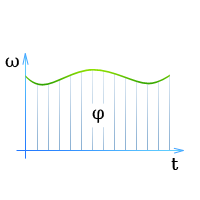
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t).
Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
[ [n] = [f] = frac{Обороты}{Секунда} = frac{(об)}{с} = frac{1}{c} = Герц ]
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
ω — угловая частота,
то
Период
[
T = frac{1}{f} = frac{1}{n}
]
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2π:
[
φ = 2 π N
]
Угловая скорость
Из формулы для одного оборота следует:
[
ω = 2 π f = frac{2π}{T}
]
Обратите внимание:
• формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.
Вращательное движение (движение тела по окружности) |
стр. 422 |
|---|