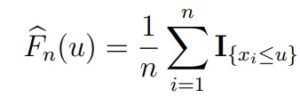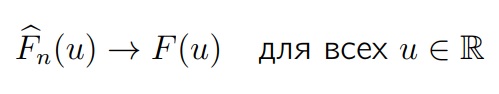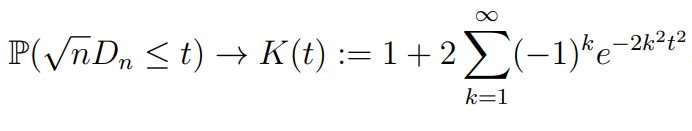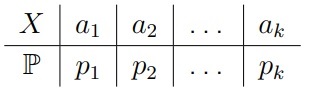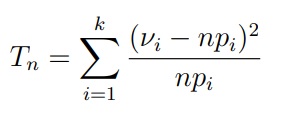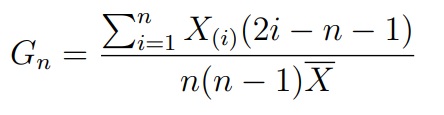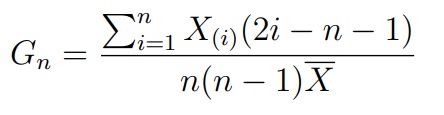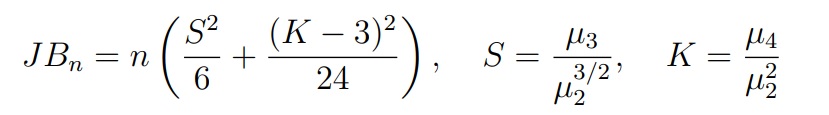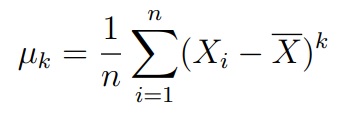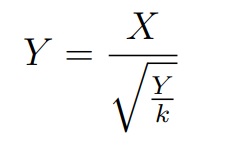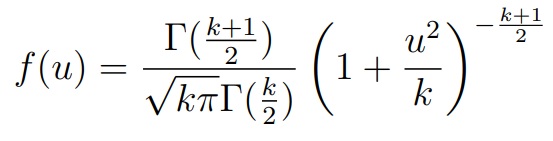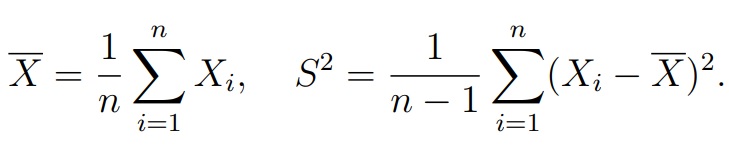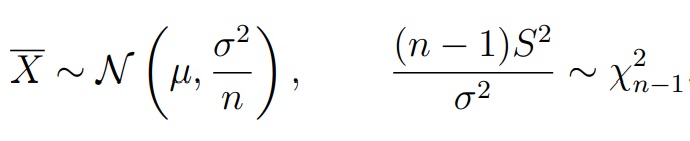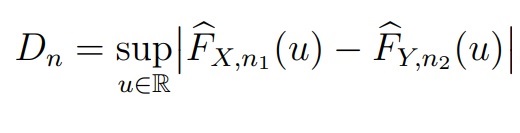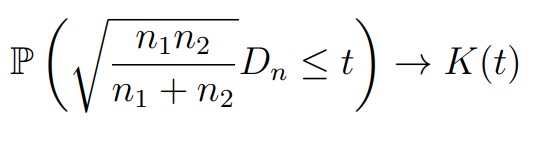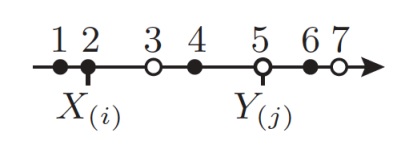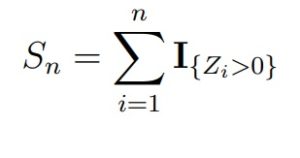Статистический критерий
Статистическим
критерием называется вычисленная по
определенному алгоритму величина
,
которая используется для проверки
основной гипотезы.
Критерий
вычисляется на основе экспериментальных
данных. При этом вычисленное эмпирическое
значениеможет оказаться таким, что, действуя по
определенному алгоритму, на данном
уровне значимости мы примем основную
гипотезу, а может оказаться таким, что
мы вынуждены будем ее отвергнуть, то
есть, принять конкурирующую гипотезу.
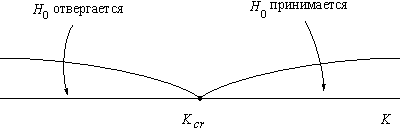
Критические точки статистического критерия
Критической
областью называется множество таких
значений критерия
,
при которых основная гипотезаотвергается. Областью принятия гипотезы,
напротив, называется множество тех
значений критерия,
при которых основная гипотезапринимается. Критическими значениями
критерияназываются точки
,
отделяющие область принятия гипотезы
от критической области.
Так как статистический
критерий является одномерной величиной,
критическая область, как и область
принятия гипотезы — это некоторый
интервал на числовой прямой, ограниченный
одной или двумя критическим точками. В
связи с этим различают односторонние
и двусторонние критические области.
Двусторонняя
критическая область
Односторонняя
критическая область
Допустим, по
результатам эксперимента мы вычислили
некоторое эмпирическое значение критерия
.
Как выяснить принадлежит ли это значение
области принятия гипотезы, или наоборот:
критической области?
Следует понимать,
что нахождение критических точек и, как
следствие, области принятия гипотезы
для каждого критерия является отдельной,
сложной теоретико-вероятностной задачей.
Однако, следует также понимать, что эти
значения известны. Они табулированы и
представлены в виде приложений в
большинстве книг по теории вероятностей
и математической статистике. Так ими и
следует пользоваться: как известным
научным фактом, не задумываясь особенно
о том, откуда они берутся. Если речь идет
о критерии Пирсона, то следует
воспользоваться соответствующей
таблицей и сказать спасибо Пирсону за
то, что он избавил нас от необходимости
вычислять критическую область, если
речь идет о критерии Колмогорова-Смирнова,
следует сказать спасибо Колмогорову и
Смирнову и т. д.
Пример применения статистического критерия
Закончим, наконец,
рассмотрение примера о делении отрезка
двумя группами испытуемых: группой
студентов-инженеров и группой
студентов-дизайнеров. В этом исследовании
мы предположили, что сообщество дизайнеров
демонстрирует более широкий разброс
мнений по поводу гармоничности деления
отрезка точкой на две части. Такова наша
экспериментальная гипотеза. После
проведения эксперимента и получения
экспериментальных данных (а именно:
для студентов-инженеров и
для студентов-дизайнеров) мы можем
сформулировать статистические гипотезы:
Обратите внимание,
что в экспериментальной гипотезе мы
предполагали существенное неравенство
дисперсий, а в основной статистической
гипотезе — наоборот: их равенство. Таким
образом, для подтверждения экспериментальной
гипотезы нам необходимо опровергнуть
основную статистическую гипотезу.
Такова специфика применяемого нами
критерия Фишера-Снедекора.
Алгоритм
Фишера-Снедекора состоит в следующем:
-
По данным двух
выборок вычисляются выборочные
дисперсии. Напомню, что мы получили
следующие результаты:
,
.
-
Эмпирическое
значение
-критерия
Фишера-Снедекора вычисляется как
отношение большей дисперсии к меньшей,
в нашем случае это
-
По таблице
критических значений Фишера-Снедекора
определяют
для
уровня значимостии степеней свободы
,
,
где—
это объем выборки, обладающей большей
дисперсией, а—
объем выборки, обладающей меньшей
дисперсией. Зададимся уровнем значимостии вычислим числа степеней свободы:
,
.
Откуда
-
Сравниваем
эмпирическое и критическое значение
критерия:
Следовательно,
основная гипотеза отвергается и
принимается альтернативная:
.
Итак, проведенный
нами статистический анализ показывает,
что распределение коэффициентов деления
отрезка среди студентов-дизайнеров
обладает значимо большим разбросом
значений, нежели то же распределение
среди студентов-инженеров. Тем самым —
на уровне значимости
теперь
нами подтверждена наша экспериментальная
гипотеза:
сообщество
дизайнеров, то есть сообщество
производителей дизайна, демонстрирует
более широкий разброс мнений по поводу
гармоничности деления отрезка точкой
на две части, нежели сообщество
потребителей дизайна.
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #
Проверка корректности А/Б тестов
Время на прочтение
8 мин
Количество просмотров 7.5K
Хабр, привет! Сегодня поговорим о том, что такое корректность статистических критериев в контексте А/Б тестирования. Узнаем, как проверить, является критерий корректным или нет. Разберём пример, в котором тест Стьюдента не работает.
Меня зовут Коля, я работаю аналитиком данных в X5 Tech. Мы с Сашей продолжаем писать серию статей по А/Б тестированию, это наша третья статья. Первые две можно посмотреть тут:
-
Стратификация. Как разбиение выборки повышает чувствительность A/Б теста
-
Бутстреп и А/Б тестирование
Корректный статистический критерий
В А/Б тестировании при проверке гипотез с помощью статистических критериев можно совершить одну из двух ошибок:
-
ошибку первого рода – отклонить нулевую гипотезу, когда на самом деле она верна. То есть сказать, что эффект есть, хотя на самом деле его нет;
-
ошибку второго рода – не отклонить нулевую гипотезу, когда на самом деле она неверна. То есть сказать, что эффекта нет, хотя на самом деле он есть.
Совсем не ошибаться нельзя. Чтобы получить на 100% достоверные результаты, нужно бесконечно много данных. На практике получить столько данных затруднительно. Если совсем не ошибаться нельзя, то хотелось бы ошибаться не слишком часто и контролировать вероятности ошибок.
В статистике ошибка первого рода считается более важной. Поэтому обычно фиксируют допустимую вероятность ошибки первого рода, а затем пытаются минимизировать вероятность ошибки второго рода.
Предположим, мы решили, что допустимые вероятности ошибок первого и второго рода равны 0.1 и 0.2 соответственно. Будем называть статистический критерий корректным, если его вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно.
Как сделать критерий, в котором вероятности ошибок будут равны допустимым вероятностям ошибок?
Вероятность ошибки первого рода по определению равна уровню значимости критерия. Если уровень значимости положить равным допустимой вероятности ошибки первого рода, то вероятность ошибки первого рода должна стать равной допустимой вероятности ошибки первого рода.
Вероятность ошибки второго рода можно подогнать под желаемое значение, меняя размер групп или снижая дисперсию в данных. Чем больше размер групп и чем ниже дисперсия, тем меньше вероятность ошибки второго рода. Для некоторых гипотез есть готовые формулы оценки размера групп, при которых достигаются заданные вероятности ошибок.
Например, формула оценки необходимого размера групп для гипотезы о равенстве средних:
где и
– допустимые вероятности ошибок первого и второго рода,
– ожидаемый эффект (на сколько изменится среднее),
и
– стандартные отклонения случайных величин в контрольной и экспериментальной группах.
Проверка корректности
Допустим, мы работаем в онлайн-магазине с доставкой. Хотим исследовать, как новый алгоритм ранжирования товаров на сайте влияет на среднюю выручку с покупателя за неделю. Продолжительность эксперимента – одна неделя. Ожидаемый эффект равен +100 рублей. Допустимая вероятность ошибки первого рода равна 0.1, второго рода – 0.2.
Оценим необходимый размер групп по формуле:
import numpy as np
from scipy import stats
alpha = 0.1 # допустимая вероятность ошибки I рода
beta = 0.2 # допустимая вероятность ошибки II рода
mu_control = 2500 # средняя выручка с пользователя в контрольной группе
effect = 100 # ожидаемый размер эффекта
mu_pilot = mu_control + effect # средняя выручка с пользователя в экспериментальной группе
std = 800 # стандартное отклонение
# исторические данные выручки для 10000 клиентов
values = np.random.normal(mu_control, std, 10000)
def estimate_sample_size(effect, std, alpha, beta):
"""Оценка необходимого размер групп."""
t_alpha = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
t_beta = stats.norm.ppf(1 - beta, loc=0, scale=1)
var = 2 * std ** 2
sample_size = int((t_alpha + t_beta) ** 2 * var / (effect ** 2))
return sample_size
estimated_std = np.std(values)
sample_size = estimate_sample_size(effect, estimated_std, alpha, beta)
print(f'оценка необходимого размера групп = {sample_size}')оценка необходимого размера групп = 784Чтобы проверить корректность, нужно знать природу случайных величин, с которыми мы работаем. В этом нам помогут исторические данные. Представьте, что мы перенеслись в прошлое на несколько недель назад и запустили эксперимент с таким же дизайном, как мы планировали запустить его сейчас. Дизайн – это совокупность параметров эксперимента, таких как: целевая метрика, допустимые вероятности ошибок первого и второго рода, размеры групп и продолжительность эксперимента, техники снижения дисперсии и т.д.
Так как это было в прошлом, мы знаем, какие покупки совершили пользователи, можем вычислить метрики и оценить значимость отличий. Кроме того, мы знаем, что эффекта на самом деле не было, так как в то время эксперимент на самом деле не запускался. Если значимые отличия были найдены, то мы совершили ошибку первого рода. Иначе получили правильный результат.
Далее нужно повторить эту процедуру с мысленным запуском эксперимента в прошлом на разных группах и временных интервалах много раз, например, 1000.
После этого можно посчитать долю экспериментов, в которых была совершена ошибка. Это будет точечная оценка вероятности ошибки первого рода.
Оценку вероятности ошибки второго рода можно получить аналогичным способом. Единственное отличие состоит в том, что каждый раз нужно искусственно добавлять ожидаемый эффект в данные экспериментальной группы. В этих экспериментах эффект на самом деле есть, так как мы сами его добавили. Если значимых отличий не будет найдено – это ошибка второго рода. Проведя 1000 экспериментов и посчитав долю ошибок второго рода, получим точечную оценку вероятности ошибки второго рода.
Посмотрим, как оценить вероятности ошибок в коде. С помощью численных синтетических А/А и А/Б экспериментов оценим вероятности ошибок и построим доверительные интервалы:
def run_synthetic_experiments(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты, возвращаем список p-value."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
def print_estimated_errors(pvalues_aa, pvalues_ab, alpha):
"""Оценивает вероятности ошибок."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
ci_first = estimate_ci_bernoulli(estimated_first_type_error, len(pvalues_aa))
ci_second = estimate_ci_bernoulli(estimated_second_type_error, len(pvalues_ab))
print(f'оценка вероятности ошибки I рода = {estimated_first_type_error:0.4f}')
print(f' доверительный интервал = [{ci_first[0]:0.4f}, {ci_first[1]:0.4f}]')
print(f'оценка вероятности ошибки II рода = {estimated_second_type_error:0.4f}')
print(f' доверительный интервал = [{ci_second[0]:0.4f}, {ci_second[1]:0.4f}]')
def estimate_ci_bernoulli(p, n, alpha=0.05):
"""Доверительный интервал для Бернуллиевской случайной величины."""
t = stats.norm.ppf(1 - alpha / 2, loc=0, scale=1)
std_n = np.sqrt(p * (1 - p) / n)
return p - t * std_n, p + t * std_n
pvalues_aa = run_synthetic_experiments(values, sample_size, effect=0)
pvalues_ab = run_synthetic_experiments(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)оценка вероятности ошибки I рода = 0.0991
доверительный интервал = [0.0932, 0.1050]
оценка вероятности ошибки II рода = 0.1978
доверительный интервал = [0.1900, 0.2056]Оценки вероятностей ошибок примерно равны 0.1 и 0.2, как и должно быть. Всё верно, тест Стьюдента на этих данных работает корректно.
Распределение p-value
Выше рассмотрели случай, когда тест контролирует вероятность ошибки первого рода при фиксированном уровне значимости. Если решим изменить уровень значимости с 0.1 на 0.01, будет ли тест контролировать вероятность ошибки первого рода? Было бы хорошо, если тест контролировал вероятность ошибки первого рода при любом заданном уровне значимости. Формально это можно записать так:
Для любого выполняется
.
Заметим, что в левой части равенства записано выражение для функции распределения p-value. Из равенства следует, что функция распределения p-value в точке X равна X для любого X от 0 до 1. Эта функция распределения является функцией распределения равномерного распределения от 0 до 1. Мы только что показали, что статистический критерий контролирует вероятность ошибки первого рода на заданном уровне для любого уровня значимости тогда и только тогда, когда при верности нулевой гипотезы p-value распределено равномерно от 0 до 1.
При верности нулевой гипотезы p-value должно быть распределено равномерно. А как должно быть распределено p-value при верности альтернативной гипотезы? Из условия для вероятности ошибки второго рода следует, что
.
Получается, график функции распределения p-value при верности альтернативной гипотезы должен проходить через точку , где
и
– допустимые вероятности ошибок конкретного эксперимента.
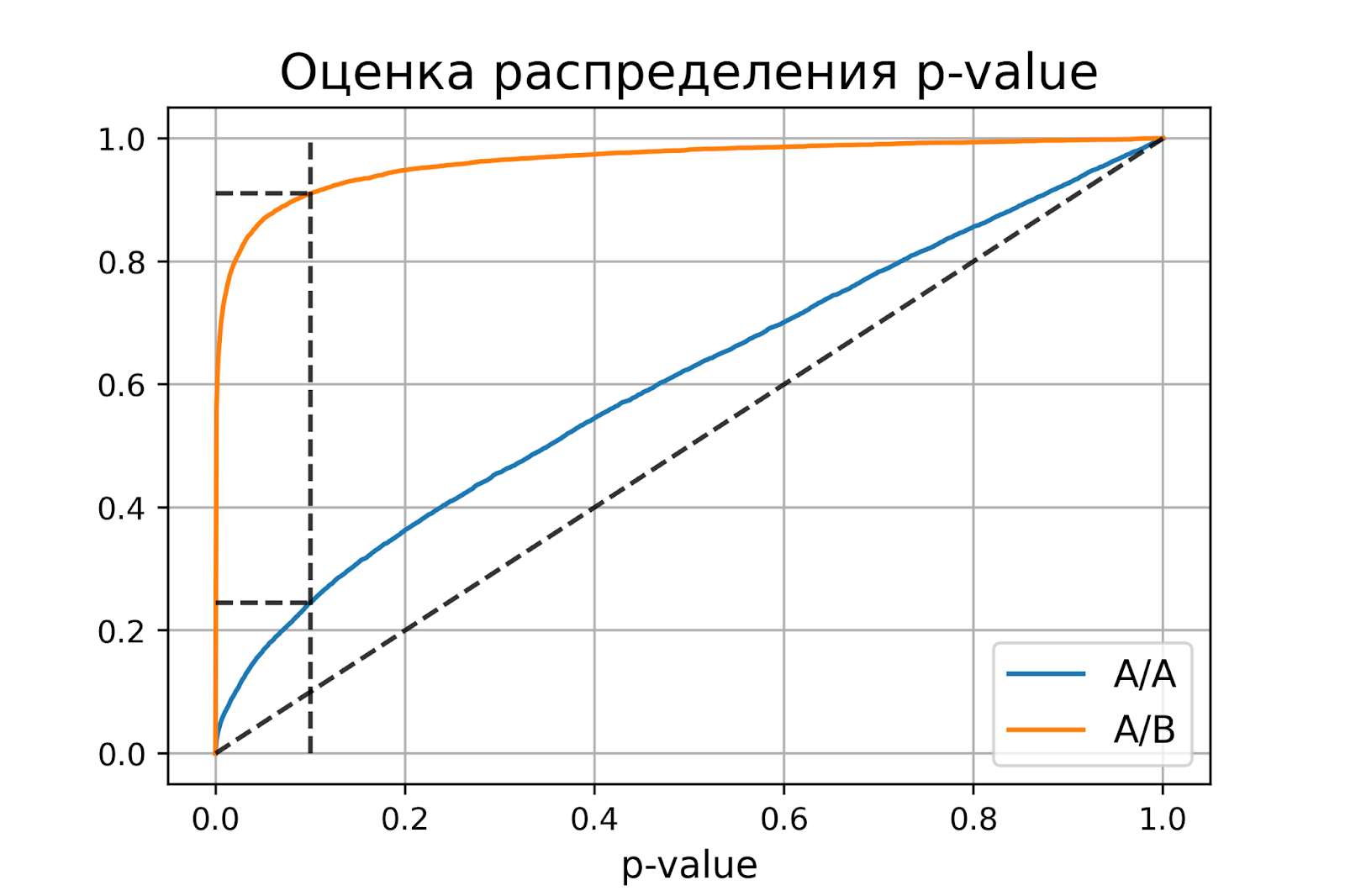
Проверим, как распределено p-value в численном эксперименте. Построим эмпирические функции распределения p-value:
import matplotlib.pyplot as plt
def plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta):
"""Рисует графики распределения p-value."""
estimated_first_type_error = np.mean(pvalues_aa < alpha)
estimated_second_type_error = np.mean(pvalues_ab >= alpha)
y_one = estimated_first_type_error
y_two = 1 - estimated_second_type_error
X = np.linspace(0, 1, 1000)
Y_aa = [np.mean(pvalues_aa < x) for x in X]
Y_ab = [np.mean(pvalues_ab < x) for x in X]
plt.plot(X, Y_aa, label='A/A')
plt.plot(X, Y_ab, label='A/B')
plt.plot([alpha, alpha], [0, 1], '--k', alpha=0.8)
plt.plot([0, alpha], [y_one, y_one], '--k', alpha=0.8)
plt.plot([0, alpha], [y_two, y_two], '--k', alpha=0.8)
plt.plot([0, 1], [0, 1], '--k', alpha=0.8)
plt.title('Оценка распределения p-value', size=16)
plt.xlabel('p-value', size=12)
plt.legend(fontsize=12)
plt.grid()
plt.show()
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)P-value для синтетических А/А тестах действительно оказалось распределено равномерно от 0 до 1, а для синтетических А/Б тестов проходит через точку .
Кроме оценок распределений на графике дополнительно построены четыре пунктирные линии:
-
диагональная из точки [0, 0] в точку [1, 1] – это функция распределения равномерного распределения на отрезке от 0 до 1, по ней можно визуально оценивать равномерность распределения p-value;
-
вертикальная линия с
– пороговое значение p-value, по которому определяем отвергать нулевую гипотезу или нет. Проекция на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А тестов – это вероятность ошибки первого рода. Проекция точки пересечения вертикальной линии с функцией распределения p-value для А/Б тестов – это мощность теста (мощность = 1 —
).
-
две горизонтальные линии – проекции на ось ординат точки пересечения вертикальной линии с функцией распределения p-value для А/А и А/Б тестов.
График с оценками распределения p-value для синтетических А/А и А/Б тестов позволяет проверить корректность теста для любого значения уровня значимости.
Некорректный критерий
Выше рассмотрели пример, когда тест Стьюдента оказался корректным критерием для случайных данных из нормального распределения. Может быть, все критерии всегда работаю корректно, и нет смысла каждый раз проверять вероятности ошибок?
Покажем, что это не так. Немного изменим рассмотренный ранее пример, чтобы продемонстрировать некорректную работу критерия. Допустим, мы решили увеличить продолжительность эксперимента до 2-х недель. Для каждого пользователя будем вычислять стоимость покупок за первую неделю и стоимость покупок за второю неделю. Полученные стоимости будем передавать в тест Стьюдента для проверки значимости отличий. Положим, что поведение пользователей повторяется от недели к неделе, и стоимости покупок одного пользователя совпадают.
def run_synthetic_experiments_two(values, sample_size, effect=0, n_iter=10000):
"""Проводим синтетические эксперименты на двух неделях."""
pvalues = []
for _ in range(n_iter):
a, b = np.random.choice(values, size=(2, sample_size,), replace=False)
b += effect
# дублируем данные
a = np.hstack((a, a,))
b = np.hstack((b, b,))
pvalue = stats.ttest_ind(a, b).pvalue
pvalues.append(pvalue)
return np.array(pvalues)
pvalues_aa = run_synthetic_experiments_two(values, sample_size)
pvalues_ab = run_synthetic_experiments_two(values, sample_size, effect=effect)
print_estimated_errors(pvalues_aa, pvalues_ab, alpha)
plot_pvalue_distribution(pvalues_aa, pvalues_ab, alpha, beta)оценка вероятности ошибки I рода = 0.2451
доверительный интервал = [0.2367, 0.2535]
оценка вероятности ошибки II рода = 0.0894
доверительный интервал = [0.0838, 0.0950]Получили оценку вероятности ошибки первого рода около 0.25, что сильно больше уровня значимости 0.1. На графике видно, что распределение p-value для синтетических А/А тестов не равномерно, оно отклоняется от диагонали. В этом примере тест Стьюдента работает некорректно, так как данные зависимые (стоимости покупок одного человека зависимы). Если бы мы сразу не догадались про зависимость данных, то оценка вероятностей ошибок помогла бы нам понять, что такой тест некорректен.
Итоги
Мы обсудили, что такое корректность статистического теста, посмотрели, как оценить вероятности ошибок на исторических данных и привели пример некорректной работы критерия.
Таким образом:
-
корректный критерий – это критерий, у которого вероятности ошибок первого и второго рода равны допустимым вероятностям ошибок первого и второго рода соответственно;
-
чтобы критерий контролировал вероятность ошибки первого рода для любого уровня значимости, необходимо и достаточно, чтобы p-value при верности нулевой гипотезы было распределено равномерно от 0 до 1.
В заключительной части блока по теории вероятностей мы рассмотрим как применять критерии на практике и принцип их работы.
В проверке гипотез мы делаем предположение о распределении данных, и наша задача состоит в том, чтобы определить, содержит ли выборка достаточно информации, чтобы отвергнуть это предположение или нет. Но прямо «в лоб» говорить, что эта гипотеза верная мы не можем:
Чтобы иметь возможность отвергнуть предположение, нам необходимо предоставить альтернативу — иное предположение о распределении данных, относительно которого мы будем решать, отвергать основную гипотезу или нет. Т.е. мы сравниваем обе гипотезы и выбираем ту, которая наиболее вероятна.
Статистический критерий
Обратимся к классическому примеру: предположим, что кто-то подбросил 16 раз монетку, и в 12 случаях она упала орлом вверх. Можно ли считать эту монетку симметричной?
Здесь у нас такое же классическое распределение Бернулли: X1, . . . , Xn ∼ Ber(p).
H0: p = 1/2 (основная или нулевая гипотеза).
H1: p ≠ 1/2 (альтернативная гипотеза).
Правило, позволяющее принять или отвергнуть гипотезу H0 на основе выборки называется статистическим критерием. Сам статистический критерий задается при помощи функции от выборки T(x1, . . . , xn), называемой статистикой критерия. Каждый критерий считает некоторую функцию от данных.
Статистика любого критерия T(x1, . . . , xn) должна обладать двумя основными свойствами:
- При верной H0 статистика T должна принимать умеренные значения, а при неверной H0 — другие, экстремальные.
- При верной H0 статистика T должна иметь известное распределение G0 (называется нулевым распределением), а при неверной H0 — распределение отличное от G0 (возможно, неизвестное).
Проверка гипотезы
Как узнать, что гипотеза H0 верная? В нашем примере в качестве статистики T можно взять
T(x1, . . . , xn) = x1 + . . . + xn.
При верной типичными значениями H0 будут значения, близкими к n/2, а экстремальными — значения, близкие к 0 или n. Итого:
- При верной H0 имеет распределение Bin(n, p) с p = 1/2
- При верной H1 имеет распределение Bin(n, p), но с p ≠ 1/2
Давайте объединим все данные, которые мы имеем:
Выборка: X = (x1, . . . , xn), Xi ∼ F (все случайные величины имеют какое-то конкретное распределение)
Нулевая гипотеза: H0 : F ∈ Ϝ0 (F принадлежит какому-то классу распределений Ϝ)
Альтернативная гипотеза: H1 : F ∈ Ϝ1, Ϝ1 ∩ Ϝ0 = ∅ (два класса не должны пересекаться)
Статистика: T(x1, . . . , xn), T(X) ∼ G0 при H0 (если мы подставляем в статистику подставляем выборку из случайных величин, то статистика H0 должна иметь какое-то конкретное распределение) , T(X) не∼ G0 при H1
Фактический уровень значимости или p-value — это вероятность для статистики T при верной H0 принять значение t = T(x), которое получилось на выборке x = (x1, . . . , xn) или ещё более экстремальное. Иногда p-value называют достигаемым уровнем значимости.
Если p-value будет маленьким, то это означает, что значение, которое будет получено, будет экстремальным, т.е. вероятность получить именно такое значение крайне мало (0,001% например). Это будет свидетельствовать о том, что альтернативная гипотеза (H1) более вероятна (лучше не использовать слово «верна»). Если p-value большое — мы попали в область типичных значений для данной статистики, а значит данные не свидетельствуют против нулевой гипотезы H0 в пользу альтернативы H1
Если для статистики T экстремальными значениями являются большие значения, то это можно записать так:
p(x) = P(T(X) ≥ t | H0).
Нулевая гипотеза H0 отвергается при p(x) ≤ α, α — уровень значимости, который мы задаем. Вероятность отвергнуть нулевую гипотезу зависит не только от того, насколько она отличается от истины, но и от размера выборки: по мере увеличения n нулевая гипотеза может сначала приниматься, но потом выявятся более тонкие несоответствия выборки гипотезе H0, и она будет отвергнута.
При помощи инструментов проверки гипотез нельзя доказать, что нулевая
гипотеза верна!
Пример
Ваш закадычный друг утверждает, что у него есть некоторый скилл: он различает чем разбавлен коньяк в коктейле — кока-колой или пепси, и предпочитает только колу. Протестируем его предложим ему выпить n-количестве коктейлей, чтобы проверить: сможет ли он отличить колу от пепси.
Выборка: X = (x1, . . . , xn), где Xi ∼ Ber(p).
Реализация выборки: x = (x1, . . . , xn) — это вектор длины n, где
- 0 — Друг выбрал коктейль с пепси
- 1 — Друг выбрал коктейль с колой
Статистика: T(x1, . . . , xn) = x1 + . . . + xn.
Реализация статистики: t = T(x).
Гипотезы:
- H0: друг не может различить колу от пепси p = 1/2.
- H1: друг может различить колу от пепси, p > 1/2.
Какие значения T считаются экстремальными? При альтернативе H1 экстремальными являются большие значения t (они свидетельствуют против H0 в пользу H1).
Если нулевая гипотеза H0 справедлива и друг не может различить колу от пепси, то
T будет иметь биномиальное распределение Bin(n, 1/2).
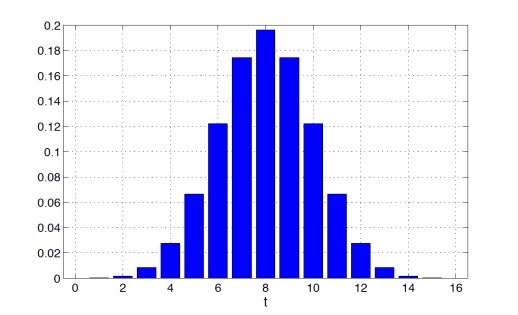
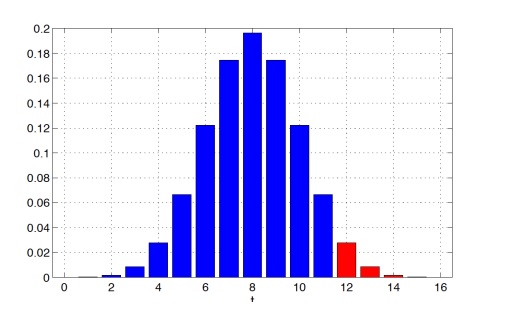
Пусть количество коктейлей n = 16, тогда Bin(n, 1/2) будет иметь следующий вид
Предположим, что t = 12, то есть в 12 случаях из 16 друг действительно угадал, что в стакане кола. В таком случае p-value будет равен:
P(T(X) ≥ 12 | H0) = 2517 / 65536 ≈ 0.0384
Здесь у нас p-value достаточно мало — это указывает на то, что альтернативная гипотеза (H1) более вероятна, т.е. друг действительно различит колу от пепси
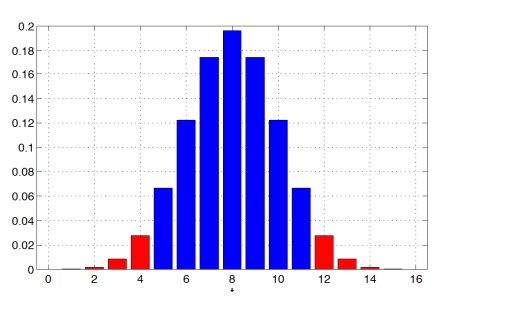
Теперь немного изменим альтернативную гипотезу:
H1: Друг любит определенный коктейль, но неизвестно какой (с колой или с пепси), то есть p ≠ 1/2. При такой альтернативе и большие, и маленькие значения t будут
свидетельствовать против H0 в пользу H1
Предположим (снова), что t = 12, то есть в 12 случаях из 16 друг действительно угадал, что в стакане кола (опять). Тогда p-value будет равен:
P(T(X) ≥ 12 или T(X) ≤ 4|H0) = 5034 / 65536 ≈ 0.0768
Чем больше, «шире» альтернатива, тем сильнее данные свидетельствуют против нулевой гипотезы H0 (тем больше значений будут считаться экстремальными). С помощью инструментов проверки гипотез нельзя доказать верность нулевой гипотезы в принципе
Критерии согласия
Критерии, которые отвечают на вопрос согласуется ли распределения данных с каким-либо видом распределения, называют критериями согласия.
Пусть нам дана выборка x1, . . . , xn ∼ F, где F — некоторое неизвестное распределение. Давайте рассмотрим критерии согласия, в которых в качестве H0 будем рассматривать гипотезу о принадлежности F какому-то параметрическому семейству, то есть F ∈ Ϝ0. Альтернативой H1 мы будем считать принадлежность F всем остальным распределениям
• H0: F ∈ Ϝ0 (нулевая гипотеза), проверяем гипотезу, что наше распределение F, которое мы не знаем, принадлежит некоторому классу распределений Ϝ0
• H1: F ∉ Ϝ0 (альтернативная гипотеза)
где Ϝ0 — некоторое параметрическое семейство распределений.
Критерии согласия так называются, потому что они отвечают на вопрос, согласуется ли наша выборка с каким-то параметрическим семейством или нет. В англоязычной литературе такие критерии называют Goodness of Fit
Чтобы построить критерий согласия достаточно найти такое свойство, которое будет выполняться для всех распределений в классе и на его основе реализовать статистику. Возьмем за правило, что произвольная гипотеза H является простой, если H : F = F0, то есть гипотеза заключается в равенстве одному конкретному распределению F0. В противном случае мы будем называть гипотезу сложной, т.е. нулевая гипотеза состоит из нескольких распределений (двух и более)
Произведем проверку простой нулевой гипотезы:
- H0 : F = F0 для некоторого конкретного распределения F0.
- H1 : F ≠ F0.
Критерий Колмогорова
Критерий Колмогорова позволяет проверить гипотезу согласия для непрерывного случая и основан на отклонении функции распределения F0 построенной по выборке эмпирической функции распределения
Функцией распределения случайной величины X называют функцию
FX : R → [0, 1], задаваемая следующей формулой
FX(u) = P(X ≤ u)
Значение F в точке u сосредотачивает вероятности всех возможных значений X вплоть до u (включительно).
Основное свойство функций распределения:
Любую случайную величину X можно задать через функцию распределения. То есть по функции распределения можно восстановить распределение случайной величины X:
- В дискретном случае можно восстановить ak и pk (т.е. сможем найти возможные значения и вероятности)
- В непрерывном случае можно восстановить f(u) (т.е. восстановить функцию плотности)
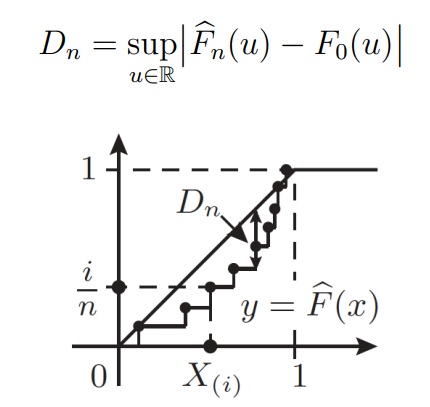
Эмпирическая функция распределения — это функция, которая оценивает истинную функцию распределения выборки F. Она задается формулой
где I{xi≤u} — индикатор события {xi ≤ u} — это функция, которая равна 1, если событие
произошло, и 0 в обратном случае).
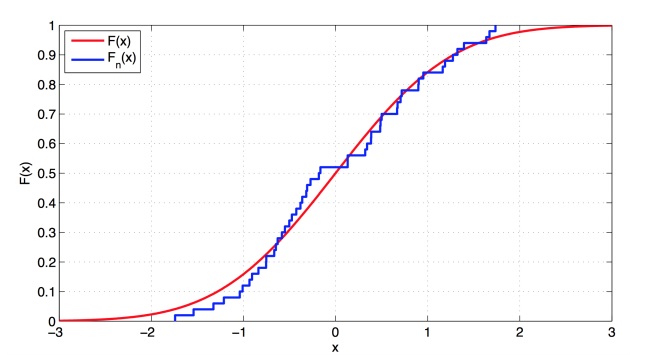
Визуально график представляет собой кусочно-постоянную функцию, у которой скачки происходят в точках выборки x1, . . . , xn, а высота скачков равна 1/n. По графику видимо, что истинная функция распределения хорошо аппроксимируется с эмпирической функцией распределения
Для выборки достаточно большого размера, эмпирическая функция распределения Fbn(u) не должна существенно отклоняться от истинной функции распределения F.
Теорема (Гливенко-Кантелли)
Если F — это функция распределения элементов выборки, то Fn(u) будет эмпирической функцией распределения, построенной по этой выборке. Тогда, для всех одновременно аргументов функции (u) и при n → ∞
Эмпирическая функция распределения будет стремиться к истинной функции распределения с вероятностью 1
Статистика критерия Колмогорова основана на такой величине максимального отклонения одной функции от другой:
Теорема (Колмогоров)
Пусть верна гипотеза H0, то есть F0 является функцией распределения элементов выборки. Если F0 непрерывна, то, при n → ∞, для любого t > 0
K(t) называется функцией Колмогорова, а соответствующее ему распределение — распределением Колмогорова. Быстрая сходимость к предельному закону позволяет пользоваться этим приближением уже при n ≥ 20. Условие непрерывности функции распределения необходимо
Критерий Пирсона (хи-квадрат)
Критерий Пирсона можно использовать для проверки простой гипотезы согласия в дискретном случае (можно и для непрерывного — но это
Пусть F0 является (пока конечным) дискретным законом, который задается таблицей распределения
Критерий Пирсона базируется уже на другой статистике — частотах. Статистикой критерия является величина
где Vi (греческая буква ню) — количество значений ai в выборке x1, . . . , xn.
Распределением χ2k (хи-квадрат) с k степенями свободы называется распределение случайной величины
Y = χ21 + . . . + χ2k
где x1, . . . , xk независимы и стандартно нормально распределены, то есть Xi ∼ N (0, 1).
Теорема (Пирсон)
Если при n → ∞ распределение статистики Tn сходится к распределению χ2k-1 то нулевая гипотеза верна, т.е. F0 является функцией распределения элементов выборки
Приближение распределения статистики Tn с помощью закона χ2k-1 является достаточно точным при n ≥ 50 и npi ≥ 5 для всех i = 1, . . . , k.
Сложные нулевые гипотезы
Лучше всего проверять гипотезы со специализированными критериями. Поэтому давайте посмотрим на самые чувствительные критерии, которые построены для конкретных семейств распределений.
Проверка экспоненциальности (показательности)
Исключение неизвестного параметра
Положим Sk = X1 + . . . + Xk, k = 1, . . . , n.
Можно доказать, что для экспоненциального распределения вектор (т.е. выборка Xi-тых заменённая на такую) S1/Sn, . . . , Sn−1/Sn, распределен так же, как и упорядоченный ряд из равномерного распределения на [0, 1] размера n − 1.
Данное преобразование сводит задачу к проверке равномерности, которую можно решить с помощью критерия Колмогорова. Но за исключение «мешающего» параметра λ приходится платить уменьшением размера выборки на 1.
Критерий Джини (Gini)
Этот критерий базируется на статистике, а по сути индексу Джини:
где X(i) — это i-ый элемент в упорядоченной по возрастанию выборке (вариационном ряду). Известно, что при верной H0 величина 12(n − 1)(Gn − 0.5) сходится к нормальному распределению. На этом факте и основан критерий Джини.
Проверка экспоненциальности (показательности)
Для проверки экспоненциальности существует и ряд других критериев (например, Шапиро-Уилка для экспоненциального случая или Андерсона-Дарлинга).
Проверка нормальности
Критерий Шапиро-Уилка (Shapiro-Wilk).
Критерий Шапиро-Уилка базируется на статистике, которая является отношением квадрата линейной оценки стандартного отклонения к смещенной оценке дисперсии:
где ai — некоторые константы. При верной H0 распределение SWn является табличным. На этом факте и основан критерий Шапиро-Уилка.
Критерий Харке-Бера (Jarque-Bera). Этот критерий основан на статистике, которая использует выборочные коэффициенты асимметрии и эксцесса:
где µk — центрированный выборочный момент порядка k
Данная статистика сходится к распределению χ22. На этом факте и основан критерий Харке-Бера.
Квантильный график
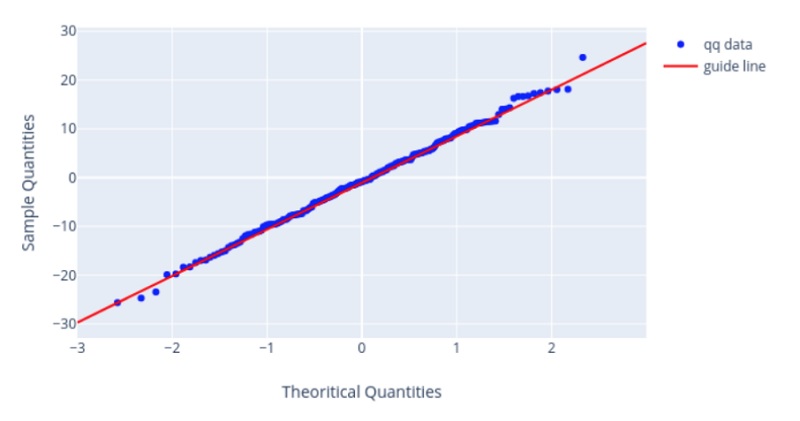
До проверки критериев мы делаем визуальный анализ данных. Согласия хорошо проверять с помощью гистограммы. Но по ней довольно сложно судить о правильности убывания хвостов. Чтобы это проверить был придуман квантильный график
Согласие выборки с распределением, которое образовано с помощью сдвига/масштаба, можно проверить визуально с помощью квантильного графика (Q-Q Plot). К таким распределениям относятся: равномерное, экспоненциальное, нормальное и т.д.
На квантильном графике имеются точки, которые должны расположится вдоль некоторой прямой. Если они располагаются как на графике ниже — тогда у нас отличное согласие.
Критерии однородности (A/B тесты)
Критерия однородности, в отличии от критериев согласия, не проверяют согласия выборки с каким-то конкретным распределением, а рассматривают согласие двух выборок, т.е. мы хотим проверить гипотезу, что у них одинаковое распределение.
Например, у нас есть автолюбители, которые предпочитают шины марки А — это будет первая выборка, а есть те, которые без ума от шин марки Б — это будет вторая выборка. Значения в этих выборках — это эффективность работы автомобильных шин (длина тормозного пути, эффективность торможения, шум и т.д.). Требуется выяснить, имеется ли значимое различие эффективности шин А и Б
Есть еще и другой пример: Первая выборка — характеристики до переобувания в зимнюю резину (пусть будут все те же самые, что и выше). Вторая выборка — характеристики после переобувания в зимнюю резину. Требуется выяснить, имеется ли значимое отличие в характеристиках до и после переобувания.
Эти примеры разные в том плане, что в одном случае мы имеем дело с независимым выборкам, а в другом — с зависимыми выборками. Мы будем применять для этих случаев разные критерии.
Параметрические и непараметрические критерии
Параметрические критерии предполагают, что выборка имеет нормальное распределение, т.е. взята из некоторого параметрического семейства распределений. Статистики параметрических критериев более чувствительны к отклонениям от нулевой гипотезы и, в целом, работаю лучше, чем непараметрические (грубо говоря p-value у параметрических обычно ниже, чем у непараметрических критериев)
Но есть одна интересная особенность: непараметрические критерии работают лучше в случае, если совсем немного отходим от нормального распределения. При небольших отклонениях от идеальных условий — они не требуют идеальных условий, например, нормальности данных.
Независимые выборки
Двухвыборочный t-критерий Стьюдента (Уэлча)
Данные критерии основаны на распределении Стьюдента tk с k степенями свободы называется распределение случайной величины, где в числителе стандартная случайная величина, в знаменателе — квадратный корень распределения хи-квадрат с k степенями свободы деленный на количество степеней свободы
где X ∼ N (0, 1), Y ∼ χ2k и являются независимыми.
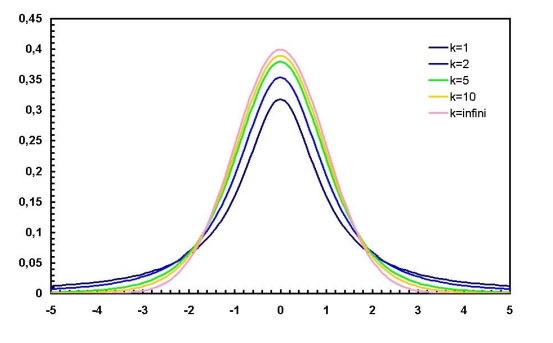
Плотность распределения Стьюдента с k степенями свободы:
где Γ(u) — гамма-функция Эйлера (специальная функция). Как мы видим, здесь хвосты убывают «тяжелее», чем у нормального распределения
Теорема (Лемма Фишера).Пусть X1, . . . , Xn — выборка из нормального распределения N (µ, σ2). Обозначим среднее арифметическое по выборке и несмещенную оценку для дисперсии:
Тогда случайные величины X и S2 независимы
- Выборки: X = (X1, . . . , Xn1), Xi ∼ N (µ1, σ21) и Y = (Y1, . . . , Yn2), Yi ∼ N (µ2, σ22). Выборки могут быть разного размера и имеют нормально распределение. Нюанс: X, Y независимые, σ1 и σ2 неизвестны
- Нулевая гипотеза: H0 : µ1 = µ2
- Альтернатива: H1 : µ1 ≠ µ2 или µ1 > µ2, или µ1 < µ2
- Нулевое распределение: Tn ≈ tk для некоторого k ∈ N
В целом сравнение средних двух нормальных выборок при неизвестных и неравных дисперсиях известна как проблема Беренса-Фишера. При этом рассмотренная аппроксимация (критерий Уэлча) достаточно точна в двух ситуациях:
- Если выборки одинакового размера n1 = n2.
- Если знак неравенства между n1 и n2 такой же, как между σ1 и σ2,
то есть выборка с большей дисперсией имеет больший объем.
Критерий Колмогорова-Смирнова
В качестве первого непараметрического критерия можно использовать модификацию критерия Колмогорова (для непрерывных распределений). Например, две выборки X = (X1, . . . , Xn) и Y = (Y1, . . . , Yn2) с функциями распределения FX и FY соответственно. Обозначим их эмпирические функции распределения и рассмотрим статистику
Если FX = FY , то Dn должна принимать малые значения
При выполнении нулевой гипотезы FX = FY , для любого t > 0 выполняется
где K(t) — функция Колмогорова (при n1, n2 ≥ 20 аппроксимация является достаточно точной)
- Выборки: X = (X1, . . . , Xn1), Xi ∼ FX и Y = (Y1, . . . , Yn2), Yi ∼ Fy (X, Y независимые; FX, FY непрерывные)
- Нулевая гипотеза: H0 : FX = FY
- Альтернатива: H1 : FX ≠ FY
Критерий Манна-Уитни
Критерий Манна-Уитни (или ранговых сумм Уилкоксона) — еще один непараметрический критерий для проверки гипотезы однородности. Он был предложен Уилкоксоном для выборок одинакового размера. Манн и Уитни обобщили его на случай выборок разного размера.
Напомним, что по любой выборке X1, . . . , Xn всегда можно сопоставить вариационный ряд, то есть упорядочить её по неубыванию:
Рангом наблюдения Xi называется:
- Его позиция в вариационном ряду, если Xi не попадает в связку
- (j1 + j2)/2, если xi попадает в связку от j1 до j2; то есть в связке все
объекты получают одинаковый средний ранг.
Критерий Манна-Уитни основан на следующей статистике Vn:
- Обозначим через Rj ранг порядковой статистики Y(j), j = 1, . . . , m, в вариационном ряду, построенном по объединенной выборке (X1, . . . , Xn1, Y1, . . . , Yn2).
- Положим Vn = R1 + . . . + Rn2
- Выборки: X = (X1, . . . , Xn1), Xi ∼ FX и Y = (Y1, . . . , Yn2), Yi ∼ Fy (X, Y независимые)
- Нулевая гипотеза: H0 : FX = FY
- Альтернатива: H1 : FX ≠ FY
- Статистика: Vn = R1 + . . . + Rn2
- Нулевое распределение: табличное для малых выборок нормальное приближение для больших выборок
Зависимые выборки
Двухвыборочный t-критерий Стьюдента
В некоторых случаях связанные выборки имеют элементы Xi и Yi
соответствуют одному и тому же объекту, но измерения сделаны в
разные моменты (например, до и после применения лекарства).
Размеры выборок в этом случае должны совпадать:
n1 = n2 = n
Рассмотрим выборку, образованную разностями Xi и Yi
Zi = Yi − Xi, i = 1, . . . , n.
Сравнение средних в зависимых выборках ничем не отличается от сравнения среднего разности Zi с нулём.
- Выборки: X = (X1, . . . , Xn1), Y = (Y1, . . . , Yn2), Zi = Yi − Xi и Zi ∼ N (µ, σ2). При этом X, Y зависимые, σ неизвестна
- Нулевая гипотеза: H0 : µ = 0
- Альтернатива: H1 : µ ≠ 0 или µ > 0, или µ < 0
- Нулевое распределение: Tn ∼ tn−1
Далее, чтобы сформулировать непараметрические критерии, возьмем каждое приращение Zi и разложим их на две части:
Zi = θ + εi, i = 1, . . . , n
где θ — систематический сдвиг, который не зависит от человека, а εi — случайные ошибки, включающие в себя влияние неучтенных факторов на Zi
В данных обозначениях нулевую гипотезу H0 можно записать как H0: θ = 0. Мы будем предполагать, что ε1, . . . , εn независимы и имеют непрерывные и разные распределения с равной нулю медианой.
Критерий знаков
Самым простым непараметрическим критерием однородности для двух зависимых выборок является критерий знаков. Статистикой критерия знаков является величина
При верной H0 статистика Sn будет иметь биномиальное распределение Bin(n, 1/2), т.е. с успехом 1/2. Для больших n можно использовать сходимость к нормальному закону.
- Выборки: X = (X1, . . . , Xn1), Xi ∼ FX, Y = (Y1, . . . , Yn2), Yi ∼ FY, Zi = Yi − Xi и Zi = θ + εi
- Нулевая гипотеза: H0 : θ = 0
- Альтернатива: H1 : θ ≠ 0 или θ > 0, или θ < 0
- Нулевое распределение: Sn ∼ Bin(n, 1/2)
Критерий знаковых рангов Уилкоксона
Предположим, что случайные величины ε1, . . . , εn имеют одинаковое распределение, симметричное относительно медианы (или же нуля). Условие строгой симметрии относительно медианы является почти столь же нереалистичным, как и предположение, что распределение величин Zi в точности нормально. Как правило, надежно проверить симметрию можно лишь по выборке из нескольких сотен наблюдений
Критерий знаковых рангов Уилкоксона основан на статистике
Wn = R1U1 + . . . + RnUn,
где Ui = I{Zi>0} и Ri — ранги величин |Zi| в ряду |Z1|, . . . , |Zn|.
При верной H0 статистика Wn будет иметь табличное распределение (его можно посчитать явно). Для больших n можно использовать сходимость к нормальному
закону.
- Выборки: X = (X1, . . . , Xn1), Xi ∼ FX, Y = (Y1, . . . , Yn2), Yi ∼ FY, Zi = Yi − Xi и Zi = θ + εi, X, Y зависимые, εi симметрично распределены
- Нулевая гипотеза: H0 : θ = 0
- Альтернатива: H1 : θ ≠ 0 или θ > 0, или θ < 0
- Нулевое распределение: табличное для малых выборок нормальное приближение для больших выборок
Ведение статистики, тестирование различных вариантов данных с отслеживанием эффективности изменений имеет огромное значение в отношении выбора той или иной концепции развития. Однако для анализа важно выбрать только значимые для статистики данные. В этой статье разберемся с понятием статистическая значимость в целом и в A/B тестах, а также рассмотрим, как ее оценивать и рассчитывать.
Что такое статистическая значимость
В процессе любого исследования стоит задача выявить связи между переменными, которые, как правило, характеризуются направлением, силой и надежностью. Чем выше вероятность повторного обнаружения связи, тем она надежнее.
Для проверки гипотез при проведении различных тестов применяется методика статистического анализа. Результатом оценки уровня надежности связи и проверки гипотезы выступает статистическая значимость (statistical significance). Чем меньше вероятность, тем надежнее будет связь.
Статистическая значимость – это параметр, который подтверждает, что результаты исследования были достигнуты не случайно.
Аналитик делает такое заключение, используя метод статистической проверки гипотез. По итогам теста определяется p-значение или значение уровня значимости. Чем оно меньше, тем больше будет статистическая значимость.
Обратите внимание! Слово «значимость» в данном контексте отличается по смыслу от общепринятого. Статистически значимые значения не обязательно являются значимыми или важными. Если же уровень значимости низкий, это не говорит о том, что итоги эксперимента не имеют ценности на практике.
Говоря о статистической значимости, стоит иметь ввиду:
- уровень значимости дает понять, что связь между переменными не случайна;
- уровень значимости в статистике может служить доказательством правдоподобности нулевой гипотезы;
- в ходе проверки получаем информацию о том, что результат эксперимента является или не является статистически значимым.
Значимость статистического критерия применяют при испытаниях вакцин, эффекта новых лекарственных препаратов, изучении болезней, а также при определении, насколько успешна и эффективна работа компании, при A/B тестировании сайтов в маркетинге, а также в различных областях науки, психологии.
История понятия уровня значимости
Статистика помогает решать задачи в различных сферах много веков, однако о статистической значимости заговорили лишь в начале XX столетия. Ввел это понятие в 1925 году британский генетик и статистик сэр Рональд Фишер, который работал над методикой проверки гипотез.
В процессе анализа любого процесса есть вероятность, что произойдут те или иные явления. Итоги эксперимента, которые имели высокую вероятность стать действительными, Фишер описывал словом «значимость» (в переводе с английского significance).
Если данные были недостаточно конкретные для проверки, возникала проблема нулевой гипотезы. Для таких систем в качестве удобной для отклонения нулевой гипотезы выборки исследователем было предложено считать вероятность событий как 5%.
Как оценить статистическую значимость
Для проверки гипотезы используют статистический анализ, при этом уровень значимости определяется с помощью p-значения. Последнее показывает вероятность события, если предположить, что определенная нулевая гипотеза верна.
Весь процесс оценивания уровня значимости можно разделить на 3 стадии, которые, в свою очередь, включают следующие промежуточные этапы.
Постановка эксперимента
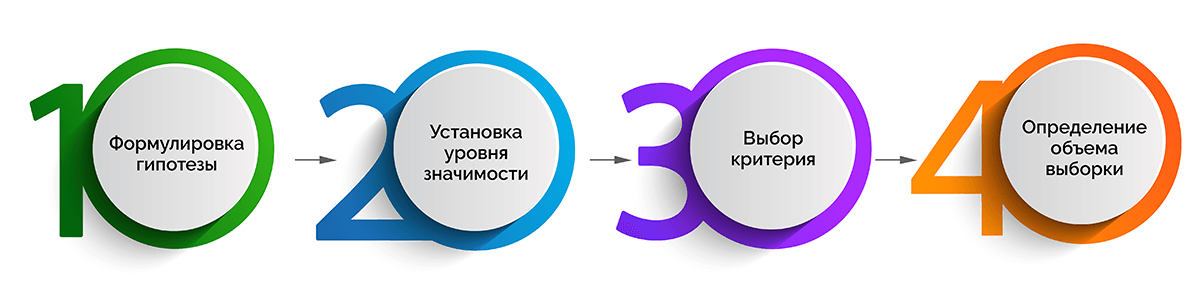
- Формулировка гипотезы.
- Установка уровня значимости, который поможет определить отклонение в распределении данных для идентификации значимого результата.
Если р-значение меньше или равно уровню значимости, данные можно считать статистически значимыми.
- Выбор критерия – одностороннего или двустороннего.
Первый подходит для случаев, когда известно, в какую сторону от нормального значения могут отклониться данные. Второй критерий лучше выбирать, если трудно понять возможное направление отклонения данных от контрольной группы значений. - Определение объема выборки с использованием статистической мощности. Она показывает вероятность того, что при заданной выборке будет получен именно ожидаемый результат. Зачастую пороговая (критическая) цифра мощности – 80%.
Вычисление стандартного отклонения

- Расчет стандартного отклонения, которое показывает величину разброса данных на заданной выборке.
- Поиск среднего значения в каждой исследуемой группе. Для этого осуществляют сложение всех значений, а сумму делят на их количество.
- Определение стандартного отклонения (xi – µ). Разница вычисляется путем вычитания каждого полученного значения из средней величины.
- Возведение полученных величин в квадрат и их суммирование. На данном этапе все числа со знаком «минус» должны исчезнуть.
- Деление суммы на общий объем выборки минус 1. Единица – это генеральная совокупность, которая не учитывается в расчете.
- Извлечение корня квадратного.
Определение значимости
- Определение дисперсии между двумя группами данных по формуле:
sd = √((s1/N1) + (s2/N2)), где:
s1 – стандартной отклонение в первой группе;
s2 – стандартное отклонение во второй группе;
N1 – объем выборки в первой группе;
N2 – объем выборки во 2-й группе. - Поиск t-оценки данных. С ее помощью можно переводить данные в такую форму, которая позволит использовать их в сравнении с другими значениями. T-оценка рассчитывается по формуле:
t = (µ1 – µ2)/sd, где:
µ1 – среднее значение для 1-й группы;
µ2 – среднее значение для 2-й группы;
sd – дисперсия между двумя группами. - Определение степени свободы выборки. Для этого объемы двух выборок складывают и вычитают 2.
- Оценка значимости. Ее осуществляют по таблице значений t-критерия (критерия Стьюдента).
- Повышение уверенности в достоверности выводов путем проведения дальнейшего исследования.
Статистическая значимость и гипотезы
Гипотеза – это теория, предположение. Если требуется проверка гипотез, всегда используется статистическая значимость. Предположение же называется гипотезой до тех пор, пока это утверждение не будет опровергнуто или доказано.

Гипотезы бывают двух типов:
- нулевая гипотеза – теория, не требующая доказательств. Согласно нее, при внесении изменений ничего не произойдет, т. е. стоит задача не доказать это, а опровергнуть;
- альтернативная гипотеза (исследовательская) – теория, в пользу которой нужно отклонить нулевую гипотезу, т. е. предстоит доказать, что одно решение лучше другого.
Рассмотрим, как статистическая значимость влияет на подтверждение или опровержение альтернативной гипотезы на простом примере.
У компании запущена реклама, которая стала давать меньше конверсий и продаж, чем месяц назад. По мнению маркетолога, причина кроется в рекламных креативах, которые приелись аудитории и требуют замены. Специалист предлагает заменить текстовый материал объявления. Гипотеза состоит в том, что после внесенных изменений будет достигнута главная цель эксперимента: клиенты, пришедшие на сайт с рекламы, станут покупать больше. Теперь маркетологу нужно проводить A/B тестирование обоих креативов, чтобы выяснить, какой текст объявления лучше работает. При высоком уровне достоверности данные условия позволят учитывать результаты такого тестирования.
Проверка статистических гипотез
В случаях, когда информация говорит о незначительных изменениях в сравнении с предыдущими значениями, требуется проверка гипотез. Она позволяет определить, действительно ли происходят изменения или это всего лишь результат неточности измерений.
Для этого принимают или отвергают нулевую гипотезу. Задача решается на основании соотношения p-уровня (общей статистической значимости) и α (уровня значимости).
- p-уровень < α – нулевая гипотеза отвергается;
- p-уровень > α – нулевая гипотеза принимается.
Чем меньше значение p-уровня, тем больше шансов, что тестовая статистика актуальна.
Критерии оценки
Уровень значимости для определения степени правдивости полученных результатов обычно устанавливается на отметке 0,05. Таким образом, интервал вероятности между разными вариантами составляет 5%.
После этого необходимо найти подходящий критерий, по которому будут оцениваться выдвинутые гипотезы: односторонний или двусторонний. Для этого применяют разные методы расчета:

- t-критерий Стьюдента;
- u-критерий Манна-Уитни;
- w-критерий Уилкоксона;
- критерий хи-квадрата Пирсона.
T-критерий Стьюдента
предполагает сравнение данных по двум вариантам исследования и позволяет делать выводы о том, по каким параметрам они отличаются. Метод актуален, когда есть сомнения, что данные располагаются ниже или выше относительно нормального распределения.
Установить, все ли данные лежат в заданном пределе, можно с помощью специальной таблицы значений. Но чаще применяют автоматический расчет t-критерия Стьюдента. Существует много калькуляторов, которые работают по схожему принципу:
- Указываем вид расчета (связанные выборки или несвязанные).
- Вносим данные о первой выборке в первую колонку, о второй – во вторую. В одну строку вписываем одно значение, без пропусков и пробелов. Для отделения дробной части от основной используется точка.
- После заполнения обеих колонок, нажимаем кнопку запуска.
Преимущество коэффициента Стьюдента в том, что он применим для любой сферы деятельности, поэтому является самым популярным и используется на практике чаще всего.
Критерий Манна-Уитни
Рассчитывается по иному алгоритму, но предполагает использование аналогичных исходных данных. Его также зачастую рассчитывают онлайн с помощью специальных сервисов.
При расчете критерия Манна-Уитни есть особенности. Показатель применим для малых выборок или выборок с большими выбросами данных. Чем меньше совпадающих значений в выборках, тем корректнее будет работать критерий.
W-критерий Уилкоксона
Непараметрический аналог t-критерия Стьюдента для сравнения показателей до и после эксперимента, основанный на рангах. Его принцип заключается в том, что для каждого участника определяется величина изменения признака. Затем все значения упорядочиваются по абсолютной величине, рангам присваивается знак изменения, после чего «знаковые ранги» суммируются. Данный критерий применяется в медицинской статистике для сравнения показателей пациентов до лечения и после его завершения.
Критерий хи-квадрата Пирсона
Еще один непараметрический метод для оценки уровня значимости двух и более относительных показателей. Применяется для анализа таблиц сопряженности, в которых приведены данные о частотах различных исходов с учетом фактора риска.
Проблема множественного тестирования гипотез
Если сравнивать группы по различным срезам аудитории или метрикам, может возникать проблема множественного тестирования. Дело в том, что учесть абсолютно все проверки достаточно сложно. Это связано со сложностью предварительного прогнозирования их количества. К тому же, зачастую они всё равно не независимы.
Не существует универсального рецепта решения проблемы множественного тестирования гипотез. Аналитики рекомендуют руководствоваться здравым смыслом. Если протестировать много срезов по различным метрикам, любое исследование может показать якобы значимый для статистики результат. Это означает, итоги тестирования следует читать и интерпретировать с осторожностью.
Вычисление объема выборки и стандартного отклонения
После вычисления критерия оценки (критерия Стьюдента или Манна-Уитни) можно определить, какого оптимального объема должна быть выборка. При этом условии должно быть достаточное для признания достоверности результатов исследования количество людей в фокус-группах, на которых будут проверяться разные варианты.
Недостаточное количество участников эксперимента может стать причиной нехватки выборочных данных для того, чтобы сделать статистически значимый вывод и привести к повышению риска получения случайных результатов.
Объем выборки определяют с помощью статистической мощности (распространенный порог находится на уровне 80%). Этот показатель рассчитывают обычно с помощью специального калькулятора.
Затем можно переходить к вычислению уровня стандартного отклонения, по которому можно узнать величину разброса данных. Его рассчитывают по формуле:

s = √∑((xi – µ)2/(N – 1)), где:
xi – i-е значение или полученный результат эксперимента;
µ – среднее значение для конкретной исследуемой группы;
N – общее количество данных.
Для упрощения расчетов также используют онлайн-калькуляторы.
Значение p-уровня
Имея две гипотезы – нулевую и альтернативную, необходимо доказать одну из них (истинную) и опровергнуть другую (ложную).
Для этого основатель теории статистической значимости доктор Рональд Фишер создал определитель, с помощью которого можно было оценить, был эксперимент удачным или нет. Такой определитель получил название индекс достоверности или p-уровень (p-value).
P-уровень или уровень статистической значимости результатов – это показатель, который находится в обратной зависимости от истинного результата и отражает вероятность его ошибочной интерпретации.
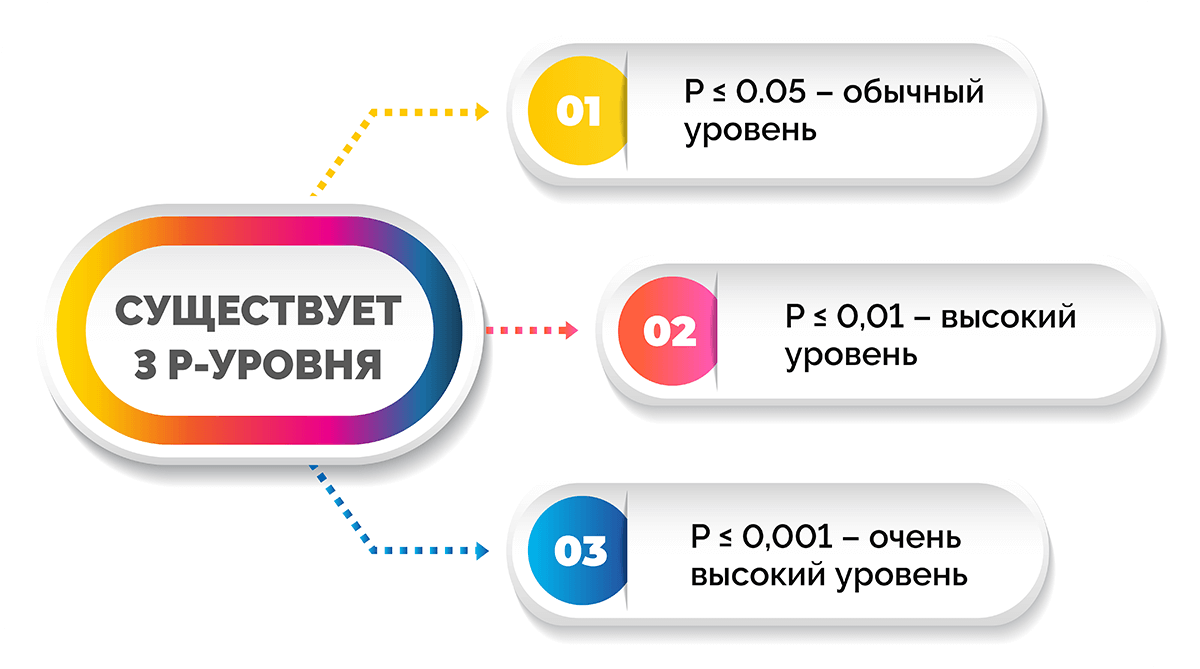
Существует 3 p-уровня.
- P ≤ 0,05 – обычный уровень, т. е. получен статистически значимый результат.
- P ≤ 0,01 – высокий уровень, т. е. выявлена выраженная закономерность.
- P ≤ 0,001 – очень высокий уровень.
Есть и другие значения статистической значимости. Например, уровень p ≥ 0,1 свидетельствует о том, что итог эксперимента не является статистически значимым.
Приближенные к статистически значимым результаты с уровнями p = 0,06 ÷ 0,09 говорят о том, что есть тенденция к существованию искомой закономерности.
Говоря проще, чем ниже значение p-уровня, тем более статистически значимым будет результат эксперимента и тем ниже вероятность ошибки.
Расчет статистической значимости
Выше в статье мы рассматривали порядок оценки уровня статистической значимости. Что касается расчета, то вручную он выполняется редко. Большинство аналитиков определяют уровень значимости с помощью онлайн-калькулятора.
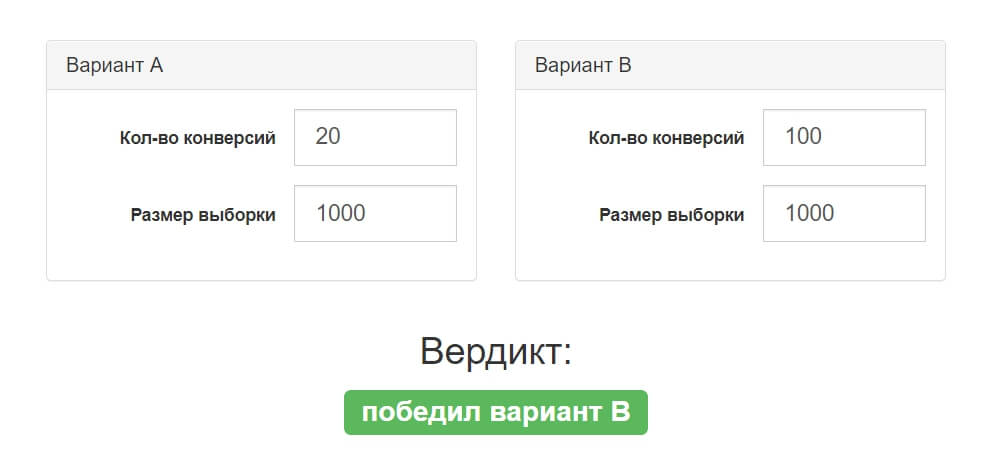
В анализе участвуют две гипотезы, для каждой из которых необходимо задать количество конверсий и размер выборки. Сервис автоматически рассчитывает показатель и определяет уровень значимости результата.
Порог вероятности
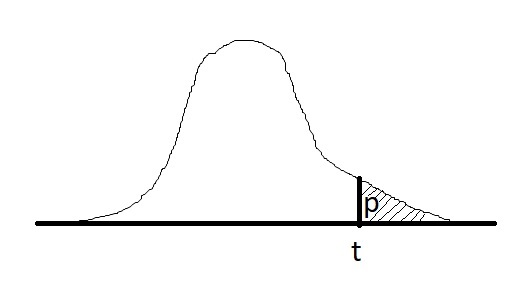
Основа статистической значимости – это вероятность получения нужного значения, если принять как факт, что нулевая гипотеза верна. Если предположить, что в процессе эксперимента было получено некое число Х, то при помощи функции плотности вероятности можно узнать, будет ли вероятность получить значение Х или любое другое значение с меньшей вероятностью, чем Х.
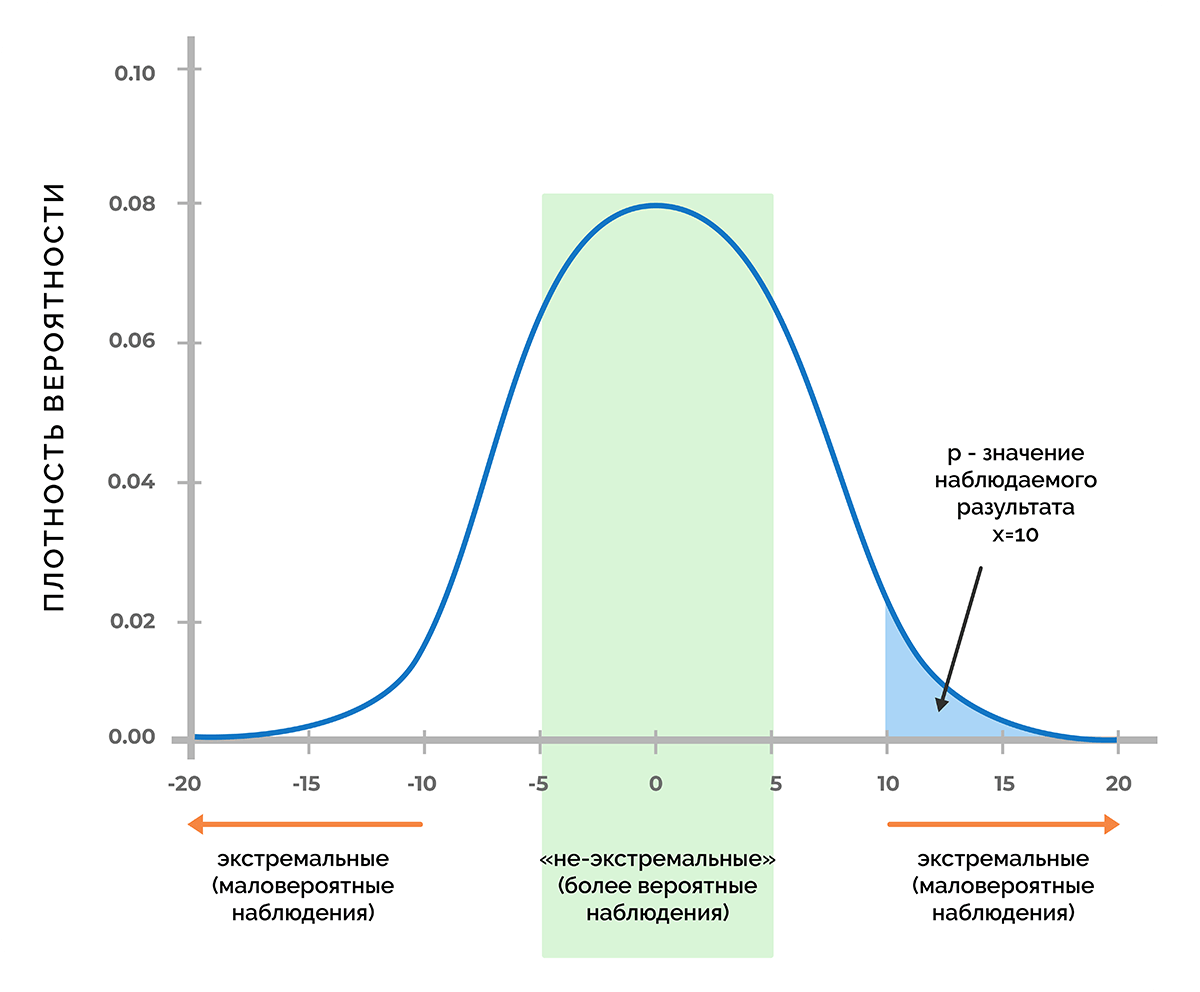
На рисунке изображена кривая Гаусса, соответствующая функции плотности вероятности, которая отвечает распределению значений показателя, при котором верна нулевая гипотеза.
При достаточно низком значении p-уровня не имеет смысла продолжать считать, что переменные не связаны друг с другом. Это позволяет отвергнуть нулевую гипотезу и принять факт того, что связь существует.
Пороги значимости в разных областях могут значительно отличаться. Так, при исследовании вероятности существования бозона Хиггса p-значение равно 1/3,5 млн, в сфере исследования геномов его уровень может достигать 5×10-8.
Статистическая значимость в A/B тестах
Одной из сфер широкого применения статистической значимости является маркетинг. Аналитики используют исследования для поиска оптимальных путей развития бизнеса, интернет-маркетологи оценивают эффективность рекламных кампаний и посещаемость ресурсов.
A/B тестирование – самый распространенный способ оптимизации страниц сайтов. Его результат невозможно предугадать, можно лишь строить алгоритм работы так, чтобы в конце тестирования получить максимальное количество данных, которые позволят сделать вывод о самом удачном варианте.
Важно, чтобы A/B тестирование длилось минимум 7 дней. Это позволит учесть колебания уровней конверсии и других показателей в разные дни.
Процедура A/B тестирования кажется довольно простой:
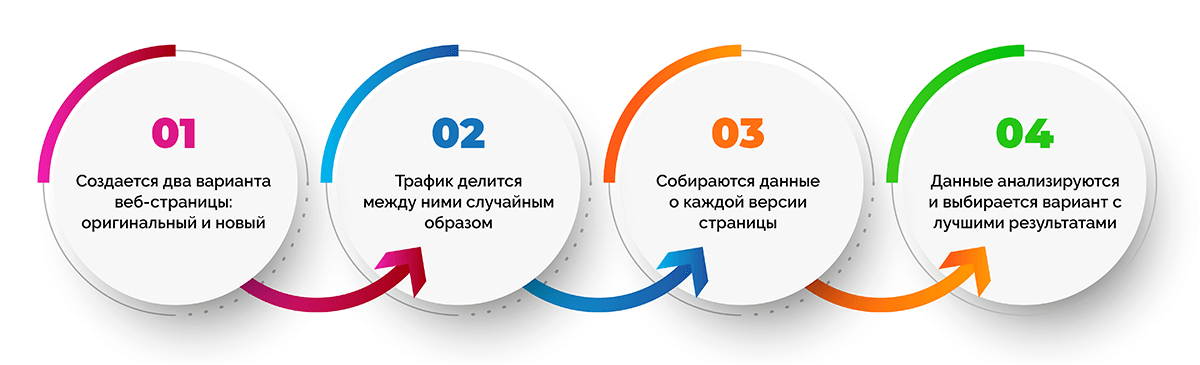
- Создается две веб-страницы (оригинальная и новая).
- Трафик делится между двумя версиями веб-страницы случайным образом.
- Собираются данные о каждой версии страницы.
- Данные анализируются и выбирается вариант с лучшими показателями, а второй отключается.
Важно, чтобы тестирование было достоверным, в противном случае неверное решение может привести к негативным последствиям для сайта.
В данном случае гипотезой считается достижение нужной достоверности. Сама достоверность будет статистической значимостью. Для тестирования гипотезы нужно сформулировать нулевую гипотезу и оценить возможность ее отклонения из-за малой вероятности.
Возможные ошибки
На этапе оценки результатов тестирования можно допустить два типа ошибок:
- ошибка первого рода (type I error) – ложноположительный итог, когда кажется, что различия между показателями двух тестируемых страниц есть, на самом же деле их нет;
- ошибка второго рода (type II error) – ложноотрицательный итог, когда существенная разница между тестируемыми страницами не заметна, но на самом деле она есть, при этом в тестировании видимое ее отсутствие является случайностью.
Как избежать ошибок
Избежать обоих типов ошибок можно, устанавливая при тестировании правильный размер выборки. Чтобы его определить, предстоит в настройках теста задать несколько параметров.
- Чтобы исключить ложноположительные результаты, понадобится указать уровень значимости. Обычно задают значение 0,05, которое будет гарантировать достоверность, превышающую 95%.
- Чтобы избежать ложноотрицательных результатов потребуется минимальная разница в ответах и вероятность обнаружить эту разницу, т. е. статистическая мощность. Последнюю по умолчанию устанавливают на уровне 80%.
Этого достаточно, чтобы вычислить требуемый размер выборки. Обычно расчеты проводятся с помощью спец. калькуляторов.
Можно ли доверять результатам на 100%
К сожалению, даже при правильно проведенной проверке гипотез могут быть допущены ошибки. Это связано с человеческим фактором, а точнее – со скрытыми предположениями, которые зачастую не имеют ничего общего с реальностью.
Вот распространенные предположения, которые приводят к ошибкам:
- посетители сайта, которые просматривают разные варианты веб-страницы, не связаны друг с другом;
- для всех посетителей вероятность конверсии одинакова;
- показатели, которые измеряются в процессе тестирования, имеют нормальное распределение.
На что обратить внимание
Без A/B теста сложно представить развитие современного интернет-продукта. Однако, несмотря на кажущийся простым инструмент, специалисты порой на практике встречаются с подводными камнями. Если знать о них заранее, можно повысить точность тестирования.
Первый узкий момент – проблема подглядывания. Наблюдение за итогами тестирования в реальном времени выступает в качестве соблазна для активных действий, предпринимаемых раньше времени. Обработка «сырых» данных неизменно приводит к статистической погрешности. Чем чаще смотреть на промежуточные результаты A/B теста, тем больше вероятность обнаружить разницу, которой в действительности нет:
- 2 подглядывания с желанием завершить тестирование повышают p-значение в 2 раза;
- 5 подглядывания – в 3,2 раза;
- 10 000 подглядываний – в 12 раз и более.
Решить проблему подглядывания можно тремя способами:
- Заблаговременно фиксировать размер выборки и не смотреть итоги теста до его окончания.
- С помощью математических методов: комбинация Sequential experiment design и байесовского подхода к A/B-тесту.
- С помощью продуктового метода, который предполагает предварительную оценку размера выборки, обеспечивающего эффективность тестирования, и принятие во внимание природы проблемы подглядывания в процессе промежуточных проверок.
Еще один подводный камень заключается в том, что от выигравшей гипотезы ожидают слишком многого. На самом деле в долгосрочной перспективе показатели победителя могут быть менее выдающимися, чем те, которые выдал тест.
Пример статистической значимости
Предположим, разработчики онлайн-игры тестируют два дизайна интерфейса. При A/B тестировании было привлечено 2000 новых игроков: по 1000 пользователей в каждую версию.
В первый день тестирования первая версия дизайна получила 370 возвратов пользователей, вторая – 510.
Как видно, вторая версия дизайна показала лучший результат возвратов. Но разработчики не были уверены, действительно ли это произошло из-за изменения продукта, а не стало следствием случайной погрешности.
Чтобы выяснить это, было принято решение рассчитать уровень значимости для наблюдаемой разницы. Поскольку метрика является простой, можно воспользоваться онлайн-сервисом и вычислить статистическую значимость автоматически.

P-значение < 0,001 в нашем примере свидетельствует о том, что при одинаковых тестовых группах вероятность увидеть наблюдаемую разницу чрезвычайно мала. Это говорит о том, что рост возвратов в первый день с высокой долей вероятности зависит от изменений продукта.
Часто задаваемые вопросы
Маркетинговые исследования статистики чаще всего проводятся путем A/B тестирования. О нем мы рассказали в одном из предыдущих разделов статьи. Однако при тестировании могут возникать некоторые трудности. Например, некорректное определение статистически значимого различия или невозможность определить, чем обусловлено различие. Решить подобные проблемы позволяет увеличение выборки и вариантов.
Оценка необходимости ранжирования данных статистики исключительно на основании статистической значимости может привести к серьезным ошибкам. Предпочтение лишь «значимых» результатов повышает риск искажения фактов.
В процессе тестирования регулярная проверка показателей с готовностью принять решение о завершении теста при обнаружении существенной разницы приводит к кумулятивному накоплению вероятных случайных моментов, при которых разница покидает пределы диапазона. В результате этого каждая новая проверка приводит к росту p-значения.
Заключение
Статистическая значимость является важным методом в ходе проведения экспериментов и исследований несмотря на риск ее неправильной интерпретации. При грамотном подходе погрешность можно свести к минимуму, используя значение в целях повышения достоверности результатов.
Олег Вершинин
Специалист по продукту
Все статьи автора
Нашли ошибку в тексте? Выделите нужный фрагмент и нажмите
ctrl
+
enter
Выбор статистического критерия для тестирования гипотез
Прежде чем приступать к выбору статистического критерия, нужно определиться с тем, от чего зависит применение тех или иных статистических методов. Ранее мы уже подразделяли наши данные на количественные и качественные (см. статью «Типы данных»), изучали способы их описания в зависимости от типов признаков и видов распределения (см. статью «Описательная статистика» и «Виды распределений»). Для вариационных рядов, которые имеют нормальное распределение, мы рассчитывали определенные параметры, с помощью которых можно описать вариационный ряд. Для нормального распределения это – средняя величина и стандартное отклонение. В случае распределения, отличного от нормального, используются медиана и интерквартильный интервал, с помощью которых можно было описать большую часть данных.
Определение задачи, которая будет решаться с использованием статистических методов.
До того, как выбирать тот или иной статистический критерий исследователь прежде всего должен определиться, какие именно задачи будут решаться, и какие методы (статистические тесты) для этого будут подбираться.
Как таковые задачи можно разделить на несколько групп:
Предварительные задачи: Описание данных
Само по себе описание данных не является аналитической задачей. Задача описания данных состоит в упорядочивании и компактном представлении данных. Методы описательной статистики напрямую зависит от типа данных, с которым мы имеем дело. Ранее мы уже подразделяли наши данные на количественные и качественные (см. статью «Типы данных»), изучали способы их описания в зависимости от типов признаков и видов распределения (см. статью «Описательная статистика» и «Виды распределений»). Для вариационных рядов, которые имеют нормальное распределение, мы рассчитывали определенные параметры, с помощью которых можно описать вариационный ряд. Для нормального распределения это – средняя величина и стандартное отклонение. В случае распределения, отличного от нормального, используются медиана и интерквартильный интервал, с помощью которых можно было описать большую часть данных. Для качественных данных описание заключается в нахождении частот, долей, пропорций, представление в виде абсолютных и относительных величин.
- Оценка динамики явления — решается прежде всего через инструменты оценки динамических рядов
- Анализ различий между группами (статистическими совокупностями) в зависимости от типа данных и распределения количественных данных, количества и связанности групп может применяться большое количество инструментов. Этот пункт будет изложен в этой статье подробным образом
- Выявление и оценка взаимовлияний в динамике — в зависимости от типа данных и их распределения используются различные методы корелляционного анализа.
- Прогноя явлений — используются линейные и логистические регрессии (возможно, в связке с ROC-analysis), деревья решений, нейронные сети, различные вариантры дискриминативного анализа
- Группировка явлений и выявление общих свойств группы — варианты кластерного анализа.
Выбор статистического критерия для тестирования гипотез о различии групп
Наиболее частой задачей является сравнение статистических совокупностей (групп, выборок) на предмет статистически значимых различий между ними (подробнее см. «Ошибка первого рода, статистическая значимость»). К примеру в результате исследования «случай-контроль» или когортного исследования необходимо сравнить показатели длительности послеоперационного периода, частоты осложнений, функционального состояния импланта и пр.
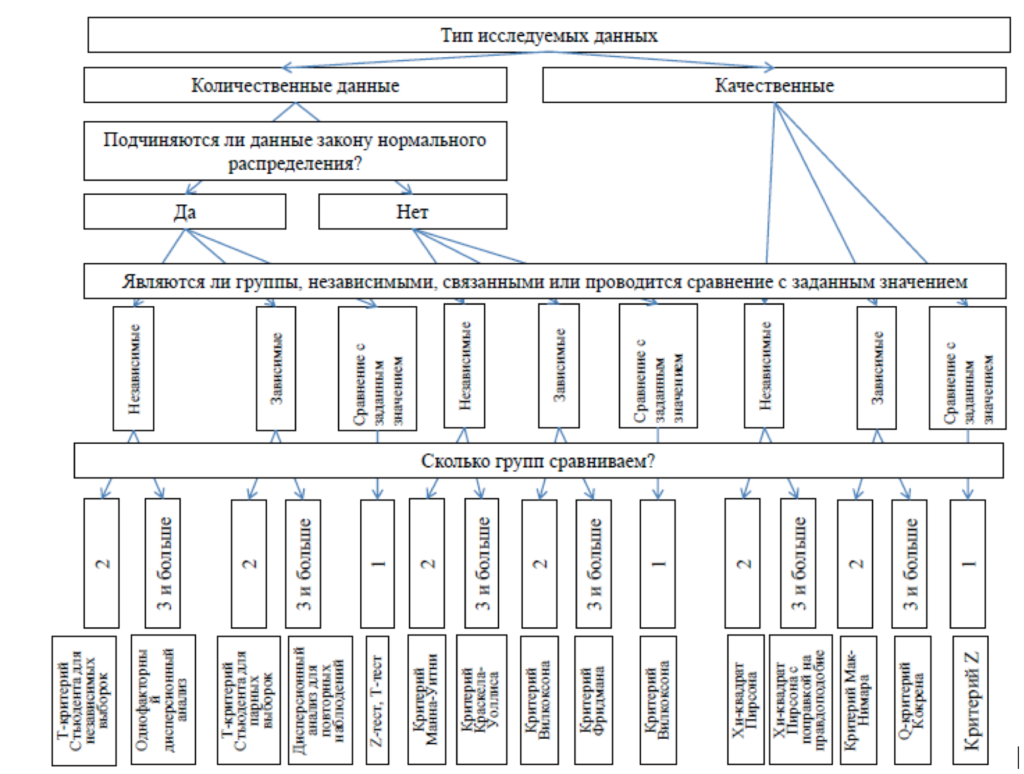
Алгоритм выбора (Рисунок 1).
- Уточните тип данных (количественные или качественные)
- В случае количественных данных уточните тип распределения (нормальное или отличное от нормального)
- Уточните количество групп сравнения. Важный пункт, о котором часто забывают сравнивать группы 1 раз попарно в случае двух групп и три раза попарно в случае трех не одно и тоже. В данном контексте нужно учитывать увеличение ошибки первого рода в случае множественных сравнений. Для таких ситуаций есть отдельные статистические методы (к примеру вместо т-критерия стьюдента используется дисперсионный анализ).
- Уточните, связан ли группы сравнения между собой (в данном случае речь идет об идентичности единиц наблюдения в группах), т.е. являются ли единицы наблюдения в группах разными носителями признака (независимые или «опыт-контроль»), или это одни и те же пациенты, опрашиваемые, предметы, сопряженные «до и после эксперимента». В зависимости от ответа на этот вопрос меняется логика выбора статистического критерия.
В случае выбора статистического критерия для сравнения количественных данных нужно учитывать распределение признака: является ли оно нормальным или отличным от нормального. В первом случае, как и при описании вариационного ряда, мы будет использовать параметры распределения, отсюда и название этой группы методов: параметрические методы, в случае отличного от нормального распределения следует использовать непараметрические методы.
Параметрические статистические методы
Класс статистических методов, используемых для анализа данных, которые образуют известное распределение (обычно нормальное). Названы так потому, что основываются на оценке параметров (таких как среднее или стандартное отклонение) выборочного распределения интересующей величины.
Непараметрические методы
Непараметрические методы не основываются на оценке параметров (таких как среднее или стандартное отклонение) при описании выборочного распределения интересующей величины. Поэтому эти методы иногда также называются свободными от параметров или свободно распределенными.
Статистические методы с (некоторыми) желательными свойствами, сохраняющимися при относительно слабых допущениях о рассматриваемых генеральных совокупностях. Непараметрические методы позволяют обрабатывать данные «низкого качества» из выборок малого объёма с переменными, про распределение которых мало что или вообще ничего неизвестно.
Рисунок 1. Выбор статистического критерия для сравнения статистических совокупностей (По Мильчаков К.С.)
Пример выбора статистического критерия для сравнения статистических совокупностей
Пример 1: Для оценки успешности реабилитации после эндопротезирования коленного сустава было проведено исследование у двух выборок (n1=10; n2=10) на предмет скорости восстановления к сгибанию в колене. В первой выборке оказались люди прошедшие полный курс реабилитации, во второй пациенты, отказавшиеся от услуг реабилитолога. Сделайте статистический вывод о пользе реабилитологического сопровождения на основании представленных данных, прдположим, что данные распределены отличным от нормального образом.
| Группа «Реабилитация», срок в днях | Группа «без реабилитации», срок в днях |
| 22.1 | 32.5 |
| 22.3 | 37.1 |
| 26.2 | 39.1 |
| 29.6 | 40.5 |
| 31.7 | 45.5 |
| 33.5 | 51.3 |
| 38.9 | 52.6 |
| 39.7 | 55.7 |
| 43.2 | 55.9 |
| 43.2 | 57.7 |
Ответ: Тип данных: количественный, непрерывный, распределение: отличное от нормального, количество групп: 2, связанность групп: не связаны. необходимо использовать критерий Манна-Уитни
Пример 2:
При заболеваниях сетчатки повышается проницаемость ее сосудов. Дж. Фишмен и соавт. (G. Fishman et al. Blood-retinal barrier function in patients with cone or cone-rod dystrophy. Arch. Ophthalmol., 104:545—548, 1986) измерили проницаемость сосудов сетчатки у здоровых и у больных с ее поражением. Полученные результаты приведены в таблице. Сделайте вывод о проницаемости сетчатки у больных с дистрофией и относительно здорового контроля.
Проницаемость сосудов сетчатки, мм:
| Здоровые | Больные |
| 0,5 | 1,2 |
| 0,7 | 1,4 |
| 0,7 | 1,6 |
| 1 | 1,7 |
| 1 | 1,7 |
| 1,2 | 1,8 |
| 1,4 | 2,2 |
| 1,4 | 2,3 |
| 1,6 | 2,4 |
| 1,6 | 6,4 |
| 1,7 | 19 |
| 2,2 | 23,6 |
Ответ: Тип данных: количественный, непрерывный, распределение: неизвестно. Количество групп: 2, связанность групп: не связаны.
Необходимо использовать критерий Манна-Уитни или после проверки распределения (в случае нормального распределения величины) использовать т-критерий Стьюдента для несвяазанных совокупностей.
Пример 3:
Бишоп (Т. Bishop. High frequency neural modulation in dentistry. J. Am. Dent. Assoc., 112:176—177, 1986) изучил эффективность высокочастотной стимуляции нерва в качестве обезболивающего средства при удалении зуба. Все больные подключались к прибору, но в одних случаях он работал, в других был выключен. Ни стоматолог, ни больной не знали, включен ли прибор. Позволяют ли следующие данные считать высокочастотную стимуляцию нерва действенным анальгезируюшим средством?
| Прибор включен | Прибор выключен | |
| Боли нет | 24 | 3 |
| Боли есть | 6 | 17 |
Ответ: Тип данных: качественный, абсолютные частоты, количество групп: 2, связанность групп: не связаны.
Необходимо использовать хи-квадрат Пирсона (или точный критерий Фишера).
NB! о выборе статистического критерия
Каждый статистический критерий работает с определенным набором данных и в условиях определенный групп. Аккуратно выбирайте статистические критерии, не упускайте логику выбора и результат Ваших расчетов будет корректным и не вызывающим сомнения о профессиональных статистических рецензентов, как при презентации материала на конференции, сдаче отчета о клиническом исследовании или публикации статьи. Удачи на научном поприще!
Если Вам понравилась статья и оказалась полезной, Вы можете поделиться ею с коллегами и друзьями в социальных сетях: