Мы можем использовать неправильные дроби и смешанные числа для представления одних и тех же значений. Рассмотрим на примере равенство неправильной дроби и смешанного числа 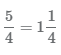
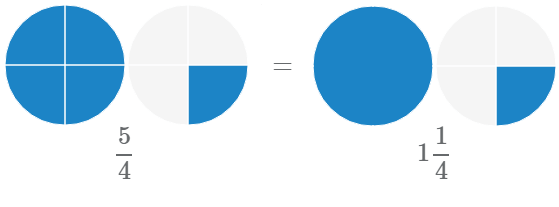
Перевод неправильной дроби в смешанное число
Для перевода неправильной дроби 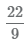
- 1 Разделим числитель на знаменатель 22 ÷ 9, получим 2 целых и 4 в остатке.
- 2 Число 2 будет целой частью смешанного числа.
-
3 Остаток от деления 4 будет числителем дроби, а знаменатель останется прежним, равным 9. В результате получаем
Пример Перевести неправильные дроби  в смешанные числа.
в смешанные числа.
Перевод смешанного числа в неправильную дробь
Для перевода смешанного числа 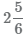
- 1 Умножим целую часть на знаменатель 2×6 и прибавим числитель 5. Полученное число 17=2×6+5запищем в числитель неправильной дроби.
- 2 Запищем в знаменатель неправильной дроби число 6, знаменатель при преобразование в неправильную дробь остается неизменным.
-
3 В результате шагов 1-2 получаем неправильную дробь
Рассмотрим на примерах как переводить смешанные числа в неправильные дроби.
Пример Перевести смешанные числа  в неправильные дроби.
в неправильные дроби.
Сумму натурального числа правильной дроби принято записывать без знака «+». Такую сумму называют смешанным числом. Можно сказать немного иначе: запись числа, которая содержит целую и дробную части, называют смешанной. Для краткости вместо «число в смешанной записи» говорят смешанное число.

Например,
целая часть этого смешанного числа равна 31, дробная –
Смешанное число можно представить в виде неправильной дроби. Чтобы представить смешанное число в виде неправильной дроби, нужно:
1) умножить его целую часть на знаменатель дробной части;
2) к полученному произведению прибавить числитель дробной части;
3) записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.
Например,
Неправильную дробь можно представить в виде смешанного числа.
Запись неправильной дроби в виде смешанного числа называют выделением целой части дроби.
Чтобы выделить целую часть неправильной дроби, надо разделить её числитель на знаменатель и записать смешанное число в виде:
- целая часть – частное от деления;
- числитель дробной части – остаток от деления;
- знаменатель дробной части – знаменатель данной неправильной дроби.
Если остаток от деления числителя неправильной дроби на её знаменатель равен 0, неправильная дробь равна получившемуся при делении натуральному числу.
Например, выделим целую часть неправильной дроби
131 : 8 = 16 (и 3 в остатке);
Выделим целую часть неправильной дроби
13104 : 13 = 1008.

Чтобы найти сумму смешанных чисел, нужно сложить отдельно целые и дробные части.
Если при сложении дробных частей получилась неправильная дробь, выделяют целую часть этой дроби и добавляют к уже имеющейся целой части.
Например,
Вычитание смешанных чисел
Чтобы найти разность смешанных чисел, нужно найти отдельно разность целых частей и отдельно разность дробных частей.
Если дробная часть уменьшаемого меньше дробной части вычитаемого, то одну единицу целой части уменьшаемого необходимо предварительно прибавить к его дробной части.
Например,
Остались вопросы? Хотите знать больше о смешанных числах?
Чтобы получить помощь репетитора – зарегистрируйтесь.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Что такое смешанная дробь
Определение
Число, содержащее в себе целую и дробную части, называется смешанной дробью.
По сути, данное понятие представляет собой сумму целого числа и правильной дроби:
(afrac bc;=;a+frac bc)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Пример:
(7frac34;=;7+frac34)
Превращение смешанной дроби в неправильную
Любое смешанное число можно преобразовать в неправильную дробь. Для этого необходимо к произведению целой части и знаменателя дробной части прибавить числитель. Полученная сумма будет числителем неправильной дроби, а знаменатель останется прежним.
Преобразование смешанной дроби в неправильную можно записать в виде формулы:
(afrac bc;=;frac{atimes c+b}c)
Пример:
(15frac89;=;frac{15times9+8}9;=;frac{143}9)
Выполнение действий со смешанными дробями, формулы и примеры
Сложение
Чтобы посчитать сумму смешанных дробей необходимо отдельно сложить их целые компоненты и дробные составляющие. Правильные дроби в составе смешанных чисел суммируются при помощи приведения к наименьшему общему знаменателю.
Формульное выражение сложения смешанных чисел:
(afrac bc+dfrac ef=left(a+dright)+left(frac bc+frac efright))
Пример:
(2frac13+5frac47;)
Вычисляем наименьший общий знаменатель дробных слагаемых:
3×7=21
(2frac13+5frac47=2+5+frac13+frac47;=7+frac7{21}+frac{12}{21}=7+frac{7+12}{21}=7frac{19}{21})
Вычитание
Чтобы из одной смешанной дроби вычесть другую, нужно дробные компоненты уменьшаемого и вычитаемого привести к минимальному общему знаменателю, затем выполнить вычитание отдельно целых и дробных частей.
Формула для ситуации, когда дробь в составе уменьшаемого больше, чем дробная часть вычитаемого:
(afrac bc-dfrac ef=left(a+frac bcright)-left(d+frac efright);=left(a-dright)+left(frac bc-frac efright))
В случае, когда дробь в составе уменьшаемого меньше дроби в составе вычитаемого, необходимо меньшую дробь превратить в неправильную, отняв единицу от целой части уменьшаемого, то есть:
(afrac bc-dfrac ef=left(left(a-dright)-frac efright)+frac bc)
Пример:
(13frac38-6frac12)
Для решения этого выражения найдем наименьший общий знаменатель:
8=2×2×2, следовательно, 8 — это наименьший общий знаменатель.
(13frac38-6frac12=13frac38-6frac48=left(12+1+frac38right)-6frac48=left(12+frac{1times8+3}8right)-6frac48=12frac{11}8-6frac48=left(12-6right)+left(frac{11}8-frac48right)=6+frac{11-4}8=6frac78)
Умножение и деление
Перед тем, как умножать или делить смешанные числа, необходимо преобразовать их в неправильные дроби. После этого можно производить нужное действие по правилам умножения и деления обыкновенных дробей.
Формула умножения смешанных чисел выглядит так:
(afrac bctimes dfrac ef=frac{atimes c+b}ctimesfrac{dtimes f+e}f=frac{left(atimes c+bright)timesleft(dtimes f+eright)}{ctimes f}=frac{left(ac+bright)left(df+eright)}{cf})
Формула деления смешанных дробей:
(afrac bcdiv dfrac ef=frac{atimes c+b}cdivfrac{dtimes f+e}f=frac{atimes c+b}ctimesfrac f{dtimes f+e}=frac{left(atimes c+bright)times f}{ctimesleft(dtimes f+eright)}=frac{fleft(ac+bright)}{cleft(df+eright)})
Пример 1:
(5frac2{19}times2frac79=frac{5times19+2}{19}timesfrac{2times9+7}9=frac{97}{19}timesfrac{25}9=frac{97times25}{19times9}=frac{2425}{171}=14frac{31}{171})
Пример 2:
(4frac23div3frac57=frac{4times3+2}3divfrac{3times7+5}7=frac{14}3divfrac{26}7=frac{14}3timesfrac7{26}=frac{14times7}{3times26}=frac{98}{78}=frac{98div2}{78div2}=frac{49}{39}=1frac{10}{39})
При умножении смешанной дроби на натуральное число преобразование в неправильную дробь делать не нужно. Такого рода вычисления производятся с помощью распределительного закона умножения.
Пример 3:
(3frac56times4=left(3+frac56right)times4=3times4+frac56times4=12+frac{5times4}6=12+frac{20div2}{6div2}=12+frac{10}3=12+3frac13=15frac13)
Если требуется разделить смешанную дробь на натуральное число или натуральное число на смешанную дробь, нужно представить делимое и делитель в виде неправильной дроби, затем выполнить необходимое действие, как с обыкновенными дробями.
Пример 4:
(5div3frac27=frac51divfrac{3times7+2}7=frac51divfrac{23}7=frac51timesfrac7{23}=frac{5times7}{1times23}=frac{35}{23}=1frac{12}{23})
Если нужно выполнить умножение или деление смешанной дроби на обыкновенную дробь, смешанное число необходимо преобразовать в неправильную дробь. После преобразований нужное действие производится по такому же алгоритму, как с обыкновенными дробями.
Пример 5:
(frac34div6frac12=frac34divfrac{6times2+1}2=frac34divfrac{13}2=frac34timesfrac2{13}=frac{3times1}{2times13}=frac3{26})
Определение смешанного числа
Определение
Смешанными числами называются числа, которые состоят из
натуральных чисел и простых дробей.
При этом число, выраженное натуральным числом, называют целой частью, а простая дробь является дробной частью числа.
Например. Числа 1$frac{2}{3}$; 101$frac{35}{117}$; 23$frac{12}{13}$
Для того чтобы выполнять арифметические действия смешанные числа переводят в
неправильную дробь, а далее производят
действия как и с рациональными числами.
Чтобы смешанное число перевести в неправильную дробь, необходимо:
- Целую часть умножить на знаменатель и к полученному произведению прибавить числитель. Результат записать в числитель.
-
Знаменатель переписать без изменений.
$$k frac{m}{n}=frac{k cdot n+m}{n}$$
Пример
Задание. Перевести смешанное число 4$frac{6}{7}$ в неправильную дробь.
Решение. Воспользуемся инструкцией выше:
$$4 frac{6}{7}=frac{4 cdot 7+6}{7}=frac{28+6}{7}=frac{34}{7}$$
Ответ. $4 frac{6}{7}=frac{34}{7}$
Читать дальше: что такое взаимно простые числа.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

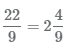
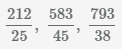 в смешанные числа.
в смешанные числа.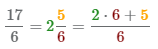
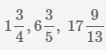 в неправильные дроби.
в неправильные дроби.