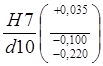Smax как найти метрология

Для характеристики
деталей при проектировании устанавливают
номинальные
поверхности
и их расположение, которые задаются
исходя из функционального назначения
детали.

Две или несколько
подвижно или неподвижно соединяемых
дета­лей называют сопрягаемыми.
Поверхности, по которым происхо­дит
соединение деталей, также называют
сопрягаемыми.
Остальные поверхности называют свободными
или несопрягаемыми.

Посадкой
называется характер соединения дета­лей,
определяемый получающимися в нем
зазорами или на­тягами.

Различают посадки
с зазором, с натягом и переход­ные (в
которых возможен как зазор, так и натяг).

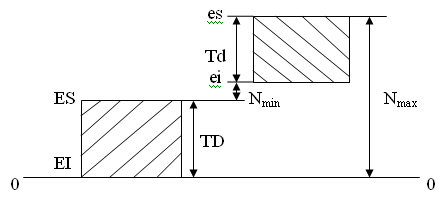
Натяг N
– разность
размеров отверстия и вала до сборки
со­единения, если размер вала больше
размера отверстия. Собранное с натягом
соединение обеспечивает взаимную
неподвижность дета­лей после сборки
(d₂D).

Зазор S
– разность
размеров вала и отверстия (рисунок 2),
если размеры вала меньше размеров
отверстия. Собранное с зазором соединение
до­пускает перемещение деталей друг
относительно друга (Dd₁).

Рисунок 2 – Варианты
образования посадки с зазором и натягом.
Переходная посадка.

3. Предельные зазоры и натяги в посадках. Допуск посадки.

При изготовлении
сопрягаемых деталей требуемые зазоры
или натяги в соединениях не могут быть
выдержаны абсолютно точно. Действительные
значения зазоров или натягов будут
колебаться в зависимости от допусков
на размеры сопрягаемых деталей, т.е.
рассеяние значений зазоров или натягов
зависит от рассеяния размеров отверстия
и вала.

Посадка с
зазором
– посадка,
при которой размеры вала меньше размера
отверстия. Поле допуска отверстия
располагается выше поля допуска вала
или нижняя граница поля допуска отверстия
совпадает с верхней границей поля
допуска вала, т.е. D_min
= d_max
. В этом
случае S_min
= 0.

В подвижных посадках
зазор может изменяться от наименьшего
до наибольшего предельного значения.

Наименьший
(гарантированный) зазор S_min
есть положительная разность между
наименьшим предельным размером отверстия
и наибольшим предельным размером вала,
или между нижним предельным отклонением
отверстия и верхним предельным отклонением
вала:

S_min
= D_min
– d_max
= /
EI
– es /

Наибольший зазор
S_max
есть положительная разность между
наибольшим предельным размером отверстия
и наименьшим предельным размером вала,
или между верхним предельным отклонением
отверстия и нижним предельным отклонением
вала:

S_max
= D_max
– d_min
= /
ES – ei /

Средний (наиболее
вероятный) зазор S_m
есть положительная разность между
средними размерами или средними
отклонениями отверстия и вала, или
среднее арифметическое наибольшего и
наименьшего зазора:

S_m
=

Допуск зазора TS
(допуск посадки)
определяет возможное (или допустимое)
колебание величины зазора в соединении,
т.е. определяет точность посадки. Чем
меньше допуск посадки, тем она точнее.
Разность предельных значений зазора
(наибольшего и наименьшего) или сумма
допусков отверстия и вала, составляющих
соединение и есть допуск зазора или
допуск посадки:

TS
= S_max
–
S_min
=
TD
+ Td

Расположение полей
допусков при сопряжении деталей с
гарантированным зазором представлено
на рисунке 3:

Рисунок 3 – Посадка
с зазором

К посадкам с зазором
относится также посадка, у которой
наименьший зазор S_min
= 0 (рисунок 4). Такую посадку называют
скользящей.
На схеме
посадки нижняя граница поля допуска
отверстия совпадает с верхней границей
поля допуска вала.

Рисунок 4 –
Скользящая посадка

Посадка с
натягом
– посадка,
при которой размеры вала больше размера
отверстия. Поле допуска отверстия
располагается ниже поля допуска или
нижняя граница поля допуска вала
сов­падает с верхней границей поля
допуска отверстия, т.е. D_max
= d_min.
В этом случае N_min
= 0.

В посадке с натягом
определяют:

— наибольший натяг:
N_max
= d_max
– D_min
= / es
– EI
/;

— наименьший натяг:
N_min
= d_min
– D_max
= / ei
– ES
/;

— средний натяг:
N_m
= (N_max
+ N_min)
/ 2;

— допуск посадки:
TN
= N_max
–
N_min
=
TD
+ Td.

Рисунок 5 – Посадка
с натягом

Переходная
посадка
– посадка,
при которой возможен как зазор, так и
натяг (поля допусков вала и отверстия
перекры­ваются полностью или частично).

В переходной
посадке определяют:

— наибольший зазор:
S_max
= D_max
– d_min
= / ES
– ei
/;

— наибольший натяг:
N_max
= d_max
– D_min
= / es
– EI
/;

— допуск посадки:
TSN
= S_max
+ N_max
= TD
+ Td.

Рисунок 6 – Посадка
переходная

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Допуском размера – называется разность между наибольшим и наименьшим предельными размерами или алгебраическая разность между верхним и нижним отклонениями /2/.

Допуск обозначают буквой «Т» (от лат. тolerance – допуск):

TD = D max – Dmin = ES – EI –         допуск размера отверстия;

Td = dmax  — dmin = es – ei – допуск размера вала.

Для рассмотренных ранее примеров 1 – 6 (раздел 1.1) допуски размеров определяются следующим образом:

1) Td = 24,015 – 24,002 = 0,015 – 0,002 = 0,013 мм;

2) Td = 39,975 – 39,950 = (-0,025) – (-0,050) = 0,025 мм;

3) TD = 32,007 – 31,982 = 0,007 – (-0,018) = 0,025 мм;

4) TD = 12,027 – 12 = 0,027 – 0 = 0,027 мм;

5) Td = 78 – 77,954 = 0 – (- 0,046) = 0,046 мм;

6) Td = 100,5 – 99,5 = 0,5 – (- 0,5) = 1 мм.

Допуск – величина всегда положительная. Допуск характеризует точность изготовления детали. Чем меньше допуск, тем труднее обрабатывать деталь, так как повышаются требования к точности станка, инструмента, приспособлений, квалификации рабочего. Неоправданно большие допуски снижают надежность и качество работы изделия.

В некоторых соединениях при различных сочетаниях предельных размеров отверстия и вала могут возникать зазоры или натяги. Характер соединения деталей, определяемый величиной получающихся в нем зазоров или натягов, называется посадкой. Посадка характеризует большую или меньшую свободу относительного перемещения соединяемых деталей или степень сопротивления их взаимному смещению /1/.

Различают три группы посадок:

1) с гарантированным зазором;

2) переходные;

3) с гарантированным натягом.

Если размеры отверстия больше размеров вала, то в соединении возникает зазор.

Зазор – это положительная разность между размерами отверстия и вала /1/:

S = D – d 0 – зазор;

Smax = Dmax – dmin – наибольший зазор,

Smin = Dmin – dmax – наименьший зазор.

Если до сборки размеры вала больше размеров отверстия, то в соединении возникает натяг. Натяг – это положительная разность между размерами вала и отверстия /1/:

N = d – D 0 –   натяг,

Nmax = dmax – Dmin – наибольший натяг;

Nmin = dmin – Dmax –  наименьший натяг.

Посадки, в которых есть вероятность возникновения зазора или натяга, называют переходными.

Допуск посадки – это допуск зазора для посадок с гарантированным зазором (определяется, как разность между наибольшим и наименьшим зазорами) или допуск натяга для посадок с гарантированным натягом (определяется, как разность между наибольшим и наименьшим натягами). В переходных посадках допуск посадки – это допуск зазора или натяга /1/.

Обозначение допуска посадки:

TS = Smax – Smin – допуск посадки для посадок с гарантированным зазором.

TN = Nmax – Nmin – допуск посадки для посадок с гарантированным натягом.

T(S,N)=Smax + Nmax – допуск посадки для переходных посадок.

Для любой группы посадок допуск посадки можно определить по формуле

T(S,N) = TD + Td.

Допуски
ГЦС по ГОСТ 25347-82. Все расчеты в миллиметрах.

1.1. Соединение  Ø 60.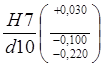

1.1.1 Отверстие  Ø 60:

D = 60; ES = 0,030; EI = 0;

D_max = D + ES = 60 + 0,030 = 60,03;

D_min = D — EI = 60 — 0= 60,00;

TD = ES — EI = 0,03 — 0= 0,03;

TD = D_max – D_min = 60,03 – 60 = 0,03;

E_m =  =  = 0.015

E_m = ES —  = 0.03 —   = 0.015

E_m = EI +  = 0 +  = 0,015

1.1.2 Вал Ø 60  :

d = 60; es = -0,100; ei = -0,220

d_max = d + es = 60 — 0,1 = 59,9;

d_min = d + ei = 60 -0,22 = 59,78

Td = d_max – d_min = 59,9 – 59,78 = 0,12;

Td = es – ei = -0,1 + 0,22 = 0,12;

e_m =  =  = -0,16

e_m = es —  = -0,1 —  = -0,16

e_m = ei +  = -0,22
—  = 0.16

1.1.3. Соединение  Ø 60  

                                    S_max
= D_max — d_min = 60,03 – 59.78=0,25;

                                    S_max
= ES – ei = 0,03+0,22 = 0,25;

                                   
S_min = D_min – d_max = 60 – 59,9 = 0,1

                                   
S_min  = EI – es = 0 + 0,1 = 0,1;

                                    
S_min =  =  = 0.175

                                   S_m
= E_m – e_m = 0,015 + 0,16 = 0,175;

                                  
TS = S_max – S_min = 0,25 – 0,1 = 0,15;

                                  
TS = TD +Td = 0,03 + 0,12 = 0,15.

Посадка Ø 60   в системе
отверстия,отверстие – высокой точности, вал – средней точности, с
гарантированным зазором. Схема расположения полей допусков посадки            Ø 60   приведена в
приложении 1.1.

1.2. Соединение  Ø 105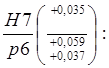   

1.2.1. Отверстие Ø 105 

                                       
D = 105; ES =
0,035; EI = 0;

D_max = D + ES = 105+ 0,035 = 105,035;

D_min = D — EI = 105 — 0= 105,00;

TD = ES — EI = 0,035 — 0= 0,035;

TD = D_max – D_min = 105,035 – 105 = 0,035;

E_m =  =  = 0.0175

E_m = ES —  = 0.035 —   = 0.0175

E_m = EI +  = 0 +  = 0,0175

1.2.2. Вал Ø 105 

d = 105; es = +0,059; ei = +0,037

d_max = d + es = 105 + 0,059 = 105,059

d_min = d + ei = 105 + 0,037 = 105,037

Td = d_max – d_min = 105,059 – 105,037 = 0,022;

Td = es – ei = 0,059 – 0,037 = 0,022;

e_m =  =  = 0,048

e_m = es —  = 0,059 –  = 0,048

e_m = ei +  = 0,037 –  = 0,048

1.2.3. Соединение Ø105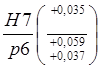    

                                            
N_max = d_max – D_min = 105,059 – 105 = 0,059

                                            
N_max
= es – EI = 0,059 — 0= 0,059;

                                            N_min
= d_min – D_max = 105,037 – 105,035 = 0,002

                                            N_min
 = ei – ES = 0,037 — 0,035 = 0,002;

                                             N_min
=  =  = 0,0305

                                            N_m
= e_m – E_m = 0,048 — 0,0175 = 0,0305;

                                            TN
= N_max – N_min = 0,059 – 0,002 = 0,057;

                                          
 TN = TD +Td = 0,035 + 0,022 =
0,057.

Посадка Ø 105  в системе отверстия высокой точности с минимальным
натягом.

smax = ± Мх  / Wх   .

Осевые моменты сопротивления стандартных профилей приводятся в справочной литературе. Размерность осевого момента сопротивления – [м³].

Поперечная сила Q_у представляет собой равнодействующую силу внутренних касательных сил – касательных напряжений t, действующих   в плоскости сечения. Величина касательных напряжений по высоте поперечного сечения также различна (рис. 5).

Рис. 5. Эпюра  касательных напряжений  по  высоте  сечения

Касательные напряжения в произвольной точке поперечного сечения можно вычислить  по  формуле:

t = (Q_y ∙ S_xω) / (J_x ∙ b_y) ,

где Q_y –поперечная сила в рассматриваемом сечении; S_xω – статический моментотносительно нейтральной оси х той части сечения, которая расположена по одну сторону прямой, проведённой параллельно оси х через данную точку; J_x – момент инерции всего сечения относительно нейтральной оси; b_y – ширина поперечного сечения на уровне рассматриваемой точки.

Для прямоугольного сечения эта формула после подстановки соответствующих величин преобразуется в следующее выражение для определения касательных напряжений:

t = 6 ∙ Q_y ∙ ( h²/4 – y² ) / b ∙ h³ .

В точках сечения, наиболее удаленных от нейтральной оси (у = h/2), касательные напряжения равны нулю. Максимальные касательные напряжения  действуют  в  точках нейтрального  слоя (у = 0). Они равны :

t_max = 3 ∙ Q_y / (2 ∙ b ∙ h) .

Под действием внешних изгибающих нагрузок ось балки искривляется, поперечные сечения балки   перемещаются  относительно своих   начальных

положений на определенные величины. Эти величины называются прогибами f. Они характеризуют жёсткость балки и являются основной мерой деформации изгиба.

В области упругих деформаций прогибы прямо пропорциональны приложенным нагрузкам: F = k × f . Коэффициент пропорциональности k зависит от схемы нагружения балки, от формы и размеров её поперечных сечений, от материала, из которого она изготовлена, от места расположения рассматриваемого сечения.

В общем случае для определения коэффициентов k, а следовательно и прогибов f , необходимо решать дифференциальные уравнения упругой линии балки. Для наиболее простых случаев нагружения эти уравнения решены и результаты решений приводятся в литературе.

Для случая нагружения, изображённого на рис. 3, максимальным будет прогиб сечения, расположенного в месте приложения силы F. Для данного сечения решение дифференциального уравнения упругой линии балки даёт следующее значение коэффициента пропорциональности:

k = 48 ∙ E ∙ J_x / l³ ,

где  Е  –  модуль  упругости  материала балки.

Тогда прогиб данного сечения будет равен:

f = F / k = (F ∙ l³) / (48 ∙ E ∙ J_x) .

Коэффициент пропорциональности можно найти экспериментально с помощью лабораторной установки. Для этого необходимо построить зависимость  прогибов  сечения  от  нагрузки  (рис. 6).

                                О

Рис. 6. Зависимость  прогибов сечения  балки  от  нагрузки

Коэффициент пропорциональности определяется углом α наклона прямой ОАС :

k = tg α = (F_C – F_A) / (f_C – f_A) .

По результатам испытаний можно определить модуль упругости материала, из которого изготовлена балка:

E = (k ∙ l³) / 48 ∙ J_x .