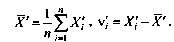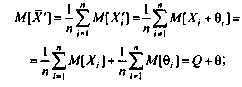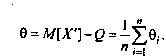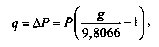Системная погрешность как найти

Систематическая
погрешность,
в отличие от случайной, сохраняет свою
величину (и знак) во время эксперимента.
Систематические погрешности появляются
вследствие ограниченной точности
приборов, неучета внешних факторов и
т.д.

Обычно
основной вклад в систематическую
погрешность
дает погрешность, определяемая точность
приборов, которыми производят измерения.
Т.е. сколько бы раз мы не повторяли
измерения, точность полученного нами
результата не превысит точности,
обеспеченной характеристиками данного
прибора. Для обычных измерительных
инструментов (линейка, пружинные весы,
секундомер) в качестве абсолютной
систематической погрешности берется
половина шкалы деления прибора. Так в
рассматриваемом нами случае работы N
24 величина h’
может измеряться с точностью =0.05
см,
если линейка имеет миллиметровые
деления, и =0.5
см,
если только сантиметровые.

Систематические
погрешности электроизмерительных
приборов, выпускаемых промышленностью,
определяется их классом точности,
который обычно выражается в процентах.
Электроизмерительные приборы по степени
точности подразделяются на 8 основных
классов точности:0.05, 0.1, 0.2, 0.5, 1, 1.5, 2.5, 4.
Класс
точности
есть
величина, показывающая максимально
допустимую
относительную погрешность в процентах.
Если например прибор имеет класс
точности 2, то это означает, что его
максимальная относительная погрешность
при измерении, например тока, равна 2 %,
т.е.

где
—
верхний предел шкалы измерений амперметра.
При этом величина
(абсолютная погрешность в измерении
силы тока) будет равна

(6)

для
любых измерений силы тока на данном
амперметре. Так как ,
вычисленное по формуле (6), это максимально
допустимая данным прибором погрешность,
то обычно считают, что для определения
,
погрешность, определяемую классом
точности прибора, нужно разделить на
два. Т.е.

и
при этом
будет так же одинакова для всех измерений
на данном приборе. Однако, относительная
погрешность (в нашем случае

где
I—
показания прибора) будет тем меньше,
чем ближе значение измеряемой величины
к максимально возможному на данном
приборе. Следовательно, лучше выбирать
прибор так, чтобы стрелка прибора при
измерениях заходила за середину шкалы.

В
реальных опытах присутствуют как
систематические, так и случайные ошибки.
Пусть они характеризуются абсолютными
погрешностями
и .
Тогда суммарная погрешность опыта
находится по формуле

(7)

Из
формулы (7) видно, что если одна из этих
погрешностей мала, то ей можно пренебречь.
Например, пусть
в 2 раза больше ,
тогда

т.е.
с точностью до 12% =.
Таким образом, меньшая погрешность
почти ничего не добавляет к большей,
даже если она составляет половину от
нее. В том случае, если случайная ошибка
опытов хотя бы вдвое меньше систематической,
нет смысла производить многократные
измерения, так как полная погрешность
опыта при этом практически не уменьшается.
Достаточно произвести 2 — 3 измерения,
чтобы убедиться, что случайная ошибка
действительно мала.

В
случае рассматриваемой нами работы N
24 =0.26
см,
а
равна либо 0.05 см,
либо 0.5 см.
В этом случае

Как
видно, в первом случае можно пренебречь
,
а во втором .

Соседние файлы в папке физика

• #
• #

  29.03.201687.04 Кб6mekh1.doc

• #
• #
• #
• #

Систематической погрешностью называется составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же величины. При этом предполагается, что систематические погрешности представляют собой определенную функцию неслучайных факторов, состав которых зависит от физических, конструкционных и технологических особенностей средств измерений, условий их применения, а также индивидуальных качеств наблюдателя. Сложные детерминированные закономерности, которым подчиняются систематические погрешности, определяются либо при создании средств измерений и комплектации измерительной аппаратуры, либо непосредственно при подготовке измерительного эксперимента и в процессе его проведения. Совершенствование методов измерения, использование высококачественных материалом, прогрессивная технология — все это позволяет на практике устранить систематические погрешности настолько, что при обработке результатов наблюдений с их наличием зачастую не приходится считаться.

Систематические погрешности принято классифицировать в зависимости от причин их возникновения и по характеру их проявления при измерениях.

В зависимости от причин возникновения рассматриваются четыре вида систематических погрешностей.

1. Погрешности метода, или теоретические погрешности, проистекающие от ошибочности или недостаточной разработки принятой теории метода измерений в целом или от допущенных упрощений при проведении измерений.

Погрешности метода возникают также при экстраполяции свойства, измеренного на ограниченной части некоторого объекта, на весь объект, если последний не обладает однородностью измеряемого свойства. Так, считая диаметр цилиндрического вала равным результату, полученному при измерении в одном сечении и в одном направлении, мы допускаем систематическую погрешность, полностью определяемую отклонениями формы исследуемого вала. При определении плотности вещества по измерениям массы и объема некоторой пробы возникает систематическая погрешность, если проба содержала некоторое количество примесей, а результат измерения принимается за характеристику данного вещества -вообще.

К погрешностям метода следует отнести также те погрешности, которые возникают вследствие влияния измерительной аппаратуры на измеряемые свойства объекта. Подобные явления возникают, например, при измерении длин, когда измерительное усилие используемых приборов достаточно велико, при регистрации быстропротекаюших процессов недостаточно быстродействующей аппаратурой, при измерениях температур жидкостными или газовыми термометрами и т.д.

2. Инструментальные погрешности, зависящие от погрешностей применяемых средств измерений.. Среди инструментальных погрешностей в отдельную группу выделяются погрешности схемы, не связанные с неточностью изготовления средств измерения и обязанные своим происхождением самой структурной схеме средств измерений. Исследование инструментальных погрешностей является предметом специальной дисциплины — теории точности измерительных устройств.

3.   Погрешности, обусловленные неправильной установкой и взаимным расположением средств измерения, являющихся частью единого комплекса, несогласованностью их характеристик, влиянием внешних температурных, гравитационных, радиационных и других полей, нестабильностью источников питания, несогласованностью входных и выходных параметров электрических цепей приборов и т.д.

4. Личные погрешности, обусловленные индивидуальными особенностями наблюдателя. Такого рода погрешности вызываются, например, запаздыванием или опережением при регистрации сигнала, неправильным отсчетом десятых долей деления шкалы, асимметрией, возникающей при установке штриха посередине между двумя рисками.

По характеру своего поведения в процессе измерения систематические погрешности подразделяются на постоянные и переменные.

Постоянные систематические погрешности возникают, например, при неправильной установке начала отсчета, неправильной градуировке и юстировке средств измерения и остаются постоянными при всех повторных наблюдениях. Поэтому, если уж они возникли, их очень трудно обнаружить в результатах наблюдений.

Среди переменных систематических погрешностей принято выделять прогрессивные и периодические.

Прогрессивная погрешность возникает, например, при взвешивании, когда одно из коромысел весов находится ближе к источнику тепла, чем другое, поэтому быстрее нагревается и

удлиняется. Это приводит к систематическому сдвигу начала отсчета и к монотонному изменению показаний весов.

Периодическая погрешность присуща измерительным приборам с круговой шкалой, если ось вращения указателя не совпадает с осью шкалы.

Все остальные виды систематических погрешностей принято называть погрешностями, изменяющимися по сложному закону.

В тех случаях, когда при создании средств измерений, необходимых для данной измерительной установки, не удается устранить влияние систематических погрешностей, приходится специально организовывать измерительный процесс и осуществлять математическую обработку результатов. Методы борьбы с систематическими погрешностями заключаются в их обнаружении и последующем исключении путем полной или частичной компенсации. Основные трудности, часто непреодолимые, состоят именно в обнаружении систематических погрешностей, поэтому иногда приходится довольствоваться приближенным их анализом.

Способы обнаружения систематических погрешностей. Результаты наблюдений, полученные при наличии систематических погрешностей, будем называть неисправленными и в отличие от исправленных снабжать штрихами их обозначения (например, Х1, Х₂ и т.д.). Вычисленные в этих условиях средние арифметические значения и отклонения от результатов наблюдений будем также называть неисправленными и ставить штрихи у символов этих величин. Таким образом,

Поскольку неисправленные результаты наблюдений включают в себя систематические погрешности, сумму которых для каждого /-го наблюдения будем обозначать через 8., то их математическое ожидание не совпадает с истинным значением измеряемой величины и отличается от него на некоторую величину 0, называемую систематической погрешностью неисправленного среднего арифметического. Действительно,

Если систематические погрешности постоянны, т.е. 0_/ = 0, /=1,2, …, п, то неисправленные отклонения могут быть непосредственно использованы для оценки рассеивания ряда наблюдений. В противном случае необходимо предварительно исправить отдельные результаты измерений, введя в них так называемые поправки, равные систематическим погрешностям по величине и обратные им по знаку:

q = -Oi.

Таким образом, для нахождения исправленного среднего арифметического и оценки его рассеивания относительно истинного значения измеряемой величины необходимо обнаружить систематические погрешности и исключить их путем введения поправок или соответствующей каждому конкретному случаю организации самого измерения. Остановимся подробнее на некоторых способах обнаружения систематических погрешностей.

Постоянные систематические погрешности не влияют на значения случайных отклонений результатов наблюдений от средних арифметических, поэтому никакая математическая обработка результатов наблюдений не может привести к их обнаружению. Анализ таких погрешностей возможен только на основании некоторых априорных знаний об этих погрешностях, получаемых, например, при поверке средств измерений. Измеряемая величина при поверке обычно воспроизводится образцовой мерой, действительное значение которой известно. Поэтому разность между средним арифметическим результатов наблюдения и значением меры с точностью, определяемой погрешностью аттестации меры и случайными погрешностями измерения, равна искомой систематической погрешности.

Одним из наиболее действенных способов обнаружения систематических погрешностей в ряде результатов наблюдений является построение графика последовательности неисправленных значений случайных отклонений результатов наблюдений от средних арифметических.

Рассматриваемый способ обнаружения постоянных систематических погрешностей можно сформулировать следующим образом: если неисправленные отклонения результатов наблюдений резко изменяются при изменении условий наблюдений, то данные результаты содержат постоянную систематическую погрешность, зависящую от условий наблюдений.

Систематические погрешности являются детерминированными величинами, поэтому в принципе всегда могут быть вычислены и исключены из результатов измерений. После исключения систематических погрешностей получаем исправленные средние арифметические и исправленные отклонения результатов наблюдении, которые позволяют оценить степень рассеивания результатов.

Для исправления результатов наблюдений их складывают с поправками, равными систематическим погрешностям по величине и обратными им по знаку. Поправку определяют экспериментально при поверке приборов или в результате специальных исследований, обыкновенно с некоторой ограниченной точностью.

Поправки могут задаваться также в виде формул, по которым они вычисляются для каждого конкретного случая. Например, при измерениях и поверках с помощью образцовых манометров следует вводить поправки к их показаниям на местное значение ускорения свободного падения

где Р — измеряемое давление.

Введением поправки устраняется влияние только одной вполне определенной систематической погрешности, поэтому в результаты измерения зачастую приходится вводить очень большое число поправок. При этом вследствие ограниченной точности определения поправок накапливаются случайные погрешности и дисперсия результата измерения увеличивается.

Систематическая погрешность, остающаяся после введения поправок на ее наиболее существенные составляющие включает в себя ряд элементарных составляющих, называемых неисключенными остатками систематической погрешности. К их числу относятся погрешности:

•   определения поправок;

•   зависящие от точности измерения влияющих величин, входящих в формулы для определения поправок;

•   связанные с колебаниями влияющих величин (температуры окружающей среды, напряжения питания и т.д.).

Перечисленные погрешности малы, и поправки на них не вводятся.

Систематические погрешности при повторных измерениях остаются постоянными или изменяются по определенному закону.

Когда судят о погрешности, подразумевают не значение, а интервал значений, в котором с заданной вероятностью находится истинное значение. Поэтому говорят об оценке погрешности. Если бы погрешность оказалась измеренной, т.е. стали бы известны её знак и значение, то её можно было бы исключить из действительного значения измеряемой физической величины и получить истинное значение.

Для получения результатов, минимально отличающихся от истинного значения измеряемой физической величины, проводят многократные наблюдения и проводят математическую обработку полученного массива с целью определения и минимизации случайной составляющей погрешности.

Минимизация систематической погрешности в процессе наблюдений выполняется следующими методами: метод замещения (состоит в замещении измеряемой величины мерой), метод противопоставления (состоит в двух поочерёдных измерениях при замене местами меры и измеряемого объекта), метод компенсации погрешности по знаку (состоит в двух поочерёдных измерениях, при которых влияющая величина становится противоположной).

При многократных наблюдениях возможно апостериорное (после выполнения наблюдений) исключение систематической погрешности в результате анализа рядов наблюдений. Рассмотрим графический анализ. При этом результаты последовательных наблюдений представляются функцией времени либо ранжируются в порядке возрастания погрешности.

Рассмотрим временную зависимость. Будем проводить наблюдения через одинаковые интервалы времени. Результаты последовательных наблюдений являются случайной функцией времени. В серии экспериментов, состоящих из ряда последовательных наблюдений, получаем одну реализацию этой функции. При повторении серии получаем новую реализацию, отличающуюся от первой.

Реализации отличаются преимущественно из-за влияния факторов, определяющих случайную погрешность, а факторы, определяющие систематическую погрешность, одинаково проявляются для соответствующих моментов времени в каждой реализации. Значение, соответствующее каждому моменту времени, называется сечением случайной функции времени. Для каждого сечения можно найти среднее по всем реализациям значение. Очевидно, что эта составляющая и определяет систематическую погрешность. Если через значения систематической погрешности для всех моментов времени провести плавную кривую, то она будет характеризовать временную закономерность изменения погрешности. Зная закономерность изменения, можем определить поправку для исключения систематической погрешности. После исключения систематической погрешности получаем «исправленный ряд результатов наблюдений».

Известен ряд способов исключения систематических погрешностей, которые условно можно разделить па 4 основные группы:

•  устранение источников погрешностей до начала измерений;
•  исключение почетностей в процессе измерения способами замещения, компенсации погрешностей по знаку, противопоставления, симметричных наблюдений;
•  внесение известных поправок в результат измерения (исключение погрешностей начислением);
•  оценка границ систематических погрешностей, если их нельзя ис­ключить.

По характеру проявления систематические погрешности подразделяют на постоянные, прогрессивные и периодические.

Постоянные систематические погрешности сохраняют свое значение в течение всего времени измерений (например, погрешность в градуировке шкалы прибора переносится на все результаты измерений).

Прогрессивные погрешности – погрешности, которые в процессе из­мерении подрастают или убывают (например, погрешности, возникающие вследствие износа контактирующих деталей средств измерения).

И группу систематических погрешностей можно отнести: инструментальные погрешности; погрешности из-за неправильной установки измерительного устройства; погрешности, возникающие вследствие внешних влияний; погрешности метода измерения (теоретические погрешности); субъективные погрешности.

Систематическая погрешность

Систематической погрешностью называется составляющая погрешности измерения, остающаяся постоянной или закономерно меняющаяся при повторных измерениях одной и той же величины. При этом предполагается, что систематические погрешности представляют собой определенную функцию неслучайных факторов, состав которых зависит от физических, конструкционных и технологических особенностей средств измерений, условий их применения, а также индивидуальных качеств наблюдателя. Сложные детерминированные закономерности, которым подчиняются систематические погрешности, определяются либо при создании средств измерений и комплектации измерительной аппаратуры, либо непосредственно при подготовке измерительного эксперимента и в процессе его проведения. Совершенствование методов измерения, использование высококачественных материалов, прогрессивная технология — все это позволяет на практике устранить систематические погрешности настолько, что при обработке результатов наблюдений с их наличием зачастую не приходится считаться.

Или: Систематическая погрешность измерения — составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины.

В зависимости от характера измерения систематические погрешности подразделяют на постоянные, прогрессивные и погрешности, изменяющиеся по сложному закону.

В зависимости от причин появления систематические погрешности подразделяют на инструментальные, погрешности метода измерений, субъективные и др.

Любая процедура измерения вне зависимости от условий, в которых она проводится, сопряжена с погрешностями. Они представляют собой отклонения, искажающие представление о реальном значении величины.

Источники погрешностей

Отклонения возникают по самым разным причинам. К основным следует отнести:

• Несовершенство конструкций измерительных средств или неточность их изготовления.
• Несоблюдение правил при проведении процедуры.
• Человеческий фактор.
• Несовершенство методов и пр.

Классификация отклонений

В процессе измерения могут возникать систематические и случайные погрешности.

Систематические отклонения классифицируют по разным основаниям. В частности, в зависимости от характера проявления, их разделяют на периодические, постоянные и прогрессивные погрешности.

Также могут появиться грубые погрешности или промахи. Они возникают вследствие:

• Ошибок специалиста.
• Внезапного изменения условий измерения.
• Неисправности оборудования и пр.

Систематические погрешности

Эти отклонения, как правило, можно изучить до начала измерения. Такие показатели остаются постоянными или изменяются закономерно при повторных измерениях одной величины. Результат исследования может корректироваться путем внесения поправок, если числовое значение отклонения известно, или с помощью таких измерительных средств, которые позволяют исключить влияние этих погрешностей без определения их значения.

При повторных измерениях действуют определенные законы, в соответствии с которыми изменяются значения систематических погрешностей. Эти отклонения можно иногда определить экспериментально. Соответственно, результат можно уточнить путем поправки.

Характер проявления

Как говорилось выше, по этому признаку выделяют три группы систематических погрешностей. Это:

• Постоянные отклонения. К ним относят такие погрешности, которые на протяжение всего процесса измерения сохраняют свою величину. К примеру, если для определения какого-то показателя специалист использует шкалу прибора, градуировка которой имеет погрешность, то ее величина переносится на все результаты эксперимента.
• Прогрессивные отклонения. Такие погрешности убывают или возрастают в ходе измерений. К ним относят, к примеру, отклонения, появляющиеся в результате износа контактирующих элементов измерительных средств, постепенное уменьшение напряжения токового источника, от которого питается измерительная цепь, и пр.
• Периодические погрешности. Их значения определяются периодической функцией времени либо функцией перемещения указателя на приборе, используемом для измерения. Они возникают в индикаторах с круговой шкалой и стрелками.

Показатели отклонений могут изменяться за счет одновременного влияния нескольких систематических погрешностей. Это проявляется, например, при измерении температуры.

Другие виды

К систематическим отклонения относят также:

• Теоретические погрешности. Их еще называют погрешностями измерительного метода.
• Инструментальные погрешности.
• Отклонения, возникающие вследствие неправильного расположения измерительного прибора.
• Личные погрешности.
• Отклонения, обусловленные влиянием внешних факторов.

Инструментальные погрешности

К ним относят отклонения, обусловленные свойствами используемых измерительных средств. К примеру, равноплечие весы идеально равноплечими быть не могут.

Отклонения возникают также вследствие трения сочленений подвижных элементов измерительных устройств. Они могут возникать из-за износа оборудования. Показатель износа, соответственно, будет зависеть от интенсивности эксплуатации прибора.

Погрешность результата

Правильность показаний некоторых измерительных средств зависит от положения их подвижных элементов относительно неподвижных. Речь, в частности, о таких приборах, как равноплечие весы, средства, частью конструкции которых является маятник или иные подвижные подвешенные детали. При отклонении прибора от правильного положения смещается точка отсчета и возникает погрешность результата. Для предупреждения ее появления при установке приборов используются специальные устройства: уровни, отвесы и пр.

Влияние внешних факторов

Температура, влажность, давление воздуха являются внешними условиями, влекущими появление погрешностей при изменении их величин. Если показатели тех или иных факторов выходят за рамки заданных границ, то могут возникнуть и дополнительные отклонения.

Погрешности измерительного метода

Они могут возникать в случае, когда между измеряемым свойством или явлением и принципом работы измерительного прибора отсутствует теоретически доказанная зависимость.

Погрешность метода обуславливается допущениями или упрощениями при применении эмпирических зависимостей и формул. Такая ситуация возникает, к примеру, при измерении твердости металлов разными способами: методами Бринелля, Роквелла, Виккерса и т. д. В каждом из них заданы свои условные единицы. Перевод результатов осуществляется приближенно.

Субъективные отклонения

Личные погрешности обусловливаются индивидуальными свойствами человека. Они, в свою очередь, связаны с особенностями организма, укоренившимися навыками (зачастую неправильными). К примеру, у всех людей разная скорость реакции на сигнал: на звук она варьируется в пределах 0,082-0,195 с., а на свет – 0,15-0,225 с.

Исключение погрешностей

Систематические отклонения влекут смещение результатов измерений. Наибольшую опасность в этих ситуациях представляют отклонения, которые остаются невыявленными и о наличии которых специалисты даже не подозревают. Такие погрешности становились причиной неверных научных выводов, установления ложных законов физики, несовершенных конструкций измерительных средств, брака в производстве.

Систематические погрешности необходимо выявить и исключить либо учесть при измерении. Способы исключения и учета отклонения разделяют на несколько групп:

• Устранение источников отклонений до начала процедуры измерения (профилактика).
• Исключение погрешностей в ходе процесса (экспериментальные методы).
• Внесение поправок в результаты измерения. В этом случае погрешности исключаются методом вычисления.
• Оценка пределов систематических погрешностей, если их исключение невозможно.

Устранение источников

Профилактические мероприятия перед началом измерения считаются наиболее рациональным способом исключения погрешностей. В этом случае специалист частично или полностью освобождается от необходимости выявлять и устранять отклонения в ходе измерения.

К наиболее эффективным профилактическим мероприятиям относятся:

• Регулирование или ремонт измерительных средств. Необходимость в проведении этих мероприятий определяется при поверке.
• Корректировка установки прибора. Для предотвращения смещения точки отсчета, перекосов и прочих негативных явлений используются отвесы и прочие приспособления.

Для устранения погрешностей, возникающих вследствие влияния внешних факторов, можно удалить непосредственный их источник или обеспечить защиту измерительного прибора от воздействия.

Исключение погрешностей в ходе экспериментов предполагает обычно проведение повторного измерения. В этой связи, описанные выше способы целесообразнее применять при работе со стабильными явлениями, показателями и пр.

Внесение поправок в результаты

Этот способ исключения систематических погрешностей предполагает исправление результата измерения путем вычисления.

Самым распространенным вариантом внесения поправок считается алгебраическое суммирование результата и самой поправки (с учетом знака). Ее числовое значение равно систематическому отклонению, а знак – противоположен. Таким способом исключается аддитивное отклонение.

В отдельных случаях систематическую погрешность можно исключить посредством умножения показателя, полученного в результате измерения, на поправочный коэффициент. Его значение приближается к единице (больше или меньше ее). Поправочным коэффициентом целесообразно пользоваться при необходимости исключить мультипликативную погрешность.

Оценка пределов отклонения

Она производится, когда исключить систематические погрешности на практике невозможно. Такое явление имеет место, если отклонения изучены недостаточно или изучены, но не могут использоваться для корректировки результата. Последнее характерно для интегрирующих измерительных средств (счетчиков).

Случайные погрешности

При повторном измерении постоянного физического показателя в одних и тех же условиях зачастую результаты незначительно отличаются. При этом отклонения между величинами не являются систематическими, не подчиняются каким-либо закономерностям. Такие погрешности принято именовать случайными.

Отклонения возникают при одновременном воздействии на процесс (объект, измерительное средство, специалиста и пр.) ряда факторов. Каждый источник может незначительно влиять на результат, но их совокупное воздействие приведет к значительному отклонению от действительного показателя измеряемого объекта.

Источники воздействия по-разному проявляют себя в тот или иной временной промежуток. При этом они действуют обособленно друг от друга, не имея какой-либо закономерной связи. Это приводит к различиям по знаку и размеру расхождений в результатах измерений. Они изменяются без какой-либо связи как с прежними, так и с последующими величинами. Соответственно, каким-либо образом их учесть невозможно.

В рамках теории вероятности используются математические методы, позволяющие изучать свойства случайных явлений в их больших совокупностях. В ходе развития измерительной техники и метрологии было установлено, что они полностью соответствуют задаче исследования случайных отклонений. Во многих случаях результаты, получаемые с их помощью, согласуются с данными, полученными опытным путем.

В теории вероятности случайным считается такое событие, наступление которого однозначно предугадать невозможно. Другими словами, в определенной совокупности условий это событие может наступить, а может и не наступить. При применении этого определения к сфере измерений можно говорить о том, что при выполнении повторных экспериментов с некоторым физическим показателем в одних и тех же условиях каждый из вероятных незначительных источников случайного изменения результатов может либо появиться, либо не появиться. Следовательно, отклонения становятся непредсказуемыми и по своей величине, и по знаку.

Учитывая вышесказанное, можно дать следующее определение случайным погрешностям: это такие отклонения, которые изменяются от одного измерения к другому, не поддаются непосредственному учету в связи с хаотическим изменением, обусловлены одновременным влиянием на результат нескольких факторов, обособленных друг от друга.

Наличие случайных погрешностей, в отличие от систематических, достаточно легко обнаруживается при повторном измерении.