|
Как найти синус 270 градусов Для решения этой задачки (этого вопроса) можно использовать таблицу значений синуса. Эта табличка изучается в школе, она пропечатывается на многих современных тетрадях по математике и является допустимой, в том числе и на контрольных. Находим слева sin, а сверху значение 270 градусов и видим на пересечении значение «-1». Ответ: синус 270 градусов равен -1. автор вопроса выбрал этот ответ лучшим Валерий Альбертович 3 года назад На этот вопрос можно дать ответ несколькими способами. Можно просто посмотреть в таблице значений тригонометрический функций, а можно посмотреть на окружности. 270 градусов — это 3пи/2, то есть «3/4 оборотка по окружности». Как видим, значение синуса в этой точке равняется -1 => синус 270 градусов равен -1 Ответ: -1 Степан БВ 3 месяца назад Синус 270 градусов равен -1. Синус угла в 270 градусов равен минимальному отрицательному значению, что соответствует точке на единичной окружности, находящейся слева. Таким образом, синус 270 градусов равен -1. Александр2207 4 года назад Чтобы вычислить значение sin от 270 градусов найдем на окружности значение угла. Далее спроецируем найденную точку на ось sin, то есть на Оу. Получим значение –1. Таким образом, sin 270 градусов равен –1. Знаете ответ? |
Смотрите также: В треугольнике ABC AB=BC, AC=14, CH=7. Как найти синус угла ACB? Как узнать синус угла в треугольнике если известны синусы остальных углов? Можно построить треугольник по сторонам АВ.ВС и биссектрисе BL угла <ABC? Как решить: Точки D и Е лежат на сторонах АВ и АС треугольника АВС? В треугольнике ABC угол C равен 90°… Как найти длину отрезка AH.? Теорема о вычислении площади треугольника, как сформулировать и доказать? Как доказать теорему о биссектрисе равнобедренного треугольника? Теорема, выражающая первый признак равенства треугольников, как доказать? Что такое тангенс, катангенс, синус, косинус, секанс, касеканс? Будет ли выполняться теорема Пифагора в геометрии Лобачевского на шаре? |
Вычислять значение тригонометрического выражения sin 270 градусов будем некоторыми из возможных методов. Эти же методы можно применять для определения значения sin от различных углов.
Метод 1. Таблица значений sin
Метод используют чаще всего для вычисления sin от основных значений углов, среди которых и угол 270 градусов.
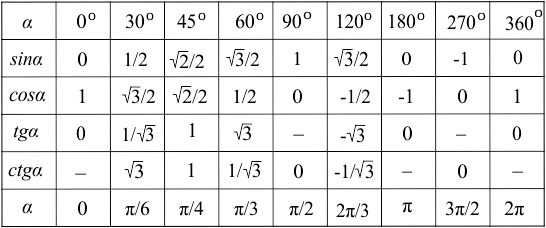
Из этой таблицы нам нужен столбец со значением угла 270 градусов и строка со значениями sin. На пересечении этих столбца и строки располагается значение ф-ции синус от выбранного угла:
sin 270 = 1.
Метод 2. Тригонометрический круг
Таблица синусов не всегда может быть под рукой. В таком случае пригодится умение пользоваться тригонометрическим кругом, с помощью которого кроме синуса можно также узнать значение косинуса, тангенса и котангенса.
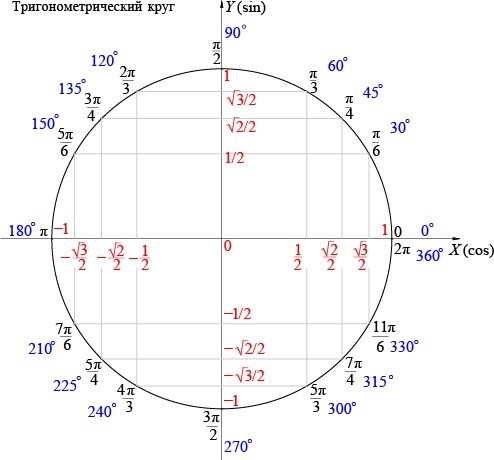
Основное, что нужно помнить, это:
— значения sin расположены на оси Оу;
— значения cos – на оси Ох;
— все значения углов располагаются непосредственно на линии окружности.
Чтобы вычислить значение sin от 270 градусов найдем на окружности значение угла. Далее спроецируем найденную точку на ось sin, то есть на Оу. Получим значение –1. Таким образом, sin 270 градусов равен –1.
Аналогичным образом можно вычислить и остальные выше упомянутые тригонометрические ф-ции.
Метод 3. Использование графика
Основным, что нужно знать о тригонометрической функции, – это как строиться ее график (достаточно уметь строить его схематически).
На оси Ох находим значение угла, далее на Оу определяем соответствующее этому углу значение синуса.
| sin(270°0′0″) = -1 | sin(270°20′0″) = -0.9999830769 | sin(270°40′0″) = -0.999932308 |
| sin(270°1′0″) = -0.9999999577 | sin(270°21′0″) = -0.9999813422 | sin(270°41′0″) = -0.9999288811 |
| sin(270°2′0″) = -0.9999998308 | sin(270°22′0″) = -0.999979523 | sin(270°42′0″) = -0.9999253697 |
| sin(270°3′0″) = -0.9999996192 | sin(270°23′0″) = -0.9999776192 | sin(270°43′0″) = -0.9999217736 |
| sin(270°4′0″) = -0.9999993231 | sin(270°24′0″) = -0.9999756307 | sin(270°44′0″) = -0.9999180929 |
| sin(270°5′0″) = -0.9999989423 | sin(270°25′0″) = -0.9999735576 | sin(270°45′0″) = -0.9999143276 |
| sin(270°6′0″) = -0.9999984769 | sin(270°26′0″) = -0.9999713999 | sin(270°46′0″) = -0.9999104777 |
| sin(270°7′0″) = -0.9999979269 | sin(270°27′0″) = -0.9999691576 | sin(270°47′0″) = -0.9999065431 |
| sin(270°8′0″) = -0.9999972923 | sin(270°28′0″) = -0.9999668307 | sin(270°48′0″) = -0.999902524 |
| sin(270°9′0″) = -0.9999965731 | sin(270°29′0″) = -0.9999644192 | sin(270°49′0″) = -0.9998984203 |
| sin(270°10′0″) = -0.9999957692 | sin(270°30′0″) = -0.9999619231 | sin(270°50′0″) = -0.9998942319 |
| sin(270°11′0″) = -0.9999948807 | sin(270°31′0″) = -0.9999593423 | sin(270°51′0″) = -0.999889959 |
| sin(270°12′0″) = -0.9999939077 | sin(270°32′0″) = -0.9999566769 | sin(270°52′0″) = -0.9998856014 |
| sin(270°13′0″) = -0.99999285 | sin(270°33′0″) = -0.999953927 | sin(270°53′0″) = -0.9998811593 |
| sin(270°14′0″) = -0.9999917076 | sin(270°34′0″) = -0.9999510924 | sin(270°54′0″) = -0.9998766325 |
| sin(270°15′0″) = -0.9999904807 | sin(270°35′0″) = -0.9999481732 | sin(270°55′0″) = -0.9998720211 |
| sin(270°16′0″) = -0.9999891692 | sin(270°36′0″) = -0.9999451694 | sin(270°56′0″) = -0.9998673251 |
| sin(270°17′0″) = -0.999987773 | sin(270°37′0″) = -0.9999420809 | sin(270°57′0″) = -0.9998625445 |
| sin(270°18′0″) = -0.9999862922 | sin(270°38′0″) = -0.9999389079 | sin(270°58′0″) = -0.9998576793 |
| sin(270°19′0″) = -0.9999847269 | sin(270°39′0″) = -0.9999356503 | sin(270°59′0″) = -0.9998527296 |
Mathway | Популярные задачи
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. |
|
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) |
|
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) |
|
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.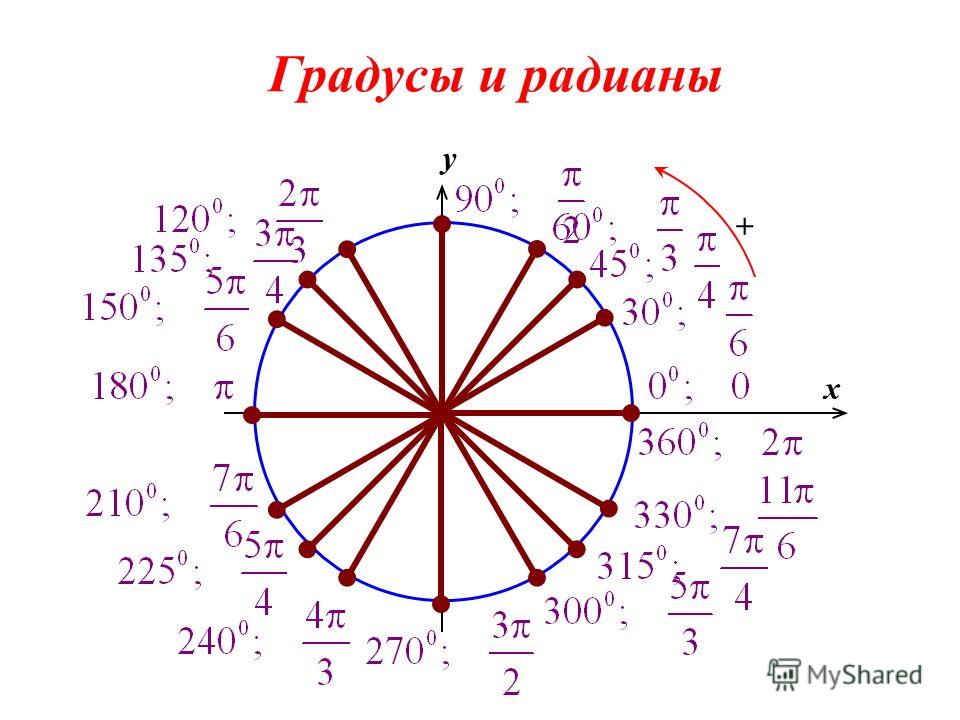 ) ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.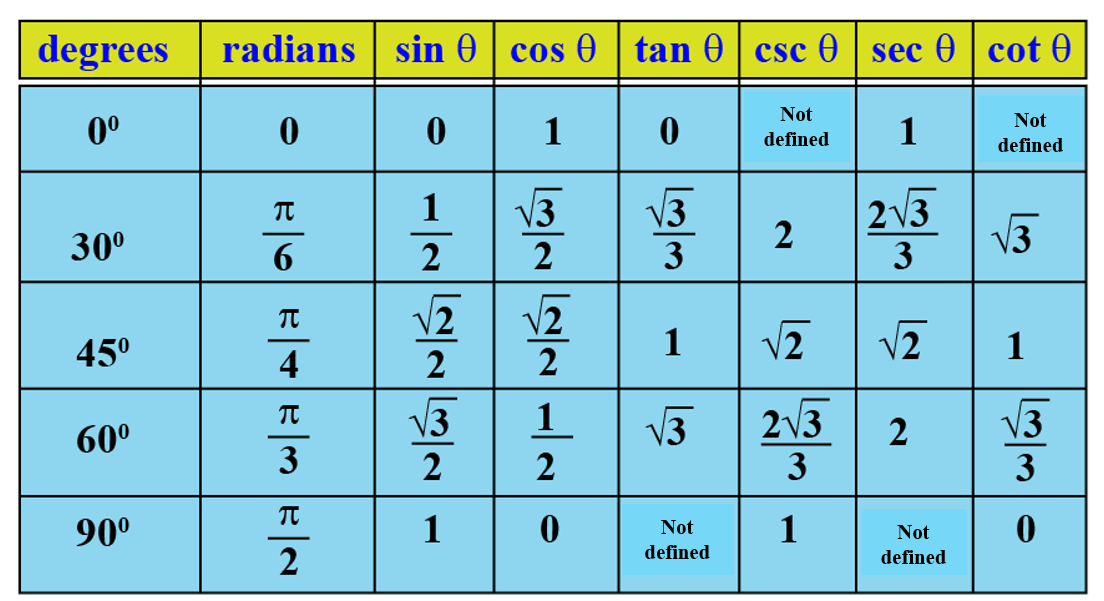 ) ) |
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) |
|
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) |
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Открытая Математика. Алгебра. Основные понятия тригонометрии
В геометрии угол определяется как часть плоскости, ограниченная двумя лучами. При таком определении получаются углы от 0° до 180°. Однако угол можно рассматривать и как меру поворота.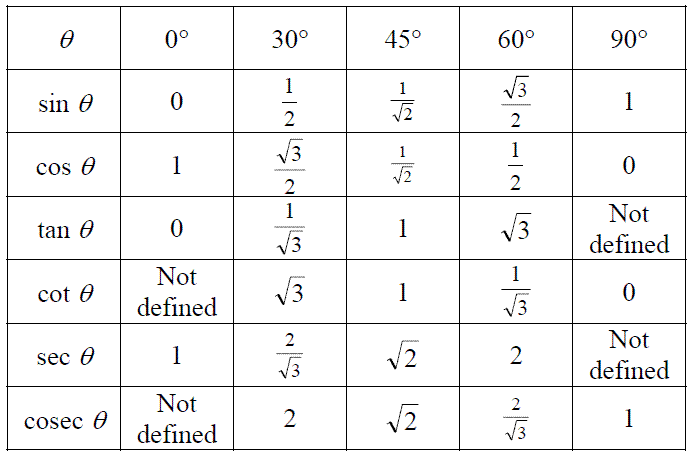
α=lR.
Такая мера называется радианной мерой угла и используется наравне с угловой. Говорят, что угол равен определённому числу радиан. Ясно, что угол в один радиан опирается на длину дуги окружности, равную её радиусу. В самом деле: α=RR=1 радиан.
Обозначение радиана – «рад». Так как длина всей окружности радиуса
R равна 2πR, то всей окружности соответствует угол α=2πRR=2π
радиан. Поскольку вся окружность содержит 360°, то один радиан соответствует 360°2π=180°π
градусов:
1 рад=180°π≈57°17′.
И наоборот,
1°=π180 рад.
Значит, можно написать следующие формулы перехода от градусного измерения к радианному:
α=πα°180° рад,
и от радианного измерения к градусному:
α°=180°πα.
Обозначение «рад» при записи часто опускают и вместо, например, 180° = π рад пишут просто 180° = π.
Пользуясь этими формулами, легко получить следующую таблицу перевода некоторых наиболее часто встречающихся углов из градусной меры в радианную и обратно.
| Угол, градусы | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
|---|---|---|---|---|---|---|---|---|
| Угол, радианы | 0 | π6 | π4 | π3 | π2 | π | 3π2 | 2π |
Определите радианную меру угла, если его градусная мера равна: 1) 2°; 2) 225°.
1) α=π180ċ2=π90;
2) α=π180ċ225=5π4.
Ответ.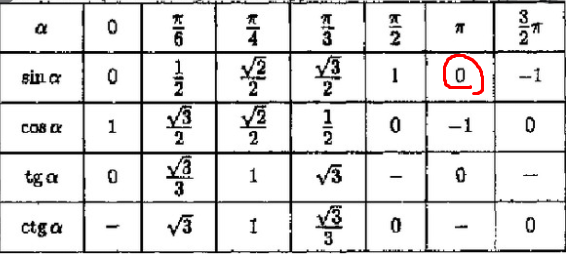
2) 5π4.
Снова рассмотрим на координатной плоскости окружность радиуса R с центром O в начале координат. Как известно, координатные оси делят окружность на четыре дуги, которые называют четвертями.
Окружность радиуса R
Рассмотрим произвольный угол α. Изобразим его как угол поворота радиус-вектора OA⟶
против часовой стрелки. При таком повороте точка A (R; 0) перейдёт в некоторую точку B (x; y) на этой окружности, при этом ∠AOB=α
(α может быть больше не только 180°, но и больше 360°). В зависимости от того, в какой четверти лежит точка B, угол α называется углом этой четверти.
Докажем, что отношения xR
и yR
не зависят от величины радиуса R. Действительно, выберем на отрезке OA точку A1
такую, что A1≠O.
Построим окружность с центром в начале координат радиуса OA1=R1.
Построенная окружность пересекает радиус-вектор OB⟶
в точке B1 (x1, y1).
Так как векторы OB⟶
и OB1⟶
коллинеарны и одинаково направлены, то
OB1⟶=λOB⟶, где λ=OB1⟶OB⟶=R1R.
Однако равные векторы имеют равные координаты, следовательно,
x1=R1Rx и y1=R1Ry.
Откуда следует после деления обеих частей последних равенств на R1, что
x1R1=xR и y1R1=yR.
Итак, для любого угла поворота отношение координат радиус-вектора к его длине не зависит от этой длины радиус-вектора. Следовательно, отношения xR
и yR
характеризуют не окружность, а лишь угол поворота. Значит, для того, чтобы рассмотреть основные свойства этих отношений, можно взять окружность любого радиуса, например, R = 1. Так мы и сделаем. Окружность единичного радиуса с центром в начале координат называется тригонометрической окружностью.
Координатная окружность
Ввиду всего вышесказанного, рассмотренные отношения xR
и пр. как характеристики только угла (но не окружности) удобно как-либо обозначить.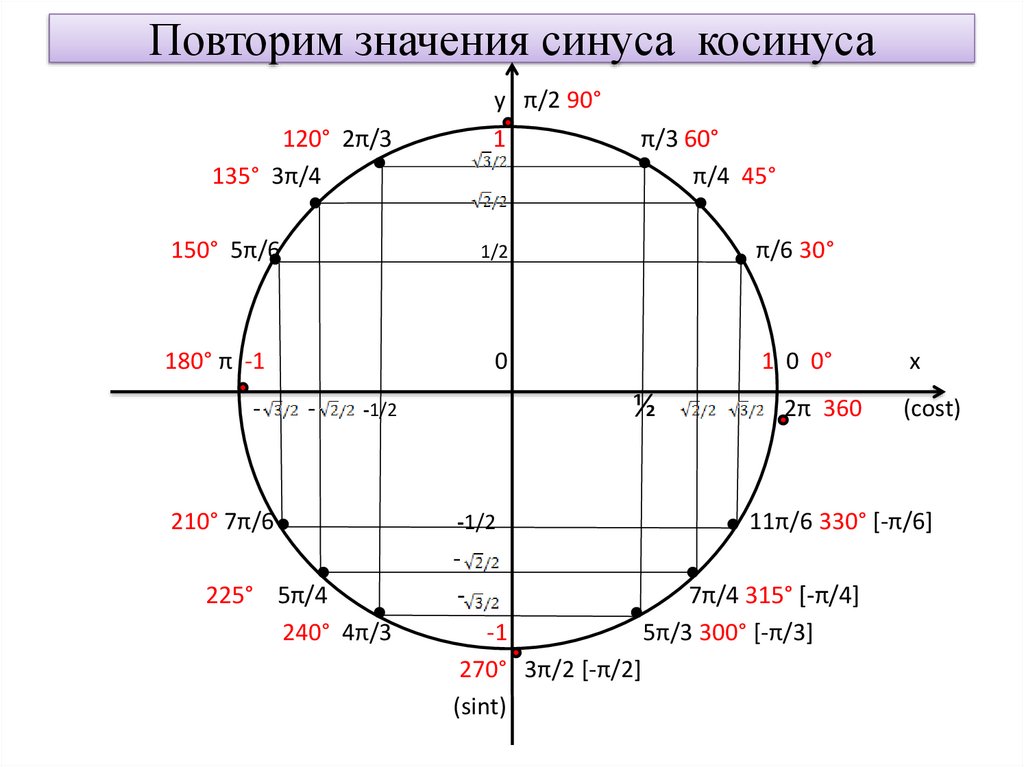
Косинусом угла α называется абсцисса x точки B − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс.
cos α = x.
Функция y = cos x
Синусом угла α называется ордината y точки B − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс.
sin α = y.
Функция y = sin x
Тангенсом угла α называется отношение ординаты y к абсциссе x точки B − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс.
tg α=yx=sin αcos α.
Функция y = tg x
Котангенсом угла α называется отношение абсциссы x к ординате y точки B − конца радиус-вектора единичной окружности, образующего угол α с осью абсцисс.
ctg α=xy=cos αsin α.
Функция y = ctg x
Ясно, что для данного угла α функции sin α, cos α, tg α и ctg α, которые называются тригонометрическими функциями, определены однозначно (поскольку каждому углу соответствует единственная точка на тригонометрической окружности). Однако если функции sin α и cos α определены для любого угла α, то функции tg α и ctg α определены только для тех углов, для которых не равен нулю знаменатель дробей xy
и yx.
Значит, tg α не определён для углов вида α=π2+πk,
где k∈ℤ;
ctg α не определён для углов вида α=πk, где k∈ℤ.
Поскольку синус по определению равен ординате точки на единичной окружности, а косинус − абсциссе, то знаки тригонометрических функций по четвертям будут такими:
| Функция | Знаки тригонометрических функций по четвертям | |||
|---|---|---|---|---|
| I | II | III | IV | |
| sin α | + | + | − | − |
| cos α | + | − | − | + |
| tg α | + | − | + | − |
| ctg α | + | − | + | − |
Вычисление тригонометрических функций некоторых угловВычисление углов
Найдём значения тригонометрических функций некоторых наиболее часто встречающихся углов.
-
sin 90° = 1, cos 90° = 0, ctg 90° = 0, tg 0° не определён.
-
sin 180° = 0, cos 180° = –1, tg 180° = 0, ctg 180° не определён.
-
sin 270° = –1, cos 270° = 0, ctg 270° = 0, tg 270° не определён.
Данные нами определения совпадают для острых углов с определениями тригонометрических функций в геометрии. В самом деле, например, синусом острого угла прямоугольного треугольника AOC (см. рис. 2.4.1.4) называлось отношение противолежащего катета к гипотенузе: sin O=ACOA.
Кроме того, в курсе геометрии было доказано, что значения тригонометрических функций острых углов не зависят от размеров прямоугольного треугольника.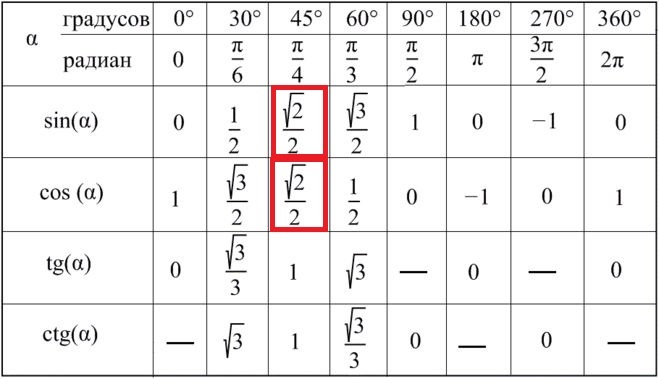
Однако если мы поместим наш прямоугольный треугольник так, что его вершина – точка O – совпадёт с началом координат, а точка A будет лежать на единичной окружности (то есть мы выбираем тем самым гипотенузу OA = 1), то геометрическое определение синуса примет вид:
sin O=ACOA=AC1=AC.
Значит, синус острого угла равен ординате точки, лежащей на тригонометрической окружности. А это как раз совпадает с нашим определением синуса. Совершенно те же самые рассуждения приводят нас к полной эквивалентности геометрического определения тригонометрических функций с тем, что дано в настоящем разделе. Следовательно, для вычисления значений тригонометрических функций мы можем воспользоваться их геометрическим определением.
Прямоугольный треугольник
Правильный треугольник
Рассмотрим правильный треугольник ABC со стороной, равной 1. Тогда по теореме Пифагора легко найти, что длина его высоты BH равна
BH=AB2-Ah3=1-(12)2=32.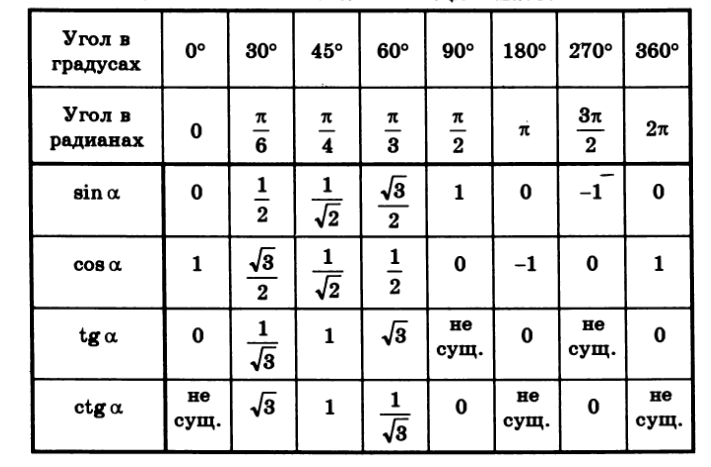
Прямоугольный равнобедренный треугольник
Значит, sin 60°=BHAB=32, cos 60°=AHAB=12.
Рассматривая угол ABH, найдём, что sin 30°=AHAB=12, cos 30°=BHAB=32.
Соответственно, tg 60°=sin 60°cos 60°=3, ctg 60°=cos 60°sin 60°=13, tg 30°=sin 30°cos 30°=13, ctg 30°=cos 30°sin 30°=3.
Рассмотрим теперь прямоугольный равнобедренный треугольник ABC с катетами, равными CA = CB = 1, ∠ CAB = 45°. Тогда по теореме Пифагора AB=2, ∠CAB=45°
и sin 45°=CAAB=12=cos 45°.
Следовательно, tg 45°=ctg 45°=1.
Итак, мы вычислили значения тригонометрических функций основных углов. Составим таблицу значений тригонометрических функций, которую мы только что получили.
| Функция | Углы | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° | Градусы | |
| 0° | Радианы | ||||||||
| sin α | 0 | 12 | 12 | 32 | 1 | 0 | –1 | 0 | |
| cos α | 1 | 32 | 12 | 12 | 0 | –1 | 0 | 1 | |
| tg α | 0 | 13 | 1 | 3 | – | 0 | – | 0 | |
| ctg α | – | 3 | 1 | 13 | 0 | – | 0 | – |
Найдите значения выражений
1) cos 0°ċsin 270°-2cos180°cos2 0°;
2) sin π2ċcos3 π3+1cos 2π+1sin (3π2).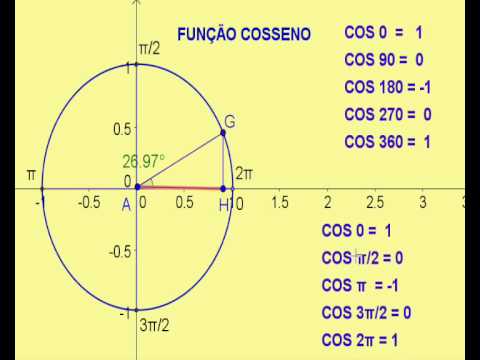
Имеем:
1) cos 0°ċsin 270°-2cos 180°cos2 0°=1ċ(-1)-2ċ(-1)12=-1+2=1;
2) sin π2ċcos3 π3+1cos 2π+1sin (3π2)=1ċ(12)3+11+1-1=18+1-1=18.
Ответ. 1) 1; 2) 18.
Периодические функции
Функция f называется периодической с периодом T ≠ 0, если для любого x из области определения функции выполнено:
f (x+T)=f (x-T)=f (x).
Если функция f имеет период T, то она, очевидно, имеет период nT, где n∈ℤ.
Поэтому говорят о наименьшем положительном периоде (НПП) функции f. Существуют периодические функции, не имеющие НПП. Так, например, f (x) = C, где C − произвольная постоянная, является периодической, однако любое положительное число является её периодом. Очевидно, среди них нет наименьшего.
Доказать, что НПП функции y = sin x является 2π.
Из определения функции следует, что у точек x и x + 2π одинаковая ордината, следовательно, sin x = sin (x + 2π), а это означает, что 2π является периодом функции sin x.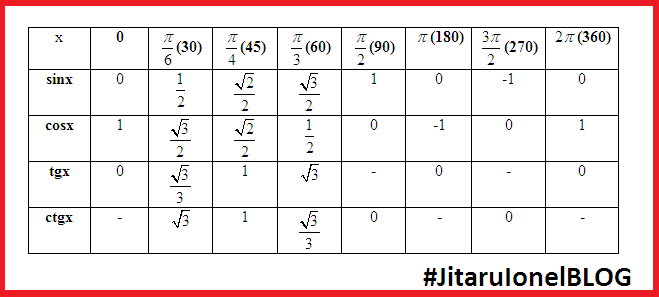
Нас интересуют T < 2π. Таким периодом может быть только T = π, однако T = π не является периодом данной функции, так как равенство sin x = sin (x + π) неверно при x=π2.
Значит, НПП функции y = sin x является T = 2π.
Аналогично можно показать, что функция y = cos x также имеет НПП T = 2π. А функции y = tg x и y = ctg x имеют НПП T = π.
Смотрите также:
Математика,
Английский язык,
Химия,
Биология,
Физика,
География,
Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ «Облако знаний».
LearnPracticeDownload
Значение sin 270 градусов равно -1 .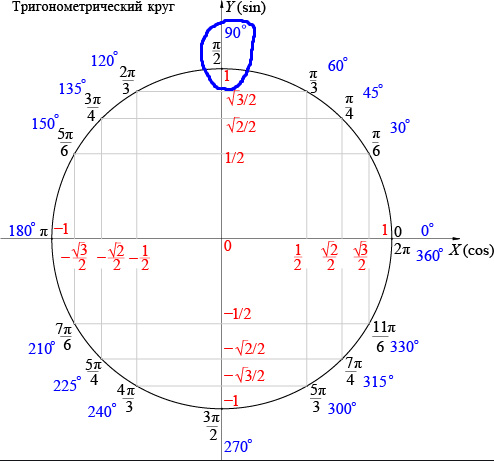
- Sin 270°: -1
- Грех (-270 градусов): 1
- Sin 270° в радианах: грех (3π/2) или грех (4,7123889 . . . .)
Каково значение греха 270 градусов?
Значение sin 270 градусов равно -1. Sin 270 градусов также можно выразить с помощью эквивалента заданного угла (270 градусов) в радианах (4,71238 . . .).
Используя преобразование градусов в радианы, мы знаем, что θ в радианах = θ в градусах × (pi/180°)
⇒ 270 градусов = 270° × (π/180°) рад = 3π/2 или 4,7123. . .
∴ sin 270° = sin(4,7123) = -1
Объяснение:
Для sin 270 градусов угол 270° лежит на отрицательной оси y. Таким образом, значение sin 270° = -1
Поскольку функция синуса является периодической функцией, мы можем представить sin 270° как sin 270 градусов = sin(270° + n × 360°), n ∈ Z.
⇒ sin 270° = sin 630° = sin 990° и так далее.
Примечание: Поскольку синус является нечетной функцией, значение sin(-270°) = -sin(270°).
Методы определения значения sin 270 градусов
Значение sin 270° принимается равным -1. Мы можем найти значение sin 270 градусов по:
- Использование единичного круга
- Использование тригонометрических функций
Sin 270 градусов с помощью единичной окружности
Чтобы найти значение sin 270 градусов с помощью единичной окружности:
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол 270° с положительной осью x.
- Синус 270 градусов равен координате y(-1) точки пересечения (0,-1) единичной окружности и r.
Отсюда значение sin 270° = y = -1
Sin 270° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить sin 270 градусов как:
- ± √(1-cos²(270°))
- ± тангенс 270°/√(1 + тангенс²(270°))
- ± 1/√(1 + раскладушка²(270°))
- ± √(сек²(270°) — 1)/сек 270°
- 1/косек 270°
Примечание.
Мы можем использовать тригонометрические тождества, чтобы представить sin 270° как
- sin(180° — 270°) = sin(-90°)
- -sin(180° + 270°) = -sin 450°
- cos(90° — 270°) = cos(-180°)
- -cos(90° + 270°) = -cos 360°
☛ Также проверьте:
- грех 2 градуса
- грех 270 градусов
- грех 120 градусов
- грех 46 градусов
- грех 315 градусов
- грех 765 градусов
Примеры использования Sin 270 градусов
-
Пример 1: Используя значение sin 270°, решите: (1-cos²(270°)).
Решение:
Мы знаем, (1-cos²(270°)) = (sin²(270°)) = 1
⇒ (1-cos²(270°)) = 1 -
Пример 2: Упростить: 2 (sin 270°/sin 630°)
Решение:
Мы знаем sin 270° = sin 630°
⇒ 2 sin 270°/sin 630° = 2(sin 270°/sin 270°)
= 2(1) = 2 -
Пример 3.
Найдите значение 5 sin(270°)/7 cos(-180°).
Решение:
Используя тригонометрические тождества, мы знаем, что sin(270°) = cos(90° — 270°) = cos(-180°).
⇒ sin(270°) = cos(-180°)
⇒ Значение 5 sin(270°)/7 cos(-180°) = 5/7
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о Sin 270 Degrees
Что такое Sin 270 Degrees?
Sin 270 градусов — значение тригонометрической функции синуса для угла, равного 270 градусам. Значение sin 270° равно -1.
Каково значение Sin 270° в пересчете на Cosec 270°?
Поскольку функция косеканса является обратной величиной функции синуса, мы можем записать sin 270° как 1/cosec(270°).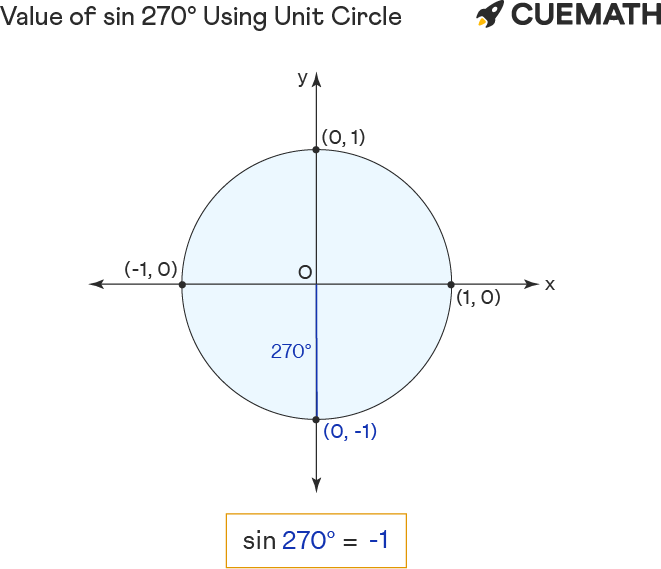
Как найти значение греха 270 градусов?
Значение sin 270 градусов можно вычислить, построив угол 270° с осью x и затем найдя координаты соответствующей точки (0, -1) на единичной окружности. Значение sin 270° равно координате y (-1). ∴ sin 270° = -1.
Каково значение Sin 270 градусов в пересчете на Cot 270°?
Мы можем представить функцию синуса в терминах функции котангенса, используя тригонометрические тождества, sin 270° можно записать как -1/√(1 + cot²(270°)). Здесь значение ctg 270° равно 0,
Как найти Sin 270° в терминах других тригонометрических функций?
Используя формулу тригонометрии, значение sin 270° может быть выражено через другие тригонометрические функции следующим образом:
- ± √(1-cos²(270°))
- ± тангенс 270°/√(1 + тангенс²(270°))
- ± 1/√(1 + раскладушка²(270°))
- ± √(сек²(270°) — 1)/сек 270°
- 1/косек 270°
☛ Также проверьте: Тригонометрическая таблица
Скачать БЕСПЛАТНЫЕ учебные материалы
Тригонометрия
Рабочие листы по математике и
визуальные учебные программы
Mathway | Популярные проблемы
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктический(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найдите точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.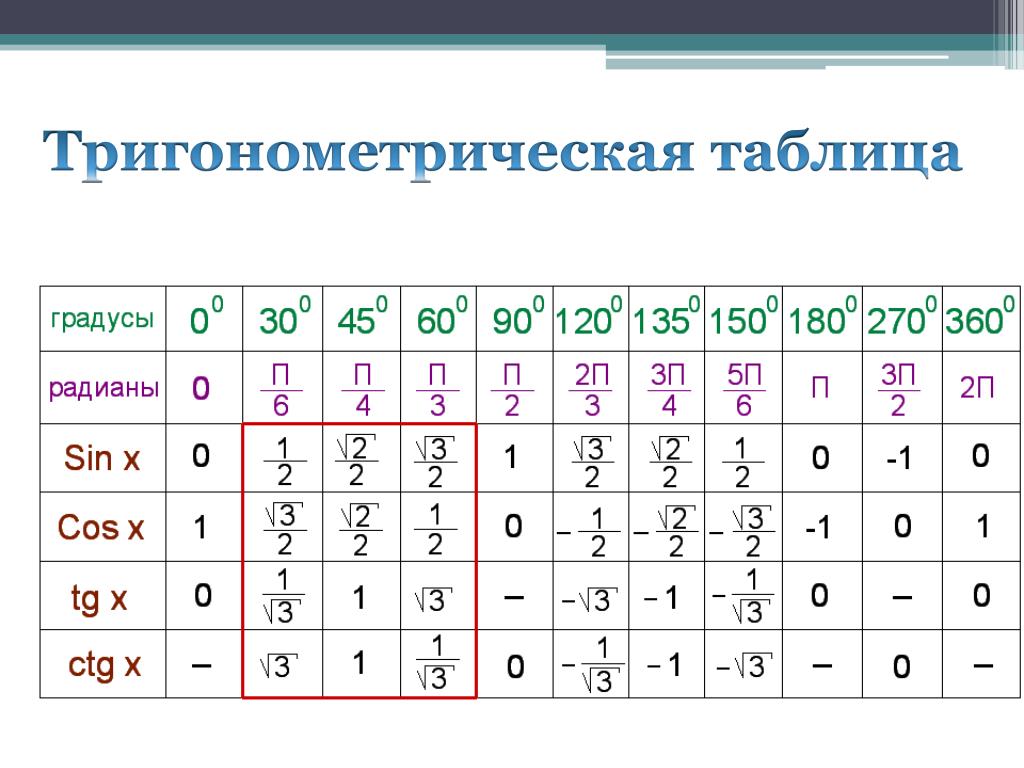 )/3 )/3 |
|
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | рыжевато-коричневый (пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найдите точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | соз(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желто-коричневый(45) | |
| 69 | Оценка | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | желтовато-коричневый ((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 шт.
No related posts. |
92
Таблица синусов.
Таблица синусов — это записанные в таблицу посчитанные значения синусов углов от 0° до 360°. Используя таблицу синусов вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение синуса от нужного Вам угла достаточно найти его в таблице.
Калькулятор — синус угла
sin(°) = 0
Калькулятор — арксинус угла
arcsin() = 90°
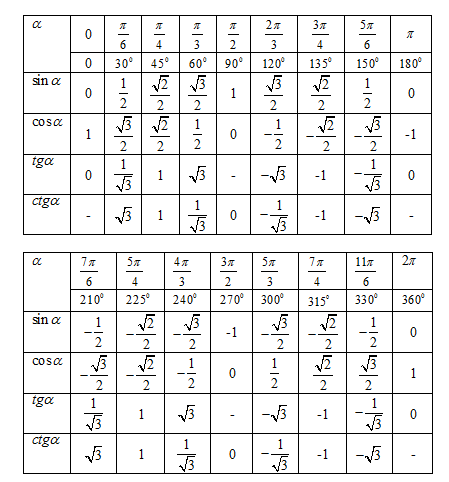
Таблица синусов в радианах
| α | 0 | π6 | π4 | π3 | π2 | π | 3π2 | 2π |
| sin α | 0 | 12 | √22 | √32 | 1 | 0 | -1 | 0 |
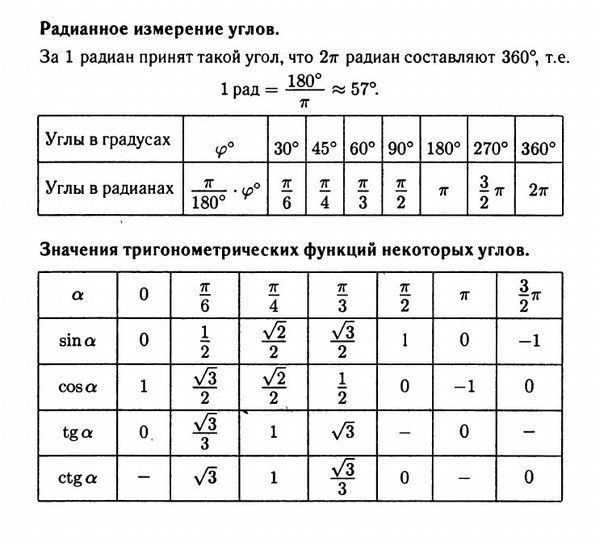
Таблица синусов углов от 0° до 180°
| sin(0°) = 0 sin(1°) = 0.017452 sin(2°) = 0.034899 sin(3°) = 0.052336 sin(4°) = 0.069756 sin(5°) = 0.087156 sin(6°) = 0.104528 sin(7°) = 0.121869 sin(8°) = 0.139173 sin(9°) = 0.156434 sin(10°) = 0.173648 sin(11°) = 0.190809 sin(12°) = 0.207912 sin(13°) = 0.224951 sin(14°) = 0.241922 sin(15°) = 0.258819 sin(16°) = 0.275637 sin(17°) = 0.292372 sin(18°) = 0.309017 sin(19°) = 0.325568 sin(20°) = 0.34202 sin(21°) = 0.358368 sin(22°) = 0.374607 sin(23°) = 0.390731 sin(24°) = 0.406737 sin(25°) = 0.422618 sin(26°) = 0.438371 sin(27°) = 0.45399 sin(28°) = 0.469472 sin(29°) = 0.48481 sin(30°) = 0.5 sin(31°) = 0.515038 sin(32°) = 0.529919 sin(33°) = 0.544639 sin(34°) = 0.559193 sin(35°) = 0.573576 sin(36°) = 0.587785 sin(37°) = 0.601815 sin(38°) = 0.615661 sin(39°) = 0.62932 sin(40°) = 0.642788 sin(41°) = 0.656059 sin(42°) = 0.669131 sin(43°) = 0.681998 sin(44°) = 0.694658 sin(45°) = 0.707107 |
sin(46°) = 0.71934 sin(47°) = 0.731354 sin(48°) = 0.743145 sin(49°) = 0.75471 sin(50°) = 0.766044 sin(51°) = 0.777146 sin(52°) = 0.788011 sin(53°) = 0.798636 sin(54°) = 0.809017 sin(55°) = 0.819152 sin(56°) = 0.829038 sin(57°) = 0.838671 sin(58°) = 0.848048 sin(59°) = 0.857167 sin(60°) = 0.866025 sin(61°) = 0.87462 sin(62°) = 0.882948 sin(63°) = 0.891007 sin(64°) = 0.898794 sin(65°) = 0.906308 sin(66°) = 0.913545 sin(67°) = 0.920505 sin(68°) = 0.927184 sin(69°) = 0.93358 sin(70°) = 0.939693 sin(71°) = 0.945519 sin(72°) = 0.951057 sin(73°) = 0.956305 sin(74°) = 0.961262 sin(75°) = 0.965926 sin(76°) = 0.970296 sin(77°) = 0.97437 sin(78°) = 0.978148 sin(79°) = 0.981627 sin(80°) = 0.984808 sin(81°) = 0.987688 sin(82°) = 0.990268 sin(83°) = 0.992546 sin(84°) = 0.994522 sin(85°) = 0.996195 sin(86°) = 0.997564 sin(87°) = 0.99863 sin(88°) = 0.999391 sin(89°) = 0.999848 sin(90°) = 1 |
sin(91°) = 0.999848 sin(92°) = 0.999391 sin(93°) = 0.99863 sin(94°) = 0.997564 sin(95°) = 0.996195 sin(96°) = 0.994522 sin(97°) = 0.992546 sin(98°) = 0.990268 sin(99°) = 0.987688 sin(100°) = 0.984808 sin(101°) = 0.981627 sin(102°) = 0.978148 sin(103°) = 0.97437 sin(104°) = 0.970296 sin(105°) = 0.965926 sin(106°) = 0.961262 sin(107°) = 0.956305 sin(108°) = 0.951057 sin(109°) = 0.945519 sin(110°) = 0.939693 sin(111°) = 0.93358 sin(112°) = 0.927184 sin(113°) = 0.920505 sin(114°) = 0.913545 sin(115°) = 0.906308 sin(116°) = 0.898794 sin(117°) = 0.891007 sin(118°) = 0.882948 sin(119°) = 0.87462 sin(120°) = 0.866025 sin(121°) = 0.857167 sin(122°) = 0.848048 sin(123°) = 0.838671 sin(124°) = 0.829038 sin(125°) = 0.819152 sin(126°) = 0.809017 sin(127°) = 0.798636 sin(128°) = 0.788011 sin(129°) = 0.777146 sin(130°) = 0.766044 sin(131°) = 0.75471 sin(132°) = 0.743145 sin(133°) = 0.731354 sin(134°) = 0.71934 sin(135°) = 0.707107 |
sin(136°) = 0.694658 sin(137°) = 0.681998 sin(138°) = 0.669131 sin(139°) = 0.656059 sin(140°) = 0.642788 sin(141°) = 0.62932 sin(142°) = 0.615661 sin(143°) = 0.601815 sin(144°) = 0.587785 sin(145°) = 0.573576 sin(146°) = 0.559193 sin(147°) = 0.544639 sin(148°) = 0.529919 sin(149°) = 0.515038 sin(150°) = 0.5 sin(151°) = 0.48481 sin(152°) = 0.469472 sin(153°) = 0.45399 sin(154°) = 0.438371 sin(155°) = 0.422618 sin(156°) = 0.406737 sin(157°) = 0.390731 sin(158°) = 0.374607 sin(159°) = 0.358368 sin(160°) = 0.34202 sin(161°) = 0.325568 sin(162°) = 0.309017 sin(163°) = 0.292372 sin(164°) = 0.275637 sin(165°) = 0.258819 sin(166°) = 0.241922 sin(167°) = 0.224951 sin(168°) = 0.207912 sin(169°) = 0.190809 sin(170°) = 0.173648 sin(171°) = 0.156434 sin(172°) = 0.139173 sin(173°) = 0.121869 sin(174°) = 0.104528 sin(175°) = 0.087156 sin(176°) = 0.069756 sin(177°) = 0.052336 sin(178°) = 0.034899 sin(179°) = 0.017452 sin(180°) = 0 |
Таблица синусов углов от 181° до 360°
| sin(181°) = -0.017452 sin(182°) = -0.034899 sin(183°) = -0.052336 sin(184°) = -0.069756 sin(185°) = -0.087156 sin(186°) = -0.104528 sin(187°) = -0.121869 sin(188°) = -0.139173 sin(189°) = -0.156434 sin(190°) = -0.173648 sin(191°) = -0.190809 sin(192°) = -0.207912 sin(193°) = -0.224951 sin(194°) = -0.241922 sin(195°) = -0.258819 sin(196°) = -0.275637 sin(197°) = -0.292372 sin(198°) = -0.309017 sin(199°) = -0.325568 sin(200°) = -0.34202 sin(201°) = -0.358368 sin(202°) = -0.374607 sin(203°) = -0.390731 sin(204°) = -0.406737 sin(205°) = -0.422618 sin(206°) = -0.438371 sin(207°) = -0.45399 sin(208°) = -0.469472 sin(209°) = -0.48481 sin(210°) = -0.5 sin(211°) = -0.515038 sin(212°) = -0.529919 sin(213°) = -0.544639 sin(214°) = -0.559193 sin(215°) = -0.573576 sin(216°) = -0.587785 sin(217°) = -0.601815 sin(218°) = -0.615661 sin(219°) = -0.62932 sin(220°) = -0.642788 sin(221°) = -0.656059 sin(222°) = -0.669131 sin(223°) = -0.681998 sin(224°) = -0.694658 sin(225°) = -0.707107 |
sin(226°) = -0.71934 sin(227°) = -0.731354 sin(228°) = -0.743145 sin(229°) = -0.75471 sin(230°) = -0.766044 sin(231°) = -0.777146 sin(232°) = -0.788011 sin(233°) = -0.798636 sin(234°) = -0.809017 sin(235°) = -0.819152 sin(236°) = -0.829038 sin(237°) = -0.838671 sin(238°) = -0.848048 sin(239°) = -0.857167 sin(240°) = -0.866025 sin(241°) = -0.87462 sin(242°) = -0.882948 sin(243°) = -0.891007 sin(244°) = -0.898794 sin(245°) = -0.906308 sin(246°) = -0.913545 sin(247°) = -0.920505 sin(248°) = -0.927184 sin(249°) = -0.93358 sin(250°) = -0.939693 sin(251°) = -0.945519 sin(252°) = -0.951057 sin(253°) = -0.956305 sin(254°) = -0.961262 sin(255°) = -0.965926 sin(256°) = -0.970296 sin(257°) = -0.97437 sin(258°) = -0.978148 sin(259°) = -0.981627 sin(260°) = -0.984808 sin(261°) = -0.987688 sin(262°) = -0.990268 sin(263°) = -0.992546 sin(264°) = -0.994522 sin(265°) = -0.996195 sin(266°) = -0.997564 sin(267°) = -0.99863 sin(268°) = -0.999391 sin(269°) = -0.999848 sin(270°) = -1 |
sin(271°) = -0.999848 sin(272°) = -0.999391 sin(273°) = -0.99863 sin(274°) = -0.997564 sin(275°) = -0.996195 sin(276°) = -0.994522 sin(277°) = -0.992546 sin(278°) = -0.990268 sin(279°) = -0.987688 sin(280°) = -0.984808 sin(281°) = -0.981627 sin(282°) = -0.978148 sin(283°) = -0.97437 sin(284°) = -0.970296 sin(285°) = -0.965926 sin(286°) = -0.961262 sin(287°) = -0.956305 sin(288°) = -0.951057 sin(289°) = -0.945519 sin(290°) = -0.939693 sin(291°) = -0.93358 sin(292°) = -0.927184 sin(293°) = -0.920505 sin(294°) = -0.913545 sin(295°) = -0.906308 sin(296°) = -0.898794 sin(297°) = -0.891007 sin(298°) = -0.882948 sin(299°) = -0.87462 sin(300°) = -0.866025 sin(301°) = -0.857167 sin(302°) = -0.848048 sin(303°) = -0.838671 sin(304°) = -0.829038 sin(305°) = -0.819152 sin(306°) = -0.809017 sin(307°) = -0.798636 sin(308°) = -0.788011 sin(309°) = -0.777146 sin(310°) = -0.766044 sin(311°) = -0.75471 sin(312°) = -0.743145 sin(313°) = -0.731354 sin(314°) = -0.71934 sin(315°) = -0.707107 |
sin(316°) = -0.694658 sin(317°) = -0.681998 sin(318°) = -0.669131 sin(319°) = -0.656059 sin(320°) = -0.642788 sin(321°) = -0.62932 sin(322°) = -0.615661 sin(323°) = -0.601815 sin(324°) = -0.587785 sin(325°) = -0.573576 sin(326°) = -0.559193 sin(327°) = -0.544639 sin(328°) = -0.529919 sin(329°) = -0.515038 sin(330°) = -0.5 sin(331°) = -0.48481 sin(332°) = -0.469472 sin(333°) = -0.45399 sin(334°) = -0.438371 sin(335°) = -0.422618 sin(336°) = -0.406737 sin(337°) = -0.390731 sin(338°) = -0.374607 sin(339°) = -0.358368 sin(340°) = -0.34202 sin(341°) = -0.325568 sin(342°) = -0.309017 sin(343°) = -0.292372 sin(344°) = -0.275637 sin(345°) = -0.258819 sin(346°) = -0.241922 sin(347°) = -0.224951 sin(348°) = -0.207912 sin(349°) = -0.190809 sin(350°) = -0.173648 sin(351°) = -0.156434 sin(352°) = -0.139173 sin(353°) = -0.121869 sin(354°) = -0.104528 sin(355°) = -0.087156 sin(356°) = -0.069756 sin(357°) = -0.052336 sin(358°) = -0.034899 sin(359°) = -0.017452 sin(360°) = 0 |





 Найдите значение 5 sin(270°)/7 cos(-180°).
Найдите значение 5 sin(270°)/7 cos(-180°).