Как найти расстояние между зарядами
Многие физические явления, наблюдаемые в природе и окружающей нас жизни, не могут быть объяснены только на основе законов механики, молекулярно-кинетической теории и термодинамики. В этих явлениях проявляются силы, действующие между телами на расстоянии, причем эти силы не зависят от масс взаимодействующих тел и, следовательно, не являются гравитационными. Эти силы называют электромагнитными силами .
О существовании электромагнитных сил знали еще древние греки. Но систематическое, количественное изучение физических явлений, в которых проявляется электромагнитное взаимодействие тел, началось только в конце XVIII века. Трудами многих ученых в XIX веке завершилось создание стройной науки, изучающей электрические и магнитные явления. Эта наука, которая является одним из важнейших разделов физики, получила название электродинамики .
Основными объектами изучения в электродинамике являются электрические и магнитные поля, создаваемые электрическими зарядами и токами.
Электрическое поле
1.1. Электрический заряд. Закон Кулона
Подобно понятию гравитационной массы тела в механике Ньютона, понятие заряда в электродинамике является первичным, основным понятием.
Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.
Электрический заряд обычно обозначается буквами или .
Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:
Существует два рода электрических зарядов, условно названных положительными и отрицательными.
Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.
Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.
Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда .
Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.
С современной точки зрения, носителями зарядов являются элементарные частицы. Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному заряду .
В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером . Атом данного вещества может потерять один или несколько электронов или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион.
Заряд может передаваться от одного тела к другому только порциями, содержащими целое число элементарных зарядов. Таким образом, электрический заряд тела – дискретная величина:
Физические величины, которые могут принимать только дискретный ряд значений, называются квантованными . Элементарный заряд является квантом (наименьшей порцией) электрического заряда. Следует отметить, что в современной физике элементарных частиц предполагается существование так называемых кварков – частиц с дробным зарядом и Однако, в свободном состоянии кварки до сих пор наблюдать не удалось.
В обычных лабораторных опытах для обнаружения и измерения электрических зарядов используется электрометр – прибор, состоящий из металлического стержня и стрелки, которая может вращаться вокруг горизонтальной оси (рис. 1.1.1). Стержень со стрелкой изолирован от металлического корпуса. При соприкосновении заряженного тела со стержнем электрометра, электрические заряды одного знака распределяются по стержню и стрелке. Силы электрического отталкивания вызывают поворот стрелки на некоторый угол, по которому можно судить о заряде, переданном стержню электрометра.
Электрометр является достаточно грубым прибором; он не позволяет исследовать силы взаимодействия зарядов. Впервые закон взаимодействия неподвижных зарядов был открыт французским физиком Ш. Кулоном в 1785 г. В своих опытах Кулон измерял силы притяжения и отталкивания заряженных шариков с помощью сконструированного им прибора – крутильных весов (рис. 1.1.2), отличавшихся чрезвычайно высокой чувствительностью. Так, например, коромысло весов поворачивалось на 1° под действием силы порядка .
Идея измерений основывалась на блестящей догадке Кулона о том, что если заряженный шарик привести в контакт с точно таким же незаряженным, то заряд первого разделится между ними поровну. Таким образом, был указан способ изменять заряд шарика в два, три и т. д. раз. В опытах Кулона измерялось взаимодействие между шариками, размеры которых много меньше расстояния между ними. Такие заряженные тела принято называть точечными зарядами .
Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь.
На основании многочисленных опытов Кулон установил следующий закон:
Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:
Силы взаимодействия подчиняются третьему закону Ньютона: Они являются силами отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках (рис. 1.1.3). Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой .
Закон Кулона справедлив для точечных заряженных тел. Практически закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними.
Коэффициент пропорциональности в законе Кулона зависит от выбора системы единиц. В Международной системе СИ за единицу заряда принят кулон (Кл).
Кулон – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А. Единица силы тока (ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения .
Коэффициент в системе СИ обычно записывают в виде:
где – электрическая постоянная .
В системе СИ элементарный заряд равен:
Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции.
Если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.
Рис. 1.1.4 поясняет принцип суперпозиции на примере электростатического взаимодействия трех заряженных тел.
Принцип суперпозиции является фундаментальным законом природы. Однако, его применение требует определенной осторожности, в том случае, когда речь идет о взаимодействии заряженных тел конечных размеров (например, двух проводящих заряженных шаров 1 и 2). Если к системе из двух заряженных шаров поднсти третий заряженный шар, то взаимодействие между 1 и 2 изменится из-за перераспределения зарядов .
Принцип суперпозиции утверждает, что при заданном (фиксированном) распределении зарядов на всех телах силы электростатического взаимодействия между любыми двумя телами не зависят от наличия других заряженных тел.
Закон Кулона
Закон Кулона количественно описывает взаимодействие заряженных тел. Он является фундаментальным законом, то есть установлен при помощи эксперимента и не следует ни из какого другого закона природы. Он сформулирован для неподвижных точечных зарядов в вакууме. В реальности точечных зарядов не существует, но такими можно считать заряды, размеры которых значительно меньше расстояния между ними. Сила взаимодействия в воздухе почти не отличается от силы взаимодействия в вакууме (она слабее менее чем на одну тысячную).
Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.
Впервые закон взаимодействия неподвижных зарядов был открыт французским физиком Ш. Кулоном в 1785 г. В опытах Кулона измерялось взаимодействие между шариками, размеры которых много меньше расстояния между ними. Такие заряженные тела принято называть точечными зарядами.
На основании многочисленных опытов Кулон установил следующий закон:
Сила взаимодействия двух неподвижных точечных электрических зарядов в вакууме прямо пропорциональна произведению их модулей и обратно пропорциональна квадрату расстояния между ними. Она направлена вдоль прямой, соединяющей заряды, и является силой притяжения, если заряды разноименные, и силой отталкивания, если заряды одноименные.
Если обозначить модули зарядов через |q1| и |q2|, то закон Кулона можно записать в следующей форме:
Коэффициент пропорциональности k в законе Кулона зависит от выбора системы единиц.
Полная формула закона Кулона:
( F ) — Сила Кулона
( q_1 q_2 ) — Электрический заряд тела
( r ) — Расстояние между зарядами
( varepsilon_0 = 8,85*10^ ) — Электрическая постоянная
( varepsilon ) — Диэлектрическая проницаемость среды
( k = 9*10^9 ) — Коэффициент пропорциональности в законе Кулона
Силы взаимодействия подчиняются третьему закону Ньютона: ( vec_=vec_ ) . Они являются силами отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках.
Электрический заряд обычно обозначается буквами q или Q .
Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:
Существует два рода электрических зарядов, условно названных положительными и отрицательными.
Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.
Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.
Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.
Закон Кулона справедлив для точечных заряженных тел. Практически закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними.
Отметим, чтоб выполнялся закон Кулона необходимо 3 условия:
- Точечность зарядов — то есть расстояние между заряженными телами много больше их размеров.
- Неподвижность зарядов. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд .
- Взаимодействие зарядов в вакууме.
В Международной системе СИ за единицу заряда принят кулон (Кл) .
Кулон – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А . Единица силы тока (Ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения.
Закон Кулона простым языком
Взаимодействия электрических зарядов исследовали ещё до Шарля Кулона. В частности, английский физик Кавендиш в своих исследованиях пришёл к выводу, что неподвижные заряды при взаимодействии подчиняются определённому закону. Однако он не обнародовал своих выводов. Повторно закон Кулона был открыт французским физиком, именем которого был назван этот фундаментальный закон.
Рисунок 1. Закон Кулона
История открытия
Эксперименты с заряженными частицами проводили много физиков:
- Г. В. Рихман;
- профессор физики Ф. Эпинус;
- Д. Бернулли;
- Пристли;
- Джон Робисон и многие другие.
Все эти учёные очень близко подошли к открытию закона, но никому из них не удалось математически обосновать свои догадки. Несомненно, они наблюдали взаимодействие заряженных шариков, но установить закономерность в этом процессе было непросто.
Кулон проводил тщательные измерения сил взаимодействия. Для этого он даже сконструировал уникальный прибор – крутильные весы (см. Рис. 2).
Рис. 2. Крутильные весы
У придуманных Кулоном весов была чрезвычайно высокая чувствительность. Прибор реагировал на силы порядка 10 -9 Н. Коромысло весов, под действием этой крошечной силы, поворачивалось на 1 º . Экспериментатор мог измерять угол поворота, а значит и приложенную силу, пользуясь точной шкалой.
Благодаря гениальной догадке учёного, идея которой состояла в том, что при соприкосновении заряженного и незаряженного шариков, электрический заряд делился между ними поровну. На это сразу реагировали крутильные весы, коромысло которых поворачивалось на определённый угол. Заземляя неподвижный шарик, Кулон мог нейтрализовать на нём полученный заряд.
Таким образом, учёный смог уменьшать первоначальный заряд подвижного шарика кратное число раз. Измеряя угол отклонения после каждого деления заряда, Кулон увидел закономерность в действии отталкивающей силы, что помогло ему сформулировать свой знаменитый закон.
Формулировка
Кулон исследовал взаимодействие между шариками, ничтожно малых размеров, по сравнению с расстояниями между ними. В физике такие заряженные тела называются точечными. Другими словами, под определение точечных зарядов подпадают такие заряженные тела, если их размерами, в условиях конкретного эксперимента, можно пренебречь.
Для точечных зарядов справедливо утверждение: Силы взаимодействия между ними направлены вдоль линии, проходящей через центры заряженных тел. Абсолютная величина каждой силы прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними (см. рис. 3). Данную зависимость можно выразить формулой: |F1|=|F2|=(ke*q1*q2) / r 2
Рис. 3. Взаимодействие точечных зарядов
Остаётся добавить, что векторы сил направлены друг к другу для разноименных зарядов, и противоположно, в случае с одноимёнными зарядами. То есть между разноимёнными зарядами действует электрическое притяжение, а между одноимёнными – отталкивание.
Таким образом, закон Кулона описывает взаимодействие между двумя электрическими зарядами, которое лежит в основе всех электромагнитных взаимодействий.
Для того чтобы действовал сформулированный выше закон, необходимо выполнение следующий условий:
- соблюдение точечности зарядов;
- неподвижность заряженных тел;
- закон выражает зависимости между зарядами в вакууме.
Границы применения
Описанная выше закономерность при определённых условиях применима для описания процессов квантовой механики. Правда, закон Кулона формулируется без понятия силы. Вместо силы используется понятие потенциальной энергии кулоновского взаимодействия. Закономерность получена путём обобщения экспериментальных данных.
Следует отметить, что на сверхмалых расстояниях (при взаимодействиях элементарных частиц) порядка 10 – 18 м проявляются электрослабые эффекты. В этих случаях закон Кулона, строго говоря, уже не соблюдается. Формулу можно применять с учётом поправок.
Нарушение закона Кулона наблюдается и в сильных электромагнитных полях (порядка 10 18 В/м), например поблизости магнитаров (тип электронных звёзд). В такой среде кулоновский потенциал уменьшается не обратно пропорционально, а экспоненциально.
Кулоновские силы подпадают под действие третьего закона Ньютона: F1 = – F2. Они используются для описания законов всемирного тяготения. В этом случае формула приобретает вид: F = ( m1* m2 ) / r 2 , где m1 и m2 – массы взаимодействующих тел, а r – расстояние между ними.
Закон Кулона стал первым открытым количественным фундаментальным законом, обоснованным математически. Его значение в исследованиях электромагнитных явлений трудно переоценить. С момента открытия и обнародования закона Кулона началась эра изучения электромагнетизма, имеющего огромное значение в современной жизни.
Коэффициент k
Формула содержит коэффициент пропорциональности k, который для согласования соразмерностей в международной системе СИ. В этой системе единицей измерения заряда принято называть кулоном (Кл) – заряд, проходящий за 1 секунду сквозь проводник, где силы тока составляет 1 А.
Коэффициент k в СИ выражается следующим образом: k = 1/4πε0, где ε0 – электрическая постоянная: ε0 = 8,85 ∙10 -12 Кл 2 /Н∙м 2 . Выполнив несложные вычисления, мы находим: k = 9×10 9 H*м 2 / Кл 2 . В метрической системе СГС k =1.
На основании экспериментов было установлено, что кулоновские силы, как и принцип суперпозиции электрических полей, в законах электростатики описывают уравнения Максвелла.
Если между собой взаимодействуют несколько заряженных тел, то в замкнутой системе результирующая сила этого взаимодействия равняется векторной сумме всех заряженных тел. В такой системе электрические заряды не исчезают – они передаются от тела к телу.
Закон Кулона в диэлектриках
Выше было упомянуто, что формула, определяющая зависимость силы от величины точечных зарядов и расстояния между ними, справедлива для вакуума. В среде сила взаимодействия уменьшается благодаря явлению поляризации. В однородной изотопной среде уменьшение силы пропорционально определённой величине, характерной для данной среды. Эту величину называют диэлектрической постоянной. Другое название – диэлектрическая проницаемость. Обозначают её символом ε. В этом случае k = 1/4πεε0.
Диэлектрическая постоянная воздуха очень близка к 1. Поэтому закон Кулона в воздушном пространстве проявляется так же как в вакууме.
Интересен тот факт, что диэлектрики могут накапливать электрические заряды, которые образуют электрическое поле. Проводники лишены такого свойства, так как заряды, попадающие на проводник, практически сразу нейтрализуются. Для поддержания электрического поля в проводнике необходимо непрерывно подавать на него заряженные частицы, образуя замкнутую цепь.
Применение на практике
Вся современная электротехника построена на принципах взаимодействия кулоновских сил. Благодаря открытию Клоном этого фундаментального закона развилась целая наука, изучающая электромагнитные взаимодействия. Понятие термина электрического поля также базируется на знаниях кулоновских сил. Доказано, что электрическое поле неразрывно связано с зарядами элементарных частиц.
Грозовые облака не что иное как скопление электрических зарядов. Они притягивают к себе индуцированные заряды земли, в результате чего появляется молния. Это открытие позволило создавать эффективные молниеотводы для защиты зданий и электротехнических сооружений.
На базе электростатики появилось много изобретений:
- конденсатор;
- различные диэлектрики;
- антистатические материалы для защиты чувствительных электронных деталей;
- защитная одежда для работников электронной промышленности и многое другое.
На законе Кулона базируется работа ускорителей заряженных частиц, в частности, функционирование Большого адронного коллайдера (см. Рис. 4).
Рис. 4. Большой адронный коллайдер
Ускорение заряженных частиц до околосветовых скоростей происходит под действием электромагнитного поля, создаваемого катушками, расположенными вдоль трассы. От столкновения распадаются элементарные частицы, следы которых фиксируются электронными приборами. На основании этих фотографий, применяя закон Кулона, учёные делают выводы о строении элементарных кирпичиков материи.
Закон Кулона. Калькулятор онлайн.
Онлайн калькулятор Закона Кулона с решением позволит вычислить силу взаимодействия двух зарядов, электрический заряд, а так же расстояние между зарядами, единицы измерения которых, могут включать любые приставки Си. Калькулятор автоматически переведет одни единицы в другие и даст подробное решение.
Калькулятор вычислит:
Силу взаимодействия двух точечных зарядов.
Точечный электрический заряд.
Расстояние между зарядами.
Сила взаимодействия двух точечных зарядов F
Сила взаимодействия двух точечных неподвижных зарядов в вакууме направлена вдоль прямой, соединяющий эти заряды, прямо пропорциональна произведению модулей этих зарядов и обратно пропорциональна квадрату расстояния между ними. Коэффициент пропорциональности k = 8.9875517873681764 × 109
Единицей измерения силы в СИ является Ньютон (Н). Международное обозначение: N
Первый заряд q1 =
Второй заряд q2 =
Расстояние r =
Единица измерения силы F
Точечный электрический заряд Q
Заряд, равный одному кулону, характеризуется как заряд, проходящий через поперечное сечение проводника, по которому идет постоянный ток силы 1 Ампер за одну секунду. Заряд 1 кулон — это заряд , который в вакууме воздействует на такой же равный ему заряд, находящийся на расстоянии 1 метр с силой 8.9875517873681764 × 109 ньютонов.
Сила F =
Второй заряд q2 =
Расстояние r =
Единица измерения заряда q1
Расстояние между зарядами R
Исходя из закона Кулона расстояние между зарядами, можно выразить как корень квадратный из частного, где числителем
выступает Коэффициент пропорциональности k = 8.9875517873681764 × 109 умноженный на произведение первого и второго зарядов, а знаменатель равен силе F взаимодействия двух зарядов.
Первый заряд q1 =
Второй заряд q2 =
Сила F =
Единица измерения расстояния r
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (физика) |
|
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
|
Оптика |
| Калькулятор отражения и преломления света |
|
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
|
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер по математике |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Еще в древности было известно, что наэлектризованные тела взаимодействуют. Силу взаимодействия двух небольших заряженных шариков с помощью крутильных весов впервые измерил Шарль Кулон. Он сформулировал закон, который позже назвали его именем.
Так же, было выяснено, что сила, с которой два заряда притягиваются, или отталкиваются, зависит не только от самих зарядов, но и от вещества, в котором эти заряды находятся.
Опыт Кулона
Кулон нашел способ измерить взаимное действие двух зарядов. Для этого он использовал крутильные весы.
Ему не пришлось применять дополнительную особо чувствительную аппаратуру. Потому, что взаимное действие зарядов имело достаточную для наблюдения интенсивность.
Примечание: Опыт Кулона похож на опыт Кавендиша, который экспериментально определил гравитационную постоянную G.
Устройство крутильных весов
Такие весы (рис. 1) содержат перекладину — тонкий стеклянный стержень, расположенный горизонтально. Он подвешен на тонкой вертикально натянутой упругой проволоке.
На одном конце стержня находится небольшой металлический шарик. К другому концу прикреплен груз, который используется, как противовес.
Еще один металлический шарик, прикрепленный ко второй палочке из стекла, можно располагать неподалеку от первого шарика. Для этого в верхней крышке корпуса весов проделано отверстие.
Рис. 1. Устройство крутильных весов, использованных Кулоном для обнаружения силы взаимодействия зарядов
Если наэлектризовать шарики, они начнут взаимодействовать. А прикрепленная к проволоке перекладина, на которой находится один из шариков, будет поворачиваться на некоторый угол.
На корпусе весов на уровне палочки располагается шкала с делениями. Угол поворота связан с силой взаимного действия шариков. Чем больше угол поворота, тем больше сила, с которой шарики действуют друг на друга.
Чтобы сдвинувшийся шарик вернуть в первоначальное положение, нужно закрутить проволоку на некоторый угол. Так, чтобы сила упругости скомпенсировала силу взаимодействия шариков.
Для закручивания проволоки в верхней части весов есть рычажок. Рядом с ним расположен диск, а на нем – еще одна угловая шкала с делениями.
По нижней шкале определяют точку, в которую необходимо вернуть шарик. Верхней шкалой пользуются, чтобы установить угол, на который нужно рычажком закрутить проволоку.
С помощью крутильных весов Шарль Кулон выяснил, как именно сила взаимного действия зависит от величины зарядов и расстояния между зарядами.
В те годы единиц для измерения заряда не было. Поэтому ему пришлось изменять заряд одного шарика с помощью метода половинного деления.
Когда он касался заряженным шариком второго такого же шарика, заряды между ними распределялись поровну. Таким способом, можно было уменьшать заряд одного из шариков, участвующих в опыте, в 2, 4, 8, 16 и т. д. раз.
Так опытным путем Кулон получил закон, формула которого очень похожа на закон всемирного тяготения.
В память о его заслугах, силу взаимодействия зарядов называют Кулоновской силой.
Закон Кулона для зарядов в вакууме
Рассмотрим два точечных заряда, которые находятся в вакууме (рис. 2).
Рис. 2. Два положительных заряда q и Q, расположенных в вакууме на расстоянии r, отталкиваются. Силы отталкивания направлены вдоль прямой, соединяющей заряды
На рисунке 2 сила (large F_{Q} ) – это сила, с которой положительный заряд Q отталкивает второй положительный заряд q. А сила (large F_{q} ) принадлежит заряду q, с такой силой он отталкивает заряд Q.
Примечание: Точечный заряд – это заряженное тело, размером и формой которого можно пренебречь.
Силы взаимодействия зарядов, по третьему закону Ньютона, равны по величине и направлены противоположно. Поэтому, для удобства можно ввести обозначение:
[large F_{q} = F_{Q} = F]
Для силы взаимодействия зарядов в вакууме Шарль Кулон сформулировал закон так:
Два точечных заряда в вакууме,
взаимодействуют с силой
прямо пропорциональной
произведению величин зарядов
и обратно пропорциональной
квадрату расстояния между ними.
Формула для этого закона на языке математики запишется так:
[large boxed { F = k cdot frac {|q| cdot |Q| }{r^{2}} } ]
(F left( H right) ) – сила, с которой два точечных заряда притягиваются, или отталкиваются;
(|q| left( text{Кл}right) ) – величина первого заряда;
(|Q| left( text{Кл}right) ) – величина второго заряда;
(r left( text{м}right) ) – расстояние между двумя точечными зарядами;
(k ) – постоянная величина, коэффициент в системе СИ;
Сила – это вектор. Две главные характеристики вектора – его длина и направление.
Формула позволяет найти одну из характеристик вектора F — модуль (длину) вектора.
Чтобы определить вторую характеристику вектора F – его направление, нужно воспользоваться правилом: Мысленно соединить два неподвижных точечных заряда прямой линией. Сила, с которой они взаимодействуют, будет направлена вдоль этой прямой линии.
Сила Кулона – это центральная сила, так как она направлена вдоль прямой, соединяющей центры тел.
Примечание: Еще один пример центральной силы — сила тяжести.
Что такое коэффициент k с точки зрения физики
Постоянная величина (k ), входящая в формулу силы взаимодействия зарядов, имеет такой физический смысл:
(k ) — это сила, с которой отталкиваются два положительных точечных заряда по 1 Кл каждый, когда расстояние между ними равно 1 метру.
Значение постоянной k равно девяти миллиардам!
[large boxed { k = 9cdot 10^{9} left( H cdot frac{text{м}^{2}}{text{Кл}^{2}}right) } ]
Это значит, что заряды взаимодействуют с большими силами.
Рис. 3. Коэффициент k в формуле взаимодействия зарядов
Константу k можно вычислить опытным путем, расположив два известных заряда (не обязательно по 1 Кулону каждый) на удобном для измерений расстоянии (не обязательно 1 метр) и измерив силу из взаимного действия.
Нужно подставить известные величины зарядов, расстояние между ними и измеренную силу в такую формулу:
[large boxed { k = frac {F cdot r^{2}}{|q| cdot |Q|} } ]
Величина k связана с электрической постоянной (varepsilon) такой формулой:
[large boxed { k = frac{1}{4pi cdot varepsilon_{0}} } ]
Поэтому дробь из правой части этой формулы можно встретить в различных справочниках физики, где она заменяет коэффициент k.
Закон Кулона для зарядов в веществе
Если два точечных заряда находятся в веществе, то сила их взаимного действия будет меньше, чем в вакууме. Для зарядов в веществе закон Кулона выглядит так:
[large boxed { F = frac{1}{varepsilon} cdot k cdot frac {|q| cdot |Q| }{r^{2}} } ]
(F left( H right) ) – сила взаимодействия зарядов в веществе;
(|q| ; |Q| left( text{Кл}right) ) – величины зарядов;
(r left( text{м}right) ) – расстояние между зарядами;
( k = 9cdot 10^{9} ) – постоянная величина;
( varepsilon ) – диэлектрическая проницаемость вещества, для разных веществ различается, ее можно найти в справочнике физики;
Рис. 4. Два заряда -q и +Q, расположенные в вакууме на расстоянии r, притягиваются сильнее, нежели те же заряды, расположенные на таком же расстоянии в диэлектрике
Силы, с которыми заряды действуют друг на друга в веществе, отличаются от сил взаимодействия в вакууме в ( varepsilon ) раз:
[large boxed { F_{text{(в диэлектрике)}} = frac{1}{varepsilon} cdot F_{text{(в вакууме)}} } ]
Примечание: Читайте отдельную статью, рассказывающую, что такое диэлектрическая проницаемость и электрическая постоянная.
Calculate the electrostatic force of attraction/repulsion, distance, or charge using Coulomb’s Law by entering known values in the calculator below.
Calculate Force
Calculate Distance
Calculate Charge
Electrostatic Force:
Learn how we calculated this below
scroll down
On this page:
-
Coulomb’s Law Calculator
-
How to Calculate Electrostatic Force
-
Coulomb’s Law Formula
-
How to Calculate the Distance Between Objects
-
How to Calculate the Charge of an Object
How to Calculate Electrostatic Force
When two charges are brought together, they experience a force of attraction if they are opposite charges and a force of repulsion if they are like charges. Using Coulomb’s Law it’s possible to calculate the electrostatic force between two charges if the distance between them is known.
Coulomb’s Law Formula
Coulomb’s Law defines the following formula for this.
FE = keq1q2 / r2
Where:
FE = electrostatic force in newtons
ke = Coulomb constant, which is equal to 8,987,551,787.3681764 Nm2C−2 (8.988×109 Nm2C-2)
q1 = charge of the first object in coulombs
q2 = charge of the first object in coulombs
r = distance between the objects in meters
The electrostatic force FE between two charges is equal to the Coulomb constant ke times the charge of an object q1 times the charge of the other object q2 divided by the distance between them r squared.
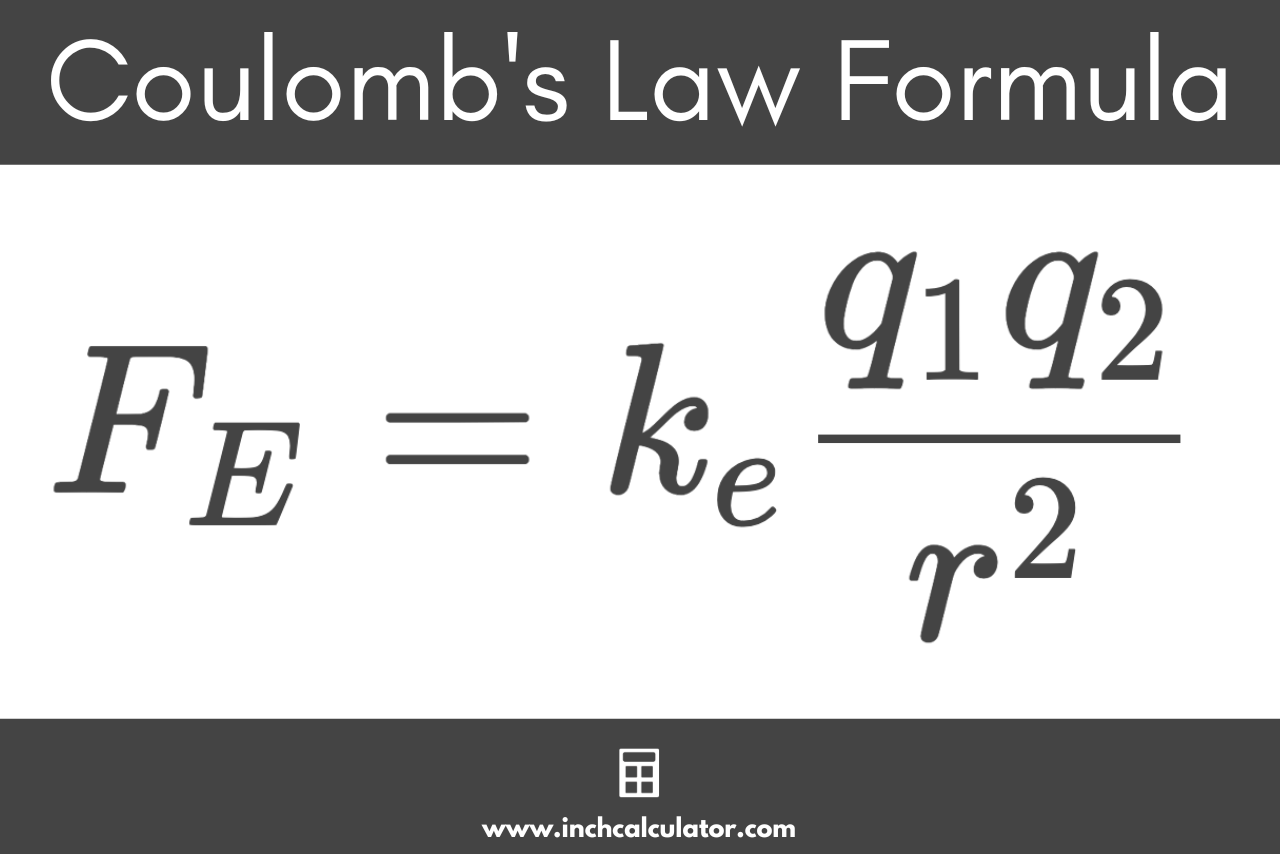
For example, let’s find the electrostatic force between two +2µC and +4µC point charges if a distance of 10 millimeters separates them.
F(N) = (8.988×109 Nm2C-2)(2×10-6 C)(4×10-6 C) / (10×10-3 m)2
F(N) = 719 N
So, the electrostatic force is equal to 719 newtons.
How to Calculate the Distance Between Objects
If the electrostatic charge and force are known, then it’s possible to use Coulomb’s Law to find the distance between the objects.
r = √ (ke × q1 × q2 ÷ FE)
So, the distance between objects r is equal to the square root of the Coulomb constant ke times the charge of an object q1 times the charge of the other object q2 divided by the electrostatic force FE.
For example, let’s find the separation between two charges, 3µC and 6µC, when a force of 2 N acts between them.
r(m) = √ ((8.988×109 Nm2C-2)(3×10-6 C)(6×10-6 C) ÷ 2 N)
r(m) = 0.288 m
Thus, the distance between the charges is 0.288 meters.
How to Calculate the Charge of an Object
If the electrostatic charge of one object, the force, and the distance are known, then the following formula can be used to solve the charge of the second object.
q2 = FE × r2 ÷ ke ÷ q1
Thus, the charge of an object q2 is equal to the electrostatic force FE times the distance between objects r squared divided by the Coulomb constant ke divided by the charge of the other object q1.
For example, let’s find the charge on an object if the other object has a charge of 8µC, a separation of 5 millimeters, and a force of 10N acts between them.
q2 (nC) = 10 N × (5×10-3 m)2 ÷ 8.988×109 Nm2C-2 ÷ 8×10-6 C
q2 (nC) = 3.5 nC
The charge of the object is equal to 3.5 nC.
Два неподвижных тела, обеспеченные определенным зарядом, взаимодействуют.
Они притягиваются либо отталкиваются. И математическое описание той самой величины действия и является законом Кулона.
Но речь идет именно о точечном заряде, когда отсутствуют сторонние источники электромагнитных полей и не учитывается стороннее воздействие.
Закон Кулона же описывает ту самую силу, исходя из формы и размеров тех самых тел.
Где F — сила воздействия, q1 b q2 — уровень заряда (в кулонах), r — расстояние (от центра тел, в метрах), k — индекс пропорциональности.
Содержание
- История открытия
- Формулировка
- Коэффициент пропорциональности K и электрическая постоянная с точки зрения физики
- Направление силы Кулона и векторный вид формулы
- Устройство крутильных весов Шарля Кулона
- Закон Кулона для зарядов в вакууме
- Закон Кулона для зарядов в веществе
- Закон Кулона в диэлектриках
- Где применяется на практике
- Ограничение в применении
- Прямая и обратная пропорциональность
- Закон Амонтона-Кулона
История открытия
Физическое свойство открыто в 1785 году Шарлем Кулоном.
Точнее, он его подтвердил, а в дальнейшем — вывел математическую зависимость.
Опыты он проводил с помощью обычных металлических шариков.
Итоговое заключение: сила взаимодействия в условиях безвоздушного пространства имеет прямую зависимость от произведения этих модулей и обратную пропорциональность корню расстояния.
И на основе этого в дальнейшем был выведен закон сохранения точечного электрического заряда закон Кулона, что сейчас является основной электростатики.
Кстати, воздействие зарядов ранее на протяжении 20 лет изучал английский физик-теоретик Кавендиш.
И именно он предложил теорию, что два не движущихся тела с имеющимся точечным зарядом взаимодействуют между собой.
Но какая именно сила действует при этом, в каком направлении и от каких параметров она может меняться — он не определил (точнее, не опубликовал информацию о своих выводах).
Математического обоснования он также не предоставил.
Аналогичные исследования проводил и Бернулли, и Робинсон, и Пристли.
Но никто из них не смог вывести окончательную математическую формулу для расчета взаимодействия и перевести её в общепринятую меру.
Формулировка
Текущее формулирование закона Кулона звучит следующим образом:
Но есть условия, при которых получается рассчитать взаимодействие двух точечных зарядов по закону:
- В пространстве расстояние между зарядами должно существенно превышать их физические габариты.
- Тела — статичны относительно окружающей среды.
- Тела расположены в вакууме (нивелируется возможное воздействие окружающей среды).
Но в теории, закон Кулона можно применять и для расчета электростатического взаимодействия между двумя точечными движущимися телами.
В итоговую формулу лишь потребуется добавить вектор от заряда q1 к q2.
Но расчет взаимодействия между собой точечных зарядов актуален только если тела находятся в условиях вакуума.
Для движущихся тел, находящихся в окружении определенной среды, применять радиус-вектор не представляется возможным, так как при смене положения меняется также и направление внешних действующих сил.
То есть в данном случае невозможно определить статический коэффициент зависимости.
Коэффициент пропорциональности K и электрическая постоянная с точки зрения физики
Рассчитывается сила взаимодействия при помощи индекса k, который по СГСЭ обозначает единицу заряда.
Его рассчитывать не нужно, так как с математической точки зрения он всегда равен 1 (при условии, что заряды расположены в условиях вакуума).
А вот индекс К — постоянный для заданных условий.
Это не статический показатель, заблаговременно его рассчитать невозможно.
Но для двух тел в одной среде значение К всегда остается одинаковым.
Направление силы Кулона и векторный вид формулы
Направление действующей силы Кулона зависит от того, одноименные или разноимённые точечные заряды взаимодействуют между собой.
Здесь действует основное правило электростатики, согласно которому два тела с одинаковым потенциалом отталкиваются, с разным — притягиваются.
Заряд при этом не имеет значения, учитывается именно потенциал (положительный или отрицательный).
Соответственно, в векторном виде формула выглядит так:
Где q — это электрический заряд (в кулонах), r — радиус-вектор (1/с), ℇ — постоянная (≈ 8,85 Ф/м).
Устройство крутильных весов Шарля Кулона
Для опытов Кулон использовал так называемые «крутильные весы».
Их основа — это шелковая нить (в безвоздушном пространстве).
На ней — уравновешенный рычаг, на краях которого — заряды (аналогично помещенные в вакуум).
При возникновении внешней движущей силы рычаг двигается по горизонтали. И смещается он до уравновешивания силой упругости имеющейся шелковой нити.
Рычаг при этом отклоняется от оси (обозначается как d). И зная это отклонение можно рассчитать крутящий момент кулоновского взаимодействия.
Допускается замена нити на любой другой материал, главное — рассчитать её обратное сопротивление, которое и уравновешивает всю конструкцию.
Но это — уже современная вариациях весов.
Непосредственно Шарль Кулон опыт проводил иначе.
Сперва фиксировалось положение горизонтального рычага, когда оба тела — не заряжены.
Далее одному из шариков придавался определенный заряд. По возвращению обратно в вакуум тела между собой начинали взаимодействовать.
С какой именно силой — как раз и показывала шкала отклонения (с поправкой на силу упругости нити, которая и удерживала всю конструкцию).
Данное физическое явление и позволило определить, что сила прямо пропорциональна заряду.
Чем выше потенциал тел — тем больше отклонение по шкале.
В дальнейшем аналогичный опыт проводился и в условиях воздуха.
Разница в результатах — минимальная, поэтому условно считается, что закон Кулона действует как для вакуума, так и для воздуха (за счет схожей диэлектрической проводимости пространства в единицу).
Поэтому опыт Шарля вполне реально повторить в домашних условиях при наличии источника тока и высокоточного измерительного прибора (мультиметра).
В качестве тел можно использовать все те же металлические шарики.
Закон Кулона для зарядов в вакууме
Сила отталкивания в вакууме рассчитывается с учетом эффекта поляризации (по квантовой электродинамике).
Что это означает? Что необходимо учитывать условное сопротивление электронно-позитронных пар, экранирующих непосредственно заряд.
И оно увеличивается при большем расстоянии.
То есть эффективный заряд электрона считается убывающей функцией по логарифмическому соотношению к расстоянию.
Но при этом формой, массой и габаритами точечного заряда в данном правиле также пренебрегают, оценивая их в условную единицу.
На практике, поправку с учетом эффекта поляризации делать не нужно, так как она играет роль только для микрочастиц размером в несколько атомов.
Закон Кулона для зарядов в веществе
Действие тел друг на друга, размещенных в каком-нибудь веществе, будет ниже, чем в вакууме.
Сила взаимодействия точечных зарядов рассчитывается аналогично, но добавляются 2 дополнительные составляющие:
- объем вещества (который условно взаимодействует с телами);
- проницаемость вещества (диэлектрическая).
Закон Кулона в диэлектриках
Диэлектрик приравнивается к среде, в которой из-за поляризации он снижает силу Кулона.
Уменьшение F пропорционально диэлектрической проницаемости.
Для воздуха он близок к 1, поэтому закон в этом случае рассчитывается точно так же, как и для вакуума.
Но нивелируется факт, что модуль рассматриваемого заряда может передавать заряженные частицы непосредственно диэлектрику (процесс формирования статического заряда).
И это актуально только в том случае, если данный процесс постоянный.
Если же телу придали заряд, а в дальнейшем извлекли из электромагнитного поля, то уровень заряженности постепенно меняется.
Соответственно, если между телами находится диэлектрик, чья проницаемость близка или равна бесконечности, то взаимодействия между ними не будет.
Увеличение заряда до бесконечности тоже не меняет данную формулу.
Где применяется на практике
Основной действующий закон электростатики как раз и выстроен на базовых понятиях кулоновской силы и взаимодействия электромагнитных полей.
Даже самая обычная молния — это ничто иное, как процесс формирования определенной силы взаимодействия между землей и грозовой тучей (где каждое из «тел» снабжено определенным зарядом).
И на основании этого и был придуман громоотвод, так как его потенциал всегда выше, чем у земли и других окружающих тел (даже если это антенна для приема и передачи сотового сигнала).
Схожим образом работает и защита от возможного попадания молнии в летательных аппаратах.
Там имеется специальный громоотвод (выступающая металлическая часть, имеющая больший заряд, чем корпус) и среда, поглощающая электромагнитное поле.
Также адронный коллайдер в своей работе тоже использует закон Кулона.
С его помощью рассчитывается потенциально возможное высвобождение кинетической энергии при движении или столкновении двух заряженных частиц.
Таким образом, например, удалось в 2014 году рассчитать потенциальную силу действия двух атомов в момент соприкосновения, когда у них световая скорость движения (порядка 300000 километров в секунду).
Ещё закон используется в производстве конденсаторов, кремниевых транзисторов (включая все компьютерные и мобильные процессоры), антистатических материалов (рассеивающих попадающий на них заряд), специализированной защитной одежды (для работы в условиях активных электромагнитных полей).
Также распространенный вариант использования закона Кулона — в промышленном оборудовании для очистки зерна.
Есть 2 основных их варианта:
- когда вся масса получает определенный статический заряд и при прохождении через электромагнитное поле — разделяется (по уровню силы взаимодействия);
- когда в массу добавляют металлическую стружку, а после — просеивают через сепаратор на основе электромагнита (железные опилки притягивают к себе остаточный мусор и «связываются» с ним).
Ещё одна сфера использования — это производство электромагнитных накопителей (карты памяти, жесткие диски, ленточные носители).
В них информация сохраняется в двоичном виде (0 и 1) при помощи так называемых «ячеек», взаимодействующих с точечными заряженными частицами.
И именно за счет диэлектрических свойств основания накопителя потенциальный срок хранения данных составляет более 5 лет (далее требуется либо повторно сформировать заряд, либо обеспечить установленный уровень намагниченности).
Схожая технология применяется ещё в производстве квантовых компьютеров.
Ограничение в применении
Закон Кулона является основной любых электромагнитных взаимодействий.
Но действует только на сравнительно небольших расстояниях.
Минимальное — это 10-16 метров, максимальное — несколько километров.
И рассчитывается только для не движущихся тел, расстояние между которыми не меняется.
И условное действие всех окружающих сил приравнено к нулю (за исключением поляризации среды, в которой и находятся тела с зарядом).
Соответственно, сумма моментов тоже приравнивается к нулю и не учитывается в формуле.
Но также известно, что при избыточно высоких зарядах (когда между телами формируется облако плазмы) сила взаимодействия растет в геометрической прогрессии.
Но по какой именно формуле — ученым ещё не удалось установить.
И здесь же можно заметить практическое значение силы Кулона.
Молния возникает только между землей и грозовыми тучами, которые расположены над уровнем почвы менее чем в 2 километра.
Тогда как поля заряженных ионов, находящихся в более высоких слоях атмосферы, взаимодействуют только между собой.
В противном бы случае Земля являлась бы необитаемой планетой.
Также закон не может применяться, если заряды помещаются в среду, не являющейся диэлектриком, так как имеющийся потенциал мгновенно нивелируется.
Поэтому его нельзя использовать, к примеру, для расчета потенциально опасного расстояния между трансформатором и человеком.
Прямая и обратная пропорциональность
Под пропорциональностью в данном случае необходимо понимать зависимость одной действующей силы от иной.
Взаимодействие между телами производно от их текущего заряда (чем выше — тем больше сила действует).
Обратная же пропорциональность актуальна по отношению к расстоянию: чем оно больше, тем сила меньше.
Но это актуально только для тех расстояний, при котором закон действует.
Если выполняется расчет для зарядов, расположенных в веществе или диэлектрике, то здесь тоже наблюдается обратная пропорциональность.
Чем выше показатель диэлектрической проницаемости — тем сила меньше, так как среда «поглощает» часть электромагнитного поля и рассеивает его.
Закон Амонтона-Кулона
Шарль Кулон известен не только своими открытиями в электростатике.
Он также сформулировал закон, описывающий линейную связь между силой трения, и действием (нормальной реакцией), оказываемым на тело со стороны поверхности.
Первичную формулировку предложил Гийом Амонтон ещё в 1699 году.
Кулон же подтвердил закон и описал его математической формулой F=A+ μN, где А — условный показатель «сцепления» поверхности, по которой и производится скольжение (трение), N — сила нормальной реакции, μ — коэффициент трения поверхностей.
А согласно 3 закону Ньютона, сила Амонтона-Кулона — взаимодействующая.
То есть она актуальна и в отношении статического, и динамичного тела.
И действие оказывается одновременно также на саму поверхность.
Данный закон активно используется при производстве смазочных материалов.
С его помощью можно также рассчитать условную устойчивость и эксплуатационный ресурс материалов.
Кулон, в свою очередь, только сформулировал математическое описание открытия Амонтона, без определения статических индексов.
Итого, закон Кулона — это фундаментная сила в электростатике в целом.
И на её основе было сделано множество новых открытий, связанных с электромагнитным воздействием.
Вся современная электроника, компоненты печатных плат — всё это прямо связано с законом Кулона.

















