Шаг винтовой линии как найти - AvtoShod.ru - решение различных проблем

Винтовая линия

Винтовая линия относится к пространственным кривым. Различают цилиндрические, конические, сферические и другие винтовые линии.

Цилиндрическая винтовая линия описывается точкой, которая совершает равномерное движение вдоль образующей кругового цилиндра,
а образующая вращается с постоянной угловой скоростью вокруг оси цилиндра.

Винтовая линия

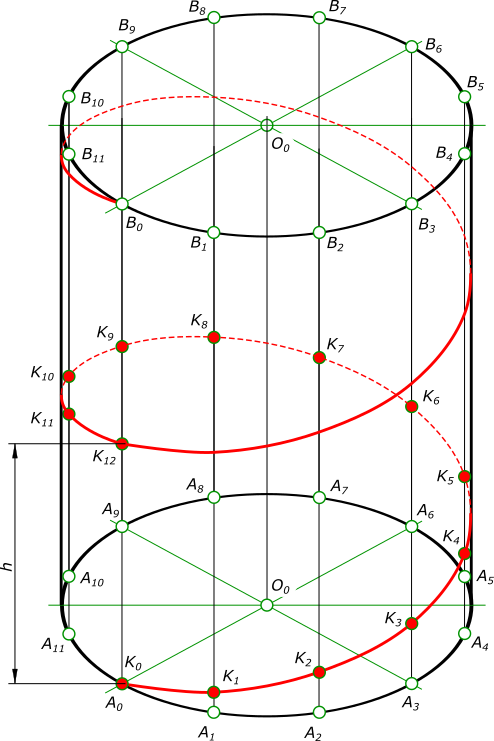
Образующая занимает 12 последовательных положений: A⁰B⁰.
Дуги A⁰A¹, A¹A² A²A³ и т. д. равны между собой и каждая равна pd/n, где d — диаметр
цилиндра, p = 3,14 и n — число положений образующей цилиндра, принятое для построения. Пусть образующая занимает 12 последовательных положений:
A⁰B⁰, A¹B¹, A²B² и т. д.
Начальному положению образующей AB соответствует A⁰B⁰, а точки K — K⁰.
При перемещении образующей AB в положение A¹B¹ точка K займет положение K¹, и поднимется по образующей на величину отрезка A¹K¹ = h/12. При последующем перемещении образующая займет положение A²B², а точка K положение
K² и поднимется на высоту равную A²B² = 2A¹B¹ = 2(h/12), и т. д.
Когда образующая совершит полный оборот и снова займет начальное положение, точка K будет находится на ней на высоте A¹²B¹² = 12(h/12) = h, величине шага винтовой линии. При этом точка описывает кривую K⁰K⁶K¹², длина которой равна длине одного витка.
На практике эти движения достигаются на токарном станке, где острие резца соответствует данной точке.

Винтовая линия

Резец оставит на цилиндрической поверхности след — винтовую линию.
Винтовая линия может быть правой или левой. Правой винтовой линией называют линию, совершающую подъем вокруг своей оси против
часовой стрелки, а левой — винтовую линию, совершающую подъем по часовой стрелке.
Правая цилиндрическая винтовая линия

Винтовая линия

может быть построена, когда заданы ее элементы.

Винтовая линия характеризуется следующими элементами: шаг, виток и угол подъема.
Шагом винтовой линии называется расстояние между смежными витками, измеренное вдоль образующей кругового цилиндра.
Витком называют винтовую линию, описанную точкой за один оборот образующей вокруг оси кругового цилиндра. Длина витка равна L.
Углом подъема винтовой линии называют отношение tg(φ)= h/(pd), тогда φ = arctg(φ), где d — диаметр цилиндра, p=3,14.

Винтовая линия может быть получена на конической поверхности

Винтовая линия

В этом случае, точка совершает равномерно-поступательное движение вдоль образующей прямого кругового конуса, а сама образующая SA вращается вокруг
его оси с постоянной угловой скорости.
Расстояние между точками смежных витков, измеренное параллельно оси конуса (например между точками A₀K₈), является шагом h конической винтовой линии.
Проекция винтовой линии на фронтальной плоскости проекций представляет собой синусоиду с затухающим колебанием (затухающей волной), а на
горизонтальной — спираль Архимеда.
При построении развертки боковой поверхности конуса винтовая линия развернется в спираль, а конус — в сектор, угол при вершине
которого равен φ= 360°×(h/L), а длина дуги радиуса R, соответствующая углу φ, равна 2πR.

Источник

Винтовая линия — кривая в трёхмерном пространстве, расположенная на круглом цилиндре
или круглом конусе и пересекающая образующие под одинаковым углом. Формы винтовых линий имеют многие детали
машин и механизмов — пружины, часть винтовых свёрл, соединительные винты и болты, шпильки, винты (шнеки)
мясорубок и экструдеров, винт Архимеда, винтовые конвейеры и др. Винтовые линии могут быть правыми и левыми, одно-
и многозаходными. Смещение винтовой линии за один оборот — называют шагом.

Рисунок 1 — Угол наклона винтовой линии

Источник

Наглядное представление и определение соединяются в параметрическом задании винтовой линии
в прямоугольной декартовой системе координат: $$ x=a cos t,quad y=a sin t,quad z=ht. $$
Первые два уравнения показывают, что проекция точки бежит по основанию прямого кругового цилиндра радиуса $a$.
Третье уравнение задаёт движение вдоль оси цилиндра с постоянной скоростью.

У «хороших» кривых в трёхмерном пространстве есть две базовые характеристики — кривизна и кручение.

Кривизна — характеризует скорость искривления линии в плоскости и определяется радиусом окружности,
дуга которой наилучшим образом приближает небольшой отрезок кривой, содержащий данную точку).
Кручение — скорость, с которой кривая стремится не быть плоской, насколько кривая хочет покинуть плоскость.

Замечательно, что для достаточно гладких кривых кривизна и кручение полностью определяют форму линии.

У винтовой линии кривизна и кручение постоянны, а из приведённого утверждения следует,
что подобным свойством обладают только такие линии!

Постоянство кривизны и кручения во всех точках означает, что устройство винтовой линии всюду одно и то же.
Как следствие, получаем, что отрезок винтовой линии может скользить вдоль неё точно так же,
как отрезок — по прямой, дуга окружности — по своей окружности. (Прямую и окружность можно рассматривать
как вырожденные, предельные случаи винтовой линии.)

Резьбовые соединения, в частности резьба болта или винта основаны на винтовой линии.
При закручивании резьба скользит как будто по лыжне.

Источник

Пространственные кривые	423

Поэтому пространственные кривые линии иногда называют как линии «двоя-

кой кривизны».

Радиус R соприкасающейся окружности (см. рис. 15.5, а) определяет радиус кривизны пространственной кривой линии, а обратная ей величина — кривизну этой линии. Соприкасающаяся окружность всегда лежит в соприкасающейся плоскости, а ее центр — на главной нормали, проведенной из точки касания.

На рис. 15.6 приведена пространственная кривая b, к которой через точки K1 и K2 проведены две соприкасающиеся плоскости — соответственно плоскости 1 и 2. Средним кручением дуги K1K2 является отношение величины линейного угла между соприкасающимися плоскостями, проведенными

вточках K1 и K2, к длине этой дуги. Линейный угол между соприкасающимися плоскостями может быть измерен углом между бинормалями к кривой b

вточках K1 и K2.

Предельное положение среднего кручения при стремлении точки K2 к точке K1 называется кручением кривой b в точке K1. Чем меньше величина кручения, тем она ближе располагается к соприкасающейся плоскости. Для плоской кривой линии кручение во всех ее точках равно нулю, т. к. кривая целиком лежит в одной плоскости — общей соприкасающейся плоскости всех ее точек.

Рис. 15.6. Пространственная кривая b и две соприкасающиеся плоскости 1 и 2

15.2.1. Свойства винтовых линий

Винтовой линией называется пространственная кривая линия, являющаяся траекторией точки, которая равномерно вращается вокруг неподвижной прямой (оси винтовой линии) и одновременно перемещается поступательно вдоль этой оси.

Винтовая линия может быть правой (с правым ходом) или левой (с левым ходом). Винтовая линия называется правой, если при подъеме она закручивается в направлении против движения часовой стрелки. В обратном случае винтовая линия является левой.

Величина перемещения вдоль оси винтовой линии, соответствующая одному полному обороту вокруг оси, называется шагом, а длина дуги, соответствующая полному обороту точки вокруг оси, — витком. Если величина перемещения точки вдоль оси прямо пропорциональна угловым перемещениям, то винтовая линия имеет постоянный шаг. Если перемещение образующей точки вдоль оси происходит по своему закону, то получается винтовая линия с переменным шагом.

Угол наклона касательной, проведенной в некоторой точке винтовой линии к плоскости, перпендикулярной оси, называется углом подъема винтовой линии.

В зависимости от вида поверхности, по которой происходит перемещение образующей точки, винтовые линии подразделяются на цилиндрические, конические и глобоидные винтовые линии.

15.2.2. Цилиндрическая винтовая линия

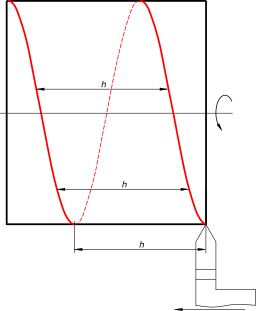
Цилиндрическая винтовая линия или гелиса образуется при движении точки по поверхности кругового цилиндра (рис. 15.7). Диаметр цилиндра D и размер шага h являются параметрами цилиндрической винтовой линии.

При равномерном перемещении точки по поверхности цилиндра она совершает сложный вид движения, состоящего из вращательного движения по окружности и поступательного перемещения, перпендикулярного этой окружности. При повороте на некоторый угол точка А переместится в точку А1, а величина ее поступательного перемещения вдоль оси будет равна

h 360,

где h — шаг цилиндрической винтовой линии.

При этом ее горизонтальная проекция будет перемещаться по окружности, а фронтальная — по синусоиде.

Построение фронтальной проекции цилиндрической винтовой линии проводится аналогично построению синусоиды (рис. 15.8). Окружность основания цилиндра на горизонтальной плоскости проекций делится на n равных частей (например, на двенадцать). Отрезок оси цилиндра, равный шагу h винтовой линии, делится на то же количество n равных частей. Фронтальные проекции точек, лежащих на винтовой линии, находятся в пересечении горизонтальных и вертикальных прямых, проведенных через соответствующие точки деления.

Пространственные кривые	425

Рис. 15.7. Цилиндрическая винтовая линия	Рис. 15.8. Построение цилиндрической
	винтовой линии

На горизонтальной проекции точка при ее подъеме вращается против часовой стрелки, следовательно, построенная цилиндрическая винтовая линия является правой.

Основные свойства цилиндрической винтовой линии:

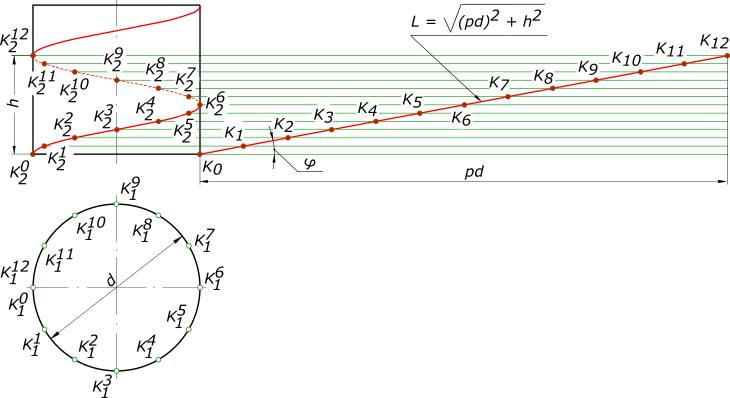
на плоскость проекций, перпендикулярную оси, цилиндрическая винтовая линия проецируется в окружность; на плоскость проекций, параллельную оси, — в синусоиду;

 угол подъема цилиндрической винтовой линии с постоянным шагом h не изменяется и может быть определен по формуле

h arctg D ;

винтовая линия пересекает все образующие цилиндра под постоянным углом, равным 90 – ;

кривизна и кручение цилиндрической винтовой линии во всех ее точках постоянны;

цилиндрическая винтовая линия обладает симметрией переноса в направлении по ее оси на расстояние, равное шагу; при этом две симметричные дуги полностью совпадают при наложении друг на друга.

15.2.3. Коническая винтовая линия

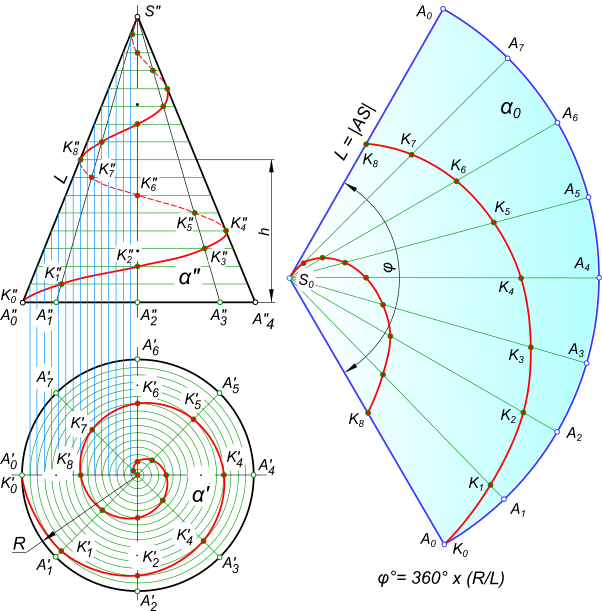
Коническая винтовая линия образуется при движении точки по поверхности кругового конуса. При этом точка совершает равномерное поступательное движение по образующей конуса, которая в свою очередь равномерно вращается вокруг оси конуса (рис. 15.9). Размеры конуса (например, диаметр его основания D и высота H), а также размер шага h являются параметрами конической винтовой линии. Иногда шагом конической винтовой линии называют расстояние h1 между точками смежных витков, измеренное по образующей.

Рис. 15.9. Коническая винтовая линия

Для построения проекций конической винтовой линии окружность основания конуса делится на n равных частей (например, на двенадцать), и через точки деления проводятся образующие конуса (рис. 15.10). На оси винтовой линии откладывается отрезок, равный ее шагу h, который делится на то же количе-

Пространственные кривые	427

ство n равных частей. В пересечении горизонтальных прямых, проведенных из точек деления шага, с соответствующими образующими конуса находятся фронтальные проекции точек, принадлежащих искомой винтовой линии. По фронтальным проекциям этих точек строятся их горизонтальные проекции.

Рис. 15.10. Построение конической винтовой линии

На горизонтальной проекции точка при ее подъеме вращается по часовой стрелке, следовательно, построенная коническая винтовая линия является левой.

Основные свойства конической винтовой линии:

на плоскость проекций, перпендикулярную оси, коническая винтовая линия проецируется в архимедову спираль; на плоскость проекций, параллельную оси, — в синусоиду с затухающей амплитудой;

угол подъема конической винтовой линии, имеющей постоянный шаг, не изменяется;

коническая винтовая линия пересекает все образующие под одинаковым углом.

Источник

: Категория: В; Просмотров: 2001

ВИНТОВАЯ ЛИНИЯ м. б. построена следующим образом: берем плоский прямоугольник с основанием 2πа и проводим из его нижней вершины наклонную прямую под углом δ к основанию (например, диагональ); если навернуть этот прямоугольник на круглый цилиндр с радиусом основания а так, чтобы основание прямоугольника совпало с окружностью основания цилиндра, то наклонная прямая обратится в пространственную кривую, которая составит один виток или ход винтовой линии. Ось цилиндра называется осью винтовой линии. Винтовая линия пересекает все образующие цилиндра под одинаковыми углами, благодаря чему называется локсодромией для данного цилиндра.

Винтовая линия — кратчайшее расстояние между точками цилиндра, т. е. геодезическая линия. Винтовая линия пересекает какую-либо одну образующую цилиндра бесконечное число раз; расстояние h по образующей между двумя смежными пересечениями, т. е. высота хода, называется шагом винтовой линии. Уравнения винтовой линии в параметрической форме:

где k = a·tg δ; h = 2πk (а, k, h — постоянные). Винтовая линия есть траектория точки, движение которой составляется из двух равномерных движений: вращательного — по кругу радиуса а и поступательного — в направлении, перпендикулярном к плоскости этого круга; параметр ϕ есть угол поворота этого вращения. Радиусы кривизны винтовой линии постоянны, причем радиус первой кривизны = (a²+k²)/a и радиус второй кривизны = (a²+k²)/k.

В механике винтовая линия имеет важное значение, т. к. (по теореме Шаля) всякое перемещение твердого тела из одного положения в другое м. б. получено одним винтовым движением. Как следствие этой теоремы, всякое движение твердого тела в бесконечно малый промежуток времени м. б. рассматриваемо как винтовое, т. е. как одновременное вращение и скольжение относительно некоторой прямой (оси винта), называемой мгновенной осью вращения и скольжения.

Источник: Мартенс. Техническая энциклопедия. Том 3 — 1928 г.

Источник

Винтовая линия

15.2.1. Свойства винтовых линий

15.2.2. Цилиндрическая винтовая линия

15.2.3. Коническая винтовая линия

Не пропустите также: