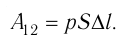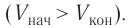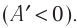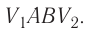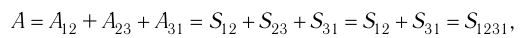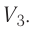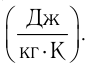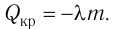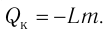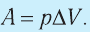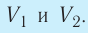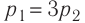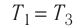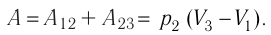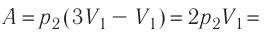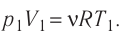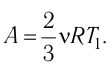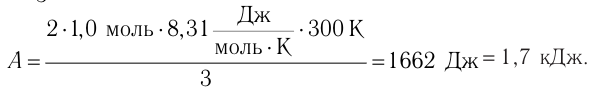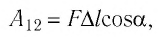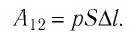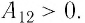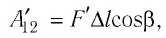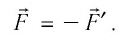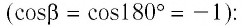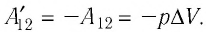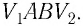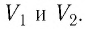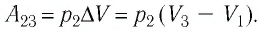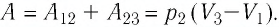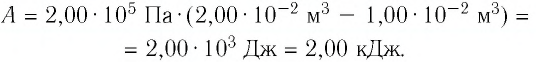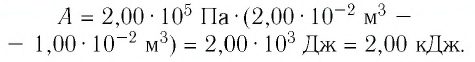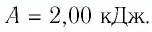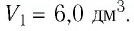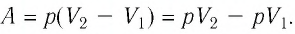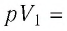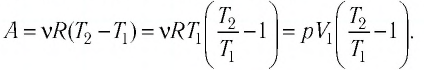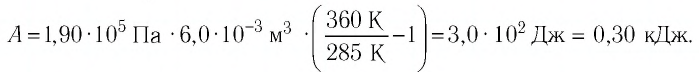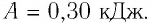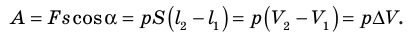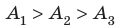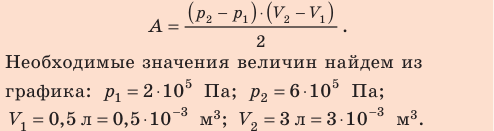Е
сли
изменение
задано
в виде графика
,
то работа выражается криволинейным
интегралом
.
Графически этот интеграл равен площади
криволинейной трапеции
,
которую можно заменить суммой площадей
трапеций равных
,
то есть
.
1 3.1.7 Теоремы о работе силы:
Теорема
1:
Работа
равнодействующей силы
на
некотором перемещении равна алгебраической
сумме работ составляющих сил на этом
же перемещении
.
Теорема
2:
Работа
постоянной
по модулю и направлению силы
на результирующем перемещении равна
алгебраической сумме работ этой силы
на соответствующих перемещениях
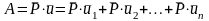
Следствие
1:Работу
постоянной силы на криволинейном
перемещении можно заменить работой на
прямолинейном перемещении.
Следствие
2:
В случае замкнутого контура перемещения
и работа постоянной силы равна нулю.
13.1.8 Работа сил приложенных к вращающемуся телу
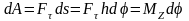
.
Элементарная
работа силы приложенной к вращающемуся
телу равно произведению момента
относительно оси вращения на элементарный
угол
.
Работа
момента относительно оси вращения при
повороте на угол φ
равна
.
Если
,
то
.
Если
значение
задано в виде графика, то работа может
быть определена графически аналогично
работе силы.
13.2 Мощность. Коэффициент полезного действия
13.2.1
Мощностью
называют скалярную величину равную
работе совершаемую силой в единицу
времени.
.
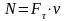
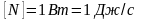
736
Вт=75кГм/с.
Работу,
произведенную машиной, измеряют
произведением мощности на время
.
.
Мощность,
развиваемая моментом силы (пары сил)
равна
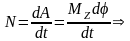

13.2.2
Коэффициентом полезного действия
(КПД) системы (механизма, машины, агрегата
и т.д.) за некоторый промежуток времени
называют отношение совершенной полезной
работы к затраченной работе сил,
действующих на систему. Это средний
КПД
за этот промежуток времени.
.
Мгновенный
КПД равен:
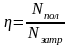
13.3 Кинетическая энергия
13.3.1
Кинетической энергией материальной
точки
называется скалярная величина равная
половине произведения массы точки на
квадрат ее скорости
,
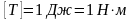
Теорема
об изменении кинетической энергии
материальной точки:
Изменение кинетической энергии
материальной точки при некотором ее
перемещении равно алгебраической сумме
работ всех действующих на точку сил на
этом же перемещении.
.
Следствие
1:
При несвободном движении точки с любыми
связями N:
.
Следствие
2:
В случае идеально гладкой поверхности
реакции связей N
перпендикулярны к траектории движения
точки и

.
Следствие
3:
Этим выражением можно пользоваться и
в случае шероховатых связей. Для этого
в число активных сил включают силы
трения.
13.3.2
Кинетической энергией материальной
системы
называют скалярную величину равную
сумме кинетических энергий всех точек
системы
.
Если
система состоит из нескольких тел, то
ее кинетическая энергия равна сумме
кинетических энергий этих тел.
13.3.3
Формулы для определения кинетической
энергии твердых тел
определяются видом их движения.
Поступательное
движение:
,
где
М — масса тела;
—
скорость любой
точки тела.
Вращение
вокруг неподвижной оси Z:
,
где
— момент инерции тела относительно оси
вращения Z;
—
угловая скорость тела.
Плоское
движение:
,
где
— скорость центра масс тела;
—
момент инерции тела относительно оси
проходящей через центр масс перпендикулярно
плоскости движения.
При
плоском движении тела его кинетическая
энергия равна сумме поступательного
движения всех его точек со скоростью
центра масс и вращения вокруг центра
масс.
13.3.4
Теорема об изменении кинетической
энергии системы:
Изменение кинетической энергии системы
при некотором ее перемещении равно
сумме работ всех внешних и внутренних
сил действующих на систему при этом
перемещении.
.
Частные
случаи:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
| Механическая работа, или работа постоянной силы (скалярная величина) |
(A = vec{F} · Deltavec{r}), ((1)) где произведение векторов силы (vec{F}) и перемещения (Deltavec{r}) является скалярным. (A = FDelta rcosalpha), ((2)) где (alpha) — угол между направлениями (vec{F}) и (Deltavec{r}) |
| Единицы работы | [(A)] (= 1 Н · 1 м =1 Дж) |
|
Работа силы — аддитивная физическая величина (получаемая суммированием) |
Если на физический объект действует (N) сил (vec{F}_1, vec{F}_2)… (vec{F}_N), то (A = sumlimits_{i = 1}^{N}vec{F}_i · Deltavec{r}). ((3)) Например, на тело действуют силы тяжести (vec{F}_т), реакции опоры (vec{N}) и трения скольжения (vec{F}_{тр}), тогда работа результирующей всех сил при перемещении тела равна (A = (vec{F}_т + vec{F}_{тр} + vec{N}) · Deltavec{r}) ((4)) |
| Работа переменной силы |
Если сила, совершающая работу по перемещению тела, изменяется, то траектория движения объекта разбивается на такие участки, где значение силы постоянно и работа силы на данном участке вычисляется по формуле: (A_k = F_kDelta r_kcosalpha_k). ((5)) Работа силы на всей траектории вычисляется через суммирование по (k)-м участкам: (A = sumlimits_kA = sumlimits_kvec{F}_k · Deltavec{r}_k = sumlimits_kF_kDelta r_kcosalpha_k) ((6)) |
| Геометрическая интерпретация механической работы |
Работа постоянной силы вычисляется как площадь (S) фигуры (рис. (1)) в координатах ((F_x), (Delta r)), где (F_x = Fcosalpha). Рис. (1). Графическое представление работы силы |
| Мощность |
Средняя мощность: (P_{ср} = frac{A}{Delta t}), ((7)) где (Delta t) — конечный временной интервал совершения работы. Мгновенная мощность (мощность): (P = limlimits_{Delta tto 0}frac{A}{Delta t} = limlimits_{Delta tto 0}frac{vec{F} · Deltavec{r}}{Delta t} = limlimits_{Delta tto 0}vec{F} · frac{Deltavec{r}}{Delta t} = vec{F} · vec{v},) ((8)) где (vec{v}) — вектор мгновенной скорости, символ (limlimits_{Delta tto 0}) — обозначение математического предела |
| Единицы мощности | [(P)] (= frac{1 Дж}{1 с} = 1 Вт) |
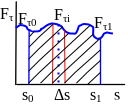
13.1.6 Графический способ вычисления работы силы
Е
сли
изменение
задано
в виде графика
,
то работа выражается криволинейным
интегралом
.
Графически этот интеграл равен площади
криволинейной трапеции
,
которую можно заменить суммой площадей
трапеций равных
,
то есть
.
1 3.1.7 Теоремы о работе силы:
Теорема
1:
Работа
равнодействующей силы
на
некотором перемещении равна алгебраической
сумме работ составляющих сил на этом
же перемещении
.
Теорема
2:
Работа
постоянной
по модулю и направлению силы
на результирующем перемещении равна
алгебраической сумме работ этой силы
на соответствующих перемещениях
Следствие
1:Работу
постоянной силы на криволинейном
перемещении можно заменить работой на
прямолинейном перемещении.
Следствие
2
:
В случае замкнутого контура перемещения
и работа постоянной силы равна нулю.
13.1.8 Работа сил приложенных к вращающемуся телу
.
Элементарная
работа силы приложенной к вращающемуся
телу равно произведению момента
относительно оси вращения на элементарный
угол
.
Работа
момента относительно оси вращения при
повороте на угол φ
равна
.
Если
,
то
.
Если
значение
задано в виде графика, то работа может
быть определена графически аналогично
работе силы.
13.2 Мощность. Коэффициент полезного действия
13.2.1
Мощностью
называют скалярную величину равную
работе совершаемую силой в единицу
времени.
.
736
Вт=75кГм/с.
Работу,
произведенную машиной, измеряют
произведением мощности на время
.
.
Мощность,
развиваемая моментом силы (пары сил)
равна
13.2.2
Коэффициентом полезного действия
(КПД) системы (механизма, машины, агрегата
и т.д.) за некоторый промежуток времени
называют отношение совершенной полезной
работы к затраченной работе сил,
действующих на систему. Это средний
КПД
за этот промежуток времени.
.
Мгновенный
КПД равен:
13.3 Кинетическая энергия
13.3.1
Кинетической энергией материальной
точки
называется скалярная величина равная
половине произведения массы точки на
квадрат ее скорости
,
Теорема
об изменении кинетической энергии
материальной точки:
Изменение кинетической энергии
материальной точки при некотором ее
перемещении равно алгебраической сумме
работ всех действующих на точку сил на
этом же перемещении.
.
Следствие
1:
При несвободном движении точки с любыми
связями N:
.
Следствие
2:
В случае идеально гладкой поверхности
реакции связей N
перпендикулярны к траектории движения
точки и
.
Следствие
3:
Этим выражением можно пользоваться и
в случае шероховатых связей. Для этого
в число активных сил включают силы
трения.
13.3.2
Кинетической энергией материальной
системы
называют скалярную величину равную
сумме кинетических энергий всех точек
системы
.
Если
система состоит из нескольких тел, то
ее кинетическая энергия равна сумме
кинетических энергий этих тел.
13.3.3
Формулы для определения кинетической
энергии твердых тел
определяются видом их движения.
Поступательное
движение:
,
где
М — масса тела;
—
скорость любой
точки тела.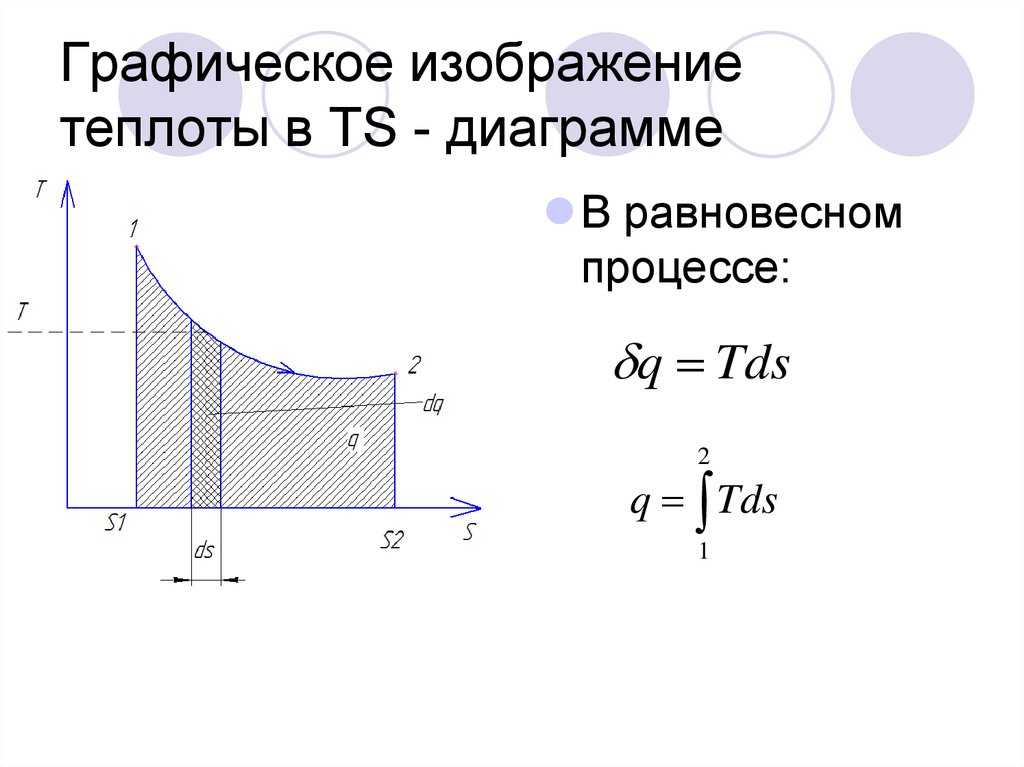
Вращение
вокруг неподвижной оси Z:
,
где
— момент инерции тела относительно оси
вращения Z;
—
угловая скорость тела.
Плоское
движение:
,
где
— скорость центра масс тела;
—
момент инерции тела относительно оси
проходящей через центр масс перпендикулярно
плоскости движения.
При
плоском движении тела его кинетическая
энергия равна сумме поступательного
движения всех его точек со скоростью
центра масс и вращения вокруг центра
масс.
13.3.4
Теорема об изменении кинетической
энергии системы:
Изменение кинетической энергии системы
при некотором ее перемещении равно
сумме работ всех внешних и внутренних
сил действующих на систему при этом
перемещении.
.
Частные
случаи:
Работа в термодинамике.

Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Работа в термодинамике.
|
Работа в термодинамике. |
|
|
В термодинамике движение тела как целого не рассматривается и речь идет о перемещении частей макроскопического тела относительно друг друга. При совершении работы меняется объем тела, а его скорость остается раной нулю. Носкорости молекул тела меняются! Поэтому меняется температура тела. Причина в том, что при столкновении с движущимся поршнем (сжатие газа) кинетическая энергия молекул изменяется — поршень отдает часть своей механической энергии. При столкновении с удаляющимся поршнем (расширение) скорости молекул уменьшаются, газ охлаждается. |
|
|
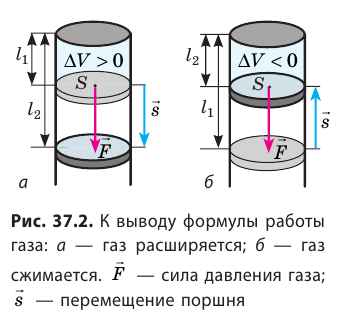
— сила, действующая на газ со стороны поршня. А — работа внешних сил по сжатию газа. — сила, действующая на поршень со стороны газа. А’ — работа газа по расширению. = — — по 3-ему з-ну Ньютона. Следовательно: А= — А’ = pS, где p— давление, S — площадь поршня. Если газ расширяется: Δh=h2 — h1 — перемещение поршня. V1=Sh1; V2=Sh2. |
|
|
Тогда: A’=F’Δh=pS(h2 — h1)=p(Sh2 — Sh1)=p(V2-V1)=pΔV |
|
|
При расширении работа газа положительна. A= — pΔV — работа внешних сил. |
|
|
Используя уравнение Менделеева-Клапейрона, получим: |
|
|
Эти выражения справедливы при очень малых (!) изменениях объема или при постоянном давлении (т.е. в изобарном процессе) |
|
|
Физический смысл универсальной газовой постоянной. — универсальная газовая постоянная численно равна работе 1 моля идеального газа при изобарном нагревании на 1 К. |
|
|
Геометрическое истолкование работы. |
|
|
В изобарном процессе площадь под графиком в координатах p,V численно равна работе (вспомните — перемещение на графике скорости!). |
|
|
В общем случае надо процесс разбить на малые части и сосчитать элементарные работы, а затем их сложить (процесс интегрирования): Например, в изотермическом процессе . |
|
|
В изохорном процессе объем не меняется, следовательно, в изохорном процессе работа не совершается! В адиабатном процессе . |
Теги:
конспект
Работа, выполненная на основе графиков сила-перемещение – Физика GCSE в Сент-Робертсе
Это навык продвинутого уровня, знания которого не требуются для GCSE по физике. Эта тема предназначена для того, чтобы обогатить ваше понимание того, как работает физика, и не будет рассматриваться.
Если мы построим силу , F , действующую на объект (ось Y) на расстояние , перемещенное , s , (ось X), мы построим график силы-перемещения .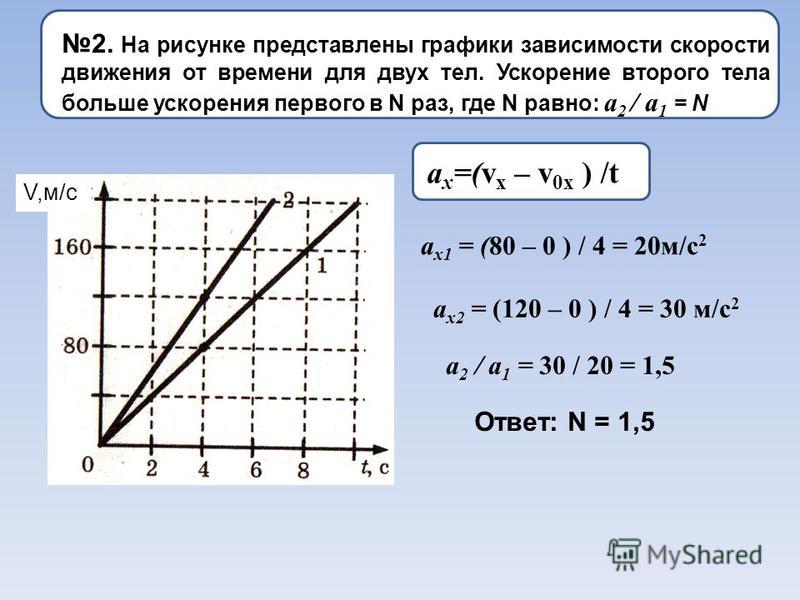
Постоянная сила
Когда сила, действующая на систему, постоянна, т.е. сила тяжести (вес объекта) или трение при движении с постоянной скоростью, график силы-перемещения представляет собой просто горизонтальную линию, потому что сила не изменяется.
В этом случае площадь под графиком представляет собой прямоугольник с основанием длиной s и высотой F. Площадь прямоугольника равна основанию x высоте, поэтому
Это знакомая нам формула механической работы, совершаемой постоянной силой.
Мы можем использовать этот метод для расчета работы, совершаемой при ускорении объекта из состояния покоя до конечной скорости v с использованием постоянной силы F. [Примечание: сила F вызывает ускорение a в соответствии со вторым законом Ньютона , F=ma].
При постоянном ускорении из состояния покоя пройденное расстояние можно записать через среднюю скорость v av ,
, а ускорение можно записать как
Итак, проделанная работа, W=Fs,
Это просто знакомое уравнение для кинетической энергии, запасенной в движущемся объекте.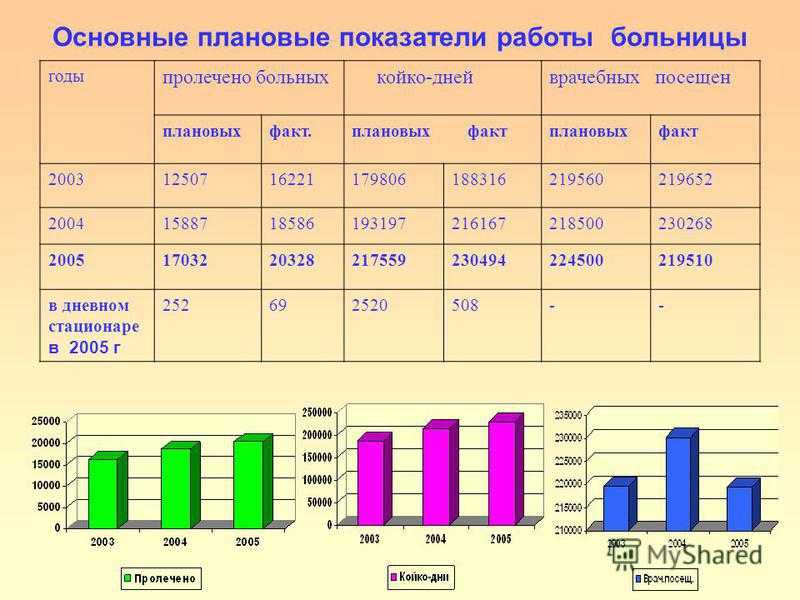
Непостоянная сила
Преимущество использования графика силы-перемещения для определения проделанной работы состоит в том, что метод также дает правильный ответ, когда сила непостоянна.
Хорошим примером является нахождение работы при растяжении пружины. В этом случае сила непостоянна, потому что согласно закону Гука
восстанавливающая сила равна постоянной пружины, умноженной на растяжение (смещение), поэтому чем больше вы растягиваете пружину, тем больше сила. В этом примере смещение является расширением, поэтому, если мы нанесем эту функцию на график силы-смещения, мы получим
. В этом случае площадь под графиком образует треугольник, поэтому мы используем формулу для площади треугольника ( 1/2 х основание х высота), чтобы рассчитать проделанную работу.
Это знакомое уравнение для энергии, запасенной в растянутой пружине, потому что работа, выполняемая для растяжения пружины, должна быть равна энергии, запасенной в пружине за счет сохранения энергии .
Mathematical link
Причина, по которой мы можем найти работу, выполненную из площади под графиком силы-перемещения, заключается в том, что общая формула для работы, совершаемой любой системой, задается интегралом ,
.
где переменная интегрирования x — смещение. Значение любого определенного интеграла равно площади под графиком функции, которую вы интегрируете, в данном случае F. Таким образом, найти площадь под графиком силы-перемещения — это то же самое, что вычислить интеграл выше! Вот почему мы всегда можем найти проделанную работу как площадь под графиком сила-перемещение.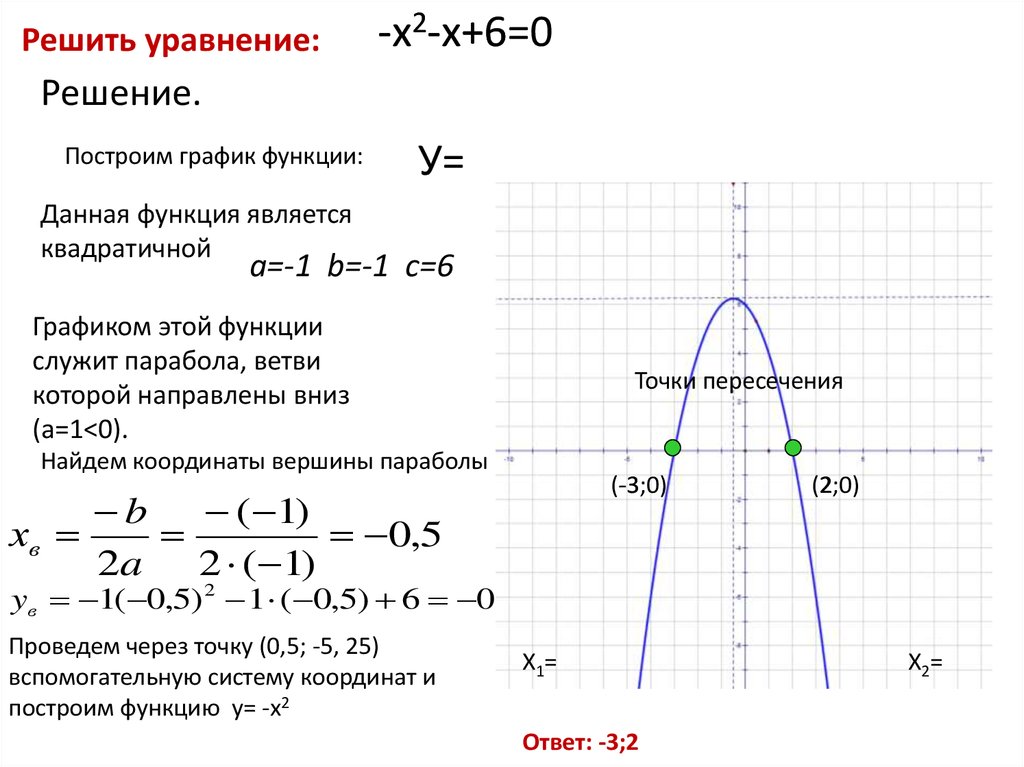
Для постоянной силы F сила может быть вынесена за пределы интеграла, поэтому
Где s — расстояние, пройденное параллельно действию силы.
Для непостоянной силы нам нужно интегрировать силу, которая в примере силы пружины представляет собой простое полиномиальное интегрирование,
, где e — расширение.
Нравится:
Нравится Загрузка…
График силы и положения: изображение и наклон
В каком из этих сценариев вы выполняете больше работы: изо всех сил вытаскиваете свой нелепо полный мусорный бак на обочину дороги и не сдвигаете его ни на дюйм… или поднимаете в воздух единственный карандаш? Теперь ваша мама может заставить вас вынести мусор независимо от того, но оказывается, что, используя определение работы в физике, мы можем доказать, что вы выполняете больше работы в сценарии с карандашом, чем в сценарии с мусорным ведром. Сумасшедший, верно? В этой статье описывается взаимосвязь между силой и позицией и их отношение к работе.
А какой самый интересный способ показать взаимосвязь между двумя физическими принципами природы, такими как сила и положение? Да, вы уже догадались: графики! К концу этой статьи вы еще не насытитесь чудесами, которые предлагают графики зависимости силы от положения.
Отношения силы и положения
Прежде чем мы погрузимся во все самое интересное с графиками (я просто чувствую ваше волнение), мы должны рассмотреть ключевое определение: прямо пропорциональные отношения.
Чтобы две вещи имели прямо пропорциональное отношение , их отношение должно быть равно постоянному значению.
Это определение пригодится вам, когда вы продолжите чтение, особенно когда вы перейдете к разговорам о пружинных константах. Когда вы туда доберетесь, подумайте о том, что означает, что сила и положение имеют прямо пропорциональные отношения. Если (k) — это наклон нашего графика зависимости силы от положения, а также константа, что это означает для связи между силой и положением?
Интерпретация силы и положения
Одним из основных навыков в физике, который необходимо развивать, является нахождение взаимосвязей.
Площадь под графиком зависимости силы от положения
Площадь под графиком зависимости силы от положения равна работе, совершаемой силой над любым смещаемым объектом. Вспомните уравнение
$$W = F Delta x$$
, который описывает проделанную работу, которую вы изучили в AP Physics 1.
Обратите внимание, что работа является просто произведением силы и положения. Распознавание этой взаимосвязи облегчает понимание площади графика зависимости силы от положения. Площадь под кривой равна работе, потому что интеграл графика будет связывать силу с положением объекта. Следовательно, более сложное уравнение для работы можно получить, применяя интегрирование следующим образом: 9{vec b} vec{F}cdot mathrm{d}vec{r}$$
где (W) — выполненная работа, (vec a) и (vec b ) — ваше начальное и конечное положения, а (vec F) — сила как функция положения (vec r).
Рис. 1. Здесь площадь под кривой зависимости силы от положения заштрихована и обозначена как работа.
Обратите внимание, что уравнение работы включает вычисление скалярного произведения двух векторов.
Скалярное произведение — это операция, используемая для векторов, равная произведению величин векторов на косинус угла между ними.
Выражаясь математически, скалярное произведение равно
$$vec{A} cdot vec{B} = A B cos{theta},$$
, где (vec A) и ( vec B) — наши два вектора, (A) и (B) — их величины, а (theta) — угол между ними.
На рис. 1 выше показан график зависимости силы от смещения с постоянным наклоном. Итак, что происходит, когда наша сила не постоянна, а у нас переменный наклон? Давайте проиллюстрируем эту возможность, а также включим наш сценарий мусорного бака и карандаша.
Твоя мама просит тебя вынести мусор. После нескольких секунд попыток сдвинуть массивный жестяной бак вы сдаетесь, так и не двигая его вообще.
Давайте начнем наше решение с построения графика зависимости силы от положения для нашего карандашного сценария.
Рис. 2. Площадь (синяя) под этой кривой от (0,000,mathrm{m}) до (0,750,mathrm{m}) дает нам общую работу, которую вы выполняете над карандашом .
Хорошо, теперь, когда у нас есть лучшее представление о том, что происходит в этой задаче, мы углубимся в наше решение. 92 \ &+1,00,mathrm{N}(0,750,mathrm{m}) — 0,mathrm{J} \ &= 1,03,mathrm{J}. \ end{align*}$$
Таким образом, мы делаем (1.03,mathrm{J}) больше работы с карандашом, чем с мусорным ведром. Мы также заключаем, что площадь под кривой на рисунке выше равна (1,03,mathrm{J}).
Сила и положение Наклон
Помните, мы говорили, что вся физика заключается в поиске взаимосвязей? Давайте посмотрим, сможем ли мы найти взаимосвязь между силой и положением, которая объяснит наклон графика зависимости силы от положения.
Сила в зависимости от положения Наклон Значение
Наклон равен подъему по ходу; таким образом, наклон нашего графика будет выглядеть примерно так:
$$frac{F}{Delta x}\mathrm{.}$$
Это уравнение звонит в колокола? Это формула для жесткости пружины (k), которая появляется в законе Гука .
Закон Гука связывает силу, действующую на пружину, с ее смещением, умноженным на константу, которая количественно определяет растяжимость этой конкретной пружины (k).
Математически записанный закон Гука выглядит примерно так:
$$F_text{пружина}=-kx,$$
где (F_text{пружина}) — величина силы пружины и (х) — расстояние пружины от равновесия.
Это означает, что график зависимости силы от положения, относящийся к влиянию смещения на силу пружины, будет иметь жесткость пружины, которую можно рассчитать по формуле
$$k = frac{F}{Delta х}\mathrm{.}$$
Рис. 3. Обратите внимание, что переменная (k) умножается на (x), чтобы показать, что (k) — это наклон.
Наклон графика зависимости силы от положения постоянен, как видно на рис. 2 выше, когда мы ссылаемся на пружины и закон Гука: в этом конкретном случае наклон нашего графика сила-перемещение постоянен и равен константе пружины. (к). Однако при обобщении наклона графика зависимости силы от смещения наклон не обязательно должен быть постоянным. Например, (F(x)) может быть переменной силой, описываемой уравнением более высокого порядка, а это означает, что наклон нашего графика может следовать более параболической или кубической траектории. Поэтому, в общем смысле, мы должны сказать, что наклон графика зависимости силы от положения является его производной, которая может иметь приложения для многих других физических сценариев: постоянная пружины (k) является лишь одним примером в случае, если сила прямо пропорциональна перемещению.
Следовательно, мы можем переписать наше уравнение для «переменной жесткости пружины» (k_text{variable}) в новом свете, используя наши знания о производных:
$$k_text{variable}=frac {mathrm{d}}{mathrm{d}x}F(x).
Приведенное выше уравнение переводится как «(k_text{variable}) равно производной нашей силы, совершающей работу, совершаемую с относительно нашего смещения (x).»
Пристальный взгляд на (k)
Для идеальных пружин (k) не является переменной величиной, а является константой, зависящей от внутренних характеристик пружины.
Рис. 4. Когда пружина расширяется или сжимается (смещает некоторую величину (x) от равновесия), прилагаемая сила изменяется; константа (k) количественно определяет эластичность пружины.
График на рис. 4 более подробно рассматривает значение жесткости пружины (k). Когда пружина смещает некоторую величину (x) из равновесия, восстанавливающая сила пытается оттянуть ее назад (обозначается зеленой стрелкой (F_text{s})). Сила, действующая на пружину, заставляющая ее смещаться, представлена фиолетовой стрелкой (F). Постоянная пружины (k) — это эластичность пружины, она количественно определяет, насколько трудно нашим двум силам сместить пружину или, другими словами, изменить (x).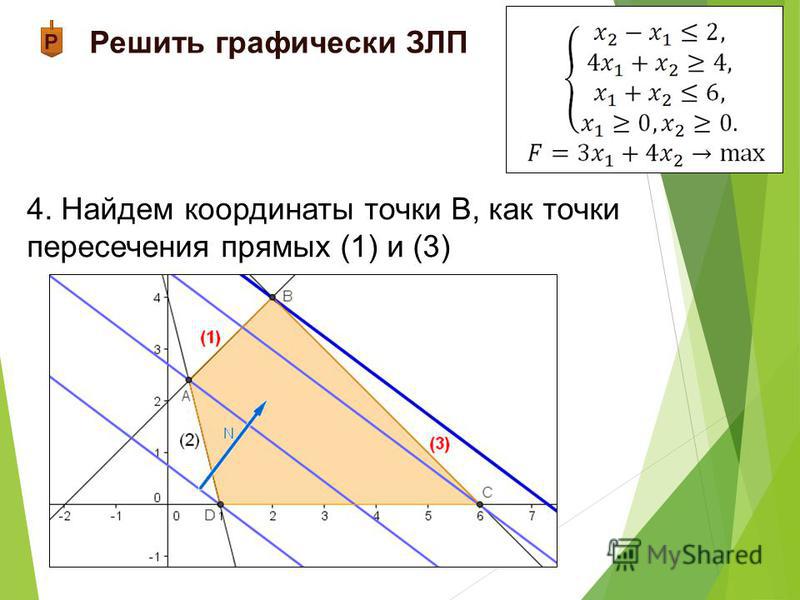
Единицы наклона силы и положения
С помощью аналогичного процесса можно найти единицы измерения наклона графика зависимости силы от положения. Начните с нашего рабочего уравнения,
$$frac{F}{Delta x}\mathrm{,}$$
и поймите, что единицами измерения силы являются ньютоны, а для положения – метры:
$ $mathrm{frac{N}{m}\}mathrm{.}$$
Эти единицы имеют большой логический смысл. Учитывая, что (k) является жесткостью пружины, тот факт, что ее единицами измерения являются ньютоны на метры, показывает, что ее можно найти, вычислив силу на единицу длины. Это придает упругость пружине. Напомним, что ньютоны равны 9.2}\}mathrm{.}$$
Если пойти еще дальше, мы увидим, как жесткость пружины связана с поверхностным натяжением. Поверхностное натяжение определяется путем приложения силы к длине, и оно выражается в килограммах на секунды в квадрате, как и константа пружины.
График зависимости силы от положения и скорости
Графики зависимости силы от положения дают нам достаточно информации, чтобы найти скорость объекта.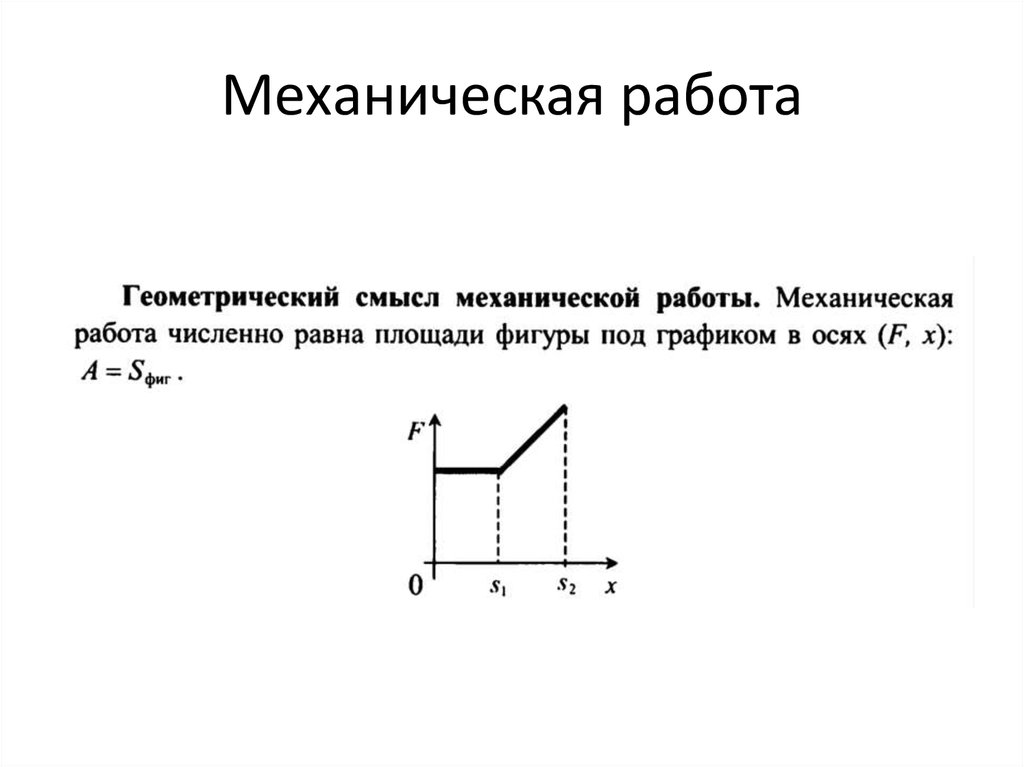
Помните, что теорема о работе и энергии утверждает, что работа, совершаемая силой над объектом, равна изменению кинетической энергии этого объекта.
Горизонтальная сила действует на объект массой (10,0,mathrm{kg}). Этот объект находится в состоянии покоя со смещением (x = 0,00,mathrm{m}). Затем он продолжается по горизонтали, пока не достигнет позиции (5.00,mathrm{m}) вдали от того места, где он начался и остановился. Сила, действующая на объект в зависимости от положения, приведена ниже. 92$$
настроены, давайте решим это символически,
$$v=sqrt{frac{2W}{m}\}mathrm{,}$$
, прежде чем мы подставим любые числа.
Выглядит хорошо. Теперь мы подключим и пыхтем,
$$sqrt{frac{2times 12,5,mathrm{N,m}}{10,0,mathrm{kg}}\} = 1,58, mathrm{frac{m}{s}\}mathrm{,}$$
, чтобы получить ответ:
$$v = 1,58,mathrm{frac{m}{s}\ }mathrm{.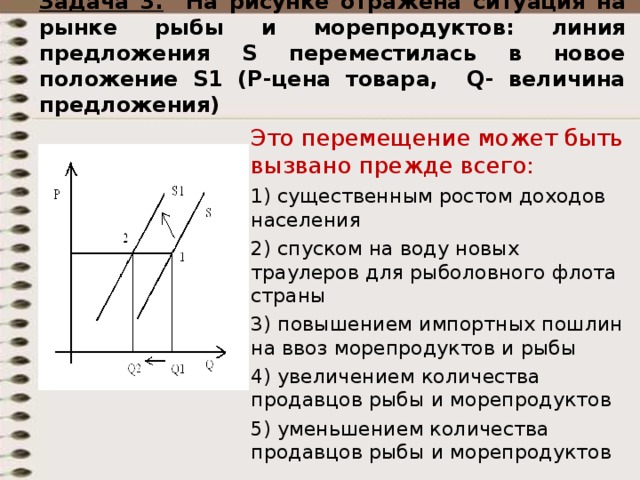
Наш ответ для скорости объекта равен (1,58) метрам в секунду.
Итак, теперь, когда ваша мама говорит вам вынести мусор, скажите ей, что вы могли бы сделать больше работы, просто подняв карандаш (то есть, если вы действительно не переместите мусорное ведро).
Графики силы и положения – ключевые выводы
- Чтобы две вещи имели прямо пропорциональную связь , они должны взаимно приносить пользу друг другу. Это означает, что по мере увеличения одного увеличивается и другой; когда один уменьшается, другой делает то же самое.
- Площадь под графиком зависимости силы от положения равна работе, совершаемой силой над любым смещаемым объектом. 9{vec b} vec{F}cdot mathrm{d}vec{r}.$$
- Скалярное произведение — это операция, используемая для векторов, которая по существу является их умножением. Он дает значение, которое показывает, насколько параллельны два вектора. Выражаясь математически, скалярное произведение равно $$vec{A} cdot vec{B} = A B cos{theta}mathrm{.
Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.
Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:
U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV
i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.
Изменение внутренней энергии идеального газа в изопроцессах
| Основная формула |
ΔU=32·mMRT=32νRT=32νR(T2−T1) |
| Изотермический процесс |
ΔU=0 Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной. |
| Изобарное расширение |
ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV |
| Изохорное увеличение давления |
ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp |
| Произвольный процесс |
ΔU=32νR(T2−T1)=32(p2V2−p1V1) |
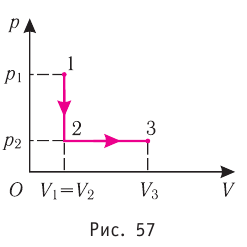
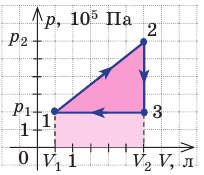
Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?
Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.
Работа идеального газа
Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.
Механическая работа вычисляется по формуле:
A=Fscosα
Перемещение равно разности высот поршня в конечном и начальном положении:
s=h2−h1
Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:
Работа идеального газа
F=pS
p — давление газа, S — площадь поршня
Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:
A‘=p(V2−V1)=pΔV>0
Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.
Работа идеального газа при изобарном сжатии:
A‘=p(V2−V1)=pΔV<0
Работа идеального газа при нагревании газа:
A‘=νRΔT=νR(T2−T1)=mMνRΔT
Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.
Геометрический смысл работы в термодинамике
В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).
Примеры графических задач
| Изобарное расширение:
A‘=p(V2−V1) A‘>0 |
 |
| Изобарное сжатие:
A‘=p(V2−V1) A‘<0 |
 |
| Изохорное охлаждение:
V=const A‘=0 |
 |
|
Изохорное охлаждение и изобарное сжатие: 1–2: A‘=0 2–3: A‘=pΔV<0 |
 |
| Замкнутый цикл:
1–2: A‘>0 2–3: A‘=0 3–4: A‘<0 4–1: A‘=0 A‘=(p1−p3)(V2−V1) |
 |
| Произвольный процесс:
A‘=p1+p22(V2−V1) |
 |
Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A2 к A1 в этих процессах.
Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:
A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV
A1=p(V2−V1)=p(5V−V)=4pV
Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.
Задание EF17505

Для каждой величины подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Определить по графику, как меняется давление.
- Определить, как меняется объем.
- Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.
Решение
На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.
Ответ: 123
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17966
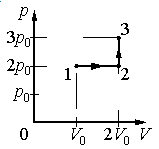
Ответ:
а) р0V0
б) 2р0V0
в) 4р0V0
г) 6р0V0
Алгоритм решения
1.Определить, на каком участке графика совершается работа.
2.Записать геометрический смысл работы.
3.Извлекая данные из графика, вычислить работу, совершенную газом.
Решение
Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.
Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).
Давление газа при этом равно 2p0, а объем равен разности 2V0 и V0. Следовательно, работа, совершенная газом, будет равна произведению:
A=2p0(2V0−V0)=2p0V0
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15.1k
Содержание:
Работа в термодинамике:
В 9 классе вы узнали, что работа силы (механическая работа) связана с превращением одного вида энергии в другой, например, механической энергии во внутреннюю. Работу силы рассматривают как меру изменения энергии физической системы. А как определить работу в термодинамике? Как может быть выражена эта работа через макроскопические параметры — давление и об1
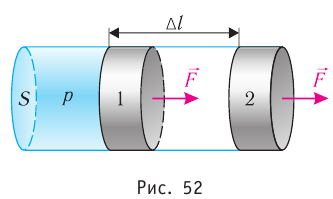
Рассмотрим газ, находящийся в цилиндрическом сосуде с площадью основания S, закрытом подвижным поршнем (рис. 52).
Взаимодействие газа с поршнем, а также со стенками сосуда можно характеризовать давлением р, которое газ оказывает на них. Допустим, что в результате изобарного расширения газа поршень переместился из положения 1 в положение 2 на расстояние
Модуль силы давления газа, действующей на поршень, F = pS. Эта сила совершает работу по перемещению поршня
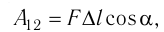
где а — угол между направлениями силы и перемещения. В рассматриваемом примере а = 0, тогда
Произведение 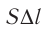
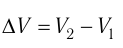
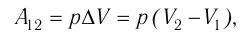
где 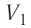
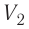
Так как давление р газа всегда величина положительная, из формулы (10.2) следует, что, если газ расширяется 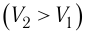
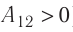
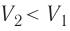
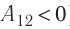
Процесс медленного изобарного сжатия газа из состояния 2 с начальным объёмом 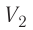
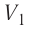
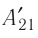
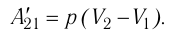
Из сравнения равенств (10.2) и (10.3) вытекает соотношение между работой 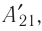
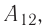
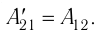
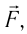
направление, противоположное силе давления 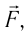
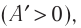
Если газ расширяется 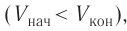
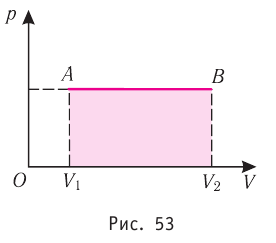
Геометрическое толкование работы
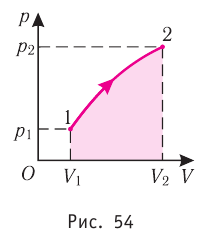
Построим график зависимости давления газа от его объёма при р = const. Как видно из рисунка 53, при изобарном расширении газа работа, совершённая силой давления газа, численно равна площади прямоугольника
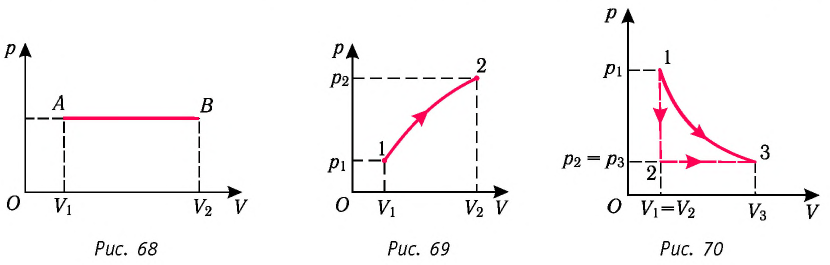
Если процесс перехода газа из начального состояния в конечное не является изобарным, то работа, совершённая силой давления газа при изменении его объёма от 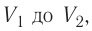
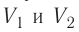
Процесс, при котором термодинамическая система, прошедшая некоторую последовательность состояний, снова возвращается в исходное состояние, называют циклическим процессом или циклом (рис. 55). Работа, совершаемая системой при циклическом процессе, или работа цикла, равна площади фигуры, ограниченной линиями, которые изображают цикл:
где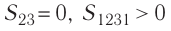
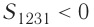
Если «кривая расширения» (изобара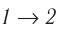
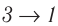
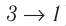
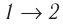
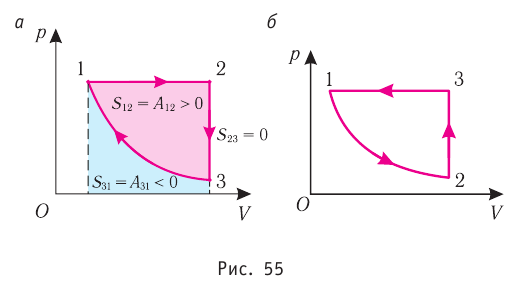
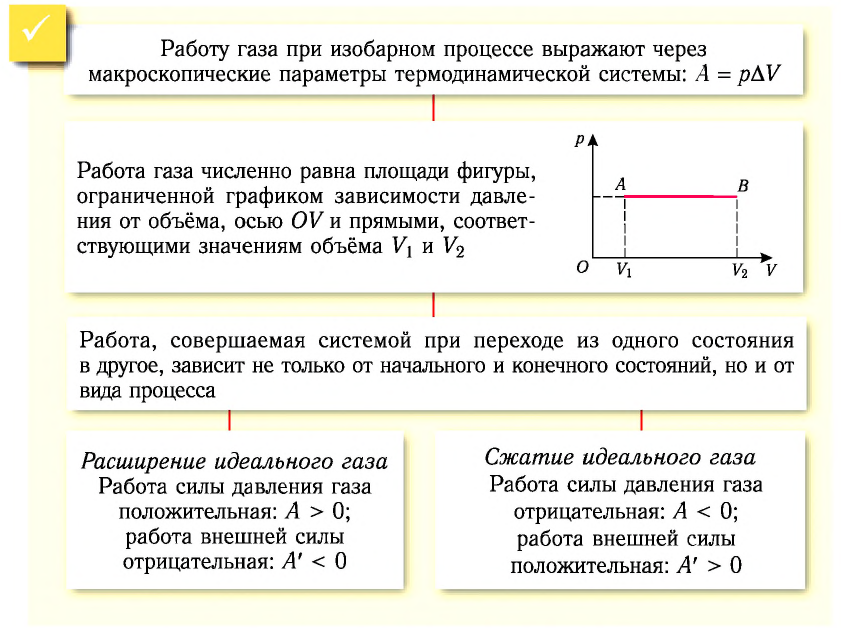
Из рисунка 56 видно, что численное значение работы цикла определяется не только начальным и конечным состояниями системы, но и видом процесса. Например, газ из состояния 1 можно перевести в состояние 3 либо в результате изотермического расширения, либо сначала изохорно понизив его давление до значения 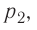
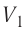
Как видно из рисунка 56, в первом случае работа, совершённая силами давления газа, больше, чем во втором. Следовательно, работа, совершаемая при переходе термодинамической системы из одного состояния в другое, зависит не только от начального и конечного состояний системы, но и от вида процесса.
Количество теплоты и удельная теплоёмкость
Итак, существуют два способа передачи энергии от одного тела к другому. Первый характеризуется передачей энергии в процессе механического взаимодействия тел — механическая энергия одного тела переходит в энергию хаотического движения частиц вещества другого тела или, наоборот, убыль энергии хаотического движения частиц вещества одного тела сказывается на увеличении механической энергии другого тела. Такую форму передачи энергии в термодинамике (как и в механике) называют работой. Так, например, в рассмотренной нами ранее термодинамической системе (газ в цилиндрическом сосуде под поршнем) расширение газа приводит к перемещению поршня. При этом убыль внутренней энергии газа равна работе, совершённой силой давления газа, под действием которой поршень переместился.
Второй способ передачи энергии осуществляется при непосредственном обмене энергией между хаотически движущимися частицами взаимодействующих тел. За счёт переданной при этом энергии увеличивается внутренняя энергия одного тела и уменьшается внутренняя энергия другого. Если, например, привести в соприкосновение два тела с разными температурами, то частицы более нагретого тела будут передавать часть своей энергии частицам более холодного тела. В результате внутренняя энергия первого тела уменьшается, а второго тела увеличивается. Процесс передачи энергии от одного тела к другому без совершения работы называют теплопередачей. Как вы уже знаете, существуют три вида теплопередачи: теплопроводность, конвекция и излучение.
Количественной мерой энергии, переданной телу в процессе теплопередачи, является количество теплоты Q. В СИ единицей количества теплоты является джоуль (Дж). Иногда для измерения количества теплоты используют внесистемную единицу — калорию (1 кал = 4,19Дж).
Если процесс теплопередачи не сопровождается изменением агрегатного состояния вещества, то
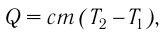
где m — масса тела, 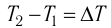
теплоемкость измеряют в джоулях, деленных на килограмм, кельвин
Физическая величина, равная произведению массы тела на удельную теплоёмкость вещества, носит название теплоёмкости тела. Обозначают теплоёмкость тела С и измеряют в джоулях на кельвин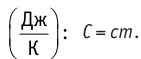
Удельная теплота плавления
Физическую величину, численно равную количеству теплоты, необходимому для превращения кристаллического вещества массой 1 кг, взятого при температуре плавления, в жидкость той же температуры, называют удельной теплотой плавления 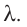
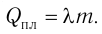
Удельная теплота парообразования
Физическую величину, численно равную количеству теплоты, которое необходимо передать жидкости массой 1 кг, находящейся при температуре кипения, для превращения её при постоянной температуре в пар, называют удельной теплотой парообразования L. Количество теплоты, необходимое для превращения жидкости массой m, предварительно нагретой до температуры кипения, в пар, определяют по формуле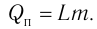
Удельная теплота сгорания топлива
Физическую величину, численно равную количеству теплоты, выделяющемуся при полном сгорании топлива массой 1 кг, называют удельной теплотой сгорания топлива q. Количество теплоты, выделившееся при полном сгорании некоторой массы m топлива, определяют по формуле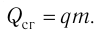
Отметим, что в результате теплопередачи могут изменяться как обе составляющие внутренней энергии тела, так и одна из них. При нагревании (охлаждении) изменяются кинетическая энергия хаотического движения частиц, которые составляют тело, и потенциальная энергия их взаимодействия. При плавлении (кристаллизации), кипении (конденсации) изменяется только потенциальная энергия взаимодействия частиц вещества.
При совершении работы также может изменяться как кинетическая, так и потенциальная энергия частиц вещества. Следовательно, как при теплопередаче, так и при совершении работы происходит изменение кинетической и потенциальной энергий частиц вещества, что приводит к изменению внутренней энергии тела.
1. Работу газа при изобарном процессе выражают через макроскопические параметры термодинамической системы:
2. Работа газа численно равна площади фигуры, ограниченной графиком зависимости давления от объёма, осью OV и прямыми, соответствующими значениям объёмов
3. Работа, совершаемая при переходе системы из одного состояния в другое, зависит не только от начального и конечного состояний, но и от вида процесса.
4. Процесс передачи энергии от одного тела к другому без совершения работы называют теплопередачей.
Пример №1
Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от 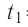
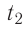
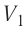
Дано:
Пример №2
Состояние идеального газа, взятого в количестве v=l,0 моль при температуре 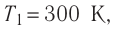
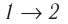
Дано:
v = 1,0 моль
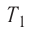
А — ?
Решение. Работа Л газа в ходе всего процесса равна сумме работ на участках 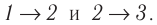
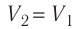
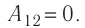
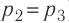
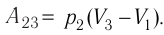
Так как по условию 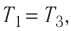
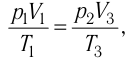
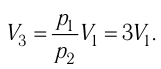
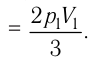
Тогда
Ответ: А = 1,7 кДж.
Работа в термодинамике
В 9-м классе вы узнали, что передача энергии путём совершения работы происходит в процессе силового взаимодействия тел. То есть работа, совершённая над рассматриваемым телом, есть не что иное, как работа сил, приложенных к этому телу со стороны всех остальных (внешних) тел, с которыми оно взаимодействует. Работа, совершённая над телом, может непосредственно изменить любой вид энергии этого тела, например внутреннюю энергию, поэтому работу силы рассматривают как меру изменения энергии физической системы.
Одним из способов изменения внутренней энергии термодинамической системы является совершение работы. Этот способ характеризуется передачей энергии в процессе механического взаимодействия тел. При этом механическая энергия одного тела переходит во внутреннюю энергию другого тела или, наоборот, убыль внутренней энергии одного тела сказывается на увеличении механической энергии другого тела.
Таким образом, при совершении работы происходит превращение энергии из одной формы в другую.
Поскольку для описания термодинамических систем используют макропараметры (давление, объём, температура), то работу в термодинамике необходимо выражать, применяя эти параметры.
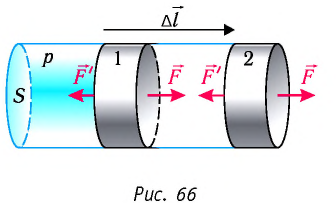
Рассмотрим газ в цилиндре, закрытом поршнем, площадь которого S (рис. 66). Давление газа в цилиндре 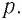
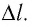
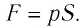
где 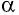
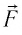
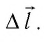
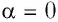
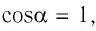
Произведение 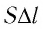
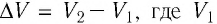
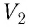
Таким образом, работа силы давления газа при его изобарном расширении:
Так как давление р газа — величина положительная, то из формулы (12.1) следует, что
При изобарном расширении газа из состояния 1 в состояние 2 работа силы 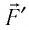
где 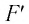
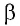
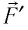
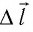
Перемещение 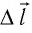
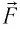
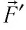
Следовательно, работы 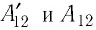
Таким образом, можно сделать следующие выводы.
Геометрическое толкование работы:
Работу газа можно определить графически. Изобразим график зависимости давления газа от его объёма при 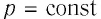
Если процесс перехода газа из начального состояния в конечное не является изобарным (рис. 69), то работа силы давления газа при изменении объёма от 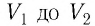
Работу газа определяют не только начальное и конечное состояния системы, но и вид процесса. Например, газ из состояния 1 можно перевести в состояние 3 либо в результате изотермического расширения (рис. 70), либо сначала изохорно понизив его давление до значения 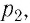
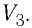
Следовательно, работа, совершаемая термодинамическом системой при переходе из одного состояния в другое, зависит не только от начального и конечного состояний системы, но и от вида процесса.
Пример №3
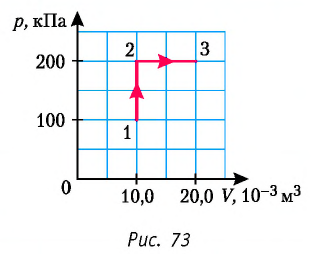
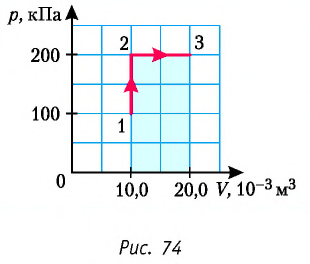
Определите работу, совершаемую силой давления идеального газа определённой 200 массы при переходе из состояния 1 в состояние 3 (рис. 73).
Решение. 1 способ. Работа А газа в ходе всего процесса равна сумме работ на участках 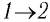
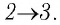
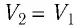
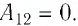
Тогда при переходе из состояния 1 в состояние 3 работа
2 способ. Работа газа численно равна площади заштрихованной фигуры, ограниченной графиком зависимости давления от объёма, осью OV и прямыми, соответствующими значениям объёма 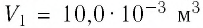
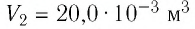
Ответ:
Пример №4
Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от 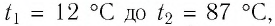
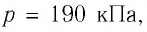
Решение. Сила давления газа совершает положительную работу, поскольку при изобарном нагревании увеличивается его объём. Поэтому
Согласно уравнению Клапейрона—Менделеева,
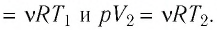
Ответ:
Как определить работу в термодинамике
В конце XVIII в. английский физик Бенджамин Томпсон (граф Румфорд) исследовал тепло, выделяющееся при сверлении бронзовых пушек. Румфорд успевал вскипятить поставленные на пушки котлы с водой за счет тепла, которое выделялось, пока лошади приводили в движение очень тупое сверло. В данном случае энергия механического движения сверла превращалась в энергию хаотического движения молекул бронзы и воды. А можно ли сделать наоборот?
Почему при изменении объема газа изменяется его внутренняя энергия
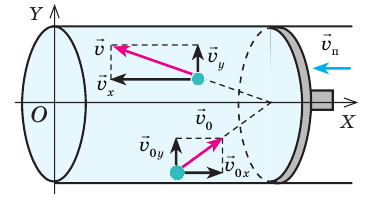
Внутренняя энергия газа может изменяться, если действующие на него внешние силы совершают работу (положительную или отрицательную). Например, если газ сжимают (газ совершает отрицательную работу) (рис. 37.1) и он при этом не отдает энергию окружающей среде, то скорость движения молекул газа, а соответственно, и внутренняя энергия, и температура газа увеличиваются. И наоборот: если газ расширяется (то есть совершает положительную работу), то скорость движения молекул, температура и внутренняя энергия газа уменьшаются.
Рис. 37.1. При сжатии газа скорость его молекул после столкновения с поршнем увеличивается (v > 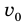
Как вычислить работу газа
Вычислим работу, которую совершает сила давления газа при изменении его объема от 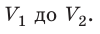
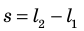
Таким образом, работа газа при его изобарном расширении равна:
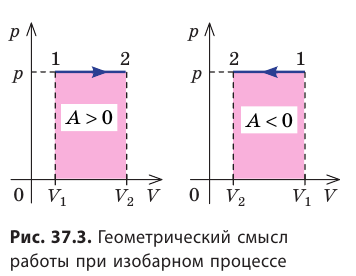
Работе газа при изобарном расширении (или сжатии) можно дать простое геометрическое толкование: работа газа численно равна площади прямоугольника под графиком зависимости p(V) (рис. 37.3).
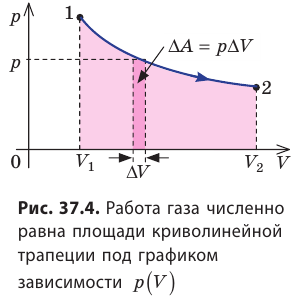
Пусть некоторый газ переходит из состояния 1 в состояние 2 (рис. 37.4). Если изменение объема газа (∆V) достаточно мало, то давление газа можно считать неизменным. Тогда работа газа численно равна площади выделенной на рисунке полосы. Полная работа при изменении объема от 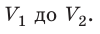
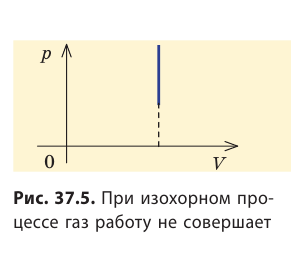
Очевидно, что при изохорном процессе (V = const) площадь фигуры под графиком зависимости p (V) равна нулю (рис. 37.5), — газ работу не совершает (A = 0) . Работа газа зависит от того, каким образом происходил переход газа из начального состояния в конечное (рис. 37.6).
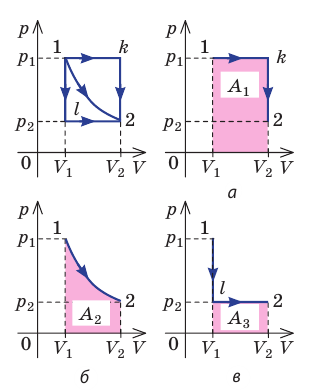
Рис. 37.6. три пути перехода газа из состояния 1 в состояние 2: а — газ изобарно расширяется (участок 1k), затем изохорно охла ждается (участок k2); б — газ изотермически расширяется; в — газ изохорно охлаждается (участок 1l), затем изобарно расширяется (участок l2). сравнив площади фигур под графиками, видим, что:
Пример №5
На рисунке графически изображен циклический процесс, совершаемый идеальным газом. Определите работу газа за цикл.
Решение:
Полная работа за цикл равна сумме работ, совершенных газом в ходе каждого процесса цикла. Работа газа в ходе процесса 1–2 численно равна площади трапеции, основания которой равны 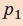
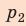
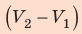
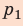
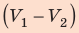
Выводы:
- При отсутствии теплообмена с окружающей средой, если над газом совершают работу, внутренняя энергия газа увеличивается; если газ сам совершает работу, его внутренняя энергия уменьшается.
- Если объем газа увеличивается, то газ совершает положительную работу. Если объем газа уменьшается, то работа газа отрицательна.
- Работа газа численно равна площади фигуры под графиком зависимости p (V). При изобарном процессе работу газа можно определить по формуле A=p∆V, при изохорном процессе работа газа равна нулю: A = 0.
- Первый закон термодинамики
- Второй закон термодинамики
- Тепловые двигатели и их КПД
- Тепловое состояние тел
- Термодинамика — основные понятия, формулы и определения
- Необратимость тепловых процессов
- Адиабатический процесс
- Молекулярно-кинетическая теория



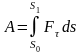
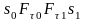

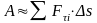

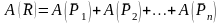




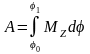
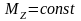
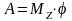

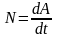




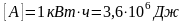

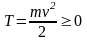
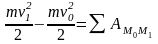


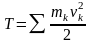


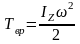
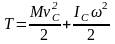
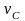
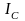
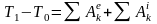

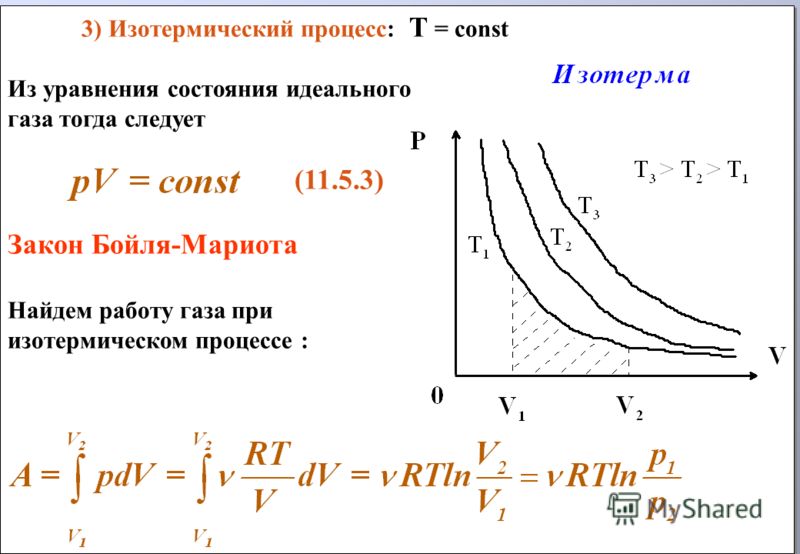
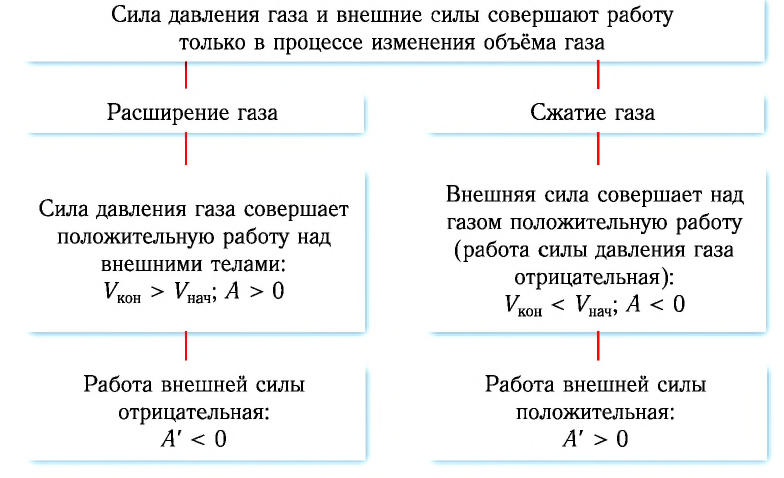
 При совершении работы в термодинамике меняется состояние макроскопических тел: их объем и температура.
При совершении работы в термодинамике меняется состояние макроскопических тел: их объем и температура.
 При сжатии — отрицательна. Таким образом: A’ = pΔV — работа газа
При сжатии — отрицательна. Таким образом: A’ = pΔV — работа газа