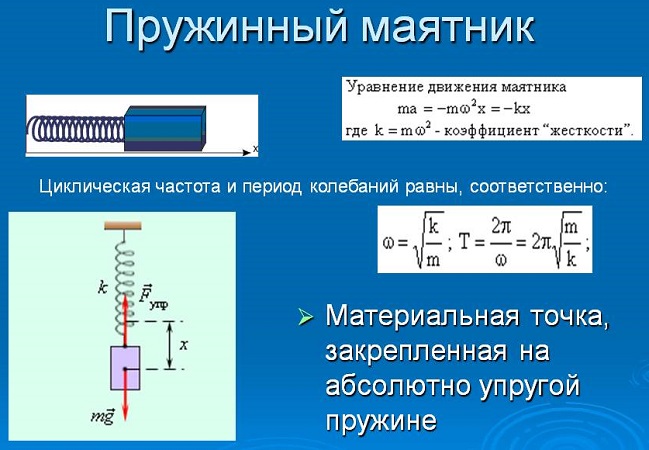
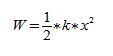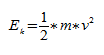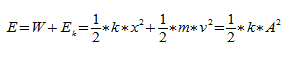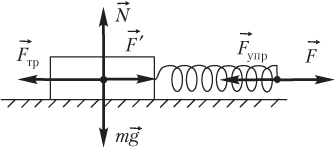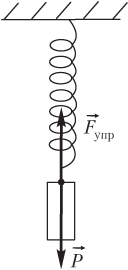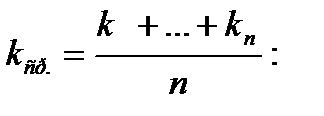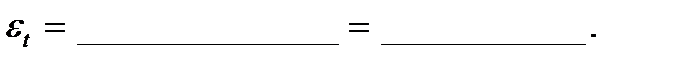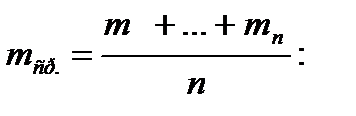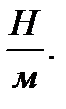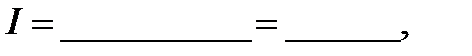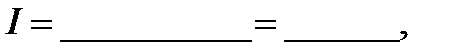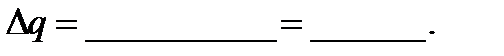Пружинный маятник как найти коэффициент жесткости

Пружинный маятник .

Пружинный маятник представляет из себя груз на пружине.

(T=2 pi sqrt{dfrac{m}{k}} )

(k) — жесткость пружины маятника

(m) — масса груза

Задача 1.

Показать ответ
Показать решение
Видеорешение

Задача 2.

Показать ответ
Показать решение
Видеорешение

Задача 3.

Показать ответ
Показать решение
Видеорешение

Задача 4.

Найти массу груза пружинного маятника, если его период ( T=1 с )
, а коэффициент жесткости пружины ( k=400 Н/м ; )
(pi=3,14 ).
Ответ округлить до целых.

Показать ответ
Показать решение
Видеорешение

Задача 5.

Найти массу груза пружинного маятника, если его период ( T=0,3 с )
, а коэффициент жесткости пружины ( k=350 Н/м ; )
(pi=3,14 ).
Ответ округлить до десятых.

Показать ответ
Показать решение
Видеорешение

Задача 6.

Найти массу груза пружинного маятника, если его период ( T=0,07 с )
, а коэффициент жесткости пружины ( k=150 Н/м ; )
(pi=3,14 ).
Ответ округлить до сотых.

Показать ответ
Показать решение
Видеорешение

Задача 7.

Найти коэффициент жесткости пружины пружинного маятника, если его период ( T=0,07 с )
, а масса груза ( m=0,0186 кг )
(pi=3,14 ).
Ответ округлить до целых.

Показать ответ
Показать решение
Видеорешение

Задача 8.

Найти коэффициент жесткости пружины пружинного маятника, если его период ( T=0,32 с )
, а масса груза ( m=0,8 кг )
(pi=3,14 ).
Ответ округлить до целых.

Показать ответ
Показать решение
Видеорешение

Задача 9.

Найти коэффициент жесткости пружины пружинного маятника, если его период ( T=0,6 с )
, а масса груза ( m=4 кг )
(pi=3,14 ).
Ответ округлить до целых.

Показать ответ
Показать решение
Видеорешение

Задача 10.

Показать ответ
Показать решение
Видеорешение

Задача 15.

Показать ответ
Показать решение
Видеорешение

Задача 16.

Показать ответ
Показать решение
Видеорешение

Задача 25.

Показать ответ
Показать решение
Видеорешение

Задача 30.

Показать ответ
Показать решение
Видеорешение

Рано или поздно при изучении курса физики ученики и студенты сталкиваются с задачами на силу упругости и закон Гука, в которых фигурирует коэффициент жесткости пружины. Что же это за величина, и как она связана с деформацией тел и законом Гука?

Сила упругости и закон Гука

Для начала определим основные термины, которые будут использоваться в данной статье. Известно, если воздействовать на тело извне, оно либо приобретет ускорение, либо деформируется. Деформация — это изменение размеров или формы тела под влиянием внешних сил. Если объект полностью восстанавливается после прекращения нагрузки, то такая деформация считается упругой; если же тело остается в измененном состоянии (например, согнутом, растянутом, сжатым и т. д. ), то деформация пластическая.

Примерами пластических деформаций являются:

• лепка из глины;
• погнутая алюминиевая ложка.

В свою очередь, упругими деформациями будут считаться:

• резинка (можно растянуть ее, после чего она вернется в исходное состояние);
• пружина (после сжатия снова распрямляется).

В результате упругой деформации тела (в частности, пружины) в нем возникает сила упругости, равная по модулю приложенной силе, но направленная в противоположную сторону. Сила упругости для пружины будет пропорциональна ее удлинению. Математически это можно записать таким образом:

F = — k·x;

где F — сила упругости, x — расстояние, на которое изменилась длина тела в результате растяжения, k — необходимый для нас коэффициент жесткости. Указанная выше формула также является частным случаем закона Гука для тонкого растяжимого стержня. В общей форме этот закон формулируется так: «Деформация, возникшая в упругом теле, будет пропорциональна силе, которая приложена к данному телу». Он справедлив только в тех случаях, когда речь идет о малых деформациях (растяжение или сжатие намного меньше длины исходного тела).

Определение коэффициента жесткости

Коэффициент жесткости (он также имеет названия коэффициента упругости или пропорциональности) чаще всего записывается буквой k, но иногда можно встретить обозначение D или c. Численно жесткость будет равна величине силы, которая растягивает пружину на единицу длины (в случае СИ — на 1 метр). Формула для нахождения коэффициента упругости выводится из частного случая закона Гука:

k = F/x.

Чем больше величина жесткости, тем больше будет сопротивление тела к его деформации. Также коэффициент Гука показывает, насколько устойчиво тело к действию внешней нагрузки. Зависит этот параметр от геометрических параметров (диаметра проволоки, числа витков и диаметра намотки от оси проволоки) и от материала, из которого она изготовлена.

Единица измерения жесткости в СИ — Н/м.

Расчет жесткости системы

Встречаются более сложные задачи, в которых необходим расчет общей жесткости. В таких заданиях пружины соединены последовательно или параллельно.

Последовательное соединение системы пружин

При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:

1/k = 1/k1 + 1/k2 + … + 1/ki,

где k — общая жесткость системы, k1, k2, …, ki — отдельные жесткости каждого элемента, i — общее количество всех пружин, задействованных в системе.

Параллельное соединение системы пружин

В случае когда пружины соединены параллельно, величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:

k = k1 + k2 + … + ki.

Измерение жесткости пружины опытным путем — в этом видео.

Вычисление коэффициента жесткости опытным методом

С помощью несложного опыта можно самостоятельно рассчитать, чему будет равен коэффициент Гука. Для проведения эксперимента понадобятся:

• линейка;
• пружина;
• груз с известной массой.

Последовательность действий для опыта такова:

1. Необходимо закрепить пружину вертикально, подвесив ее к любой удобной опоре. Нижний край должен остаться свободным.
2. При помощи линейки измеряется ее длина и записывается как величина x1.
3. На свободный конец нужно подвесить груз с известной массой m.
4. Длина пружины измеряется в нагруженном состоянии. Обозначается величиной x2.
5. Подсчитывается абсолютное удлинение: x = x2-x1. Для того чтобы получить результат в международной системе единиц, лучше сразу перевести его из сантиметров или миллиметров в метры.
6. Сила, которая вызвала деформацию, — это сила тяжести тела. Формула для ее расчета — F = mg, где m — это масса используемого в эксперименте груза (переводится в кг), а g — величина свободного ускорения, равная приблизительно 9,8.
7. После проведенных расчетов остается найти только сам коэффициент жесткости, формула которого была указана выше: k = F/x.

Примеры задач на нахождение жесткости

Задача 1

На пружину длиной 10 см действует сила F = 100 Н. Длина растянутой пружины составила 14 см. Найти коэффициент жесткости.

1. Рассчитываем длину абсолютного удлинения: x = 14—10 = 4 см = 0,04 м.
2. По формуле находим коэффициент жесткости: k = F/x = 100 / 0,04 = 2500 Н/м.

Ответ: жесткость пружины составит 2500 Н/м.

Задача 2

Груз массой 10 кг при подвешивании на пружину растянул ее на 4 см. Рассчитать, на какую длину растянет ее другой груз массой 25 кг.

1. Найдем силу тяжести, деформирующей пружину: F = mg = 10 · 9.8 = 98 Н.
2. Определим коэффициент упругости: k = F/x = 98 / 0.04 = 2450 Н/м.
3. Рассчитаем, с какой силой действует второй груз: F = mg = 25 · 9.8 = 245 Н.
4. По закону Гука запишем формулу для абсолютного удлинения: x = F/k.
5. Для второго случая подсчитаем длину растяжения: x = 245 / 2450 = 0,1 м.

Ответ: во втором случае пружина растянется на 10 см.

Видео

Из этого видео вы узнаете, как определить жесткость пружины.

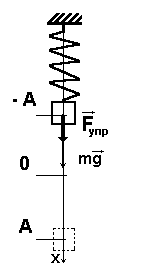
Пружинный маятник — колебательная система, которая состоит из тела, подвешенного к пружине. Эта система способна к совершению свободных колебаний.

Подобные системы довольно широко распространены за счет своей функциональной гибкости. Механизмы на основе таких маятников часто используются как элементы средств автоматики. 

В том числе они нашли применение в контактных взрывателях различных боеприпасов, в качестве акселерометров в контурах управления ракет. Так же они активно используются в предохранительных клапанах, устанавливаемых в трубопроводах.

Что такое пружинный маятник

Пружинным маятником в физике называют систему, совершающую колебательные движения под действием силы упругости. 

Приняты следующие обозначения:

• m — масса тела;

• k — коэффициент жесткости пружины.

Общий вид маятника:

Особенностями пружинных маятников являются:

1. Сочетание тела и пружины. Массой пружины обычно в расчетах пренебрегают. Роль тела могут играть различные объекты. На них оказывают действие внешние силы. Груз может крепиться разными способами. Витки пружины, которыми она начинается и заканчивается, изготавливают с учетом повышенной нагрузки;

2. У любой пружины есть исходное положение, предел сжатия и растяжения. При максимальном сжатии зазора между витками нет. Когда она максимально растянута, возникает необратимая деформация;

3. Полная механическая энергия появляется с началом процесса обратимого деформирования. В этот момент на объект не оказывает действие сила упругости;

4. Колебательные движения происходят под влиянием силы упругости. Масштаб влияния определяется несколькими причинами (тип сплава, расположение витков и т. д.). Так как может происходить и сжатие и растяжение, можно сделать вывод, что сила упругости действует в двух противоположных направлениях;

5. От массы тела, величины и направления прикладываемой силы зависит скорость в плоскости его перемещения. Например, если подвесить груз к пружине и, растянув её, отпустить, то груз будет перемещаться в двух плоскостях: вертикально и горизонтально.

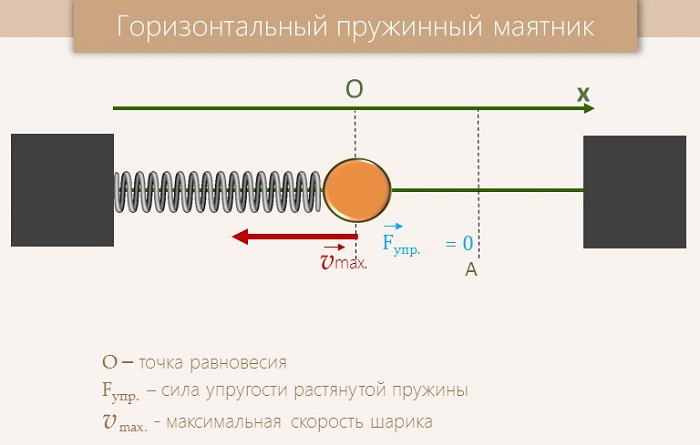
Виды пружинных маятников

Существует два типа данной системы:

1. Вертикальный маятник — на тело довольно сильно влияет сила тяжести. Это влияние обуславливает увеличение инерционных движений, которые совершает тело в исходной точке.

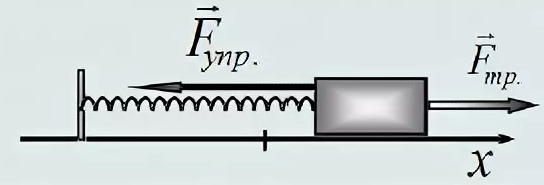
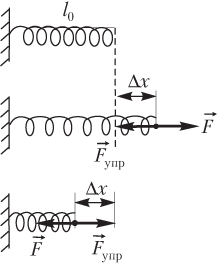
2. Горизонтальный — в таком варианте при движении на груз начинает действовать сила трения, возникающая по причине того, что груз лежит на поверхности.

Сила упругости в пружинном маятнике

До начала деформирования пружина находится в равновесном состоянии. Прикладываемое усилие может как растягивать, так и сжимать её. 

Применяя к пружинному маятнику закон сохранения энергии, мы можем рассчитать силу упругости в нем. Упругость прямо пропорциональна расстоянию, на которое сместился груз.

Расчёт силы упругости может быть проведен таким образом:

F_упр = — k*x

где k — коэффициент жесткости пружины (Нм),

x – смещение (м).

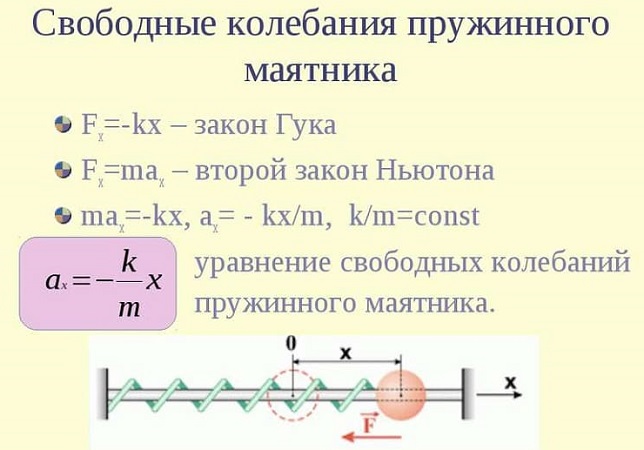
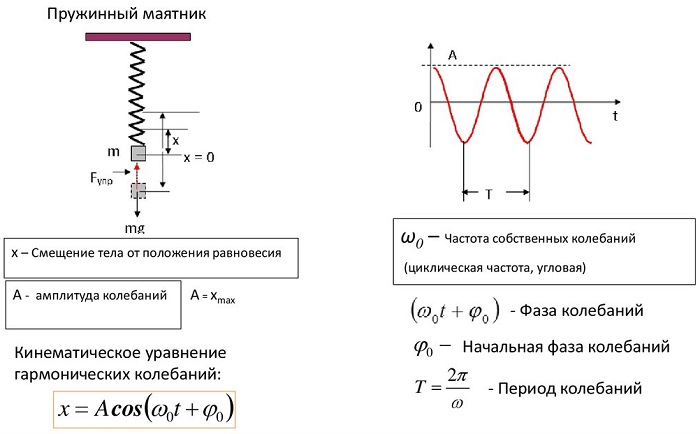
Уравнения колебаний пружинного маятника

Свободные колебания пружинного маятника описываются с помощью гармонического закона. 

Если допустить вероятность того, что колебания идут вдоль оси Х, и при этом выполняется закон Гука, то уравнение примет вид:

F(t) = ma(t) = — mw2x(t),

где w — радиальная частота гармонического колебания.

Для проведения расчета колебаний, учитывая все вероятности, применяют следующие формулы:

Период и частота свободных колебаний пружинного маятника

При разработке проектов всегда определяется период колебаний и их частота. Для их измерения используются известные в физике формулы.

Изменение циклической частоты покажет формула, приведенная на рисунке:

Факторы, от которых зависит частота:

1. Коэффициент упругости. На этот коэффициент влияет количество витков, их диаметр, расстояние между ними, длина пружины, жесткость используемого сплава и т. д.

2. Масса груза. От этого фактора зависит возникающая инерция и скорость перемещения.

Амплитуда и начальная фаза пружинного маятника

Учитывая начальные условия и рассчитав уравнение колебаний, можем точно описать колебания пружинного маятника. 

В качестве начальных условий используются: амплитуда (А) и начальная фаза колебаний (ϕ).

Энергия пружинного маятника

При рассмотрении колебания тел учитывают, что груз движется прямолинейно. Полная механическая энергия тела в каждой точке траектории является константой и равняется сумме его потенциальной энергии и кинетической энергии.

Потенциальная энергия:

Кинетическая энергия:

Полная энергия:

Расчет имеет особенности. При его проведении нужно учитывать несколько условий:

1. Колебания проходят в двух плоскостях: вертикальной и горизонтальной.

2. В качестве равновесного положения выбирается ноль потенциальной энергии. Находясь в этом положении пружина сохраняет свою форму.

3. Влияние силы трения при расчете не учитывают.

Дифференциальное уравнение гармонических колебаний пружинного маятника 

Отметим, что пружинный маятник — это обобщенное определение. Скорость движения груза (тела) напрямую зависит от комплекса условий, в том числе приложенного к нему усилия.

Порядок выполнения работы

I. Определение коэффициента жесткости пружины k по удлинению пружины

1.
Подвесить к концу пружины держатель
(рис. 1).

Рис. 1

2.
Пользуясь зеркальной шкалой, заметить
начальное положение держателя l₀
(отсчет делают таким образом, чтобы
нижняя грань держателя совпала с его
зеркальным изображением) и записать
данные отсчета в таблицу 1.

3.
Постепенно нагружать держатель грузами
(их масса в граммах намаркирована на
них), записывая положение нижней грани
держателя l₁
для каждого значения растягивающей
силы, соответствующей общей массе m
грузов (масса держателя в m
не входит).

4.
Нагрузив держатель всеми грузами,
начинают их по одному снимать, записывая
в таблицу в обратном порядке снизу-вверх
соответствующее положение нижней грани
держателя l₂
для каждого значения m.

5.
Вычислить среднее арифметическое
величин l₁
и l₂
для каждой массы

l_ср


.

6.
Вычислить удлинение пружины для каждого
значения массы грузов вычитая l₀
из соответствующего l_ср

Δl

l_ср
– l₀.

Таблица
1

7.
Построить проходящий через начало
координат график зависимости удлинения
пружины Δl
от массы m
(рис. 2).

l

0
m

Рис.2

По нему определить
коэффициент жесткости пружины k


,
взяв значения m
и Δl
для любой точки усредненной прямой.

8.
Рассчитать погрешность определения
коэффициента жесткости по формуле

k

k.

Для
расчета погрешности следует использовать
те значения m
и Δl,
по которым рассчитывался коэффициент
жесткости, а в качестве Δ(Δl),
Δm
и Δg
взять
абсолютную погрешность измерения
удлинения и точности, с которыми задаются
массы грузов и ускорение свободного
падения. Результат расчета k
и погрешности его определения Δk
занести в таблицу 1, выполнив предварительно
соответствующее округление [3].

II. Определение коэффициента жёсткости k пружины по зависимости периода собственных колебаний пружинного маятника от массы груза

1. Поместить на
держатель груз. Значение массы груза с
держателем и результаты последующих
измерений занести в таблицу 2. Измерить
секундомером время 10 полных колебаний
маятника. Опыт повторить не менее 4 раз.
Найти среднее значение времени t_ср
10 полных колебаний и среднее значение
периода колебаний Т_ср,
гдеn

10, при расчетах оставляя на одну значащую
цифру больше, чем в результатах наблюдений.

2.
Подобные измерения провести для различных
значений грузов.

Таблица
2

Силы упругости возникают при деформации тел.

Вычисление силы упругости производится по закону Гука :

где k — коэффициент жесткости (упругости) пружины; Δ x = | l − l 0 | — абсолютная деформация (растяжения или сжатия) пружины, l 0 — длина пружины в недеформированном состоянии, l — длина растянутой (или сжатой) пружины.

Направление силы упругости F → упр (рис. 2.9) противоположно направлению силы, вызывающей деформацию:

Относительная деформация определяется отношением:

ε = Δ x l 0 или ε = Δ x l 0 ⋅ 100 % ,

где Δ x = | l − l 0 | — абсолютная деформация (растяжения или сжатия) пружины, l 0 — длина недеформированной пружины, l — длина растянутой (сжатой) пружины.

Коэффициент жесткости (упругости) k нескольких пружин одинаковой длины , но разной жесткости вычисляется для последовательного соединения по формуле (рис. 2.10)

1 k = 1 k 1 + 1 k 2 + . + 1 k N ;

где k 1 , k 2 , . k N — коэффициенты жесткости (упругости) этих пружин.

Коэффициент жесткости (упругости) k нескольких пружин одинаковой длины , но разной жесткости (рис. 10), вычисляется для параллельного соединения по формуле (рис. 2.11)

k = k 1 + k 2 + . + k N ,

где k 1 , k 2 , . k N — коэффициенты жесткости (упругости) этих пружин.

• для последовательного соединения N одинаковых пружин с коэффициентами жесткости (упругости) k 0 :

для параллельного соединения N одинаковых пружин с коэффициентами жесткости (упругости) k 0 :

Пример 16. При последовательном соединении трех пружин, коэффициенты жесткости которых относятся как 1 : 2 : 3, сила 12 Н вызвала растяжение системы на 4,0 см. Рассчитать коэффициенты жесткости указанных пружин.

Решение. Величина силы упругости, действующей на пружину, определяется формулой

F упр = k общ ∆ x ,

где k общ — коэффициент жесткости составной пружины; ∆ x — указанное в условии задачи растяжение пружины.

Величина силы упругости, с другой стороны, совпадает с величиной приложенной силы:

Значение данной силы и величина растяжения пружины под действием этой силы позволяют рассчитать коэффициент жесткости составной пружины:

k общ = F Δ x = 12 4,0 ⋅ 10 − 2 = 300 Н/м.

Для определения коэффициентов жесткости каждой пружины запишем их коэффициенты жесткости в следующем виде:

так как указанные коэффициенты по условию задачи соотносятся между собой как

k 1 : k 2 : k 3 = 1 : 2 : 3.

Для расчета величины k запишем формулу для коэффициента жесткости пружины, состоящей из трех последовательно соединенных пружин, и подставим в нее выражения k 1 , k 2 , k 3 :

1 k общ = 1 k 1 + 1 k 2 + 1 k 3 = 1 k + 1 2 k + 1 3 k = 11 6 k , или k общ = 6 k 11 .

Найденное ранее значение k общ = 300 Н/м позволяет рассчитать k = 550 Н/м.

Тогда коэффициенты жесткости каждой из пружин имеют значения:

k 2 = 2 k = 1100 Н/м;

k 3 = 3 k = 1650 Н/м.

Пример 17. Вычислить абсолютную деформацию пружины с коэффициентом жесткости 100 Н/м, присоединенной к бруску, лежащему на горизонтальной поверхности, в момент начала скольжения бруска по поверхности. Сила, вызывающая скольжение бруска, прикладывается к пружине. Коэффициент трения между бруском и поверхностью равен 0,1. Масса бруска составляет 1,0 кг.

Решение. На рисунке показаны силы, действующие на брусок.

Абсолютную деформацию пружины рассчитаем по формуле

где F упр = F — модуль силы упругости, возникающей в пружине (величина силы упругости равна величине приложенной силы); k — коэффициент жесткости пружины.

Со стороны пружины на брусок действует сила, модуль которой совпадает с силой упругости:

В момент начала скольжения величина силы трения равна силе, приложенной к бруску в направлении движения:

где µ — коэффициент трения; N = mg — модуль силы нормальной реакции опоры.

Поэтому величина силы упругости может быть вычислена по формуле

Из исходного уравнения следует, что величина деформации пружины в момент начала скольжения определяется выражением

Расчет позволяет определить ее значение:

Δ x = 0,1 ⋅ 1,0 ⋅ 10 100 = 10 − 2 м = 1,0 см .

Пример 18. Вычислить массу груза, подвешенного к пружине жесткостью 250 Н/м, если известно, что относительная деформация пружины составляет 25 %. Длину нерастянутой пружины считать равной 100 мм.

Решение. Проиллюстрируем условие задачи рисунком.

Сила упругости определяется формулой

где k — коэффициент жесткости (упругости) пружины; ∆ x = l − l 0 — абсолютная деформация пружины (величина ее растяжения под действием груза); l 0 — длина недеформированной пружины; l — длина пружины в деформированном состоянии.

Из определения относительной деформации

где ε = 0,25 — относительная деформация (в долях).

С учетом значения относительной деформации формула для вычисления силы упругости принимает вид:

F упр = k ε l 0 = 0,25 k l 0 .

С другой стороны, сила упругости, возникающая в пружине, численно равна весу тела, вызвавшего деформацию пружины:

где m — масса тела; g — модуль ускорения свободного падения.

Таким образом, имеем равенство

позволяющее вычислить массу груза, подвешенного к пружине:

m = 0,25 k l 0 g = 0,25 ⋅ 250 ⋅ 0,100 10 = 0,625 кг = 625 г .

I. Жесткость пружины

Что такое жесткость пружины?
Одним из важнейших параметров, относящимся к упругим изделиям из металла разного назначения, является жесткость пружины. Она подразумевает, насколько пружина будет устойчива к воздействию других тел и насколько сильно сопротивляется им при воздействии. Силе сопротивления равен коэффициент жесткости пружины.

На что влияет этот показатель?
Пружина – это достаточно упругое изделие, обеспечивающее передачу поступательных вращательных движений тем приборам и механизмам, в которых она находится. Надо сказать, что встретить пружину можно повсеместно, каждый третий механизм в доме оснащен пружиной, не говоря уже о количестве этих упругих элементов в приборах на производстве. При этом надежность функционирования этих приборов будет определяться степенью жесткости пружины. Эта величина, называемая коэффициентом жесткости пружины, зависит от усилия, которое нужно приложить, чтобы сжать или растянуть пружину. Распрямление пружины до исходного состояния определяется тем металлом, из которого она изготовлена, но не степенью жесткости.

От чего зависит данный показатель?
Такой простой элемент, как пружина, обладает массой разновидностей в зависимости от степени назначения. По способу передачи деформации механизму и форме выделяют спиральные, конические, цилиндрические и другие. Поэтому жесткость конкретного изделия определяется также и способом передачи деформации. Деформационная характеристика будет разделять пружинные изделия на пружины кручения, сжатия, изгиба и растяжения.

При использовании в приборе сразу двух пружин, степень их жесткости будет зависеть от способа крепления – при параллельном соединении в приборе жесткость пружин будет увеличиваться, а при последовательном – уменьшаться.

II. Коэффициент жесткости пружины

Коэффициент жесткости пружины и пружинных изделий – один из важнейших показателей, который определяет срок службы изделия. Для расчета коэффициента жесткости в ручную — существует несложная формула (см. рис. 1), а так же есть возможность воспользоваться нашим калькулятором пружин, который достаточно легко поможет произвести Вам все необходимые расчеты. Однако на срок эксплуатации всего механизма жесткость пружины будет влиять лишь косвенно – большее значение будут иметь другие качественные особенности прибора.

Цель работы: научиться опытным путем определять коэффициент жесткости пружины физического маятника.

Средства обучения:

· оборудование: физический маятник, штатив, секундомер, набор грузов известной массы;

· методические указания к выполнению лабораторной работы, калькулятор.

Ход выполнения лабораторной работы

Теоретическая часть

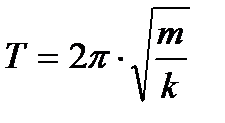
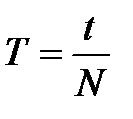
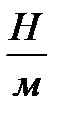
Период колебаний физического маятника можно рассчитать по формуле: (1), где (2); π=3,14; m – масса груза, а k – коэффициент жесткости пружины, [k]= .

Для увеличения точности измерений необходимо взять достаточно большое число полных колебаний (например, N=30, 40, 50).

Получим расчетную формулу для определения k:

→ → → → (3).

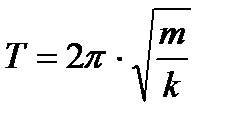
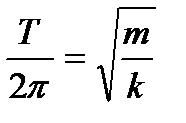
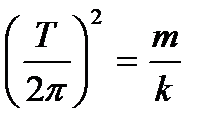
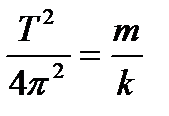
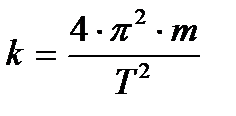
Для определения коэффициента жесткости пружины необходимо знать массу груза, подвешенного на пружине m и период колебаний – Т.

2. Вычисления и измерения

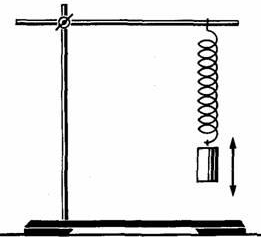
1. Закрепите физический маятник в штативе (к пружине подвесьте один груз известной массы) и приведите его в колебательное движение. Измерьте время t фиксированного числа полных колебаний N, рассчитайте период колебаний по формуле (2):

Опыт №1: ,

2. Зная массу груза, рассчитайте коэффициент жесткости пружины физического маятника k по формуле (3):

3. Повторите измерения и вычисления п.1-2, подвесив к пружине сначала два груза той же массы и оставив первоначальное число колебаний; а затем три груза той же массы, но изменив число колебаний маятника.

Опыт №2:

Опыт №3:

4. Вычислите среднее значение коэффициента жесткости пружины:

5. Результаты измерений и вычислений занесите в отчетную таблицу 1:

№

N

t, с

Т, с

tср, с

m, кг

mср, кг

k,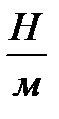

kср,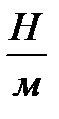

Δtср, с

εt

εm

εk

Δk,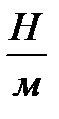

Таблица 1 –Результаты измерений и вычислений

6.

Рассчитайте абсолютную и относительную погрешности измерений:

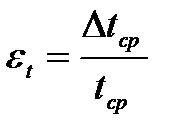
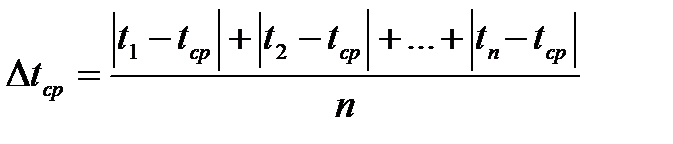
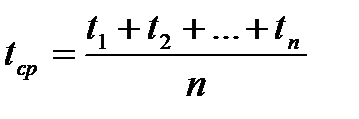
Относительная погрешность измерения времени: , где , и :

Относительная погрешность измерения массы груза: 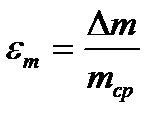; где

Относительная и абсолютная погрешности измерения k: ε_k=2ε_t+ε_m; Δk=k_ср∙ ε_k;

ε_k=______________________=____________, Δk=_________________=________

Окончательный результат запишите в виде: k_cр–Δk≤k≤ k_cр+Δk:

______________________ ≤k≤_____________________ .

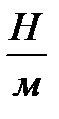
Обобщите результаты своей работы. Сделайте вывод по проделанной работе.

Вывод: ______________________________________________________________________

_____________________________________________________________________________

Контрольные вопросы

1. Как зависит период колебаний физического маятника от жёсткости пружины?

2. Зависит ли частота колебаний физического маятника от массы груза на пружине и от амплитуды колебаний?

3. Каким был бы результат опыта в условиях невесомости?

Ответы:

Лабораторная работа №14

Тема: «Определение заряда и электроемкости конденсатора»

Цель работы: определить опытным путем величину заряда конденсатора и рассчитать его электроемкость.

Средства обучения:

· оборудование: источник тока, ключ, мультиметр, конденсатор 4700мкФ, резистор 20кОм, секундомер;

· методические указания к выполнению лабораторной работы, калькулятор.

Ход выполнения лабораторной работы

Теоретическая часть

Электроемкость конденсатора — это отношение величины заряда, имеющегося на его обкладках, к напряжению на конденсаторе 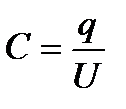(1). Следовательно, для определения электроемкости необходимо знать заряд и напряжение на конденсаторе, которое можно измерить с помощью мультиметра.

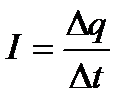
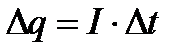
Заряд на обкладках появляется в процессе зарядки конденсатора, т. е. при протекании тока в электр. цепи. Т. к. сила тока – это заряд, протекающий через проводник в единицу времени, то величину заряда, прошедшего по цепи, можно найти, умножив силу тока на время: → (2).

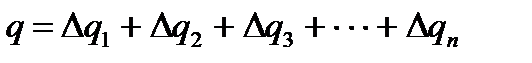
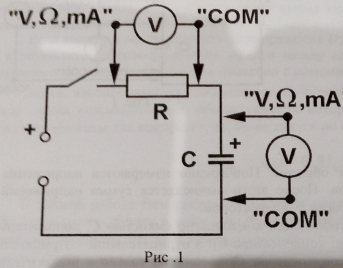
По мере зарядки конденсатора сила тока в цепи изменяется, поэтому для подсчета заряда весь период зарядки разбивают на малые интервалы времени Δt, в течение которых можно считать силу тока I постоянной. Величина заряда Δq, на которую изменился заряд конденсатора за Δt, рассчитывается по формуле (2). Просуммировав Δq, можно получить величину заряда конденсатора q: (3).

2. Вычисления и измерения

1. Соберите электрическую цепь по схеме, представленной на рис.1.

2. Переведите мультиметр в режим измерения постоянного напряжения. Установите диапазон 20 В.

3. Убедитесь в том, что конденсатор разряжен. Для этого подключите мультиметр к выводам конденсатора и убедитесь, что его показания равны нулю. Если это не так, замкните выводы конденсатора проводником на короткое время.

4. Подключите мультиметр параллельно сопротивлению R.

5. Замкните ключ и одновременно начните отсчет времени. Через каждые 15 с фиксируйте в табл.1 показания вольтметра на протяжении 3,5 минут зарядки конденсатора.

6. Спустя указанное время с начала зарядки разомкните ключ.

7. Отключите мультиметр от резистора и измерьте с его помощью напряжение U_к, до которого зарядился конденсатор: .

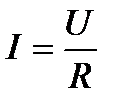
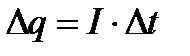
8. Используя закон Ома , рассчитайте силу тока в цепи и вычислите величины зарядов Δq, накапливаемые конденсатором каждые 15с: , Δt=15с:

1)

2)

3)

4)

5)

6)

7)

9)

10)

11)

12)

13)

14)

15)

9. Определите заряд qна обкладках конденсатора :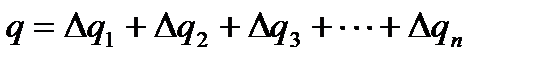

.

10. Рассчитайте электроемкость конденсатора : .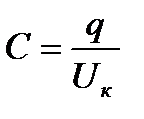

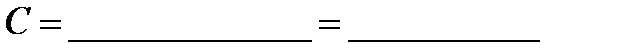
11. Сравните полученное значение электроемкости с величиной, указанной на конденсаторе: ________________________________________________________________________________.

12. Результаты измерений и вычислений занесите в отчетную таблицу 1.

3. Таблица 1 –Результаты измерений и вычислений

4.Обобщите результаты своей работы. Сделайте вывод по проделанной работе.

Вывод:___________________________________________________________________________________________________________________________________________________

Контрольные вопросы

1. Дайте определение конденсатора.

2. От чего зависит величина тока зарядки конденсатора?

3. Как вычислить электроемкость двух конденсаторов, соединенных последовательно?

4. Как рассчитать электроемкость трех конденсаторов, соединенных параллельно?

Ответы:

Лабораторная работа №15

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ – конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.