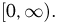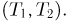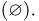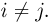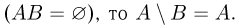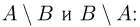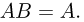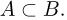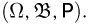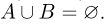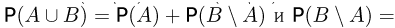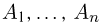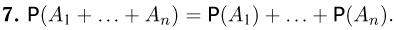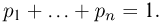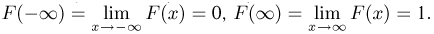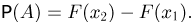События и операции над ними
Пространство элементарных исходов. Основным понятием теории вероятностей является множество всех возможных результатов
данного случайного эксперимента.
Определение 1. Пространством элементарных исходов
называется множество 
результаты данного случайного эксперимента.
Элементы множества 
и обозначаются буквой 
Отметим сразу, что любое непустое множество 
элементарных исходов какого-то случайного эксперимента.
Определение 2.
Событиями называются подмножества множества 
Говорят, что произошло событие 
если эксперимент завершился одним из элементарных исходов,
входящих в множество 
Замечание.
Вообще говоря, можно называть событиями не любые
подмножества множества 
некоторого набора подмножеств.
О смысле такого ограничения мы поговорим позднее.
Итак, элементарный исход — это мельчайший неделимый результат эксперимента,
а событие может состоять из одного или нескольких исходов.
Напомним, что конечные и счетные множества удобно задавать перечислением
их элементов. Например, 
ста натуральных чисел. Несчетные множества
обычно задают указанием свойства, которым обладают все элементы
множества. Так, 
множество действительных чисел из интервала 
Пример 1.
Один раз подбрасывают игральную кость.
Рассмотрим пространство элементарных исходов 




Элементарные исходы здесь
соответствуют числу выпавших очков.
Событие 
одно или два очка; событие 

означает, что выпадет нечетное число очков. Событие
состоит из одного элементарного исхода и означает появление шести очков.
Пример 2.
Подбрасываются две игральные кости. Будем считать их различимыми и назовем одну
из них первой, другую — второй.
Пространством элементарных исходов является множество пар чисел 
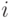
кости, 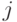

В этом множестве 
![begin{equation}
begin{matrix}
(1,1) & (1,2) & cdots & (1,6) \
(2,1) & (2,2) & cdots & (2,6) \
hdotsfor[1.5]{4} \
(6,1) & (6,2) & cdots &(6,6)
end{matrix}
end{equation}](https://intuit.ru/sites/default/files/tex_cache/93d9174df16be50d4b506c0a72f7fc9f.png) |
( 1.1) |
Заметим, что для симметричных костей
все эти 
ни одна из этих комбинаций не имеет больше шансов выпасть, чем другая.
Действительно, на первой кости с равными шансами выпадает любая грань.
Это означает, что результат бросания двух костей имеет столько же шансов оказаться
в первой строке матрицы ( 1 ), что и во второй, в третьей и т. д.
Но на второй кости снова с одинаковыми шансами
выпадает любая грань, поэтому и каждое место в строке равновозможно.
Событие «на первой кости выпадет одно очко» можно записать так: 


сумма выпавших очков равна четырем; событие
— на костях выпадет одинаковое число очков.
Пример 3. Подбрасываются две неразличимые игральные кости.
Элементарными исходами будем считать пары чисел 

случается, если на одной из костей выпадает одно очко, на другой —
два очка. В множестве 
Для симметричных костей эти исходы равновозможными уже не будут: например,
исход 

Мы просто перестали различать исходы из примера 2,
симметричные друг другу относительно главной диагонали матрицы (1).
Теперь событие «сумма выпавших очков равна четырем»
состоит из двух элементарных исходов 
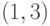
Событие «на костях выпадет одинаковое число очков» по-прежнему включает
шесть исходов.
Слова «на первой кости выпадет одно очко»
никакого события уже не описывают, а
событие 
что хотя бы на одной из костей выпало одно очко (ср. с примером 2).
Пример 4.
На поверхность стола бросается монета. Результатом эксперимента
можно считать положение центра монеты.
Пространство элементарных исходов такого
эксперимента — множество всех точек стола.
Оно бесконечно и несчетно.
Событием можно назвать, например, попадание центра монеты на
лист бумаги, лежащий на столе, в левую или правую половину стола.
Пример 5.
Монета подбрасывается до тех пор, пока не выпадет вверх гербом.
Пространство элементарных исходов является бесконечным, но счетным множеством: 
где 

при одном подбрасывании.
Событие «герб выпал при броске с четным номером» выглядит так:
Пример 6.
В коробке лежат один черный и два белых шара. Из коробки достают
наугад один шар.
Можно определить два разных пространства элементарных исходов. Первое из
них состоит из двух исходов 
мог появиться белый шар или черный. Эти исходы, очевидно, не будут равновозможными:
появление белого шара вдвое вероятнее, чем появление черного.
Если мы хотим иметь дело с равновозможными элементарными исходами,
шары следует занумеровать (или различать как-нибудь иначе). Тогда множество
будет состоять из трех равновозможных элементарных исходов.
Пример 7.
В коробке лежат один черный и два белых шара. Из коробки достают наугад два шара.
Порядок следования шаров нам безразличен.
Занумеруем шары, чтобы элементарные исходы были равновозможными
(это может оказаться удобным).
Пространство элементарных исходов состоит из трех элементов:
Событие «вынуты два белых шара» включает один исход
а событие «вынуты разноцветные шары» состоит из двух исходов: 

Можно, как в примере 6,
рассмотреть пространство элементарных исходов, состоящее из двух
элементов: 
вынуты два белых шара или шары разных цветов.
Но в таком пространстве второй исход имеет вдвое больше шансов случиться, чем
первый.
Пространство элементарных событий. Определение вероятности
- Опыт (испытание) и событие (исход)
- Пространство элементарных событий
- Классическое определение вероятности
- Геометрическое определение вероятности
- Статистическое определение вероятности
- Примеры
п.1. Опыт(испытание) и событие (исход)
Опыт – некоторый набор условий, который можно воспроизвести, чтобы наблюдать то или иное явление.
Событие – любое явление, которое наблюдается в результате опыта.
Например:
Опыт (испытание)
Событие (исход)
Подбрасывание монеты
Выпадение орла или решки
Выстрел
Попадание в 10 или в 9,… на мишени, или в молоко, или выстрел мимо мишени
Подбрасывание игрального кубика
Выпадение 6 или 5,… или 1
Выбор карты из колоды
Выбор пикового туза или любой другой из 54 карт
Ставка при игре в рулетку
Выигрыш на «7 красное» или любой другой из ставок
Событие называется достоверным, если оно обязательно произойдёт в условиях данного опыта.
Событие называется возможным (случайным), если в результате опыта оно может появиться, но может и не появиться.
Событие называется невозможным, если оно не может произойти в условиях данного опыта.
Например:
1) При бросании кубика выпадение 2 – это возможное событие, а выпадение 8 – невозможное. Достоверное событие «1 или 2 или 3 или 4 или 5 или 6».
2) При бросании монеты выпадение орла – это возможное событие, а зависание монеты в воздухе – невозможное. Достоверное событие «орёл или решка».
События называют несовместными, если они не могут произойти одновременно в результате одного опыта.
Например:
1) Нельзя одновременно A=«попасть в 10» и B=«промахнуться» при стрельбе. События A и B – несовместны.
2) Нельзя одновременно C=«достать белый шарик» и D=«достать черный шарик» из коробки. События C и D – несовместны.
События называют равновозможными, если по условиям опыта ни одно из событий не имеет преимуществ перед другими при появлении.
п.2. Пространство элементарных событий
Пространство элементарных событий Ω – это множество, содержащее все возможные результаты опыта, которые взаимно исключают друг друга. Элементами этого множества являются элементарные события, каждое из которых – и только одно – происходит в результате опыта.
Элементарные события обладают свойствами несовместности и равновозможности.
Пространство элементарных событий обладает свойством полноты.
Например:
1) Пространство элементарных событий при бросании кубика Ω={1;2;3;4;5;6}
2) Пространство элементарных событий при бросании двух монет $$Omega=left{ begin{array}{ l l} mathrm{00} & mathrm{01}\ mathrm{10} & mathrm{11} end{array}right} $$ где на первом месте – результат бросания 1-й монеты, на втором – 2-й монеты.
«0» – выпадение решки; «1» – выпадение орла.
Событие A – это подмножество пространства элементарных событий A⊆Ω.
Событие A произошло, если в опыте произошло одно из элементарных событий, входящих в множество A.
Например:
Пусть при бросании кубика A={1;3;5} – выпадение нечётного числа. Событие A будет происходить каждый раз при наблюдении элементарных событий 1 или 3 или 5.
п.3. Классическое определение вероятности
Данное определение сформулировано Лапласом в 1795 г. в курсе лекций «Опыт философии теории вероятностей».
Рассмотрим пространство элементарных событий, которое состоит из конечного числа элементарных исходов:
Ω={ω1, ω2, …, ωn}, |Ω|=n
Событие A является его подмножеством A⊆Ω: $$ mathrm{ A={widetilde{omega_1}, widetilde{omega_2}, …, widetilde{omega_k}}, widetilde{omega_i}=omega_j, |A|=k, kleq n } $$
Вероятностью события A называется отношение числа элементарных исходов, способствующих появлению события A, к общему числу исходов: $$ mathrm{ P(A)=frac{k}{n} } $$
Например:
Пространство элементарных событий при бросании кубика Ω={1;2;3;4;5;6}
Пусть при бросании кубика A={1;3;5} – выпадение нечётного числа. $$ mathrm{ n=6, k=3, P(A)=frac{3}{6}=0,5 } $$ Вероятность выпадение нечётного числа равна 0,5.
п.4. Геометрическое определение вероятности
Недостатком классического определения вероятности является требование конечности множества событий.
Но нам известны удачные модели бесконечных множеств, которые используются даже в элементарной математике: числовые прямые, системы координат на плоскости и в пространстве. Попробуем их использовать.
Например, рассмотрим опыт со стрельбой в мишень радиуса R=1. Пусть стрелок всегда попадает в мишень. Пространство элементарных событий ограничено кругом x2 + y2 ≤1. Круг содержит в себе бесконечное множество точек и все возможные исходы (свойство полноты). Случайное попадание в эту область равновероятно для любой точки (свойство равновозможности). Одновременно попасть в две разные точки области невозможно (свойство несовместности).
Пусть событие A, которое нас интересует, описывается другим ограничением: попаданием в круг (mathrm{ left(x-frac12right)^2+y^2leq frac14. })
Тогда:
Вероятностью события A называется отношение площади (меры) области, соответствующей событию A, к общей площади (мере) области всех исходов: $$ mathrm{ P(A)=frac{S_A}{S_{Omega}} } $$
 |
begin{gather*} mathrm{ Omega: x^2+y^2leq 1, left(x-frac12right)^2+y^2leq frac14. }\ mathrm{ S_A=frac{pi r^2}{2}=frac{pi}{2}cdot frac14=frac{pi}{8} }\ mathrm{ S_{Omega}=frac{pi r^2}{2}=frac{pi}{2}cdot 1=frac{pi}{2} }\ mathrm{ P(A)=frac{pi}{8}:frac{pi}{2}= frac14 } end{gather*} |
Геометрическое определение вероятности можно использовать при моделировании бесконечных множеств любой размерности: от одномерных (прямая, на которой определена длина) до многомерных (N-мерные пространства, на которых определены свои меры) (см. также §38 данного справочника).
п.5. Статистическое определение вероятности
Многочисленные опыты с подбрасыванием монеты показывают, что число выпадений «орла» приближается к 1/2, может быть немного больше или меньше, но никогда не равно половине в точности.
Экспериментатор
К-во бросков монеты
Частота выпадения орла
Огастес Де Морган
4092
0,5005
Уильям Джевонс
20480
0,5068
Вс. Романовский
80640
0,4923
Уильям Феллер
10000
0,4979
В принципе, чем больше будет проведено опытов, тем ближе будет экспериментальная величина к теоретической. Поэтому, с точки зрения статистики:
Вероятностью события A называется предел отношения числа наблюдений этого события к общему числу опытов (однородных независимых испытаний): $$ mathrm{ P(A)=lim_{Nrightarrowinfty}frac{n}{N} } $$ где N – общее количество испытаний, n – количество наблюдений события A.
Такое понимание вероятности очень продуктивно, т.к. позволяет вывести важные теоремы, которые широко используются в статистике и других областях прикладной математики.
В современной математике вероятность определяется аксиоматически, в рамках аксиоматики Колмогорова. Если ваша будущая профессия будет связана с математикой, вам обязательно об этом расскажут.
п.6. Примеры
Пример 1. Из хорошо тасованной колоды в 32 карты выбирается наугад одна карта. Какова вероятность того, что это:
1) туз;
2) карта бубновой масти;
3) либо король, либо дама, либо валет;
4)* какова вероятность, что в данной колоде сверху – пиковая дама?
1) Всего карт n = 32, тузов k = 4
Вероятность выбрать туз: (mathrm{ P=frac{k}{n}=frac{4}{32}=frac{1}{8}=0,125 })
2) Всего карт n = 32, бубновой масти k = 8
Вероятность выбрать карту бубновой масти: (mathrm{ P=frac{k}{n}=frac{8}{32}=frac{1}{4}=0,25 })
3) Всего карт n = 32, королей, дам и валетов k = 12
Вероятность выбрать короля, даму или валета: (mathrm{ P=frac{k}{n}=frac{12}{32}=frac{3}{8}=0,375 })
4) Каждое тасование колоды – это перестановка без повторений (см.§34 данного справочника)
Общее количество возможных перестановок: P32=32!
Если зафиксировать первую карту – пиковую даму, то общее количество возможных перестановок оставшихся карт P31=31! – количество вариантов колод с пиковой дамой наверху.
n = 32!, k = 31!
Искомая вероятность:(mathrm{ P=frac{k}{n}=frac{31!}{32!}=frac{1}{32}=0,03125 })
Ответ: 1) 0,125; 2) 0,25; 3) 0,375; 4) 0,03125.
Пример 2. В слове «КОРОНАВИРУС» наугад выбирается одна буква.
Какова вероятность, что это буква:
1) гласная;
2) согласная;
3) буква «Р»;
4) буква «Ц».
1) Всего букв n = 11, гласных букв k = 5
Вероятность выбрать гласную букву: (mathrm{ P=frac{k}{n}=frac{5}{11} })
2) Всего букв n = 11, согласных букв k = 6
Вероятность выбрать согласную букву: (mathrm{ P=frac{k}{n}=frac{6}{11} })
3) Всего букв n = 11, букв «Р» k = 2
Вероятность выбрать букву «Р»: (mathrm{ P=frac{k}{n}=frac{2}{11} })
4) Всего букв n = 11, букв «Ц» k = 0
Вероятность выбрать букву «Ц»: (mathrm{ P=frac{k}{n}=0 }) – невозможное событие.
Ответ: (mathrm{ 1) frac{5}{11}; 2) frac{6}{11}; 3) frac{2}{11}; 4) 0. })
Пример 3. В семье четверо детей, близнецов нет.
1) Какова вероятность, что мальчиков и девочек поровну?
2) Какова вероятность, что старший ребенок – девочка, и младший — мальчик?
Дети в семье появляются по очереди, т.е. выборка является упорядоченной. Рассматриваем размещение с повторениями (см.§35 данного справочника)
n = 2, k = 4 $$ mathrm{ overline{A}_2^4=2^4=16 } $$ Пространство элементарных событий состоит из N = 16 вариантов:
1) Мальчиков и девочек поровну в 6 случаях из 16: (mathrm{ P=frac{6}{16}=frac{3}{8}=0,375 })
2) Старший ребенок – девочка, и младший – мальчик в 4 случаях из 16:
(mathrm{ P=frac{4}{16}=frac{1}{4}=0,25 })
Ответ: 1) 0,375; 2) 0,25.
Пример 4. Деревянный куб покрасили и распилили на 1000 кубиков.
Какова вероятность, что случайно выбранный кубик имеет:
1) три окрашенных грани;
2) две окрашенных грани;
3) одну окрашенную грань;
4) ни одной окрашенной грани?
1) Три окрашенных грани будут иметь кубики на вершинах куба.
Вершин у куба 8, значит k = 8. Вероятность (mathrm{ P=frac{8}{1000}=0,008})
2) Две окрашенных грани будут иметь кубики на ребрах куба, кроме вершин.
Всего ребёр у куба 12, на каждом ребре по 8 кубиков без вершин, k = 12 · 8 = 96.
Вероятность (mathrm{ P=frac{96}{1000}=0,096})
3) Одну окрашенную грань будут иметь кубики на гранях куба, кроме ребер и вершин.
Всего граней у куба 6, на каждой грани по 8 · 8 = 64 внутренних кубика, k = 6 · 64 = 384. Вероятность (mathrm{ P=frac{384}{1000}=0,384})
4) Неокрашенными будут k = 8 · 8 · 8 = 512 кубиков.
Вероятность (mathrm{ P=frac{512}{1000}=0,512})
Ответ: 1) 0,008; 2) 0,096; 3) 0,384; 4) 0,512.
Взяв практически любую статью по теории вероятностей, мы увидим, что либо она начинается словами: «Пусть 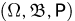
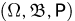
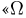
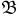
Пространство элементарных исходов
Рассмотрим простейший вариант случайного испытания — подбрасывание монеты. Если отвлечься от чисто гипотетических возможностей — падения монеты на ребро или вообще исчезновения монеты, то возможны только два исхода: выпадение «герба» и выпадение «цифры». Эти два исхода в рамках данного опыта уже нельзя разбить на более мелкие составляющие, т.е. они являются в некотором роде «элементарными». При бросании игральной кости такими неделимыми исходами являются: выпадение одного очка, выпадение двух очков, …, выпадение шести очков. Значит, мы имеем уже 6 элементарных исходов. Более сложный пример получим, если рассмотрим падение идеальной (т. е. не имеющей размера) частицы на плоскость. Тогда результат испытания представляет собой попадание частицы в определенную точку плоскости и его можно отождествить с двумерным вектором в некоторой системе координат на плоскости.
Аналогично, если проанализировать любое испытание со случайным исходом, можно заметить, что его результат представляет собой один из множества допустимых исходов. Поскольку в математике принято абстрагироваться от несущественных деталей, то всегда можно рассматривать все возможные в данном опыте исходы как некоторое множество 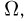
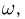
Пример:
При подбрасывании монеты пространство элементарных исходов 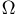
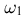
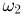
Пример:
При бросании игральной кости возможны 6 элементарных исходов: 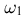
Пример:
При подбрасывании двух монет пространство элементарных исходов 
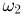
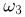
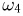
Пример:
При определении времени жизни элементарной частицы пространство элементарных исходов 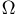
Следует отметить, что в практических исследованиях существует определенный произвол в описании пространства элементарных исходов 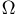
События, действия над ними
Понятие «событие» лингвистически отличается от понятия «элементарное событие» только отсутствием прилагательного «элементарное». Естественно поэтому определить событие так же, как исход испытания, но только не обязательно неделимый.
Пример:
При бросании игральной кости (см. пример 2) событиями являются: выпадение четного числа очков (это событие происходит тогда и только тогда, когда появляется один из элементарных исходов 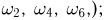
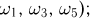
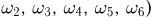
Пример:
При подбрасывании двух монет примерами событий будут: падение обеих монет на одну и ту же сторону (появлению этого события благоприятствуют элементарные исходы 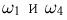
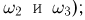
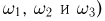
Пример:
При определении времени безотказной работы электрической лампочки можно привести следующие примеры событий: безотказная работа лампочки до момента Т; отказ лампочки до момента Т; отказ лампочки между моментами 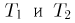
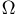
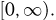
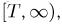
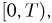
Вспоминая, что в результате опыта может произойти один и только один элементарный исход 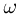
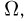
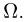
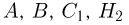
Заметим, что приведенное выше определение события не всегда позволяет построить логически безупречную аксиоматику теории вероятностей. Поэтому в следующем параграфе мы уточним понятие «событие». Сейчас же наша цель состоит в описании теоретико-множественных операций над событиями, и нам удобно отказаться от несущественных пока деталей.
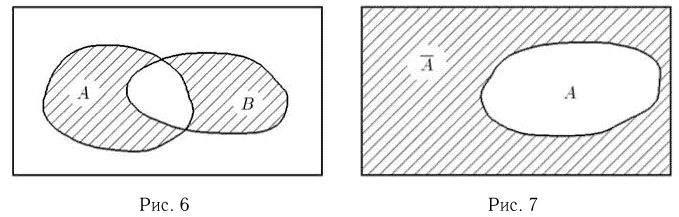
Часто бывает полезным наглядное представление событий в виде так называемой диаграммы Эйлера-Венна. Будем изображать все пространство элементарных исходов прямоугольником (рис.1). Тогда каждый элементарный исход 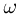
Само пространство элементарных исходов 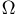
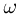
Для дальнейшего нам удобно ввести еще одно событие 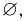
Пример:
При бросании игральной кости событие «выпадение не менее одного очка» является достоверным 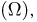
Над событиями как над подмножествами фиксированного множества можно производить действия, которые мы сейчас опишем.
Пересечением (произведением) двух событий А и В называется событие С, происходящее тогда и только тогда, когда наступают одновременно оба события А и В, или, иными словами, состоящее из тех элементарных исходов, которые принадлежат и А, и В (рис. 2).
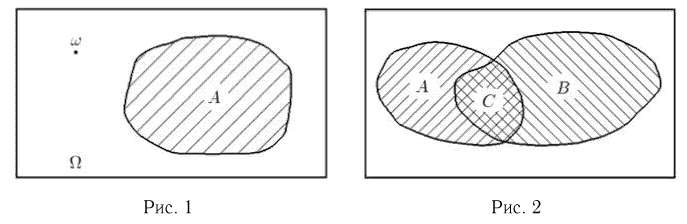
Пересечение событий А и В записывается следующим образом:
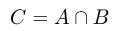
или
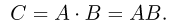
Аналогично определяется пересечение трех и более событий.
Пример:
Событие А — при подбрасывании двух монет падение их одной стороной, событие В — выпадение хотя бы одного «герба». Пересечением событий А и В является событие С, состоящее в выпадении двух «гербов».
Пример:
Событие А — выпадение четного числа очков при бросании игральной кости, событие В — выпадение не менее 3 очков. Пересечение А ий — событие С, состоящее в выпадении 4 или 6 очков. □
События А и В называются непересекающимися или несовместными, если их пересечение является невозможным событием, т.е. 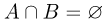
Для трех и более событий понятие несовместности можно определить разными способами. Мы будем, в основном, пользоваться следующим понятием несовместности n событий, которое также называется попарной несовместностью событий: события 
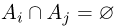
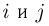
Пример:
Событие А — выпадение четного числа очков при бросании игральной кости, событие В — выпадение нечетного числа очков. События А и В несовместны.
Нетрудно видеть, что справедливы следующие простейшие формулы для пересечения двух событий, одно из которых достоверно или невозможно:

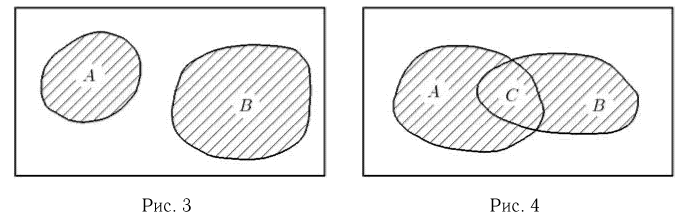
Объединением (суммой) двух событий А и В называется событие С, происходящее тогда и только тогда, когда наступает хотя бы одно из событий А или В, т. е. состоящее из тех элементарных исходов, которые принадлежат хотя бы одному из множеств А или В (рис.4).
Для объединения событий А и В применяется запись
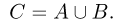
Пример:
Событие А — выпадение 1 или 3 очков при бросании игральной кости, событие В — выпадение 3 или 5 очков. Объединением событий А и В является событие С, состоящее в выпадении нечетного числа очков.
Для объединения двух событий, одно из которых достоверно или невозможно, имеют место следующие формулы:

В том случае, когда события А и В несовместны, наряду со знаком 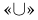
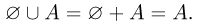
Аналогично определяется объединение трех и более событий. При этом знак «+» используется в случае попарной несовместности входящих в объединение событий.
Разностью двух событий А и В называется событие С, происходящее тогда и только тогда, когда происходит событие А, но не происходит событие В, т. е. состоящее из тех элементарных исходов, которые принадлежат ,4, но не принадлежат В (рис.5).
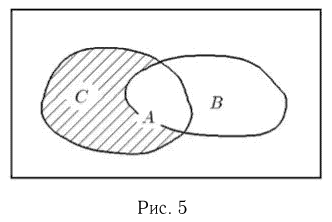
Разность событий А и В записывается в виде
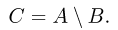
Пример:
Событие А — выпадение хотя бы одного «герба» при подбрасывании двух монет, событие В — падение обеих монет одной стороной. Разность С событий А к В представляет собой событие, заключающееся в выпадении ровно одного «герба».
Справедливы следующие формулы для разности двух событий, одно из которых достоверно или невозможно:
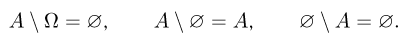
Кроме того, если А и В несовместны
Симметрической разностью двух событий А и В (обозначается знаком 
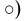
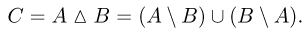
Поскольку события 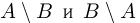
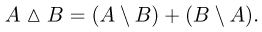
Нетрудно заметить, что симметрическая разность есть объединение событий а и в без их общей части:
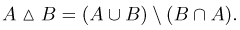
Пример:
Событие А — выпадение не менее 2 очков при бросании игральной кости, событие в — выпадение не более 4 очков. Симметрической разностью событий а и в является событие С, заключающееся в выпадении 1, 5 или 6 очков.
Если А и В несовместны, то
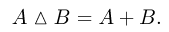
Дополнением события А (обычно обозначается 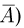
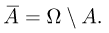
Пример:
Событие А — выпадение четного числа очков при бросании игральной кости. Дополнительное событие 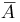
Справедливы формулы:
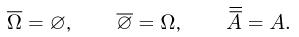
Если некоторое событие записано в виде нескольких действий над различными событиями, то сначала вычисляются дополнения, затем выполняются умножения и, наконец, сложения и вычитания событий. Так, формула
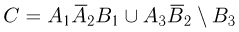
эквивалентна формуле
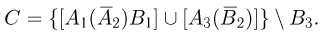
Пользуясь диаграммой Эйлера-Венна, нетрудно показать справедливость следующих формул (формулы де Моргана):

Формулы де Моргана элементарно переносятся на произвольное число событий. В частности, для n событий 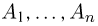

Следует отметить, что все действия над событиями можно получить с помощью только двух действий — объединения и дополнения (или пересечения и дополнения). Основанием для этого утверждения служат формулы де Моргана, а также соотношение
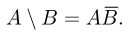
Кроме вышеперечисленных действий над событиями нам в дальнейшем понадобится понятие включения. Событие А принадлежит (содержится в, включается в) событию В (записывается 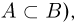
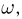
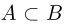
Используют и обратное понятие: событие В содержит (включает) событие 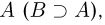
Пример:
Событие А — выпадение четного числа очков при бросании игральной кости, событие В — выпадение не менее 2 очков. Событие А принадлежит событию В, поскольку если выпало четное число очков (2, 4 или 6), то обязательно выпало не менее 2 очков.
Следующие включения очевидны:
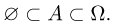
Кроме того, если 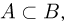
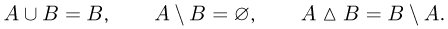
Алгебра событий
Итак, мы назвали событием произвольное подмножество пространства элементарных исходов 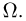
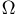
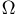
то, вообще говоря, мы уже не сможем построить логически непротиворечивую теорию, называя событием произвольное подмножество 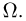
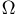
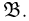
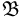
С точки зрения повседневной практики подмножества пространства элементарных исходов 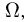

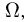

Алгеброй событий 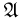
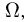
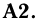
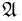
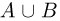
Как мы знаем, любую из рассмотренных нами операций над подмножествами можно получить с помощью только двух операций: дополнения и объединения. Поэтому пересечение и разность двух событий также будут событиями. Поскольку 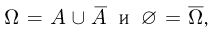
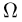
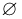
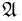
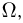
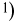
Однако понятие алгебры событий также оказывается недостаточным для аксиоматического построения теории вероятностей в том случае, когда пространство элементарных исходов 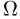


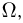
2′. Если подмножества 



Основываясь на формулах де Моргана, нетрудно показать, что пересечение счетного числа событий снова будет событием. Таким образом, 

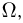
.Любая 

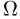



Пример:
Для любого пространства элементарных исходов 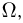
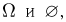

Пример 18. Пусть пространство элементарных исходов 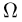
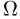
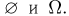
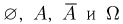





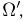
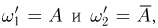
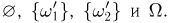
В качестве иллюстрации рассмотрим время работы электрической лампочки. Первоначально пространство элементарных исходов представляет собой полупрямую 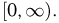
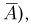
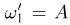
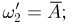

Пример:
Пусть пространство элементарных исходов 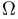
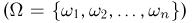
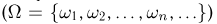



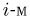
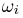
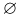
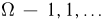


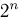
В случае дискретного 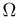


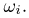
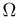
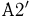

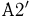
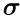
В частности, в случае конечного 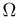


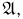
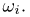
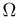
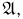
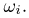


Пример:
Пусть пространство элементарных исходов 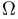
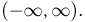



О невозможности использования «максимальной» 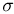
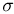
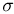
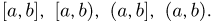
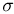
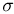
Все сказанное относительно прямой в полной мере относится и к пространствам элементарных исходов, представляющим собой плоскость, трехмерное пространство и пространства более высоких размерностей, а также их невырожденные части (отрезки, многоугольники, круги, шары и т.д.). В теории вероятностей такие пространства элементарных исходов называются непрерывными. □
Определение вероятности
Приступим теперь к аксиоматическому определению последней составляющей вероятностного пространства 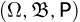
Предположим сначала, что пространство элементарных исходов конечно. Пусть каждому событию А ( т.е. подмножеству А пространства элементарных исходов 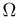
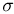

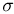

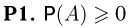
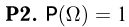
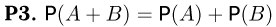
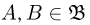
Как говорилось во введении, аксиомы вероятности представляют собой не что иное, как математическое отражение основных свойств частоты.
Из аксиом Р1-РЗ можно вывести ряд очевидных свойств вероятности.
Поскольку 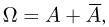
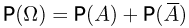
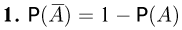
Далее, поскольку 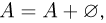
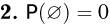
Пусть 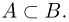
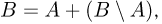
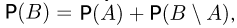
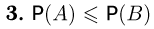
В частности, так как всегда 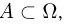
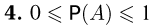
Наконец, поскольку 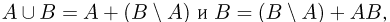
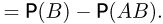
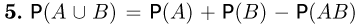
Последнее свойство допускает очевидное, но весьма полезное обобщение на случай произвольного числа слагаемых
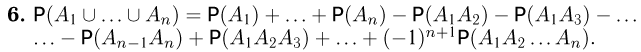
Свойство 6 доказывается индукцией по n. Так, для трех событий А, В и С
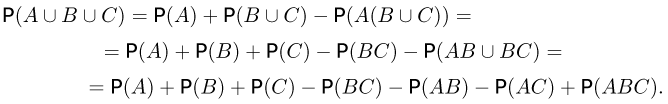
Из свойств 6 и 2 имеем для любого числа n (попарно) непересекающихся событий
В случае, когда 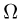
Действительно, с одной стороны, пусть на пространстве элементарных исходов 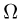
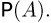

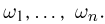
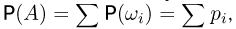
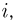

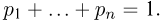
С другой стороны, пусть 
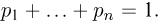
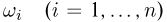
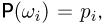
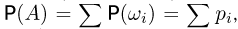
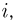
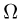
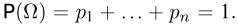
Итак, существует взаимно однозначное соответствие между всеми вероятностями Р(А) на 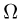

В частности, мы можем всем элементарным исходам 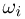
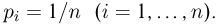
В случае произвольного (не обязательно конечного) пространства элементарных исходов 
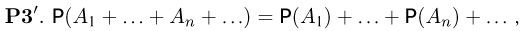
справедливой для счетного числа попарно несовместных событий.
Именно аксиомы 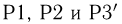
Очевидно, что свойства вероятности 1-7 сохраняются и в этом случае.
Пример:
Пусть 
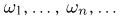
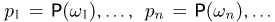
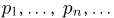
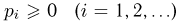
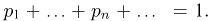
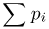
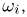
Пример:
Пусть пространство элементарных исходов 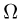
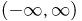
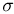
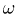
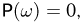
Для того чтобы показать это, предположим сначала, что она каким-то образом уже задана для всех событий (элементов борелевской 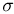
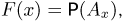
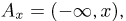
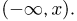
Во-первых, значения функции F(x) как вероятности должны лежать между 0 и 1.
Во-вторых, так как для любых 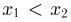
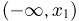
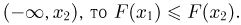
В-третьих, поскольку событие 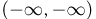
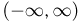
Наконец, так как событие 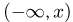
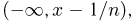
Зная функцию F(a-), можно определить вероятности любых других событий. В частности, вероятность события 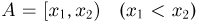
Таким образом, любая вероятность на прямой полностью определяется своей функцией F(x), которая удовлетворяет перечисленным выше свойствам.
Справедливо и обратное. Любая неубывающая непрерывная слева функция F(x), удовлетворяющая условиям 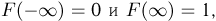
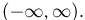
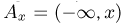
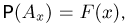
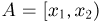
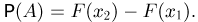
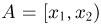
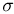
Вероятное пространство
Смотрите также:
Предмет теория вероятностей и математическая статистика
Решение заданий и задач по предметам:
- Теория вероятностей
- Математическая статистика
Дополнительные лекции по теории вероятностей:
- Случайные события и их вероятности
- Случайные величины
- Функции случайных величин
- Числовые характеристики случайных величин
- Законы больших чисел
- Статистические оценки
- Статистическая проверка гипотез
- Статистическое исследование зависимостей
- Теории игр
- Вероятность события
- Теорема умножения вероятностей
- Формула полной вероятности
- Теорема о повторении опытов
- Нормальный закон распределения
- Определение законов распределения случайных величин на основе опытных данных
- Системы случайных величин
- Нормальный закон распределения для системы случайных величин
- Классическое определение вероятности
- Геометрическая вероятность
- Условная вероятность
- Схема Бернулли
- Многомерные случайные величины
- Предельные теоремы теории вероятностей
- Оценки неизвестных параметров
- Генеральная совокупность
Пространство элементарных исходов
Определение
Элементарным исходом (или элементарным событием) называют любой простейший (т.е. неделимый в рамках данного опыта) исход опыта. Множество всех элементарных исходов будем называть пространтсвом элементарных исходов.
Другими словами, множество исходов опыта образует пространство элементарных исходов, если выполнены следующие требования:
- в результате опыта один из исходов обязательно происходит;
- появление одного из исходов опыта исключает появление остальных;
- в рамках данного опыта нельзя разделить элементарный исход на более мелкие составляющие.
В дальнейшем пространство элементарных исходов будем обозначать прописной буквой %%Omega%%, а сами элементарные исходы — строчной буквой %%omega%%, снабженной, при необходимости, индексами. То, что элемент %%omega%% принадлежит %%Omega%%, записывают в виде %%omega in Omega%%, а тот факт, что множество %%Omega%% состоит из элементов %%omega_1, omega_2, ldots, omega_n, ldots,%% и только из них, записывают в виде
$$
Omega = {omega_1, omega_2, ldots, omega_n, ldots}
$$
или в виде
$$
Omega = {omega_i, i=1, 2, ldots, n,ldots}.
$$
В частности, %%Omega%% может содержать конечное число элементарных исходов.
Примеры
Пример 1
Пусть опыт состоит в однократном подбрасывании монеты. При математическом описании этого опыта естественно отвлечься от несущественных возможностей (например, монета встанет на ребро) и ограничиться только двумя элементарными исходами: выпадением «герба» (можно обозначить этот исход как %%w_1%%) и выпаденим «цифры» (%%w_2%%). Таким образом, %%Omega = {w_1, w_2}%%.
При двукратном подбрасывании монеты (или однократном подбрасывании двух монет) пространство элементарных исходов будет содержать четыре элемента, т.е.
$$
Omega = {w_{11}, w_{12}, w_{21}, w_{22}},
$$
где, например, %%w_{12}%% — появление «герба» при первом броске и появление «цифры» при втором.
Пример 2
При однократном бросании игральной кости возможен любой из 6 элементарных исходов %%w_1, w_2, ldots, w_6%%, где %%w_i, i=overline{1,6}%%, означает появление %%i%% очков на верхней грани кости, т.е.
$$
Omega = {w_i, i=overline{1,6}}.
$$
При двукратном бросании игральной кости, каждый из шести возможных исходов, при первом бросании может сочетаться с каждым из шести исходов второго бросания, т.е.
$$
Omega = {w_{ij}, i, j=overline{1,6}},
$$
где, %%w_{ij}%% — исход опыта, при котором сначала выпало %%i%%,а затем %%j%% очков.
Нетрудно посчитать, что пространство элементарных исходов %%Omega%% содержит %%36%% элементарных исходов.
Основные определения
| Определение: |
| Дискретным вероятностным пространством (англ. discrete probability space) называется пара из некоторого (не более, чем счетного) множества и функции ( называется множеством элементарных исходов (англ. sample space), — элементарным исходом (англ. elementary outcome), такая, что . |
| Определение: |
| называют дискретной вероятностной мерой (англ. discrete probability measure), или дискретной плотностью вероятности (англ. discrete probability density). |
— вероятность элементарного исхода.
| Определение: |
| Множество называется событием (англ. event). |
, то есть вероятность события равна сумме вероятностей входящих в него элементарных исходов.
| Определение: |
| Прямым произведением вероятностных пространств (англ. direct product of probability spaces) и называется такое вероятностное пространство , что |
Другими словами, — множество всех пар элементарных исходов из и (т.е. декартово произведение этих множеств).
Примеры вероятностных пространств
- Конечные вероятностные пространства
- Честная монета
Множество исходов , где — выпадает орел, — выпадает решка.
Рассмотрим все возможные события и их вероятности для этого пространства.
: . То есть вероятность того, что не выпадет ничего, равна нулю.
: . Вероятность того, что выпадет орел, равна одной второй.
: . Вероятность того, что выпадет решка, равна одной второй.
: . Действительно, вероятность того, что выпадет орел или решка, равна единице. - Нечестная монета
Множество исходов здесь такое же, как и в предыдущем пространстве, однако , где . - Игральная кость
Множество исходов . Рассмотрим некоторые события этого пространства.
: Вероятность выпадения одного из трех чисел из множества равна одной второй.
: Числа или выпадут с вероятностью одна треть. - Колода карт
. Здесь — масть, — достоинство карты.
Вероятность элементарного исхода этого пространства
- Честная монета
- Бесконечное вероятностное пространство
Пусть задано множество следующих элементарных исходов: выпадение орла на -ом подбрасывании честной монеты в первый раз.
Тогда вероятность исхода с номером равна:
Очевидно, что вероятности этих событий образовывают убывающую геометрическую прогрессию с знаменателем прогрессии равным Найдем сумму этой прогрессии:
Так как сумма всех элементарных исходов равна то это множество является вероятностным пространством.
См. также
- Дискретная случайная величина
Источники информации
- Википедия — Вероятностное пространство
- MachineLearning.ru — Дискретное вероятностное пространство
- Ширяев А.Н. Вероятность. — М.: МЦНМО, 2004.












![begin{matrix}
(1,1) & (1,2) & cdots & (1,6) \
& (2,2) & cdots & (2,6) \
& hdotsfor[1.5]{2} \
& & & (6,6)
end{matrix}](https://intuit.ru/sites/default/files/tex_cache/db0083d0f7cdb270105cc7cf0b22ab01.png)