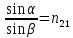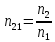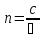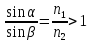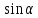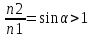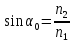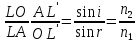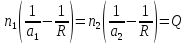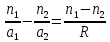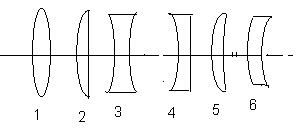Есть ничто иное, как отношение синуса угла падения к синусу угла преломления
Показатель преломления зависит от свойств вещества и длины волны излучения, для некоторых веществ показатель преломления достаточно сильно меняется при изменении частоты электромагнитных волн от низких частот до оптических и далее, а также может ещё более резко меняться в определённых областях частотной шкалы. По умолчанию обычно имеется в виду оптический диапазон или диапазон, определяемый контекстом.
Величина n, при прочих равных условиях, обычно меньше единицы при переходе луча из среды более плотной в среду менее плотную, и больше единицы при переходе луча из среды менее плотной в среду более плотную (например, из газа или из вакуума в жидкость или твердое тело). Есть исключения из этого правила, и потому принято называть среду оптически более или менее плотной, чем другая (не путать с оптической плотностью как мерой непрозрачности среды).
В таблице приведены некоторые значения показателя преломления для некоторых сред:
Среда, обладающая большим показателем преломления, называется оптически более плотной. Обычно измеряется показатель преломления различных сред относительно воздуха. Абсолютный показатель преломления воздуха равен . Таким образом, абсолютный показатель преломления какой-либо среды связан с ее показателем преломления относительно воздуха формулой:
Показатель преломления зависит от длины волны света, то есть от его цвета. Различным цветам соответствуют различные показатели преломления. Это явление, называемое дисперсией, играет важную роль в оптике.
Цифровой ресурс может использоваться для обучения в рамках программы основной и средней школы (базового уровня).
Модель представляет собой анимированную иллюстрацию по теме «Закон преломления света». Рассматривается система вода–воздух. Прорисовывается ход падающего, отраженного и преломленного лучей.
Краткая теория
Закон преломления света находит объяснение в волновой физике. Согласно волновым представлениям, преломление является следствием изменения скорости распространения волн при переходе из одной среды в другую. Физический смысл показателя преломления – это отношение скорости распространения волн в первой среде υ 1 к скорости их распространения во второй среде υ 2:
Работа с моделью
Кнопка Старт
/Стоп
позволяет начать или поставить на паузу эксперимент, кнопка Сброс
– начать новый эксперимент.
Данная модель может быть применена в качестве иллюстрации на уроках изучения нового материала по теме «Закон преломления света». На примере этой модели можно рассмотреть с учащимися ход луча при переходе из оптически менее плотной среды в оптически более плотную.
Пример планирования урока с использованием модели
Тема «Преломление света»
Цель урока: рассмотреть явление преломления света, ход луча при переходе из одной среды в другую.
|
||||||||||||||||||||||||
|
Таблица 1. |
Примеры вопросов и заданий
- Свет переходит из вакуума в стекло, при этом угол падения равен α, угол преломления β. Чему равна скорость света в стекле, если скорость света в вакууме равна c
? - Показатели преломления воды, стекла и алмаза относительно воздуха равны 1,33, 1,5, 2,42 соответственно. В каком из этих веществ предельный угол полного отражения имеет минимальное значение?
- Водолаз рассматривает снизу вверх из воды лампу, подвешенную на высоте 1 м над поверхностью воды. Чему равна кажущаяся высота лампы под водой?
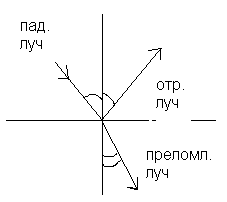
Угол падения —
угол
a
между направлением падающего луча и перпендикуляром к границе раздела двух сред, восстановленным в точке падения
.
Угол отражения
— угол β
между этим перпендикуляром и направлением отраженного луча.
Законы отражения света:
1. Луч падающий, перпендикуляр к границе раздела двух сред в точке падения и луч отраженный лежат в одной плоскости.
2. Угол отражения равен углу падения
.
Преломлением света
называют изменение направления световых лучей при переходе света из одной прозрачной среды в другую.
Угол преломления
— угол
b
между тем же перпендикуляром и направлением преломленного луча.
Скорость света в вакуумес
= 3*10 8 м/с
Скорость света в среде V<
c
Абсолютный показатель преломления среды
показывает, во сколько раз скорость света
v
в данной среде меньше, чем скорость света с
в вакууме.
Абсолютный показатель преломления первой среды
Абсолютный показатель преломления второй среды
Абсолютный показатель преломления для вакуума
равен 1
Скорость света в воздухе очень мало отличается от значения с,
поэтому
Абсолютный показатель преломления для воздуха
будем считать равным 1
Относительный показатель преломления
показывает, во сколько раз изменяется скорость света при переходе луча из первой среды во вторую.
где V 1 и V 2 – скорости распространения света в первой и второй среде.
С учетом показателя преломления закон преломления света можно записать в виде
где n 21
– относительный показатель преломления
второй среды относительно первой;
n 2
и n 1
– абсолютные показатели преломления
второй и первой среды соответственно
Показатель преломления среды относительно воздуха (вакуума) можно найти в таблице 12 (задачник Рымкевича). Значения приведены для случая падения света из воздуха в данную среду.
Например,
находим в таблице показатель преломления алмаза n= 2,42.
Это показатель преломления алмаза относительно воздуха
(вакуума), то есть для абсолютных показателей преломления:
Законы отражения и преломления справедливы при обратном направлении хода световых лучей.
Из двух прозрачных сред оптически менее плотной
называют среду с большей скоростью распространения света, или с меньшим показателем преломления
.
При падении в оптически более плотную среду
угол преломления меньше угла падения.
При падении в оптически менее плотную среду
угол преломления больше угла падения
Полное внутреннее отражение
Если световые лучи из оптически более плотной среды 1 падают на границу раздела с оптически менее плотной средой 2 (n 1
> n 2
), то угол падения меньше угла преломления
a
<
b
. При увеличении угла падения можно подойти к такому его значению
a пр
, когда преломленный луч заскользит по границе раздела двух сред и не попадет во вторую среду,
Угол преломления b
= 90°, при этом вся световая энергия отражается от границы раздела.
Предельным углом полного внутреннего отражения a пр
называется угол, при котором преломленный луч скользит вдоль поверхности двух сред,
При переходе из среды оптически менее плотной в среду более плотную полное внутреннее отражение невозможно.
К ЛЕКЦИИ №24
«ИНСТРУМЕНТАЛЬНЫЕ МЕТОДЫ АНАЛИЗА»
РЕФРАКТОМЕТРИЯ.
Литература:
1.
В.Д. Пономарёв «Аналитическая химия» 1983год 246-251
2.
А.А. Ищенко «Аналитическая химия» 2004 год стр 181-184
РЕФРАКТОМЕТРИЯ.
Рефрактометрия является одним их самых простых физических методов анализа с затратой минимального количества анализируемого вещества и проводится за очень короткое время.
Рефрактометрия
— метод, основанный на явлении преломления или рефракции т.е. изменении направления распространения света при переходе из одной среды в другую.
Преломление, так же как и поглощение света, является следствием взаимодействия его со средой. Слово рефрактометрия означает измерение
преломления света, которое оценивается по величине показателя преломления.
Величина показателя преломления n
зависит
1)от состава веществ и систем,
2) от того, в какой концентрации
и какие молекулы встречает световой луч на своем пути, т.к. под действием света молекулы разных веществ поляризуются по-разному. Именно на этой зависимости и основан рефрактометрический метод.
Метод этот обладает целым рядом преимуществ, в результате чего он нашел широкое применение как в химических исследованиях, так и при контроле технологических процессов.
1)Измерение показатели преломления являются весьма простым процессом, который осуществляется точно и при минимальных затратах времени и количества вещества.
2) Обычно рефрактометры обеспечивают точность до 10% при определении показателя преломления света и содержания анализируемого вещества
Метод рефрактометрии применяют для контроля подлинности и чистоты, для идентификации индивидуальных веществ, для определения строения органических и неорганических соединений при изучении растворов. Рефрактометрия находит применение для определения состава двухкомпонентных растворов и для тройных систем.
Физические основы метода
ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ.
Отклонение светового луча от первоначального направления при переходе его из одной среды в другую тем больше, чем больше разница в скоростях распространения света в двух
данных средах.
Рассмотрим преломление светового луча на границе каких-либо двух прозрачных сред I и II(См. Рис.). Условимся, что среда II обладает большей преломляющей способностью и, следовательно, n 1
и n 2
— показывает преломление соответствующих сред. Если среда I -это не вакуум и не воздух, то отношение sin угла падения светового луча к sin угла преломления даст величину относительного показателя преломления n отн. Величина n отн. может быть так же определена как отношение показателей преломления рассматриваемых сред.
n отн. = —— = —
Величина показателя преломления зависит от
1) природы веществ
Природу вещества в данном случае определяет степень деформируемости его молекул под действием света — степень поляризуемости. Чем интенсивней поляризуемость, тем сильнее преломление света.
2)длины волны падающего света
Измерение показателя преломления проводится при длине волны света 589,3 нм (линия D спектра натрия).
Зависимость показателя преломления от длины световой волны называется дисперсией. Чем меньше длина волны, тем значительнее преломление
. Поэтому, лучи разных длин волн преломляются по-разному.
3)температуры
, при которой проводится измерение. Обязательным условием определения показателя преломления является соблюдение температурного режима. Обычно определение выполняется при 20±0,3 0 С.
При повышении температуры величина показателя преломления уменьшается, при понижении — увеличивается
.
Поправку на влияние температуры рассчитывают по следующей формуле:
n t =n 20 + (20-t) ·0,0002, где
n t –
показатель преломления при данной температуре,
n 20 -показатель преломления при 20 0 С
Влияние температуры на значения показателей преломления газов и жидких тел связано с величинами их коэффициентов объемного расширения. Объем всех газов и жидких тел при нагревании увеличивается, плотность уменьшается и,следовательно, уменьшается показатель
Показатель преломления, измеренный при 20 0 С и длине волны света 589,3 нм, обозначается индексом n D 20
Зависимость показателя преломления гомогенной двухкомпонентной системы от ее состояния устанавливается экспериментально, путем определения показателя преломления для ряда стандартных систем(например,растворов), содержание компонентов в которых известно.
4)концентрации вещества в растворе.
Для многих водных растворов веществ показатели преломления при разных концентрациях и температурах надежно измерены, и в этих случаях можно пользоваться справочными рефрактометрическими таблицами
. Практика показывает, что при содержании растворенного вещества, не превышающем 10-20%, наряду с графическим методом в очень многих случаях можно пользоваться линейным уравнением типа:
n=n о +FC,
n-
показатель преломления раствора,
nо
— показатель преломления чистого растворителя,
C
— концентрация растворенного вещества,%
F
-эмпирический коэффициент, величина которого найдена
путем определения коэффициентов преломления растворов известной концентрации.
РЕФРАКТОМЕТРЫ.
Рефрактометрами называют приборы, служащие для измерения величины показателя преломления. Существует 2 вида этих приборов: рефрактометр типа Аббе и типа Пульфриха. И в тех и в др. измерения основаны на определении величины предельного угла преломления. На практике применяются рефрактометры различных систем: лабораторный-РЛ, универсальный РЛУ и др.
Показатель преломления дистиллированной воды n 0 =1,33299, практически же этот показатель принимает в качестве отсчетного как n 0 =1,333.

Ручной рефрактометр

Преломление света
— явление, при котором луч света, переходя из одной среды в другую, изменяет направление на границе этих сред.
Преломление света происходит по следующему закону:
Падающий и преломленный лучи и перпендикуляр, проведенный к границе раздела двух сред в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения к синусу угла преломления есть величина постоянная для двух сред:
,
где α
— угол падения,
β
— угол преломления,
n
— постоянная величина, не зависящая от угла падения.
При изменении угла падения изменяется и угол преломления. Чем больше угол падения, тем больше угол преломления.
Если свет идет из среды оптически менее плотной в более плотную среду, то угол преломления всегда меньше угла падения: β < α.
Луч света, направленный перпендикулярно к границе раздела двух сред, проходит из одной среды в другую без преломления.
абсолютный показатель преломления вещества
— величина, равная отношению фазовых скоростей света (электромагнитных волн) в вакууме и в данной среде n=c/v
Величина n, входящая в закон преломления, называется относительным показателем преломления для пары сред.
Величина n есть относительный показатель преломления среды В по отношению к среде А, а n» = 1/n есть относительный показатель преломления среды А по отношению к среде В.
Эта величина при прочих равных условиях больше единицы при переходе луча из среды более плотной в среду менее плотную, и меньше единицы при переходе луча из среды менее плотной в среду более плотную (например, из газа или из вакуума в жидкость или твердое тело). Есть исключения из этого правила, и потому принято называть среду оптически более или менее плотной, чем другая.
Луч, падающий из безвоздушного пространства на поверхность какой-нибудь среды В, преломляется сильнее, чем при падении на нее из другой среды А; показатель преломления луча, падающего на среду из безвоздушного пространства, называется его абсолютным показателем преломления.
(Абсолютный — относительно вакуума.
Относительный — относительно любого другого вещества (того же воздуха, например).
Относительный показатель двух веществ есть отношение их абсолютных показателей.)
Полное внутреннее отражение
— внутреннее отражение, при условии, что угол падения превосходит некоторый критический угол. При этом падающая волна отражается полностью, и значение коэффициента отражения превосходит его самые большие значения для полированных поверхностей. Коэффициент отражения при полном внутреннем отражении не зависит от длины волны.
В оптике это явление наблюдается для широкого спектра электромагнитного излучения, включая рентгеновский диапазон.
В геометрической оптике явление объясняется в рамках закона Снелла. Учитывая, что угол преломления не может превышать 90°, получаем, что при угле падения, синус которого больше отношения меньшего показателя преломления к большему показателю, электромагнитная волна должна полностью отражаться в первую среду.
В соответствии с волновой теорией явления, электромагнитная волна всё же проникает во вторую среду — там распространяется так называемая «неоднородная волна», которая экспоненциально затухает и энергию с собой не уносит. Характерная глубина проникновения неоднородной волны во вторую среду порядка длины волны.
Законы преломления света.

1 . На границе раздела двух сред различной оптической плотности луч света при переходе из одной среды в другую меняет своё направление.
2. При переходе луча света в среду с большей оптической плотностью угол преломления меньше угла падения; при переходе луча света из оптически более плотной среды в среду менее плотную угол преломления больше угла падения.
Преломление света сопровождается отражением, причём с увеличением угла падения яркость отражённого пучка возрастает, а преломлённого ослабевает. Это можно увидеть проводя опыт, изображённом на рисунке. Следовательно, отражённый пучок уносит с собой тем больше световой энергии, чем больше угол падения.
Пусть MN
-граница раздела двух про зрачных сред, например, воздуха и воды, АО
-падающий луч, ОВ
— преломленный луч, -угол падения, -угол преломления, -скорость распространения света в первой среде, — скорость распространения света во второй среде.
Преломление света.
-
Закон преломления (частный случай).
-
Обратимость световых лучей.
-
Закон преломления (общий случай).
-
Полное внутреннее отражение.
-
Разберем задачи ЕГЭ по теме: Преломление света.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: закон преломления света, полное внутреннее отражение.
На границе раздела двух прозрачных сред наряду с отражением света наблюдается его преломление — свет, переходя в другую среду, меняет направление своего распространения.
Преломление светового луча происходит при его наклонном падении на поверхность раздела (правда, не всегда — читайте дальше про полное внутреннее отражение). Если же луч падает перпендикулярно поверхности, то преломления не будет — во второй среде луч сохранит своё направление и также пойдёт перпендикулярно поверхности.
к оглавлению ▴
Закон преломления (частный случай).
Мы начнём с частного случая, когда одна из сред является воздухом. Именно такая ситуация присутствует в подавляющем большинстве задач. Мы обсудим соответствующий частный случай закона преломления, а уж затем дадим самую общую его формулировку.
Предположим, что луч света, идущий в воздухе, наклонно падает на поверхность стекла, воды или какой-либо другой прозрачной среды. При переходе в среду луч преломляется, и его дальнейший ход показан на рис. 1.
 |
| Рис. 1. Преломление луча на границе «воздух–среда» |
В точке падения проведён перпендикуляр (или, как ещё говорят, нормаль)
к поверхности среды. Луч
, как и раньше, называется падающим лучом, а угол
между падающим лучом и нормалью — углом падения. Луч
— это преломлённый луч; угол
между преломлённым лучом и нормалью к поверхности называется углом преломления.
Всякая прозрачная среда характеризуется величиной , которая называется показателем преломления этой среды. Показатели преломления различных сред можно найти в таблицах. Например, для стекла
, а для воды
. Вообще, у любой среды
; показатель преломления равен единице только в вакууме. У воздуха
, поэтому для воздуха с достаточной точностью можно полагать в задачах
(в оптике воздух не сильно отличается от вакуума).
Закон преломления (переход «воздух–среда»).
1) Падающий луч, преломлённый луч и нормаль к поверхности, проведённая в точке падения, лежат в одной плоскости.
2) Отношение синуса угла падения к синусу угла преломления равно показателю преломления среды:
. (1)
Поскольку из соотношения (1) следует, что
, то есть
— угол преломления меньше угла падения. Запоминаем: переходя из воздуха в среду, луч после преломления идёт ближе к нормали.
Показатель преломления непосредственно связан со скоростью распространения света в данной среде. Эта скорость всегда меньше скорости света в вакууме:
. И вот оказывается,что
. (2)
Почему так получается, мы с вами поймём при изучении волновой оптики. А пока скомбинируем формулы . (1) и (2):
. (3)
Так как показатель преломления воздуха очень близок единице, мы можем считать, что скорость света в воздухе примерно равна скорости света в вакууме . Приняв это во внимание и глядя на формулу . (3), делаем вывод: отношение синуса угла падения к синусу угла преломления равно отношению скорости света в воздухе к скорости света в среде.
к оглавлению ▴
Обратимость световых лучей.
Теперь рассмотрим обратный ход луча: его преломление при переходе из среды в воздух. Здесь нам окажет помощь следующий полезный принцип.
Принцип обратимости световых лучей. Траектория луча не зависит от того, в прямом или обратном направлении распространяется луч. Двигаясь в обратном направлении, луч пойдёт в точности по тому же пути, что и в прямом направлении.
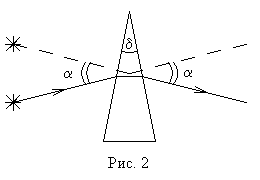
Согласно принципу обратимости, при переходе из среды в воздух луч пойдёт по той же самой траектории, что и при соответствующем переходе из воздуха в среду (рис. 2) Единственное отличие рис. 2 от рис. 1 состоит в том, что направление луча поменялось на противоположное.
 |
| Рис. 2. Преломление луча на границе «среда–воздух» |
Раз геометрическая картинка не изменилась, той же самой останется и формула (1): отношение синуса угла к синусу угла
по-прежнему равно показателю преломления среды. Правда, теперь углы поменялись ролями: угол
стал углом падения, а угол
— углом преломления.
В любом случае, как бы ни шёл луч — из воздуха в среду или из среды в воздух — работает следующее простое правило. Берём два угла — угол падения и угол преломления; отношение синуса большего угла к синусу меньшего угла равно показателю преломления среды.
Теперь мы целиком подготовлены для того, чтобы обсудить закон преломления в самом общем случае.
к оглавлению ▴
Закон преломления (общий случай).
Пусть свет переходит из среды 1 с показателем преломления в среду 2 с показателем преломления
. Среда с большим показателем преломления называется оптически более плотной; соответственно, среда с меньшим показателем преломления называется оптически менее плотной.
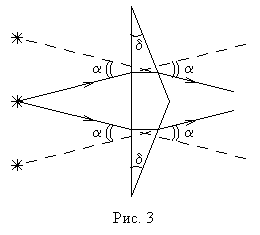
Переходя из оптически менее плотной среды в оптически более плотную, световой луч после преломления идёт ближе к нормали (рис. 3). В этом случае угол падения больше угла преломления: .
Наоборот, переходя из оптически более плотной среды в оптически менее плотную, луч отклоняется дальше от нормали (рис. 4). Здесь угол падения меньше угла преломления:
Оказывается, оба этих случая охватываются одной формулой — общим законом преломления, справедливым для любых двух прозрачных сред.
Закон преломления.
1) Падающий луч, преломлённый луч и нормаль к поверхности раздела сред, проведённая в точке падения, лежат в одной плоскости.
2) Отношение синуса угла падения к синусу угла преломления равно отношению показателя преломления второй среды к показателю преломления первой среды:
. (4)
Нетрудно видеть, что сформулированный ранее закон преломления для перехода «воздух–среда» является частным случаем данного закона. В самом деле, полагая в формуле (4) , мы придём к формуле (1).
Вспомним теперь, что показатель преломления — это отношение скорости света в вакууме к скорости света в данной среде: . Подставляя это в (4), получим:
. (5)
Формула (5) естественным образом обобщает формулу (3). Отношение синуса угла падения к синусу угла преломления равно отношению скорости света в первой среде к скорости света во второй среде.
к оглавлению ▴
Полное внутреннее отражение.
При переходе световых лучей из оптически более плотной среды в оптически менее плотную наблюдается интересное явление — полное внутреннее отражение. Давайте разберёмся, что это такое.
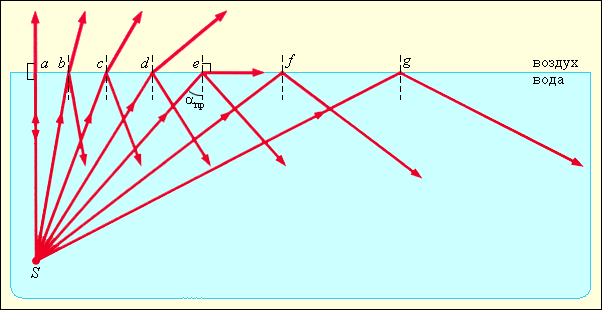
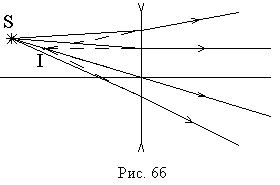
Будем считать для определённости, что свет идёт из воды в воздух. Предположим, что в глубине водоёма находится точечный источник света , испускающий лучи во все стороны. Мы рассмотрим некоторые из этих лучей (рис. 5).
 |
| Рис. 5. Полное внутреннее отражение |
Луч падает на поверхность воды под наименьшим углом. Этот луч частично преломляется (луч
) и частично отражается назад в воду (луч
). Таким образом, часть энергии падающего луча передаётся преломлённому лучу, а оставшаяся часть энергии -отражённому лучу.
Угол падения луча больше. Этот луч также разделяется на два луча — преломлённый и отражённый. Но энергия исходного луча распределяется между ними по-другому: преломлённый луч
будет тусклее, чем луч
(то есть получит меньшую долю энергии), а отражённый луч
— соответственно ярче, чем луч
(он получит большую долю энергии).
По мере увеличения угла падения прослеживается та же закономерность: всё большая доля энергии падающего луча достаётся отражённому лучу, и всё меньшая — преломлённому лучу. Преломлённый луч становится всё тусклее и тусклее, и в какой-то момент исчезает совсем!
Это исчезновение происходит при достижении угла падения , которому отвечает угол преломления
. В данной ситуации преломлённый луч
должен был бы пойти параллельно поверхности воды, да идти уже нечему — вся энергия падающего луча
целиком досталась отражённому лучу
.
При дальнейшем увеличении угла падения преломлённый луч и подавно будет отсутствовать.
Описанное явление и есть полное внутреннее отражение. Вода не выпускает наружу лучи с углами падения, равными или превышающими некоторое значение — все такие лучи целиком отражаются назад в воду. Угол
называется предельным углом полного отражения.
Величину легко найти из закона преломления. Имеем:
.
Но , поэтому
,
откуда
.
Так, для воды предельный угол полного отражения равен:
.
Явление полного внутреннего отражения вы легко можете наблюдать дома. Налейте воду в стакан, поднимите его и смотрите на поверхность воды чуть снизу сквозь стенку стакана. Вы увидите серебристый блеск поверхности — вследствие полного внутреннего отражения она ведёт себя подобно зеркалу.
Важнейшим техническим применением полного внутреннего отражения является волоконная оптика. Световые лучи, запущенные внутрь оптоволоконного кабеля (световода) почти параллельно его оси, падают на поверхность под большими углами и целиком, без потери энергии отражаются назад внутрь кабеля. Многократно отражаясь, лучи идут всё дальше и дальше, перенося энергию на значительное расстояние. Волоконно-оптическая связь применяется, например, в сетях кабельного телевидения и высокоскоростного доступа в Интернет.
к оглавлению ▴
Разберем задачи ЕГЭ по теме: Преломление света.
Задача 1. Нижняя грань AC прозрачного клина посеребрена и представляет собой плоское зеркало. Угол при вершине клина . Луч света падает из воздуха на клин перпендикулярно грани AB, преломляется и выходит в воздух через ту же грань AB, но уэе под углом преломления
Определите показатель преломления материала клина. Сделайте рисунок, поясняющий ход луча в клине.
Дано:
n-?
Решение. Решение задач по геометрической оптике необходимо начинать с построения чертежа (рисунка), моделирующего условия, описанные в тексте задачи.
Световой луч падает на прозрачный клин перпендикулярно стороне АВ (см.рис.1). В этом случае, световой луч не преломляется на границе раздела воздух-клин, так как угол падения равен 0, соответственно, угол преломления также равен 0. Следовательно, внутри клина световой луч попадает на нижнюю грань АС, которая представляет собой плоское зеркало. Согласно рис.1 величина угла
Тогда угол падения луча на плоское зеркало будет равен
То есть угол падения равен .
Согласно закону отражения света, угол падения светового луча равен углу отражения. В треугольнике МКО угол КОМ образован суммой двух углов α, поэтому он равен 60°. Тогда угол падения светового луча на грань АВ также будет равен (равенство накрест лежащих углов).
На следующем этапе задачи надо применить закон преломления света, так как луч переходит из одной среды в другую.
При записи этой формулы учтено, что второй средой является воздух с показателем преломления равным 1, а первой средой является материал клина с показателем преломления n, который необходимо определить. Из последней формулы можно выразить и рассчитать n.
Ответ: 1,15
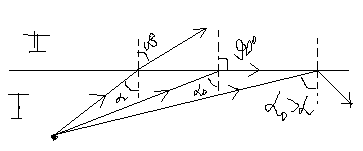
Задача 2. На тонкую собирающую линзу от удалённого источника падает пучок параллельных лучей (см. рисунок). Как изменится положение изображения источника, создаваемого линзой, если между линзой и её фокусом поставить
плоскопараллельную стеклянную пластинку с показателем преломления n (на рисунке положение пластинки отмечено пунктиром)? Ответ поясните, указав, какие физические закономерности Вы использовали. Сделайте рисунок, поясняющий ход лучей до и после установки плоскопараллельной стеклянной пластинки.
Решение. Рассмотрим ход световых лучей от удаленного источника через линзу при отсутствии плоскопараллельной стеклянной пластинки (см.рис.1).
Луч 1-1ʹ проходит через оптический центр линзы и не преломляется. Луч 2-2ʹ идет через фокус и после прохождения через линзу, идет параллельно главной оптической оси. Пересечение этих двух лучей дает действительное изображение удаленного источника, которое расположено в фокальной плоскости линзы. Этот факт также можно доказать, используя формулу тонкой линзы.
Так как источник света расположен на расстоянии то
Тогда формула тонкой линзы (1) примет вид следовательно, f=F, т.е. изображение формируется в фокальной плоскости линзы.
Рассмотрим ход световых лучей через плоскопараллельную стеклянную пластинку. Для этого необходимо использовать закон преломления света.
Рис.2
Согласно рис.2 угол падения луча на пластину равен α. Закон преломления света на границе раздела воздух-пластинка имеет вид:
Здесь учтено, что показатель преломления воздуха равен 1, а пластинки n.
При переходе светового луча из пластинки в воздух, закон преломления света будет иметь вид:
В этом случае первой средой является пластинка с показателем преломления n, а второй средой будет воздух с показателем преломления равным 1.
Из (1) и (2) выразим и
.
и
Так как правые части этих уравнений равны, то
Отсюда вытекает равенство углов . Следовательно, луч, падающий на стеклянную пластину, выходит из нее, оставаясь параллельным входящему лучу. Но при этом выходящий луч немного смещается вверх.
Исходя из этого можно сделать вывод, что изображение удаленного источника после прохождения через плоскопараллельную стеклянную пластину, не изменится. Из удаленного источника выходит бесконечное количество параллельных лучей, которые собираются в фокальной плоскости линзы.
Ответ: не изменится.
Задача 3. Ученик провел опыт по преломлению света, представленный на фотографии. Как изменится при уменьшении угла падения угол преломления светового пучка и скорость света, распространяющегося в стекле? Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшиться
3) не изменится
Запишите в таблицу выбранные цифры для каждой величины. Цифры в ответе могут повторяться.
| Угол преломления | Скорость света в стекле |
Решение. Для ответа на первый вопрос задачи необходимо применить закон преломления света для границы раздела воздух-стекло.
Показатель преломления стекла равен n, а воздуха 1.
При уменьшении угла падения α, будет уменьшаться и значение Так как показатель преломления стекла не изменяется, то значение
так же будет уменьшаться. Поэтому угол преломления уменьшится.
Для ответа на второй вопрос надо учесть, что скорость света в данной среде определяется значением показателя преломления где с – скорость света в вакууме, а n – показатель преломления среды (стекла). Так как эти обе величины не изменяются, то скорость света в стекле так же не изменяется.
Ответ: 23.
Задача 4. Чему равен синус предельного угла полного внутреннего отражения при переходе света из вещества с в вещество с
?
Решение.
Явление полного внутреннего отражения наблюдается при переходе светового луча из оптически более плотной среды в оптически менее плотную (см.рис.1). Источник света S должен находиться в среде с большим показателем преломления.
Для нахождения синуса угла полного внутреннего отражения необходимо воспользоваться законом преломления света.
При полном внутреннем отражении преломленный луч скользит по границе раздела двух сред и угол преломления . С учетом того, что
уравнение (1) примет вид:
Ответ: 0,8.
Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Преломление света.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
The frequency always remain the same in all media. So the speed of light and the wavelength change. The refractive index tells you how much the speed of light changes:
$$ v = frac{c}{n} , $$
where $n$ is the refractive index, $c$ is the speed of light in vacuum and $v$ is the speed of light in the medium.
In vacuum, the speed of light, wavelength $lambda$ and frequency $nu$ are related by
$$ c = lambda nu , $$
and in the medium, it is related by
$$ v = lambda_m nu . $$
So now one can substitute these two equations into the first equation, cancel off the frequency and get
$$ lambda_m = frac{lambda}{n} . $$
Physically, one can understand it as follows. In the medium, light propagates slower. Therefore, the wavelength would needs to be shorter.
Условие задачи:
В дно водоема глубиной 2 м вбита свая, выступающая из воды на 0,5 м. Найти длину тени от сваи на дне водоема при угле падения лучей 30°.
Задача №10.3.24 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(H=2) м, (h=0,5) м, (alpha=30^circ), (L-?)
Решение задачи:
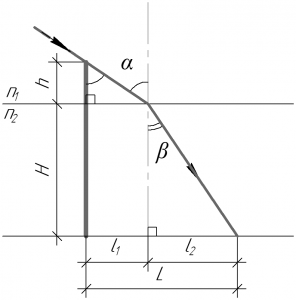
[L = {l_1} + {l_2};;;;(1)]
При этом из прямоугольных треугольников можно найти длины (l_1) и (l_2) по следующим формулам:
[left{ begin{gathered}
{l_1} = h cdot tgalpha hfill \
{l_2} = H cdot tgbeta hfill \
end{gathered} right.]
То есть формула (1) примет вид:
[L = h cdot tgalpha + H cdot tgbeta;;;;(2)]
Запишем закон преломления света (также известен как закон преломления Снеллиуса):
[{n_1}sin alpha = {n_2}sin beta]
Здесь (alpha) и (beta) – угол падения и угол преломления соответственно, (n_1) и (n_2) – показатели преломления сред. Показатель преломления воздуха (n_1) равен 1, показатель преломления воды (n_2) равен 1,33.
Тогда:
[sin beta = frac{{{n_1}sin alpha }}{{{n_2}}}]
[beta = arcsin left( {frac{{{n_1}sin alpha }}{{{n_2}}}} right)]
Полученное выражение подставим в формулу (2), тогда:
[L = h cdot tgalpha + H cdot tgleft( {arcsin left( {frac{{{n_1}sin alpha }}{{{n_2}}}} right)} right)]
Задача решена в общем виде, подставим данные задачи в полученную формулу и посчитаем численный ответ:
[L = 0,5 cdot tg30^circ + 2 cdot tgleft( {arcsin left( {frac{{1 cdot sin 30^circ }}{{1,33}}} right)} right) = 1,1;м]
Ответ: 1,1 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.3.23 В дно пруда вертикально вбита свая так, что она целиком находится под водой. Определите
10.3.25 Высота солнца над горизонтом 60°. Высота непрозрачного сосуда 25 см. На сколько
10.3.26 Кубический сосуд с непрозрачными стенками расположен так, что глаз наблюдателя
19.
Лучевая (геометрическая) оптика.
Геометрическая оптика как предельный
случай волновой оптики. Основные
понятия и законы геометрической оптики.
Полное внутреннее отражение. Преломление
света в призме и на сферической
поверхности. Линза. Построение
изображений.
Раздел
оптики, в к-м законы распространения
света рассм-ся на основе представления
о световых лучах, н-ся геометрической
оптикой.
Световой
луч
– это линия, вдоль которой распространяется
поток световой энергии. Представление
о независимо расп-ся световых лучах
возникло ещё в античной науке. Древне-греч.
учёный Евклид сф-л закон прямолинейного
распространения света и закон зеркального
отражения света. В 17 в. Г. о. бурно
развивалась в связи с изобретением
ряда оптич. приборов (зрительная
труба,
телескоп, микроскоп
и т. д.) и началом их широкого исп-ия.
Основные
законы оптики: закон прямолинейного
распространения света, закон независимости
световых лучей, закон отражения света,
закон преломления света.
Закон
прямолинейного распространения света:
свет в оптически однородной среде
распространяется прямолинейно.
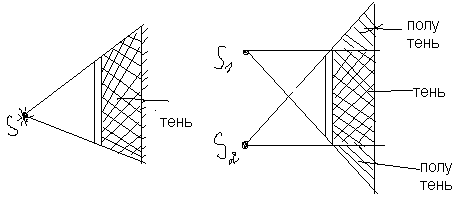
Доказательством
этого закона является наличие тени с
резкими границами от непрозрачных
предметов при освещении их точечными
источниками света (источники, размеры
которых значительно меньше освещаемого
предмета и расстоянии до него).
Углом
падения
называется угол между падающим лучом
света и перпендикуляром к границе
раздела двух сред, восстановленным в
точке падения.
Углом
отражения
называется угол между отраженным лучом
и перпендикуляром к поверхности,
отразившей луч света, восстановленным
в точке падения.
Закон
независимости световых лучей:
Распространение световых лучей в среде
происходит независимо друг от друга.
Эффект,
производимый отдельным пучком, не
зависит от того, действуют ли одновременно
остальные пучки или они устранены.
Разбивая световой поток на отдельные
световые пучки (например, с помощью
диафрагм), можно показать, что действие
выделенных световых пучков независимо.
Закон
отражения световых лучей:
отраженный луч лежит в одной плоскости
с падающим лучом и перпендикуляром,
проведенным к границе раздела двух
сред в точке падения; угол отражения
равен углу падения.
Изображение
называется действительным, если оно
образовано самими лучами (т.е. в данную
точку поступает световая энергия).
____
Виды
отражения света:
зеркальное
–
лучи света, падающие на зеркальную
поверхность параллельным пучком, после
отражения остаются параллельными;
рассеянное
(диффузное)
– поверхность, размеры неровностей
которой больше световой волны, отражает
лучи света по всевозможным направлениям.
Преломление
света
– это изменение направления распространения
света при прохождении через границу
раздела двух прозрачных сред.
Закон
преломления света:
Лучи падающий и преломленный лежат в
одной плоскости с перпендикуляром,
проведенным в точке падения луча к
плоскости границы раздела двух сред;
отношение синуса угла падения α к синусу
угла преломления β есть величина
постоянная для двух данных сред:
Где
n21
– показатель преломления второй среды
относительно первой (относительный
показатель преломления).
Относительный
показатель преломления
двух сред равен отношению их абсолютных
показателей преломления:
Абсолютным
показателем преломления
среды называется величина n,
равная отношению скорости с
электромагнитных
волн в вакууме к их фазовой скорости
υ в среде:
Полное
внутреннее отражение.
Если свет переходит из оптически менее
плотной среды в оптически более плотную
(n2>n1),
то всегда существуют как отраженный,
так и преломленный пучки, энергии
которых соответствуют условию. Несколько
иной результат получается при переходе
света из оптически плотной в оптически
менее плотную среду (n2<n1)
например, из воды в воздух или из стекла
в воду.
Если
угол падения небольшой, то существуют
оба пучка – как отраженный, так и
преломленный. Если же угол падения
возрастает, то энергия отраженного
пучка резко возрастает, а преломленного
– столь же сильно убывает. При некотором
угле падения α1→αпр
угол преломления α2→900,
а энергия преломленного пучка падает
до нуля. Следовательно, окажутся равными
энергии отраженного и падающего пучка.
Это явление называется полным отражением.
При
переходе света из среды с большим
показателем преломления n1
(оптически более плотной) в среду с
меньшим показателем n2
(оптически менее плотную согласно
и преломленный луч удаляется от
перпендикуляра. С увеличением угла
падения α растет и угол преломления
β>α.
Когда
угол падения достигает некоторого
предельного значения iпред,
определявшегося из условия:
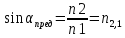
то
преломленный луч направлен вдоль
границы раздела. При еще большем угле
падения α>αпред·Sin
α>n2/n1,
Sin
β=
(1.8)
Для
таких углов падения уравнение (1.8) дает
мнимое значение угла преломления.
Следовательно, α>αпред,
преломление прекращается и остается
лишь отраженный луч. Это явление носит
название полного внутреннего отражения
– вся энергия света, падающего на
границу раздела, при этом полностью
отражается обратно в первую среду.
Явление
полного внутреннего отражения
используется в различных оптических
приборах (бинокли, перископы и др.), а
также для измерения показателя
показателей преломления (рефрактометры).
Показатель преломления различных
сортов стекла – около 1.5. поэтому
предельный угол для границы стекло
воздух составляет αпред=arcsin(1/1,5)=420
и при падении лучей на эту границу под
несколько большим углом, равным 450,
будет всегда происходить полное
внутренне отражение.
Наименьший
угол, с которого начинается полное
отражение, называется предельным
углом
полного отражения.
Призма.
В
задачах с призмами поворот света призмой
можно рассматривать как два последовательных
преломления света на плоских гранях
призмы при входе света в призму и при
его выходе.
Особый
интерес представляет частный случай
призмы с малым углом при вершине (
на рис. 2). Такую призму называют тонкой
призмой. Обычно рассматриваются задачи,
в которых свет падает на тонкую призму
почти перпендикулярно ее поверхности.
При этом за два преломления лучи света
поворачивают на малый угол
в
плоскости перпендикулярной ребру
призмы в сторону утолщения призмы (рис.
2). Угол поворота не зависит от угла
падения света в приближении малых углов
падения. Это означает, что призма
поворачивает «кажущееся» положение
источника света на угол
в
плоскости перпендикулярной ребру
призмы.
Из
двух таких тонких призм состоит, в
частности, бипризма Френеля (рис. 3),
проходя через которую свет от точечного
источника распространяется далее так,
как если бы свет излучался двумя
точечными когерентными
источниками.
Преломление
и отражение
света
на сферической поверхности.
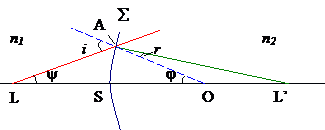
Предположим,
что две среды с показателями преломления
n1
и
n2
разделяются
сферической поверхностью Σ (рис. 3.2.).
На линии LL‘,
проходящей
через центр нашей сферы О,
поместим точечный источник света L.
Рассмотрим
узкий гомоцентрический
конус лучей, падающий из L
на
поверхность раздела двух сред.
|
|
|
Рис. |
Мы
предполагаем пучок настолько узким,
т.е. угол
настолько
малым, что практически можно считать
отрезок LS
равным
LA,
L‘S равным
L‘A
и
т.д. Такой узкий пучок будем называть
параксиальным.
Итак, условие параксиальности пучка
есть
LS
»
LA
и
L‘S
»
L‘A.
Возьмем
какой-либо луч из этого пучка, например
LA,
падающий
на Σ под углом i,
построим
сопряженный ему преломленный луч AL‘
(угол
преломления r)
и найдем положение точки, в которой
преломленный луч пересечет ось системы.
Из
треугольника ALO
имеем
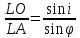
, из треугольника OAL
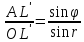
Отсюда
(1)
В
дальнейшем все отрезки вдоль оси будем
отсчитывать от точки S,
считая положительными отрезки,
откладываемые от S
вправо
(в
направлении распространяющегося
света), и отрицательными – отрезки,
откладываемые влево. Т. о, AL
» SL= – а1
,
AL‘»
SL‘= а2,
AO
= SO = R (радиус
нашей сферы). В таком
случае
LO
= -а1
+ R, OL‘ = а2
– R. Используя
закон преломления при переходе из
первой среды во вторую, получим
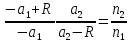
т.е.
(2)
Последняя
формула показывает, что произведение
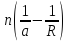
при преломлении сохраняет свою величину
Q.
Его называют нулевым
инвариантом Аббе. Для
многих целей этой формуле удобно придать
вид
(3)
Соотношение
(3) позволяет найти длину а2
= SL‘,
если задано а1
= LS,
т.е. позволяет отыскать положение точки
L‘
по
заданному L.
При выводе его мы, кроме закона
преломления, пользовались еще
допущением, что луч LA
принадлежит
к параксиальному пучку. Следовательно,
соотношение справедливо для любого
луча параксиального пучка.
Из формулы (3) видно, что а2
при заданных параметрах задачи (п1,
n2,
R)
зависит только от а1.
Таким
образом, все лучи параксиального
гомоцентрического пучка, выходящего
из L,
пересекают ось в одной и той же точке
L‘,
которая является, следовательно,
стигматическим изображением источника
L.
Итак, гомоцентрический пучок при
преломлении на сферической поверхности
остается гомоцентрическим, если он
удовлетворяет условию параксиальности.
Основное уравнение (3) охватывает все
случаи преломления лучей на сферической
поверхности. Пользуясь установленным
выше правилом знаков, мы можем разобрать
случай выпуклой (R>0)
или
вогнутой (R
<
0) поверхности.
Точно
так же в зависимости от того, будут ли
а1
и a2
иметь разные знаки или одинаковые, мы
будем иметь случаи, когда изображение
располагается с противоположной по
сравнению с источником стороны
преломляющей поверхности или лежит по
одну сторону с ним. В первом случае (а2
> 0) точка, именуемая изображением,
есть действительно точка пересечения
преломленных лучей. Такое изображение
называется действительным.
Во втором случае (а2
< 0), очевидно, преломленные лучи, идущие
во второй среде, остаются расходящимися
и реально не пересекаются. В этом случае
название изображения относится к той
воображаемой точке, которая представляет
собой место пересечения предполагаемого
продолжения преломленных лучей. Такое
изображение называется мнимым.
Наши рассуждения и формула (3) показывают,
что гомоцентрический пучок после
преломления направлен так, что его лучи
или пересекаются в одной точке
(действительное изображение), или могут
быть представлены как пересекающиеся
в одной точке (мнимое изображение).
Именно в этом смысле он и остается
гомоцентрическим.
Так как для всех наших рассуждений нам
важно знать направление
световых лучей, то при всех построениях
мы одинаково можем пользоваться как
действительным, так и мнимым изображением.
Формула
(3) показывает также, что если бы источник
был в L‘,
то изображение расположилось бы в L
(взаимность).
Линза.
Сферическая
линза
– прозрачное тело, ограниченное с двух
сторон сферическими поверхностями.
Линзы
п/с прозрачные тела, ограниченные двумя
поверхностями ( одна из них обычно
сферическая, иногда цилиндрическая, а
вторая – сферическая или плоская),
преломляющими световые лучи, способные
формировать оптические изображения
предметов.
Материалом
для линз служат стекло, кварц, кристаллы,
пластмассы и т.п. По внешней форме линзы
делятся на: 1) двояковыпуклые; 2)
плосковыпуклые; 3) двояковогнутые; 4)
плосковогнутые; 5) выпукло-вогнутые; 6)
вогнуто-выпуклые. По оптическим свойствам
линзы делятся на собирающие и рассеивающие.
Линза
наз-ся тонкой,
если ее толщина (расстояние между
ограничивающими поверхностями)
значительно меньше по сравнению с
радиусами поверхностей, ограничивающих
линзу. Прямая, проходящая через центры
кривизны поверхностей линзы, наз-ся
главной
оптической осью.
Точка
О – это точка, называемая оптическим
центром линзы,
лежащая на главной оптической оси и
обладающая тем свойством, что лучи
проходят сквозь нее не преломляясь.
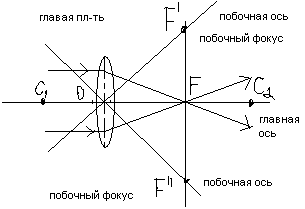
Главная
плоскость
– плоскость, проходящая через центр
тонкой линзы перпендикулярно к главной
оптической оси.
Главный
фокус линзы F
– точка, в которую собирается параллельный
пучок света, распространяющийся
параллельно главной оптической оси.
Фокусное
расстояние линзы
– расстояние OF
от оптического центра линзы до ее
главного фокуса.
Фокальная
плоскость
– плоскость, проходящая через главный
фокус перпендикулярно к главной
оптической оси.
Построение
изображений. В
задачах на построение изображений
подразумевается, что протяженный
источник света состоит из некогерентных
точечных источников. В этом случае
изображение протяженного источника
света состоит из изображений каждой
точки источника, полученных независимо
друг от друга.
Изображение
точечного источника — это точка
пересечения всех лучей после прохождения
через систему, лучей испущенных точечным
источником света. Точечный источник
испускает сферическую световую волну.
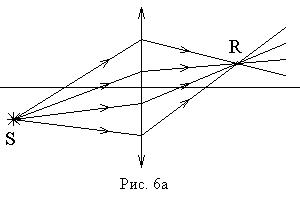
В приближении параксиальной оптики
сферическая волна, проходя через линзу
(рис. 6), распространяется и далее в виде
сферической волны, но с другим значением
радиуса кривизны. Лучи за линзой либо
сходятся в одну точку (рис. 6а), которую
называют действительным изображением
источника (точка
),
либо расходятся (рис. 6б). В последнем
случае продолжения лучей назад
пересекаются в некоторой точке
,
которая называется мнимым изображением
источника света.
В
параксиальном приближении все лучи,
исходящие из одной точки до линзы, после
линзы пересекаются в одной точке,
поэтому для построения изображения
точечного источника достаточно найти
точку пересечения «удобных нам»
двух лучей, эта точка и будет изображением.
Если
перпендикулярно оптической оси поставить
лист бумаги (экран) так, чтобы изображение
точечного источника попало на экран,
то в случае действительного изображения
на экране будет видна светящаяся точка,
а в случае мнимого изображения — нет.
Построение
изображения в тонкой линзе. Есть
три луча, удобных для построения
изображения точечного источника света
в тонкой линзе.
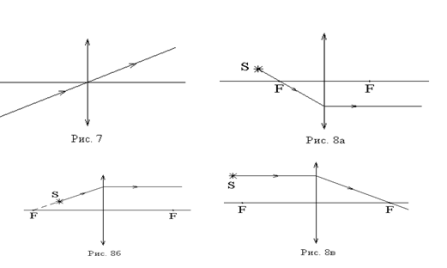
Первый
луч проходит через центр линзы. После
линзы он не изменяет своего направления
(рис. 7) как для собирающей так и для
рассеивающей линзы. Это справедливо
только в том случае, если среда с обеих
сторон линзы имеет одинаковый показатель
преломления.
Два других удобных луча рассмотрим на
примере собирающей линзы. Один из них
проходит через передний фокус
(рис. 8а), или его продолжение назад
проходит через передний фокус
(рис. 8б). После линзы такой луч пойдет
параллельно оптической оси. Другой луч
проходит до линзы параллельно оптической
оси, а после линзы через задний фокус
(рис. 8в).
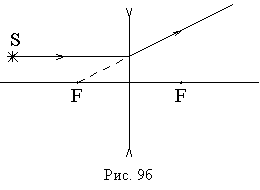
Удобные
для построения изображения лучи в
случае рассеивающей линзы показаны на
рис. 9а,9б.
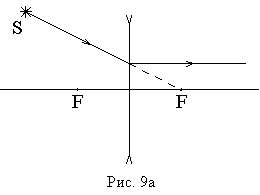
Точка
пересечения, мнимого или действительного,
любой пары из этих трех лучей, прошедших
линзу, совпадает с изображением
источника. 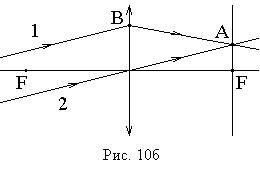
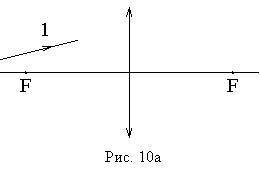
В
задачах по оптике иногда возникает
потребность найти ход луча не для одного
из удобных нам трех лучей, а для
произвольного луча (1 на рис. 10), направление
которого до линзы определено условиями
задачи.
В
таком случае полезно рассмотреть,
например, параллельный ему луч (2 на
рис. 10б), проходящий через центр линзы,
независимо от того есть или нет такой
луч на самом деле.
Параллельные
лучи собираются за линзой в фокальной
плоскости. Эту точку (
на рис. 10б) можно найти как точку
пересечения фокальной плоскости и
вспомогательного луча 2, проходящего
линзу без изменения направления. Вторая
точка, необходимая и достаточная для
построения хода луча 1 после линзы, это
точка на тонкой линзе (
на рис. 10б), в которую упирается луч 1 с
той стороны, где его направление
известно.
Построение
изображения в толстой линзе. Тонкая
линза — линза, толщина которой много
меньше ее фокусного
расстояния.
Если линзу нельзя считать тонкой, то
каждую из двух сферических поверхностей
линзы можно рассматривать как отдельную
тонкую линзу.
Тогда
изображение в толстой линзе можно найти
как изображение изображения. Первая
сферическая поверхность толстой линзы
дает изображение источника как
изображение в тонкой линзе. Вторая
сферическая поверхность дает изображение
этого изображения.
Другой
подход при построении изображений
состоит в том, что вводится понятие
главных плоскостей центрированной
оптической системы, частным случаем
которой может быть толстая линза.
Центрированная оптическая система,
которая может состоять и из большого
числа линз, полностью характеризуется
двумя фокальными и двумя главными
плоскостями. Полностью характеризуется
в том смысле, что знание положения этих
четырех плоскостей достаточно для
построения изображений. Все четыре
плоскости перпендикулярны оптической
оси, следовательно свойства оптической
системы полностью определяются четырьмя
точками пересечения четырех плоскостей
с оптической осью. Эти точки называются
кардинальными точками системы.
Для
тонкой линзы обе главные плоскости
совпадают с положением самой линзы.
Для более сложных оптических систем
существуют формулы расчета положения
кардинальных точек через радиусы
кривизны поверхностей линз и показатели
их преломления
[2].
Для
построения изображения точечного
источника достаточно рассмотреть
прохождение через оптическую систему
двух удобных нам лучей и найти точку
их пересечения после линзы, либо точку
пересечения продолжений лучей назад
(для мнимого изображения).
Построение
хода лучей проводится так, как будто
между главными плоскостями системы
находится тонкая линза, а пространство
между главными плоскостями отсутствует.
Пример построения приведен на рис. 11.
и
—
главные плоскости системы. 
Задача
прохождения света через центрированную
оптическую систему может быть решена
не только геометрическим построением
хода лучей, но и аналитически. Для
аналитического решения задач удобен
матричный метод [2].
Формулы
тонкой линзы. Если
в задаче требуется аналитический
результат, а не построение изображения,
то для решения обычно достаточно трех
формул:
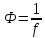
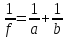
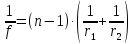
Здесь
—
оптическая сила линзы,
—
фокусное
расстояние,
—
расстояние от линзы до источника света,
—
расстояние от линзы до изображения,
и
—
радиусы кривизны обоих поверхностей
линзы,
—
показатель
преломления
материала линзы.
В
этих формулах все величины с размерностью
длины могут принимать как положительные,
так и отрицательные значения. Фокусное
расстояние
положительно
для собирающей линзы,
положительно
для действительного изображения,
и
положительны
для двояковыпуклой линзы. Расстояние
от линзы до источника — положительная
величина, но и тут можно представить
себе мнимый точечный источник, для
которого это расстояние будет
отрицательным.
Реже
встречаются задачи, в которых показатели
преломления
среды с двух сторон от линзы различаются.
Тогда потребуются следующие формулы:
Может
быть полезна и формула для оптической
силы одной сферической поверхности, в
частности при рассмотрении толстой
линзы как двух сферических поверхностей:
Сферическое
зеркало. Чтобы
удовлетворить приближению параксиальной
оптики, нужно потребовать, чтобы
сферическое зеркало было малой частью
сферы. Другими словами, размер зеркала
должен быть много меньше радиуса
кривизны сферы.
Сферическое
зеркало отражает световые лучи аналогично
оптической системе, состоящей из тонкой
линзы и вплотную поставленного плоского
зеркала. Вогнутое зеркало аналогично
собирающей линзе, выпуклое — рассеивающей.
Модуль
фокусного
расстояния
сферического зеркала равен половине
радиуса кривизны сферы
Фокус
расположен посередине между зеркалом
и центром сферы.
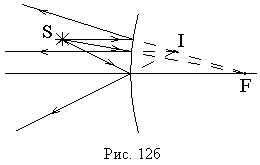
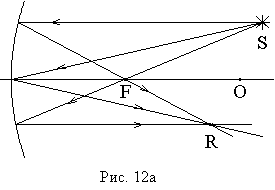
На
рис. 12а,б приведены примеры построения
изображений точечного источника света
в сферическом зеркале.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #