Что такое предельный цикл системы дифференциальных уравнений
Система обыкновенных дифференциальных уравнений называется автономной, если независимая переменная не входит явно в систему.
Рассмотрим автономные системы второго порядка:
Будем полагать, что правые части системы f1(x1, x2), f2(x1, x2) непрерывно дифференцируемы в области определения, т.е. справедлива теорема существования и единственности.
Название автономная система оправдано тем, что решение само управляет своим изменением, поскольку производные dx1/dt и dx2/dt зависят только от x1 и x2. Автономные системы называют также динамическими системами.
Пусть x1= j 1(t), x2= j 2(t) — решение автономной системы второго порядка. Тогда уравнения
задают в параметрической форме кривую на плоскости (x1, x2). Эта кривая называется фазовой кривой или фазовой траекторией системы. Плоскость, на которой расположены фазовые траектории называется фазовой плоскостью автономной системы. Именно поэтому автономные системы второго порядка принято называть автономными системами на плоскости.
Для фазовых траекторий автономной системы с непрерывно дифференцируемой правой частью справедливы следующие утверждения:
- две фазовые кривые либо не имеют общих точек, либо совпадают;
- фазовая траектория, отличная от точки, есть гладкая кривая (в каждой ее точке есть ненулевой касательный вектор);
- всякая фазовая кривая принадлежит к одному из трех типов— гладкая кривая без самопересечений, замкнутая гладкая кривая (цикл), точка.
ПРИМЕР 1. Виды фазовых кривых.
Если фазовая траектория x1= j1(t), x2= j2(t) — замкнутая гладкая кривая g, в некоторой окрестности которой нет других замкнутых траекторий, то она является предельным циклом: все траектории, которые начинаются достаточно близко от g, спиралевидно приближаются к ней либо при , либо при .
Предельные циклы бывают трех типов:
- устойчивые — близкие траектории «навиваются» на него при (пример 2);
- неустойчивые— близкие траектории уходят от него при (пример 3);
- полуустойчивые — траектории, лежащие по одну сторону от цикла, «навиваются» на него при , а лежащие по другую строну — «отходят» от цикла (пример 4).
ПРИМЕР 2. Устойчивый предельный цикл.
ПРИМЕР 3. Неустойчивый предельный цикл.
ПРИМЕР 4. Полуустойчивый предельный цикл.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Что такое предельный цикл системы дифференциальных уравнений
КОЛЕБАНИЯ В БИОЛОГИЧЕСКИХ СИСТЕМАХ
Понятие автоколебаний. Изображение автоколебательной системы на фазовой плоскости. Предельные циклы. Условия существования предельных циклов. Рождение предельного цикла. Бифуркация Андронова ‑ Хопфа. Мягкое и жесткое возбуждение колебаний. Модель брюсселятор. Примеры автоколебательных моделей процессов в живых системах. Колебания в темновых процессах фотосинтеза. Автоколебания в модели гликолиза. Внутриклеточные колебания концентрации кальция. Клеточные циклы.
Для биологических систем характерно периодическое изменение различных характеристик. Период этих колебаний может быть связан с периодическими изменениями условий жизни на Земле — смена времен года, смена дня и ночи. Существуют и другие геофизические ритмы –солнечные, лунные, связанные с периодами атмосферных явлений. Геофизические и биологические ритмы сопоставлены на рис. 8.1. Но многие периодические процессы имеют частоту изменения, не связанную очевидным образом с внешними геокосмическими циклами. Это так называемые «биологические часы» различной природы, начиная от колебаний биомакромолекул, биохимических колебаний, вплоть до популяционных волн.
Внутриклеточные колебания задают эндогенные биологические ритмы, которые свойственны всем живым системам. Именно они определяют периодичность деления клеток, отмеряют время рождения и смерти живых организмов. Модели колебательных систем используются в ферментативном катализе, теории иммунитета, в теории трансмембранного ионного переноса, микробиологии и биотехнологии.
С некоторыми из типов периодических движений мы уже имели дело при рассмотрении особых точек типа центр и затухающих или нарастающих колебаний в случае устойчивого и неустойчивого фокуса. Однако «биологические часы» имеют свойство, отличающее их от рассмотренных типов колебаний — неизменность во времени периода и амплитуды таких колебаний, означающую стационарность и устойчивость колебательного режима.
Рис. 8.1. Космофизические, геофизические и биологические ритмы. Справа – шкала периодов, слева – шкала частот
В данном случае периодическое изменение величин представляет собой один из типов стационарного поведения системы. Если колебания в системе имеют постоянные период и амплитуду, устанавливаются независимо от начальных условий и поддерживаются благодаря свойствам самой системы, а не вследствие воздействия периодической силы, система называется автоколебательной.
Незатухающие колебания в таких системах устойчивы, так как отклонения от стационарного колебательного режима затухают. К классу автоколебательных систем относятся колебания в гликолизе и других метаболических системах, периодические процессы фотосинтеза, колебания концентрации кальция в клетке, колебания численности животных в популяциях и сообществах.
Предельный цикл. В фазовом пространстве такому типу поведения соответствует притягивающее множество (аттрактор), называемое предельным циклом .
Предельный цикл есть изолированная замкнутая кривая на фазовой плоскости, к которой в пределе при t ® ¥ стремятся все интегральные кривые . Предельный цикл представляет стационарный режим с определенной амплитудой, не зависящий от начальных условий, а определяющийся только организацией системы. Существование предельного цикла на фазовой плоскости есть основной признак автоколебательной системы. Очевидно, что при автоколебательном процессе фаза колебаний может быть любой.
Остановимся на общих характеристиках автоколебательных систем. Рассмотрим систему уравнений общего вида:
(8.1)
Если T (T > 0) — наименьшее число, для которого при всяком t
то изменение переменных x = x ( t ), y = y ( t ) называется периодическим изменением с периодом T .
Периодическому изменению соответствует замкнутая траектория на фазовой плоскости, и обратно: всякой замкнутой траектории соответствует бесконечное множество периодических изменений, отличающихся друг от друга выбором начала отсчета времени.
Если периодическому изменению на фазовой плоскости соответствует изолированная замкнутая кривая, к которой с внешней и внутренней стороны приближаются (при возрастании t) соседние траектории по спиралям, эта изолированная замкнутая траектория есть предельный цикл.
Простые примеры позволяют убедиться, что система общего вида (8.1) допускает в качестве траекторий предельные циклы.
Например, для системы
(8.2)
траектория является предельным циклом. Его параметрические уравнения будут:
а уравнения всех других фазовых траекторий запишутся в виде:
.
Значениям постоянной интегрирования С > 0 соответствуют фазовые траектории, накручивающиеся на предельный цикл изнутри (при t ® ¥ ), а значениям –1 C 0 траектории, накручивающиеся снаружи.
Предельный цикл называется устойчивым, если существует такая область на фазовой плоскости, содержащая этот предельный цикл, — окрестность e , что все фазовые траектории, начинающиеся в окрестности e , асимптотически при t ® ¥ приближаются к предельному циклу.
Если же, наоборот, в любой сколь угодно малой окрестности e предельного цикла существует по крайней мере одна фазовая траектория, не приближающаяся к предельному циклу при t ® ¥ , то такой предельный цикл называется неустойчивым . Такие циклы разделяют области влияния (бассейны) разных притягивающих множеств.
На рис. 8.2 изображены устойчивый предельный цикл ( а) и неустойчивые ( б) и ( в).
Рис. 8.2. Устойчивый (а) и неустойчивые (б и в) предельные циклы на фазовой плоскости
Неустойчивые предельные циклы, подобные изображенному на рис. 8.2 б, такие, что все траектории с одной стороны (например, изнутри) приближаются к ним, а с другой стороны (например, извне) удаляются от них при t ® ¥ , называют «полуустойчивыми» или двойными. Последнее название связано с тем, что обычно такие циклы при подходящем изменении параметра системы расщепляются на два, один из которых устойчив, а другой неустойчив.
А.М. Ляпунов показал, что для исследования устойчивости периодического движения x = j ( t), y = y ( t) можно идти по пути линеаризации уравнений, подобно тому, как мы это делали при исследовании устойчивости состояний равновесия. Если положить
подставить эти выражения в уравнения (8.1), разложить правые части этих уравнений — функции
в ряды по степеням x и h и отбросить нелинейные члены, то мы получим линейные уравнения (уравнения первого приближения) для координат возмущения x и h :
Коэффициенты в правой части:
Это система линейных дифференциальных уравнений с периодическими коэффициентами периода T, поскольку a, b, c, d суть функции от j , y — периодических функций времени с периодом T. Общий вид ее решения
Здесь — некоторые периодические функции с периодом T. От показателей и которые носят название «характеристических показателей», зависят свойства решений для отклонений от стационарного периодического решения x и h . А именно, знаки их действительных частей определяют, являются ли эти решения нарастающими или затухающими. Можно показать, что в силу автономности исходной системы (8.1) один из характеристических показателей равен нулю, а другой равен h.
где x = j ( t ), y = y ( t ) — любое периодическое решение, соответствующее рассматриваемому предельному циклу, T — период решения.
Таким образом, устойчивость предельного цикла (и устойчивость в смысле Ляпунова соответствующих периодических движений) определяется знаком характеристического показателя. Предельный цикл устойчив, если h 0 и неустойчив, если h > 0. Если же h = 0, уравнения первого приближения не решают вопроса об устойчивости периодического движения.
Для нахождения предельных циклов не существует таких простых аналитических методов, как для нахождения стационарных точек и исследования их устойчивости. Однако, исследование фазовой плоскости системы позволяет ответить на вопрос, есть в данной системе предельный цикл, или нет.
Сформулируем несколько теорем, определяющих наличие предельного цикла по топологическому строению фазовой плоскости. Они могут быть полезны как при аналитическом, так и при компьютерном анализе системы.
Теорем а 1. Пусть на фазовой плоскости существует область, из которой фазовые траектории не выходят, и в которой нет положений равновесия (особых точек). Тогда в этой области обязательно существует предельный цикл, причем все остальные траектории обязательно наматываются на него.
На рис. 8.3. изображена такая область G, из которой фазовые траектории не выходят. Это означает, что фазовые траектории либо входят, пересекая границу, внутрь области, либо сама граница является траекторией. Легко видеть, что такая область не может быть односвязной. Поскольку траектория наматывается на предельный цикл изнутри, это означает, что внутри этого предельного цикла на фазовой плоскости существует либо неустойчивая особая точка, либо неустойчивый предельный цикл, очевидно, не принадлежащие рассматриваемой области G.
Таким образом, если найти на фазовой плоскости такую двусвязную область, что направления фазовых траекторий на всей границе обращены внутрь этой области, то можно утверждать, что внутри этой области имеется предельный цикл.
Теорема 2. Если существует на фазовой плоскости некоторая замкнутая область, такая, что все фазовые траектории, пересекающие границу этой области, входят в нее, и внутри этой области находится неустойчивая особая точка, то в этой области обязательно имеется хотя бы один предельный цикл (рис. 8.4)
Рис. 8.4. Иллюстрация к теореме 2
Рис. 8.3. Иллюстрация к теореме 1. Жирная кривая – предельный цикл
Приведем также некоторые критерии отсутствия замкнутых фазовых траекторий (в том числе предельных циклов).
1. Если в системе не существует особых точек, то в ней не может быть и замкнутых фазовых траекторий.
2. Если в системе существует только одна особая точка, отличная от узла, фокуса и центра (например, седло), то такая система не допускает замкнутых фазовых траекторий.
3. Если в системе имеются только простые особые точки, причем через все точки типа узел и фокус проходят интегральные кривые, уходящие на бесконечность, то в такой системе нет замкнутых фазовых траекторий.
В случае, если критерии 1–3 выполнены, можно с уверенностью утверждать, что в системе нет предельных циклов. Однако невыполнение этих критериев еще не позволяет сделать вывод о наличии в системе предельных циклов и, следовательно, автоколебаний.
Рис. 8.5. Фазовый портрет системы, имеющий устойчивый и неустойчивый (пунктир) предельные циклы
Неустойчивый предельный цикл также может содержаться в фазовом портрете грубых систем. Однако такой предельный цикл не соответствует реальному периодическому процессу, он играет лишь роль «водораздела», по обе стороны которого траектории имеют различное поведение. Например, на рис. 8.5 представляет собой сепаратрису, отделяющую область тяготения траекторий к устойчивой особой точке, с одной стороны, и к устойчивому предельному циклу, с другой.
Рождение предельного цикла. Бифуркация Андронова-Хопфа.
Существование предельных циклов возможно лишь в системе типа (8.1), правые части которой представлены нелинейными функциями.
На бифуркационной диаграмме 4.11 мы видели, что при пересечении оси абсцисс происходит смена устойчивости фокуса. Нулевым значениям действительной части характеристических чисел (ляпуновских показателей) соответствует особая точка типа центр. В нелинейной системе, где возникает неустойчивый фокус, при этом возможно рождение предельного цикла. Такой переход легко проследить в «модельной» системе:
(8.3)
Схематически возникновение предельного цикла в системе (8.3) изображено на фазопараметрической диаграмме на рис. 8.6.
Рис. 8.6. Закритическая (суперкритическая) бифуркация Андронова-Хопфа. Мягкое возбуждение. При с>0 возникают автоколебания, амплитуда которых растет с увеличением с.
Выполнению условия Re l 1,2 = 0, причем Im l 1,2 ¹ 0, соответствует бифуркация Андронова–Хопфа или бифуркация рождения (исчезновения) предельного цикла. Бифуркация впервые была исследована А.А. Андроновым для случая N = 2 и обобщена Е. Хопфом на системы с произвольной размерностью. (Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М., Наука, 1981; Hopf E ., 1942)
Существуют два типа бифуркации Андронова–Хопфа. Только что мы рассмотрели суперкритическую бифуркацию (мягкое возбуждение автоколебаний). Возможна также субкритическая бифуркация (жесткое возбуждение автоколебаний). В этом случае при бифуркационном значении параметра устойчивый фокус теряет устойчивость из-за «влипания» в него неустойчивого предельного цикла (рис. 8.7). Фокус становится неустойчивым, а аттрактором при этом может стать предельный цикл большой амплитуды.
Рис. 8.7. Докритическая (субкритическая) бифуркация Андронова – Хопфа. Жесткое возбуждение автоколебаний. «Локальные события» при изменении параметра при переходе через бифуркационное значение: устойчивый фокус и неустойчивый предельный цикл пунктир, ( а) при уменьшении параметра с переходят в центр (б) , а затем в неустойчивый фокус ( в). Внешний большой устойчивый предельный цикл находится за пределами локальной системы, в которой происходит бифуркация.
«Модельной» системой (см. лекция 6), описывающей рождение предельного цикла при жестком возбуждении, является система:
(8.4)
Приравняв правую часть первого уравнения нулю, получим стационарные значения r :
Ветвь r = 0 устойчива при c c > 0.
Рис 8.8. Фазовые траектории в окрестности «черной дыры» при разных значениях параметра c .
устойчивый предельный цикл
При с > –1 стационарное решение — устойчивый предельный цикл.
При –1 с 0 стационарное решение — неустойчивый предельный цикл.
Рассмотрим, что произойдет, если двигаться по параметру с, начиная с отрицательных значений (Рис.8.8). Первоначально имеется единственное устойчивое стационарное состояние r = 0, колебаний нет. При c > –1 существует также устойчивый предельный цикл, но система не покидает своего устойчивого стационарного состояния. Однако после того как с становится положительным, стационарное состояние становится неустойчивым, и происходит резкий скачок к устойчивому предельному циклу. В системе начинаются колебания сразу большой амплитуды. Если двигаться от положительных значений с к отрицательным, колебания большой амплитуды сохраняются до тех пор, пока с не станет меньше –1, а затем внезапно исчезнут. Таким образом при –1 с 0 могут существовать два различных типа поведения. Какой из них реализуется, зависит от предыстории системы. Такой феномен называется эффектом гистерезиса.
При увеличении параметра с и его переходе через ноль скачком возникают устойчивые автоколебания конечной амплитуды и частоты. Для промежуточных значений параметра с существуют два типа устойчивого поведения (два аттрактора) — устойчивое стационарное состояние и устойчивый предельный цикл.
Винфри ( Winfree A . T . ) назвал области, в которых возможны два режима: устойчивая точка покоя и предельный цикл, — черной дырой (рис. 8.8 б) . В этой области параметров можно так приложить возмущение к колебательной системе, что она попадет в область притяжения точки покоя, что приведет к прекращению колебаний. В частности, это показано для уравнений Ходжкина–Хаксли, моделирующих проведение нервного импульса (см. ниже).
Брюсселятор. Простейшим классическим примером существования автоколебаний в системе химических реакций является тримолекулярная модель «Брюсселятор», предложенная в Брюсселе Пригожиным и Лефевром (1965). Основной целью при изучении этой модели было установление качественных типов поведения, совместимых с фундаментальными законами химической и биологической кинетики.
В этом смысле блюсселятор играет роль базовой модели, такую же как гармонический осциллятор в физике, или модели Вольтерра в динамике популяций. Во 2-й части лекций мы остановимся на пространственно‑временных свойствах распределенной системы, локальным элементом которой является брюсселятор. Здесь мы рассмотрим свойства брюсселятора как автоколебательной системы.
Брюсселятор содержит простейшую реализацию кубической нелинейности посредством химической реакции
Хотя тримолекулярная стадия в химической кинетике не столь распространена, как бимолекулярные процессы, выражения для скорости ряда биохимических реакций в определенных случаях можно свести к кубическому виду. В качестве примера приведем следующую последовательность ферментативных реакций:
Здесь предполагается что фермент E имеет по крайней мере три каталитических центра, способных одновременно фиксировать две молекулы X и одну молекулу Y . Если образующиеся комплексы распадаются с достаточно большой скоростью, а ферменты присутствуют в небольших количествах, легко показать, что всю последовательность реакций можно свести к одной стадии, дающей нелинейный член типа X 2 Y в выражении для скорости реакции.
Брюсселятор представляет собой следующую схему гипотетических химических реакций:
ПРЕДЕ́ЛЬНЫЙ ЦИКЛ
В книжной версии
Том 27. Москва, 2015, стр. 404
Скопировать библиографическую ссылку:
ПРЕДЕ́ЛЬНЫЙ ЦИКЛ, изолированная замкнутая траектория динамич. системы (заданной нелинейной системой обыкновенных дифференциальных уравнений) в фазовом пространстве, изображающая периодич. движение. П. ц. может быть грубым (структурно устойчивым) и негрубым. Негрубый П. ц. исчезает в фазовом пространстве при сколь угодно малых изменениях параметров динамической системы , а грубый – сохраняется даже при изменениях параметров в конечных пределах. П. ц. является орбитально асимптотически устойчивым (далее просто устойчивым), если все траектории, начинающиеся в его малой окрестности, приближаются к нему при времени $t→+∞$ . Если же хотя бы одна из траекторий уходит из этой окрестности, то П. ц. неустойчив. Устойчивый П. ц. (рис. 1, а ) является математич. образом в фазовом пространстве устойчивых периодич. автоколебаний (рис. 1, б ).
http://www.library.biophys.msu.ru/LectMB/lect08.htm
http://bigenc.ru/physics/text/3174941
-
Предельные циклы
Мы рассмотрели два типа особых траекторий:
особые точки и сепаратрисы. Очень важным
видом особой траектории является
«предельный цикл». В линейной системе
второго порядка описываемой дифференциальным
уравнением (1), при
имеем замкнутую фазовую траекторию
(эллипс), которую мы не можем отнести к
предельным циклам, т.к. в этом случае
имеем в системе не автоколебания, а
границу устойчивости линейной системы.
Во всех остальных случаях изолированные,
замкнутые фазовые траектории принято
называть предельными циклами.
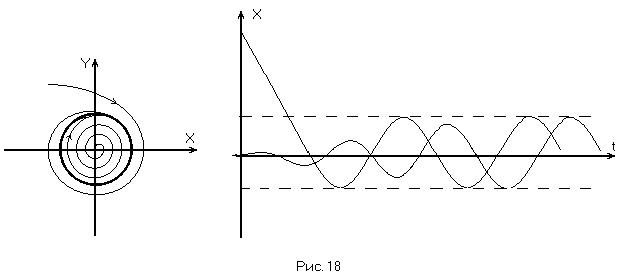
Предельный цикл соответствует устойчивому
периодическому режиму – автоколебаниям,
если все фазовые траектории «наматываются»
на предельный цикл (устойчивый предельный
цикл) (Рис. 18).
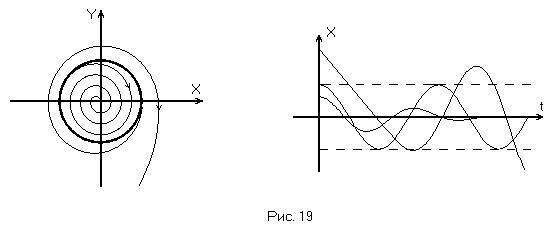
Если же все фазовые траектории
«сматываются» с предельного цикла, как
изнутри, так и снаружи, такой предельный
цикл неустойчив и соответствует
неустойчивым автоколебаниям. (Рис. 19).
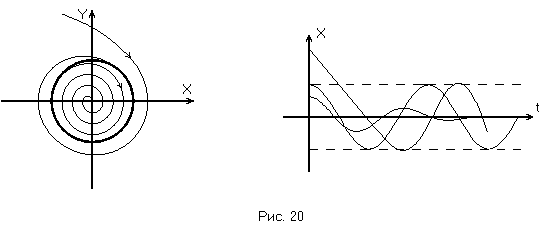
Если же соседние траектории «навёртываются»
на предельный цикл с одной стороны и
«свёртываются» с другой, такой предельный
цикл называется полуустойчивым. (Рис.
20).
Итак, при исследовании НСАР особыми
траекториями являются «особые точки»
(положение равновесия) и предельные
циклы (устойчивые периодические
колебания). Они и составляют схему
фазового портрета.
-
Метод точечного преобразования
М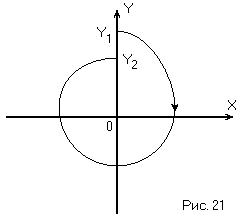
точечных преобразований предложен
академиком Андроновым и является
дополнением к методу фазовой плоскости.
Он служит для анализа возможных режимов
в НСАР и их количественной оценки. Пусть
изображающая точка в какой-то момент
времени находится на верхней полуоси
ординат (·Y1). При
движении изображающей точки по фазовой
траектории она обходит начало координат
и снова возвращается на полуось (·Y2).
(Рис. 21)
При этом «Y2» может
быть больше, меньше или равно «Y1».
Операция нахождения точкиY2по заданной точкеY1называетсяточечным преобразованием.
Аналитическое взаимно однозначное и
непрерывное соответствие точек Y2с точкамиY1на одной
и той же полупрямой (т.е. точечное
преобразование) устанавливается с
помощью так называемойфункции
последования, которая может быть
получена из уравнения фазовой траектории
(14)
С помощью этой зависимости можно
осуществить точечное преобразование
всех точек положительной полуоси
ординат, или, другими словами, точечное
преобразование положительной полуоси
Y, в саму себя.
Г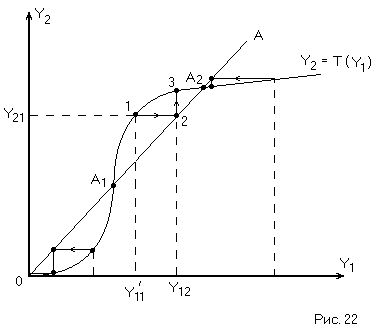
изображениеназываетсядиаграммой точечного
преобразования. По этой диаграмме мы
и можем исследовать всевозможные режимы
в НСАР, не строя фазового портрета.
Точечное преобразование можно осуществлять
необязательно для положительной полуоси.
В принципе это можно делать для полуосиXи других прямых.
Предположим, что имеется диаграмма
точечного преобразования. (Рис. 22)
Характер процессов, происходящих в НСАР
определяется взаимным расположением
диаграммы точечного преобразования
[]
и биссектрисы координатного угла,
уравнение которойY2=Y1. Это означает,
что после обхода вокруг начала (·)Y1возвращается на своё место и, следовательно,
в системе имеют место незатухающие
колебания (предельный цикл).
Область ниже биссектрисы ОА означает,
что после обхода начала координат Y1<Y1, т.е. колебания
в системе затухают и фазовая траектория
представляет закручивающуюся
логарифмическую спираль (затухающие
колебания).
Область выше биссектрисы ОА соответствует
Y2>Y1,
и, следовательно, в этой области фазовые
траектории представляют раскручивающуюся
спираль (расходящиеся колебания).
Рассмотрим характер процессов в САР
при любых начальных условиях:
Точечное
преобразование точки— точка 1 (Рис. 22). К точке 1 применим ещё
раз точечное преобразование, для чего
найдём на оси абсцисс значение.
Для этого проведём через точку 1 прямую,
параллельную оси абсцисс до пересечения
с биссектрисой (точка 2). Точечное
преобразование точки 2 – точка 3. Повторяя
эти преобразования получаем ступенчатую
линию, приводящую нас в точку равновесия
А2. Точки касания ступенчатой
линией биссектрисы ОА определяют
последовательность точек пересечения
фазовой траекторией полуосиY.
При начальных условиях Y0=Y11(справа от точки
А2) точечные преобразования опять
приводят нас к точке А2, следовательно
точка А2является точкой устойчивого
равновесия и соответствует устойчивому
предельному циклу.
Аналогичные рассуждения в окрестностях
точки А1показывают, что точка А1является точкой неустойчивого равновесия
(неустойчивый предельный цикл).
Итак, устойчивым предельным циклам
соответствуют такие точки пересечения
диаграммы точечного преобразования с
биссектрисой Y2=Y1, в которых диаграмма
точечного преобразования имеет меньший
наклон к оси абсцисс, чем биссектриса.
Аналитически это записывается так:
,
т.к.биссектрисы = 1. При
имеем неустойчивый предельный цикл.
Другими словами, устойчивый предельный
цикл получается, если диаграмма точечного
преобразования пересекает биссектрисуY2=Y1сверху вниз, а неустойчивый – если снизу
вверх. Таким образом, кривая точечного
преобразования позволяет проанализировать
возможные режимы поведения НСАР, а
именно:
-
система
устойчива в малом, т.к. при Y1<YA1изображающая точка стремится к нулю; -
в
системе возможен один предельный
устойчивый цикл (точка А2).
З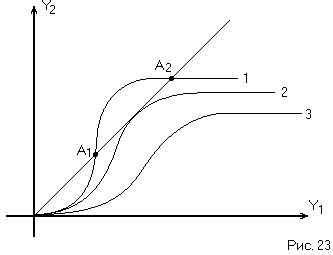
координаты точки А2, можно
рассчитать частоту и амплитуду
автоколебаний. При изменении параметров
НСАР диаграмма точечного преобразования
перемещается относительно биссектрисы
угла. При этом поведение НСАР может
качественно меняться (Рис. 23).
Кривая 1, как мы видели ранее, соответствует
устойчивости в малом и двум предельным
циклам: устойчивому (А2) и
неустойчивому (А1). Кривая 3
соответствует устойчивости в целом (ни
одного предельного цикла). Кривая 2
касается биссектрисы и соответствует
полуустойчивому предельному циклу. При
изменении параметров НСАР мы переходим
от кривой 2 к кривой 1 или 3, т.е. кривая 2
является границей между совершенно
разными режимами работы НСАР. Значения
параметров НСАР, при которых имеет место
полуустойчивый предельный цикл,
называютсябифуркационными.
(Бифуркация (лат.) – разделение,
разветвление).
Соседние файлы в папке TAU_Teorija_NSAR
- #
- #
- #
- #
22.02.201415.93 Кб52Рис43.cdr
From Wikipedia, the free encyclopedia
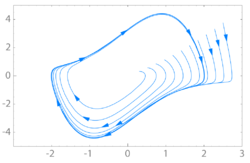
Stable limit cycle (shown in bold) and two other trajectories spiraling into it
In mathematics, in the study of dynamical systems with two-dimensional phase space, a limit cycle is a closed trajectory in phase space having the property that at least one other trajectory spirals into it either as time approaches infinity or as time approaches negative infinity. Such behavior is exhibited in some nonlinear systems. Limit cycles have been used to model the behavior of many real-world oscillatory systems. The study of limit cycles was initiated by Henri Poincaré (1854–1912).
Definition[edit]
We consider a two-dimensional dynamical system of the form
where
is a smooth function. A trajectory of this system is some smooth function 





Properties[edit]
By the Jordan curve theorem, every closed trajectory divides the plane into two regions, the interior and the exterior of the curve.
Given a limit cycle and a trajectory in its interior that approaches the limit cycle for time approaching 


Stable, unstable and semi-stable limit cycles[edit]
In the case where all the neighboring trajectories approach the limit cycle as time approaches infinity, it is called a stable or attractive limit cycle (ω-limit cycle). If instead, all neighboring trajectories approach it as time approaches negative infinity, then it is an unstable limit cycle (α-limit cycle). If there is a neighboring trajectory which spirals into the limit cycle as time approaches infinity, and another one which spirals into it as time approaches negative infinity, then it is a semi-stable limit cycle. There are also limit cycles that are neither stable, unstable nor semi-stable: for instance, a neighboring trajectory may approach the limit cycle from the outside, but the inside of the limit cycle is approached by a family of other cycles (which wouldn’t be limit cycles).
Stable limit cycles are examples of attractors. They imply self-sustained oscillations: the closed trajectory describes the perfect periodic behavior of the system, and any small perturbation from this closed trajectory causes the system to return to it, making the system stick to the limit cycle.
Finding limit cycles[edit]
Every closed trajectory contains within its interior a stationary point of the system, i.e. a point 

Open problems[edit]
Finding limit cycles, in general, is a very difficult problem. The number of limit cycles of a polynomial differential equation in the plane is the main object of the second part of Hilbert’s sixteenth problem. It is unknown, for instance, whether there is any system 

Applications[edit]
Examples of limit cycles branching from fixed points near Hopf bifurcation. Trajectories in red, stable structures in dark blue, unstable structures in light blue. The parameter choice determines the occurrence and stability of limit cycles.
Limit cycles are important in many scientific applications where systems with self-sustained oscillations are modelled. Some examples include:
- Aerodynamic limit-cycle oscillations[1]
- The Hodgkin–Huxley model for action potentials in neurons.
- The Sel’kov model of glycolysis.[2]
- The daily oscillations in gene expression, hormone levels and body temperature of animals, which are part of the circadian rhythm,[3][4] although this is contradicted by more recent evidence.[5]
- The migration of cancer cells in confining micro-environments follows limit cycle oscillations.[6]
- Some non-linear electrical circuits exhibit limit cycle oscillations,[7] which inspired the original Van der Pol model.
- The control of respiration and hematopoiesis, as appearing in the Mackey-Glass equations.[8]
See also[edit]
- Attractor
- Hyperbolic set
- Periodic point
- Self-oscillation
- Stable manifold
References[edit]
- ^ Thomas, Jeffrey P.; Dowell, Earl H.; Hall, Kenneth C. (2002), «Nonlinear Inviscid Aerodynamic Effects on Transonic Divergence, Flutter, and Limit-Cycle Oscillations» (PDF), AIAA Journal, American Institute of Aeronautics and Astronautics, 40 (4): 638, Bibcode:2002AIAAJ..40..638T, doi:10.2514/2.1720, retrieved December 9, 2019
- ^ Sel’kov, E. E. (1968). «Self-Oscillations in Glycolysis 1. A Simple Kinetic Model». European Journal of Biochemistry. 4 (1): 79–86. doi:10.1111/j.1432-1033.1968.tb00175.x. ISSN 1432-1033. PMID 4230812.
- ^ Leloup, Jean-Christophe; Gonze, Didier; Goldbeter, Albert (1999-12-01). «Limit Cycle Models for Circadian Rhythms Based on Transcriptional Regulation in Drosophila and Neurospora». Journal of Biological Rhythms. 14 (6): 433–448. doi:10.1177/074873099129000948. ISSN 0748-7304. PMID 10643740. S2CID 15074869.
- ^ Roenneberg, Till; Chua, Elaine Jane; Bernardo, Ric; Mendoza, Eduardo (2008-09-09). «Modelling Biological Rhythms». Current Biology. 18 (17): R826–R835. doi:10.1016/j.cub.2008.07.017. ISSN 0960-9822. PMID 18786388. S2CID 2798371.
- ^ Meijer, JH; Michel, S; Vanderleest, HT; Rohling, JH (December 2010). «Daily and seasonal adaptation of the circadian clock requires plasticity of the SCN neuronal network». The European Journal of Neuroscience. 32 (12): 2143–51. doi:10.1111/j.1460-9568.2010.07522.x. PMID 21143668. S2CID 12754517.
- ^ Brückner, David B.; Fink, Alexandra; Schreiber, Christoph; Röttgermann, Peter J. F.; Rädler, Joachim; Broedersz, Chase P. (2019). «Stochastic nonlinear dynamics of confined cell migration in two-state systems». Nature Physics. 15 (6): 595–601. Bibcode:2019NatPh..15..595B. doi:10.1038/s41567-019-0445-4. ISSN 1745-2481. S2CID 126819906.
- ^ Ginoux, Jean-Marc; Letellier, Christophe (2012-04-30). «Van der Pol and the history of relaxation oscillations: Toward the emergence of a concept». Chaos: An Interdisciplinary Journal of Nonlinear Science. 22 (2): 023120. arXiv:1408.4890. Bibcode:2012Chaos..22b3120G. doi:10.1063/1.3670008. ISSN 1054-1500. PMID 22757527. S2CID 293369.
- ^ Mackey, M.; Glass, L (1977-07-15). «Oscillation and chaos in physiological control systems». Science. 197 (4300): 287–289. Bibcode:1977Sci…197..287M. doi:10.1126/science.267326. ISSN 0036-8075. PMID 267326.
Further reading[edit]
- Steven H. Strogatz (2014). Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Avalon. ISBN 9780813349114.
- M. Vidyasagar (2002). Nonlinear Systems Analysis (Second ed.). SIAM. ISBN 9780898715262.
- Philip Hartman, «Ordinary Differential Equation», Society for Industrial and Applied Mathematics, 2002.
- Witold Hurewicz, «Lectures on Ordinary Differential Equations», Dover, 2002.
- Solomon Lefschetz, «Differential Equations: Geometric Theory», Dover, 2005.
- Lawrence Perko, «Differential Equations and Dynamical Systems», Springer-Verlag, 2006.
- Arthur Mattuck, Limit Cycles: Existence and Non-existence Criteria, MIT Open Courseware http://videolectures.net/mit1803s06_mattuck_lec32/#
External links[edit]
- «limit cycle». planetmath.org. Retrieved 2019-07-06.