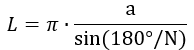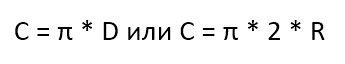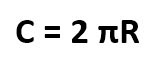Загрузить PDF
Загрузить PDF
Окружность – это плоская замкнутая кривая, все точки которой равноудалены от центральной точки.[1]
Длина окружности (С) – это длина замкнутой кривой, которая и образует окружность.[2]
Площадь круга (А) – это величина пространства, которое ограничено окружностью.[3]
Площадь круга и длина окружности вычисляются по формулам, в которых присутствует радиус (или диаметр) окружности и число «пи».
-
1
Формула для вычисления длины окружности. Длину окружности можно вычислить по двум формулам: C = 2πr или C = πd, где π – число «пи» (математическая константа, приблизительно равная 3,14)[4]
, r – радиус окружности, d – диаметр окружности.[5]
- Приведенные формулы по сути одинаковые, так как диаметр равен удвоенному радиусу.
- Длина окружности измеряется в любых единицах измерения длины: в метрах, сантиметрах, миллиметрах и так далее.
-
2
Величины формулы. В формулу для нахождения длины окружности входят три величины: радиус, диаметр и число «пи». Радиус и диаметр связаны друг с другом: радиус равен половине диаметра, а диаметр равен удвоенному радиусу.
- Радиус окружности (r) – это отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности.
- Диаметр окружности (d) – это отрезок, проходящий через центр окружности и соединяющий любые две точки, лежащие на окружности.[6]
- Число «пи» (π) равно отношению длины окружности к ее диаметру; число «пи» представляет собой иррациональное число, которое примерно равно 3,14159265 и не имеет конечной цифры и повторяющихся сочетаний цифр.[7]
В большинстве математических вычислений число «пи» округляется до 3,14.
-
3
Измерьте радиус или диаметр окружности. Совместите начало линейки с любой точкой на окружности и сделайте так, чтобы линейка соприкасалась с центром окружности. Измерьте расстояние от точки до центра окружности, чтобы получить значение радиуса. Измерьте расстояние между двумя точками, лежащими на окружности, чтобы получить значение диаметра.
- В большинстве математических задач радиус или диаметр будет дан.
-
4
Подставьте значения величин в формулу. Найдя радиус и/или диаметр окружности, подставьте значение в соответствующую формулу. Если вы нашли радиус, воспользуйтесь формулой C = 2πr, а если диаметр, формулой C = πd.
- Пример: найдите длину окружности, радиус которой равен 3 см.
- Напишите формулу: C = 2πr
- Подставьте данное значение в формулу: C = 2π3
- Перемножьте: C = (2*3*π) = 6π = 18,84 см
- Пример: найдите длину окружности, диаметр которой равен 9 м.
- Напишите формулу: C = πd
- Подставьте данное значение в формулу: C = 9π
- Перемножьте: C = (9*π) = 28,26 м
- Пример: найдите длину окружности, радиус которой равен 3 см.
-
5
Попрактикуйтесь на нескольких примерах. Теперь, когда вы знаете формулу, попробуйте решить несколько задач. Чем больше задач вы решите, тем быстрее научитесь справляться с ними.
- Найдите длину окружности с диаметром 5 м.
- C = πd = 5π = 15,7 м
- Найдите длину окружности с радиусом 10 м.
- C = 2πr = C = 2π10 = 2*10* π = 62,8 м
Реклама
- Найдите длину окружности с диаметром 5 м.
-
1
Формула для вычисления площади круга. Площадь круга можно вычислить по двум формулам, включающим диаметр или радиус: A = πr2 или A = π(d/2)2[8]
, где π – число «пи» (математическая константа, приблизительно равная 3,14)[9]
, r – радиус круга, d – диаметр круга.- Приведенные формулы по сути одинаковые, так как диаметр равен удвоенному радиусу.
- Площадь круга измеряется в любых единицах измерения длины, возведенных в квадрат: в квадратных метрах (м2), в квадратных сантиметрах (см2), в квадратных миллиметрах (мм2) и так далее.
-
2
Величины формулы. В формулу для нахождения площади круга входят три величины: радиус, диаметр и число «пи». Радиус и диаметр связаны друг с другом: радиус равен половине диаметра, а диаметр равен удвоенному радиусу.
- Радиус круга (r) – это отрезок, соединяющий центр круга с любой точкой, лежащей на окружности, которая ограничивает этот круг.
- Диаметр круга (d) – это отрезок, проходящий через центр круга и соединяющий любые две точки, лежащие на окружности, которая ограничивает этот круг.[10]
- Число «пи» (π) равно отношению длины окружности к ее диаметру; число «пи» представляет собой иррациональное число, которое примерно равно 3,14159265 и не имеет конечной цифры и повторяющихся сочетаний цифр.[11]
В большинстве математических вычислений число «пи» округляется до 3,14.
-
3
Измерьте радиус или диаметр круга. Совместите начало линейки с любой точкой на окружности, ограничивающей круг, и сделайте так, чтобы линейка соприкасалась с центром круга. Измерьте расстояние от точки до центра круга, чтобы получить значение радиуса. Измерьте расстояние между двумя точками, лежащими на окружности, чтобы получить значение диаметра.
- В большинстве математических задач радиус или диаметр будет дан.
-
4
Подставьте значения величин в формулу. Найдя радиус и/или диаметр круга, подставьте значение в соответствующую формулу. Если вы нашли радиус, воспользуйтесь формулой A = πr2, а если диаметр, формулой A = π(d/2)2.
- Пример: найдите площадь круга с радиусом 3 м.
- Напишите формулу: A = πr2
- Подставьте данное значение: A = π32
- Возведите радиус в квадрат: r2 = 32 = 9
- Умножьте на число «пи»: A = 9π = 28,26 м2
- Пример: найдите площадь круга с диаметром 4 м.
- Напишите формулу: A = π(d/2)2
- Подставьте данное значение: A = π(4/2)2
- Разделите диаметр на 2: d/2 = 4/2 = 2
- Результат возведите в квадрат: 22 = 4
- Умножьте на число «пи»: A = 4π = 12,56 м2
- Пример: найдите площадь круга с радиусом 3 м.
-
5
Попрактикуйтесь на нескольких примерах. Теперь, когда вы знаете формулу, попробуйте решить несколько задач. Чем больше задач вы решите, тем быстрее научитесь справляться с ними.
- Найдите площадь круга с диаметром 7 м.
- A = π(d/2)2 = π(7/2)2 = π(3,5)2 = 12,25 * π= 38,47 м2.
- Найти площадь круга с радиусом 3 м.
- A = πr2 = π32 = 9 * π = 28,26 м2
Реклама
- Найдите площадь круга с диаметром 7 м.
-
1
Найдите радиус или диаметр окружности. В некоторых задачах радиус или диаметр дается в виде выражения с участием переменной, например, г = (х + 7) или d = (х + 3). В этом случае вы можете найти площадь круга или длину окружности, но окончательный ответ будет также содержать переменную. Запишите радиус или диаметр так, как дается в задаче.
- Пример: вычислите длину окружности с радиусом (х + 1).
-
2
Напишите формулу с данным значением. Вычисляя площадь круга или длину окружности, вы подставляете данное значение в соответствующую формулу. Сначала запишите формулу для вычисления площадь круга или длину окружности, а затем подставьте в нее значение диаметра или радиуса, выраженное переменной.
- Пример: вычислите длину окружности с радиусом (х + 1).
- Напишите формулу: C = 2πr
- Подставьте данное значение: C = 2π(х + 1)
-
3
Вычислите длину окружности так, как если бы переменная была представлена числом. На данный момент решите задачу, рассматривая переменную в качестве обычного числа. Возможно, вам придется использовать свойство дистрибутивности для упрощения окончательного ответа.
- Пример: вычислите длину окружности с радиусом (х + 1).
- C = 2πr = 2π (х + 1) = 2πx + 2π1 = 2πx + 2π = 6,28x + 6,28
- Если вы знаете значение переменной «х», подставьте его в найденное выражение, чтобы получить численный ответ.
-
4
Попрактикуйтесь на нескольких примерах. Теперь, когда вы знаете формулу, попробуйте решить несколько задач. Чем больше задач вы решите, тем быстрее научитесь справляться с ними.
- Найдите площадь круга с радиусом 2х.
- A = πr2 = π(2x)2 = π4x2 = 12,56x2
- Найдите площадь круга с диаметром (х + 2).
- A = π(d/2)2 = π((x +2)/2)2 = ((x +2)2/4)π
Реклама
- Найдите площадь круга с радиусом 2х.
Об этой статье
Эту страницу просматривали 212 798 раз.
Была ли эта статья полезной?
8 способов найти длину окружности
Выбирайте формулу, ориентируясь на известные величины.
1. Как найти длину окружности через диаметр
Просто умножьте диаметр на число пи.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- d —диаметр окружности.
2. Как найти длину окружности через радиус
Умножьте число пи на два радиуса.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- r — радиус окружности.
3. Как вычислить длину окружности через площадь круга
Умножьте число пи на четыре площади круга.
Найдите корень из результата.
- O — искомая длина окружности.
- S – площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
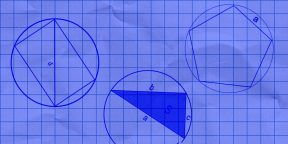
4. Как найти длину окружности через диагональ вписанного прямоугольника
Умножьте число пи на диагональ.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- d – любая диагональ прямоугольника.
5. Как вычислить длину окружности через сторону описанного квадрата
Умножьте число пи на сторону квадрата.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- a – любая сторона квадрата.
6. Как найти длину окружности через стороны и площадь вписанного треугольника
Перемножьте стороны треугольника.
Поделите результат на площадь и на два.
Умножьте полученное число на пи.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- S – площадь треугольника.
- a, b, c – стороны треугольника.
7. Как найти длину окружности через площадь и полупериметр описанного треугольника
Поделите площадь треугольника на его полупериметр.
Умножьте результат на число пи и на два.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- S – площадь треугольника.
- p – полупериметр треугольника (равен половине от суммы всех сторон).
8. Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разделите 180 градусов на количество сторон многоугольника.
Найдите синус полученного числа.
Разделите сторону многоугольника на результат.
Умножьте получившееся число на пи.
- O — искомая длина окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- π (пи) — константа, равная 3,14.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✏️🎓
- Как найти периметр прямоугольника
- 8 способов найти периметр треугольника
- 7 способов найти площадь прямоугольника
- Как перевести обычную дробь в десятичную
- Как освоить устный счёт школьникам и взрослым
Содержание:
- Формула
- Примеры вычисления длины окружности
Формула
Чтобы найти длину окружности, нужно либо диаметр окружности умножить на
$pi approx 3,1415926535 dots$, либо найти удвоенное произведение радиуса и числа
$pi$.
То есть нужно воспользоваться одной из формул:
$l=2 pi r text { или } l=pi d$
Здесь $r$ — это радиус заданной окружности,
а $d$ — диаметр,
$pi approx 3,1415926535 dots$. Радиусом окружности — отрезок, который соединяет центр
окружности с точкой окружности. Диаметром называют отрезок, который соединяет две точки окружности и проходит через её центр. Число
$pi$ — математическая константа , выражающая
отношение длины окружности к длине её диаметра.
Примеры вычисления длины окружности
Пример
Задание. Найти длину окружности, диаметр которой равен 3 см.
Решение. Для вычисления длины заданной окружности воспользуемся формулой
$$l=pi d$$
Подставляя в неё исходные данные, получим:
$l=3 pi approx 3.14 cdot 3=9.42$ (см)
Ответ. $l=3 pi approx 9.42$ (см)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти длину окружности, описанной около правильного треугольника со стороною
$a=4 sqrt{3}$ дм.
Решение. Радиус окружности, описанной около правильного треугольника, равен
$R=frac{a}{sqrt{3}}$. В нашем случае он будет равен
$R=frac{4 sqrt{3}}{sqrt{3}}=4$ (дм)
Для нахождения длины рассматриваемой окружности воспользуемся формулой
$l=2 pi r$
Подставляя в нее найденное значение радиуса и значение
$pi approx 3.14 ldots$, окончательно получим
$l=2 cdot pi cdot 4 approx 8 cdot 3,14=25,12$ (дм)
Ответ. $l=8 pi approx 25,12$ (дм)
Остались вопросы?
Здесь вы найдете ответы.
Каким образом можно вычислить длину окружности при условии, что площадь
круга (S) является известной величиной?
Площадь круга (S) рассчитывается путем умножения числа Пи на длину его
радиуса (R), возведенную в квадратную степень (S = ПR²). Из указанного
равенства можно выразить радиус:
R² = S/ П
Если избавиться от квадратной степени, то получится:
R = √(S/П)
Длина окружности (L) рассчитывается путем умножения числа Пи на длину
радиуса, и последующего умножения на два полученного в результате числа:
L = 2ПR
Если R = √(S/П), то L = 2П*√(S/П)
Каким образом можно найти длину окружности, диаметр которой составляет 2 см?
Длина окружности (L) представляет собой число, которое получено в
результате умножения числа Пи на диаметр данной окружности:
L = П*D
В конкретном случае:
L = 3,14*2 = 6,28 см.
Ответ: Длина окружности с диаметром 2 см составляет 6,28 см.
Дан квадрат, вокруг которого описана окружность. Ее длина составляет 12 Пи
см. Как можно найти длину окружности, вписанной в этот же квадрат?
Известно, что длина окружности (L) рассчитывается путем умножения на два
произведения числа Пи и длины ее радиуса (R). Формула выглядит так:
2ПиR
Из данной формулы можно выразить радиус
R = 12пи/2пи = 6 см
Радиус окружности, описанной около квадрата, равен 6 см.
Теперь можно вычислить сторону квадрата, вокруг которого описана данная
окружность. Ее длина составляет R корней из 2:
а = 6 корней из 2.
Рассчитываем длину малого радиуса (r), который равен половине длины
стороны квадрата:
r = а/2 = 6 корней из 2/2 = 3 корней из 2.
Длина окружности, вписанной в квадрат, рассчитывается по той же формуле:
L = 6 корней из 2 Пи.
Каким образом можно вычислить длину окружности, а также найти ее площадь,
при условии, что радиус этой окружности равен 30 см?
Радиус окружности, равный 30 см, обозначается как R.
Площадь окружности можно найти, умножив число Пи на квадрат длины ее
радиуса:
S = πR²
Подставим в формулу известные величины:
S = π*30² = 900π см. кв.
Длина окружности обозначается как С и рассчитывается путем умножения на 2
произведения числа Пи и ее радиуса:
C = 2πR
Снова подставляем в формулу величины, которые известны:
C = 2π*30 = 60π см
Ответ: Площадь окружности равна 900π см², а ее длина составляет 60π см.
Дана окружность, в которую вписан правильный треугольник. Его площадь
составляет 12√3 см кв. Как можно вычислить длину окружности в данном случае?
По условию задачи известно, что треугольник является правильным, что
означает равенство всех его трех сторон. В данном случае его площадь может
быть рассчитана по следующей формуле:
S = а^2 * √3 ÷ 4
Зная площадь, мы получаем возможность вычислить длину стороны а. Она будет
равна ± √48. Учитывая то, что сторона не может быть отрицательной
величиной, можно говорить о том, что сторона а равна √48.
После того как длина стороны стала известна, можно приступить к вычислению
площади описанной и вписанной окружности. Для этого не достает еще одного
элемента – длины радиуса.
Радиус описанной окружности (R) равен длине стороны треугольника,
разделенной на √3:
R = √48 ÷ √3 = 4 см.
Радиус вписанной окружности (r) можно получить, разделив на 2 радиус
описанной окружности:
r = 4/2 = 2 см.
Вычисленные длины радиусов вписанной и описанной окружностей позволяют
определить ее длину ℓ, которая равна произведению числа Пи и радиуса
окружности, умноженному на 2:
ℓ = 2πR
В нашем случае длина описанной окружности рассчитывается как:
ℓ= 2πR = 2π4 = 8π
Длина вписанной окружности будет составлять:
ℓ= 2πR = 2π2 = 4π
Известно, что радиус окружности равен 12 см. Как вычислить ее площадь и
длину при Пи=3,14?
В условии задачи говорится о том, что радиус окружности R равен 12 см. Ее
длина может быть вычислена посредством умножения на 2 произведения длины
радиуса и числа Пи:
C=2πR
Известно, что число Пи – это константа, равная 3,14. Тогда длина
окружности (С)высчитывается следующим образом:
C=2*3*12=72 см
Площадь окружности можно найти, умножив число Пи на длину ее радиуса,
возведенную в квадратную степень:
S=πR²=3,14*12²=3,14*144=452,16 см кв.
Как можно вычислить радиус окружности и ее диаметр, если известно, что ее
длина составляет 20 Пи см?
По условию задачи длина окружности равна 20 Пи см. Зная формулу, по
которой вычисляется длина окружности, можно записать следующее равенство:
2Пи = 2ПиR
Можно сократить Пи в обеих частях записанного равенства, в результате чего
получится, что:
2R = 20
Теперь высчитаем, чему равна длина радиуса окружности:
R = 20/2 = 10 см.
Длина диаметра равна длине радиуса, умноженной на 2:
D = R*2 = 10*2 = 20 cм.
Длина дуги окружности составляет 6Пи см, при этом ее градусная мера равна
120 градусов. Каким образом можно вычислить радиус окружности?
Полная градусная мера любой окружности равна 360 градусов. В случае,
описанном в задании, градусная мера окружности составляет 120 градусов,
что равно 1/3 части 360 градусов. Это позволяет сделать вывод о том, что
длина окружности (L) может быть рассчитана следующим образом:
L = 6Пи * 3 = 18Пи
Формула, по которой вычисляется длина окружности, выглядит так:
L =2пR
Из данной формулы можно выразить радиус (R):
R = L/2Пи
В заданном случае длина радиуса будет равна:
18Пи/2Пи = 9 см.
Как на радиус окружности повлияет увеличение ее длины на 9,42 см?
Обозначим прежнюю длину окружности как L, а новую – как L₁. Тогда можно
записать следующее равенство:
L₁ — L = 9,42 см
Прежний радиус окружности примем за R, а новый ее радиус, который
получится в результате увеличения длины, обозначим как R₁. Для того чтобы
вычислить ее значение, следует сначала записать формулу, по которой
вычисляется прежняя длина данной окружности:
L = 2πR
Тогда формула для вычисления новой длины окружности будет иметь такой вид:
L + 9,42 = 2πR₁
Отнимем от новой длины старую, и в итоге получим:
2πR₁ — 2πR = 9,42 см.
Перенесем 2Пи из левой части равенства в правую:
R₁ — R = 9,42 : 2π = 1,5 см.
Ответ: В результате увеличения длины окружности на 9,42 см ее радиус
станет больше на 1,5 см.
Как можно вычислить радиус окружности, вписанной в правильный треугольник,
зная то, что площадь данного треугольника превышает площадь окружности на
27√3-9π?
Радиус окружности, которая вписана в правильный треугольник, обозначим r.
Ее площадь (S) является произведением числа Пи и квадрата ее радиуса:
S = πr²
В случае треугольника, все стороны которого одинаковы, радиус вписанной в
него окружности равен третьей части высоты, являющейся также и медианой.
Площадь правильного треугольника рассчитывается так:
Sтр = (1/2)*(2r/tg30)*3r = (1/2)*(2r√3)*3r = 3√3r².
Согласно условию задачи 3√3r² = πr² + 27√3 — 9π.
Перенесем πr² из левой части равенства в правую, изменив его знак на
противоположный:
3√3r² — πr² = 27√3 — 9π
Вынесем в правой части равенства r² за скобки. То же самое сделаем с
числом 9 в левой части равенства:
r²(3√3 — π) = 9(3√3 — π)
Сокращаем в обеих частях одинаковый множитель (3√3 — π) и получаем:
r² = 9
Таким образом, радиус окружности равен корню квадратному из 9:
r =3 см.
Дано две окружности, радиус одной из которых пятикратно превышает радиус
другой. Каким образом вычислить радиус каждой из этих окружностей, если
известно, что диаметр второй из окружностей на 240 мм меньше, чем диаметр
первой?
Обозначим радиус второй окружности буквой х. В данном случае радиус первой
окружности нужно обозначить как 5х. Известно, что разница между длинами
диаметров двух окружностей равна 240 мм. На основании этого можно
составить следующее равенство:
5х-х=240:2, что равно 4х=120
Теперь можно найти значение х:
х=120:4=30 мм.
Таким образом, радиус второй окружности равен 30 мм. Это позволяет
вычислить радиус первой окружности, который в 5 раз больше радиуса второй
из них:
30*5=150 мм.
Как можно высчитать радиус окружности, когда известна ее градусная мера и
длина дуги?
Длина дуги обозначена как L. В качестве обозначения ее градусной меры
используется α. Через R обозначена длина радиуса данной окружности.
Формула расчета длины дуги выглядит так:
L = πR · α / 180°
Это же равенство может быть переписано следующим образом:
πR · α = L · 180°
Отсюда выведем радиус:
R = L · 180° / (π·α).
Как высчитать радиус окружности, длина дуги которой составляет 3,14 см, а ее
градусная мера равна 18 градусам?
Длина окружности (L) равна произведению числа Пи и радиуса, которое
умножено на 2:
L = 2Пиr
Согласно заданию, длина дуги равна 3,14, что равно значению константы Пи.
Дуга способна поместиться в длине окружности 2 пи r/пи =2 r раз
Подставив в равенство значения, которые известны, мы получим:
360:18=20 раз
Длина окружности будет равна:
3,14*20=20Пи
2Пиr = 20Пи
Сократим 2Пи в каждой из частей равенства и получим, что:
r=10 см.
Площадь круга составляет 169Пи см. Чему равна длина окружности в данном
случае?
Для решения поставленной задачи следует записать формулу расчета площади
круга:
S=πr2
Эта величина указана в задании, и составляет 169Пи. Это значит, что:
πr2 = 169π
Можно сократить одинаковый множитель Пи в обеих частях равенства:
r2= 169
r = √169 = 13 см.
Длина окружности обозначена С. Она считается по следующей формуле:
С = 2πr
Длина радиуса уже известна, и ее можно подставить в формулу расчета длины
окружности:
С = 2* π*13 = 26π см.
В окружность вписан квадрат площадью 36 дм кв. Чему в этом случае будет
равна площадь круга и длина окружности?
Известно, что площадь круга представляет собой величину, равную длине
стороны этого квадрата, возведенной во вторую степень Sкв = а². Это
значит, что в данном случае а² = 36 дм. Для того чтобы найти значение а,
нужно извлечь квадратный корень из 36:
а = √36 = 6 дм.
Длина диагонали (d) квадрата считается по приведенной ниже формуле:
d = a√2 = 6√2 дм.
Радиус (R)окружности, которая описана около квадрата, равен половине длины
ее диагонали:
R = d/2 = 3√2 дм.
Площадь круга можно посчитать, умножив число Пи на квадрат его радиуса:
S = πR² = π · (3√2)² = 18π дм. кв.
Длина окружности рассчитывается посредством умножения на два числа Пи,
после чего полученное число умножается на длину радиуса окружности:
C = 2πR = 2π · 3√2 = 6√2π дм.
Длина окружности составляет 3,5 дм. Диаметр второй окружности равен 5/7 ее
диаметра. Как вычислить длину второй окружности?
Ниже записана формула, которая используется для того, чтобы рассчитать
длину окружности:
С = Пи*d,
где Пи – это константа, равная 3,14, а d – это диаметр окружности.
Отношение длины первой окружности к длине второй окружности равно
отношению их диаметров:
C/C1 = d/d1
d1 = 5/7 d
В условии сказано, что длина первой окружности С = 3,5 дм. Таким образом:
C1 = 5/7 *C = 5/7 * 3,5 = 2,5 дм.
Длина радиуса окружности составляет 14 см. Какова будет ее длина при
условии, что П=22/7?
Для того чтобы узнать длину окружности (C), следует воспользоваться
формулой, предназначенной для ее расчета. Она выглядит так:
C = П*R*2
Если подставить в эту формулу величины, которые даны по условию задачи, то
получим:
22/7*14*2=22/7*28/1=88 см.
Ответ: Длина окружности равна 88 см.
Какой будет длина окружности при условии, что ее половина составляет 25,5
см?
Длина окружности равна длине ее половины, умноженной на 2. Это значит, что
в данном случае нужно умножить число 25,5, обозначающее половину длины
окружности, на 2:
25,5*2 = 51 см.
Круг имеет площадь Пи м кв. Какова будет длина окружности данного круга?
Для вычисления длины окружности необходимо число Пи умножить на два и
умножить на длину его радиуса (2πR). Для данной задачи это будет выглядеть
следующим образом:
2π · 3√2 = 6√2π дм.
Для того чтобы посчитать площадь круга, необходимо умножить число Пи на
радиус, взятый в квадрат (S = πR²). По условию задачи площадь круга равна
Пи м кв. Это значит, что:
πR² = π
Из данного равенства можно выразить R
R — √π/π = 1
Зная длину радиуса, можно переходить к вычислению длины окружности (С):
C = 2πR = 2π x 1 = 2π
Ответ: Длина окружности равна 2π.
Какова формула длины окружности, при условии, что длина ее радиуса
составляет R?
С целью вычисления длины окружности (С) используется приведенная ниже
формула:
C=2πR
Ее составляющими является постоянное число Пи и радиус окружности (R),
длину которой необходимо вычислить.
Какова формула расчета длины окружности, диаметр которой составляет 15 см?
Если длина диаметра окружности является известной величиной, то его нужно
умножить на постоянное число Пи, равное 3,14, для того чтобы найти длину
этой окружности. Формула выглядит так:
С = πD
В условии говорится, что диаметр окружности равен 15 см:
С = 3,14 * 15 = 47,1 cм.
Ответ: Длина окружности равна 47,1 см.
В результате деления длины окружности на величину ее диаметра получается
число, приблизительно равное 22/7. Каким образом можно высчитать длину
окружности с диаметром 10 см?
Для расчета длины окружности (С) нужно знать длину ее радиуса (R) или
диаметра (d). Тогда могут быть использованы следующие формулы:
C = 2πR или C = πd
По условию задания d = 10 см, а π = 22/7. Тогда длина окружности будет
равна:
C = πd = (22/7) * 10 = 220/7 ≈ 31,4 см.
В каком виде представлены формулы, которые используются для вычисления
площади круга и длины окружности (через диаметр и через радиус)?
В случае, если длина диаметра (d) или длина радиуса (R) окружности
известны, то эти величины можно использовать для нахождения длины
окружности. При этом следует воспользоваться одной из формул:
С=πd или С=2πR.
Эти величины также помогут вычислить площадь круга. Формулы выглядят
следующим образом:
S=πr² или S=π(d2)².
Можно ли вычислить длину диаметра окружности, если известна только ее длина?
Нужно записать формулу расчета длины окружности, для того чтобы понять,
существует ли взаимосвязь между этой величиной и диаметром окружности:
L = π·d
Очевидно, что длина окружности является результатом умножения числа Пи на
длину ее диаметра.
Если длина окружности известна, то ее можно использовать для определения
диаметра (d). Это можно сделать следующим образом:
d = L/π.
Во сколько раз длина окружности превышает ее диаметр, и в каком виде
представлена формула ее расчета через диаметр?
Длину окружности (С) можно рассчитать через диаметр (d), если
воспользоваться нижеприведенной формулой:
С = π*d
Это формула демонстрирует, что длина окружности больше длины ее диаметра в
π раз. Именно отношение длины окружности к величине ее диаметра и является
числом π.
Какова формула вычисления отношения длины окружности к величине, означающей
ее диаметр?
Число π представляет собой константу, которая получается в результате
деления длины окружности (С) на ее диаметр (d). В виде формулы это
выглядит так:
π = С/d
Площадь круга составляет 185 см кв. Как вычислить 30% от длины окружности
при заданных исходных?
Располагая информацией о том, что площадь круга равна произведению числа
Пи и квадрата ее радиуса (S=πr²), можно через нее выразить радиус:
r² = S/π = 185/π
Избавляемся от квадратной степени:
r = √(185/π) см.
Следующим шагом в решении задачи станет вычисление длины окружности,
которая находится путем умножения на 2 числа Пи и радиуса окружности:
С=2πr= C=2π√(185/π) = 2√(185π) см.
На последнем этапе находим 30%. Принимаем всю длину окружности за 100%:
2√(185π) — 100%
х — 30%
Тогда х можно найти следующим образом:
х=(30*2√(185π))/100 = 0,6√(185π) см.
Как выглядят формулы определения длины окружности через радиус и через
диаметр? В какое количество раз длина диаметра окружности меньше ее длины?
Существует две формулы, которые предназначены для расчета длины окружности
(С). Они отличаются друг от друга тем, что элементом одной из них является
радиус (r), а другой – диаметр (D):
C=2Пr и C=ПD.
Для того чтобы понять, во сколько раз длина окружности превышает длину ее
диаметра, нужно произвести деление этих величин:
С/D
В результате получается число Пи, которое является постоянным и имеет
значение примерно 3,14.
Длина окружности, обозначаемая как L, может быть вычислена при условии, что
известен ее диаметр (D). При этом следует воспользоваться формулой L = Пи*D.
Можно ли использовать данную формулу с целью вычисления длины диаметра
окружности, длина которой составляет 126 м. (число Пи считать равным 3)?
Формула расчета длины окружности (С) через диаметр (D) выглядит так:
С = Пи*D
Исходя из условий задания, это равенство может быть записано в следующем
виде:
126=3*D
Отсюда можно выразить диаметр:
D=126:3=42 м.
Читать дальше: как найти периметр квадрата.
Длина (периметр) окружности калькулятор онлайн умеет вычислять длину восемью способами:
- По радиусу.
- По диаметру.
- По площади окружности.
- По диагонали вписанного прямоугольника.
- По стороне описанного квадрата.
- По сторонам и площади описанного треугольника.
- По площади вписанного треугольника.
- По стороне вписанного многогранника.
Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.
Длина окружности или периметр окружности — это длина кривой из множества точек которая ограничивает собой круг.
Длина окружности может быть найдена по длине пути, который проедет круг сделав один полный оборот.
Как найти длину окружности?
Найти длину окружности очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
1) По радиусу
где R — радиус окружности.
2) По диаметру
где D — диаметр окружности.
3) По площади окружности
ггде S — площадь окружности.
4) По диагонали вписанного прямоугольника
где d — диагональ вписанного прямоугольника.
5) По стороне описанного квадрата
где a — сторона описанного квадрата.
6) По сторонам и площади описанного треугольника
где a,b,c — стороны описанного треугольника, S — его площадь.
7) По площади вписанного треугольника
где p — полупериметр вписанного треугольника, S — его площадь.
 По стороне вписанного многогранника
По стороне вписанного многогранника
где a — сторона вписанного многогранника, N — количество сторон.
Скачать все формулы в формате Word
Длина окружности
О чем эта статья:
6 класс, 9 класс, ЕГЭ/ОГЭ
Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так — l
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Как найти длину окружности через диаметр
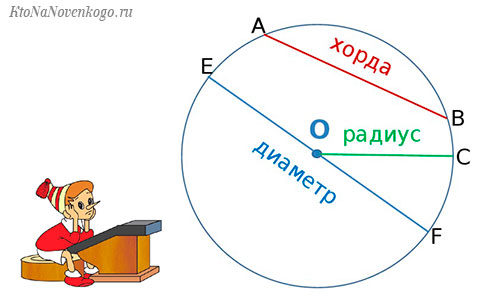
Хорда — это отрезок, который соединяет две точки окружности.
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, примерно равное 3,14
r — радиус окружности
Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, примерно равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
π — математическая константа, примерно равная 3,14
a — сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен Подставим туда наши переменные и получим
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Обучение на курсах по математике поможет закрепить полученные знания на практике.
Урок 25 Бесплатно Длина окружности и площадь круга
На этом уроке мы рассмотрим одни из самых древнейших геометрических фигур: окружность и круг.
Определим, какими элементами характеризуются круг и окружность, в чем сходство и различие этих фигур.
Узнаем, как рассчитать длину окружности и площадь круга.
Окружность и круг
Мы часто встречаем такие понятия, как окружность и круг.
Давайте попробуем разобраться, что называют окружностью, а что кругом.
Окружность — это замкнутая плоская кривая, все точки которой удалены на одинаковые расстояния от заданной точки, называемой центром окружности.
Центр окружности— это точка, которая находится на одинаковом расстоянии (равноудаленная) от любой точки окружности, ее обозначают обычно заглавной буквой О.
По сути, окружность — это изогнутая линия. Наглядно представить данную геометрическую фигуру можно, обведя стакан или блюдце карандашом, — оставшийся нарисованный след и будет окружностью.
Круг — это часть плоскости, ограниченная окружностью. Можно также сказать что это часть плоскости, которая находится внутри линии окружности.
Круг — плоская фигура, ее можно получить, закрасив окружность или вырезав его из бумаги по контуру окружности.
Свои имена окружность и круг приобрели не сразу.
В древние времена специальных названий для этих фигур не существовало. Люди пытались описать различные геометрические формы, сравнивая объекты. Например, говоря про что-то круглое, говорили: «такой, как солнце» или «такой, как орех» и т.п.
Только в Древней Греции окружность и круг приобрели себе свои названия.
Круг всегда привлекал к себе внимание как самая простая фигура из кривых, но самая загадочная.
У меня есть дополнительная информация к этой части урока!

Древние греки считали круг и окружность символом бесконечности и совершенства. Поражало то, что в каждой своей точке окружность устроена одинаково, представляя собой бесконечную линию, которая движется сама по себе.
У древних славян еще за долго до христианства круг был символом солнца.
В Древнем Египте и Греции круг изображали в виде змея Уробороса, который кусает свой хвост, образуя тем самым, окружность — этот символ обозначал бесконечность и цикличность во всей вселенной (смена дня и ночи, жизни и смерти т.д.).
Символика круга в различных религиях сопоставляется с целостностью, вечностью и бесконечной мудростью.
Например, в масонских учениях круг как форма без начала и конца — это источник бесконечного времени и пространства, в котором заключена тайна творения.
У буддистов круг символизирует единство внутреннего и внешнего мира.
В дзен-буддизме круг — это символ высшей степени просветления и совершенства. На основе этого представления построены принципы инь и янь (в виде круга, разделенного на две части, — символа взаимодействия и борьбы двух начал).
В христианстве круг служит эталоном божественного и духовного совершенства.
В живой и неживой природе круги и окружности встречаются как на макроуровнях, так и на микроуровнях. Например, движение электронов вокруг атомного ядра; вращение планет вокруг солнца; распространение волн на воде от упавшего груза; образование солнечного и лунного гало; срез дерева; зрачок глаза у человека и многое другое.
Рассмотрим подробней элементы, характерные для окружности.
Радиус окружности— это отрезок, соединяющий центр окружности и любую другую точку, расположенную на линии окружности.
С латинского радиус (radius)- луч, спица колеса. Радиус не сразу приобрел себе такое название.
Слово радиус впервые встречается в 1569 году у французского ученого П. Рамуса, а общепризнанным становится к концу XVII века.
Радиус обозначается маленькой латинской буквой (r) или заглавной (R).
В окружности можно провести столько же радиусов, сколько точек имеет линия окружности; все эти радиусы равны.
Диаметр — это отрезок прямой, проходящий через центр окружности и соединяющий две точки на этой окружности.
Диаметр в переводе с греческого (diametros) — поперечник.
Обычно диаметр обозначают латинской маленькой буквой d или заглавной D.
По величине диаметр равен двум радиусам, лежащим на одной прямой.
d = 2r
Следовательно, радиус- это половина диаметра.
r = d: 2
Пример 1
Радиус окружности равен 6 см.
Чему равен диаметр окружности?
r = 6 см
d — ?
Решение:
d = 2r
d = 2r= 2*6 = 12 (см) диаметр окружности
Ответ: d= 12 см
Пример 2
Диаметр окружности равен 12 см.
Чему равен радиус окружности?
d = 12 см
r — ?
Решение:
r = d : 2
r = 12 : 2 = 6 (см) радиус окружности
Ответ: r = 6 см
У меня есть дополнительная информация к этой части урока!

Секущая окружности — это прямая, пересекающая окружность в двух точках. В результате окружность делится на дуги.
Точки А и В — точки пересечения секущей с окружностью.
Образовались две дуги: (mathbf<cup AB и cup BA>)
Отрезок, который соединяет любые две точки на окружности (отрезок секущей), называется хордой.
Отрезок АВ (отрезок секущей) на рисунке — хорда окружности.
Хорда в переводе с греческого — струна, тетива.
На рисунке отрезок MN является хордой.
Если хорда проходит через центр окружности, то она является самой большой хордой для этой окружности. По своей сути она является диаметром для данной окружности и делит окружность на две равные дуги.
По мере удаления хорды от центра размеры ее уменьшаются, а дуги делятся на большую и малую.
АВ— самая большая хорда окружности- диаметр окружности.
CD, N1M1, NM, FE— хорды окружности.
Хорды окружности, удаленные на равные расстояния от центра, равны.
Хорды NM и N1M1 равны.
Если две хорды пересекаются в точке, то их отрезки пропорциональны.
Важно отметить, что все рассмотренные элементы окружности одинаковы и для круга.
Пройти тест и получить оценку можно после входа или регистрации
Длина окружности и площадь круга
Давайте выясним, что такое длина окружности и как ее определить.
Представьте, что окружность обернута нитью.
Если разрезать эту нить в некоторой точке и размотать ее, то длина нитки будет равна длине окружности.
Обычно длина окружности обозначается заглавной буквой С
Длина окружности (С) зависит от длины ее диаметра (d)
Обратите внимание на рисунок.
Вы можете заметить, что чем больше диаметр, тем больше длина окружности.
Из этого следует, что длина окружности прямо пропорционально зависит от диаметра окружности.
А значит, для любых окружностей отношение длины окружности (С) к длине диаметра (d) является числом постоянным.
Это число (коэффициент пропорциональности) обозначают греческой буквой (mathbf<pi>), читается «пи».
С— это длина окружности
d— диаметр окружности
запишем отношение (mathbf)
отсюда следует, что длина окружности равна
Так как диаметр окружности вдвое больше радиуса d = 2r, получим еще одну формулу для вычисления длины окружности
Выясним, чему равна постоянная величина — число (mathbf<pi>)
Число (mathbf<pi>)- это иррациональное число, т.е. число, которое представлено в виде бесконечной непериодической десятичной дроби.
У меня есть дополнительная информация к этой части урока!

История числа (mathbf< pi>) насчитывает около 4 тысячелетий.
Одно из первых доказательств древнего существования этого числа (mathbf< pi>) заключено в папирусе Ахмеса, в одном из старейших задачников (1650 год до н.э.), найденного в Древнем Египте.
В папирусе дано достаточно точное, особенного для того времени, значение числа, равного 3,1605.
Точнее число (mathbf< pi>) рассчитал древнегреческий математик Архимед. Он приближенно представил значение константы в виде обыкновенной дроби (mathbf<frac <22><7>>)
Архимеду удалось найти точное приближение числа (mathbf< pi>) (т.е. узкий числовой промежуток к которому принадлежит число (mathbf< pi>)).
Пройти тест и получить оценку можно после входа или регистрации
Решения задач по теме «Длина окружности и площадь круга»
Рассмотрим примеры решения задач
Задача 1
Найдите длину окружности, если ее радиус равен 4 см.
Число (mathbf<<pi>>) округлите до сотых.
r = 4 см
Длину окружности С — ?
Решение:
Подставив в формулу известные значения радиуса и постоянной (mathbf<pi>), получим:
Ответ: (mathbf)(см)
Задача 2
Длина окружности надувного бассейна 15,7м.
Найдите диаметр этого бассейна.
Число (mathbf<pi>) округлите до сотых.
C = 15,7 м
Диаметр d — ?
Решение:
Подставив в формулу известные значения длины окружности и постоянной (mathbf<pi>), получим:
Ответ: (mathbf) (м)
Задача 3
Диаметр окружности равен 6 см.
Найдите площадь круга, ограниченного этой окружностью.
Значение числа (mathbf<pi>) округлить до сотых.
d = 6 cм
Площадь круга S — ?
Решение:
Подставим в формулу известные значения диаметра окружности и постоянной , получим:
(mathbf<4><cdot>3,14<cdot>6^2 = frac <3,14<cdot>36> <4>> = 3,14<cdot>9=28,26) (cм 2 ) площадь круга
Ответ: (mathbf) (см 2 )
Задача 4
Вычислите площадь полукруга, если радиус круга равен 5 см.
Значение (mathbf<pi >) округлить до целых.
r = 5 cм
Площадь полукруга Sп — ?
Решение:
Площадь круга найдем по формуле:
Площадь полукруга будет равна половине площади всего круга.
Следовательно, формула для расчета площади полукруга получится вида:
Подставим в формулу известные значения радиуса круга и постоянной (mathbf<pi>), получим:
(mathbf <2>=37,5>) (cм 2 ) площадь полукруга
Ответ: (mathbf) (см 2 )
Задача 5
Найдите площадь круга, если известна длина окружности С.
Длина окружности С
Площадь круга S — ?
Решение:
Длина окружности выражается формулой:
Выразим неизвестный радиус окружности через длину окружности:
Площадь круга определяем по формуле:
Подставим, полученные выражения для радиуса окружности, в формулу площади круга, получим:
Сократим полученную дробь:
У меня есть дополнительная информация к этой части урока!

Кроме вычислительных задач, существуют задачи на построение окружности и круга.
Окружность и круг можно начертить с помощью чертежного инструмента, который называется циркуль.
В переводе с латинского языка circulus означает «окружность», «круг».
Циркуль использовали еще с древности, много тысяч лет назад, об этом свидетельствуют найденные на раскопках находки, изображения.
Циркуль представляет собой две одинаковые по длине «ножки». На конце одной из них игла, а на второй- грифель.
Есть циркуль, у которого вместо «ножки» с грифелем помещается карандаш.
Рассмотрим, как построить окружность (круг) на бумаге с помощью циркуля и линейки.
Если задан радиус окружности (круга), то в нулевую отметку на линейке ставим иголку циркуля, другая «ножка» циркуля с грифелем в точку на линейке, равной по значению заданному радиусу.
Ставим точку на листе бумаги — это будет центр окружности (круга), в эту точку ставим иголку циркуля.
Не отрывая грифеля второй «ножки» циркуля от бумаги проводим окружность с заданным радиусом.
Если в задаче задан диаметр, то, прежде чем совершать замер по линейке, необходимо диаметр разделить пополам.
Таким образом, устанавливаем раствор циркуля по линейке на расстояние d:2 = r и чертим окружность по выше изложенной схеме.
Чтобы начертить окружность на местности, пользуются колышком и веревкой. Колышек вбивают в землю — предполагаемый центр окружности; веревка одним концом закрепляется к этому колышку, второй конец веревки туго натягивается; далее очерчивают окружность.
Данный способ построения окружности (круга) может быть применен и на бумаге, если под рукой не оказалось циркуля.
В качестве колышка берется кнопка, к ней привязывается нить определенной длинны (длина нити равна значению заданного радиуса), ко второму концу привязывается карандаш
Пройти тест и получить оценку можно после входа или регистрации
Длина окружности
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня у нас очередная математическая тема. Ее проходят в 6-м классе. Называется она – ДЛИНА ОКРУЖНОСТИ.
Эта важная величина для решения многих задачек. В том числе и во время Единого госэкзамена.
Так что наша статья будет крайне полезна школьникам-выпускникам. А для всех остальных это хороший повод освежить свои знания.
Что такое окружность
Но для начала напомним, что называют окружностью.
Окружность – это кривая замкнутая линия, которая состоит из множества точек. И эти точки находятся на одном расстоянии от центра окружности.
Определение несколько «тяжеловатое», но это официальная формулировка, которая также приводится в школьных учебниках. Графически все выглядит гораздо проще.
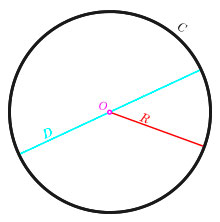
Вот пример окружности, у которой все точки на кривой «С» равноудалены от центра «О».
Кстати, расстояние от центра до границы окружности называется радиус и обозначается он буквой «R».
А отрезок, который соединяет две точки на окружности и проходит через ее центр – это диаметр «D». И, как всем известно, диаметр – это два сложенных радиуса (D = 2R).
Интересный факт! Точка тоже является в некотором роде окружностью. В математике ее называют «окружностью нулевого радиуса».
А чтобы начертить правильную окружность, нужно воспользоваться специальным прибором – циркулем. Им же можно нарисовать и окружность нужного радиуса.
Длина окружности через диаметр
Зачем мы так подробно рассказали о самой окружности, ее радиусе и диаметре? Все просто – без них не обойтись при расчете длины окружности.
Эту зависимость заметили еще в Древнем Египте. Тогдашние математики были весьма продвинуты в различных инженерных расчетах. Достаточно вспомнить, насколько надежно построены пирамиды. Им более 5 тысяч лет, а кажется, что простоят еще столько же и даже больше.
Так вот, египтяне определили, что соотношение длины окружности и ее диаметра – величина постоянная.
Другими словами, если взять совершенно разные по размерам окружности, а потом поделить их длины на их же диаметры, то получится одно и то же число.
У египтян это было число 3. Но впоследствии было получено более точное значение, которое равно 22/7 или 3 целых и 1/7.
Так появилась математическая постоянная «ПИ». Сейчас это один из столпов науки, с помощью которого решаются многие задачи.
Кстати, само название «пи» происходит от греческого слова «περιφέρεια», что как раз переводится как окружность. А «περίμετρος» — это диаметр.
Этими обозначениями и воспользовался математик Леонард Эйлер, когда в 1737 году представил научному сообществу число «пи», обозначив его изначально буквой выше упомянутых слов.
И сейчас уже каждый школьник знает, что число «пи» равно 3,14. Это значение взято за базовое, хотя на самом деле в нем бесконечное количество знаков после запятой.
Формула длины окружности
Ну а теперь главный вывод из этого исторического экскурса. Согласно вычислениям еще древнеегипетских ученых, формула длины окружности выглядит так:
Но чаще всего эту формулу принято писать без знаков умножения:
Формула эта единственная. И других возможностей рассчитать длину окружности — нет. Хотя ее можно представить, как диаметр умноженный на ПИ, но это уже банальность.
Вот и все, что мы хотели рассказать по этой теме, а более подробно смотрите в приведенном видеоролике:
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Вот объясните, как длина окружности может иметь конечное значение, если её можно разбить на отрезки, а те отрезки на ещё меньшие отрезки и так до бесконечности. Как то, что состоит из бесконечного количества отрезков, может быть конечно?
http://ladle.ru/education/matematika/6class/dlina-okruzhnosti
http://ktonanovenkogo.ru/voprosy-i-otvety/dlina-okruzhnosti-formula-kak-ee-najti.html















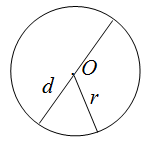
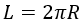
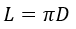
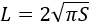
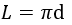
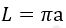
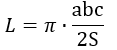
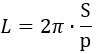
 По стороне вписанного многогранника
По стороне вписанного многогранника