Правила как найти разность сумму

В начальной школе ребенок впервые знакомится с математикой, и его первыми примерами являются такие простые действия, как складывание или вычитание. Но иногда ребенку сложно объяснить даже такие, казалось бы, несложные и привычные взрослым примеры. Как же научиться находить сумму и разность чисел?

Что такое сумма, и как ее найти

Сумма – это результат складывания двух чисел (слагаемых), между которыми стоит знак +. Чтобы получить сумму, нужно к одному слагаемому прибавить второе слагаемое. В общем виде пример можно показать так: a + b = s, где а – первое слагаемое, b – второе слагаемое, а s – результат сложения этих двух слагаемых. При этом нужно знать, что от перестановки слагаемых сумма не меняется, — это одно из самых первых правил в математике, которое проходят в начальной школе.

Чтобы наглядно показать ребенку, как сложить числа, возьмите конфеты или любые другие вещи. Покажите ребенку две конфеты, а затем прибавьте к этим конфетам еще две. Пусть ребенок посчитает и скажет, что теперь конфет оказалось четыре. Объясните ему, что он только что сложил эти числа, то есть прибавил к одному числу другое число и в конечном итоге получил сумму.

Немного сложнее объяснить сложение разрядных слагаемых, эта тема может быть непонятна ребенку. Итак, существует множество разрядов: единицы, десятки, тысячи. Возьмите, к примеру, число 2564. Если разложить его на разряды, то получится: 2564 = 2000 + 500 + 60 + 4. Чтобы прибавить к этому числу, например, число 305, воспользуйтесь сложением в столбик. При таком сложении нужно прибавлять одни разряды к другим, начиная с конца: единицы к единицам, десятки к десяткам, тысячи к тысячам. То есть, для начала складываем 4 и 5, затем 6 и 0, после 5 и 3, и в конце 2 и 0. В конечном итоге получаем число 2869.

Как найти разность чисел

 Разность – результат вычитания одного числа из другого. В отличие от суммы, здесь мы не можем воспользоваться правилом «от перестановки слагаемых разность не меняется», так как в вычитании всегда есть уменьшаемое и вычитаемое. Чтобы найти вычитаемое и разность, для начала нужно разобраться с этими понятиями. Уменьшаемое – это то, из чего мы «вычитаем», то есть убираем, а вычитаемое – количество того, что мы у этого уменьшаемого вернем.

В общем виде вычитание можно записать так: a — b = r.
Обратимся к тем же конфетам, с которыми мы разбирали сумму чисел. Чтобы помочь ребенку найти разность чисел, возьмите пять конфет. Пусть ребенок посчитает и убедится, что их пять. Затем заберите себе три конфеты. Ребенок скажет, что их осталось две. А сколько тогда забрали? Три.

А что касается разрядных слагаемых, то здесь мы делаем то же самое, что и с суммой, только теперь не прибавляем, а вычитаем. Возьмем число 6845 и вычтем из него 4231. Для этого мы вычитаем один разряд из другого разряда, производя вычитание с конца: 5-1 = 4, 4-3 = 1, 8-2 = 6, 6-4 = 2. В ответе получим 2614.

Сумма и разность чисел

Что такое сумма, и как ее найти

Сумма – это результат складывания двух чисел (слагаемых), между которыми стоит знак +. Чтобы получить сумму, нужно к одному слагаемому прибавить второе слагаемое. В общем виде пример можно показать так: a + b = s, где а – первое слагаемое, b – второе слагаемое, а s – результат сложения этих двух слагаемых. При этом нужно знать, что от перестановки слагаемых сумма не меняется, — это одно из самых первых правил в математике, которое проходят в начальной школе.

Чтобы наглядно показать ребенку, как сложить числа, возьмите конфеты или любые другие вещи. Покажите ребенку две конфеты, а затем прибавьте к этим конфетам еще две. Пусть ребенок посчитает и скажет, что теперь конфет оказалось четыре. Объясните ему, что он только что сложил эти числа, то есть прибавил к одному числу другое число и в конечном итоге получил сумму.

Немного сложнее объяснить сложение разрядных слагаемых, эта тема может быть непонятна ребенку. Итак, существует множество разрядов: единицы, десятки, тысячи. Возьмите, к примеру, число 2564. Если разложить его на разряды, то получится: 2564 = 2000 + 500 + 60 + 4. Чтобы прибавить к этому числу, например, число 305, воспользуйтесь сложением в столбик. При таком сложении нужно прибавлять одни разряды к другим, начиная с конца: единицы к единицам, десятки к десяткам, тысячи к тысячам. То есть, для начала складываем 4 и 5, затем 6 и 0, после 5 и 3, и в конце 2 и 0. В конечном итоге получаем число 2869.

Как найти разность чисел

Разность – результат вычитания одного числа из другого. В отличие от суммы, здесь мы не можем воспользоваться правилом «от перестановки слагаемых разность не меняется», так как в вычитании всегда есть уменьшаемое и вычитаемое. Чтобы найти вычитаемое и разность, для начала нужно разобраться с этими понятиями. Уменьшаемое – это то, из чего мы «вычитаем», то есть убираем, а вычитаемое – количество того, что мы у этого уменьшаемого вернем.

В общем виде вычитание можно записать так: a — b = r.
Обратимся к тем же конфетам, с которыми мы разбирали сумму чисел. Чтобы помочь ребенку найти разность чисел, возьмите пять конфет. Пусть ребенок посчитает и убедится, что их пять. Затем заберите себе три конфеты. Ребенок скажет, что их осталось две. А сколько тогда забрали? Три.

А что касается разрядных слагаемых, то здесь мы делаем то же самое, что и с суммой, только теперь не прибавляем, а вычитаем. Возьмем число 6845 и вычтем из него 4231. Для этого мы вычитаем один разряд из другого разряда, производя вычитание с конца: 5-1 = 4, 4-3 = 1, 8-2 = 6, 6-4 = 2. В ответе получим 2614.

Источник

Как найти разность чисел в математике

Слово «разность» может употребляться во многих значениях. Это может означать и разницу чего-либо, например, мнений, взглядов, интересов. В некоторых научных, медицинских и других профессиональных сферах этим термином обозначают разные показатели, к примеру, уровня сахара в крови, атмосферного давления, погодных условий. Понятие «разность», как математический термин тоже существует.

Арифметические действия с числами

Основными арифметическими действиями в математике являются:

Каждый результат этих действий также имеет своё название:

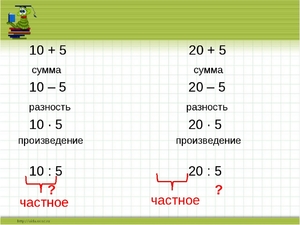
• сумма — результат, получившийся при сложении чисел;
• разность — результат, получившийся при вычитании чисел;
• произведение — результат умножения чисел;
• частное — результат деления.

Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:

• сумма — прибавить;
• разность — отнять;
• произведение — умножить;
• частное — разделить.

Разность в математике

Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:

• Разность чисел означает, насколько одно из них больше другого.
• Разностью в математике называется итог, получившийся при отнимании друг от друга двух и более чисел.
• Это вычитание одного числа из другого.
• Это цифра, составляющая остаток при минусовании двух величин.
• Это величина, являющаяся результатом вычитания двух значений.
• Разность показывает количественное различие между двумя цифрами.
• Это результат одного из четырёх арифметических действий, которым является вычитание.
• Это то, что получится, если из уменьшаемого отнять вычитаемое.

Видео: Математика 6 Делимость суммы и разности чисел

И все эти определения являются верными.

Как найти разницу величин

Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:

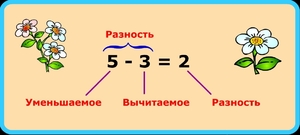
• Разностью называется результат вычитания одного числа из другого. Первое из этих чисел, из которого осуществляется вычитание, называется уменьшаемым, а второе, которое вычитают из первого, называется вычитаемым.

Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:

• Чтобы найти разность, надо от уменьшаемого отнять вычитаемое.

Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?

• Уменьшаемое — это математическое число, от которого отнимают и оно уменьшается (становится меньше).
• Вычитаемое — это математическое число, которое вычитают из уменьшаемого.

Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:

• Чтобы найти уменьшаемое, надо к вычитаемому прибавить разность.
• Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.

Математические действия с разностью чисел

Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.

Видео: Математика 2 класс. Разность двухзначных чисел

Простые примеры

• Пример 1. Найти разницу двух величин.

20 — уменьшаемое значение,

Решение: 20 — 15 = 5

Ответ: 5 — разница величин.

• Пример 2. Найти уменьшаемое.

32 — вычитаемое значение.

Решение: 32 + 48 = 80

• Пример 3. Найти вычитаемое значение.

17 — уменьшаемая величина.

Решение: 17 — 7 = 10

Ответ: вычитаемое значение 10.

Более сложные примеры

На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.

• Пример 4. Найти разницу трёх значений.

Даны целые значения: 56, 12, 4.

56 — уменьшаемое значение,

12 и 4 — вычитаемые значения.

Решение можно выполнить двумя способами.

1 способ (последовательное отнимание вычитаемых значений):

1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым);

2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):

1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым);

Ответ: 40 — разница трёх значений.

• Пример 5. Найти разницу рациональных дробных чисел.

Даны дроби с одинаковыми знаменателями, где

4/5 — уменьшаемая дробь,

Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.

Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5

• Пример 6. Утроить разницу чисел.

А как выполнить такой пример, когда требуется удвоить или утроить разницу?

Вновь прибегнем к правилам:

• Удвоенное число — это величина, умноженная на два.
• Утроенное число — это величина, умноженная на три.
• Удвоенная разность — это разница величин, умноженная на два.
• Утроенная разность — это разница величин, умноженная на три.

7 — уменьшаемая величина,

5 — вычитаемая величина.

2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.

• Пример 7. Найти разницу величин 7 и 18.

7 — уменьшаемая величина;

Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?

И опять есть применяемое для конкретного случая правило:

• Если вычитаемое больше уменьшаемого, разница окажется отрицательной.

Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.

Математика для блондинок

Во Всемирной паутине можно найти массу тематических сайтов, которые ответят на любой вопрос. Точно так же в любых математических расчётах вам помогут онлайн-калькуляторы на любой вкус. Все расчёты, производимые на них, прекрасное подспорье для торопливых, нелюбознательных, ленивых. Математика для блондинок — один из таких ресурсов. Причём прибегаем к нему мы все, независимо от цвета волос, пола и возраста.

В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.

И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:

• сумму — сложением слагаемых;
• произведение — умножением множителей;
• частное — делением делимого на делитель.

Источник

Свойства сложения и вычитания

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Свойства сложения

Сложение — это арифметическое действие, в котором единицы двух чисел объединяются в одно новое число

Для записи сложения используют знак «+» (плюс), который ставят между слагаемыми.

Слагаемые — это числа, единицы которых складываются.

Сумма — это число, которое получается в результате сложения.

Рассмотрим пример 2 + 5 = 7, в котором:

• 2 — это первое слагаемое,
• 5 — второе слагаемое,
• 7 — это сумма.

При этом саму запись (2 + 5) можно тоже назвать суммой.

Сложение двух чисел можно проверить вычитанием. Для этого вычитаем из суммы одно из слагаемых. Если разность окажется равной другому слагаемому — сложение выполнено верно.

Впервые мы сталкиваемся со свойствами сложения во 2 классе. С каждым годом задания усложняются, и появляются новые правила и законы. Рассмотрим свойства сложения для 4 класса.

1. Переместительное свойство сложения
   От перестановки мест слагаемых сумма не меняется.
   a + b = b + a
2. Сочетательное свойство сложения
   Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа.
   (a + b) + c = a + (b + c)
3. Свойство нуля при сложении
   Если к числу прибавить нуль, получится само число.
   a + 0 = 0 + a = a

Свойства вычитания

Вычитание— это арифметическое действие, в котором отнимают меньшее число от большего.

Для записи вычитания используется знак «-» (минус), который ставится между уменьшаемым и вычитаемым.

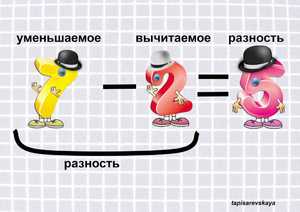
Уменьшаемое — это число, из которого вычитают.

Вычитаемое — это число, которое вычитают.

Разность — это число, которое получается в результате вычитания.

Рассмотрим пример 9 — 4 = 5, в котором:

Инфоурок

›

Математика

›Другие методич. материалы›Памятка по математике «Сумма, разность, произведение, частное».

Памятка по математике «Сумма, разность, произведение, частное».

I. Математические понятия СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ, ЧАСТНОЕ взаимосвязаны с математическими терминами СЛОЖЕНИЕ, ВЫЧИТАНИЕ, УМНОЖЕНИЕ, ДЕЛЕНИЕ.

Все определения даются здесь на множестве натуральных чисел.

Каждой паре чисел ставится в соответствие число, называемое их СУММОЙ.

Сумма состоит из стольких единиц, сколько их содержится в числах (слагаемых) из данной пары.

СУММА есть результат сложения чисел-слагаемых.

Вычитание — это операция, обратная сложению. Она состоит в нахождении одного из слагаемых по сумме и другому слагаемому. Данная сумма называется уменьшаемым, данное слагаемое — вычитаемым, а искомое слагаемое — РАЗНОСТЬЮ.

РАЗНОСТЬ — это число, являющееся результатом вычитания, остаток вычитания.

Каждой паре чисел можно поставить в соответствие число, которое состоит из стольких единиц, сколько их содержится в первом числе из пары, взятых столько раз, сколько единиц содержится во втором числе из пары. Это соответствующее таким образом паре чисел (они называются сомножителями) число называется ПРОИЗВЕДЕНИЕМ.

ПРОИЗВЕДЕНИЕ — это результат умножения.

Деление есть операция, обратная умножению.

Деление — это нахождение одного из сомножителей по произведению и другому сомножителю. Данное произведение называется делимым, данный сомножитель — делителем, а искомый сомножитель — это ЧАСТНОЕ, то есть число, полученное от деления одного числа на другое.

II. ДРУГИЕ ЗНАЧЕНИЯ СЛОВ СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ, ЧАСТНОЕ.

Все используемые в качестве математических понятий слова могут иметь и другие лексические значения.

СУММА в переносном значении означает совокупность, общее количество чего-либо.

Например. Профессионализм педагога заключается в сумме знаний, умений и навыков, передаваемых им своим ученикам. Отсутствие нужной суммы денег заставило отказаться от покупки.

РАЗНОСТЬ имеет значения разницы, несходства, отличия в чем-либо.

Например. Разность интересов намного хуже разницы в возрасте. Дружба может начаться с представления об общности взглядов , а вражда — с разности взглядов.

ПРОИЗВЕДЕНИЕ означает что-либо произведенное в процессе труда, создание чего-нибудь, продукт труда, творчества, искусства и т.п.

Например. Высокое художественное произведение заставляет человека думать над своей жизнью. На конкурсе юных пианистов мальчик играл произведение П.И. Чайковского. Эта шкатулка — настоящее произведение искусства.

ЧАСТНОЕ — это что-то личное, персональное, принадлежащее только одному человеку, это его собственность, его и только его достояние. И будь то самоличные мысли, будь то имущество или что-нибудь другое, но оно принадлежит только ему, частному лицу.

Например. Подруга подарила мне записную книжку с надписью «Частное». Хорошо ли противопоставлять частное общественному?