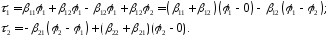Потенциальные коэффициенты как найти - AvtoShod.ru

Уединенный проводник.

Электроемкостью проводника называется величина, измеряемая отношением заряда q, сообщенного этому проводнику к потенциалу этого проводника

(9.1)

Электроемкость измеряется в фарадах: .

Фарад – очень большая величина, поэтому на практике пользуются более мелкими величинами 1мкФ=10-6Ф, 1пФ=10-12Ф.

Вычислим электроемкость шара радиусом R. Так как , то .

Система проводников.

Если имеется система проводников, то потенциал каждого из них зависит не только от заряда проводника, но и от напряженности полей, создаваемых другими проводниками, т. е. от зарядов других проводников, причем по принципу суперпозиции он прямо пропорционален этим зарядам.

Потенциалы первого и второго проводников можно записать в виде

(9.2)

Коэффициенты Называют потенциальными коэффициентами. Они зависят от формы, размеров, взаимного расположения проводников. Если вначале заряды на проводниках И , а потенциалы , а затем заряды стали , а потенциалы , то можно показать, что справедливо соотношение

, (9.3)

Которое называется теоремой взаимности. Из нее непосредственно получается условие, которому удовлетворяют коэффициенты : они симметричны относительно своих индексов. Теорему взаимности в общем случае для системы из n проводников можно записать в виде

. (9.4)

Если теперь обобщить (9.2) на систему из n заряженных проводников, т. е.

, (9.5)

То непосредственно после подстановки (9.5) в (9.4) легко получить, что . Соотношение (9.5) можно рассматривать как систему, решение которой можно записать виде уравнений относительно при заданных потенциалах

(9.7)

где – емкостные коэффициенты. – емкостной коэффициент i-го проводника, -коэффициент взаимной емкости i-го и j-го проводников. Поскольку положительный заряд на уединенном проводнике создает положительный потенциал, то все емкостные коэффициенты >0.

Емкостные коэффициенты двух проводящих шаров.

Предположим, имеется два проводящих шара с радиусами a, центры которых расположены на расстоянии r, содержащие заряды И и пусть . Последнее условие позволяет сохранить сферическую симметрию поля каждого из зарядов.

Умножим первое уравнение на r, второе на (-a) и после преобразований

Получим:

Но , а . Сопоставляя эти выражения с полученными для и Легко найти, что

Если емкостную связь разорвать, т. е. устремить r к бесконечности, то емкостные коэффициенты что совпадает с выражением для электроемкости уединенного шара, а коэффициенты .

Конденсаторы.

Конденсатор – совокупность двух любых проводников, расположенных на некотором расстоянии друг от друга, пространство между которыми обычно заполняют диэлектриком. Заряжают проводники равными по величине, но противоположными по знаку зарядами. Проводники называют обкладками конденсатора, а сам конденсатор – это устройство, позволяющее накапливать электрическую энергию и отдавать ее в нужный момент времени. Вернемся к (9.2), где положим , , тогда ,

Электроемкостью системы двух проводников, будет величина . (9.9)

Так как , то C>0.

Электроемкость конденсатора можно выразить и через емкостные коэффициенты:

Достаточно положить , найти И , затем и можно получить (9.10)

В большинстве случаев форма обкладок конденсатора и их взаимное расположение подбирают таким образом, чтобы внешние поля не влияли существенно на электрическое поле между ними, и силовые линии, начинающиеся на одной из обкладок, обязательно заканчивались на другой. Благодаря этому всегда обеспечивается равенство абсолютных значений зарядов на обкладках. В зависимости от формы обкладок конденсаторы бывают сферическими, цилиндрическими и плоскими. Вычисление емкости конденсатора производится следующим образом: мысленно заряжаем обкладки равными по величине и противоположными по знаку зарядами , затем вычисляем разность потенциалов между обкладками . И затем вычисляем емкость .

Фактически вычисление емкости конденсатора сводится к определению разности потенциалов между обкладками при известном заряде на обкладках.

Сферический конденсатор.

Даны 2 сферы с общим центром. Пусть на внутренней обкладке

Сферического конденсатора имеется заряд +Q, на внешней –Q.

Используя Электростатическую теорему Гаусса легко видеть, что

Напряженность полей . Напряженность поля между внешней и внутренней обкладкой равна:

Разность потенциалов между обкладками :

Тогда емкость:

(9.11)

Цилиндрический конденсатор.

Рассмотрим два коаксиальных цилиндра с радиусами R1 и R2. . Согласно теореме Гаусса , где L – длина цилиндров.

Тогда емкость цилиндрического конденсатора:

. (9.12)

Плоский конденсатор.

Даны 2 проводящие пластины площадью S, расстояние между которыми D

Поле внутри конденсатора

Тогда емкость плоского конденсатора

. (9.13)

Последовательное соединение конденсаторов.

Очевидно:

или, обобщая, получим:

. (9.14)

Формула (9.14) определяет электроемкость K параллельно соединенных конденсаторов.

Параллельное соединение конденсаторов.

На основании закона сохранения заряда , , т. к. напряжение на каждом конденсаторе равно U, следовательно. Обобщить систему из K конденсаторов, получаем:

. (9.15)

Источник

Как
пример практического применения метода
зеркальных изображений рассмотрим
расчет потенциалов и зарядов в системе
проводящих тел. Задачи такого типа
возникают, в частности, при исследовании
процессов в линиях электропередач.

Два
длинных провода
расположенны параллельно проводящей
плоскости (над землею). Радиусы проводов
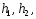
высоты подвесокмежосевое расстояниепри этомh>>R,
d>>R.
Известны
.

На
основании второго следствия из теоремы
единственности заменим проводящую
среду (землю) диэлектриком с
,
а поверхностные заряды земли – системой
зеркальных зарядов проводов с
противоположными знаками. Смещением
электрических осей пренебрегаем,
так как по условиюh>>R.

Потенциальные
коэффициенты.

Потенциалы
проводов можно определить через линейные
плотности зарядов:

или

(2.12)

Здесь
обозначены:

собственные
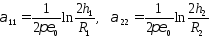
потенциальные коэффициенты;

взаимные
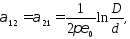
потенциальные коэффициенты.

Систему
уравнений (2.12) принято называть первой
группой формул Максвелла.
Первая группа формул Максвелла позволяет
определить потенциалы проводов через
их заряды.

Коэффициент
численно равен потенциалуn-го
провода, если на нем находится единичный
заряд (),
а на остальных проводах заряды отсутствуют.
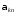
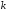
Коэффициентчисленно равен потенциалу-го
провода, если заряд-го
провода равен единице, а остальных
проводов – нулю.

Емкостные
коэффициенты (коэффициенты элетростатической
индукции).

Если
заданы потенциалы проводов
,
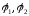
то их зарядымогут быть определены из совместного
решения системы потенциальных уравнений
(первой группы формул Максвелла). Тогда
получим вторую группу формул Максвелла

(2.13)

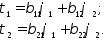
Здесь
приняты обозначения:

—
собственные емкостные коэффициенты
(коэффициенты элетростатической
индукции) всегда положительны,

— взаимные
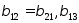
емкостные коэффициенты, всегда
отрицательны.

Частичные
ёмкости.

Систему
уравнений (2.13) можно записать в другой
форме, выражая заряды на проводящих
телах через разности
потенциалов (напряжения)
между некоторым телом и всеми остальными,
в т.ч. и землей.

Запишем
систему уравнений (2.13) в виде

Введем
обозначения:;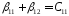
;.

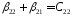
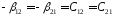
С учетом
введенных обозначений выражение (2.13)
перепишется в форме:

(2.14)

Здесь
обозначены: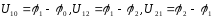
напряжения между соответствующими
элементами схемы;
=0
.

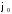
Итак,
чстичные емкости определяются через
коэффициенты элетростатической индукции.

Частичные
емкости являются важными характеристиками
системы заряженных проводящих тел. С
их помощью такая система может быть
представлена в виде определенной
комбинации емкостей.

На рис.
2.13 в виде схемы соединений частичных
емкостей представлена система двух
проводящих тел.

Частичные
емкости используют при расчетах не
только электростатических полей, но и
быстропротекающих процессов в
электрических цепях, а также при расчетах
таких процессов в электрических цепях,
в основу которых положено использование
частичных емкостей, например, при
емкостном отборе мощности от высоковольтной
линии электропередачи. При расчете
быстропротекающих процессов учитывают,
в частности, емкости между электродами
полупроводниковых приборов (тиристоров,
транзисторов).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
15.03.20166.58 Mб44Бандурин Теоретич основы электротехн Теория электрич цепей электромагн поля С.А.Башарин 2004.djvu
#
#
#
#
10.04.2015403.46 Кб251БЖ.doc
#
#

Источник

Виталий Викторович Карабут

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Рассмотрим систему, которая состоит из некоторого количества (N) заряженных стационарных проводников. Пространство между этими проводящими телами заполняет диэлектрик. Предположим, что в диэлектрике свободных зарядов нет. Нормировку потенциала примем на бесконечность ($varphi left(infty right)=0$).

Что такое потенциальные коэффициенты

Считаем, что в начале наблюдения заряд всех проводников равен нулю. Зарядим один из проводников (допустим i-й) на 1 Кл. Так мы определим, причем однозначно, электрическое поле во всем пространстве ($overrightarrow{E_{i }}left(overrightarrow{r}right) и зная их связь через градиент {varphi }_i(overrightarrow{r})$). Потенциал в месте нахождения проводника с номером j обозначим как: ${varphi }_{ji}.$

Определение

Коэффициенты ${varphi }_{ji}$ зависят исключительно от формы проводников, их местоположения, диэлектрической проницаемости среды между ними (диэлектрика). Такие коэффициенты называют потенциальными коэффициентами.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Так как уравнения электростатики по большей части линейные и однородные, то произвольная комбинация векторов напряженности и электрического смещения ($overrightarrow{E_{i }}left(overrightarrow{r}right), overrightarrow{D_{i }}left(overrightarrow{r}right)$) c постоянными коэффициентами $q_i$ удовлетворяют уравнениям вида:

[overrightarrow{E}left(overrightarrow{r}right)=sumlimits^N_{i=1}{q_i}overrightarrow{E_{i }}left(overrightarrow{r}right)left(1right),]

[overrightarrow{D}left(overrightarrow{r}right)=sumlimits^N_{i=1}{q_i}overrightarrow{D_{i }}left(overrightarrow{r}right)left(2right).]

Потенциал проводника и потенциальные коэффициенты

Электростатические поля потенциальны, следовательно, вектор напряженности так же потенциален. В диэлектрике $divoverrightarrow{D}=0.$ В проводниках $overrightarrow{E}=0. $ Выражения $overrightarrow{D} и overrightarrow{E}$ могут быть рассмотрены как напряжённость и индукция какого-то электростатического поля. Заряды этого поля не могут находиться внутри диэлектрика, так как $divoverrightarrow{D}=0.$ Необходимо выяснить физический смысл коэффициентов $q_i$, которые ранее мы ввели формально. По теореме Остроградского — Гаусса заряд на поверхности проводника с номером i равен:

[Q_i=ointlimits_{S_i}{overrightarrow{D}doverrightarrow{S}=sumlimits_j{q_jointlimits_{S_i}{overrightarrow{D_j}doverrightarrow{S}=q_i}}}ointlimits_{S_i}{overrightarrow{D_i}doverrightarrow{S}=q_i}left(3right).]

На основании теоремы о единственности можно сказать, что уравнение (1) определяет электростатическое поле системы N проводников, заряды которых равны $q_1,q_2,dots q_N.$ Потенциал поля при этом можно вычислить в соответствии с формулой:

[varphi left(overrightarrow{r}right)=sumlimits^N_{j=1}{q_j{varphi }_jleft(overrightarrow{r}right)}left(4right).]

Зададим точку на поверхности проводника номера i с помощью вектора $overrightarrow{r}$, найдем потенциал проводника как:

[{varphi }_i=sumlimits^N_{j=1}{q_j{varphi }_{ij}left(overrightarrow{r}right)}left(5right).]

Решив уравнения (4) и (5) относительно $q_i$, получим, что:

[q_i=sumlimits^N_{i=0}{C_{ij}{varphi }_jleft(6right),}]

где $C_{ij}$ — постоянные емкостные коэффициенты. Как и потенциальные коэффициенты они определяются только размерами, конфигурацией, расположением проводников и $varepsilon $ среды.

Мы получили, что заряды проводников — линейные однородные функции их потенциалов, а потенциалы — линейные однородные функции зарядов. В случае однородного диэлектрика $C_{ij}sim varepsilon .$ Для конденсатора количество обкладок — 2. Тогда:

[q_1=C_{11}{varphi }_1+C_{12}{varphi }_2, q_2=C_{21}{varphi }_1+C_{22}{varphi }_2left(7right),]

где $q_1=-q_2$. Из уравнений (7) емкость конденсатора равна:

[C=frac{C_{11}C_{22}-C_{12}C_{21}}{C_{11}+C_{22}+C_{12}+C_{21}}left(8right).]

Все потенциальные коэффициенты положительны. Емкостные коэффициенты с одинаковыми индексами положительны, с разными — отрицательны. Емкостные и потенциальные коэффициенты симметричны, то есть:

[C_{ij}=C_{ji},left(9right),]

[{varphi }_{ij}={varphi }_{ji}left(10right).]

«Связь между зарядом и потенциалом проводника» 👇

Пример 1

Задание: Проводник заряжают, поднося к нему несколько раз пластинку, которая каждый раз имеет заряд $Q$. Предположим, что $q_1$- заряд, который остался на проводнике после того, как его зарядили в первый раз. Найдите заряд проводника после бесконечно большого количества операций по его зарядке.

Решение:

Когда пластинку подносят к проводнику, заряд распределяется между двумя этими телами. Когда пластинку поднесли к проводнику в первый раз, проводник получил заряд $q_1$, на пластинка этот заряд потеряла, следовательно, у нее остался заряд $Q-q_1$. В случае многократного повторения операции зарядки при следующих соприкосновениях проводника и пластинки его заряд практически изменяться не будет. Заряд пластинки не изменится так же, он останется равным Q. Искомый заряд можно определить из пропорции:

[frac{q}{Q}=frac{q_1}{Q-q_1}left(1.1.right).]

Следовательно,

[q=frac{q_1Q}{Q-q_1}.]

Ответ: Заряд проводника равен $q=frac{q_1Q}{Q-q_1}.$

Пример 2

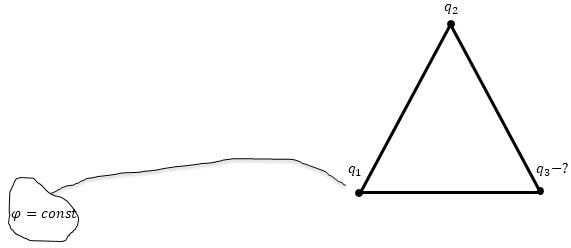
Задание: Три одинаковых металлических шарика находятся в вершинах равностороннего треугольника. Проводником (тонкой проволокой), который подключён удаленному заряженному телу, потенциал которого не известен, но постоянен, по очереди касаются каждого шарика. Заряды первых двух после касания стали равны${ q}_1$ $ $и $q_2$, каким будет заряд на третьем шаре? Считать шарики изолированными.

Решение:

Рис. 1

Так как потенциальные коэффициенты симметричны, то мы можем записать:

[{varphi }_{11}={varphi }_{22}={varphi }_{33}=A left(2.1right).]

[{varphi }_{12}={varphi }_{21}={varphi }_{23}=B left(2.2right).]

При зарядке первого шарика он получает потенциал равный:

[{varphi }_1=Aq_{1 }left(2.3right).]

Когда происходит зарядка двух других шаров, потенциал первого шара изменяется, но в нашем случае это не имеет значения. При зарядке второго шара его потенциал будет:

[{varphi }_1=Aq_2+Bq_1left(2.4right).]

Для третьего шарика имеем:

[{varphi }_1=Aq_3+B{(q}_1+q_2) left(2.5right).]

Следовательно, из (2.2) — (2.4) получаем:

[Aq_{1 }=Aq_2+Bq_1=Aq_3+B{(q}_1+q_2) left(2.6right).]

Выразим из (2.6) искомый заряд, получим:

[q_3=frac{q^2_2}{q_1}.]

Ответ: $q_3=frac{q^2_2}{q_1}.$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

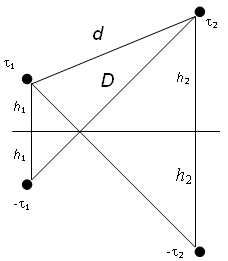
Определим потенциальные коэффициенты двухпроводной линии, провода которой подвешены на одинаковой высоте h от земли и на расстоянии D друг от друга (рис. 1.36). Радиусы проводов одинаковы и равны R. Для определения коэффициентов достаточно положить q₁ ? 0 и q₂ = 0. При этом уравнения (1.47) приобретают вид

(1.48)

Поле заряженного первого провода будет таким же, как и при одном проводе, протянутом над поверхностью земли. Поэтому потенциал этого провода можно определить по формуле (1.46), если предположить, что точка М, находится на поверхности провода, а электрические оси данного и отраженного провода совпадают с их геометрическим осями (вследствие малости размера провода по сравнению с расстоянием до земли). В этом случае формула (1.46) приобретает вид:

(1.49)

Потенциал второго провода будет равен потенциалу той точки, через которую проходит его ось (поскольку искажением поля пренебрегаем) и его также можно определить с помощью формулы (1.46)

(1.50)

Сравнивая первую формулу (1.48) с выражением (1.49), получаем уравнение для определения собственного потенциального коэффициента a₁₁

Здесь l – длина провода. Аналогичным образом, сравнивая вторую формулу (1.48) с выражением (1.50), получаем уравнение для определения взаимного потенциального коэффициента a₂₁,

Собственный потенциальный коэффициент a₂₂ второго провода, с учетом его размеров, а также то, что он находится на том же расстоянии от поверхности земли, что и первый провод, равен a₁₁.

Что касается взаимного потенциального коэффициента a₁₂, то он равен a₂₁, поскольку всегда имеет место равенство a_kp = a_pk, что вытекает из условия независимости энергии системы заряженных тел от последовательности, в которой устанавливаются заряды системы.

Зная потенциальные коэффициенты, определим теперь емкость двухпроводной линии с учетом влияния земли. Пусть заряды проводов равны по абсолютному значению и противоположны по знаку: q₁ = -q₂. Заменяя q₂ в выражении (1.47) на – q₁, получаем