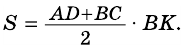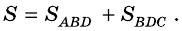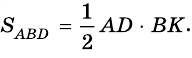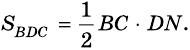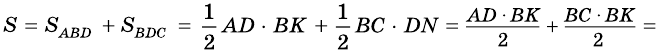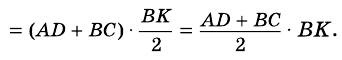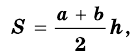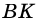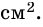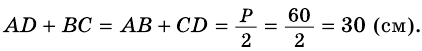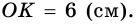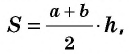Администрация Таймырского Долгано-Ненецкого
муниципального района
Управление образования
Таймырское муниципальное казенное общеобразовательное
учреждение
«Диксонская средняя школа»
Муниципальная Конференция
исследовательских и проектных работ «Золотое перо»
Исследовательская работа
Секция: физико-математическая
«9 способов нахождения площади трапеции»
Работу выполнил:
Низовцев Руслан Алексеевич,
10.09.2000 г
г.п. Диксон, ул. Водопьянова д.24 кв.36
ТМКОУ «Диксонская средняя школа»
9 класс
Научный руководитель:
Низовцева Джамиля Ахмедулловна
ТМКОУ «Диксонская средняя школа»
учитель математики
e—mail: yaporova@yandex.ru
тел: 89050911271
2015-2016 уч. год
Аннотация
Автор: Низовцев Руслан Алексеевич
ТМКОУ «Диксонская средняя школа» 9 класс
Тема: «9 способов нахождения площади трапеции»
Руководитель: Низовцева Джамиля Ахмедулловна, ТМКОУ «Диксонская
средняя школа», учитель математики
Цель научной работы: определить, существуют ли другие способы нахождения
площади трапеции
Методы проведенных исследований: поисковый метод с использованием научной и
учебной литературы, интернета; исследовательский метод; практический метод при
выполнении вычислений; составление буклета; видео опрос «Что знают учащиеся школы
о трапеции, о нахождении ее площади»
Основные результаты
научного исследования:
· существует много способов нахождения площади
трапеции;
· при решении задач используется тот метод,
который удобен.
Содержание
1.
Введение
2. Значение геометрии в нашей жизни
3. Способы нахождения
площади трапеции
3.1. Исследование 1 «Нахождение площади трапеции по учебнику «Геометрия
7-9» А.В. Погорелов
3.2. Исследование 2 «Нахождение площади трапеции через построение
внешних высот трапеции»
3.3. Исследование 3 «Нахождение площади
трапеции через построение прямой, параллельной одной из боковых сторон»
3.4. Исследование 4 «Нахождение площади
трапеции через построение прямой, проходящей через середину боковой стороны»
3.5.
Исследование 5 «Нахождение площади
трапеции с помощью построения перпендикуляров через середины боковых сторон»
3.6. Исследование 6 «Нахождение площади
трапеции с помощью построения внутренних высот трапеции»
3.7. Исследование 7 «Нахождение площади
трапеции, если известны диагонали и угол между ними»
3.8. Исследование 8 «Нахождение площади
трапеции через среднюю линию»
3.9.Исследование 9 «Нахождение
площади трапеции при проведении перпендикуляра к боковой стороне из середины
другой боковой стороны»
3.10.
Исследование 10 «Анализ тестов
ОГЭ по математике модуль «Геометрия»: частота задач на нахождение площади
трапеции»
4.
Заключение
5. Список литературы
6. Приложения:
6.1.
Приложение 1. Буклет «Трапеция в нашей жизни»
6.2.
Приложение 2. Видео опрос «Что знают учащиеся школы о трапеции, о
нахождении ее площади»
1. Введение
Выбор темы «9 способов нахождения площади трапеции»
обусловлен моими личными интересами в области геометрии, а именно в
строительстве. Я очень люблю строить различные объекты. Это могут быть фигуры
из конструктора, а также различные «конструкции» из досок, которые мы находим
с друзьями на побережье Карского моря. Актуальность данной работы определяется
тем, что знания и умения находить площадь трапеции имеют огромное значение для
решения практических задач в жизни, в том числе и заданий основного
государственного экзамена по математике. Данное исследование, которое выходит
за рамки нашей школьной программы, поможет найти новые подходы к решению
геометрических задач. Именно поэтому данная тема явилась источником для
исследовательской работы.
В ходе работы нам предстояло подтвердить или
опровергнуть суждение о том, что существуют другие способы нахождения площади
трапеции, помимо описанного способа в учебнике.
Объект исследования: трапеция
Предмет исследования: площадь трапеции
Цель исследования: определить, существуют ли другие способы нахождения
площади трапеции.
Задачи исследования:
1.
Проанализировать
литературу по данному вопросу;
2.
Изучить вопрос по
нахождению площади трапеции в учебнике геометрии 7-9 класс А.В. Погорелов.
3.
Провести исследования
«Различные способы нахождения площади трапеции»
4.
Провести анализ тестов ОГЭ
с 2011 г по 2016г по математике и определить частоту появления задач на
нахождение площади трапеции в КИМах.
5.
Провести видео опрос «Что
знают учащиеся школы о трапеции, о нахождении ее площади»
Методы исследования:
1.
поисковый метод с
использованием научной и учебной литературы, интернета;
2.
исследовательский метод
определяется как самостоятельное решение проблемы с применением рассуждения,
доказательства и анализ фактов.
3.
практический метод при
определении частоты появления задач на нахождение площади трапеции, составлении
буклета, проведение видео опроса
Практическая значимость работы определяется возможностью
использования данного материала при решении геометрических задач, при
доказательстве некоторых положений.
Совместно с руководителем был разработан ход
исследования:
1.
Изучить теоретический
материал учебника и дополнительных источников информации и найти новые способы
нахождения площади трапеции.
2.
Провести анализ тестов ОГЭ
и определить частоту появления задач на нахождение площади трапеции.
3.
Провести видео опрос «Что
знают учащиеся школы о трапеции, о нахождении ее площади»
4.
Оформить результаты,
сделать соответствующие выводы.
2. Значение геометрии в нашей жизни1,2
Геометрия обладает целым рядом качеств, располагает
огромными возможностями для эмоционального и духовного развития человека. «Я
думаю, что никогда до настоящего времени мы не жили в такой геометрический
период. Всё вокруг – геометрия». Эти слова, сказанные великим французским
архитектором Ле Корбюзье в начале XX в., очень точно характеризуют и наше
время. Мир, в котором мы живём, наполнен геометрией домов и улиц, гор и полей,
творениями природы и человека. Лучше ориентироваться в нём, открывать новое,
понимать красоту и мудрость окружающего мира помогает нам геометрия.
Геометрия зародилась в глубокой древности. Строя
жилища и храмы, украшая их орнаментами, размечая землю, измеряя расстояния и
площади, человек применял свои знания о форме, размерах и взаимном расположении
предметов, он использовал свои геометрические знания, полученные из наблюдений
и опытов.
Среди множества различных геометрических фигур на
плоскости выделяется большое семейство четырёхугольников. В обычной жизни на
каждом шагу мы встречаемся с понятием “площадь”. Что такое “площадь”, знает
каждый. Каждый понимает смысл слов: площадь комнаты, площадь садового участка.
Подумайте и самостоятельно ответьте на вопрос: что такое “площадь”? И вы
увидите, что не так-то это просто. Даже математики смогли создать
соответствующую математическую теорию сравнительно недавно. Правда, это никому
не мешало успешно использовать понятие площади и в науке, и на практике с
незапамятных времен. Измерение площадей считают одним из самых древних разделов
геометрии; в частности название “геометрия” (т.е. “землемерие”) связывают
именно с измерением площадей. Согласно легенде, эта наука возникла в Древнем
Египте, где после каждого разлива Нила приходилось заново производить разметку
участков, покрытых плодоносным илом, и вычисление их площадей.
По-видимому, в древности приходилось рассматривать
лишь участки, мало отличающиеся от прямоугольника по форме, а для таких
участков погрешность невелика. Лишь в последствие было полностью развито учение
о площадях и получены точные формулы для вычисления площади прямоугольника,
параллелограмма, треугольника, трапеции и других многоугольников.
Определение площадей геометрических фигур –
одна из древнейших практических задач. Правильный подход к их решению был
найден не сразу, но уже древние греки умели правильно находить площади
многоугольников.
1.https://ru.wikipedia.org/wiki,
2.Математический энциклопедический словарь. — М.: «Сов. энциклопедия», 1988. — С. 587.
3. Способы нахождения площади трапеции
Одним из многоугольников является трапеция.
Трапе́ция2 (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол,
трапеза») — выпуклый четырёхугольник,
у которого две стороны параллельны,
а две другие не параллельны. Параллельные противоположные стороны называются
основаниями трапеции, а две другие боковыми сторонами. Средняя
линия — отрезок, соединяющий середины боковых сторон.
Виды трапеций
- Трапеция, у которой
боковые стороны равны, называется равнобокой, равнобочной или
равнобедренной трапецией. - Трапеция, имеющая прямые
углы при боковой стороне, называется прямоугольной.
Трапецию можно встретить как в повседневной жизни —
быту, так и в архитектуре и природе. Значение трапеции в нашей жизни я оформил
в виде буклета. Приложение 1.
Я самостоятельно изучил теорему о нахождении площади
трапеции, провел исследования. Одним, из них является видео опрос «Что знают
учащиеся школы о трапеции, о нахождении ее площади» Приложение 2
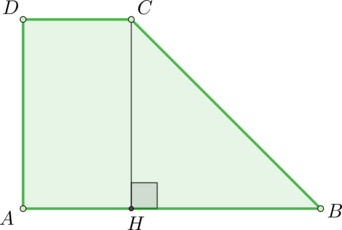
Исследование 1 «Нахождение площади трапеции по
учебнику «Геометрия 7-9» А.В. Погорелов3
Дано: ABCD — трапеция
Найти площадь SABCD

D С Е
Решение.
1.
Провели диагональ BD.
Тогда наша трапеция разбивается на две части: два треугольника ΔABD и ΔBCD.
2.
ДН= ВЕ – как высоты
трапеции (расстояние между параллельными прямыми АВ и СД)
3.
SABCD=SABD+SBCD=
Вывод: площадь трапеции равна произведению полусуммы
оснований на высоту трапеции.
2.Математический энциклопедический
словарь. — М.: «Сов. энциклопедия», 1988. — С. 587,
3 Погорелов А.В. Геометрия, 7-9 класс. – М.:
Просвещение, 2006.
Исследование 2 «Нахождение площади трапеции
через построение внешних высот трапеции»
Н В С К
А Д
Решение.
1.
Провели высоты АН и DК , AН = DК, AD = HK . Тогда наша трапеция разбивается на три части: треугольник АHВ,
прямоугольник AНDК и треугольник CKD.
2. Таким образом, SABCD = SAHKD – SAHВ —
S DKC
3. SABCD = A
= AH
=AH
Вывод: площадь трапеции равна произведению полу суммы
оснований на высоту трапеции.
Исследование 3 «Нахождение площади трапеции
через построение прямой, параллельной одной из боковых сторон»13

1.
Провели СК‖АВ, высоту ВН. Тогда наша трапеция
разбивается на две части: параллелограмм АВСК (по определению, так как АВ‖СК по построению, АК‖ ВС по условию) и ΔКСD. Причём,
высоты параллелограмма и треугольника равны.
2. Таким образом, SABCD = SABCK + S KCD
3. SABCD = = BH
=BH
Вывод: площадь
трапеции равна произведению полу суммы оснований на высоту трапеции.
Исследование 4 «Нахождение площади трапеции
через построение прямой, проходящей через середину боковой стороны»
Решение:
1.
Через середину стороны CD
(точка К) провели прямую, пересекающую сторону AD в точке L.
2.
Рассмотрим треугольники BCK и LDК: CK = DK (по
построению), ∟ВCК = ∟LDK (как внутренние накрест лежащие при
параллельных прямых ВС и LD и секущей CD ), ∟CKB = ∟DKL
(как вертикальные), Δ BCK = ΔLDК (по стороне и двум прилежащим к ней углам),
следовательно, BC = LD и SBCK = SLDК.
3.
SABCD = SABL
=
Вывод:
площадь трапеции равна произведению полу суммы оснований на высоту трапеции.
Исследование 5 «Нахождение площади трапеции с
помощью построения перпендикуляров через середины боковых сторон»
Решение:
1. Через середины сторон AB и CD (точки M и K ) провели перпендикуляры NH и PT к
основаниям трапеции.
2. Рассмотрим Δ AMH и ΔBMN: ∟H = ∟N = 900
, AM = MB (по условию), ∟AMH = ∟BMN (как вертикальные), значит, ΔAMH = ΔBMN (по гипотенузе и острому углу),
следовательно, AH = BN и SAMH = SBMN
3. Рассмотрим Δ CPK и ΔDTK: ∟T = ∟P = 900
, CK = KD (по условию), ∟CKP = ∟DKT (как вертикальные), значит, ΔCPK = ΔDTK (по гипотенузе и острому углу),
следовательно, CP = DT и S CPK = S DTK
4.
SABCD = SHNPT
= NHNP
Вывод: нахождение площади трапеции сводится к нахождению
площади прямоугольника.
Исследование 6 «Нахождение площади трапеции с
помощью построения внутренних высот трапеции»

А Н
Д
Н К
Решение.
1.
Провели высоты ВН и СК, ВН
= СК, HK = BC. Тогда наша трапеция разбивается на три
части: треугольник АВН, прямоугольник НВСK и треугольник CKD.
2.
Таким образом, SABCD = SABH + SHBCK + SCKD
3.
SABCD = = BH
=BH
Вывод: площадь трапеции равна произведению полу суммы
оснований на высоту трапеции.
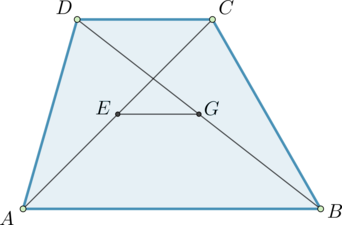
Исследование 7 «Нахождение площади трапеции,
если известны диагонали и угол между ними» 14

1.
В трапеции даны диагонали
AC = d1,
BD = d2,
∟COD = .
2.
∟AOB = ∟COD (как
вертикальные), ∟BOC = ∟AOD = 1800 – (по
свойству смежных углов), и =
.
3.
SABCD = SABO
+ SBOC + SCOD + SAOD = +
+ +
+
=
= =
= =
= =
d1d2
.
Вывод: площадь трапеции равна произведению диагоналей
трапеции на синус угла между ними деленному на 2.
14 http://2mb.ru/matematika/geometriya/ploshhad-trapecii/
, 15 А.Н. Колмогоров, А.Ф. Семенович, Р.С. Черкасов, Геометрия 6-8 классов, М.:
Просвещение, 1979г
Исследование 8 «Нахождение площади трапеции
через среднюю линию»
1.
В трапеции ABCD MN –
средняя линия, т. е. AM = MB и CN = ND,
MN = .
2.
Так как SABCD = .
Вывод: площадь трапеции равна произведению средней
линии на высоту трапеции
Исследование 9 «Нахождение площади трапеции при проведении
перпендикуляра к боковой стороне из середины другой боковой стороны»

1.
Через середину стороны CD трапеции ABCD провели перпендикуляр KM к стороне AB, т. е. CK = KD, KM = q, AB = d.
2.
PN ‖ AB.
3.
ΔCPK = ΔDNK по стороне и двум прилежащим к ней углам (∟CKP = =∟DKN (как
вертикальные, CK = DK (по условию), ∟PCK = ∟NDK (как
накрест лежащие при параллельных прямых), значит, SCPK = SDNK
4.
SABCD = SABCKN + SCPK = SABPN = dq.
Вывод: при
данных условиях нахождение площади трапеции сводится к нахождению площади
параллелограмма.
И так:
При исследовании способов решения задачи, мы увидели,
что площадь трапеции может быть найдена:
1.
С помощью площади
прямоугольника;
2.
Через площадь треугольника
(наиболее часто);
3.
С помощью площади
параллелограмма;
4.
Через среднюю линию
трапеции;
5.
Через диагонали трапеции и
угол между ними.
Таким образом, существует много способов
нахождения площади трапеции. При решении задач используется тот метод, который
удобен.
13. http://www.tutoronline.ru/blog/kak-najti-ploshhad-trapecii-formuly-i-primery
Исследование 10
«Анализ тестов ОГЭ по математике»: частота появления
тестов с задачами на нахождение площади трапеции»
Цель: определить,
как часто встречаются задачи на нахождение площади трапеции в тестах ОГЭ по
математике
Ход исследования:
1.
Рассмотреть учебные
пособия по подготовке к ОГЭ по математике с 2011г по 2016г.1,10,
11,12,13,14,15
2.
Подсчитать количество
тестов по годам
3.
Подсчитать, количество
тестов, где встречаются задания на нахождение площади трапеции.
4.
Найти частоту появления
данных задач по годам.
5.
Сделать вывод.
|
год |
Количество рассмотренных тестов |
Количество тестов с заданиями на нахождение площади трапеции |
Частота |
% |
|
2011 |
28 |
2 |
0,03 |
3 % |
|
2012 |
18 |
2 |
0,11 |
11 % |
|
2013 |
38 |
19 |
0,5 |
50 % |
|
2014 |
26 |
13 |
0,5 |
50 % |
|
2015 |
26 |
13 |
0,5 |
50 % |
|
2016 |
16 |
9 |
0,56 |
56 % |
Вывод: начиная
с 2012 года, частота появления задач на нахождение площади трапеции в тестах
ОГЭ по математике возрастает, что является доказательством актуальности и
практической значимости рассматриваемой темы лично для меня и учащихся 9
класса при сдаче экзамена.
6.Сайт: http://www.fipi.ru, 7.сайт: www.alexlarin.net, 8, 10,12
Сборник тестов для подготовки ГИА- 2011, 2013,2015г 9 класс, Ф.Ф. Лысенко, С.Ю.
Калабухова, 9 Сборник тематических тестовых заданий ГИА 2012
г, 9 класс, Л.Д.Лаппо, М.А. Попов; 8, 11 Сборник для подготовки ОГЭ-2015,2016
И.В. Ященко, С.А. Шестаков, А.В. Семенов
4. Заключение
При выполнении исследовательской работы я
использовал знания, которые имеются у меня, а так же дополнительную литературу.
В процессе выполненной работы в соответствии с ее целью и задачами получены следующие выводы и
результаты.
С помощью математических исследований мы
пришли к выводу: что существует
много способов нахождения площади трапеции. При решении задач используется тот
метод, который удобен и соответствует условию задачи.
В своей исследовательской работе я также показал
практическую значимость данной темы, проанализировав пособия для подготовки к
ОГЭ по математике. Создал буклет «Трапеция в нашей жизни», в которой показал,
что трапецию можно встретить как в повседневной жизни — быту, так и в природе,
архитектуре.
Результат проведенного опроса в нашей школе показал,
что данная тема актуальна для повторения в 10-11 классах на уроках геометрии.
Кроме того, работая над проектом, я закрепил умения и
навыки работы в текстовом редакторе WORD, Power Point, Microsoft Excel (для
составления диаграммы в ходе исследований), Microsoft Publisher
(при создании буклета)
Таким образом, цели и задачи данной работы выполнены.
Список литературы
1.
https://ru.wikipedia.org/wiki
2.
Математический
энциклопедический словарь. — М.: «Сов. энциклопедия», 1988. — С. 587.
3.
А.В. Погорелов, Геометрия,
7-9 класс. – М.: Просвещение, 2006.
4.
Л.С. Атанасян, Учебник
“Геометрия 7–9” ,М.: Просвещение, 2000г
5.
Сборник для подготовки
ОГЭ-2016 И.В. Ященко, С.А. Шекстаков, А.В. Семенов
6.
Сайт: http://www.fipi.ru
7.
Сайт: www.alexlarin.net
8.
Сборник тестов для
подготовки ГИА- 2013, 9 класс, Ф.Ф. Лысенко, С.Ю. Калабухова
9.
Сборник тематических
тестовых заданий ГИА 2012 г, 9 класс, Л.Д.Лаппо, М.А. Попов.
10.
Сборник тестов для
подготовки ГИА- 2011, 9 класс, Ф.Ф. Лысенко, С.Ю. Калабухова
11.
Сборник для подготовки
ОГЭ-2015 И.В. Ященко, С.А. Шекстаков, А.В. Семенов
12.
Сборник тестов для
подготовки ГИА- 2015, 9 класс, Ф.Ф. Лысенко, С.Ю. Калабухова
13.
http://www.tutoronline.ru/blog/kak-najti-ploshhad-trapecii-formuly-i-primery
14.
http://2mb.ru/matematika/geometriya/ploshhad-trapecii/
15.
А.Н. Колмогоров, А.Ф.
Семенович, Р.С. Черкасов, Геометрия 6-8 классов, М.: Просвещение, 1979г
Приложение 1
Создание буклета
1.
Подборка интересного
материала о трапеции: в архитектуре, быту, природе.
2.
Оформление в программе Microsoft
Publisher.
Приложение 2.
Видео опрос учащихся школы
«Что знают учащиеся школы о трапеции, о
нахождении ее площади»
1.
Опрос проведен для
учащихся 8,10,11 класса.
2.
Количество участников — 5
3.
Отношение к опросу –
положительное.
4.
Вопросы:
1.
Что Вы знаете о трапеции
2.
Знаете ли Вы как найти
площадь трапеции.
5.
Вывод по опросу
Вывод
По результатам видео опроса можно сделать вывод, что
учащиеся 8 класса знают на момент исследования только определение трапеции,
учащиеся 10-11 классов называют определение трапеции, не все учащиеся могут
правильно назвать формулу для нахождения площади трапеции.
Выбирайте формулу в зависимости от известных величин.
1. Как найти площадь трапеции через основания и высоту
Посчитайте сумму оснований трапеции.
Умножьте результат на высоту и поделите на два.
- S – искомая площадь трапеции.
- a и b – основания трапеции (её параллельные стороны).
- h – высота трапеции.
2. Как вычислить площадь трапеции через высоту и среднюю линию
Просто умножьте высоту трапеции на среднюю линию.
- S – искомая площадь трапеции.
- m – средняя линия трапеции (отрезок, соединяющий середины боковых сторон).
- h – высота трапеции.
3. Как найти площадь трапеции через диагонали и угол между ними
Умножьте одну диагональ на другую, а затем — на синус любого угла между ними.
Поделите результат на два.
- S – искомая площадь трапеции.
- x и y – диагонали трапеции.
- α – любой угол между диагоналями.
4. Как найти площадь трапеции через четыре стороны
Отнимите от большего основания меньшее.
Найдите квадрат полученного числа.
Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.
Поделите полученное число на удвоенную разность оснований.
Найдите квадрат результата и отнимите его от квадрата боковой стороны.
Найдите корень из полученного числа.
Умножьте результат на половину от суммы оснований.
- S – искомая площадь трапеции.
- a, b – основания трапеции.
- c, d – боковые стороны.
5. Как вычислить площадь равнобедренной трапеции через четыре стороны
Отнимите от большего основания трапеции меньшее и поделите результат на два.
Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.
Найдите корень из результата.
Умножьте полученное число на сумму оснований и поделите на два.
- S — искомая площадь трапеции.
- a, b — основания трапеции.
- c, d — боковые стороны (напомним, в равнобедренной трапеции они равны).
6. Как найти площадь равнобедренной трапеции через радиус вписанной окружности и угол
Найдите квадрат радиуса и умножьте его на четыре.
Поделите результат на синус известного угла.
- r — радиус вписанной окружности.
- α — любой угол трапеции.
Читайте также 📐✏️🎓
- 8 способов найти длину окружности
- 8 способов найти периметр треугольника
- 7 способов найти площадь прямоугольника
- Как перевести обычную дробь в десятичную
- Как освоить устный счёт школьникам и взрослым
Определения
Трапеция — это такой четырехугольник, у которого две стороны параллельны (они являются основаниями трапеции, указанные на рисунках a и b), а две другие — нет.
Высота трапеции — это такой отрезок h, который проведен перпендикулярно основаниям.
Нахождение высоты по площади и основаниям
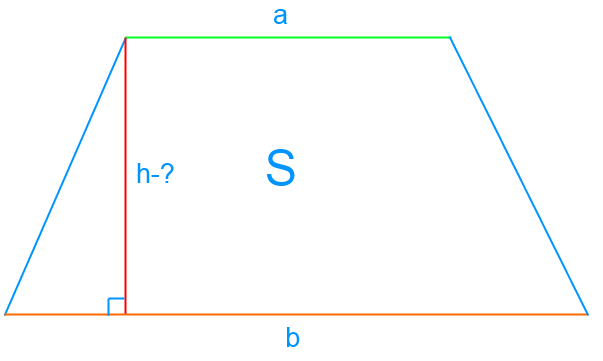
Чтобы вычислить площадь S трапеции мы используем формулу:
[S=frac{((a+b) times h)}{2}]
Здесь h — высота трапеции, а сегменты a и b являются ее основаниями.
Можем найти h:
[h=frac{2 times S}{(a+b)}]
Пример 1
Площадь трапеции S составляет 50 см2, длина ее основания a = 4 см, длина второго основания b равна 6 см, то для нахождения высоты h мы используем формулу:
[h=frac{2 times 50}{(4+6)}=10 mathrm{~cm}]
Ответ: 10 см.
Нахождение высоты, зная площадь и среднюю линию
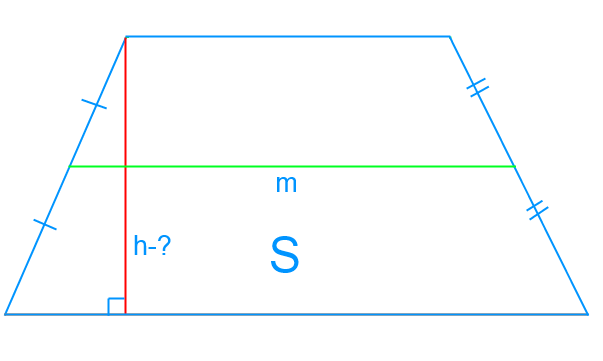
Мы используем формулу, с помощью которой можно рассчитать площадь трапеции:
S = m × h,
Здесь h — это высота трапеции, m — ее средняя линия.
Можем найти h:
[h=frac{S}{m}], будет ответом.
Пример 2
Средняя линия трапеции, обозначенная буквой m, равна 20 см, а площадь S, которая составляет 200 см2. Давайте найдем значение высоты трапеции h.
[h=frac{200}{20}=10 mathrm{~cm}]
Ответ: 10 см
Высота прямоугольной трапеции
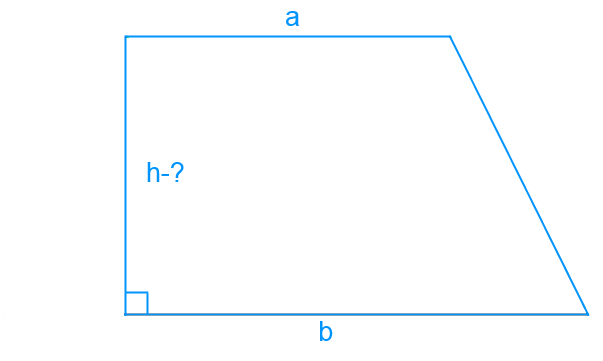
Определение
Диагональ — это сегмент, соединяющий пару противоположных вершин трапеции. Когда трапеция прямоугольная, используя диагональ, мы находим высоту данной фигуры.
Трапецию, одна из боковых сторон которой перпендикулярна основаниям, называют прямоугольной трапецией.
Таким образом, рассмотрим подобную трапецию ABCD, где AD — высота, AC — диагональ, DC-основание. Мы используем теорему Пифагора, которая говорит, что в прямоугольном треугольнике ADC квадрат гипотенузы AC равен сумме квадратов его сторон — катетов AB и BC.
Тогда мы сможем написать:
AC² = AD² + DC².
AD — это катет треугольника, сторона трапеции и, одновременно, ее высота. Так как отрезок перпендикулярен основаниям. Длина катета будет находиться как:
[A D=sqrt{left(A C^{2}-D C^{2}right)}]
Таким образом, у нас есть формула, которая поможет при вычислении найти высоту трапеции AD.
Пример 3
Основания трапеции с прямым углом(DC) равно 14 см, а ее диагональ (AC) равна 15 см, мы будем использовать теорему Пифагора для получения высоты (сторона AD).
Пусть x — неизвестная часть прямоугольного треугольника (AD), тогда
[A C^{2}=A D^{2}+D C^{2}] может быть записан
[15^{2}=14^{2}+x^{2}]
[x=sqrt{left(15^{2}-14^{2}right)}=sqrt{(225-196)}=sqrt{29} mathrm{см}]
Ответ: [sqrt{29} mathrm{см}], что составляет приблизительно 5,385 см
Нет времени решать самому?
Наши эксперты помогут!
Нахождение высоты через стороны
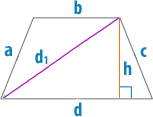
Существует еще один способ найти высоту — через стороны. Помимо высоты в трапеции стоит провести также ее диагональ, которая образует треугольник с прямым углом и даст возможность найти высоты несколькими различными способами через различные треугольники.
Если выразить все длины сторон таких треугольников через стороны трапеции и привести подобные слагаемые, то получится следующая формула:
[mathrm{h}=sqrt{C^{2}-left(frac{(a-b)^{2}+e^{2} d^{2}}{2(a-b)}right)^{2}}]
Пример 4
Дана трапеция, в ней известны основания a и b. Эти основания соответственно равны 4,5 см и 2,5 см. Известны и ее боковые стороны d и c, которые равны 2 см и используем формулу:
[h=sqrt{2^{2}-left(frac{(4,5-2,5)^{2}+2^{2}-2 sqrt{2}^{2}}{2(4,5-2,5)}right)^{2}}=sqrt{4}=2 см]
Ответ: h=2 см.
18. Площади геометрических фигур
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
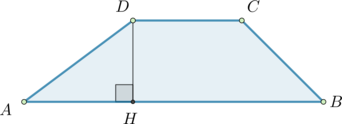
Площадь трапеции
Найдите площадь прямоугольной трапеции, основания которой равны (6) и (2), большая боковая сторона составляет с основанием угол (45^circ).
Проведем высоту (CH).
Так как (angle HBC=45^circ), то (angle HCB=45^circ). Следовательно, (triangle HBC) равнобедренный и (HB=HC).
(ADCH) – прямоугольник, следовательно, (AH=DC=2). Тогда (CH=HB=6-2=4). Тогда площадь трапеции равна [S=dfrac{AB+DC}2cdot CH=dfrac{2+6}2cdot 4=16]
Ответ: 16
Основания прямоугольной трапеции равны (12) и (4). Ее площадь равна (64). Найдите острый угол этой трапеции. Ответ дайте в градусах.
Проведем высоту (CH).
(ADCH) – прямоугольник, следовательно, (AH=DC=4). Тогда (HB=12-4=8). Площадь трапеции равна [64=dfrac{AB+DC}2cdot CH=dfrac{4+12}2cdot CHquadRightarrowquad
CH=8] Заметим, что мы получили, что (CH=HB=8). То есть (triangle
CHB) равнобедренный, значит, углы при основании равны, то есть (angle HCB=angle HBC). Так как сумма острых углов в прямоугольном треугольнике равна (90^circ), то (angle B=angle
HBC=90^circ:2=45^circ).
Ответ: 45
Основания трапеции равны (18) и (6), боковая сторона, равная (7), образует с одним из оснований угол (150^circ). Найдите площадь трапеции.
Пусть (AD=7), тогда (angle ADC=150^circ). По свойству трапеции (angle DAB=180^circ-150^circ=30^circ). Проведем (DHperp
AB).
Рассмотрим (triangle ADH). Катет, лежащий против угла (30^circ), равен половине гипотенузы, следовательно, (DH=AD:2=3,5). Тогда площадь трапеции равна [S=dfrac{AB+DC}2cdot DH=dfrac{18+6}2cdot 3,5=42]
Ответ: 42
Основания трапеции равны (27) и (9), боковая сторона равна (8). Площадь трапеции равна (72). Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ дайте в градусах.
Пусть (AD=8). Проведем (DHperp AB).
Тогда площадь трапеции равна [72=dfrac{AB+DC}2cdot DH=dfrac{27+9}2cdot DHquadRightarrowquad
DH=4] Рассмотрим прямоугольный (triangle ADH). Так как катет (DH) равен половине гипотенузы (AD), то угол (DAH) равен (30^circ).
Ответ: 30
Основания равнобедренной трапеции равны (14) и (26), а ее боковые стороны равны (10). Найдите площадь трапеции.
Проведем высоту (BH). По свойству равнобедренной трапеции (AH=(AD-BC):2=(26-14):2=6).
Тогда из прямоугольного треугольника (ABH): [BH=sqrt{AB^2-AH^2}=sqrt{10^2-6^2}=8] Тогда площадь трапеции: [S=dfrac{AD+BC}2cdot BH=dfrac{26+14}2cdot 8=160]
Ответ: 160
Основания равнобедренной трапеции равны (7) и (13), а ее площадь равна (40). Найдите боковую сторону трапеции.
Проведем высоту (BH).
Площадь трапеции равна [40=dfrac{AD+BC}2cdot BH=dfrac{7+13}2cdot BHquadRightarrowquad BH=
4] Рассмотрим прямоугольный (triangle ABH). По свойству равнобедренной трапеции (AH=(AD-BC):2=(13-7):2=3). Следовательно, [AB=sqrt{AH^2+BH^2}=5]
Ответ: 5
Основания равнобедренной трапеции равны (14) и (26), а ее периметр равен (60). Найдите площадь трапеции.
Проведем высоту (BH). По свойству равнобедренной трапеции (AH=(AD-BC):2=(26-14):2=6).
Так как периметр трапеции равен (60), а боковые стороны равны, то [AB=dfrac{60-14-26}2=10] Тогда из прямоугольного треугольника (ABH): [BH=sqrt{AB^2-AH^2}=sqrt{10^2-6^2}=8] Тогда площадь трапеции: [S=dfrac{AD+BC}2cdot BH=dfrac{26+14}2cdot 8=160]
Ответ: 160

УСТАЛ? Просто отдохни
Преподаватель который помогает студентам и школьникам в учёбе.
Площадь трапеции — определение и вычисление с примерами решения
Теорема (о площади трапеции). Площадь трапеции равна произведению полусуммы ее оснований на высоту.
Доказательство:
Пусть
Докажем, что площадь 
1) Диагональ 
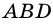
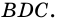
2) 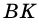
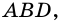
3) Проведем в трапеции высоту 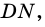
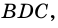
4) 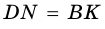
В общем виде формулу площади 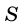
где 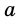
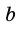
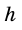
Следствие. Площадь трапеции равна произведению ее средней линии на высоту.
Пример:
В трапеции 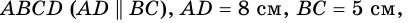
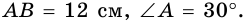
Решение:
1) Проведем в трапеции 
(рис. 245). В 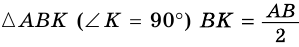
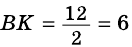
2)
Ответ. 39
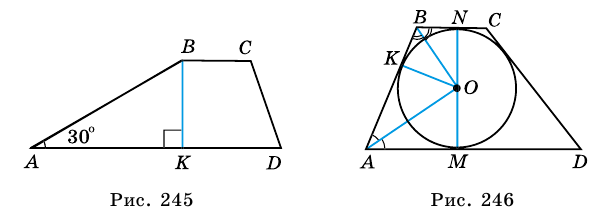
Пример:
Периметр трапеции 60 см, а одна из боковых сторон точкой касания вписанной окружности делится на отрезки 9 см и 4 см. Найдите площадь трапеции.
Решение:
1) Так как трапеция является описанной около окружности (рис. 246), то
2) Центр вписанной окружности — точка 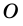
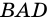
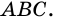
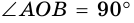
3) Точка 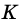
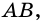
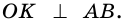
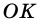
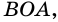
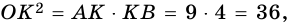
4) 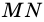
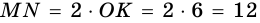
5) Следовательно,
Ответ. 180
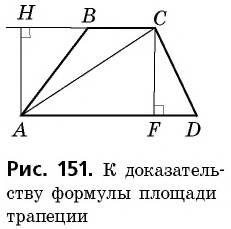
Площадь трапеции
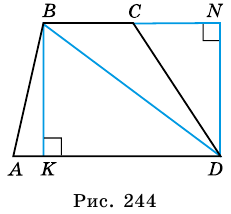
Часто для вычисления площади некоторого многоугольника его разбивают на несколько треугольников и находят искомую площадь как сумму площадей этих треугольников. Именно такой подход можно применить для вывода формулы площади трапеции.
Теорема (формула площади трапеции) Площадь трапеции равна произведению полусуммы ее оснований на высоту:
где 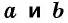
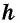
Доказательство:
Пусть дана трапеция 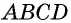
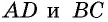
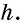
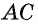
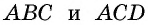
Проведем высоты этих треугольников 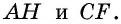
Теорема доказана.
Следствие
Площадь трапеции равна произведению средней линии на высоту.
- Центральные и вписанные углы
- Углы и расстояния в пространстве
- Подобие треугольников
- Решение прямоугольных треугольников
- Прямоугольник и его свойства
- Ромб и его свойства, определение и примеры
- Квадрат и его свойства
- Трапеция и ее свойства