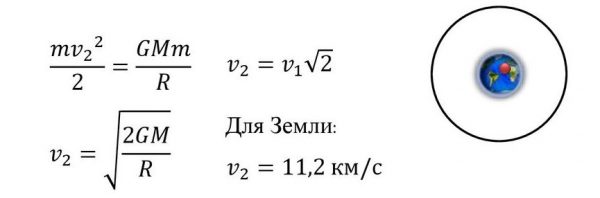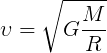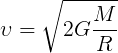Если мы подбросим камень в воздух – он упадет на Землю. Если у самолета на высоте 10 километром отключаться двигатели – он тоже упадет на Землю. Но спутники и космические корабли, что мы запускаем в космос, не падают. Почему?
Все дело в том, с какой скоростью тот или иной объект удаляется от планеты. Хватит ли этому объекту энергии преодолеть притяжение планеты.
Оглавление
- 1 Первая космическая скорость
- 1.1 Расчет
- 2 Вторая космическая скорость
- 2.1 Расчет
- 3
- 4 Третья космическая скорость
- 4.1 Расчет
- 5 Четвертая космическая скорость
- 6 Пятая космическая скорость
- 7 Почему спутники не падают на Землю
Первая космическая скорость
Это та самая минимальная скорость для выхода корабля или спутника на круговую орбиту, равную радиуса планеты, без учета вращения планеты и сопротивления ее атмосферы.
Если скорость будет превышать первую, но не достигнет второй космической скорости, то траектория тела из круговой начнет переходить в эллиптическую.
Впервые такую скорость смог достичь первый искусственный спутник Земли «Спутник-1» СССР 4 октября 1957 года.
Расчет
Вторая космическая скорость
Это минимальная скорость, которую следует придать телу для того, чтобы оно покинуло замкнутую орбиту и смогло улететь от небесного тела за пределы его гравитационного поля.
Иными словами, для Земли, это та скорость, с которой должны двигаться космические аппараты (КА) для полетов к другим объектам Солнечной системы: Луны, Марса и т.д.
Движение тела на второй космической скорости происходит по параболической траектории.
Впервые такую скорость развил Советский космический аппарат Луна-1 2 января 1959 года, чтобы преодолеть расстояние от Земли до Луны и изучить наш естественный спутник.
Расчет
Третья космическая скорость
Такую скорость необходимо придать телу, чтобы оно смогло покинуть Солнечную систему. Так как 99,8% массы Солнечной системы приходится на Солнце, то можно сказать, что КА надо преодолеть гравитационное притяжение Солнца.
Расчет
Для Солнечной системы это величина равна 16,650 км/с.
Самое выгодное расположение космодрома для подобного запуска – максимально близко к экватору, так как на экваторе самая большая скорость собственного вращения Земли вокруг своей оси и направление движения в сторону вращения Земли и в сторону орбитального движения Земли по орбите.
КА «Новые горизонты» покинул атмосферу Земли со скоростью близкой к третьей космической – 16,26 км /с. Относительно Солнца он имел скорость 45 км/с. Такой скорости недостаточно, чтобы покинуть Солнечную систему. Но благодаря гравитационному маневру у Юпитера, «Новые горизонты» добавил еще 4 км/с, что позволило ему покинуть Солнечную системы, предварительно показав нам карликовую планету Плутон.
Четвертая космическая скорость
Эта та скорость, которая позволит покинуть галактику в данной точке.
Четвертая космическая в основном не зависит от месторасположения Земли в Млечном пути. Она зависит от расположения и плотности звездного вещества в окрестностях Солнечной системы. А эти данные пока мало изучены.
Для нашей части галактики четвертая космическая скорость примерно равна 550 км/с.
Пятая космическая скорость
Эта скорость редко применима и является больше «фантазией», так как такую скорость необходимо развить для путешествия на другую планету в другую звездную систему, независимо от их взаимного расположения, с траекторией перпендикулярно плоскости эклиптики.
Для Земли эта скорость будет равна 43,6 км/с.
Почему спутники не падают на Землю
Этот вопрос поднимался в самом начале статьи. Теперь давайте на него ответим.
На спутник на орбите действует сила тяжести со стороны Земли. И под действием этой силы спутнику логичнее упасть.
Но, он летит вокруг Земли с первой космической скоростью – 7,9 км/с. Вспомните, чем больше скорость – тем сложнее затормозить. Вот и здесь, спутник и хотел бы упасть, но он не может затормозить и просто пролетает мимо Земли по инерции, тем самым продолжая бесконечное падение.
То есть, спутники падают, но промахиваются и не попадают в Землю.
Еще больше космоса и интересных фактов в телеграмм-канале.
Содержание
- Первая космическая скорость
- Вторая космическая скорость
- Третья космическая скорость
- Четвёртая и пятая космическая скорости
Любой предмет, будучи подброшенным вверх, рано или поздно оказывается на земной поверхности, будь то камень, лист бумаги или простое перышко. В то же время, спутник, запущенный в космос полвека назад, космическая станция или Луна продолжают вращаться по своим орбитам, словно на них вовсе не действует сила притяжения нашей планеты. Почему так происходит?
На нашей Земле всемирное тяготение воздействует на любое материальное тело. Тогда логично будет предположить, что есть некая сила, нейтрализующая действие гравитации. Эту силу принято называть центробежной.
Центробежную силу легко ощутить привязав на один конец нитки небольшой груз и раскрутив его по окружности. При этом чем больше скорость вращения тем сильнее натяжение нити, а чем медленнее вращаем мы груз тем больше вероятность, что он упадет вниз.
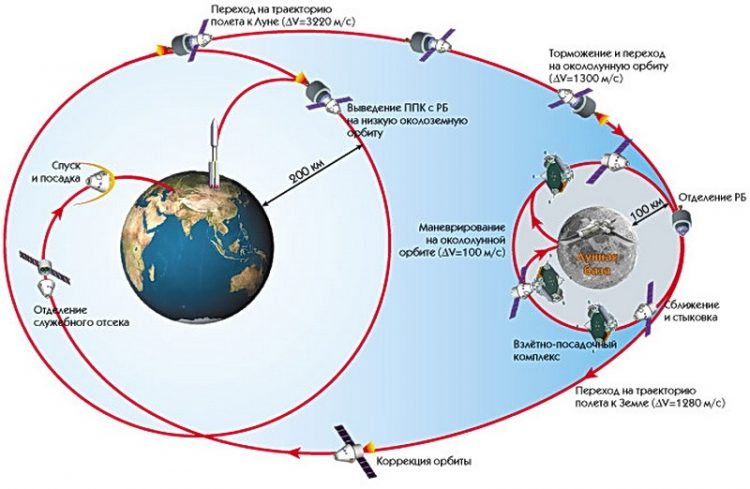
Траектория полета космических кораблей
Таким образом мы вплотную приблизились к понятию «космическая скорость». Простыми словами — это скорость, позволяющая любому объекту преодолеть тяготение небесного тела и их системы. Космические скорости используются для характеристики типа движения космического аппарата в сфере действия небесных тел: Солнца, Земли и Луны, других планет и их естественных спутников, а также астероидов и комет.
Это также значит, что космическая скорость есть у каждого объекта, который движется по орбите. Размер и форма орбиты космического объекта зависят от величины и направления скорости, которую данный объект получил на момент выключения двигателей, и высоты, на которой произошло данное событие.
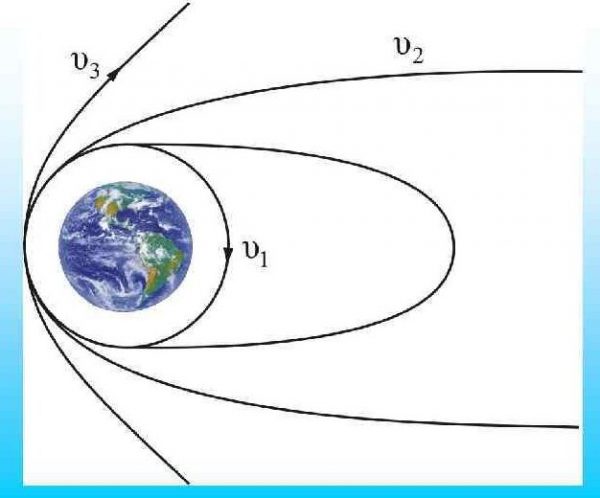
Космическая скорость (первая v1, вторая v2, третья v3 и четвёртая v4) — это минимальная скорость, при которой какое-либо тело в свободном движении сможет:
- v1 — стать спутником небесного тела (то есть способность вращаться по орбите вокруг небесного тела и не падать на его поверхность);
- v2 — преодолеть гравитационное притяжение небесного тела и начать двигаться по параболической орбите;
- v3 — покинуть при запуске планету, преодолев притяжение Звезды;
- v4 — при запуске из планетной системы объект покинул Галактику.
Космические скорости могут быть рассчитаны для любого удаления от центра Земли. Однако в космонавтике часто используются величины, рассчитанные конкретно для поверхности шаровой однородной модели Земли радиусом 6371 км.
Первая космическая скорость
Первая космическая скорость или Круговая скорость V1 — скорость, которую необходимо придать объекту без двигателя, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы вывести его на круговую орбиту с радиусом, равным радиусу планеты.
Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.
Формула
где G — гравитационная постоянная (6,67259·10−11 м³·кг−1·с−2), — первая космическая скорость. Подставляя численные значения (для Земли M = 5,97·1024 кг, R = 6 378 км), найдем
7,9 км/с
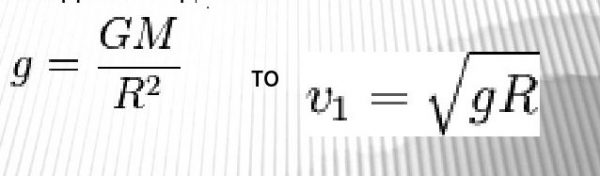
Первую космическую скорость можно определить через ускорение свободного падения —
Вторая космическая скорость
Вторая космическая скорость (параболическая скорость, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала относительно массы небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела.
Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой:
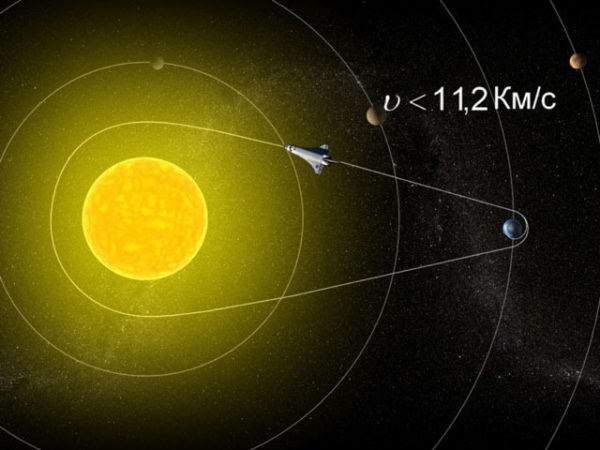
- для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца.
- для Солнца вторая космическая скорость составляет 617,7 км/с.
- для Луны скорость убегания равна 2,4 км/с, несмотря на то, что в действительности для удаления тела на бесконечность с поверхности Луны необходимо преодолеть притяжение Земли, Солнца и Галактики.
Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся по параболе.
Формула
Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния .
Третья космическая скорость
Третья космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение Солнца и в результате уйти за пределы Солнечной системы.
Только на космических кораблях, которым доступны такие скорости, принципиально могут быть осуществлены пилотируемые межзвёздные перелёты к планетным системам других звёзд.
Взлетая с поверхности Земли и наилучшим образом используя орбитальное движение планеты космический аппарат может достичь третей космической скорости уже при 16,6 км/с относительно Земли, а при старте с Земли в самом неблагоприятном направлении его необходимо разогнать до 72,8 км/с.
Здесь для расчёта предполагается, что космический аппарат приобретает эту скорость сразу на поверхности Земли и после этого не получает негравитационного ускорения (двигатели выключены и сопротивление атмосферы отсутствует). Если к тому же учесть притяжение других планет, которое может как ускорить, так и притормозить аппарат, то диапазон возможных значений 3-й космической скорости станет еще больше.
При наиболее энергетически выгодном старте скорость объекта должна быть сонаправлена скорости орбитального движения Земли вокруг Солнца. Орбита такого аппарата в Солнечной системе представляет собой параболу.
Четвёртая и пятая космическая скорости
Четвёртая космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение галактики Млечный Путь. Она используется довольно редко.
Четвёртая космическая скорость не постоянна для всех точек Галактики, а зависит от расстояния до центральной массы.
Для нашей галактики таковой является объект Стрелец A*, сверхмассивная чёрная дыра.
По грубым предварительным расчётам в районе нашего Солнца четвёртая космическая скорость составляет около 550 км/с. Значение сильно зависит не только (и не столько) от расстояния до центра галактики, а от распределения масс вещества по Галактике, о которых пока нет точных данных, ввиду того что видимая материя составляет лишь малую часть общей гравитирующей массы, а все остальное — скрытая масса.
Ещё реже в некоторых источниках встречается понятие «пятая космическая скорость». Это скорость, позволяющая добраться до иной планеты звездной системы вне зависимости от разности плоскостей эклиптики планет. Например, для Солнечной системы и, конкретно, для Земли, чтобы орбита межпланетного перелета была перпендикулярной к земной орбите, нужна скорость запуска 43,6 километра в секунду.
Видео
Источники
- https://ru.wikipedia.org/wiki/Космическая_скорость
https://mirznanii.com/a/9233/kosmicheskie-skorosti
http://www.astronet.ru/db/msg/1162252
https://fb.ru/article/54389/kosmicheskaya-skorost
Здесь приведены формулы и примеры расчета первой и второй космической скорости для небесных тел произвольной массы и радиуса.
Для быстрого расчета можно воспользоваться онлайн-калькулятором.
Первая космическая скорость
Первая космическая скорость — это скорость, которую нужно придать телу, масса которого пренебрежительно мала по сравнению с массой планеты,
чтобы это тело стало спутником планеты и вращалось вокруг нее по круговой траектории. Примечание: если скорость будет выше заданной (но меньше второй космической), то траектория орбиты будет
не круговой, а эллипсоидной.
Формула первой космической скорости:
где
G — гравитационная постоянная (постоянная Ньютона), равная 6,6743015·10-11 м3/(кг*с2), или Н*м2/кг2
R — радиус небесного тела
M — масса небесного тела
Вторая космическая скорость
Вторая космическая скорость — это минимальная скорость, которой должно обладать тело, чтобы преодолеть гравитационное притяжение планеты и покинуть замкнутую орбиту вокруг нее.
Формула второй космической скорости:
где
G — гравитационная постоянная
R — радиус небесного тела
M — масса небесного тела
Пример:
Масса планеты Земля составляет 5,9726*1024 кг, средний радиус — 6371 км (или 6371000 м). Подставив эти значения в формулы первой и второй
космических скоростей, мы получим значение соответственно 7 910 м/с и 11 187 м/с.
Теперь рассчитаем значение космических скоростей для планеты Нептун. Масса Нептуна — 1,0243*1026 кг. средний радиус — 24 622 км (24 622 000 м).
В итоге получим значения — 16 663 м/с и 23 565 м/с.
Значения для Марса (6,4171*1023 кг и 3389,5 км) будет 3 555 м/с и 5 027 м/с.
Для Венеры (4,8675*1024 кг и 6051,8 км) — 7 327 м/с и 10 362 м/с соответственно.
Калькулятор космических скоростей
Другие формулы
Несмотря на то, что отечественная космонавтика переживает не лучшие, мягко говоря, времена, космосом на сегодняшний день интересуется все больше людей разного возраста и уровня образования. Усилиями частных инвесторов и популяризаторов науки пространство за пределами нашей планеты становится все более интересным, доступным и понятным, привлекая любознательных граждан к получению новых знаний.
В этом материале мы кратко, избегая сложных пояснений и формулировок, расскажем о космических скоростях, которые необходимы для преодоления гравитационных полей астрономических объектов. В новостных сюжетах мы часто слышим такое словосочетание, как «первая (вторая, третья, четвертая) космическая скорость», однако далеко не каждый обыватель понимает о каких скоростях идет речь и как их определяют.
♥ ПО ТЕМЕ: Как хорошо выглядеть на любом фото: 5 простых советов.
Что такое космическая скорость
Космическими скоростями в космонавтике (речь идет не только о пилотируемых полетах, но для удобства мы будем называть все запуски искусственных космических аппаратов космонавтикой) пользуются для расчета минимально необходимой скорости для:
1. Выхода космических аппаратов на орбиту Земли;
2. Выхода космических аппаратов за пределы гравитационного поля Земли;
3. Выхода космических аппаратов за пределы Солнечной системы;
4. Выхода космических аппаратов за пределы галактики Млечный Путь.
Естественно, формулы расчета космических скоростей применимы не только к нашей планете, но и к любому другому объекту Вселенной, однако мы рассмотрим лишь актуальные для земных космических аппаратов значения.
♥ ПО ТЕМЕ: Что такое карат? Как определить вес драгоценного камня и пробу золота в каратах.
Первая космическая скорость — 7,9 км/сек
Чтобы вращаться на орбите Земли, спутнику необходимо иметь первую космическую или круговую скорость, которая для нашей планеты равна примерно 7,9 км/сек. В этом случае объект на орбите будет удерживать сила, называемая в народе центробежной, а движение Земли и сила притяжения не позволят спутнику покинуть гравитационное поле планеты.
Отсюда следует довольно интересное и простое умозаключение: что будет если в формуле расчета первой космической скорости (V1 = (GM/R) в степени 1/2, где M – масса объекта, R – радиус, а G – гравитационная постоянная) поиграть с цифрами и подставить данные, которые определят первую космическую скорость для выдуманного нами объекта, как равную скорости света (чуть менее 300 000 км/сек)?
Мы получим объект огромной массы и малого радиуса, на который свет может падать, но покинуть его гравитационное поле фотоны уже не в состоянии, ведь для этого нужна вторая космическая скорость, которая в данном случае будет превышать скорость света, что невозможно в известной нам Вселенной. Это есть объект, о котором слышал каждый и который астрофизики называют «черной дырой».
♥ ПО ТЕМЕ: БелАЗ-75710: 1 300 литров топлива на 100 км и другие 7 фактов о лучшем самосвале мира из Беларуси.
Вторая космическая скорость — 11,2 км/сек
В 1959 году в СССР состоялся запуск автоматической межпланетной станции Луна-1 — первого искусственного объекта, покинувшего гравитационное поле Земли и ставшего спутником Солнца. Для этого аппарату пришлось разогнаться до второй космической скорости (она же скорость убегания), которая для Земли составляет порядка 11,2 км/сек. Покинув Землю на такой скорости, объект выходит на параболическую орбиту, которая при условии отсутствия других тел во Вселенной позволила бы ему бесконечно далеко удалиться от планеты.
♥ ПО ТЕМЕ: Как появились названия брендов: Ikea, Lego, Pepsi, Reebok, Skype, Sony, Canon, Google — 16 историй о происхождении названий известных компаний.
Третья космическая скорость — 16,6 км/сек
Определить точное значение третьей космической скорости невозможно, так оно может колебаться в довольно широком диапазоне. Имеет значение угол направления запуска к траектории движения Земли по орбите и контакт с гравитационными полями других планет, которые могут как ускорять, так и притормаживать КА. Минимальное значение третьей космической скорости оценивается как 16,6 км/сек.
♥ ПО ТЕМЕ: 70 интересных фактов об IT-технологиях.
Четвертая космическая скорость — 400-600 км/сек
Редко употребляемый термин ввиду недосягаемости определяемых им величин для нашей космонавтики в обозримом будущем. Четвертая космическая скорость подразумевает вылет КА за пределы галактики, что в принципе невозможно при текущем и ожидаемом уровне развития технологий. Учитывая, что наша Солнечная система вращается вокруг галактического центра со скоростью около 220 км/сек, примерную расчетную скорость искусственного аппарата для вылета за пределы Млечного Пути можно определить как 400-600 км/сек.
Смотрите также:
- Первый велосипед: история создания, эволюция конструкции (фото).
- Корабль в бутылке: как засовывают, где купить.
- 7 известных символов, о происхождении которых вы могли не знать.
Первая космическая скорость
Первая космическая скорость – это скорость, с которой спутник движется вокруг планеты по круговой орбите, не удаляясь от планеты и не падая на нее.
То есть, для первой космической скорости орбита — это окружность. Расстояние от центра планеты до спутника равно ( R = left( r + h right) ). Это представлено на рисунке 1.
Рис. 1. Спутник (черная точка), вращается вокруг планеты (центральная окружность) по круговой орбите (пунктир).
Формула для вычисления первой космической скорости
Первую космическую скорость можно посчитать по формуле:
[ large boxed { |v| = sqrt{G cdot frac{M}{r + h}} }]
( v left( frac{text{м}}{text{c}} right) ) (метры в секунду) – первая космическая скорость
( M left( text{кг} right) ) (килограммы) — масса планеты, вокруг которой движется спутник
( r left( text{м} right) ) (метры) – радиус планеты
( h left( text{м} right) ) (метры) — расстояние от поверхности планеты до спутника
(G = 6{,}67 cdot 10^{-11} left( text{Н} cdot frac{text{м}^2}{text{кг}^2} right)) — гравитационная постоянная
Первая космическая скорость в цифрах для некоторых небесных тел
первая космическая скорость у поверхности Земли ( v = 8000 left( frac{text{м}}{text{c}} right) )
первая космическая скорость у поверхности Солнца ( v = 437000 left( frac{text{м}}{text{c}} right) )
первая космическая скорость у поверхности Луны ( v = 1680 left( frac{text{м}}{text{c}} right) )
первая космическая скорость у поверхности Марса ( v = 3530 left( frac{text{м}}{text{c}} right) )
Как выводится формула первой космической скорости
Рассмотрим движение спутника вокруг Земли.
Земля и спутник притягиваются, запишем закон притяжения между планетой и спутником
[ F = G cdot frac{mcdot M}{left( r + h right)^{2}} ]
При круговом движении на спутник действует центростремительная сила (как и на любое тело при таком движении).
[ F_{text{ц}} = m cdot frac{v^{2} }{left( r + h right)} ]
Мы можем записать эти уравнения в виде системы.
[ begin{cases} displaystyle F = Gcdot frac {m cdot M}{(r+h)^{2}} \ displaystyle F_{text{ц}} = m cdot frac {v^{2}}{(r+h)} \ end{cases} ]
Земля и спутник притягиваются, благодаря этому спутник движется вокруг Земли по круговой орбите. Значит, притяжение между спутником и Землей – это центростремительная сила. Именно она заставляет спутник двигаться вокруг планеты по окружности. На языке математики это запишется так:
[ F = F_{text{ц}} ]
А если равны левые части уравнений, то будут равны и правые:
[ G cdot frac{mcdot M}{left( r + h right)^{2}} = m cdot frac{v^{2} }{left( r + h right)} ]
Масса ( m ) спутника и расстояние ( R ) между телами встречается в обеих частях уравнения. Поделим обе части уравнения на массу спутника.
[ G cdot frac{M}{ left( r + h right)^{2}} = frac{v^{2} }{left( r + h right)} ]
Теперь умножим обе части уравнения на расстояние (left( r + h right) ). Получим:
[ G cdot frac{M}{left( r + h right)} = v^{2} ]
Извлечем корень квадратный из обеих частей уравнения, чтобы получить скорость:
[ sqrt{G cdot frac{M}{left( r + h right)}} = |v| ]
Все)
Вам будет интересно почитать:
Закон всемирного тяготения
Движение по окружности, центростремительная сила и центростремительное ускорение
Ускорение свободного падения
Вторая космическая скорость
Оценка статьи:
Загрузка…