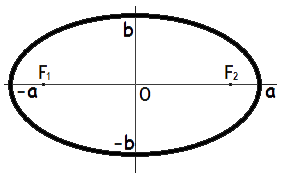Окей google как найти площадь - AvtoShod.ru - решение различных проблем

Загрузить PDF

Иногда вычисление площади сводится к простому перемножению двух чисел, но зачастую это вычисление более сложное. Прочтите эту статью для краткого обзора по вычислению площади (или площади поверхности) следующих фигур: четырехугольник, квадрат, параллелограмм, трапеция, треугольник, многоугольник, круг, пирамида, цилиндр, кривая линия.

1

Найдите длину двух смежных сторон прямоугольника. Поскольку противоположные стороны прямоугольника равны, нужно найти длины смежных сторон. Обозначьте одну сторону как (b), а другую — как (h).^[1]
2
Перемножьте значения двух смежных сторон, чтобы найти площадь. Обозначим площадь прямоугольника как (k). Тогда: k = b*h.
- Для более детальных инструкций прочтите статью «Как найти площадь четырехугольника».
Реклама

1

Найдите длину стороны квадрата. Поскольку квадраты имеют четыре равные стороны, нужно найти длину всего одной стороны.^[2]
2
Возведите в квадрат длину стороны. Это и есть площадь квадрата.
- Это верно, потому что квадрат — это прямоугольник, у которого все стороны равны. Так как для прямоугольника k = b*h, а в квадрате b=h, для вычисления площади квадрата просто умножаем его сторону на саму себя.
Реклама

1

Выберите одну сторону, на которую будет опущен перпендикуляр. Найдите длину этой стороны.
2
Опустите перпендикуляр (высоту) на выбранную ранее сторону и найдите его длину.^[3]
- Если нужно, продлите сторону, на которую опускается перпендикуляр, до ее пересечения с перпендикуляром.
3

Реклама

1

Найдите длины двух параллельных сторон. Обозначьте их как (а) и (b).
2

Найдите высоту. Опустите перпендикуляр (высоту (h)) к основанию трапеции.^[5]
3

Реклама

1

Найдите длину одной стороны треугольника (b), на которую будет опущен перпендикуляр (высота) и длину высоты (h).
2
Чтобы найти площадь треугольника, подставьте длину соответствующей стороны и длину высоты в формулу: A=0.5b*h
- Для более детальных инструкций прочтите статью «Как найти площадь треугольника».
Реклама

1

Найдите длину стороны и длину апофемы (а) (отрезок, соединяющий центр многоугольника и середину любой из его сторон).
2

Умножьте длину стороны на количество сторон, чтобы найти периметр многоугольника (р).
3

Реклама

1

Найдите радиус окружности (r). Это отрезок, соединяющий центр окружности и любую точку на окружности.
2

Реклама

1

Найдите площадь прямоугольного основания пирамиды с помощью приведенной выше формулы для нахождения площади прямоугольника: k=b*h.
2

Найдите площадь каждой треугольной грани пирамиды с помощью приведенной выше формулы для нахождения площади треугольника: A=0.5b*h.
3

Сложите все полученные площади для вычисления площади поверхности пирамиды.

Реклама

1

Найдите радиус круга в основании цилиндра.
2

Найдите высоту цилиндра.
3

Найдите площадь круга в основании, используя формулу для вычисления площади круга: А=πr^2.
4

Найдите площадь боковой поверхности, умножив высоту цилиндра на периметр основания. Периметр основания равен длине окружности: P = 2πr, поэтому площадь боковой поверхности А= 2πhr.
5
Сложите все полученные площади: две площади круговых оснований и площадь боковой поверхности. Таким образом, площадь поверхности цилиндра: SA = 2πr^2 + 2πhr.
- Для более детальных инструкций прочтите статью «Как найти площадь поверхности цилиндра».
Реклама

Допустим, вы хотите найти площадь фигуры, ограниченной кривой линией (описывается функцией f(x)), осью x и значениями функции при x=а и при x=b (то есть область определения [a,b]). Этот метод потребует знаний интегрального исчисления. Если вы не знаете его, этот метод не имеет для вас никакого смысла.

1

Определите f(x) через x.
2

Возьмите интеграл функции f(x) в интервале [а,b]. По формуле Ньютона-Лейбница: F(x)=∫f(x), ∫abf(x) = F(b) — F(a).
3

Подставьте значения а и b в интегральное выражение. Искомая площадь определяется как ∫abf(x). Поэтому, A=F(b)) — F(a).

Реклама

Об этой статье

Эту страницу просматривали 25 331 раз.

Была ли эта статья полезной?

Источник

Формулы площади геометрических фигур

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Формулы площади треугольника

Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты
Формула площади треугольника по трем сторонам

Формула Герона

S = √p(p — a)(p — b)(p — c)
Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.
Формула площади треугольника по трем сторонам и радиусу описанной окружности
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

где S — площадь треугольника,
a, b, c — длины сторон треугольника,
h — высота треугольника,
γ — угол между сторонами a и b,
r — радиус вписанной окружности,
R — радиус описанной окружности,

p = a + b + c — полупериметр треугольника.

2

Формулы площади квадрата

Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.

S = a²
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.

где S — площадь квадрата,
a — длина стороны квадрата,
d — длина диагонали квадрата.

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон

S = a · b

где S — Площадь прямоугольника,
a, b — длины сторон прямоугольника.

Формулы площади параллелограмма

Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

S = a · h
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

S = a · b · sin α
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.

где S — Площадь параллелограмма,
a, b — длины сторон параллелограмма,
h — длина высоты параллелограмма,
d₁, d₂ — длины диагоналей параллелограмма,
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма.

Формулы площади ромба

Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

S = a · h
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

S = a² · sin α
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.

где S — Площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба,
α — угол между сторонами ромба,
d₁, d₂ — длины диагоналей.

Формулы площади трапеции

Формула Герона для трапеции

S = a + b √(p-a)(p-b)(p-a-c)(p-a-d)

|a — b|
Формула площади трапеции по длине основ и высоте

Площадь трапеции равна произведению полусуммы ее оснований на высоту

где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,

p = a + b + c + d — полупериметр трапеции.

2

Формулы площади выпуклого четырехугольника

Формула площади четырехугольника по длине диагоналей и углу между ними

Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:

где S — площадь четырехугольника,
d₁, d₂ — длины диагоналей четырехугольника,
α — угол между диагоналями четырехугольника.
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)

Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности

S = p · r
Формула площади четырехугольника по длине сторон и значению противоположных углов

S = √(p — a)(p — b)(p — c)(p — d) — abcd cos²θ

где S — площадь четырехугольника,

a, b, c, d — длины сторон четырехугольника,

p = a + b + c + d2 — полупериметр четырехугольника,

θ = α + β2 — полусумма двух противоположных углов четырехугольника.
Формула площади четырехугольника, вокруг которого можно описать окружность

S = √(p — a)(p — b)(p — c)(p — d)

Формулы площади круга

Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.

S = π r²
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.

где S — Площадь круга,
r — длина радиуса круга,
d — длина диаметра круга.

Формулы площади эллипса

Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.

S = π · a · b

где S — Площадь эллипса,

a — длина большей полуоси эллипса,

b — длина меньшей полуоси эллипса.

Источник

Калькулятор для расчета площади

Данный онлайн-калькулятор позволяет рассчитать площадь различных геометрических фигур, таких как:

Прямоугольник;
Параллелограмм;
Круг;
Сектор круга;

Треугольник;
Правильный многоугольник;
Эллипс;
Трапеция.

Для удобства расчетов вы можете выбрать единицу измерения (миллиметр, сантиметр, метр, километр, фут, ярд, дюйм, миля). Также полученный результат можно конвертировать в другую единицу измерения путем выбора её из выпадающего списка.

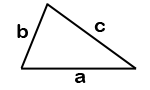
Способ нахождения площади треугольника:

a=
b=
c=

Вычислить

Рассчитать площадь круга, если известен:

Вычислить

Способ нахождения площади параллелограмма:

a=
h=

Вычислить

Рассчитать площадь сектора круга, если известен:

r=
θ=

Вычислить

Способ нахождения площади трапеции:

Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры.

Метрические единицы измерения площади:
Квадратный метр, производная единица системы СИ 1 м² =	1 са (сантиар)
Квадратный километр — 1 км² =	1 000 000 м²
Гектар — 1 га =	10 000 м²
Ар (сотка) — 1 а =	100 м² (сотка как правило применяется для измерения земельных участков и равна 100 м² или 10м х 10м)
Квадратный дециметр, 100 дм² =	1 м²;
Квадратный сантиметр, 10 000 см² =	1 м²;
Квадратный миллиметр, 1 000 000 мм² =	1 м².

Данный онлайн-калькулятор удобен при расчете площадей помещений и земельных участков.

Источник

Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне
высоты
Формула площади треугольника по трем сторонам

Формула Герона

S = √p(p — a)(p — b)(p — c)
Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между
ними.
Формула площади треугольника по трем сторонам и радиусу описанной окружности

Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

где S — площадь треугольника,
a, b, c — длины сторон
треугольника,
h — высота треугольника,
γ — угол между сторонами a и b,
r — радиус вписанной окружности,
R — радиус описанной окружности,

p =	a + b + c	— полупериметр треугольника.
2

Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.

S = a²
Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.

где S — Площадь квадрата,
a — длина стороны квадрата,
d — длина диагонали квадрата.

Площадь
прямоугольника равна произведению длин
двух его смежных сторон

S = a · b

где S — Площадь
прямоугольника,
a,
b —
длины сторон прямоугольника.

Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

S = a · h
Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

S = a · b · sin α
Формула площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.

где S — Площадь параллелограмма,
a, b — длины сторон параллелограмма,
h — длина высоты параллелограмма,
d₁, d₂ — длины диагоналей параллелограмма,
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма.

Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

S = a · h
Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

S = a² · sin α
Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.

где S — Площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба,
α — угол между сторонами ромба,
d₁, d₂ — длины диагоналей.

Формула Герона для трапеции

S =	a + b	√(p — a)(p — b)(p — a — c)(p — a — d)
4\|a — b\|

Формула площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на высоту

где S — Площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,

p =	a + b + c + d	— полупериметр трапеции.
2

Формула площади четырехугольника по длине диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:

где S — площадь четырехугольника,
d₁, d₂ — длины диагоналей четырехугольника,
α — угол между
диагоналями четырехугольника.
Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности

S = p · r

Формула площади четырехугольника по длине сторон и значению противоположных углов

S = √(p — a)(p — b)(p — c)(p — d) — abcd cos²θ

где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,

p =	a + b + c + d	— полупериметр четырехугольника,
2

θ =	α + β	— полусумма двух противоположных углов четырехугольника.
2

Формула площади четырехугольника, вокруг которого можно описать окружность

S = √(p — a)(p — b)(p — c)(p — d)

Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.

S = π r²
Формула площади круга через диаметр
Площадь круга равна четверти произведения квадрата диаметра на число пи.

где S — Площадь круга,
r — длина радиуса круга,
d — длина диаметра круга.

Площадь
эллипса равна произведению длин
большой и малой полуосей эллипса на число пи.

S = π · a · b

где S — Площадь
эллипса,
a — длина большей полуоси
эллипса,
b — длина меньшей полуоси
эллипса.

Источник

Площадь многоугольника — это величина той части плоскости, которую занимает многоугольник.

Некоторые свойства площади фигур

Если многоугольники равны, то они имеют равные площади.
Если многоугольник состоит из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

Рис. (1). Нахождение площади многоугольника

Рассмотрим, как найти площадь у разных фигур.

Площадь квадрата

Площадь квадрата равна квадрату его стороны.

S=a2

, где

— длина стороны квадрата.

Площадь прямоугольника

Площадь прямоугольника равна произведению его длины на ширину (смежные стороны).

S=a⋅b

, где

— длина и ширина.

Площадь параллелограмма равна произведению основания на высоту.

Рис. (2). Параллелограмм

S=a⋅h

(

) — основание,

(

) — высота.

Площадь ромба равна половине произведения его диагоналей.

Рис. (3). Ромб

Рис. (4). Треугольник

Площадь треугольника равна половине произведения основания на высоту.

S=a⋅h2

, где

(

) — основание,

(

) — высота треугольника.

Площадь прямоугольного треугольника равна половине произведения его катетов.

Рис. (5). Трапеция

Площадь трапеции равна половине суммы оснований, умноженной на высоту.

S=a+b2⋅h

, где

(

) и

(

) — основания,

(

) — высота.

Площадь круга и кругового сектора

Рис. (6). Круг

S=π⋅R2360°⋅α

— площадь кругового сектора.

Более подробно ознакомиться с примерами можно здесь.

Источник

S =	a + b	√(p-a)(p-b)(p-a-c)(p-a-d)
\|a — b\|

Об этой статье

Была ли эта статья полезной?

Формулы площади геометрических фигур

Формулы площади треугольника

Формула Герона

Формулы площади квадрата

Формула площади прямоугольника

Формулы площади параллелограмма

Формулы площади ромба

Формулы площади трапеции

Формулы площади выпуклого четырехугольника

Формулы площади круга

Формулы площади эллипса

Формула Герона﻿

Не пропустите также:

Формула Герона