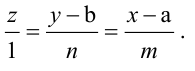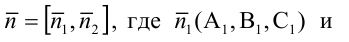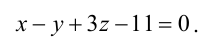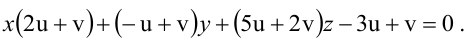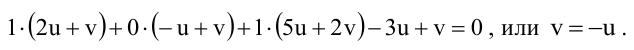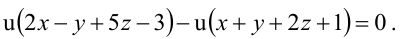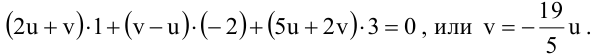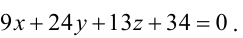Прямая как линия пересечения плоскостей
Прямая
в пространстве может быть определена
как линия пересечения двух непараллельных
плоскостей
и
,
то есть как множество точек, удовлетворяющих
системе двух линейных уравнений
(V.5)
Справедливо
и обратное утверждение: система двух
независимых линейных уравнений вида
(V.5)
определяет прямую как линию пересечения
плоскостей (если они не параллельны).
Уравнения системы (V.5)
называются общим
уравнением прямой
в пространстве
.
Пример
V.12.
Составить
каноническое уравнение прямой, заданной
общими уравнениями плоскостей
Решение.
Чтобы написать
каноническое уравнение прямой или, что
тоже самое, уравнение прямой, проходящей
через две данные точки, нужно найти
координаты каких-либо двух точек прямой.
Ими могут служить точки пересечения
прямой с какими-нибудь двумя координатными
плоскостями, например Oyz
и Oxz.
Точка
пересечения прямой с плоскостью Oyz
имеет абсциссу
.
Поэтому, полагая в данной системе
уравнений,
получим систему с двумя переменными:
Ее
решение
,
вместе с
определяет точку
искомой прямой. Полагая в данной системе
уравнений,
получим систему
решение
которой
,
вместе с
определяет точку
пересечения прямой с плоскостьюOxz.
Теперь
запишем уравнения прямой, проходящей
через точки
и
:
или
,
гдебудет направляющим векто-ром этой
прямой.
Пример
V.13.
Прямая задана
каноническим уравнением
.
Составить общее уравнение этой прямой.
Решение.
Каноническое
уравнение прямой можно записать в виде
системы двух независимых уравнений:
Получили
общее уравнение прямой, которая теперь
задана пересечением двух плоскостей,
одна из которых
параллельна осиOz
(),
а другая– осиОу
().
Данную
прямую можно представить в виде линии
пересечения двух других плоскостей,
записав ее каноническое уравнение в
виде другой пары независимых уравнений:
Замечание.
Одна и та же прямая может быть задана
различными системами двух линейных
уравнений (то есть пересечением различных
плоскостей, так как через одну прямую
можно провести бесчисленное множество
плоскостей), а также различными
каноническими уравнениями (в зависимости
от выбора точки на прямой и ее направляющего
вектора).
Ненулевой
вектор, параллельный прямой линии, будем
называть ее направляющим
вектором.
Пусть
в трехмерном пространстве
задана прямая l,
проходящая через точку
,
и ее направляющий вектор.
Любой
вектор
,
где,
лежащий на прямой, коллинеарен с вектором,
поэтому их координаты пропорциональны,
то есть
.
(V.6)
Это
уравнение называется каноническим
уравнением прямой. В частном случае,
когда ﻉ
есть
плоскость, получаем уравнение прямой
на плоскости
.
(V.7)
Пример
V.14.
Найти уравнение прямой, проходящей
через две точки
,
.
Будем
считать вектор
направляющим, тогда уравнение искомой
прямой имеет вид
,
где
,
,
.
Удобно
уравнение (V.6)
записать в параметрической форме. Так
как координаты направляющих векторов
параллельных прямых пропорциональны,
то, полагая
,
получим
где
t
– параметр,
.
Расстояние от точки до прямой
Рассмотри
двухмерное евклидовое пространство ﻉ
с
декартовой системой координат. Пусть
точка
ﻉ
и
lﻉ.
Найдем расстояние от этой точки до
прямой. Положим
,
и прямая l
задается уравнением
(рис.V.8).
Расстояние
,
вектор
,
где
– нормальный вектор прямой l,
и
– коллинеарны, поэтому их координаты
пропорциональны, то есть
,
следовательно,
,
.
Рис.
V.8
Отсюда
или умножая эти уравнения
наA
и B
соответственно и складывая их, находим
,
отсюда
или
.
Формула
(V.8)
определяет
расстояние от точки
до прямой
.
Пример
V.15.
Найти уравнение прямой, проходящей
через точку
перпендикулярно прямойl:
и найти расстояние от
до прямойl.
Из
рис. V.8
имеем
,
а нормальный вектор прямойl
.
Из условия перпендикулярности имеем
или
.
Так
как
,
то
.
(V.9)
Это
и есть уравнение прямой, проходящей
через точку
,перпендикулярно
прямой
.
Пусть
имеем уравнение прямой (V.9),
проходящей через точку
,
перпендикулярна прямойl:
.
Найдем расстояние от точкидо прямойl,
используя формулу (V.8).
Для
нахождения искомого расстояния достаточно
найти уравнение прямой, проходящей
через две точки
и точку
,
лежащую на прямой в основании
перпендикуляра. Пусть
,
тогда
.
(V.10)
Так
как
,
а вектор,
то
.
(V.11)
Поскольку
точка
лежит на прямойl,
то имеем еще одно равенство
или
Приведем систему
к виду, удобному для применения метода
Крамера
Ее решение имеет
вид


(V.12)
Подставляя
(V.12)
в (V.10),
получаем исходное расстояние.
Пример
V.16.
В двухмерном пространстве задана точка
и прямая
.
Найти расстояние от точкидо прямой; записать уравнение прямой,
проходящей через точкуперпендикулярно заданной прямой и найти
расстояние от точкидо основания перпендикуляра к исходной
прямой.
По
формуле (V.8)
имеем
.
Уравнение
прямой, содержащей перпендикуляр, найдем
как прямую, проходящую через две точки
и
,
воспользовавшись формулой (V.11).
Так как
,
то, с учетом того, что,
а,
имеем
.
Для
нахождения координат
имеем систему с учетом того, что точка
лежит на исходной прямой
Следовательно,
,
,
отсюда.
Рассмотрим
трехмерное евклидовое пространство ﻉ.
Пусть точка
ﻉ
и
плоскость ﻉ.
Найдем расстояние от этой точки
до плоскости,
заданной уравнением
(рис.V.9).
Рис.
V.9
Аналогично
двухмерному пространству имеем
и вектор
,
а,
отсюда
.
(V.13)
Уравнение
прямой, содержащей перпендикуляр к
плоскости ,
запишем как уравнение прямой, проходящей
через две точки
и
,
лежащую в плоскости:
.
(V.14)
Для
нахождения координат точки
к двум любым равенствам формулы (V.14)
добавим уравнение
.
(V.15)
Решая
систему трех уравнений (V.14),
(V.15),
найдем
,
,
– координаты точки
.
Тогда уравнение перпендикуляра запишется
в виде
.
Для
нахождения расстояния от точки
до плоскости
вместо формулой (V.13)
воспользуемся
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
5.4.4. Прямая, заданная пересечением двух плоскостей
Если плоскости 

То есть прямая задана уравнениями двух плоскостей. Типовая и распространенная задача состоит в том, чтобы переписать уравнения прямой в каноническом виде:
Задача 151
Записать канонические уравнения прямой
Решение: чтобы составить канонические уравнения прямой, нужно знать точку и направляющий вектор. А у нас даны уравнения двух плоскостей….
1) Сначала найдём какую-либо точку, принадлежащую данной прямой. Как это сделать? Методом подбора. В системе уравнений обнулим какую-нибудь координату, например, 

Таким образом, точка 
Получены верные равенства, значит, действительно 
В процессе подбора обратите внимание на следующий технический момент: желательно найти точку с целыми координатами. Если бы в системе мы обнулили «икс» или «зет», то не факт, что получилась бы «хорошая» точка без дробных координат. Такой анализ и подбор точки следует проводить мысленно или на черновике.
2) Как найти направляющий вектор прямой? Существует готовая формула: если прямая задана пересечением двух плоскостей 

В нашей задаче:
Однако всех формул не упомнишь и поэтому очень важно понимать, откуда они взялись. Направляющий вектор нашей прямой ортогонален нормальным векторам плоскостей: 





Проверим результат с помощью скалярного произведения: 
И, наконец, завершающий этап:
3) Составим канонические уравнения прямой по точке 

Ответ:
Аналогичная задача для самостоятельного решения:
Задача 152
Записать канонические уравнения прямой
Будьте внимательны! Ваш ответ может отличаться от моего ответа (смотря, какую точку подберёте). Если отличие есть, то для проверки возьмите точку из вашего уравнения и подставьте в моё уравнение (или наоборот).
Полное решение и ответ в конце книги.
И сейчас самое время перейти к простейшим задачам с пространственной прямой:
Уравнения прямой в пространстве — это уравнения двух пересекающихся плоскостей
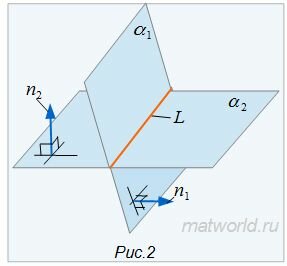
В данном разделе продолжим изучение темы уравнения прямой в пространстве с позиции стереометрии. Это значит, что мы будем рассматривать прямую линию в трехмерном пространстве как линию пересечения двух плоскостей.
Согласно аксиомам стереометрии, если две плоскости не совпадают и имеют одну общую точку, то они также имею одну общую прямую, на которой лежат все точки, которые являются общими для двух плоскостей. Используя уравнения двух пересекающихся плоскостей, мы можем определить прямую линию в прямоугольной системе координат.
По ходу рассмотрения темы приведем многочисленные примеры, ряд графических иллюстраций и развернутых решений, необходимых для лучшего усвоения материала.
Уравнения двух плоскостей, задающих прямую линию в пространстве
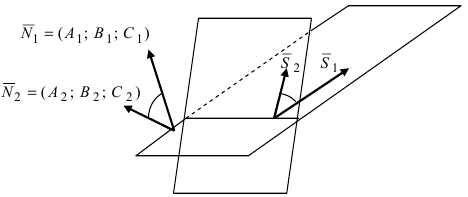
Пусть даны две плоскости, которые не совпадают между собой и пересекаются. Обозначим их как плоскость α и плоскость β . Разместим их в прямоугольной системе координат O х у z трехмерного пространства.
Как мы помним, любую плоскость в прямоугольной системе координат задает общее уравнение плоскости вида A x + B y + C z + D = 0 . Будем считать, что плоскости α соотвествует уравнение A 1 x + B 1 y + C 1 z + D 1 = 0 , а плоскости β уравнение A 2 x + B 2 y + C 2 z + D 2 = 0 . В этом случае нормальные вектора плоскостей α и β n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) не коллинеарны, так как плоскости не совпадают между собой и е размещаются параллельно друг другу. Запишем это условие следующим образом:
n 1 → ≠ λ · n 2 → ⇔ A 1 , B 1 , C 1 ≠ λ · A 2 , λ · B 2 , λ · C 2 , λ ∈ R
Чтобы освежить в памяти материал по теме «Параллельность плоскостей», смотрите соответствующий раздел нашего сайта.
Линию пересечения плоскостей обозначим буквой a . Т.е. a = α ∩ β . Эта прямая представляет собой множество точек, которые являются общими для обеих плоскостей α и β . Это значит, что все точки прямой линии a удовлетворяют обоим уравнениям плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . Фактически, они являются частным решением системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .
Общее решение системы линейных уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 определяет координаты всех точек линии, по которой происходит пересечение двух плоскостей α и β . Это значит, что с его помощью мы можем определить положение прямой в прямоугольной системе координат O x y z .
Рассмотрим описанную теорию еще раз, теперь уже на конкретном примере.
Прямая O x – это прямая, по которой пересекаются координатные плоскости O x y и O x z . Зададим плоскость O x y уравнением z = 0 , а плоскость O x z уравнением у = 0 . Такой подход мы подробно разобрали в разделе «Неполное общее уравнение плоскости», так что, в случае затруднений, можно обратиться к этому материалу повторно. В этом случае координатная прямая O x определяется в трехмерной системе координат системой из двух уравнений вида y = 0 z = 0 .
Нахождение координат точки, лежащей на прямой, по которой пересекаются плоскости
Рассмотрим задачу. Пусть в трехмерном пространстве задана прямоугольная система координат O х у z . Линия, по которой пересекаются две плоскости a , задана системой уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 . Дана точка трехмерного пространства M 0 x 0 , y 0 , z 0 .
Давайте определим, принадлежит ли точка M 0 x 0 , y 0 , z 0 заданной прямой линии a .
Для того, чтобы получить ответ на вопрос задачи, подставим координаты точки М 0 в каждое из двух уравнений плоскости. Если в результате подстановки оба уравнения превратятся в верные равенства A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 , то точка М 0 принадлежит каждой из плоскостей и принадлежит заданной линии. Если хотя бы одно из равенств A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 и A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 окажется неверным, то точка М 0 не принадлежит прямой линии.
Рассмотрим решение примера
Прямая линия задана в пространстве уравнениями двух пересекающихся плоскостей вида 2 x + 3 y + 1 = 0 x — 2 y + z — 3 = 0 . Определите, принадлежат ли точки M 0 ( 1 , — 1 , 0 ) и N 0 ( 0 , — 1 3 , 1 ) прямой линии пересечения плоскостей.
Решение
Начнем с точки М 0 . Подставим ее координаты в оба уравнения системы 2 · 1 + 3 · ( — 1 ) + 1 = 0 1 — 2 · ( — 1 ) + 0 — 3 = 0 ⇔ 0 = 0 0 = 0 .
В результате подстановки мы получили верные равенства. Это значит, что точка М 0 принадлежит обеим плоскостям и расположена на линии их пересечения.
Подставим в оба уравнения плоскости координаты точки N 0 ( 0 , — 1 3 , 1 ) . Получаем 2 · 0 + 3 · — 1 3 + 1 = 0 0 — 2 · — 1 3 + 1 — 3 = 0 ⇔ 0 = 0 — 1 1 3 = 0 .
Как вы видите, второе уравнение системы превратилось в неверное равенство. Это значит, что точка N 0 не принадлежит заданной прямой.
Ответ: точка М 0 принадлежит прямой линии, а точка N 0 не принадлежит.
Теперь предлагаем вам алгоритм нахождения координат некоторой точки, принадлежащей прямой линии, если прямая в пространстве в прямоугольной системе координат O x y z определяется уравнениями пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .
Количество решений системы из двух линейных уравнений с темя неизвестными A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 бесконечно. Любое из этих решений может стать решением задачи.
Пусть в трехмерном пространстве задана прямая линия уравнениями двух пересекающихся плоскостей вида x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 . Найдите координаты любой из точек этой прямой.
Решение
Перепишем систему уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 ⇔ x + 0 y + 3 z = — 7 2 x + 3 y + 3 z = — 2 .
Возьмем отличный от нуля минор второго порядка в качестве базисного минора основной матрицы системы 1 0 2 3 = 3 ≠ 0 . Это значит, что z – это свободная неизвестная переменная.
Перенесем слагаемые, содержащие свободную неизвестную переменную z в правые части уравнений:
x + 0 y + 3 z = — 7 2 x + 3 y + 3 z = — 2 ⇔ x + 0 y = — 7 — 3 z 2 x + 3 y = — 2 — 3 z
Введем произвольное действительное число λ и примем, что z = λ .
Тогда x + 0 y = — 7 — 3 z 2 x + 3 y = — 2 — 3 z ⇔ x + 0 y = — 7 — 3 λ 2 x + 3 y = — 2 — 3 λ .
Для решения полученной системы уравнений применим метод Крамера:
∆ = 1 0 2 3 = 1 · 3 — 0 · 1 = 2 ∆ x = — 7 — 3 λ 0 — — 3 λ 3 = — 7 — 3 λ · 3 — 0 · ( — 2 — 3 λ ) = 21 — 9 λ ⇒ x = ∆ x ∆ = — 7 — 3 λ ∆ y = 1 — 7 — 3 λ 2 — 2 — 3 λ = 1 · — 2 — 3 λ — — 7 — 3 λ · = 12 + 3 λ ⇒ y = ∆ y ∆ = 4 + λ
Общее решение системы уравнений x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 будет иметь вид x = — 7 — 3 λ y = 4 + λ z = λ , где λ ∈ R .
Для получения частного решения системы уравнений, которое даст нам искомые координаты точки, принадлежащей заданной прямой, нам необходимо взять конкретное значение параметра λ . Если λ = 0 , то x = — 7 — 3 · 0 y = 4 + 0 z = 0 ⇔ x = — 7 y = 4 z = 0 .
Это позволяет нам получить координаты искомой точки — 7 , 4 , 0 .
Проверим верность найденных координат точки методом подстановки их в исходные уравнения двух пересекающихся плоскостей — 7 + 3 · 0 + 7 = 0 2 · ( — 7 ) + 3 · 4 + 3 · 0 + 2 = 0 ⇔ 0 = 0 0 = 0 .
Ответ: — 7 , 4 , 0
Направляющий вектор прямой, по которой пересекаются две плоскости
Давайте рассмотрим, как определить координаты направляющего вектора прямой, которая задана уравнениями двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . В прямоугольной системе координат 0хуz направляющий вектор прямой неотделим от прямой линии.
Как мы знаем, прямая перпендикулярна по отношению к плоскости в том случае, когда она перпендикулярна по отношению к любой прямой, лежащей в данной плоскости. Исходя из вышесказанного, нормальный вектор плоскости перпендикулярен любому ненулевому вектору, лежащему в данной плоскости. Эти два факта помогут нам в нахождении направляющего вектора прямой.
Плоскости α и β пересекаются по линии a . Направляющий вектор a → прямой линии a расположен перпендикулярно по отношению к нормальному вектору n 1 → = ( A 1 , B 1 , C 1 ) плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и нормальному вектору n 2 → = ( A 2 , B 2 , C 2 ) плоскости A 2 x + B 2 y + C 2 z + D 2 = 0 .
Направляющий вектор прямой a представляет собой векторное произведение векторов n → 1 = ( A 1 , B 1 , C 1 ) и n 2 → = A 2 , B 2 , C 2 .
a → = n → 1 × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2
Зададим множество всех направляющих векторов прямой как λ · a → = λ · n 1 → × n 2 → , где λ — это параметр, который может принимать любые действительные значения, отличные от нуля.
Пусть прямая в пространстве в прямоугольной системе координат O х у z задана уравнениями двух пересекающихся плоскостей x + 2 y — 3 z — 2 = 0 x — z + 4 = 0 . Найдем координаты любого направляющего вектора этой прямой.
Решение
Плоскости x + 2 y — 3 z — 2 = 0 и x — z + 4 = 0 имеют нормальные векторы n 1 → = 1 , 2 , — 3 и n 2 → = 1 , 0 , — 1 . Примем за направляющий вектор прямой линии, являющейся пересечением двух заданных плоскостей, векторное произведение нормальных векторов:
a → = n → 1 × n 2 → = i → j → k → 1 2 — 3 1 0 — 1 = i → · 2 · ( — 1 ) + j → · ( — 3 ) · 1 + k → · 1 · 0 — — k → · 2 · 1 — j → · 1 · ( — 1 ) — i → · ( — 3 ) · 0 = — 2 · i → — 2 j → — 2 k →
Запишем ответ в координатной форме a → = — 2 , — 2 , — 2 . Тем, кто не помнит, как это делается, рекомендуем обратиться к теме «Координаты вектора в прямоугольной системе координат».
Ответ: a → = — 2 , — 2 , — 2
Переход к параметрическим и каноническим уравнениям прямой в пространстве
Для решения ряда задач проще использовать параметрические уравнения прямой в пространстве вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ или канонические уравнения прямой в пространстве вида x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ . В этих уравнениях a x , a y , a z — координаты направляющего вектора прямой, x 1 , y 1 , z 1 — координаты некоторой точки прямой, а λ — параметр, принимающий произвольные действительные значения.
От уравнения прямой вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 можно перейти к каноническим и параметрическим уравнениям прямой линии в пространстве. Для записи канонических и параметрических уравнений прямой нам понадобятся навыки нахождения координат некоторой точки прямой, а также координат некоторого направляющего вектора прямой, заданной уравнениями двух пересекающихся плоскостей.
Рассмотрим написанное выше на примере.
Зададим прямую линию в трехмерной системе координат уравнениями двух пересекающихся плоскостей 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 . Напишем канонические и параметрические уравнения этой прямой.
Решение
Найдем координаты направляющего вектора прямой, который является векторным произведением нормальных векторов n 1 → = 2 , 1 , — 1 плоскости 2 x + y — z — 1 = 0 и n 2 → = ( 1 , 3 , — 2 ) плоскости x + 3 y — 2 z = 0 :
a → = n 1 → × n 2 → = i → j → k → 2 1 — 1 1 3 — 2 = i → · 1 · ( — 2 ) + j → · ( — 1 ) · 1 + k → · 2 · 3 — — k → · 1 · 1 — j → · 2 · ( — 2 ) — i → · ( — 1 ) · 3 = i → + 3 · j → + 5 · k →
Координаты направляющего вектора прямой a → = ( 1 , 2 , 5 ) .
Следующим шагом является определение координат некоторой точки заданной прямой линии, которыми является одно из решений системы уравнений: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ 2 x + y — z = 1 x + 3 y — 2 z = 0 .
Возьмем в качестве минорной матрицы системы определитель 2 1 1 3 = 2 · 3 — 1 · 1 = 5 , который отличен от нуля. В этом случае переменная z является свободной. Перенесем слагаемые с ней в правые части каждого уравнения и придаем переменной произвольное значение λ :
2 x + y — z = 1 x + 3 y — 2 z = 0 ⇔ 2 x + y = 1 + z x + 3 y = 2 z ⇔ 2 x + y = 1 + λ x + 3 y = 2 λ , λ ∈ R
Применяем для решения полученной системы уравнений метод Крамера:
∆ = 2 1 1 3 = 2 · 3 — 1 · 1 = 5 ∆ x = 1 + λ 1 2 λ 3 = ( 1 + λ ) · 3 — 1 · 2 λ = 3 + λ ⇒ x = ∆ x ∆ = 3 + λ 5 = 3 5 + 1 5 · λ ∆ y = 2 1 + λ 1 2 λ = 2 · 2 λ — ( 1 + λ ) · 1 = — 1 + 3 λ ⇒ y = ∆ y ∆ = — 1 + 3 λ 5 = — 1 5 + 3 5 · λ
Получаем: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ x = 3 5 + 1 5 y = — 1 5 + 3 5 z = λ
Примем λ = 2 для того, чтобы получить координаты точки прямой линии: x 1 = 3 5 + 1 5 · 2 y 1 = — 1 5 + 3 5 · 2 z 1 = 2 ⇔ x 1 = 1 y 1 = 1 z 1 = 2 . Теперь мы имеем достаточно данных для того, чтобы записать канонические и параметрические уравнения данной прямой в пространстве: x — x 1 a x = y — y 1 a y = z — z 1 a z ⇔ x — 1 1 = y — 1 3 = z — 2 5 x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ x = 1 + 1 · λ y = 1 + 3 · λ z = 2 + 5 · λ ⇔ x = 1 + λ y = 1 + 3 · λ z = 2 + 5 · λ
Ответ: x — 1 1 = y — 1 3 = z — 2 5 и x = 1 + λ y = 1 + 3 · λ z = 2 + 5 · λ
Данная задача имеет еще один способ решения.
Нахождение координат некоторой точки прямой проводится при решении системы уравнений A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .
В общем случае ее решения можно записать в виде искомых параметрических уравнений прямой в пространстве x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ .
Получение канонических уравнений проводится следующим образом: решаем каждое из полученных уравнений относительно параметра λ , приравниваем правые части равенства.
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ λ = x — x 1 a x λ = y — y 1 a y λ = z — z 1 a z ⇔ x — x 1 a x = y — y 1 a y = z — z 1 a z
Применим данный способ к решению задачи.
Зададим положение прямой линии уравнениями двух пересекающихся плоскостей 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 . Напишем параметрическое и каноническое уравнения для этой прямой линии.
Решение
Решение системы из двух уравнений с тремя неизвестными проводится аналогично тому, как мы делали это в предыдущем примере. Получаем: 2 x + y — z — 1 = 0 x + 3 y — 2 z = 0 ⇔ x = 3 5 + 1 5 · λ y = — 1 5 + 3 5 · λ z = λ .
Это параметрические уравнения прямой в пространстве.
Канонические уравнения получаем следующим образом: x = 3 5 + 1 5 · λ y = — 1 5 + 3 5 · λ z = λ ⇔ λ = x — 3 5 1 5 λ = y + 1 5 3 5 λ = z 1 ⇔ x — 3 5 1 5 = y + 1 5 3 5 = z 1
Полученные в обоих примерах уравнения отличаются внешне, однако они эквивалентны, так как определяют одно и то же множество точек трехмерного пространства, а следовательно и одну и ту же прямую линию.
Ответ: x — 3 5 1 5 = y + 1 5 3 5 = z 1 и x = 3 5 + 1 5 · λ y = — 1 5 + 3 5 · λ z = λ
Линия пересечения плоскостей онлайн
С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Линия пересечения плоскостей − теория, примеры и решения
Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α1 и α2:
| α1: A1x+B1y+C1z+D1=0, | (1) |
| α2: A2x+B2y+C2z+D2=0, | (2) |
Найдем уравнение линии пересеченя плоскостей α1 и α2. Для этого рассмотрим следующие случаи:
Умножив уравнение (2) на λ, получим:
| α2: A1x+B1y+C1z+λD2=0, | (3) |
Если векторы n1 и n2 не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:
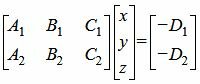 |
(4) |
Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.
Так как в системе линейных уравнений (4) векторы n1=<A1, B1, C1> и n2=<A2, B2, C2> не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:
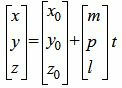 , , |
(5) |
Равенство (5) можно записать в следующем виде:
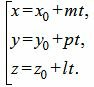 . . |
(6) |
Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей α1 и α2. Полученное уравнение прямой можно записать в каноническом виде:
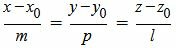
Пример 1. Найти линию пересечения плоскостей α1 и α2:
Поскольку направляющие векторы n1 и n2 неколлинеарны, то плолскости α1 и α2 пересекаются.
Для нахождения линии пересечения влоскостей α1 и α2 нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:
 . . |
(9) |
Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
 . . |
(10) |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 2 со строкой 1, умноженной на −2:
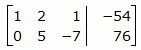
Второй этап. Обратный ход Гаусса.
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на −2/5:
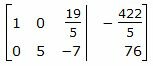
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

 . . |
(11) |
где t− произвольное действительное число.
Запишем (11) в следующем виде:
 . . |
(12) |
Получили уравнение линии пересечения плоскостей α1 и α2 в параметрическом виде. Запишем ее в каноническом виде.
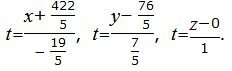 |
(13) |
Из равентсв выше получим каноническое уравнение прямой:
Ответ. Уравнение линии пересечения плоскостей α1 и α2имеет вид:
Пример 2. Найти линию пересечения плоскостей α1 и α2:
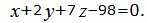 |
(14) |
 |
(15) |
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/2), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/2:
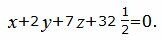 |
(16) |
Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости α1 и α2 не совпадают. Следовательно они параллельны, т.е. не пересекаются.
Пример 3. Найти линию пересечения плоскостей α1 и α2:
 |
(17) |
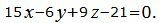 |
(18) |
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/3), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/3:
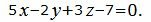 |
(19) |
Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α1 и α2 совпадают.
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenija-prjamoj-v-prostranstve-eto-uravnenija-d/
http://matworld.ru/analytic-geometry/linija-peresechenija-ploskostej.php
5.4.4. Прямая, заданная пересечением двух плоскостей
Если плоскости пересекаются, то система линейных уравнений

То есть прямая задана уравнениями двух плоскостей. Типовая и
распространенная задача состоит в том, чтобы переписать уравнения прямой в каноническом виде:
Задача 151
Записать канонические уравнения прямой
Решение: чтобы составить канонические уравнения прямой, нужно знать точку и направляющий вектор. А у нас даны уравнения двух
плоскостей….
1) Сначала найдём какую-либо точку, принадлежащую данной прямой. Как это сделать? Методом подбора. В системе уравнений обнулим
какую-нибудь координату, например, . Тогда получается система двух линейных
уравнений с двумя неизвестными: . Почленно складываем уравнения и находим
решение системы:
Таким образом, точка принадлежит данной прямой. Но принадлежит ли?
Выполним проверку – подставим её координаты в исходную систему уравнений:
Получены верные равенства, значит, действительно .
В процессе подбора обратите внимание на следующий технический момент: желательно найти точку с целыми координатами. Если бы в
системе мы обнулили «икс» или «зет», то не факт, что получилась бы «хорошая» точка без дробных координат. Такой анализ и подбор точки следует
проводить мысленно или на черновике.
2) Как найти направляющий вектор прямой? Существует готовая формула: если прямая задана пересечением двух
плоскостей 

В нашей задаче:
Однако всех формул не упомнишь и поэтому очень важно понимать, откуда они взялись. Направляющий вектор нашей прямой ортогонален нормальным векторам плоскостей: и
, поэтому вектор «пэ» можно найти как векторное произведение векторов нормали:
.

«снимаем» их векторы нормали:
и находим направляющий вектор прямой:
Проверим результат с помощью скалярного произведения:
, ч.т.п.
И, наконец, завершающий этап:
3) Составим канонические уравнения прямой по точке и
направляющему вектору :
Ответ:
Аналогичная задача для самостоятельного решения:
Задача 152
Записать канонические уравнения прямой
Будьте внимательны! Ваш ответ может отличаться от моего ответа (смотря, какую точку подберёте). Если отличие есть, то для проверки возьмите точку из вашего уравнения
и подставьте в моё уравнение (или наоборот).
Полное решение и ответ в конце книги.
И сейчас самое время перейти к простейшим задачам с пространственной прямой:


| Оглавление |
Автор: Aлeксaндр Eмeлин
Две различные плоскости в пространстве либо параллельны, либо пересекаются.
Параллельность двух плоскостей
Определение. Две плоскости в пространстве называются параллельными, если они не пересекаются.
Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то такие плоскости параллельны.
Основные свойства параллельности плоскостей.
- Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
- Отрезки параллельных прямых, заключённых между двумя параллельными плоскостями, равны по длине.
Пересечение двух плоскостей
Две плоскости пересекаются по прямой. Общая прямая двух плоскостей называется ребром двугранного угла, образованного при пересечении данных плоскостей. При пересечении двух плоскостей образуются четыре двугранных угла. Если все они равны, то плоскости называются перпендикулярными.
Признак перпендикулярности плоскостей. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.
Из признака перпендикулярности плоскостей следует, что плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.
Угол между плоскостями — наименьший из двугранных углов, образованных при пересечении плоскостей.
Угловая величина двугранного угла — это величина линейного угла данного двугранного угла.
Чтобы найти линейный угол двугранного угла надо из произвольной точки на ребре двугранного угла провести в каждой плоскости по перпендикуляру к этому ребру. Все линейные углы двугранного угла равны друг другу.
Тренировочные задания
-
Дан куб
. Найдите угол между плоскостями
и
.
-
Дан куб
. Точка
— середина ребра
. Найдите угол между плоскостями
и
.
-
В кубе
все рёбра равны
. На его ребре
отмечена точка
так, что
. Через точки
и
построена плоскость
, параллельная прямой
. Найдите угол наклона плоскости
к плоскости грани
.
-
Дана правильная треугольная призма
, у которой сторона основания равна
, а боковое ребро равно
. Через точки
,
и середину
ребра
проведена плоскость. Найдите угол между плоскостью сечения и плоскостью ABC.
-
Все рёбра правильной треугольной призмы
имеют длину
. Точки
и
— середины рёбер
и
соответственно. Найдите угол между плоскостями
и
.
-
Основанием пирамиды
является прямоугольник
, в котором
. Диагонали прямоугольника
пересекаются в точке
. Отрезок
является высотой пирамиды
. Из вершин
и
опущены перпендикуляры
и
на ребро
. Найдите двугранный угол пирамиды при ребре
, если
.
-
В основании прямой призмы
лежит квадрат
со стороной
, а высота призмы равна
. Точка
лежит на диагонали
, причём
. Найдите угол между плоскостью
и плоскостью
.
Содержание:
Плоскость в пространстве
Общее уравнение плоскости
Определение: Уравнение вида
Определение: Порядок поверхности определяется по высшему показателю степени переменных х, у и z или по сумме показателей степени в произведении этих величин.
Определение: Уравнение вида Ax+By+Cz+D=O называется общим уравнением плоскости.
Рассмотрим частные случаи приведенного уравнения:
1. D = 0; Ах + By + Сz = 0. Из этого уравнения видно, что точка О(0; 0; 0) удов- летворяет этому уравнению, следовательно, это уравнение описывает плоскость, проходящую через начало координат (Рис. 36).
Рис. 36. Плоскость, проходящая через начало координат.
2. С = 0; Ах + Ву + D = 0. Этому уравнению удовлетворяет любое значение переменной z, поэтому данное уравнение описывает плоскость, которая параллельна оси аппликат (Oz) (Рис. 37).
Рис. 37. Плоскость, проходящая параллельно оси аппликат.
Замечание: При отсутствии в уравнении плоскости одной из переменных величин говорит о том, что плоскость параллельна соответствующей координатной оси.
3. С=0; D=0; Ах+ By=0 — плоскость проходит через начало отсчета параллельно оси аппликат (Рис. 38).
Рис. 38. Плоскость, проходящая через начало координат параллельно оси аппликат.
4. 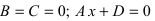
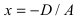
Рис. 39. Плоскость, проходящая параллельно координатной плоскости
5. В = С = D = 0; Ах = 0=>х = 0 — уравнение описывает плоскость 
Рис. 40. Координатная плоскость 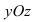
Другие уравнения плоскости
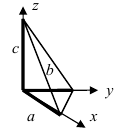
1. Уравнение плоскости в отрезках. Пусть в уравнении 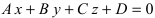
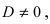
Введем следующие обозначения 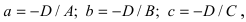
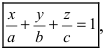
Откладывая на координатных осях точки М, N и Р, соединяя их прямыми лучим изображение данной плоскости (для определенности принято, что параметры а, b, с положительные) (Рис. 41):
Рис. 41. Отрезки, отсекаемые плоскостью на координатных осях.
Из рисунка видно, что числа а, b, с показывают отрезки, отсекаемые плоскостью на координатных осях, считая от начала координат.
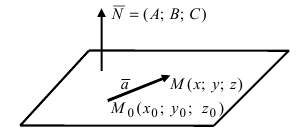
2. Уравнение плоскости, проходящей через заданную точку перпендикулярно к заданному вектору. Пусть задана точка 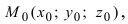
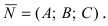
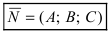
Возьмем на плоскости произвольную точку 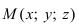
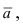
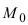
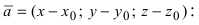
Рис. 42. Плоскость, проходящая через заданную точку перпендикулярно к нормальному вектору.
В силу того, вектор 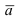
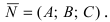
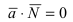
Пример:
Составить уравнение плоскости, проходящей через т. 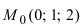
Решение:
Так как искомая плоскость параллельна плоскости (Q), то нормальный вектор этой плоскости 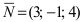
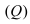
Пример:
Составить уравнение плоскости, проходящей через точки А(—1; 1 ;2) и В(0; —1; —1) параллельно вектору 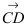
Решение:
Построим на искомой плоскости вектор 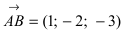
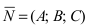
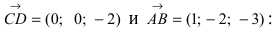
Уравнение плоскости, проходящей через заданную точку 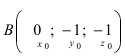
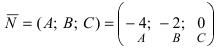
Отметим, что при выборе точки, через которую проходит искомая плоскость из точек 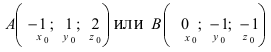
3. Уравнение плоскости, проходящей через три заданные точки. Пусть плоскость проходит через 3 известные точки 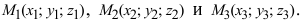
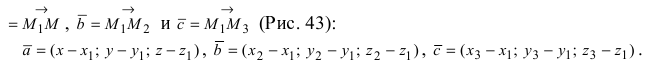
Рис. 43. Плоскость, проходящая через три заданные точки.
Вектора 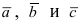
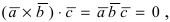
Замечание: Полученный определитель третьего порядка раскрывается по элементам первой строки.
Пример:
Составить уравнение плоскости, проходящей через три заданные точки
Решение:
Составим определитель третьего порядка 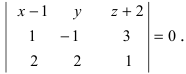
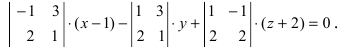
Основные задачи о плоскости в пространстве
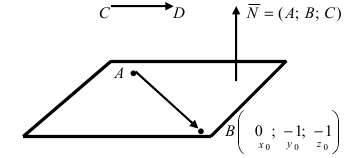
1. Угол между пересекающимися плоскостями. Пусть даны две пересекающиеся плоскости 
Пусть линия пересечения плоскостей определяется прямой (l). Из одной точки этой прямой проведем два перпендикулярных к прямой вектора 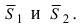
Рис.44. Угол между плоскостями.
В силу того, что 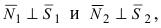
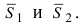
Следствие: Если плоскости перпендикулярны (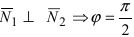
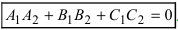
Следствие: Если плоскости параллельны, то нормальные вектора коллинеарны, следовательно, условие параллельности плоскостей:
2. Расстояние от данной точки до заданной плоскости. Расстояние от данной точки 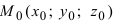
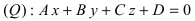
Пример:
На каком расстоянии от плоскости 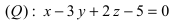
Решение:
Воспользуемся приведенной формулой:
Прямая в пространстве
Общее уравнение прямой
Прямая в пространстве может быть задана как пересечение двух плоскостей:
Определение: Геометрическое место точек пространства, удовлетворяющих системе уравнений (1), называется прямой в пространстве, а система уравнений (1) называется общим уравнением прямой.
Замечание: Для того чтобы система уравнений (1) определяла прямую в пространстве необходимо и достаточно, чтобы нормальные вектора плоскостей, определяющих прямую, 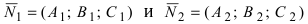
Пусть прямая проходит через точку 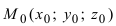
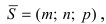
Замечание: Если в уравнении (2) одна из проекций направляющего вектора равна 0, то это означает, что прямая перпендикулярна соответствующей координатной оси.
Пример:
Как расположена прямая 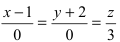
Решение:
Согласно замечанию эта прямая будет перпендикулярна осям абсцисс и ординат (параллельна оси аппликат) и будет проходить через точку 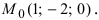
Пример:
Записать уравнение прямой 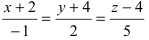
Решение:
Приравняем каждую дробь к параметру t: 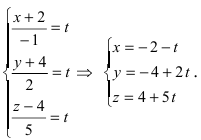
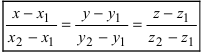
Пример:
Составить канонические и параметрические уравнения прямых, проходящих через точки А (— 1; 1; 2 ), В (0; -1; -1) И С (1; 0; -1), D (l; 0; 1 ).
Решение:
Составим каноническое уравнение прямой линии, проходящей через точки
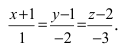
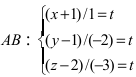
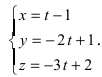
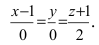
Основные задачи о прямой в пространстве
1. Переход от общего уравнения прямой к каноническому. Пусть прямая задана общим уравнением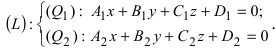
Пример:
Записать уравнение прямой 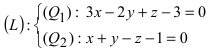
Решение:
Положив х = 0, получим СЛАУ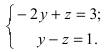
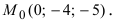
Запишем каноническое 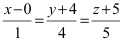
Угол между пересекающимися прямыми
Угол между двумя пересекающимися прямыми определяется как угол между их направляющими векторами. Если прямые 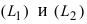
соответственно, то угол между прямыми определяется по формуле:
Следствие: Если прямые перпендикулярны (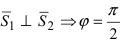
Следствие: Если прямые параллельны, то направляющие вектора коллинеарны, следовательно, условие параллельности прямых:
Координаты точки пересечения прямой и плоскости
Пусть прямая (L) задана общим уравнением 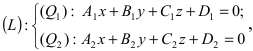
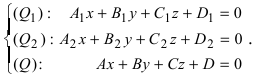
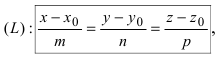
Рассмотрим возможные случаи:
- если выполняются условия
, то прямая не пересекает плоскость (прямая параллельна плоскости);
- при условиях
прямая лежит на плоскости;
- если
, прямая пересекает плоскость в одной точке.
Пример:
Найти координаты точки пересечения прямой (L), заданной уравнением 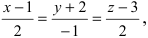
Решение:
Перепишем уравнение прямой (L) в параметрическом виде 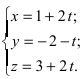
Найденное значение параметра 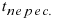
- Заказать решение задач по высшей математике
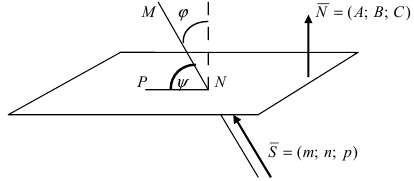
Угол между прямой и плоскостью
Пусть дана плоскость (Q) с нормальным вектором 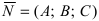
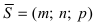
Рис. 45. Угол между прямой и плоскостью.
Угол 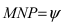
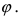
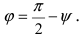
Следствие: Если прямая перпендикулярна плоскости (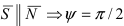
Следствие: Если прямая параллельна плоскости (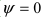
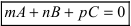
Плоскость и прямая в пространстве
Всякое уравнение первой степени относительно координат 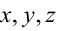

Вектор 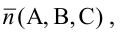
Особые случаи уравнения (3.1):
- D = 0, Ах + By + Cz = 0 — плоскость проходит через начало координат.
- С = 0, Ах + By + D = 0 — плоскость параллельна оси Oz.
- С = D = 0, Ах + By = 0 — плоскость проходит через ось Oz.
- С = В = 0, Ах + D = 0 — плоскость параллельна плоскости Oyz.
Уравнения координатных плоскостей:
Прямая в пространстве может быть задана:
- как линия пересечения двух плоскостей, т.е. системой уравнений:
- двумя своими точками
тогда прямая, через них проходящая, задается уравнениями:
- точкой
ей принадлежащей, и вектором
ей коллинеарным.
Тогда прямая определяется уравнениями:
Уравнения (3.4) называются каноническими уравнениями прямой.
Вектор 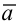
Параметрические уравнения прямой получим, приравняв каждое из отношений (3.4) параметру t: 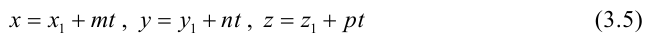
От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:
От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий вектор 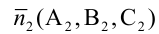
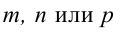
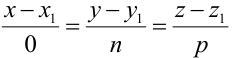
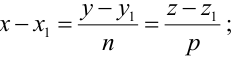
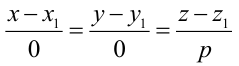
Пример:
Составьте уравнение плоскости, зная, что точка А(1,-1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
Решение:
По условию задачи вектор 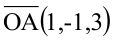
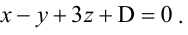
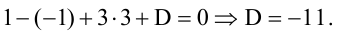
Пример:
Составьте уравнение плоскости, проходящей через ось Oz и образующей с плоскостью
Решение:
Плоскость, проходящая через ось Oz, задается уравнением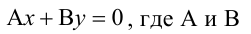
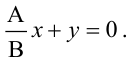
Решая квадратное уравнение 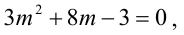
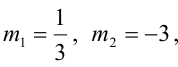
Пример:
Составьте канонические уравнения прямой: 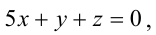
Решение:
Канонические уравнения прямой имеют вид:
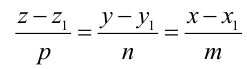
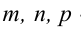
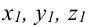
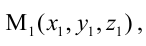
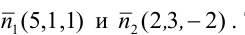
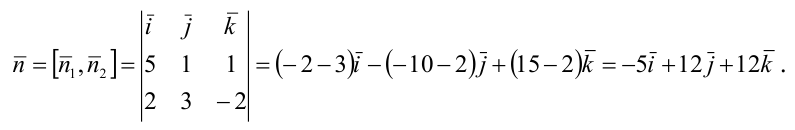
Пример:
В пучке, определяемом плоскостями 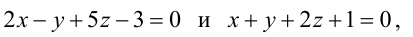
Решение:
Уравнение пучка, определяемого данными плоскостями, имеет вид 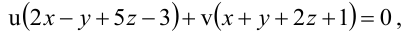
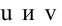
Для того, чтобы из пучка выделить плоскость, проходящую через точку М, подставим координаты точки М в уравнение пучка. Получим:
Тогда уравнение плоскости, содержащей М, найдем, подставив 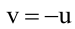
Т.к. и 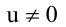
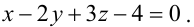
Значит, уравнение второй плоскости имеет вид: 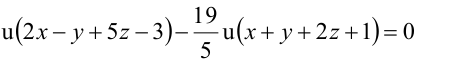
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Производная сложной функции
- Пределы в математике
- Функции многих переменных
- Уравнения прямых и кривых на плоскости














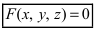
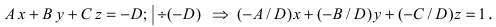
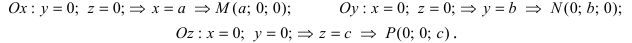
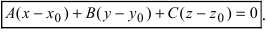
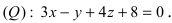
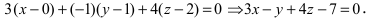
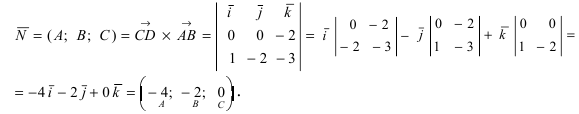
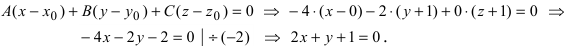

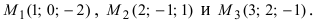
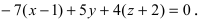
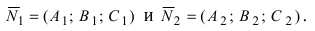
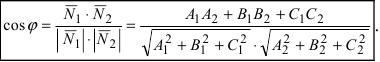
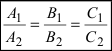
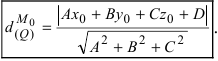
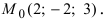
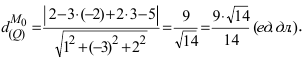
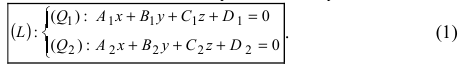
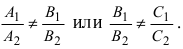

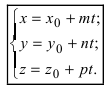
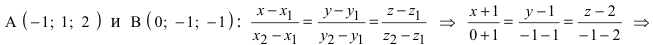
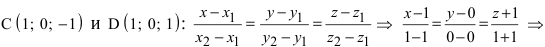
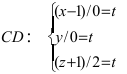
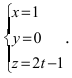
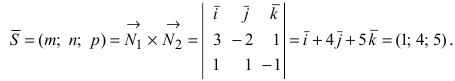
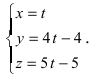
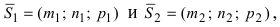

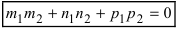
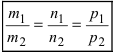
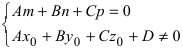 , то прямая не пересекает плоскость (прямая параллельна плоскости);
, то прямая не пересекает плоскость (прямая параллельна плоскости);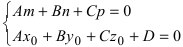 прямая лежит на плоскости;
прямая лежит на плоскости;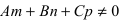 , прямая пересекает плоскость в одной точке.
, прямая пересекает плоскость в одной точке.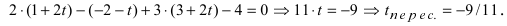
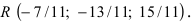
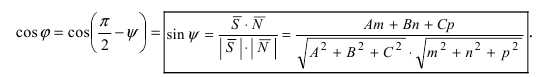
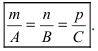
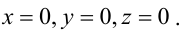
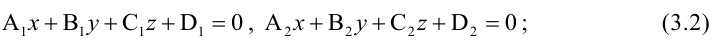
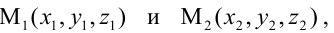 тогда прямая, через них проходящая, задается уравнениями:
тогда прямая, через них проходящая, задается уравнениями: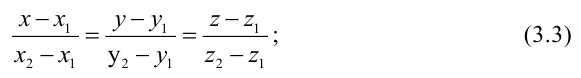
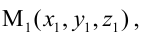 ей принадлежащей, и вектором
ей принадлежащей, и вектором 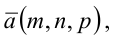 ей коллинеарным.
ей коллинеарным.