Объем это в математике как найти - AvtoShod.ru - решение различных проблем

Загрузить PDF

Объем фигуры представляет собой занимаемое этой фигурой трехмерное пространство.^[1] Представьте себе объем как количество жидкости (или воздуха, или песка), которым можно заполнить данную фигуру. Объем измеряется в кубических единицах (мм³, см³, м³).^[2] Эта статья расскажет вам, как вычислять объем шести трехмерных фигур. Вы можете заметить, что многие формулы для вычисления объема схожи, что упрощает их запоминание.

1
Куб – это трехмерная фигура, которая имеет шесть одинаковых квадратных граней, то есть все ее стороны (ребра) равны.^[3]
- Например, игральная кость – это куб.
2
Формула нахождения объема куба: V = s³, где V — объем, а s — длина ребра.
- Возведение в куб аналогично следующему умножению: s³ = s * s * s
3
Найдите длину стороны (ребра) куба. Она будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой). Так как ребра куба равны, измеряйте любое ребро.
- Если вы не уверены, что ваша фигура является кубом, измерьте каждую сторону, чтобы убедиться, что они равны. Если они не равны, перейдите к следующему разделу.
4

Подставьте длину ребра куба в формулу V = s³. Например, если ребро куба равно 5 см, напишите формулу следующим образом: V = 5³ = 5 * 5 * 5 = 125 см³ – это объем куба.
5

К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере ребро куба измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах. Если, например, сторона куба равна 3 см, то V = 3³ = 27см³.

Реклама

1
Прямоугольный параллелепипед или прямоугольная призма – это трехмерная фигура с шестью гранями, каждая из которых является прямоугольником (вспомните коробку из под обуви). ^[4]
- Куб – это частный случай прямоугольного параллелепипеда, у которого все ребра равны.
2

Формула нахождения объема прямоугольного параллелепипеда или прямоугольной призмы: V = l*w*h, где V = объем, l = длина, w = ширина, h = высота.^[5]
3
Длина прямоугольного параллелепипеда – это самое длинное ребро верхней или нижней грани, то есть грани, на которой стоит параллелепипед (нижняя грань) или параллельной ей грани (верхняя грань). Длина будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: длина прямоугольного параллелепипеда равна 4 см, то есть l = 4 см.
- Не беспокойтесь о том, какие ребра выбрать в качестве длины, ширины и высоты. В любом случае в итоге вы получите правильный ответ (только измерьте три ребра, перпендикулярные друг другу).
4
Ширина прямоугольного параллелепипеда – это самое короткое ребро верхней или нижней грани, то есть грани, на которой стоит параллелепипед (нижняя грань) или параллельной ей грани (верхняя грань). Ширина будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: ширина прямоугольного параллелепипеда равна 3 см, то есть w = 3 см.
- Если вы измеряете ребра параллелепипеда линейкой или рулеткой, не забудьте измерить их в одинаковых единицах измерения. Не измеряйте одно ребро в миллиметрах, а другое в сантиметрах.
5
Высота прямоугольного параллелепипеда – это расстояние между его нижней и верхней гранями. Высота будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: высота прямоугольного параллелепипеда равна 6 см, то есть h = 6 см.
6
Подставьте найденные значения в формулу V = l*w*h.
- В нашем примере l = 4, w = 3 и h = 6. Поэтому V = 4*3*6 = 72.
7
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере ребра измерялись в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 72 см³.
- Если в прямоугольной призме l = 2 см, w = 4 см, h = 8 см, то V = 2*4*8 = 64 см³
Реклама

1
Цилиндр – это трехмерная фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее.^[6]
- Например, банка или батарейка АА имеют форму цилиндра.
2
Формула нахождения объема цилиндра: V = πr²h, где V — объем, h — высота, r – радиус основания и πr² — площадь основания цилиндра.
- В некоторых задачах ответ требуется представить с пи, а в некоторых вместо пи подставить 3,14.
- Формула для нахождения объема цилиндра на самом деле очень похожа на формулу вычисления объема прямоугольной призмы, то есть вы перемножаете высоту и площадь основания. В прямоугольной призме площадь основания равна l*w, а в цилиндре она равна πr².
3

Найдите радиус основания. Он, скорее всего, дан в задаче. Если дан диаметр, разделите его на 2, чтобы найти радиус (d = 2r).
4
Если радиус не дан, измерьте его. Для этого измерьте основание цилиндра при помощи линейки или рулетки. Измеряйте основание в его самой широкой части (то есть измерьте диаметр основания), а затем разделите полученное значение на 2, чтобы найти радиус.
- Другой вариант – измерьте длину окружности цилиндра (то есть измерьте обхват цилиндра) при помощи рулетки, а затем найдите радиус по формуле r = с/2π, где с – обхват (длина окружности) цилиндра (2π = 6,28).
- Например, если обхват цилиндра равен 8 см, то радиус будет равен 1,27 см.
- Если вам нужно точное измерение, вы можете использовать оба метода, чтобы убедиться, что значения радиуса совпадают (нахождение радиуса через длину окружности является более точным методом).
5
Вычислите площадь круглого основания. Для этого подставьте радиус в формулу πr².
- Если радиус основания равен 4 см, то площадь основания равна π4².
- 4² = 4 * 4 = 16. 16*π = 16*3,14 = 50,24 см²
- Если дан диаметр основания, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус.
6

Найдите высоту цилиндра. Это расстояние между двумя круглыми основаниями. Высота будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
7
Умножьте площадь основания на высоту цилиндра, чтобы найти его объем. Или же просто подставьте значения соответствующих величин в формулу V = πr²h. В нашем примере, когда радиус основания равен 4 см, а высота равна 10 см:
- V = π4²10
- π4² = 50,24
- 50,24 * 10 = 502,4
- V = 502,4
8

К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 502,4 см³.

Реклама

1
Пирамида – это трехмерная фигура, в основании которой лежит многоугольник, а грани являются треугольниками, имеющими общую вершину. ^[7] Правильная пирамида – это трехмерная фигура, в основании которой лежит правильный многоугольник (с равными сторонами), а вершина проецируется в центр основания.^[8]
- Обычно мы представляем пирамиду, имеющую квадратное основание, но в основании пирамиды может лежать многоугольник с 5, 6 или даже со 100 сторонами!
- Пирамида с круглым основанием называется конусом, который будет обсуждаться в следующем разделе.
2
Формула нахождения объема правильной пирамиды: V = 1/3bh, где b – площадь основания пирамиды, h – высота пирамиды (перпендикуляр, соединяющий основание и вершину пирамиды).
- Эта формула для вычисления объема пирамиды одинаково годна как для правильных пирамид (в которых вершина проецируется в центр основания), так и для наклонных (в которых вершина не проецируется в центр основания).
3
Вычислите площадь основания. Формула будет зависеть от фигуры, лежащей в основании пирамиды. В нашем примере в основании пирамиды лежит квадрат со стороной 6 см. Площадь квадрата равна s², где s – сторона квадрата. Таким образом, в нашем примере площадь основания пирамиды равна 6² = 36 см²
- Площадь треугольника равна 1/2bh, где h – высота треугольника, b – сторона, к которой проведена высота.
- Площадь любого правильного многоугольника можно вычислить по формуле: А = 1/2ра, где А – площадь, р – периметр фигуры, а – апофема (отрезок, соединяющий центр фигуры с серединой любой стороны фигуры). Для получения дополнительной информации о нахождении площади многоугольников прочитайте эту статью.^[9]
4

Найдите высоту пирамиды. Высота будет дана в задаче. В нашем примере высота пирамиды равна 10 см.
5
Умножьте площадь основания пирамиды на ее высоту, а затем разделите полученный результат на 3, чтобы найти объем пирамиды. Формула для вычисления объема пирамиды: V = 1/3bh. В нашем примере площадь основания равна 36, а высота равна 10, поэтому объем: 36*10*1/3 = 120.
- Если, например, дана пирамида с пятиугольным основанием площадью 26, а высота пирамиды равна 8, то объем пирамиды: 1/3*26*8 = 69,33.
6

К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 120 см³.

Реклама

1
Конус – это трехмерная фигура, которая имеет круглое основание и одну вершину. Или конус – это особый случай пирамиды с круглым основанием.^[10]
- Если вершина конуса находится непосредственно над центром круглого основания, то конус называется прямым; в противном случае конус называется наклонным. Но формула для вычисления объема конуса одинаковая для обоих типов конуса.
2
Формула для вычисления объема конуса: V = 1/3πr²h, где r – радиус круглого основания, h – высота конуса.
- b = πr² – это площадь круглого основания конуса. Таким образом, формулу для вычисления объема конуса можно записать так: V = 1/3bh, что совпадает с формулой нахождения объема пирамиды!
3
Вычислите площадь круглого основания. Радиус должен быть дан в задаче. Если дан диаметр основания, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус. Для вычисления площади круглого основания подставьте радиус в формулу πr².
- Например, радиус круглого основания конуса равен 3 см. Тогда площадь этого основания равна π3².
- π3² = π(3*3) = 9π.
- = 28,27 см²
4

Найдите высоту конуса. Это перпендикуляр, опущенный из вершины к основанию пирамиды. В нашем примере высота конуса равна 5 см.
5

Перемножьте высоту конуса и площадь основания. В нашем примере площадь основания равна 28,27 см², а высота равна 5 см, поэтому bh = 28,27 * 5 = 141,35.
6
Теперь умножьте полученный результат на 1/3 (или просто разделите его на 3), чтобы найти объем конуса. В описанном выше шаге вы нашли объем цилиндра, а объем конуса всегда в 3 раза меньше объема цилиндра.
- В нашем примере: 141,35 * 1/3 = 47,12 – это объем конуса.
- Или: 1/3π3²5 = 47,12
7

К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 47,12 см³.

Реклама

1

Шар – это идеально круглая трехмерная фигура, каждая точка поверхности которой равноудалена от одной точки (центра шара). ^[11]
2

Формула для вычисления объема шара: V = 4/3πr³, где r – радиус шара.^[12]
3

Найдите радиус шара. Радиус должен быть дан в задаче. Если дан диаметр шара, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус. Например, радиус шара равен 3 см.
4
Если радиус не дан, вычислите его. Для этого измерьте длину окружности шара (например, теннисного мяча) в его самой широкой части при помощи веревки, нити или другого подобного предмета. Затем измерьте длину веревки, чтобы найти длину окружности. Разделите полученное значение на 2π (или на 6,28), чтобы вычислить радиус шара.
- Например, если вы измерили мяч и нашли, что длина его окружности равна 18 см, разделите это число на 6,28 и получите, что радиус мяча равен 2,87 см.
- Проделайте 3 измерения окружности шара, а затем усредните полученные значения (для этого сложите их и сумму разделите на 3), чтобы убедиться, что вы получили значение, близкое к истинному.
- Например, в результате трех измерений длины окружности вы получили следующие результаты: 18 см, 17,75 см, 18,2 см. Сложите эти значения: 18 + 17,5 + 18,2 = 53,95, а затем разделите их на 3: 53,95/3 = 17,98. Используйте это среднее значение в расчетах объема шара.
5

Возведите радиус в куб (r³). То есть r³ = r*r*r. В нашем примере r = 3, поэтому r³ = 3 * 3 * 3 = 27.
6

Теперь умножьте полученный результат на 4/3. Вы можете использовать калькулятор или выполнить умножение вручную, а затем упростить дробь. В нашем примере: 27*4/3 = 108/3 = 36.
7
Умножьте полученный результат на π (3,14), чтобы найти объем шара.
- В нашем примере: 36*3,14 = 113,09.
8

К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 113,09 см³.

Реклама

Об этой статье

Эту страницу просматривали 74 719 раз.

Была ли эта статья полезной?

Источник

Геометрия, 11 класс

Урок №11

Понятие объёма

Перечень вопросов, рассматриваемых на уроке:

Понятие объёма.

Свойства объёмов.

Объём прямоугольного параллелепипеда.

Формула объёма прямоугольного параллелепипеда.

Тезаурус

Объём тела– величина, характеризующая часть пространства, занимаемую телом, и определяемая формой и линейными размерами этого тела.

Основные свойства объёма:

— равные тела имеют равные объёмы;

— если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.

Основная литература:

Атанасян Л. С. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы [текст]: учеб. для общеобразоват. организаций: базовый и углубл. уровни – М.: Просвещение, 2014. – 255 с. С. 130–133.

Теоретический материал для самостоятельного изучения

С понятием объёмного тела, отличающегося от плоской фигуры, мы познакомились ещё в начальной школе.

Объёмом принято называть положительную величину, характеризующую часть пространства, занимаемую телом, и определяемую формой и линейными размерами этого тела.

Мы можем вычислить объём тела точно так же, как ранее находили площадь фигуры. Объём принято измерять в единицах измерения объёма (единицах измерения размера пространства, занимаемого телом), то есть в кубических метрах, сантиметрах, миллиметрах и так далее. За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (обозначение: см³). По аналогии, можно за единицу измерения объёма принять кубический миллиметр (1 мм³), кубический метр (1 м³) и тому подобное.

Объём выражается в положительных числах. Это число показывает, сколько единиц измерения содержится в теле. Например, сколько кубических миллиметров в аквариуме, сколько кубических метровв бассейне и так далее.

Объём обозначается заглавной латинской буквой V.

Пример:

Объём книги400 кубических сантиметров запишут: V = 400см³.

Рассмотрим свойства объёмов.

Свойство № 1. Равные тела имеют равные объёмы. Это означает, что если два тела идентичны, то есть имеют равное количество единиц измерения и частей, то равны и их объёмы. Например, 2 одинаковых пакета молока равны в объёме.

Свойство № 2. Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.

Следствие из основных свойств объёмов.

Объём куба с ребром 1/n равен 1/n³

Доказательство. Рассмотрим куб, объём которого принят за единицу измерения объёмов, тоесть равный некоторому числукубических сантиметров. Его ребро равно единице измерения отрезков. Разобьём каждое ребро этого куба на произвольное количество частей – nтак, чтобы провести плоскости, перпендикулярные к этому ребру.

По второму свойству объёмов, сумма объёмов всех кубиков равна объёму всего куба (1 см³). Следовательно, поскольку мы разбили каждое ребро на n частей, то каждый маленький куб внутри большого куба будет иметь ребро

Объём каждого из маленьких кубиков при этом будет равен 1/n³.

Объём прямоугольного параллелепипеда

Теорема

Объём прямоугольного параллелепипеда равен произведению трёх его измерений.

Доказательство

Обозначимизмеренияпрямоугольного параллелепипеда P буквами a,b,c, его объём буквой V, и докажем, что V = a ∙ b ∙ c.

Рассмотрим два возможных случая.

Случай первый. Измерения a, b и c представляют собой конечные десятичные дроби, у которых число знаков после запятой не превосходит n (можно считать, что n больше или равно 1). В этом случае числа a ∙10ⁿ, b∙10ⁿ, c∙10ⁿ, являются целыми. Разобьём каждое ребро параллелепипеда на равные части длины: 1/10ⁿ и через точки разбиения проведём плоскости, перпендикулярные к этому ребру. Параллелепипед P разобьётся на abc∙10³ⁿ равных кубов с ребром 1/10ⁿ. Так как объём каждого куба равен 1/10³ⁿ, что мы доказали ранее, то объём всего параллелепипеда P = abc, что и требовалось доказать.

Случай второй.

Хотя бы одно из измерений a, b, c представляет собой бесконечную десятичную дробь. Рассмотрим конечные десятичные дроби: a_n, b_n, c_n, которые получаются из чисел a, b, c, если отбросить в каждом из них все цифры после запятой, начиная с n + 1. Очевидно, a_n ≤ a ≤ a_n’, где a_n’= a_n+1 : 10ⁿ. Аналогичные неравенства справедливы для b и c. Перемножив эти неравенства, получим произведение a_nb_nc_n ≤ abc ≤ a_n’b_n’c_n’, где b_n’= b_n+1 : 10ⁿ, c_n’ = c_n+1 : 10ⁿ

По доказанному в первом случае, левая часть неравенства представляет собой объём V_n прямоугольного параллелепипеда P_nс измерениями a_n, b_n, c_n, а правая часть – это объём V_n’прямоугольного параллелепипеда P_n’ с измерениями a_n’, b_n’, c_n’. Так как параллелепипед P содержит в себе параллелепипед P_n, а сам содержится в параллелепипеде P_n’, то объём V параллелепипеда P заключён между V_n, = a_nb_nc_n и V_n’= a_n’b_n’c_n’. Будем неограниченно увеличивать n. Тогда 1/10ⁿ будет становиться сколь угодно малым, и поэтому произведение a_n’b_n’c_n’будет сколь угодно мало отличаться от числа, выраженного произведением a_nb_nc_n. Отсюда следует, что число V сколь угодно мало отличается от числа, выраженного произведением a_nb_nc_n, а значит, они равны.V = abc, что и требовалось доказать.

Примеры и разбор решения заданий тренировочного модуля.

№1.Длины сторон основания прямоугольного параллелепипеда равны 15 см и 20 см. Высота параллелепипеда равна диагонали основания. Найдите объём этого параллелепипеда.

Решение:

Найдём длину диагонали основания, для этого воспользуемся теоремой Пифагора:

А теперь найдём объём параллелепипеда:

V = 15 ∙ 20 ∙ 25 = 7500 см³

Ответ: V = 7500 см³.

№2.

Найдите площадь закрашенной фигуры, если объём прямоугольного параллелепипеда равен 960 см³, AB = 8 см, АА₁ ₌20 см.

Варианты ответов:

220 см²

100 см²

400 см²

200 см²

Решение.

Найдём длину АD:

AD = 960 : 8 : 20 = 6 см

Найдём АС, воспользовавшись теоремой Пифагора:

Закрашенная фигура – прямоугольник. Вычислим его площадь: 10∙20= 200 см².

Ответ: площадь закрашенной фигуры 200 см².

Верный ответ: 200 см².

Источник

Статьи

Среднее общее образование

Геометрия

Математика

Объемы геометрических тел

Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.

01 апреля 2019

Объемы геометрических тел

Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров «Российского учебника» учитель высшей категории Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.

Определение объема

Объем можно определить как функцию V на множестве многогранников, удовлетворяющую следующим аксиомам:

V сохраняется при движениях.
V удовлетворяет принципу Кавальери.
Если внутренности многогранников M и N не пересекаются, то V(M ∪ N) = V(M) + V(N).
Объем прямоугольного параллелепипеда V = abc.

Принцип Кавальери (итальянского математика, ученика Галилея). Если при пересечении двух тел плоскостями, параллельными одной и той же плоскости, в сечениях этих тел любой из плоскостей получаются фигуры, площади которых относятся как m : n, то объемы данных тел относятся как m : n.

В открытом банке заданий ЕГЭ есть много задач для отработки этого способа определения объема.

Примеры

Задача 1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

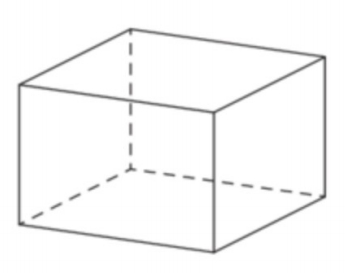
Задача 2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

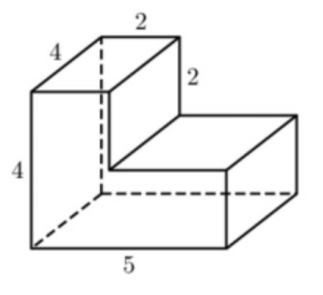
Задача 3. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

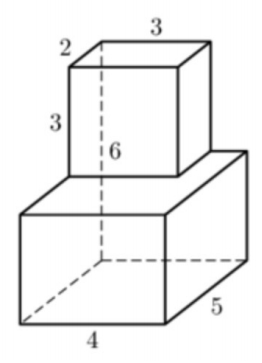
Разберем, как можно вычислять объемы изучаемых в школе фигур.

Объем призмы

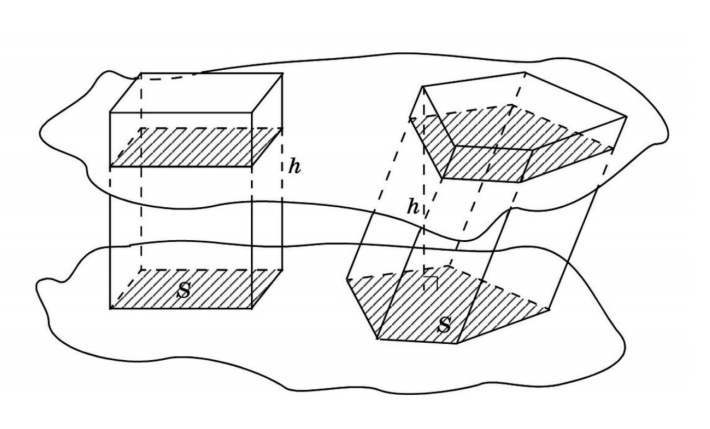
В представленном случае известны площадь основания и высота призмы. Чтобы найти объем, используем принцип Кавальери. Рядом с призмой (Ф₂) поместим прямоугольный параллелепипед (Ф₁), в основании которого — прямоугольник с такой же площадью, как у основания призмы. Высота у параллелепипеда такая же, как у наклонного ребра призмы. Обозначим третью плоскость (α) и рассмотрим сечение. В сечении виден прямоугольник с площадью S и, во втором случае, многоугольник тоже с площадью S. Далее вычисляем по формуле:

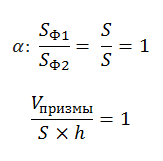
V S_осн h

Математика. Геометрия. Углублённый уровень. 11 класс. Задачник.

Задачник является Частью УМК для 10-11 классов, предназначенного для изучения предмета на углубленном уровне, и содержит более 1000 задач разной степени трудности, помогающих изучению и усвоению материала, изложенного в учебнике.
Пособие соответствует Федеральному государственному образовательному стандарту среднего (полного) общего образования.

Купить

Объем пирамиды

Лемма: две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики. Докажем это, используя принцип Кавальери.

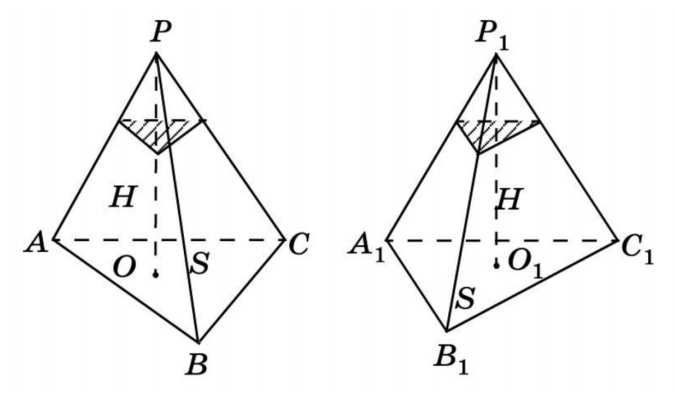
Возьмем две пирамиды одинаковой высоты и заключим их между двумя параллельными плоскостями α и β. Обозначим также секущую плоскость и треугольники в сечениях. Заметим, что отношения площадей этих треугольников связаны непосредственно с отношением оснований.

V ₁/V₂ = 1 <=> V₁= V₂

Известно, что объем любой пирамиды равен одной трети произведения площади основания на высоту. Данной теоремой апеллируют довольно часто. Однако откуда в формуле объема пирамиды появляется коэффициент 1/3? Чтобы понять это, возьмем призму и разобьем ее на 3 треугольные пирамиды:

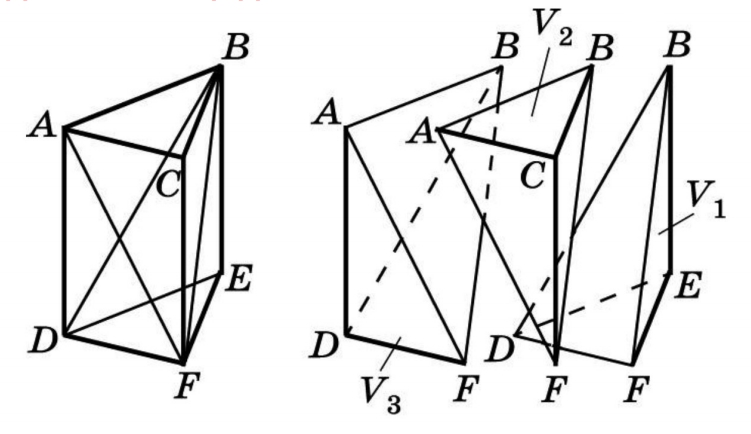
V₁= V₂

V₂ = V₃

V_призмы S h = 3V

V = 1/3 Sh

Объем цилиндра

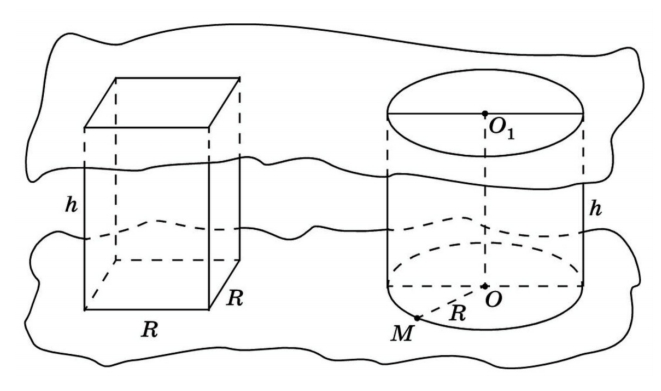
Возьмем прямой круговой цилиндр, в котором известны радиус основания и высота. Рядом поместим прямоугольный параллелепипед, в основании которого лежит квадрат. Рассмотрим:

V_цил = πh × R²

Объем конуса

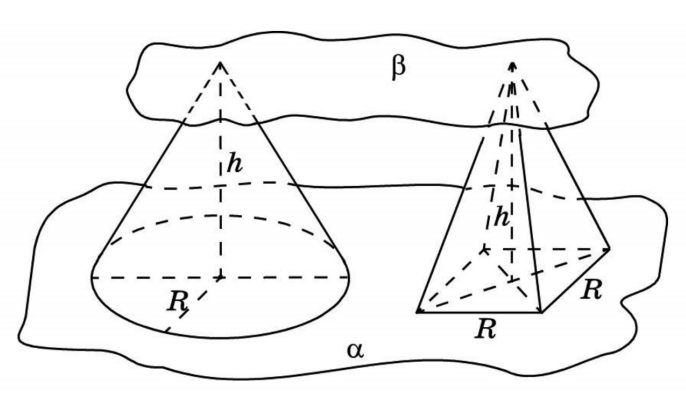
Конус лучше всего сравнивать с пирамидой. Например, с правильной четырехугольной пирамидой с квадратом в основании. Две фигуры с равными высотами заключаем в две параллельные плоскости. Обозначив третью плоскость, в сечении получаем круг и квадрат. Представления о подобиях приводят к числу π.

S_Ф1/S_Ф2 = π

V_конуса = 1/3 πR² h

Объем шара

Объем шара — одна из наиболее сложных тем. Если предыдущие фигуры можно продуктивно разобрать за один урок, то шар лучше отложить на последующее занятие.

Чтобы найти объем шара, шар часто предлагается сравнить со сложным геометрическим телом, которое связано с конусом и цилиндром. Но не стоит строить цилиндр, из которого вырезан конус, или вроде того. Возьмем половину шара с высотой R и радиусом R, а также конус и цилиндр с аналогичными высотами и радиусами оснований. Обратимся к полезным материалам на сайте
«Математические этюды», где объем шара рассматривается с использованием весов Архимеда. Цилиндр располагается на одной стороне уравновешенных весов, конус и половина шара — на другой.

Заключаем геометрические фигуры в две параллельные плоскости и смотрим, что получается в сечении. У цилиндра — круг с площадью πR². Как известно, если внутренности геометрических тел не пересекаются, то объем их объединения равен сумме объемов. Пусть в конусе и в половине шара расстояние до плоскости сечения будет x. Радиус — тоже x. Тогда площадь сечения конуса — π ∙ x². Расстояние от середины верха половины шара к краю сечения — R. Площадь сечения половины шара: π(R² — x²).

Заметим, что: πR² + πR² — πR² = πR²

V_цил = πR² × R = πR³ = 1/3 R³ π + V_шара

V_шара = 4/3 πR³

Итак, чтобы найти объем нового, не изученного геометрического тела, нужно сравнить его с тем телом, которое наиболее на него похоже. Многочисленные примеры заданий из открытого банка задач показывают, что в работе с фигурами имеет смысл использовать представленные формулы и аксиомы.

#ADVERTISING_INSERT#

Источник

Площади и объемы многогранников

Что такое многогранник

Простейшей геометрической фигурой является прямая. Ею называется линия, которая имеет свое продолжение вправо и влево. Если эту прямую ограничить с двух сторон, получится отрезок. Для определения его величины достаточно одного измерения — длины. Прямая, ограниченная с одной стороны, имеет свое название. Это отрезок.

луч

Источник: rusinfo.info

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В пределах одной плоскости, кроме прямой, которую можно измерить одной величиной, существуют геометрические фигуры, измеряемые длиной и шириной. Это многоугольники.

много

Источник: sun9-19.userapi.com

Они могут иметь различное количество углов и характеризуются таким понятием как площадь.

Фигура, которая располагается в нескольких плоскостях, характеризуется пространственными величинами или трехмерным измерением. К таким фигурам относят многогранники.

Многогранник — геометрическая фигура, имеющая замкнутую поверхность, которую можно представить совокупностью многоугольников.

Для полной характеристики многогранника необходимо назвать следующие свойства:

стороны обязательно являются смежными с одной соседней стороной;
при необходимости можно, начав движение от одного из многоугольников, достигнуть любого другого, используя принцип смежности;
площадь поверхности многогранника равна сумме площадей многоугольников, ограничивающих фигуру.

При этом каждый многоугольник — это грань, сторона — ребро, а вершина — вершина многогранника.

Многогранник, как геометрическое тело, может быть представлен несколькими параллелепипедами, которые соединены по одной из граней. В таком случае их площадь будет равна сумме площадей свободных сторон и одной стороны, по которой произошло соединение. Объем такого тела будет равен сумме объемов каждого из параллелепипедов.

куб

Источник: examer.ru

Многогранники бывают:

выпуклыми (каждая из точек фигуры находится по одну сторону от плоскости);
невыпуклыми (не все точки располагаются по одну сторону плоскости).

Проще говоря, выпуклый многогранник можно поставить на одну из сторон, и он будет на ней «уверенно стоять». С невыпуклым такого действия совершить нельзя.

Примечание 1

Важно помнить, что многогранник — это не только поверхность, состоящая из нескольких многоугольников. Это еще и тот внутренний объем, который ограничивает данная поверхность. Именно поэтому в стереометрии отделяют два понятия: площадь многогранника и его объем.

Как найти площадь: формулы

В зависимости от того, какой фигурой представлен многогранник, выбирают формулу для расчета площади его поверхности. Рассмотрим примеры.

1. Дана призма (многогранник, у которого в параллельных плоскостях расположены два многоугольника, являющихся гранями. Прочие грани представлены параллелограммами).

призма

Источник: osiktakan.ru

Найти площадь данной фигуры можно следующим образом:

фрмула

Источник: osiktakan.ru

2. Дан параллелепипед (один из вариантов призмы, все шесть граней которой являются параллелограммами).

параллел

Источник: osiktakan.ru

В этом случае S=2(ab+bc+ac)

3.Дана пирамида (вид многогранника с основанием в виде n-угольника и боковыми гранями по форме треугольниками. Обязательное условие: все треугольники имеют одну общую вершину, у которой есть свое название — вершина пирамиды).

пирамида

Источник: osiktakan.ru

Площадь пирамиды можно найти по формуле:

формула2

Источник: osiktakan.ru

Примечание 2

Особый случай, когда у пирамиды нет вершины. Такая фигура носит название усеченной. Ее можно себе представить, если мысленно параллельно основанию провести сечение (см. рисунок).

нет

Источник: osiktakan.ru

S_бок усеченной пирамиды находят по формуле:

формула3

Источник: osiktakan.ru

В стереометрии существует понятие правильного многогранника. Его вводят для фигур, у которых:

все грани представлены правильными многоугольниками;
число граней у всех углов идентично;
ребра являются равными отрезками;
величины плоских углов идентичны.

Перечисленным требованиям отвечают 5 видов многогранников, представленных в таблице:

	Наименование фигуры	Пример
1	Правильный четырехгранник	Правильный тетраэдр
2	Правильный шестигранник	Куб
3	Правильный восьмигранник	Правильный октаэдр
4	Правильный двенадцатигранник	Правильный додекаэдр
5	Правильный двадцатигранник	Правильный икосаэдр

Определить площадь правильных многогранников также несложно, зная следующие формулы (нумерация согласно строке таблицы):

1. S=a²√3

2. S=6a²

3. S=2a²√3

4. формула4

Источник: osiktakan.ru

5. S=5a²√3

Использовать данный формулы нужно в задачах, требующих определить площадь поверхности многогранника, без учета его внутреннего объема.

Объем многогранника: формулы

Объем многогранника, в отличие от площади его поверхности, не может быть определен только касательно поверхности. Ведь он представляет собой все внутреннее пространство, которое ограничивается имеющейся поверхностью. На практике говорят, что объем является величиной, с помощью которой описывают размер трехмерных фигур. Эти фигуры так и называют: объемные (тела). У объемной фигуры имеется не только длина и ширина, но и высота – параметр, измеряемый в третьей плоскости.

Решить задачи по определению объема многогранника также можно с использованием формул.

Рассмотрим следующий рисунок:

рисунок

Источник: interneturok.ru

Объем такого тела определяется по формуле:

V=a*b*c

Поскольку по рисунку видно, что a*b=S, а c является высотой (h), то формулу можно записать в виде: V=S*h

Рассмотренный вариант касается прямоугольного параллелепипеда. Если же произвольный параллелепипед имеет наклонные вертикальные грани, то данная формула также верна, однако проведенная высота отличается от бокового ребра, и, возможно, лежит внутри либо вне самого тела:

Источник: interneturok.ru

Формула определения объема через площадь и высоту подходит и для такого трехмерного тела, как призма (причем как для прямой, так и наклонной):

Источник: interneturok.ru

В быту часто происходит образование новых многогранников в процессе обрезания кусков от старых и приставления их к уже имеющимся. Как же вычислить объем такого геометрического тела? В геометрии используется принцип Кавальери. Суть его в следующем. Площади прямоугольника и параллелограмма равны потому что они в своей структуре имеют отрезки одинакового размера. Проще говоря, если представить рассечение обеих фигур плоскостями, параллельными основанию, величина отрезка слева всегда будет равна величине отрезка справа. Если третья фигура имеет такое же строение, по ее площадь будет такой же.

Источник: interneturok.ru

Объем многогранника, который может быть разделен на два и более многогранников, может определяться суммой их объемов.

найдите

Источник: image2.slideserve.com

Для систематизации формул, применяемых для определения объемов многогранников, рассмотрим таблицу:

	Наименование фигуры	Формула объема
1	Параллелепипед непрямоугольный, призма	V=S*h
	Параллелепипед прямоугольный	V=abc
2	Куб	V=a³
3	Пирамида	S=1/3(Sh)

На практике определить объем трехмерного тела можно и без формулы. Например, найти объем призмы можно, если умножить площадь ее основания на высоту фигуры. При этом вариант, когда в основании призмы лежит треугольник, предполагает, что нужно найти его площадь. Если основание квадрат, на первом этапе — нахождение площади квадрата. Величину высоты определяем, опуская перпендикуляр к основанию.

Примеры решения задач

Задача 1

Треугольник ABC — основание пирамиды DABC. При этом AC=AB=13см, BC=10см. AD=9см, это перпендикуляр к основанию. Найти S боковой поверхности.

задача1

Источник: ege-study.ru

Искомая величина равна сумме площадей боковых граней этой пирамиды.

Из вершин A и D проведем перпендикуляры к стороне BC. Тогда высота треугольника DBC — DK.

Треугольник ABC является равнобедренным, поскольку AB=AC. Тогда высота AK, которую провели по направлению основания BC, совпадает с медианой. Соответственно BK=KC=5см.

решение

Источник: ege-study.ru

Ответ: 192 см³

Задача 2

Имеется выпуклый многогранник. У него 8 граней, в т.ч. 4 пятиугольника и 4 четырехугольника. Определить, сколько у данного тела ребер и вершин. Определим сумму всех граней: 4*4+4*5=36

Поскольку смежные ребра посчитаны дважды, найденное количество необходимо разделить на два: 36/2=18

В+Г-Р=2

В+12-30=2

В+12-2=30

В+10=30

В=20

Ответ: вершин — 20, ребер — 30.

Задача 3

Если переплавить три куба из латуни, у которых ребра равны соответственно 3, 4, 5см, в один куб, какая величина ребра получится у нового куба?

Решение.

решение2

Источник: famiredo.ru

Источник

Формулы объёма и площади поверхности. Многогранники.

Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:

Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
Элементарная логика.

Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.

Куб		диагональ
Параллелепипед	$V=S_text{OCH}h, h -$ высота
Прямоугольный параллелепипед		$d=sqrt{a^2+b^2+c^2}$
Призма	$V=S_text{OCH}h$	$S = 2S_text{OCH}+$
Пирамида	$V=frac{1}{3}S_text{OCH}h$	$S = S_text{OCH}+$

Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».

Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.

Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.

Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.

Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.

Задача 1.Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Решение:

Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб

Очевидно, их 6, поскольку у куба 6 граней.

Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.

Разберем задачи, где требуется найти площадь поверхности многогранника.

Мы рассмотрим призмы и пирамиды. Начнем с призмы.

Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.

Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.

Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Многогранник на рисунке – это прямая призма с высотой 12.

$P_text{OCH}=8+6+6+2+2+4=28.$

Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:

(больший квадрат), (маленький прямоугольник), $S_text{OCH}=36+8=44$

Подставим все данные в формулу: и найдем площадь поверхности многогранника:

Ответ: 424.

Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).

Решение.

Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Площадь поверхности этой призмы находится по формуле:

$P_text{OCH}=4+5+2+1+2+4=18.$

Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:

(большой прямоугольник), $S_text{OCH}=16+2=18$ (маленький прямоугольник).

Найдем площадь полной поверхности:

Ответ: 54

Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Покажем еще один способ решения задачи.

Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.

И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
куба со стороной 1, без удвоенной площади квадрата со стороной 1:

Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело. Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.

Ответ: 42

Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.

Решение.

Пусть АВ = 5 см, ВС = 3 см, тогда $angle{ABC}=120^{circ}$

Из по теореме косинусов найдем ребро АС:

$AC^2=AB^2+BC^2-2cdot ABcdot BC cdot cos120^{circ}$

$AC^2=25+9-2cdot5cdot3cdotleft(-frac{1}{2}right)=47, ~AC = 7$

Отрезок АС – большая сторона , следовательно, большая боковая грань призмы.

Поэтому или откуда h=5.

Ответ: 75

Теперь две задачи на площадь боковой поверхности пирамиды.

Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.

Решение.

Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.

Проведем , тогда (по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.

– равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.

Из прямоугольного получим:

$AK=sqrt{AB^2-BK^2}=sqrt{13^2-5^2}=sqrt{169-25}=sqrt{144}=12.$

Из прямоугольного имеем:

$DK=sqrt{DA^2+AK^2}=sqrt{9^2+12^2}=sqrt{81+144}=sqrt{225}=15.$

(по двум катетам), тогда $S_{ADB}=S_{ADC},$ следовательно

$=2S_{ADB}+S_{BDC},$ $=2cdotfrac{1}{2}cdot13cdot9+frac{1}{2}cdot10cdot15=117+75=192.$

Ответ: 192

Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.

Решение:

Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани — равные равнобедренные треугольники.

Площадь поверхности пирамиды равна

где р – полупериметр основания, h — апофема (высота боковой грани правильной пирамиды), a – сторона основания.

Значит, полупериметр основания .

Апофему найдем по теореме Пифагора:

$h=sqrt{37^2-12^2}=sqrt{(37-12)(37+12)}=sqrt{25cdot49}=5cdot7=35$

Ответ: 2256

Как решать задачи на нахождение объема многогранника сложной формы?

Покажем два способа.

Первый способ

1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.

Второй способ.

1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.

Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

1) Достроим составной многогранник до параллелепипеда.

2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту:

3) Найдем объем лишней части, то есть маленького параллелепипеда.

Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем

4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:

Ответ: 220.

Задача 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.

Объем призмы равен $V=S_{OCH}cdot h$ , а так как призма прямая, то ее боковое ребро является и высотой, то есть h=6.

Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания

$S_{OCH}=frac{1}{2}cdot ab=frac{1}{2}cdot6cdot7=21.$

Ответ: 126

Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.

Решение.

Объем призмы равен $V = S_{OCH}cdot h$

Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.

Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда. Отношение площадей подобных фигур равно квадрату коэффициента подобия.

Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.

Объем воды не изменился, Так как высота воды h_2 должна быть в 81 раз меньше, чем h_1. Она равна (см).

Ответ: 4

Задача 12. Объем параллелепипеда Найдите объем треугольной пирамиды ABDA_1.

Решение.
Опустим из вершины A_1 высоту A_1H Н на основание ABCD.

$=S_{ABCD}cdot A_1H$

$=frac{1}{3}S_{ABD}cdot A_1H$

Диагональ основания делит его на два равных треугольника, следовательно, $S_{ABD}=frac{1}{2}S_{ABCD}.$

Имеем:

$ABDA_1=frac{1}{3}S_{ABD}cdot A_1H=frac{1}{3}cdotfrac{1}{2}S_{ABCD}cdot A_1H=frac{1}{6}V_{ABCDA_1B_1C_1D_1}=frac{1}{6}cdot21=3,5.$

Ответ: 3,5

Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна

Решение.
По формуле объема пирамиды, .

В основании пирамиды лежит правильный треугольник. Его площадь равна $S_{OCH}=frac{a^2sqrt{3}}{4}.$

$S_{OCH}=frac{8^2sqrt{3}}{4}=frac{64sqrt{3}}{4}=16sqrt{3}.$

Объем пирамиды $V=frac{1}{3}cdot16sqrt{3}cdot6sqrt{3}=16cdot6=96.$

Ответ: 96

Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.

Решение.

По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.

Пусть AD=x, тогда $S_{OCH}=x^2.$

Так как точки М и К – середины АD и DС соответственно, то $DM=DK=frac{x}{2}.$

$S_{MDK}=frac{1}{2}MDcdot DK=frac{1}{2}cdotfrac{x}{2}cdotfrac{x}{2}=frac{1}{8}x^2.$

Площадь треугольника MDK, лежащего в основании новой призмы, составляет $frac{1}{8}$ часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: $V=S_{OCH}cdot h$ , и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен 32:8=4.

Ответ: 4

Докажем полезную теорему.

Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.

Доказательство:

Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.

$S=P_{perp}cdot l.$

Больше задач на формулы объема и площади поверхности здесь.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Формулы объёма и площади поверхности. Многогранники.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Об этой статье

Была ли эта статья полезной?

Объемы геометрических тел

Объемы геометрических тел

Определение объема

Примеры

Объем призмы

Объем пирамиды

Объем цилиндра

Объем конуса

Объем шара

Площади и объемы многогранников

Что такое многогранник

Как найти площадь: формулы

Объем многогранника: формулы

Примеры решения задач

Формулы объёма и площади поверхности. Многогранники.

Не пропустите также: