Нули функции как найти гипербола - AvtoShod.ru - решение различных проблем

Свойства гиперболы

1) Область определения и область значений

По аналитическому заданию функции видно, что х ≠-a, поскольку знаменатель дроби не может ровняться нулю. Таким образом получим:

D(f)=(-∞;-а) U (-a;+∞)

Область значений

Е(f)=(-∞;+∞)

2) Нули функции

Если b=0, то график функции не пересекает ось ОХ;

Если b≠0, то гипербола имеет одну точку пересечения с ОХ:*

x=-(k+ab)/b

3) Промежутки знакопостоянства

Рассмотрим только 2 простых случая, остальные случаи вы можете рассмотреть аналитически самостоятельно по алгоритму из раздела Свойства функций -> Знакопостоянство

Случай 1: a=0, b=0, k>0

f(x)>0, при x ∈ (0; +∞)

f(x)<0, при x ∈ (-∞;0)

Случай 1: a=0, b=0, k<0

f(x)<0, при x ∈ (0; +∞)

f(x)>0, при x ∈ (-∞;0)

4) Промежутки монотонности

Аналогично с промежутками знакопостоянства рассмотрим только 2 случая

Случай 1: a=0, b=0, k>0

Функция убывает при

x ∈ (-∞;0) U (0; +∞)

Функция возрастает при

x ∈ (-∞;0) U (0; +∞)

5) Четность и нечетность

Функция является нечетной при a=0, b=0, то есть если имеет вид y=k/x

Источник

Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).

Математическая гипербола.

Функция заданная формулой (y=frac{k}{x}), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции (y=frac{k}{x}) называют гиперболой. Где х является независимой переменной, а у — зависимой.

Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:

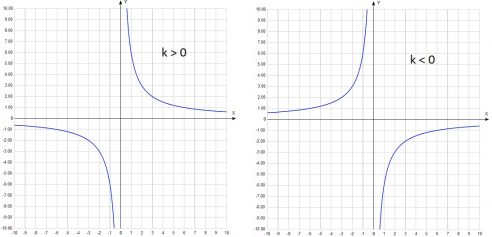
1. Ветви гиперболы. Если k>o, то ветви гиперболы находятся в 1 и 3 четверти. Если k<0, то ветви гиперболы находятся во 2 и 4 четверти.
гипербола, где k>0 ветви гиперболы находятся в 1 и 3 четверти

гипербола, где k<0 ветви гиперболы находятся во 2 и 4 четверти

2.Асимптоты гиперболы. Чтобы найти асимптоты гиперболы необходимо,иногда, уравнение гиперболы упростить. Рассмотрим на примере:
Пример №1:
$$y=frac{1}{x}$$
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х не равен 0.
$$yneqcolor{red} {frac{1}{x}}+0$$
(frac{1}{x}) дробь отбрасываем, для того чтобы найти вторую асимптоту.
Остается простое число
y≠0 это вторая асимптота.
И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.

Пример №2:
$$y=frac{1}{x+2}-1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота

Находим вторую асимптоту.

$$y=color{red} {frac{1}{x+2}}-1$$

Дробь (color{red} {frac{1}{x+2}}) отбрасываем
Остается y≠ -1 это вторая асимптота.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):

Пример №3:

$$begin{align*}
&y=frac{2+x}{1+x} \\
&y=frac{color{red} {1+1}+x}{1+x} \\
&y=frac{1}{1+x}+frac{1+x}{1+x}\\
&y=frac{1}{1+x}+1\\
&y=frac{1}{color{red} {1+x}}+1
end{align*}$$

Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.

Находим вторую асимптоту.

$$y=color{red}{frac{1}{1+x}}+1$$

(color{red}{frac{1}{1+x}}) Дробь убираем.

Остается y≠1 это вторая асимптота.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):

3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:

$$y=frac{1}{x}$$

Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.

4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:

$$y=frac{1}{x}$$

Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.

Вторая ось симметрии это прямая y=-x.

5. Гипербола нечетная функция.

$$f(-x)=frac{1}{-x}=-frac{1}{x}=-f(x)$$

6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:

$$y=frac{-1}{x-1}-1$$

а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.

Находим вторую асимптоту.

$$y=color{red} {frac{-1}{x-1}}-1$$

Дробь (color{red} {frac{-1}{x-1}}) удаляем.

Остается y≠ -1 это вторая асимптота.

б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.

в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5

г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).

д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).

е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).

7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k<0 функция возрастающая.

8. Для более точного построения взять несколько дополнительных точек. Пример смотреть в пункте №6.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
реклама

Источник

Определение

Графиком функции у=kx, где k≠0 число, а х – переменная, является кривая, которую называют гиперболой.

Гипербола имеет две ветви и может располагаться в 1 и 3 координатных четвертях, либо во 2 и 4. Это зависит от знака числа k. Рассмотрим данную кривую на рисунке, где показано ее расположение в зависимости от знака k.

Свойства гиперболы (у=kx)

График функции симметричен относительно начала координат (0;0). Поэтому функцию еще называют – обратная пропорциональность.

Область определения – любое число, кроме нуля.
Область значения – любое число, кроме нуля.
Функция не имеет наибольших или наименьших значений.

Построение графика функции

Для построения графика функции необходимо подбирать несколько положительных и несколько отрицательных значений переменной х, затем подставлять их в заданную функцию для вычисления значений у. После этого по найденным координатам построить точки и соединить их плавной линией. Рассмотрим построение графиков на примерах.

Построить график функции у=10x.

Для этого построим две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число 10 на них делилось

х	1	2	4	5	10
у

х	–1	–2	–4	–5	–10
у

Теперь делим на эти числа 10, получим значения у:

х	1	2	4	5	10
у	10	5	2,5	2	1

х	–1	–2	–4	–5	–10
у	–10	–5	–2,5	–2	–1

Выполняем построение точек, они будут располагаться в первой и третьей координатных четвертях, так как число k положительное.

Теперь для построения гиперболы соединим точки плавной линией.

Построить график функции у=−5x.

Для этого построим также две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число минус 5 на них делилось. Выполняем деление и получаем значения у. При делении обращаем внимание на знаки, чтобы не допускать ошибок.

х	1	2	5	10
у	–5	–2,5	–1	–0,5

х	–1	–2	–5	–10
у	5	2,5	1	0,5

Теперь отмечаем точки во 2 и 4 координатных четвертях (число k отрицательное) и соединяем их для получения ветвей гиперболы.

Задание OM1104o

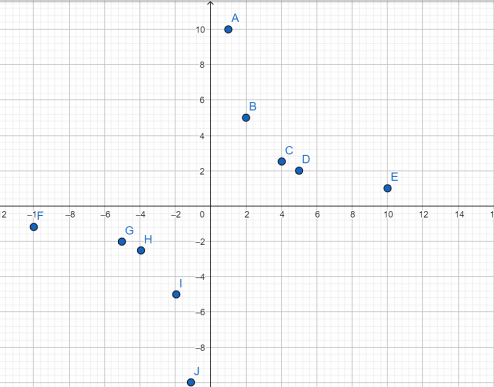
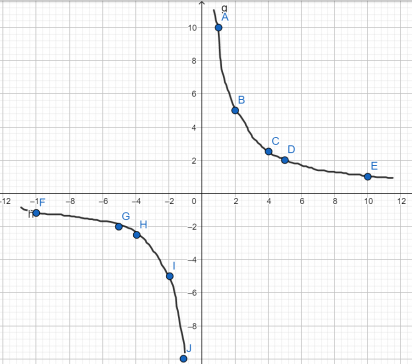
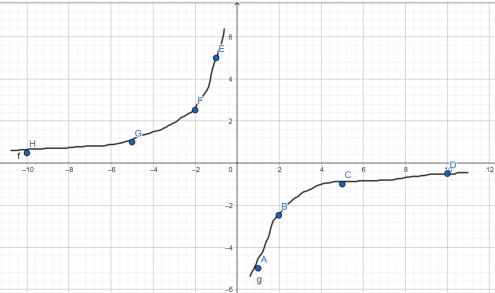
Установите соответствие между графиками функций и формулами, которые их задают.

5oge 1) y = x²

2) y = x/2

3) y = 2/x

Для решения данной задачи необходимо знать вид графиков функций, а именно:

y = x² – парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1

x/2 – прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2

y = 2/x – гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2

Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая – В.

Ответ:

А 1

Б 3

В 2

Ответ: 132

pазбирался: Даниил Романович | обсудить разбор

Задание OM1102o

Установите соответствие между функциями и их графиками.

Функции:

A) y = -3/x

Б) y = 3/x

В) y = 1/(3x)

Графики:

В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.

Общие правила:

если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях

Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.

Второе правило, которым я пользуюсь, звучит так:

чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости

и наоборот:

чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям

Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.

Ответ:

A) 2

Б) 3

В) 1

Ответ: 231

pазбирался: Даниил Романович | обсудить разбор

Даниил Романович | Просмотров: 11.7k

Источник

В данной публикации мы рассмотрим, что такое гипербола, приведем формулу, с помощью которой задается ее функция, а также на практических примерах разберем алгоритм построения данного вида графика.

Определение и функция гиперболы
Алгоритм построения гиперболы
- Пример 1
- Пример 2

Определение и функция гиперболы

Гипербола – это график функции обратной пропорциональности, которая в общем виде задается следующей формулой:

Здесь:

x – независимая переменная;
k ≠ 0;
при k > 0 гипербола расположена в I и III четвертях координатной плоскости;
при k < 0 график находится во II и IV четвертях.

На рисунке ниже изображен пример гиперболы.

Линии графика (зеленым цветом) называются его ветвями.
Оси абсцисс и ординат (Ox и Oy) являются асимптотами гиперболы, т.е. ветви бесконечно к ним приближаются, но никогда их не коснутся и не пересекут.
Ось симметрии (синим цветом) – это прямая:
- y = x (при k > 0)
- y = -x (при k < 0)

Смещение асимптот

Допустим у нас есть функция, заданная формулой:

В этом случае:

x = a – это вертикальная асимптота графика (при a ≠ 0) вместо оси Oy;
y = b – горизонтальная асимптота (при b ≠ 0) вместо оси Ox.

Канонический вид уравнения гиперболы (координатные оси совпадают с осями графика):

Алгоритм построения гиперболы

Пример 1

Дана функция y = ⁴/_x. Построим ее график.

Решение

Так как k > 0, следовательно, гипербола будет находиться в I и III координатных четвертях.

Чтобы построить график, сначала нужно составить таблицу соответствия значений x и y. То есть мы берем конкретное значение x, подставляем его в формулу функции и получаем y.


x	y	Расчет y
0,5	8	⁴ / _0,5 = 8
1	4	⁴ / ₁ = 4
2	2	⁴ / ₂ = 2
4	1	⁴ / ₄ = 1
8	0,5	⁴ / ₈ = 0,5

Теперь отмечаем найденные точки на координатной плоскости и соединяем их плавной линией, которая будет стремиться к осям координат. В итоге получится ветвь гиперболы, расположенная в первой четверти.

Чтобы построить ветвь в третьей четверти, вместо x в формулу подставляем -x. Так мы вычислим значения y.


x	y	Расчет y
-0,5	-8	⁴ / _-0,5 = -8
-1	-4	⁴ / _-1 = -4
-2	-2	⁴ / _-2 = -4
-4	-1	⁴ / _-4 = -1
-8	-0,5	⁴ / _-8 = -0,5

Соединив полученные точки получаем следующий результат. На этом построение гиперболы завершено.

Пример 2

Рассмотренный выше пример был одним из самых простых (без смещения асимптот). Давайте усложним задачу и построим гиперболу, заданную функцией ниже:

Решение

Так как k < 0, график будет располагаться во второй и четвертой четвертях.

Теперь определяемся с асимптотами, в нашем случае это x = 3 и y = 4 (см. информацию выше про их смещение).

Составим таблицу соответствия значений x и y.


x_{II четв.}	y_{II четв.}	x_{IV четв.}	y_{IV четв.}
-1	4,5	3,5	0
1	5	4	2
2	6	5	3
2,5	8	7	3.5

Остается только нанести рассчитанные точки на координатную плоскость и соединить их плавными линиями.

Источник

Нами была рассмотрена функция

y=kx

при (k= 1). Сейчас увидим поведение функции при другом положительном значении (k), например при (k = 4). Таким образом, функция будет иметь вид

y=4x

Заполним таблицу:

(x)	(-8)	(-4)	(-2)	(-1)	(-) 12	12	(1)	(2)	(4)	(8)
(y)	(-) 12	(-1)	(-2)	(-4)	(-8)	(8)	(4)	(2)	(1)	12

Отметим полученные точки на координатной плоскости и соединим их плавной линией (в точке (0) функция не определена, поэтому получили две ветви).

График функции

y=kx

называют гиперболой.

Сейчас рассмотрим случай при (k < 0), например, при (k = — 4). Тогда функция задана формулой

y=−4x

, построим её график.

График функции (y = -f(x)) симметричен графику функции (y = f(x)) относительно оси (x). Таким образом, график функции

y=−4x

симметричен графику

y=4x

относительно оси (x). Получится гипербола, ветви которой находятся во II и IV координатных углах.

Графиком функции

y=kx

(

k≠0

) является гипербола, ветви которой находятся в I и III координатных углах при (k > 0), и во II и IV координатных углах при (k < 0).

Точка ((0; 0)) — центр симметрии гиперболы, оси координат — асимптоты гиперболы.

Две величины (x) и (y) обратно пропорциональны, если выполняется условие(xy = k) (где (k) — число, не равное (0)), следовательно,

y=kx

Функция

y=kx

имеет название — обратная пропорциональность, где число (k) является коэффициентом обратной пропорциональности.

Свойства функции

y=kx

при (k > 0)

Графиком этой функции является гипербола.

1. Область определения функции — все числа, кроме нуля, то есть (x)

≠

(0).

2. (y > 0) при (x > 0); (y < 0) при (x < 0).

3. Промежутки убывания:

−∞;0 и 0;+∞

4. Функция не ограничена ни снизу, ни сверху.

5. Наименьшего значения нет; наибольшего значения нет.

6. Функция непрерывна на промежутках

−∞;0 и 0;+∞

и имеет разрыв при (x = 0).

7. Область значений функции:

−∞;0∪0;+∞

Свойства функции

y=kx

при (k < 0)

Для описания свойств данной функции будем использовать гиперболу (её геометрическую модель).

1. Область определения функции:

−∞;0∪0;+∞

2. (y > 0) при (x < 0); (y < 0) при (x > 0).

3. Возрастает на

−∞;0 и 0;+∞

4. Снизу и сверху не ограничена.

5. Не имеет наименьшего и наибольшего значений.

6. Непрерывна на промежутках

−∞;0 и 0;+∞

7. Область значений функции:

−∞;0∪0;+∞

Источник

Свойства гиперболы (у=kx)

Построение графика функции

Определение и функция гиперболы

Алгоритм построения гиперболы

Пример 1

Пример 2

Не пропустите также: