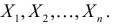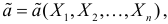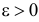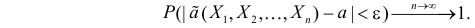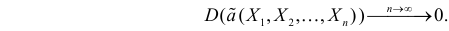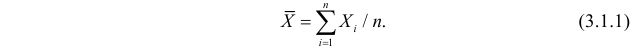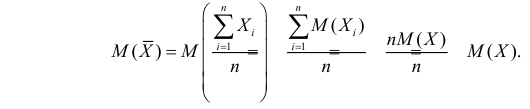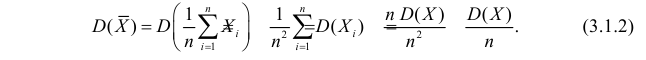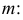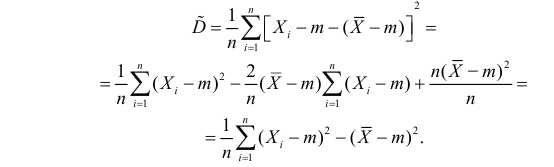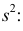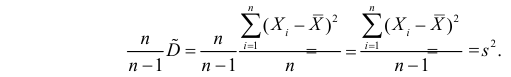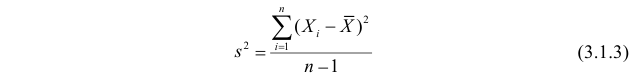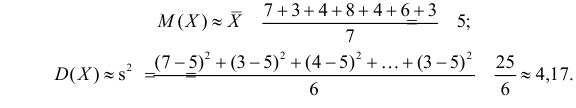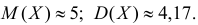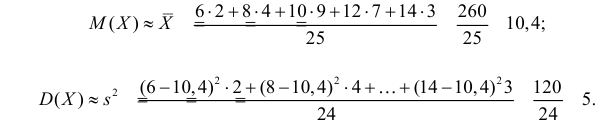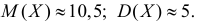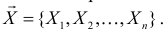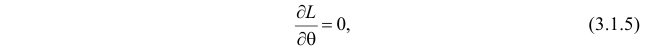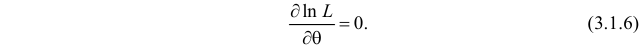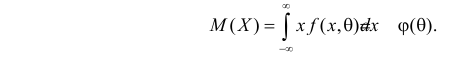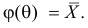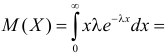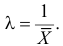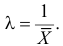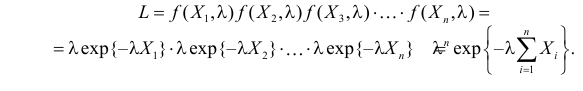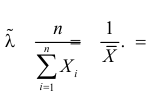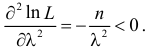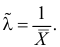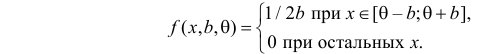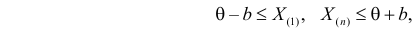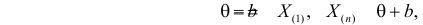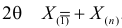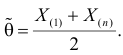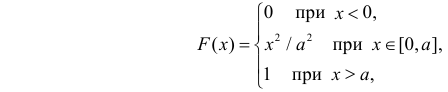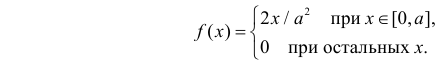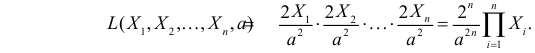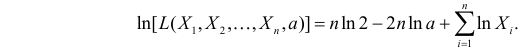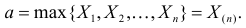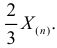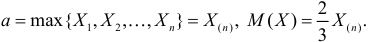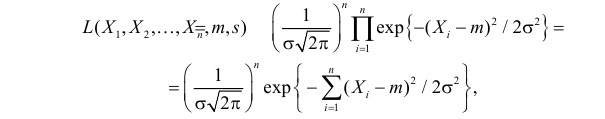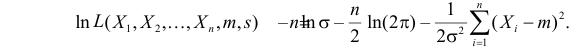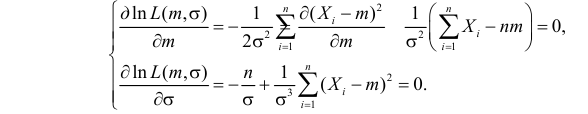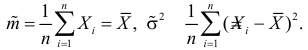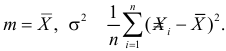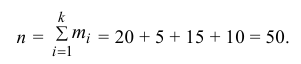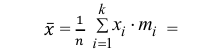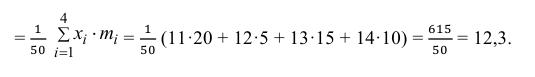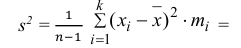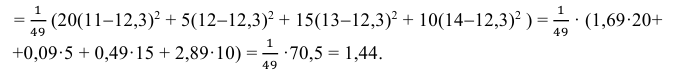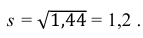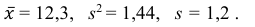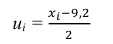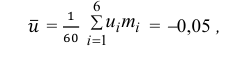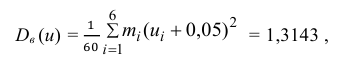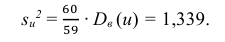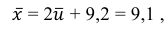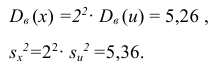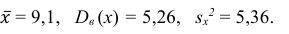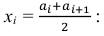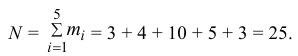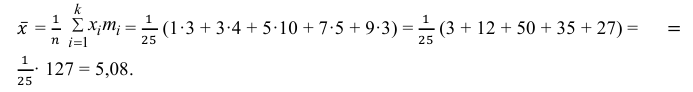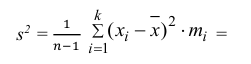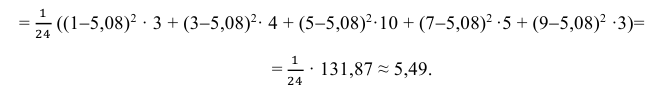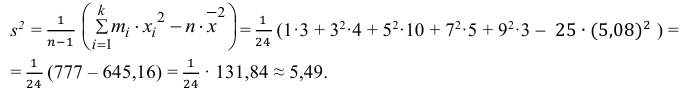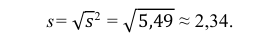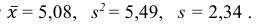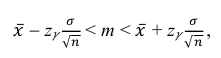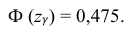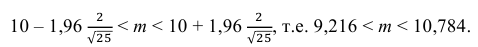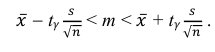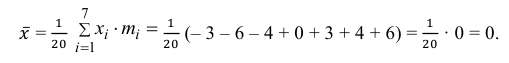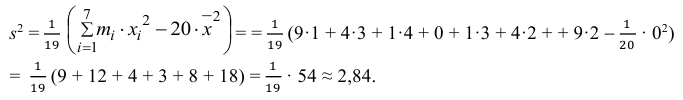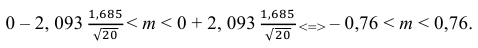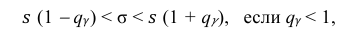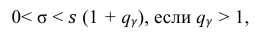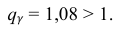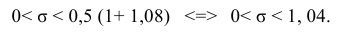Несмещенной
состоятельной, эффективной оценкой для
генерального среднего ā нормального
распределения является выборочное
среднее х,
определяемое
по формуле:
Где х1;
х2;…;хn
– совокупность значений случайных
величин х.
Несмещенную оценку
для среднего квадратического отклонения
определяют по формуле:
где
если a
неизвестно, то по формуле (1):
(1)
если а
известно,
то по формуле (2):
(2)
Значение коэффициента
Мк дается в таблице, где к = n-1, если а
неизвестно, и к = n, если а известно.
При значениях
объема выборок n
> 60 оценку для среднего квадратического
отклонения σ находят по формуле (1), а
если а неизвестно, или по формуле (2),
если а известно.
Несмещенными
оценками для дисперсии σ2
нормального распределения являются
выборочные характеристики:
при неизвестном
а
при известном а
1.14.Оценка среднего квадратического отклонения результата измерения
Среднее квадратическое
отклонение результата измерения
оценивают по формуле:
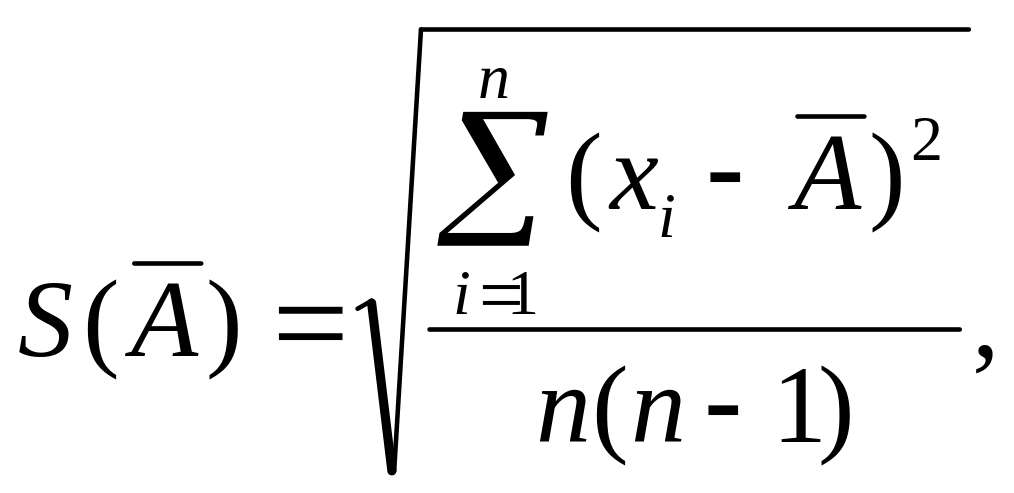
где S(Ã)
– оценка среднего квадратического
отклонения результата измерения;
à – результат
измерения (ср. арифметическое исправленных
результатов наблюдений); хi
– i-й
результат наблюдений.
1.15. Вычисление доверительных границ случайной погрешности результата измерения
Доверительные
границы случайной погрешности результата
измерения устанавливают для результатов
наблюдений, принадлежащих нормальному
распределению. Если это условие не
выполняется, то методы вычисления
доверительного интервала случайной
погрешности должны быть указаны в
методике выполнения конкретных измерений.
Если заранее
известно, что результаты наблюдений
принадлежат нормальному распределению,
доверительные границы Є (без учета
знака) случайной погрешности результата
измерения находят по формуле:
Є=tsS(
)
Где ts
– коэффициент Стьюдента, который в
зависимости от доверительной вероятности
Р и числа результатов наблюдений n
находят по таблицам. При числе наблюдений
n
> 50 для проверки принадлежности их к
нормальному распределению используют
критерий х2
(Пирсона) или ω2
(Мизеса-Смирнова). Если 50 > n
> 15, то используют составной критерий.
1.16. Вычисление доверительных границ погрешности результата измерени3
1
Если отношение
неисключенных систематических
погрешностей к среднему квадратическому
отклонению результата измерения Q/S(Ã)
< 0,8, то неисключенными систематическими
погрешностями пренебрегают и принимают
что граница погрешности результата ∆
= Є. Если Q/S(Ã)
> 8, то пренебрегают случайной погрешностью
и принимают, что граница погрешности
результата Δ = Q.
Однако , следует помнить, что погрешность,
возникающая вследствие пренебрежения
одной из составляющих погрешности
результата измерений при выполнении
указанных неравенств, не должна превышать
15 %. Если неравенства не выполняются, то
границу погрешности результата измерения
находят путем построения композиции
распределений случайных и не исключенных
систематических погрешностей,
рассматриваемых как случайные величины.
В результате
определения доверительных границ
случайных погрешностей, вычисляют
границы погрешности результата измерения
Δ без учета знака по формуле:
Δ = К*SΣ
Где
К – коэффициент, зависящий от соотношения
случайной и неслучайной систематической
погрешностей;
SΣ
– оценка суммарного среднего
квадратического отклонения результата
измерения.
К
оэффициент
К вычисляют по эмпирической формуле:
Суммарное
среднее квадратического отклонение
результата измерения оценивают по
формуле: Є
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Процедура оценки стандартного отклонения из выборки
В статистике и в конкретная статистическая теория, несмещенная оценка стандартного отклонения — это вычисление на основе статистической выборки оценочного значения стандартного отклонения ( мера статистической дисперсии ) совокупности значений таким образом, чтобы ожидаемое значение вычисления равнялось истинному значению. За исключением некоторых важных ситуаций, описанных ниже, задача не имеет большого отношения к приложениям статистики, поскольку ее потребности устраняются стандартными процедурами, такими как использование тестов значимости и доверительных интервалов, или с помощью байесовского анализа.
Однако для статистической теории он предоставляет примерную проблему в контексте теории оценивания, которую легко сформулировать и для которой результаты не могут быть получены в закрытой форме. Он также предоставляет пример, в котором введение требования объективной оценки может рассматриваться как просто добавление неудобств без реальной выгоды.
Содержание
- 1 Предпосылки
- 2 Коррекция смещения
- 2.1 Результаты для нормального распределения
- 2.2 Практическое правило для нормального распределения
- 2.3 Другие распределения
- 3 Эффект автокорреляции (последовательный корреляция)
- 3.1 Пример смещения в стандартном отклонении
- 3.2 Дисперсия среднего
- 3.3 Оценка стандартного отклонения генеральной совокупности
- 3.4 Оценка стандартного отклонения выборочного среднего
- 4 См. также
- 5 Ссылки
- 6 Внешние ссылки
Предпосылки
В статистике стандартное отклонение совокупности чисел часто оценивается как случайная выборка, составленная из населения. Это стандартное отклонение выборки, которое определяется как
- s = ∑ i = 1 n (xi — x ¯) 2 n — 1, { displaystyle s = { sqrt { frac { sum _ {i = 1} ^ {n} (x_ {i} — { overline {x}}) ^ {2}} {n-1}}},}
где {x 1, x 2,…, xn} { displaystyle {x_ {1}, x_ {2}, ldots, x_ {n} }}

Один из способов увидеть, что это смещенная оценка стандартного отклонения генеральной совокупности должно начинаться с того результата, что s является несмещенной оценкой для дисперсии σ базовой совокупности, если такая дисперсия существует и значения выборки построены самостоятельно с заменой. Квадратный корень — это нелинейная функция, и только линейные функции коммутируют с математическим ожиданием. Поскольку квадратный корень является строго вогнутой функцией, из неравенства Дженсена следует, что квадратный корень из выборочной дисперсии является заниженным.
Использование n — 1 вместо n в формуле для выборочной дисперсии известно как поправка Бесселя, которая исправляет систематическую ошибку при оценке дисперсии генеральной совокупности, и некоторые, но не вся систематическая ошибка в оценке стандартного отклонения населения.
Невозможно найти оценку стандартного отклонения, которая была бы несмещенной для всех распределений генеральной совокупности, так как систематическая ошибка зависит от конкретного распределения. Большая часть следующего относится к оценке, предполагающей нормальное распределение.
Коррекция смещения
Результаты для нормального распределения

c 4 { displaystyle c_ {4}}

Если случайная величина нормально распределена, существует небольшая поправка для устранения смещения. Чтобы получить поправку, обратите внимание, что для нормально распределенного X, теорема Кохрана означает, что (n — 1) s 2 / σ 2 { displaystyle (n-1) s ^ {2} / сигма ^ {2}}



- E [s] = c 4 (n) σ { displaystyle operatorname {E} [s] = c_ {4} (n) sigma}
где поправочный коэффициент c 4 (n) { displaystyle c_ {4} (n)}


- c 4 (n) = 2 n — 1 Γ (n 2) Γ (n — 1 2) = 1 — 1 4 n — 7 32 n 2 — 19 128 n 3 + O (n — 4) { displaystyle c_ {4} (n) = { sqrt { frac {2} {n-1}}} { frac { Gamma left ({ frac {n} {2}} right)} { Gamma left ({ frac {n-1} {2}} right)}} = 1 — { frac {1} {4n}} — { frac {7} {32n ^ {2}}} — { frac {19} {128n ^ {3}}} + O (n ^ {- 4})}
где Γ (·) — гамма-функция. Несмещенную оценку σ можно получить, разделив s { displaystyle s}





| Размер выборки | Выражение c 4 { displaystyle c_ {4}} |
Числовое значение |
|---|---|---|
| 2 | 2 π { displaystyle { sqrt { frac {2} { pi}}}} |
0,7978845608 |
| 3 | π 2 { displaystyle { frac { sqrt { pi}} {2}}} |
0,8862269255 |
| 4 | 2 2 3 π { displaystyle 2 { sqrt { frac {2} {3 pi}}}} |
0,9213177319 |
| 5 | 3 4 π 2 { displaystyle { frac {3 } {4}} { sqrt { frac { pi} {2}}}} |
0,9399856030 |
| 6 | 8 3 2 5 π { displaystyle { frac {8} {3}} { sqrt { frac {2} {5 pi}}}} |
0,9515328619 |
| 7 | 5 3 π 16 { displaystyle { frac {5 { sqrt {3 pi}}} {16}}} |
0,9593687891 |
| 8 | 16 5 2 7 π { displaystyle { frac {16} {5}} { sqrt { frac {2} {7 pi}}}} |
0,9650304561 |
| 9 | 35 π 64 { displaystyle { frac {35 { sqrt { pi}}} {64}}} |
0,9693106998 |
| 10 | 128 105 2 π { displaystyle { frac {128} {105}} { sqrt { frac {2} { pi}}}} |
0,9726592741 |
| 100 | 0,9974779761 | |
| 1000 | 0,9997497811 | |
| 10000 | 0,999974 9978 | |
| 2k | 2 π (2 k — 1) 2 2 k — 2 (k — 1)! 2 (2 к — 2)! { displaystyle { sqrt { frac {2} { pi (2k-1)}}} { frac {2 ^ {2k-2} (k-1)! ^ {2}} {(2k-2)!}}} |
|
| 2k + 1 | π k (2 k — 1)! 2 2 к — 1 (к — 1)! 2 { displaystyle { sqrt { frac { pi} {k}}} { frac {(2k-1)!} {2 ^ {2k-1} (k-1)! ^ {2}}} } |
Важно помнить, что эта поправка дает несмещенную оценку только для нормально и независимо распределенного X. Когда это условие удовлетворяется, другой результат о s, включающем c 4 (n) { displaystyle c_ {4 } (n)}

Практическое правило для нормального распределения
Если вычисление функции c 4 (n) кажется слишком сложным, есть простое практическое правило, чтобы использовать оценку
- σ ^ = 1 n — 1,5 ∑ i = 1 n (xi — x ¯) 2 { displaystyle { hat { sigma}} = { sqrt {{ frac {1} {n-1.5}} sum _ {i = 1} ^ {n} (x_ {i} — { overline {x}}) ^ {2 }}}}
Формула отличается от знакомого выражения для s только тем, что в знаменателе стоит n — 1,5 вместо n — 1. Это выражение является приблизительным; фактически
- E [σ ^] = σ ⋅ (1 + 1 16 n 2 + 3 16 n 3 + O (n — 4)). { displaystyle operatorname {E} left [{ hat { sigma}} right] = sigma cdot left (1 + { frac {1} {16n ^ {2}}} + { frac {3} {16n ^ {3}}} + O (n ^ {- 4}) right).}
Смещение относительно невелико: скажем, для n = 3 { displaystyle n = 3 }

Другие распределения
В случаях, когда статистически независимые данные моделируются параметрическим семейством распределений, отличным от нормального распределения, стандартное отклонение совокупности будет, если он существует, зависеть от параметров модели. Один из общих подходов к оценке — максимальное правдоподобие. В качестве альтернативы можно использовать теорему Рао – Блэквелла как путь к нахождению хорошей оценки стандартного отклонения. Ни в том, ни в другом случае полученные оценки обычно не были бы объективными. Теоретически можно получить теоретические поправки, которые приведут к несмещенным оценкам, но, в отличие от поправок для нормального распределения, они обычно будут зависеть от предполагаемых параметров.
Если требуется просто уменьшить систематическую ошибку оцененного стандартного отклонения, а не полностью ее устранить, то доступны два практических подхода, оба в контексте повторной выборки. Это складывание и самозагрузка. Оба могут применяться либо к параметрическим оценкам стандартного отклонения, либо к стандартному отклонению выборки.
Для ненормальных распределений приблизительная (до O (n) членов) формула для несмещенной оценки стандартного отклонения:
- σ ^ = 1 n — 1,5 — 1 4 γ 2 ∑ i = 1 n (xi — x ¯) 2, { displaystyle { hat { sigma}} = { sqrt {{ frac {1} {n-1.5 — { tfrac {1} {4}} gamma _ {2}}} sum _ {i = 1} ^ {n} left (x_ {i} — { overline {x}} right) ^ {2}}},}
где γ 2 обозначает популяцию избыточного эксцесса. Избыточный эксцесс для определенных распределений может быть известен заранее или рассчитан на основе данных.
Эффект автокорреляции (последовательная корреляция)
Приведенный выше материал, чтобы еще раз подчеркнуть, применяется только к независимым данным. Однако реальные данные часто не соответствуют этому требованию; это автокорреляция (также известная как последовательная корреляция). В качестве одного примера, последовательные показания измерительного прибора, который включает в себя некоторую форму процесса «сглаживания» (вернее, низкочастотной фильтрации), будут автокоррелированы, поскольку любое конкретное значение вычисляется из некоторой комбинации более ранних и более поздних показаний.
Оценки дисперсии и стандартного отклонения автокоррелированных данных будут смещены. Ожидаемое значение выборочной дисперсии:
- E [s 2] = σ 2 [1-2 n — 1 ∑ k = 1 n — 1 (1 — kn) ρ k] { displaystyle { rm {E} } left [s ^ {2} right] = sigma ^ {2} left [1 — { frac {2} {n-1}} sum _ {k = 1} ^ {n-1} left (1 — { frac {k} {n}} right) rho _ {k} right]}
где n — размер выборки (количество измерений), а ρ k { displaystyle rho _ {k}}

Пример смещения в стандартном отклонении
Чтобы проиллюстрировать величину смещения в стандартном отклонении, рассмотрим набор данных, который состоит из последовательных считываний из прибор, который использует определенный цифровой фильтр, ACF которого, как известно, задается как
- ρ k = (1 — α) k { displaystyle rho _ {k} = (1- alpha) ^ {k}}
где α — параметр фильтра, принимающий значения от нуля до единицы. Таким образом, ACF положительна и геометрически убывает.

На рисунке показано отношение оцененного стандартного отклонения к его известному значению (которое может быть вычислено аналитически для этого цифрового фильтра) для нескольких настроек α как функции выборки размер n. Изменение α изменяет коэффициент уменьшения дисперсии фильтра, который, как известно, равен
- VRR = α 2 — α { displaystyle { rm {VRR}} = { frac { alpha} {2- alpha}} }
, чтобы меньшие значения α приводили к большему уменьшению дисперсии или «сглаживанию». Смещение указано значениями на вертикальной оси, отличными от единицы; то есть, если бы не было смещения, отношение расчетного стандартного отклонения к известному было бы равно единице. Очевидно, что для небольших размеров выборки может быть значительная систематическая ошибка (в два или более раз).
Дисперсия среднего
Часто представляет интерес оценить дисперсию или стандартное отклонение оцененного среднего, а не дисперсию генеральной совокупности. Когда данные автокоррелированы, это оказывает прямое влияние на теоретическую дисперсию выборочного среднего, которая составляет
- V ar [x ¯] = σ 2 n [1 + 2 ∑ k = 1 n — 1 (1 — kn) ρ k]. { displaystyle { rm {Var}} left [{ overline {x}} right] = { frac { sigma ^ {2}} {n}} left [1 + 2 sum _ {k = 1} ^ {n-1} { left (1 — { frac {k} {n}} right) rho _ {k}} right].}
Дисперсия выборочного среднего может затем можно оценить, подставив оценку σ. Одна такая оценка может быть получена из уравнения для E [s], приведенного выше. Сначала определите следующие константы, снова предполагая, что известна ACF:
- γ 1 ≡ 1-2 n — 1 ∑ k = 1 n — 1 (1 — kn) ρ k { displaystyle гамма _ {1} Equiv 1 — { frac {2} {n-1}} sum _ {k = 1} ^ {n-1} { left (1 — { frac {k} {n} } right)} rho _ {k}}
- γ 2 ≡ 1 + 2 ∑ k = 1 n — 1 (1 — kn) ρ k { displaystyle gamma _ {2} Equiv 1 + 2 sum _ {k = 1} ^ {n-1} { left (1 — { frac {k} {n}} right)} rho _ {k}}
так, чтобы
- E [ s 2] = σ 2 γ 1 ⇒ E [s 2 γ 1] = σ 2 { displaystyle { rm {E}} left [s ^ {2} right] = sigma ^ {2} gamma _ {1} Rightarrow { rm {E}} left [{ frac {s ^ {2}} { gamma _ {1}}} right] = sigma ^ {2}}
Здесь сказано что ожидаемое значение величины, полученной путем деления наблюдаемой дисперсии выборки на поправочный коэффициент γ 1 { displaystyle gamma _ {1}}
- V ar [x ¯] = σ 2 n γ 2 { displaystyle { rm {Var}} left [{ overline {x}} right] = { frac { sigma ^ {2}} {n}} gamma _ {2}}
и подставив оценку вместо σ 2 { displaystyle sigma ^ {2}}
- V ar [x ¯] = E [s 2 γ 1 (γ 2 n)] = E [s 2 n {n — 1 n γ 2 — 1}] { displaystyle { rm {Var}} left [{ overline {x}} right] = { rm {E}} left [{ frac {s ^ {2}} { gamma _ {1}}} left ({ frac { gamma _ {2}} {n}} right) right] = { rm {E}} left [{ frac {s ^ {2}} {n}} left {{ frac {n-1} {{ frac {n} { gamma _ {2}}} — 1}} right } right]}
, который представляет собой объективную оценку дисперсии среднее значение с точки зрения наблюдаемой дисперсии выборки и известных величин. Обратите внимание, что, если автокорреляции ρ k { displaystyle rho _ {k}}
Оценка стандартного отклонения генеральной совокупности
Имея приведенные выше выражения, включающие дисперсию генеральной совокупности и оценку среднего для этой совокупности, казалось бы Логично просто извлечь квадратный корень из этих выражений, чтобы получить несмещенные оценки соответствующих стандартных отклонений. Однако, поскольку ожидания являются интегралами,
- E [s] ≠ E [s 2] ≠ σ γ 1 { displaystyle { rm {E}} [s] neq { sqrt {{ rm {E}} left [s ^ {2} right]}} neq sigma { sqrt { gamma _ {1}}}}
Вместо этого предположим, что существует функция θ такая, что несмещенная оценка стандартного отклонения можно записать как
- E [s] = σ θ γ 1 ⇒ σ ^ = s θ γ 1 { displaystyle { rm {E}} [s] = sigma theta { sqrt { gamma _ {1}}} Rightarrow { hat { sigma}} = { frac {s} { theta { sqrt { gamma _ {1}}}}}}
и θ зависит от размер выборки n и ACF. В случае данных NID (нормально и независимо распределенных) подкоренное выражение равно единице, а θ — это просто функция c 4, указанная в первом разделе выше. Как и в случае c 4, θ приближается к единице по мере увеличения размера выборки (как и γ 1).
С помощью имитационного моделирования можно продемонстрировать, что игнорирование θ (то есть принятие его за единицу) и использование
- E [s] ≈ σ γ 1 ⇒ σ ^ ≈ s γ 1 { displaystyle { rm {E}} [s] приблизительно sigma { sqrt { gamma _ {1}}} Rightarrow { hat { sigma}} приблизительно { frac {s} { sqrt { gamma _ {1}}}}}
удаляет все, кроме нескольких процентов смещения, вызванного автокорреляцией, что делает его оценкой с уменьшенным смещением, а не несмещенной оценкой. В практических ситуациях измерения это уменьшение систематической ошибки может быть значительным и полезным, даже если сохраняется относительно небольшая погрешность. Рисунок выше, показывающий пример смещения стандартного отклонения в зависимости от размера выборки, основан на этом приближении; фактическое смещение будет несколько больше, чем указано на этих графиках, поскольку смещение преобразования θ туда не включено.
Оценка стандартного отклонения выборочного среднего
Несмещенная дисперсия среднего в терминах дисперсии генеральной совокупности и ACF определяется как
- V ar [x ¯] = σ 2 n γ 2 { displaystyle { rm {Var}} left [{ overline {x}} right] = { frac { sigma ^ {2}} {n}} gamma _ {2}}
и поскольку здесь нет ожидаемых значений, в этом случае можно взять квадратный корень, так что
- σ x ¯ = σ n γ 2 { displaystyle sigma _ { overline {x}} = { frac { sigma} { sqrt {n}}} { sqrt { gamma _ {2}}}}
Используя выражение для несмещенной оценки выше для σ, оценка стандартного отклонения тогда среднее значение будет
- σ ^ x ¯ = s θ n γ 2 γ 1 { displaystyle { hat { sigma}} _ { overline {x}} = { frac {s} { theta { sqrt {n}}}} { frac { sqrt { gamma _ {2}}} { sqrt { gamma _ {1}}}}}
Если данные имеют NID, так что ACF исчезает, это сокращается до
- σ ^ x ¯ = sc 4 n { displaystyle { hat { sigma}} _ { overline {x}} = { frac {s} {c_ {4} { sqrt {n}}}}}
При наличии ненулевой ACF, i Наблюдение за функцией θ, как и раньше, приводит к оценке с уменьшенным смещением
- σ ^ x ¯ ≈ sn γ 2 γ 1 = snn — 1 n γ 2 — 1 { displaystyle { hat { sigma}} _ { overline {x}} приблизительно { frac {s} { sqrt {n}}} { frac { sqrt { gamma _ {2}}} { sqrt { gamma _ {1}}}} = { frac {s} { sqrt {n}}} { sqrt { frac {n-1} {{ frac {n} { gamma _ {2}}} — 1}}}}
который снова можно продемонстрировать, что устраняет значительную часть систематической ошибки.
См. Также
- Поправка Бесселя
- Оценка ковариационных матриц
- Выборочное среднее и выборочная ковариация
Ссылки
- Дуглас С. Монтгомери и Джордж К. Рангер, Прикладная статистика и вероятность для Engineers, 3-е издание, Wiley and sons, 2003. (см. Разделы 7–2.2 и 16–5)
Внешние ссылки
- A Интерактивная графика Java, показывающая PDF-файл Helmert, из которого получены коэффициенты коррекции смещения.
- Демонстрация моделирования Монте-Карло для объективной оценки стандартного отклонения.
- http://www.itl.nist.gov/div898/handbook/pmc/section3/pmc32.htm Что такое контрольные диаграммы переменных?
Эта статья включает материалы, являющиеся общественным достоянием, с веб-сайта Национального института стандартов и технологий https://www.nist.gov.
In statistics and in particular statistical theory, unbiased estimation of a standard deviation is the calculation from a statistical sample of an estimated value of the standard deviation (a measure of statistical dispersion) of a population of values, in such a way that the expected value of the calculation equals the true value. Except in some important situations, outlined later, the task has little relevance to applications of statistics since its need is avoided by standard procedures, such as the use of significance tests and confidence intervals, or by using Bayesian analysis.
However, for statistical theory, it provides an exemplar problem in the context of estimation theory which is both simple to state and for which results cannot be obtained in closed form. It also provides an example where imposing the requirement for unbiased estimation might be seen as just adding inconvenience, with no real benefit.
Motivation[edit]
In statistics, the standard deviation of a population of numbers is often estimated from a random sample drawn from the population. This is the sample standard deviation, which is defined by
where 

One way of seeing that this is a biased estimator of the standard deviation of the population (if that exists and the samples are drawn independently with replacement) is that already s2 is an estimator of the population variance σ2 with a low bias. Because only linear functions commute with taking expectations and the square root is a strictly concave function, it follows from Jensen’s inequality that the square root of the sample variance also has a low bias.
The use of n − 1 instead of n in the formula for the sample variance is known as Bessel’s correction, and it gives
It corrects the bias in the estimation of the population variance, and some, but not all of the bias in the estimation of the population standard deviation.
It is not possible to find an estimate of the standard deviation which is unbiased for all population distributions, as the bias depends on the particular distribution. Much of the following relates to estimation assuming a normal distribution.
Bias correction[edit]
Results for the normal distribution[edit]
Correction factor 
When the random variable is normally distributed, a minor correction exists to eliminate the bias. To derive the correction, note that for normally distributed X, Cochran’s theorem implies that 



where the correction factor 


where Γ(·) is the gamma function. An unbiased estimator of σ can be obtained by dividing 





| Sample size | Expression of 
|
Numerical value |
|---|---|---|
| 2 | 
|
0.7978845608 |
| 3 | 
|
0.8862269255 |
| 4 | 
|
0.9213177319 |
| 5 | 
|
0.9399856030 |
| 6 | 
|
0.9515328619 |
| 7 | 
|
0.9593687891 |
| 8 | 
|
0.9650304561 |
| 9 | 
|
0.9693106998 |
| 10 | 
|
0.9726592741 |
| 100 | 0.9974779761 | |
| 1000 | 0.9997497811 | |
| 10000 | 0.9999749978 | |
| 2k | 
|
|
| 2k+1 | 
|
It is important to keep in mind this correction only produces an unbiased estimator for normally and independently distributed X. When this condition is satisfied, another result about s involving 


Rule of thumb for the normal distribution[edit]
If calculation of the function c4(n) appears too difficult, there is a simple rule of thumb[4] to take the estimator
The formula differs from the familiar expression for s2 only by having n − 1.5 instead of n − 1 in the denominator. This expression is only approximate; in fact,
The bias is relatively small: say, for 

Other distributions[edit]
In cases where statistically independent data are modelled by a parametric family of distributions other than the normal distribution, the population standard deviation will, if it exists, be a function of the parameters of the model. One general approach to estimation would be maximum likelihood. Alternatively, it may be possible to use the Rao–Blackwell theorem as a route to finding a good estimate of the standard deviation. In neither case would the estimates obtained usually be unbiased. Notionally, theoretical adjustments might be obtainable to lead to unbiased estimates but, unlike those for the normal distribution, these would typically depend on the estimated parameters.
If the requirement is simply to reduce the bias of an estimated standard deviation, rather than to eliminate it entirely, then two practical approaches are available, both within the context of resampling. These are jackknifing and bootstrapping. Both can be applied either to parametrically based estimates of the standard deviation or to the sample standard deviation.
For non-normal distributions an approximate (up to O(n−1) terms) formula for the unbiased estimator of the standard deviation is
where γ2 denotes the population excess kurtosis. The excess kurtosis may be either known beforehand for certain distributions, or estimated from the data.
Effect of autocorrelation (serial correlation)[edit]
The material above, to stress the point again, applies only to independent data. However, real-world data often does not meet this requirement; it is autocorrelated (also known as serial correlation). As one example, the successive readings of a measurement instrument that incorporates some form of “smoothing” (more correctly, low-pass filtering) process will be autocorrelated, since any particular value is calculated from some combination of the earlier and later readings.
Estimates of the variance, and standard deviation, of autocorrelated data will be biased. The expected value of the sample variance is[5]
where n is the sample size (number of measurements) and 

Example of bias in standard deviation[edit]
To illustrate the magnitude of the bias in the standard deviation, consider a dataset that consists of sequential readings from an instrument that uses a specific digital filter whose ACF is known to be given by
where α is the parameter of the filter, and it takes values from zero to unity. Thus the ACF is positive and geometrically decreasing.
Bias in standard deviation for autocorrelated data.
The figure shows the ratio of the estimated standard deviation to its known value (which can be calculated analytically for this digital filter), for several settings of α as a function of sample size n. Changing α alters the variance reduction ratio of the filter, which is known to be
so that smaller values of α result in more variance reduction, or “smoothing.” The bias is indicated by values on the vertical axis different from unity; that is, if there were no bias, the ratio of the estimated to known standard deviation would be unity. Clearly, for modest sample sizes there can be significant bias (a factor of two, or more).
Variance of the mean[edit]
It is often of interest to estimate the variance or standard deviation of an estimated mean rather than the variance of a population. When the data are autocorrelated, this has a direct effect on the theoretical variance of the sample mean, which is[7]
The variance of the sample mean can then be estimated by substituting an estimate of σ2. One such estimate can be obtained from the equation for E[s2] given above. First define the following constants, assuming, again, a known ACF:
so that
This says that the expected value of the quantity obtained by dividing the observed sample variance by the correction factor 
and substituting the estimate for 
which is an unbiased estimator of the variance of the mean in terms of the observed sample variance and known quantities. If the autocorrelations 
Estimating the standard deviation of the population[edit]
Having the expressions above involving the variance of the population, and of an estimate of the mean of that population, it would seem logical to simply take the square root of these expressions to obtain unbiased estimates of the respective standard deviations. However it is the case that, since expectations are integrals,
Instead, assume a function θ exists such that an unbiased estimator of the standard deviation can be written
and θ depends on the sample size n and the ACF. In the case of NID (normally and independently distributed) data, the radicand is unity and θ is just the c4 function given in the first section above. As with c4, θ approaches unity as the sample size increases (as does γ1).
It can be demonstrated via simulation modeling that ignoring θ (that is, taking it to be unity) and using
removes all but a few percent of the bias caused by autocorrelation, making this a reduced-bias estimator, rather than an unbiased estimator. In practical measurement situations, this reduction in bias can be significant, and useful, even if some relatively small bias remains. The figure above, showing an example of the bias in the standard deviation vs. sample size, is based on this approximation; the actual bias would be somewhat larger than indicated in those graphs since the transformation bias θ is not included there.
Estimating the standard deviation of the sample mean[edit]
The unbiased variance of the mean in terms of the population variance and the ACF is given by
and since there are no expected values here, in this case the square root can be taken, so that
Using the unbiased estimate expression above for σ, an estimate of the standard deviation of the mean will then be
If the data are NID, so that the ACF vanishes, this reduces to
In the presence of a nonzero ACF, ignoring the function θ as before leads to the reduced-bias estimator
which again can be demonstrated to remove a useful majority of the bias.
See also[edit]
- Bessel’s correction
- Estimation of covariance matrices
- Sample mean and sample covariance
References[edit]
- ^ Ben W. Bolch, «More on unbiased estimation of the standard deviation», The American Statistician, 22(3), p. 27 (1968)
- ^ Duncan, A. J., Quality Control and Industrial Statistics 4th Ed., Irwin (1974) ISBN 0-256-01558-9, p.139
- ^ * N.L. Johnson, S. Kotz, and N. Balakrishnan, Continuous Univariate Distributions, Volume 1, 2nd edition, Wiley and sons, 1994. ISBN 0-471-58495-9. Chapter 13, Section 8.2
- ^ Richard M. Brugger, «A Note on Unbiased Estimation on the Standard Deviation», The American Statistician (23) 4 p. 32 (1969)
- ^ Law and Kelton, Simulation Modeling and Analysis, 2nd Ed. McGraw-Hill (1991), p.284, ISBN 0-07-036698-5. This expression can be derived from its original source in Anderson, The Statistical Analysis of Time Series, Wiley (1971), ISBN 0-471-04745-7, p.448, Equation 51.
- ^ Law and Kelton, p.286. This bias is quantified in Anderson, p.448, Equations 52–54.
- ^ Law and Kelton, p.285. This equation can be derived from Theorem 8.2.3 of Anderson. It also appears in Box, Jenkins, Reinsel, Time Series Analysis: Forecasting and Control, 4th Ed. Wiley (2008), ISBN 978-0-470-27284-8, p.31.
- ^ Law and Kelton, p.285
- Douglas C. Montgomery and George C. Runger, Applied Statistics and Probability for Engineers, 3rd edition, Wiley and sons, 2003. (see Sections 7–2.2 and 16–5)
External links[edit]
- A Java interactive graphic showing the Helmert PDF from which the bias correction factors are derived.
- Monte-Carlo simulation demo for unbiased estimation of standard deviation.
- http://www.itl.nist.gov/div898/handbook/pmc/section3/pmc32.htm What are Variables Control Charts?
This article incorporates public domain material from the National Institute of Standards and Technology.
Содержание:
Точечные оценки:
Пусть случайная величина имеет неизвестную характеристику а. Такой характеристикой может быть, например, закон распределения, математическое ожидание, дисперсия, параметр закона распределения, вероятность определенного значения случайной величины и т.д. Пронаблюдаем случайную величину n раз и получим выборку из ее возможных значений
Существует два подхода к решению этой задачи. Можно по результатам наблюдений вычислить приближенное значение характеристики, а можно указать целый интервал ее значений, согласующихся с опытными данными. В первом случае говорят о точечной оценке, во втором – об интервальной.
Определение. Функция результатов наблюдений
Для одной и той же характеристики можно предложить разные точечные оценки. Необходимо иметь критерии сравнения оценок, для суждения об их качестве. Оценка 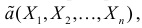
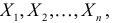
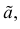
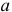
Определение. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемой величине: 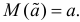
Определение. Оценка называется состоятельной, если при увеличении числа наблюдений она сходится по вероятности к оцениваемой величине, т.е. для любого сколь угодно малого
Если известно, что оценка 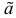
Последнее условие удобно для проверки. В качестве меры разброса значений оценки 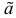
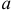
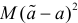
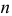
Следует отметить, что несмещенность и состоятельность являются желательными свойствами оценок, но не всегда разумно требовать наличия этих свойств у оценки. Например, может оказаться предпочтительней оценка хотя и обладающая небольшим смещением, но имеющая значительно меньший разброс значений, нежели несмещенная оценка. Более того, есть характеристики, для которых нет одновременно несмещенных и состоятельных оценок.
Оценки для математического ожидания и дисперсии
Пусть случайная величина имеет неизвестные математическое ожидание и дисперсию, причем 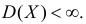
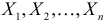
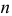
Несмещенность такой оценки следует из равенств
В силу независимости наблюдений
При условии 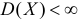
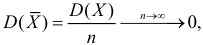
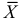
Доказано, что для математического ожидания нормально распределенной случайной величины оценка 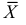
Оценка математического ожидания посредством среднего арифметического наблюдаемых значений наводит на мысль предложить в качестве оценки для дисперсии величину
Преобразуем величину 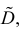
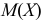
В силу (3.1.2) имеем 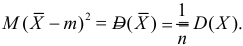
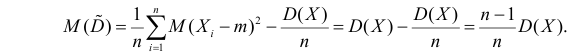
Последняя запись означает, что оценка 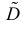
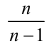
Величина
является несмещенной и состоятельной оценкой дисперсии.
Пример:
Оценить математическое ожидание и дисперсию случайной величины Х по результатам ее независимых наблюдений: 7, 3, 4, 8, 4, 6, 3.
Решение. По формулам (3.1.1) и (3.1.3) имеем
Ответ.
Пример:
Данные 25 независимых наблюдений случайной величины представлены в сгруппированном виде:
Требуется оценить математическое ожидание и дисперсию этой случайной величины.
Решение. Представителем каждого интервала можно считать его середину. С учетом этого формулы (3.1.1) и (3.1.3) дают следующие оценки:
Ответ.
Метод наибольшего правдоподобия для оценки параметров распределений
В теории вероятностей и ее приложениях часто приходится иметь дело с законами распределения, которые определяются некоторыми параметрами. В качестве примера можно назвать нормальный закон распределения 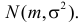
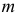
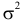
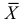
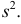
Пусть случайная величина Х имеет функцию распределения 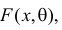
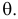
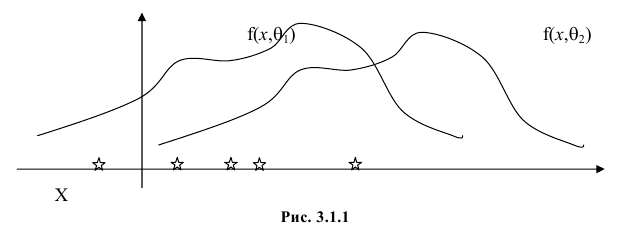
Продемонстрируем идею метода наибольшего правдоподобия на упрощенном примере. Пусть по результатам наблюдений, отмеченных на рис. 3.1.1 звездочками, нужно отдать предпочтение одной из двух функций плотности вероятности 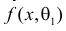
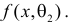
Из рисунка видно, что при значении параметра 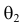
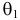
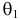
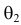
Этот принцип приводит к следующему способу действий. Пусть закон распределения случайной величины Х зависит от неизвестного значения параметра 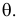
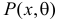
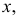
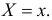
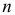
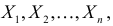
называют функцией правдоподобия. Величина 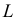
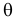
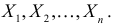
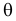


Сформулированный принцип предлагает в качестве оценки значения параметра выбрать такое 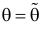

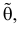
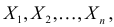
Во многих случаях, когда 
которое следует из необходимого условия экстремума. Поскольку 
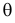

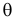
Это уравнение называют уравнением правдоподобия. Им пользоваться удобнее, чем уравнением (3.1.5), так как функция 


Если параметров несколько (многомерный параметр), то следует взять частные производные от функции правдоподобия по всем параметрам, приравнять частные производные нулю и решить полученную систему уравнений.
Оценку, получаемую в результате поиска максимума функции правдоподобия, называют еще оценкой максимального правдоподобия.
Известно, что оценки максимального правдоподобия состоятельны. Кроме того, если для q существует эффективная оценка, то уравнение правдоподобия имеет единственное решение, совпадающее с этой оценкой. Оценка максимального правдоподобия может оказаться смещенной.
Метод моментов
Начальным моментом 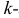
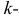
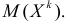
Центральным моментом 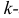
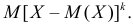
Для оценки параметров распределения по методу моментов находят на основе опытных данных оценки моментов в количестве, равном числу оцениваемых параметров. Эти оценки приравнивают к соответствующим теоретическим моментам, величины которых выражены через параметры. Из полученной системы уравнений можно определить искомые оценки.
Например, если Х имеет плотность распределения 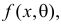
Если воспользоваться величиной 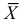
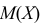
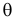
Пример:
Найти оценку параметра показательного закона распределения по методу моментов.
Решение. Плотность вероятности показательного закона распределения имеет вид 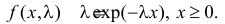
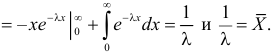
Ответ.
Пример:
Пусть имеется простейший поток событий неизвестной интенсивности 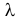
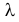
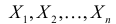

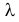
Решение. В простейшем потоке интервалы времени между последовательными моментами наступления событий потока имеют показательный закон распределения 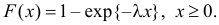
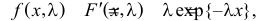
Тогда 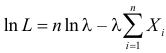
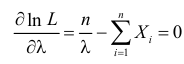
При таком значении 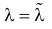
Ответ.
Определение. Пусть 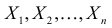
В этой записи 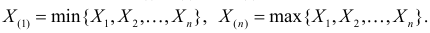
Величины 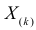
Пример:
Случайная величина Х имеет равномерное распределение на отрезке 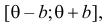


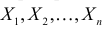


Решение. Функция плотности вероятности величины Х имеет вид
В этом случае функция правдоподобия 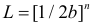




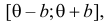
где 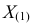
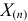

откуда 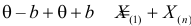
Оценкой наибольшего правдоподобия для параметра 
Ответ.
Пример:
Случайная величина X имеет функцию распределения
где 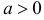
Пусть 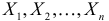

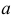
Решение. Для построения функции правдоподобия найдем сначала функцию плотности вероятности
Тогда функция правдоподобия:
Логарифмическая функция правдоподобия:
Уравнение правдоподобия
не имеет решений. Критических точек нет. Наибольшее и наименьшее значения 

По виду функции 



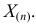
Так как 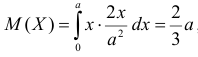
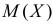
Ответ.
Пример:
Случайная величина Х имеет нормальный закон распределения 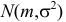
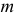
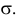
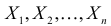
Решение. В соответствии с (3.1.4) функция правдоподобия имеет вид
а логарифмическая функция правдоподобия:
Необходимые условия экстремума дают систему двух уравнений:
Решения этой системы имеют вид:
Отметим, что обе оценки являются состоятельными, причем оценка для 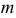
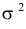
Ответ.
Пример:
По данным эксперимента построен статистический ряд:
Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения случайной величины X.
Решение. 1) Число экспериментальных данных вычисляется по формуле:
Значит, объем выборки n = 50.
2) Вычислим среднее арифметическое значение эксперимента:
Значит, найдена оценка математического ожидания 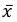
3) Вычислим исправленную выборочную дисперсию:
Значит, найдена оценка дисперсии: 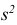
5) Вычислим оценку среднего квадратического отклонения:
Ответ:
Пример:
По данным эксперимента построен статистический ряд:
Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения случайной величины X.
Решение. По формуле
перейдем к условным вариантам:
Для них произведем расчет точечных оценок параметров:
Следовательно, вычисляем искомые точечные оценки:
Ответ:
Пример:
По данным эксперимента построен интервальный статистический ряд:
Найти оценки математического ожидания, дисперсии и среднего квадратического отклонения.
Решение. 1) От интервального ряда перейдем к статистическому ряду, заменив интервалы их серединами
2) Объем выборки вычислим по формуле:
3) Вычислим среднее арифметическое значений эксперимента:
3) Вычислим исправленную выборочную дисперсию:
Можно было воспользоваться следующей формулой:
5) Вычислим оценку среднего квадратического отклонения:
Ответ:
Пример:
Найти доверительный интервал с надежностью 0,95 для оценки математического ожидания M(X) нормально распределенной случайной величины X, если известно среднее квадратическое отклонение σ = 2, оценка математического ожидания 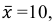
Решение. Доверительный интервал для истинного математического ожидания с доверительной вероятностью 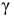
где m = M(X) – истинное математическое ожидание; 𝑥̅ − оценка M(X) по выборке; n – объем выборки; 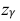
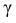
Из табл. П 2.2 приложения 2 находим: 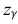
Ответ: (9,216 ; 10,784).
Пример:
По данным эксперимента построен статистический ряд:
Найти доверительный интервал для математического ожидания M (X) с надежностью 0,95.
Решение. Воспользуемся формулой для доверительного интервала математического ожидания при неизвестной дисперсии:
где n – объем выборки; 𝑥̅ оценка M(X); s – оценка среднего квадратического отклонения; 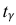
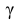
По числам 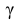
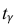
Теперь вычисляем оценки для M(X) и D(X):
Следовательно, s ≈ 1,685. Поэтому искомый доверительный интервал математического ожидания задается формулой:
Ответ: (– 0,76; 0,76).
Пример:
По данным десяти независимых измерений найдена оценка квадратического отклонения 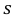
Решение. Задача сводится к нахождению доверительного интервала для истинного квадратического отклонения, так как точность прибора характеризуется средним квадратическим отклонением случайных ошибок измерений.
Доверительный интервал для среднего квадратического отклонения находим по формуле:
где 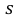
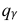
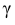
Находим:
Тогда можно записать:
Ответ: (0; 1,04).
- Доверительный интервал для вероятности события
- Проверка гипотезы о равенстве вероятностей
- Доверительный интервал для математического ожидания
- Доверительный интервал для дисперсии
- Системы случайных величин
- Вероятность и риск
- Определения вероятности событий
- Предельные теоремы теории вероятностей

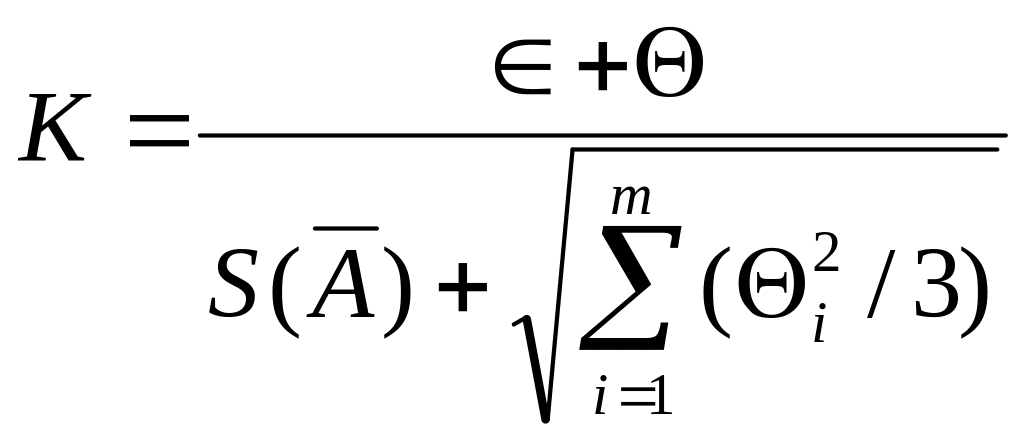

![{ displaystyle operatorname {E} [s] = c_ {4} (n) sigma}](https://wikimedia.org/api/rest_v1/media/math/render/svg/087c663bb5db8a4e93f3306024fa09be9e78786a)


![{ displaystyle operatorname {E} left [{ hat { sigma}} right] = sigma cdot left (1 + { frac {1} {16n ^ {2}}} + { frac {3} {16n ^ {3}}} + O (n ^ {- 4}) right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a125feb9c843e27c546b6752e80c8973493e3d7c)

![{ displaystyle { rm {E}} left [s ^ {2} right] = sigma ^ {2} left [1 - { frac {2} {n-1}} sum _ {k = 1} ^ { n-1} left (1 - { frac {k} {n}} right) rho _ {k} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b6c5f0408430fef974dcd29e6c40e5268a326a8)


![{ displaystyle { rm {Var}} left [{ overline {x}} right] = { frac { sigma ^ {2}} {n}} left [1 + 2 sum _ {k = 1} ^ {n-1} { left (1 - { frac {k} {n}} справа) rho _ {k}} right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d01fbd671b0ddcddc7c9a19b861f90790b048e42)


![{ displaystyle { rm {E}} left [s ^ {2} right] = sigma ^ {2} gamma _ {1} Rightarrow { rm {E}} left [{ frac {s ^ {2}} { gamma _ {1}}} right] = sigma ^ {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/514fd2e6fda33312717fd83431183719bfe31c84)
![{ displaystyle { rm {Var}} left [{ overline {x}} right] = { frac { sigma ^ {2}} {n}} gamma _ {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fdb847ca3b6eea0a8b668aea64deb62662ce761)
![{ displaystyle { rm {Var}} left [{ overline {x}} right] = { rm {E}} left [{ frac {s ^ {2}} { gamma _ {1}}} left ({ frac { gamma _ {2}} {n}} right) right] = { rm {E}} left [{ гидроразрыв {s ^ {2}} {n}} left {{ frac {n-1} {{ frac {n} { gamma _ {2 }}} - 1}} right } right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2d000e5afc787aeaa30dbbae65a8d88243aa47c)
![{ displaystyle { rm {E}} [ s] neq { sqrt {{ rm {E}} left [s ^ {2} right]}} neq sigma { sqrt { gamma _ {1}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/12b6b81c4ab7fd8b53ee4e88867ea94085f1a4f4)
![{ displaystyle { rm {E}} [s] = sigma theta { sqrt { gamma _ {1}}} Rightarrow { hat { sigma}} = { frac {s} { theta { sqrt { gamma _ {1}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4074f525fe722e999fab660492a17360bc7a756b)
![{ displaystyle { rm {E}} [s] приблизительно sigma { sqrt { gamma _ {1}}} Rightarrow { hat { sigma}} приблизительно { frac {s} { sqrt { gamma _ {1}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbb590234c6b806b2f4b15e5e29c9542c24ab8f8)