Всего: 40 1–20 | 21–40
Добавить в вариант
Тип 18 № 40
i
Найдите тангенс угла AOB, изображенного на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB.
Найдите тангенс угла AOB, в треугольнике, изображённом на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB. Размер клетки 1 × 1.
Найдите тангенс угла AOB.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB
Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс AOB
Всего: 40 1–20 | 21–40
№8. Найдите тангенс угла AOB, изображенного на рисунке.
Решение:
Опустим перпендикуляр AH на сторону OB.
Рассмотрим прямоугольный △ A O H :
Тангенс угла – отношение противолежащего катета к прилежащему.
tg ∠ A O H = A H O H = 4 2 = 2
Ответ: 2
№9. Найдите тангенс угла A треугольника ABCб изображённого на рисунке.
Решение:
Тангенс угла – это отношение противолежащего катета к прилежащему.
tg ∠ B A C = B C A C = 2 5 = 0,4
Ответ: 0,4
№10. На рисунке изображена трапеция ABCD. Используя рисунок, найдите sin ∠ B A H .
Решение:
Рассмотрим прямоугольный △ A B H :
Синус угла – отношение противолежащего катета к гипотенузе.
sin ∠ A = B H A B
Найдем AB по теореме Пифагора:
A B 2 = A H 2 + B H 2
A B 2 = 3 2 + 4 2
A B 2 = 9 + 16 = 25
A B = ± 25 = [ − 5 не подходит 5 подходит
A B = 5
sin ∠ A = B H A B = 4 5 = 0,8
Ответ: 0,8
№11. На рисунке изображен ромб ABCD. Используя рисунок, найдите tg ∠ O B C .
Решение:
Тангенс угла – это отношение противолежащего катета к прилежащему.
tg ∠ O B C = O C B O = 3 4 = 0,75
Ответ: 0,75
№12. На рисунке изображена трапеция ABCD. Используя рисунок, найдите cos ∠ H B A .
Решение:
Рассмотрим прямоугольный △ A B H :
Косинус угла – отношение прилежащего катета к гипотенузе.
cos ∠ A B H = B H A B
Найдем A B по теореме Пифагора:
A B 2 = A H 2 + B H 2
A B 2 = 6 2 + 8 2
A B 2 = 36 + 64 = 100
A B = ± 100 = [ − 10 не подходит 10 подходит
A B = 10
cos ∠ A B H = B H A B = 8 10 = 0,8
Ответ: 0,8
№13. Найдите тангенс угла, изображенного на рисунке.
Решение:
tg β = tg ( 180 ° − α ) = − tg α
Рассмотрим прямоугольный △ B C H .
Тангенс угла – отношение противолежащего катета к прилежащему.
tg α = C H B H = 3 1
tg β = − tg α = − 3
Ответ: -3
№14. Найдите тангенс угла AOB.
Решение:
Опустим высоту BH на сторону OA.
Рассмотрим прямоугольный △ O B H :
tg ∠ O = B H O H
Найдем B H и O H по теореме Пифагора:
B H 2 = 2 2 + 8 2 = = 4 + 64 = 68
B H = ± 68 = ± 4 ⋅ 17 = ± 4 ⋅ 17 = ± 2 17 = [ − 2 17 не подходит 2 17 подходит
B H = 2 17
O H 2 = 1 2 + 4 2 = 1 + 16 = 17
O H = ± 17 = [ − 17 не подходит 17 подходит
O H = 17
tg ∠ O = B H O H = 2 17 17 = 2
Ответ: 2
Обычно в задачах требуется найти тангенс именно острого угла, как, допустим, на этом примере:
Для этого мы строим прямоугольный треугольник, проведя линию (перпендикуляр) BD:
Далее вспоминаем определение тангенса, это отношение противолежащего катета к прилежащему.
То есть tg(BOA) = DB / DO.
Чтобы найти DO и DB достаточно будет посчитать количество клеточек.
DO = 2.
DB = 5.
Значит, tg(BOA) = 5 / 2 = 2,5.
Зная тангенс, мы можем легко найти и котангенс:
ctg(BOA) = 1 / tg(BOA) = 1 / 2,5 = 0,4.
_
А вот задача на нахождение тангенса угла по клеточкам немного другого плана (ищем тангенс угла AOB):
Если соединить точки A и B, то угол ABO будет прямым.
И тангенс можно вычислить как отношение BA к BO.
Как же нам их найти?
И BO, и BA будут гипотенузами 2 совершенно равных прямоугольных треугольников (для наглядности я их выделил красным).
Длина катетов их равна 2 и 8, а квадрат гипотенузы, как известно, равен сумме квадратов катетов.
Таким образом, у нас получится следующее:
tg(BOA) = BA / BO = √(2² + 8²) / √(2² + 8²) = 1.
И нетрудно догадаться, что треугольник этот равнобедренный с равными углами BOA и BAO по 45 градусов.
Подготовка к ЕГЭ и ОГЭ. Решение задачи: найти тангенс угла (на клетках).
несколько способов решения одной задачи.pptx
Несколько способов решения одной задачи
Несколько способов
решения одной задачи
Шишкина Л. В.
учитель математики
МБОУ СОШ №24
хутора Болгов
Усть-Лабинского района
Краснодарского края
Задача: Найдите тангенс угла АОВ
Задача: Найдите тангенс угла АОВ.
Размер клетки 11.
Используем систему координат х y
Используем систему координат
х
y
Несколько способов решения одной задачи
Несколько способов решения одной задачи
Используем определения и формулы тригонометрии
Используем определения и формулы тригонометрии
Используем теорему Пифагора и обратную ей теорему
Используем теорему Пифагора и обратную ей теорему
Используем понятие площади и формулы площади треугольника
Используем понятие площади и формулы площади треугольника
Несколько способов решения одной задачи
Аналогичные задачи.
Аналогичные задачи.
Несколько способов решения одной задачи
х y
х
y
Несколько способов решения одной задачи
Несколько способов решения одной задачи
Несколько способов решения одной задачи
Порешаем сами?
Порешаем сами?
Несколько способов решения одной задачи
Несколько способов решения одной задачи
Несколько способов решения одной задачи
Несколько способов решения одной задачи
Несколько способов решения одной задачи
Несколько способов решения одной задачи
Несколько способов решения одной задачи
Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
Введите ваш emailВаш email
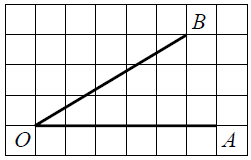
Найдите тангенс угла AOB, изображённого на рисунке.
Источник: statgrad
Решение:
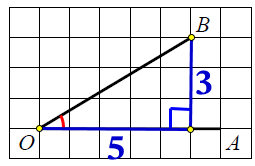
Дорисуем угол АОВ до прямоугольного треугольника:
Тангенс угла – это отношение противолежащего (дальнего) катета к прилежащему (близкому).
tgangle AOB=frac{3}{5}=0,6
Ответ: 0,6.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 4
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.