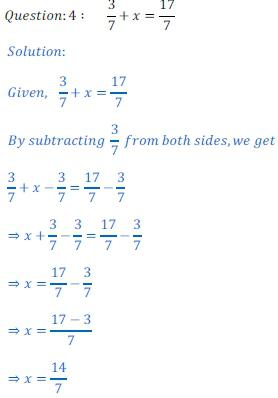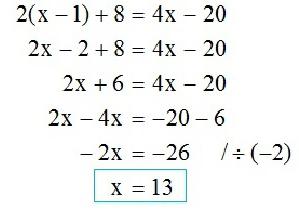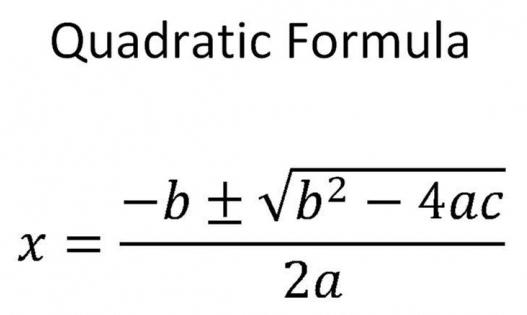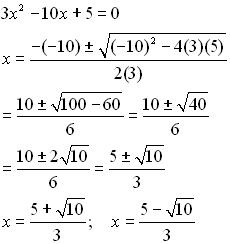Основными уравнениями школьной алгебры являются линейные и квадратные. Все остальные уравнения путём различных тождественных преобразований или путём соответствующей подстановки сводятся к ним.
Линейные уравнения
Линейные уравнения ах = b, где а ≠ 0; x=b/a.
Пример 1. Решите уравнение – х + 5,18 = 11,58.
Решение:
– х + 5,18 = 11,58;
– х = – 5,18 + 11,58;
– х = 6,4;
х = – 6,4.
Ответ: – 6,4.
Пример 2. Решите уравнение 3 – 5(х + 1) = 6 – 4х.
Решение:
3 – 5(х + 1) = 6 – 4х;
3 – 5х – 5 = 6 – 4х;
– 5х + 4х = 5 – 3+6;
– х = 8;
х = – 8.
Ответ: – 8.
Пример 3. Решите уравнение 
Решение:

2х + 3(х – 1) = 12; 2х + 3х – 3 =12; 5х = 12 + 3; 5х = 15; х = 3.
Ответ: 3.
Пример 4. Решите систему 
Решение:
Из уравнения 3х – у = 2 найдём у = 3х – 2 и подставим в уравнение 2х + 3у = 5.
Получим: 2х + 9х – 6 = 5; 11х = 11; х = 1.
Следовательно, у = 3∙1 – 2; у = 1.
Ответ: (1; 1).
Замечание.
Если неизвестные системы х и у, то ответ можно записать в виде координаты точки.
Квадратные уравнения
Квадратные уравнения ax2 + bx + c = 0, где а ≠ 0.
D = b2 – 4ac;

нет решения при D < 0.
При решении квадратных уравнений полезно помнить формулу чётного коэффициента, т.е. случай, когда b = 2k или k =b/2:

х2 + px + q = 0 – приведённое квадратное уравнение. Для него справедлива теорема Виета:
где х1 и х2 – корни уравнения.
Пример 5. Решите уравнение 3у + у2 = у.
Решение:
3у + у2 = у – неполное квадратное уравнение; у2 + 3у – у = 0;
у2 + 2у =0; у∙(у + 2) = 0.
Помните! Произведение равно нулю, когда хотя бы один из сомножителей равен нулю, но второй при этом имеет смысл.
y1 = 0, или у + 2 = 0;
у2 = – 2.
Ответ: – 2; 0.
Пример 6. Решите уравнение 18 – х2 = 14.
Решение:
18 – х2 = 14 – неполное квадратное уравнение; – х2 = 14 – 18;
– х2 = – 4; х2 =4; х = ± 2.
Ответ: ± 2.
Пример 7. Решите уравнение х2 + 6х – 3 = 2х3.
Решение:
х2 + 6х – 3 = 2х3 – уравнение 3-ей степени. Оно решается разложением на множители: х2 – 2х3 + 6х – 3 = 0;
– х2(2х – 1 ) + 3(2х – 1) = 0;
(2х – 1)(3 – х2) = 0;
2х – 1 = 0 или 3 – х2 =0;
х1 = 0,5; х2,3 =
Ответ: 0,5; 
Пример 8. Решите уравнение (х2 – 5х)2 – 30 (х2 – 5х) – 216 = 0.
Решение:
(х2 – 5х)2 – 30 (х2 – 5х) – 216 = 0 – биквадратное уравнение. Такое уравнение решается методом подстановки.
Метод подстановки позволяет перейти к уравнению, равносильному данному.
Пусть х2 – 5х = t. Тогда уравнение примет вид t2 – 30t – 216 = 0;
x2 – 5х = – 6 или х2 – 5х = 36;
х2 – 5х + 6 = 0 или х2 – 5х – 36 =0.
По теореме Виета:
х1 = 2, х2 = 3, х3 = – 4, х4 =9.
Ответ: – 4, 2, 3, 9.
Пример 9. Вычислить наибольший корень уравнения х4 – 7х3 + 14х2 – 7х + 1 = 0.
Решение:
х4 – 7х3 + 14х2 – 7х + 1 = 0 │: х2 (х ≠ 0)
t2 – 2 – 7t + 14 = 0;
t2 – 7t + 12 = 0;
t1 =3; t2 = 4.
х2 – 3х + 1 = 0 или х2 – 4х + 1 = 0;
D = 9 – 4 = 5, D = 16 – 4 = 12
x1 и х3 – меньшие корни. Остаётся сравнить х2 и х4.
– больший корень.
Ответ:
Пример 10. Найти все целые решения системы уравнений
Решение:
Решаем уравнение 2(х + у)2 + (х + у) = 21.
Пусть х + у = t. Тогда получим 2t2 + t – 21 = 0; t1 =-7/2 ; t2 = 3.
x + у = -7/2 не удовлетворяет условию задачи, так как хотя бы одно из слагаемых в данной сумме будет нецелым числом.
x + у = 3 – удовлетворяет условию.
Решением системы будут (1; 2) или (2; 1).
Ответ: (1; 2), (2; 1).
Рациональные уравнения
Уравнение, содержащее неизвестную в знаменателе, называют рациональным.
При решении рационального уравнения необходимо исключать те значения неизвестного, при которых знаменатель обращается в нуль.
Пример 11. Решить уравнение

Решение:
Область определения уравнения х – 2 ≠ 0. В данном случае левую часть уравнения можно сократить на ( ).
По т. Виета х1 = 1, х2 = 3.
Ответ: 1; 3.
Пример 12. Решить уравнение
Решение:
Ответ: 2.
Пример 13. Решить уравнение
Решение:
Так как x2+5 быть равным нулю не может, то данное уравнение будет равносильно уравнению 3(x2+5)2-23(x2+5)-8=0, которое решается методом подстановки. Пусть x2+5=t .
Имеем 3t2-23t-8=0; t1=-1/3; t2=8.
x2+5≠-1/3. Остаётся x2+5=8; x2=3; x=
Ответ: 
Пример 14. Решить систему
Решение:
Полученное решение системы удовлетворяет области определения.
Ответ: х = 2; у = 4.
Иррациональные уравнения
Уравнение, содержащее неизвестную под знаком корня n-ой степени, называется иррациональным.
Иррациональное уравнение чаще всего решается путём возведения в степень, которую имеет корень, содержащий неизвестную, или заменой неизвестной. Не следует забывать, что в степень возводятся обе части уравнения.
При возведении в нечётную степень обеих частей уравнения, получаем уравнение, равносильное исходному.
Новое уравнение, получившееся после возведения в чётную степень обеих частей, не всегда равносильно исходному уравнению, поэтому необходимо либо выполнить проверку полученных значений неизвестного путём подстановки в исходное уравнение, либо отбросить корни, не принадлежащие области определения уравнения.
Пример 15. Решить уравнение 
Решение:
Область определения: х + 1 ≥ 0.
x2 – 4 = 0 или х + 1 = 0;
х1 = – 2 , х3 = – 1.
х2 = 2,
х1 = – 2 не принадлежит области определения.
Ответ: – 1; 2
Пример 16. Решить уравнение .
Решение:
Данное уравнение решается возведением в квадрат левой и правой частей, и, так как в правой части уравнения содержится переменная, мы получим уравнение не равносильное исходному.
15 – 3х = х2 + 2х + 1; х2 + 5х – 14 = 0; х1 = – 7, х2 = 2.
Проверка. При х1 = – 7, 
При х2 = 2, 
Ответ: 3.
Пример 17. Решить систему
Решение:
В данном случае не требуется ни проверка, ни нахождение области определения, поскольку правые части обоих уравнений и до возведений в квадрат, и после – заведомо положительны.
Ответ: (29; 20).
Уравнения, содержащие знак модуля
Пример 18. Решите уравнение 
Решение:
х + 5 = 3 или х + 5 = – 3. Откуда х1 = – 2 или х2 = – 8.
Ответ: – 2; – 8.
Пример 19. Решите уравнение 
Решение:
Данное уравнение будем рассматривать на двух числовых промежутках:
Значение –1/2 назовём пограничным, т.е. при х = –1/2, 2х – 1 = 0.
При 
При 
Помните!
Пограничное значение смены знака необходимо включить хотя бы в один из интервалов.
Ответ: -4/3; 2.
Пример 20. Решите уравнение 
Решение:
Двучлен х – 3 меняет свой знак при переходе через х = 3, а х + 1 – при х = – 1. Данное уравнение будем рассматривать на трёх числовых промежутках:
1)

2) 

3) 

Ответ: – 1.
Пример 21. Решить систему
Решение:
Ответ: (3; – 1), (1; – 3).
Уравнения с параметром
Пример 22. При каком значении а уравнение х(2 – а) – х = 5 + х не имеет решений?
Решение:
Выразим х через а. 2х – ах – х – х = 5; – ах = 5; х = –5/a .
При а = 0 х не определён.
Подставим а = 0 в исходное уравнение: х(2 – 0) – х = 5 + х; 2х – 2х = 5; 0 ≠ 5, следовательно, при а =0 данное уравнение не имеет решения.
Ответ: при а = 0.
Пример 23. Корни х1 и х2 уравнения х2 + х + а = 0 обладают свойством x12+x22=5 . Найти а.
Решение:
Уравнение х2 + х + а = 0 – приведённое квадратное. По теореме Виета х1 + х2 = – 1, х1 ∙ х2 = а. Т.к. x12+x22=5, то х1 – х2 = – 5.
Имеем х1 = – 3; х2 = 2, следовательно, а = (– 3)∙2= – 6.
Ответ: а = – 6.
Пример 24. При каких значениях параметра n уравнение (n-2)x2-2nx+n+3=0 имеет корни разных знаков.
Решение:
n – 2 ≠ 0. В противном случае – нет квадратного уравнения.
Приведём исходное уравнение (путём почленного деления обеих частей равенства на n – 2) к приведённому:
Чтобы уравнение имело корни разных знаков, необходимо и достаточно выполнение двух условий одновременно:
1) D/4 > 0 (по формуле чётного коэффициента);
2) x1 ∙ x2 < 0 (по теореме Виета):
Ответ: 
Показательные уравнения и системы уравнений
Пример 25. Решите уравнение 62-x=63-2x.
Решение:
62-x=63-2x; 2 – х = 3 – 2х; х = 1.
Ответ: 1.
Пример 26. Решите уравнение 
Решение:

Ответ: – 2.
Пример 27. Решите уравнение 
Решение:
Ответ: 2.
Пример 28. Решите уравнение .
Решение:
При подстановке полученных значений х1 = 1 и х2 = 10 уравнение 
Ответ: 1, 10.
Пример 29. Укажите промежуток, на котором лежит корень уравнения
Решение:
Применим свойство степени и выделим в левой части уравнения множитель 3х:
Корень уравнения – число 0 – принадлежит промежутку 
Ответ: 1).
Логарифмические уравнения
Пример 30. Укажите отрицательный корень уравнения log5(x2-7x-35)=2.
Решение:
По определению логарифма получаем
Ответ: – 5.
Пример 31. Решите уравнение log3x+log3(3x-2)=log35.
Решение:
Область допустимых значений
В левой части уравнения на основании 3-го свойства получаем log3(x(3x-2))=log35; x(3x-2)=5; 3x2-2x-5=0; x1=5/3; x2=–1. –1 — не принадлежит области допустимых значений, т.е. не является корнем.
5/3 — принадлежит области допустимых значений, т.е. является корнем.
Ответ: 5/3.
Пример 32. Укажите целое решение уравнения
Решение:
Так как правая часть уравнения есть показательная функция, то 
Прологарифмируем обе части уравнения по основанию x2:
К правой части уравнения применим 5-е свойство логарифмов:
К обеим частям уравнения применим 7-е свойство логарифмов:
К обеим частям уравнения применим 4-е свойство логарифмов, сгруппируем и разложим на множители, получим:
(1-logx4)(1+logx4-logx3)=0
1-logx4=0 или 1+logx4-logx3=0
Из первого уравнения получаем х = 4, из второго х = 3/4.
Все найденные значения неизвестного входят в область допустимых значений уравнения, т.е. являются его корнями. Выбираем только целое — 4.
Ответ: 4.
Задачи для самостоятельного решения
Базовый уровень
Линейные уравнения и системы уравнений
1) Решите уравнение 3x=75
2) Решите уравнение 
3) Решите уравнение
4) Решите уравнение 
5) Решите уравнение 
6) Решите систему уравнений
7) Решить систему уравнений


Квадратные уравнения и системы уравнений
9) Решите уравнение х + х2=0.
10) Укажите меньший корень уравнения (2х – 1)(х+3) = 0.
11) Решить систему уравнений
Рациональные уравнения и системы уравнений
12) Решите уравнение 
13) Решите уравнение 
14) Сколько корней имеет уравнение 
Иррациональные уравнения и системы уравнений
15) Решите уравнение 
16) Решите уравнение 
17) Решите уравнение 
18) Решите уравнение 
19) Решите систему уравнений 
20) Решите систему уравнений 
21) Пусть (х0; у0) решение системы уравнений 
22) Решите систему уравнений 
Показательные уравнения и системы уравнений
23) Решите уравнение 52x-3=5 .
24) Решите уравнение 23х+1 = 4.
25) Решите уравнение 9x-5∙3x+1+54=0 .
26) Укажите отрицательный корень уравнения 23x+1-22x=2x+1-1.
27) Решите уравнение 3x+2-3x=72 .
28) Решите уравнение 
29) Решите уравнение 9x-75∙3x-1-54=0.
30) Решите уравнение 
31) Решите уравнение 
Логарифмические уравнения
32) Решите уравнение log2x=5.
33) Решите уравнение 
34) Решите уравнение 3log0.2x=log0.2x4-1 .
35) Решите уравнение 
36) Решите уравнение 
37) Решите уравнение lg(3+2lg(1+x))=0.
38) Решите уравнение log2(54-x3)=3log2x.
Уравнения и системы уравнений, содержащие модуль
39) Найдите наибольший корень уравнения |5-4x|=1.
40) Решите уравнение 2x+|x-13|=8.
41) Решить уравнение |x+1|-8x=|x-5|+4.
42) Решите систему уравнений 
Повышенный уровень
Уравнения с параметром
43) При каких значениях k уравнение x2 + kx + 9 =0 имеет корни?
44) Найти все значения а, при каждом из которых уравнение |2x+3|+|2x-3|=ax+6 имеет один корень.
Сложные уравнения
45) Решите уравнение log3|x+1|=1 .
46) Укажите наибольший корень уравнения
47) Решите уравнение
48) Пусть – решение системы 
49) Укажите целый корень уравнения xlog2x+4=32 .
50) Решите уравнение x2log3x=81x2 и укажите произведение его корней.
51) Решите уравнение lg(x+2)=lg(5x+1)-lg(4-2x).
52) Найдите сумму корней уравнения logx(5x-4)=2.
53) Сколько корней имеет уравнение ln(x2+2x-3)=ln(x-3)?
54) Решите уравнение log7(x-7)-1=log7(5x-1).
55) Укажите все пары (х, у) положительных чисел х и у, удовлетворяющих системе
56) Решите уравнение 
Найти корень уравнения? Это просто!
В математике встречаются разнообразные уравнения. Их всегда нужно решать, то есть искать все числа, которые сделают его верным равенством. Пути поиска решений определяются первоначальным видом уравнения. От него же будет зависеть и количество верных значений переменной, которые обозначаются, как корень уравнения. Это число может варьироваться от нуля до бесконечности.
Что подразумевается под уравнением и его корнем?
Из названия понятно, что оно приравнивает две величины, которые могут быть представлены числовыми или буквенными выражениями. Кроме того, они содержат еще неизвестные величины. Самое простое уравнение имеет только одну.
Видов уравнений большое количество, но понятие корня для них всегда одно и то же. Корень уравнения — это такое значение неизвестного числа, при котором уравнение принимает становится верным равенством. Бывают ситуации, когда таких чисел несколько, тогда неизвестная называется переменной.
В алгебре при решении уравнений можно прийти к такой ситуации, что корней не будет совсем. Тогда говорят о том, что оно неразрешимо. А в ответе такого уравнения нужно записать, что решений нет.
Но иногда бывает и противоположное. То есть в процессе многочисленных преобразований появляются посторонние корни. Они не дадут верного равенства при подстановке. Поэтому числа всегда нужно проверять, чтобы избежать ситуации с лишними корнями в ответе. Иначе уравнение не будет считаться решенным.
О линейном уравнении
Оно всегда может быть преобразовано в запись следующего вида: а * х + в = 0. В нем «а» всегда не равно нулю. Чтобы понять сколько корней имеет уравнение, его потребуется решить в общем виде.
- перенести в правую часть равенства слагаемое «в», заменив его знак на противоположный;
- разделить обе части получившегося равенства на коэффициент «а».
х = -в/а.
Из него ясно, что ответом будет одно число. То есть всего один корень.
Квадратное уравнение
Его общий вид: а * х 2 + в * х + с = 0. Здесь коэффициенты являются любыми числами, кроме первого, «а», которое не может быть равным нулю. Ведь тогда оно автоматически превратится в линейное. Ответ на вопрос, сколько корней имеет уравнение, уже не будет столь однозначным, как это было в предыдущем случае.
Все будет зависеть от значения дискриминанта. Он вычисляется по формуле Д = в 2 — 4 а * с. После расчетов «Д» может получиться больше, меньше или равным нулю. В первом случае корней уравнения будет два, во втором ответом будет «корней нет», а третья ситуация даст только одно значение неизвестной.
Формулы, которые используют для нахождения корней квадратного уравнения, и содержащие дискриминант
В общем случае, когда «Д» положительное число, не равное нулю, нужно использовать такую формулу:
При равенстве «Д» нулю корень уравнения — это единственное число. Просто потому что квадратный корень из нуля равен нулю. А значит, прибавлять и вычитать нужно будет ноль. От этого число не изменится. Поэтому формулу корня уравнения можно записать без упоминания «Д»:
х = (-в) / (2 * а).
При отрицательном значении дискриминанта извлечь из него квадратный корень не представляется возможным. Поэтому корней у такого уравнения не будет.
Замечание. Это верно для курса школьной программы, в которой не изучаются комплексные числа. Когда они вводятся, то получается, что и в этой ситуации ответов будет два.
Формулы для расчета корней квадратного уравнения, не использующие дискриминант
Речь идет о теореме Виета. Она действительна в случае, когда квадратное уравнение записывается в несколько другом виде:
х 2 + в * х + с = 0.
Тогда формула корней квадратного уравнения сводится к тому, чтобы выполнить решение двух линейных:
Оно решается за счет того, что из первого выводится выражение для одного из корней. И это значение нужно подставить во второе. Так будет найден второй корень, а потом первый.
К этому варианту всегда можно прийти от общего вида квадратного уравнения.
Достаточно только разделить все коэффициенты на «а».
Как быть, если нужно узнать наименьшее значение корня?
Решать уравнение и находить все возможные числа, которые подойдут для ответа. А потом выбрать самое малое. Это и будет наименьший корень уравнения.
Чаще всего такие вопросы встречаются в заданиях, которые имеют степень большую, чем 2, или содержат тригонометрические функции. Примером, когда нужно найти наименьший корень, может служить такое равенство:
2 х 5 + 2 х 4 — 3 х 3 — 3 х 2 + х + 1 = 0.
Чтобы найти каждое значение, которое можно назвать «корень уравнения», это равенство нужно преобразовать. Первое действие: сгруппировать его члены попарно: первый со вторым и так далее. Потом из каждой пары вынести общий множитель.
В каждой скобке останется (х + 1). Общим множителем в первой из пар будет 2 х 4 , во второй 3 х 2 . Теперь снова нужно выполнить вынесение общего множителя, которым будет являться одинаковая скобка.
После множителя (х + 1) будет стоять (2 х 4 — 3 х 2 + 1). Произведение двух множителей равняется нулю, только если один из них принимает значение, равное нулю.
Первая скобка равна нулю при х = -1. Это будет одним из корней уравнения.
Другие будут получены из уравнения, образованного второй скобкой, приравненной к нулю. Оно биквадратное. Для его решения нужно ввести обозначение: х 2 = у. Тогда уравнение существенно преобразится и примет привычный вид квадратного уравнения.
Его дискриминант равен Д = 1. Он больше нуля, значит корней будет два. Первый корень оказывается равным 1, второй будет 0,5. Но это значения для «у».
Нужно вернуться к введенному обозначению. х1,2 = ± 1, х3,4 = ± √0,5. Все корни уравнения: -1; 1; -√0,5; √0,5. Наименьший из них — -1. Это ответ.
В качестве заключения
Напоминание: все уравнения нужно проверять на то, подходит ли корень. Может быть, он посторонний? Стоит выполнить проверку предложенного примера.
Если подставить в изначально данное уравнение вместо «х» единицу, то получается, что 0 = 0. Этот корень верный.
Если х = -1, то получается такой же результат. Корень тоже подходящий.
Аналогично, при значениях «х» равных -√0,5 и √0,5 опять выходит верное равенство. Все корни подходят.
Этот пример не дал посторонних корней. Такое бывает не всегда. Вполне могло оказаться, что самое маленькое значение не подходило бы при проверке. Тогда пришлось бы выбирать из оставшихся.
Вывод: надо помнить о проверке и внимательно подходить к решению.
Тригонометрические уравнения
Тригонометрические уравнения. В составе экзамена по математике в первой части имеется задание связанное с решением уравнения — это простые уравнения, которые решаются за минуты, многие типы можно решить устно. Включают в себя: линейные, квадратные, рациональные, иррациональные, показательные, логарифмические и тригонометрические уравнения.
В этой статье мы рассмотрим тригонометрические уравнения. Их решение отличается и по объёму вычисления и по сложности от остальных задач этой части. Не пугайтесь, под словом «сложность», имеется виду их относительную сложность по сравнению с другими заданиями.
Кроме нахождения самих корней уравнения, необходимо определить наибольший отрицательный, либо наименьший положительный корень. Вероятность того, что вам на экзамене попадёт тригонометрическое уравнение, конечно же, мала.
Их в данной части ЕГЭ менее 7%. Но это не означает, что их нужно оставить без внимания. В части С тоже необходимо решить тригонометрическое уравнение, поэтому хорошо разобраться с методикой решения и понимать теорию просто необходимо.
Понимание раздела «Тригонометрия» в математике во многом определяет ваш успех при решении многих задач. Напоминаю, что ответом является целое число или конечная десятичная дробь. После того, как получите корни уравнения, ОБЯЗАТЕЛЬНО сделайте проверку. Много времени это не займёт, а вас избавит от ошибки.
В будущем мы также рассмотрим и другие уравнения, не пропустите! Вспомним формулы корней тригонометрических уравнений, их необходимо знать:
Знание этих значений необходимо, это «азбука», без которой невозможно будет справиться с множеством заданий. Отлично, если память хорошая, вы легко выучили и запомнили эти значения. Что делать, если этого сделать не получается, в голове путаница, да просто вы именно при сдаче экзамена сбились. Обидно будет потерять бал из-за того, что вы запишите при расчётах неверное значение.
Алгоритм восстановления этих значений прост, он также приведён в теории, полученной вами во втором письме после подписки на рассылку. Если ещё не подписались, сделайте это! В будущем также рассмотрим, как эти значения можно определить по тригонометрической окружности. Не даром её называют «Золотое сердце тригонометрии».
Сразу поясню, во избежание путаницы, что в рассматриваемых ниже уравнениях даны определения арксинуса, арккосинуса, арктангенса с использованием угла х для соответствующих уравнений: cosx=a, sinx=a, tgx=a, где х может быть и выражением. В примерах ниже у нас аргумент задан именно выражением.
Итак, рассмотрим следующие задачи:
Найдите корень уравнения:
В ответе запишите наибольший отрицательный корень.
Решением уравнения cos x = a являются два корня:
Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.
Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.
Общая рекомендация для всех подобных задач: для начала берите диапазон n от – 2 до 2. Если требуемое значение выявить не удалось, подставляем следующие значения x: – 3 и 3, – 4 и 4 и так далее.
При n = – 2 х1= 3 (– 2) – 4,5 = – 10,5 х2= 3 (– 2) – 5,5 = – 11,5
При n = – 1 х1= 3 (– 1) – 4,5 = – 7,5 х2= 3 (– 1) – 5,5 = – 8,5
При n = 0 х1= 3∙0 – 4,5 = – 4,5 х2= 3∙0 – 5,5 = – 5,5
При n = 1 х1= 3∙1 – 4,5 = – 1,5 х2= 3∙1 – 5,5 = – 2,5
При n = 2 х1= 3∙2 – 4,5 = 1,5 х2= 3∙2 – 5,5 = 0,5
Получили, что наибольший отрицательный корень равен –1,5
В ответе напишите наименьший положительный корень.
Решением уравнения sin x = a являются два корня:
Либо (он объединяет оба указанные выше):
Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от – 90 о до 90 о синус которого равен a.
Выразим x (умножим обе части уравнения на 4 и разделим на Пи):
Найдём наименьший положительный корень. Здесь сразу видно, что при подстановке отрицательных значений n мы получим отрицательные корни. Поэтому будем подставлять n = 0,1,2 …
При n = 0 х = (– 1) 0 + 4∙0 + 3 = 4
При n = 1 х = (– 1) 1 + 4∙1 + 3 = 6
При n = 2 х = (– 1) 2 + 4∙2 + 3 = 12
Проверим при n = –1 х = (–1) –1 + 4∙(–1) + 3 = –2
Значит наименьший положительный корень равен 4.
В ответе напишите наименьший положительный корень.
Решением уравнения tg x = a является корень:
Определение: Арктангенсом числа a (a – любое число) называется угол x принадлежащий интервалу – 90 о до 90 о , тангенс которого равен a.
Выразим x (умножим обе части уравнения на 6 и разделим на Пи):
Найдём наименьший положительный корень. Подставим значения n = 1,2,3. Отрицательные значения подставлять нет смысла, так как видно, что получим отрицательные корни:
Таким образом, наименьший положительный корень равен 0,25.
Определение котангенса: Арккотангенсом числа a (a – любое число) называется угол x принадлежащий интервалу (0;П), котангенс которого равен a.
Здесь хочу добавить, что в уравнениях в правой части может стоять отрицательное число, то есть тригонометрическая функция от аргумента может иметь отрицательное значение. Если в ходе решения вы не сможете определить угол, например, для
то данные формулы вам помогут:
Спасибо за внимание, учитесь с удовольствием!
Решение простых линейных уравнений
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Числовой коэффициент — число, которое стоит при неизвестной переменной.
Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:
Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.
Как решать простые уравнения
Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.
1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.
Для примера рассмотрим простейшее уравнение: x+3=5
Начнем с того, что в каждом уравнении есть левая и правая часть.
Перенесем 3 из левой части в правую и меняем знак на противоположный.
Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.
Решим еще один пример: 6x = 5x + 10.
Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.
Приведем подобные и завершим решение.
2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.
Применим правило при решении примера: 4x=8.
При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.
Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.
Разделим каждую часть на 4. Как это выглядит:
Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:
Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12
-
Разделим обе части на −4, чтобы коэффициент при неизвестной стал равен единице.
−4x = 12 | : (−4)
x = −3
Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.
Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.
Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.
| Алгоритм решения простого линейного уравнения |
|---|
|
Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Примеры линейных уравнений
Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!
Пример 1. Как правильно решить уравнение: 6х + 1 = 19.
-
Перенести 1 из левой части в правую со знаком минус.
Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.
Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1.
5х − 15 + 2 = 3х − 12 + 2х − 1
Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.
5х − 3х − 2х = −12 − 1 + 15 − 2
Приведем подобные члены.
Ответ: х — любое число.
Пример 3. Решить: 4х = 1/8.
-
Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.
Пример 4. Решить: 4(х + 2) = 6 − 7х.
- 4х + 8 = 6 − 7х
- 4х + 7х = 6 − 8
- 11х = −2
- х = −2 : 11
- х = −2/11
Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье.
Пример 5. Решить:
- 3(3х — 4) = 4 · 7х + 24
- 9х — 12 = 28х + 24
- 9х — 28х = 24 + 12
- -19х = 36
- х = 36 : (-19)
- х = — 36/19
Пример 6. Как решить линейное уравнение: х + 7 = х + 4.
5х — 15 + 2 = 3х — 2 + 2х — 1
Сгруппировать в левой части неизвестные члены, в правой — свободные члены:
Приведем подобные члены.
Ответ: нет решений.
Пример 7. Решить: 2(х + 3) = 5 − 7х.
http://matematikalegko.ru/uravnenia/trigonometricheskie-uravneniya.html
http://skysmart.ru/articles/mathematic/reshenie-prostyh-linejnyh-uravnenij
- Если b = 0, то квадратное уравнение принимает вид ax 2 + 0x+c=0 и оно равносильно ax 2 + c = 0.
- Если c = 0, то квадратное уравнение выглядит так ax 2 + bx + 0 = 0, иначе его можно написать как ax 2 + bx = 0.
- Если b = 0 и c = 0, то квадратное уравнение выглядит так ax 2 = 0.
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.
Решение неполных квадратных уравнений
Как мы уже знаем, есть три вида неполных квадратных уравнений:
- ax 2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
- ax 2 + c = 0, при b = 0;
- ax 2 + bx = 0, при c = 0.
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.
Как решить уравнение ax 2 = 0
Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0.
Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.
Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0.
Пример 1. Решить −6x 2 = 0.
- Замечаем, что данному уравнению равносильно x 2 = 0, значит исходное уравнение имеет единственный корень — нуль.
- По шагам решение выглядит так:
Как решить уравнение ax 2 + с = 0
Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.
Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.
Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:
- перенесем c в правую часть: ax 2 = — c,
- разделим обе части на a: x 2 = — c/а.
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.
Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней.
Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению х 2 = -c/a, которое:
- не имеет корней при — c/а 0.
| В двух словах |
|---|
Пример 1. Найти решение уравнения 8x 2 + 5 = 0.
- Перенесем свободный член в правую часть:
Разделим обе части на 8:
Ответ: уравнение 8x 2 + 5 = 0 не имеет корней.
Как решить уравнение ax 2 + bx = 0
Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.
Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:
Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.
Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.
Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня:
Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0
0,5x = 0,125,
х = 0,125/0,5
Ответ: х = 0 и х = 0,25.
Как разложить квадратное уравнение
С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:
Формула разложения квадратного трехчлена
Если x1 и x2 — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x1) (x − x2).
Дискриминант: формула корней квадратного уравнения
Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:
где D = b 2 − 4ac — дискриминант квадратного уравнения.
Эта запись означает:
Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.
Алгоритм решения квадратных уравнений по формулам корней
Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.
В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.
Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
- вычислить его значение дискриминанта по формуле D = b 2 −4ac;
- если дискриминант отрицательный, зафиксировать, что действительных корней нет;
- если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
- если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!
Примеры решения квадратных уравнений
Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.
Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.
- Найдем дискриминант: D = 28 2 — 4(-4)(-49) = 784 — 784 = 0
- Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
- Найдем корень
Ответ: единственный корень 3,5.
Пример 2. Решить уравнение 54 — 6x 2 = 0.
- Произведем равносильные преобразования. Умножим обе части на −1
Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
Ответ: два корня 3 и — 3.
Пример 3. Решить уравнение x 2 — х = 0.
- Преобразуем уравнение так, чтобы появились множители
Ответ: два корня 0 и 1.
Пример 4. Решить уравнение x 2 — 10 = 39.
- Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
Ответ: два корня 7 и −7.
Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.
- Найдем дискриминант по формуле
D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112
Ответ: корней нет.
В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.
Формула корней для четных вторых коэффициентов
Рассмотрим частный случай. Формула решения корней квадратного уравнения 
Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 — 4ac = 4n 2 — 4ac = 4(n 2 — ac) и подставим в формулу корней:
2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″>
Для удобства вычислений обозначим выражение n 2 -ac как D1. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:
где D1 = n 2 — ac.
Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.
Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
- вычислить D1= n 2 — ac;
- если D1 0, значит можно найти два действительных корня по формуле
Формула Виета
Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:
Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.
Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:
Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.
Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.
Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:
Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:
Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=»215″ src=»https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE» width=»393″>
Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=»52″ src=»https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG» width=»125″>
Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=»52″ src=»https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo» width=»112″>
Результат проделанных вычислений в том, что мы убедились в справедливости выражения:
Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:
Обратная теорема Виета
Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0.
Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.
Пример 1. Решить при помощи теоремы Виета: x 2 − 6x + 8 = 0.
- Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″>
Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.
Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.
Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6. А значения 4 и 2 подходят обоим равенствам:
Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p>
Упрощаем вид квадратных уравнений
Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.
Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0.
Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100.
Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.
Покажем, как это работает на примере 12x 2 — 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто.
А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения
умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0.
Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 — 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0.
Связь между корнями и коэффициентами
Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:
Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.
Например, можно применить формулы из теоремы Виета:
Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 — 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.
Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:
Как находить наибольший корень уравнения
Пример 5. Решите уравнение 3у + у 2 = у.
Решение:
3у + у 2 = у – неполное квадратное уравнение; у 2 + 3у – у = 0;
у 2 + 2у =0; у∙(у + 2) = 0.
x 2 – 5х = – 6 или х 2 – 5х = 36;
х 2 – 5х + 6 = 0 или х 2 – 5х – 36 =0.
По теореме Виета:
х1 = 2, х2 = 3, х3 = – 4, х4 =9.
Ответ: – 4, 2, 3, 9.
источники:
http://skysmart.ru/articles/mathematic/kak-reshat-kvadratnye-uravneniya
http://www.sites.google.com/a/ssga.ru/ssga4school/matematika/tema-3
5
.
01
Линейные и квадратные уравнения
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
решение уравнений
Решаем задачи
Решите уравнение:
Показать ответ и решение
Найдите корень уравнения
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Умножим левую и правую часть уравнения на 9. После умножения: , что равносильно
– подходит по
ОДЗ.
Найдите корень уравнения
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Умножим левую и правую часть уравнения на После умножения:
что равносильно
–
подходит по ОДЗ.
Решите уравнение
Показать ответ и решение
Данное уравнение является линейным. Преобразуем его, заметив, что
Решите уравнение
Показать ответ и решение
Решите уравнение Если уравнение имеет несколько корней, в ответ укажите наибольший по
модулю.
Показать ответ и решение
1 способ.
Данное уравнение является квадратным.
Дискриминант Найдем, чей это квадрат. Это число делится на 25, следовательно, корень из
него делится на 5. Так как а
проверкой убеждаемся, что
Следовательно,
корни
Следовательно, наибольший по модулю корень – это
2 способ.
Заметим, что сумма коэффициентов уравнения равна нулю: следовательно, один из корней
Тогда второй по теореме Виета (произведение корней равно ) равен
Найдите отрицательный корень уравнения
Показать ответ и решение
Данное уравнение является квадратным. Раскроем скобки:
1 способ.
Дискриминант , следовательно, корни:
Следовательно, отрицательный корень – это .
2 способ.
Заметим, что сумма коэффициентов, стоящих при четных степенях: , равна сумме коэффициентов, стоящих
при нечетных степенях: , следовательно, один из корней
. Тогда второй по теореме Виета (произведение
корней равно ) равен
.
Найдите корень уравнения
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Найдите корень уравнения
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Найдите корень уравнения
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
После упрощения имеем что равносильно
что равносильно
что равносильно
Произведение двух выражений равно нулю в том и только том случае, когда хотя бы одно из них равно 0 и оба
выражения не теряют смысл. Отсюда заключаем, что
– единственный корень – подходит по ОДЗ.
Найдите корень уравнения
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
После упрощения имеем что равносильно
что равносильно

Произведение двух выражений равно нулю в том и только том случае, когда хотя бы одно из них равно 0 и оба
выражения не теряют смысл. Отсюда заключаем, что
– единственный корень – подходит по ОДЗ.
Решите уравнение Если уравнение имеет более одного корня, в ответе укажите больший из них.
Показать ответ и решение
1 способ
Дискриминант данного уравнения
Тогда его корни
Ответ: – больший корень уравнения.
2 способ
Найдем дискриминант:
Значит, уравнение имеет 2 корня.
Тогда можно применить теорему Виета:
Произведение и сумма корней положительны, значит, оба корня положительны. Подбором чисел, произведение
которых равно 28, обнаружим, что 4 и 7 корни данной системы. Так как 7 — наибольший корень, запишем его в
ответ.
Решите уравнение
Показать ответ и решение
1 способ.
Раскроем скобки:
2 способ.
Преобразуем:
Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите больший из них.
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
После умножения на 7 левой и правой частей имеем что равносильно
что равносильно
–
подходят по ОДЗ. Таким образом, больший из корней равен 9.
Решите уравнение
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
После упрощения имеем
Найдите корень уравнения
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
После упрощения имеем
Решите уравнение
Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Показать ответ и решение
1 способ
Дискриминант данного уравнения Корни
ответ: – меньший корень уравнения.
2 способ
Найдем дискриминант:
Значит, уравнение имеет 2 корня.
Тогда можно применить теорему Виета:
Произведение и сумма корней положительны, значит, оба корня положительны. Подбором найдем, что и 3 являются
корнями системы. Так как — наименьший корень, запишем его в ответ.
Найдите больший корень уравнения
Показать ответ и решение
Данное уравнение является квадратным.
1 способ.
Дискриминант Найдем, квадрат какого числа равен
Заметим, что
следовательно,
чуть больше, чем
Подбором убеждаемся, что Следовательно, корни:
Следовательно, больший корень – это
2 способ.
Найдем корни по теореме Виета. Заметим, что их произведение равно то есть отрицательно. Следовательно,
они разных знаков, например и
(где
).
Заметим, что их сумма равна , следовательно,
Попробуем найти
и
.
Заметим, что Таким образом, если взять числа 201 и 200, то их разность равна 1.
Минус следует отнести к 200, то есть и
Решите уравнение. Если корней несколько, в ответе укажите наибольший
корень.
Показать ответ и решение
Выбираем наибольший корень
Решите уравнение:
Корни введите в порядке возрастания, через запятую. Пример ответа — если
Вы получили и
ввести нужно -1,03,2/3 .
Показать ответ и решение
Заметим, что сумма коэффицентов равна 0, следовательно, один из корней
уравнения равен 1. По теореме Виета, произведение корней равно ,
следовательно, второй корень равен -4/3.
Найдите наибольший отрицательный корень уравнения
Дата: 2018-02-02
15107
Категория: Простейшие уравнения
Метка: ЕГЭ-№5
Найдите наибольший отрицательный корень уравнения:

Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.
Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.
Общая рекомендация для всех подобных задач: для начала берите диапазон n от –2 до 2. Если требуемое значение выявить не удалось, подставляем следующие значения x: –3 и 3, –4 и 4 и так далее. Вычисляем:
При n = – 2 х1= 3(– 2) – 4,5 = – 10,5 х2= 3(– 2) – 5,5 = – 11,5
При n = – 1 х1= 3(– 1) – 4,5 = – 7,5 х2= 3(– 1) – 5,5 = – 8,5
При n = 0 х1= 3∙0 – 4,5 = – 4,5 х2= 3∙0 – 5,5 = – 5,5
При n = 1 х1= 3∙1 – 4,5 = – 1,5 х2= 3∙1 – 5,5 = – 2,5
При n = 2 х1= 3∙2 – 4,5 = 1,5 х2= 3∙2 – 5,5 = 0,5
Получили, что наибольший отрицательный корень равен –1,5
Ответ: –1,5
Найдите наименьший положительный корень уравнения:
Решением уравнения sin x = a являются два корня:
Либо (он объединяет оба указанные выше):
Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от –90о до 90о синус которого равен a.
Значит
Выразим x (умножим на 4 и разделим на Пи):

При n = 0 х = (– 1)0 + 4∙0 + 3 = 4
При n = 1 х = (– 1)1 + 4∙1 + 3 = 6
При n = 2 х = (– 1)2 + 4∙2 + 3 = 12
Проверим при n=–1 х=(–1)–1 + 4∙(–1) + 3 = –2
Значит наименьший положительный корень равен 4.
Ответ: 4
Найдите наименьший положительный корень уравнения:
Решением уравнения tg x = a является корень:
Определение: Арктангенсом числа a (a – любое число) называется угол x принадлежащий интервалу – 90о до 90о, тангенс которого равен a.
Значит


Таким образом, наименьший положительный корень равен 0,25.
Ответ: 0,25