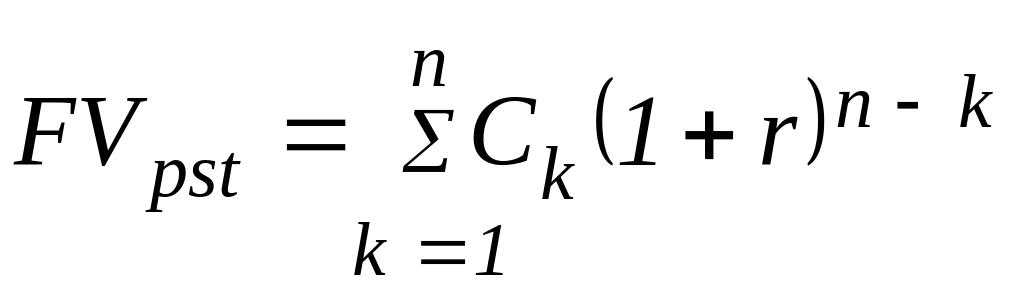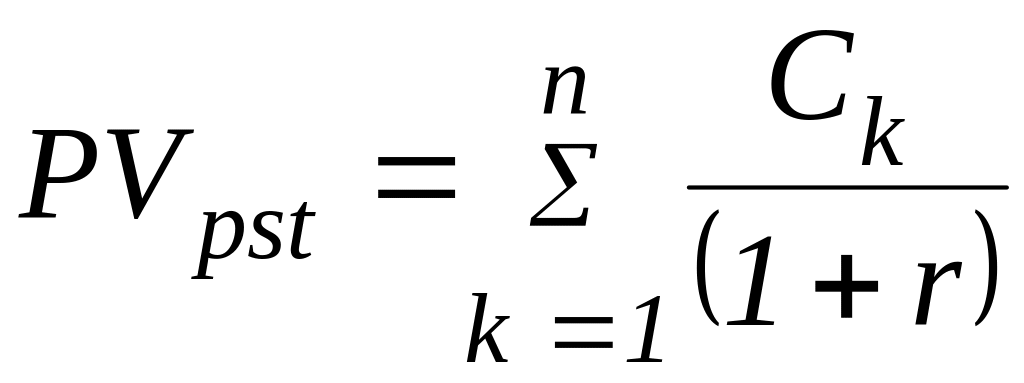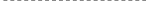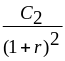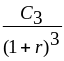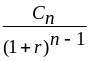Одним из важнейших критериев оценки инвестиционного проекта является коэффициент дисконтирования. Качественное бизнес-планирование предполагает обязательный учет изменения стоимости денег со временем, поэтому все будущие денежные потоки следует приводить к текущему состоянию. Остановимся подробнее на том, что такое коэффициент дисконта и как определить его величину.
Содержание статьи
- Понятие коэффициента дисконтирования и его значение
- Способ определения величины показателя
- Примеры вычисления потоков денег с использованием фактора дисконта
- Некоторые особенности практических расчетов фактора приведения
Понятие коэффициента дисконтирования и его значение

В бизнес-проектировании «деньги сейчас» всегда предпочтительнее, чем «деньги потом», поскольку их можно вложить в другое дело и получить доход или разместить на банковском депозите и получать фиксированный процент. Следовательно, перед вложением инвестор должен быть уверен, что в течение жизненного цикла проекта он не только не потеряет от удешевления денег, но и сможет получить прибыль.
Интервал времени, на протяжении которого реализуется начинание и приносит прибыль участникам, устанавливается заранее. Он, как правило, определяется по нормативным срокам применения установленного оборудования, после чего технические возможности производства продукции исчерпываются. От правильного определения временных рамок начинания во многом зависит объективность вычислений.
Значение коэффициента дисконтирования используется в разных ситуациях:
- оценка эффективности экономической деятельности какой-либо фирмы;
- расчет эффективности инвестиционного проекта;
- рассмотрение альтернативных вариантов вложения средств как между разными инициативами, так и внутри одного предприятия (выбор наиболее перспективного пути развития);
- многосторонние расчеты и кредитование.
Этот показатель фактически устанавливает некий норматив издержек или поступления капитала при вложении его в другое начинание. Иными словами, коэффициент (или фактор) дает возможность определить размер процента, на который следует множить ожидаемые доходы для того, чтобы выйти на конкретную сумму применительно к сегодняшнему состоянию.
Способ определения величины показателя
Рассмотрим подробнее, как рассчитать коэффициент дисконтирования. Обычно речь идет о многошаговом расчете перспективности и экономической эффективности инвестиционного начинания, поэтому фактор дисконтирования приводит объем потока на n-м шаге к моменту приведения.
Общая формула дисконтирования потока денег имеет такой вид:
PV = FV * 1/(1+R)n
где:
- PV – приведенная стоимость;
- FV – будущая стоимость.
В этой формуле выделяется компонент, определяющий величину фактора приведения. Собственно, формула расчета коэффициента дисконтирования выглядит так:
КД = 1/(1+R)n
в которой:
- R – установленное значение нормы дисконта;
- n – количество периодов (шагов), представляющее собой число лет (месяцев) от будущего до текущего момента.
Получившийся показатель всегда имеет значение меньше единицы. Он показывает стоимость одной инвестированной денежной единицы (рубля, евро, доллара) через определенное время при соответствии условий тем, которые приняты для вычисления.
Важнейшей составной частью для расчета коэффициента является ставка дисконтирования, которую еще называют нормой дисконта. Для ее определений существует целый ряд методик, основанных на различных принципах:
- дивидендный метод (модель Гордона);
- стоимость капитальных активов предприятия (модель CAPM и ее многочисленные модификации);
- наличие заемных и собственных средств (модель WACC);
- метод значений рентабельности капитала (ROE, ROA, ROACE, ROCE);
- метод вычисления рисковых премий (кумулятивный);
- экспертный метод, основанный на субъективных прогнозах специалистов.

Другая составляющая формулы – это жизненный цикл начинания, то есть количество рассматриваемых периодов, в течение которых проект будет генерировать денежные потоки. Чем точнее, установлены эти две вводные, тем более точным будет конечный результат.
Примеры вычисления потоков денег с использованием фактора дисконта
Рассмотрим пример расчета. Бизнесмен вкладывает в новый шестилетний проект 800 тысяч рублей. Согласно с представленным инициатором бизнес-планом, через 6 лет он сможет единоразовым платежом получить 1,5 миллиона рублей. Кумулятивным способом определена ставка дисконтирования 12%, при этом процент нормы дисконта записывается при подсчете в виде части от единицы (0,12). Теперь, используя стандартную формулу, можно посчитать величину фактора:
Kd = 1 / (1 + 0,12) 6
Kd = 1 / 1,9738
Kd = 0,5066
Мы получили коэффициент приведения в размере 0,5066. После этого по формуле дисконтирования рассчитываются показатели стоимости приведенного денежного потока:
PV = FV * 1/(1+R)n.
PV = 1500000 * 0,5066
PV = 759900
Из полученного результата можно сделать неутешительный для инвестора вывод, что при таких стартовых условиях ему не следует ожидать не только прибыли, но и даже простого возврата вложенных денег. Следовательно, от такого предложения нужно отказаться или же предложить изменить основные условия проекта, если это приемлемо (сократить срок реализации или уменьшить норму дисконта).
Предположим, что норма дисконта в нашем примере снижена до 10%. В таком случае значение коэффициента составит 0,5645, а приведенный поток денег возрастет до 846750 рублей, что сделает проект прибыльным. Аналогичная ситуация возникает и в случае сокращения срока внедрения до 5 лет при ставке 12%: фактор будет 0,5674, а поток – 851100 рублей.
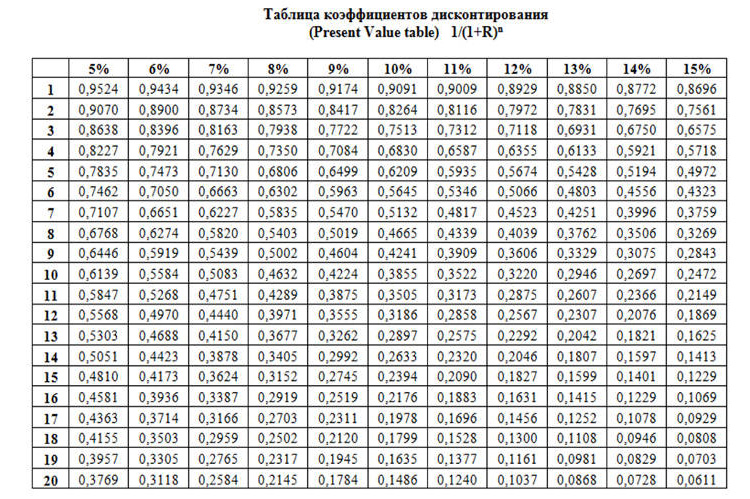
Следует отметить, что для того, чтобы определить коэффициент дисконтирования, нет необходимости каждый раз погружаться в математические формулы. Для упрощения этого задания разработана и широко применяется на практике таблица коэффициентов дисконтирования. Она построена по стандартной схеме, как таблицы Пифагора или Брадиса, то есть на одной оси указаны размеры процентных ставок, на другой – временные отрезки. Для нахождения нужного показателя достаточно найти ячейку, где они пересекаются, в ней содержится величина коэффициента с точностью до десятитысячных (до четвертого знака после запятой).
Все приведенные выше значения коэффициентов, взяты из этой таблицы. Это значительно ускоряет расчеты и дает возможность без лишних усилий просчитывать альтернативные варианты развития событий.
Мы рассматривали задачу, в которой предусматривалась выплата денег одним платежом после окончания проекта. На практике, гораздо чаще встречаются ситуации, когда выплаты производятся ежегодно. Тогда для корректности расчетов необходимо находить коэффициент приведения для каждого года отдельно. К примеру, свои полтора миллиона наш инвестор получит за 6 лет жизненного цикла инициативы при норме дисконта 10% равными частями по 250 тысяч рублей в год (т.е. как аннуитет):
Применяя формулу годовых расчетов, можно находить коэффициенты отдельно по каждому периоду, а затем просуммировать их:
| CF1 | CF2 | CFN | |||
| NPV = | —— | + | —— | +…+ | —— |
| (1+R) | (1+R)2 | (1+R)6 |
PV = 227272 + 206611 + 187828 + 170765 + 155279 + 141083 = 1088838 рублей.
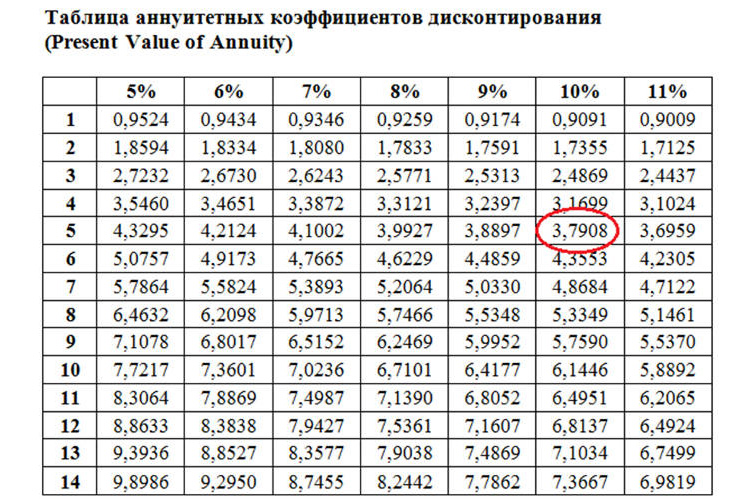
Если же использовать таблицу коэффициентов аннуитетных платежей, то достаточно будет размер среднегодового платежа умножить на фактор, указанный в нужной ячейке таблицы (в данном случае это 4,3553).
PV = 250000 * 4,3553 = 1088825 рублей
Таким образом, мы видим, что показатель, найденный по формуле, практически аналогичен величине, определенной при помощи таблиц (1088838 против 1088825).
Некоторые особенности практических расчетов фактора приведения
В заключение хотелось бы остановиться еще на нескольких моментах, связанных с приведением денежных потоков, о которых спрашивают пользователи Интернета. В частности, возникает вопрос, как вычислять фактор, когда шаг задается в разных единицах, например годах и месяцах, и различаются ли формулы при таких расчетах.
При периоде дисконтирования, равном одному месяцу, коэффициент высчитывается по такой формуле:
1 / (1 + R) в степени (Месяц – 1) / 12,
где:
- R – норма дисконта;
- Месяц – номер порядковый месяца проекта.
При годовом периоде приведения применяется такой механизм расчета:
1 / (1 + R) в степени Год – 1,
где:
- Год – номер порядковый года жизненного цикла начинания.
Если же период считается поквартально, то для каждого месяца квартала принимается во внимание показатель, равный последнему месяцу в квартале, то есть для 1, 2 и 3 месяца берется показатель 3 месяца и т.д.
Также на форумах обсуждают ситуацию, когда контролирующие органы иногда требуют считать коэффициент приведения по формуле КД = 1/(1+R)^(n-0,5) вместо стандартной КД = 1/(1+R)^n.
Такой подход называется моделью среднегодового дисконтирования.Здесь дисконтирование проводится по состоянию на середину календарного года (или периода приведения), а не на его начало или конец.
Среднепериодическое дисконтирование применяется в случаях, когда идет постоянный равномерный приток денег (например, от работы промышленного предприятия). Хотя среди специалистов мнения о целесообразности такого метода расчета расходятся.
Коэффициент дисконта, благодаря своей гибкости широко используется экономистами и финансистами. Он показывает перспективу и потенциальную доходность отдельного проекта во временном отрезке. При этом, у этого финансового инструмента есть серьезный недостаток: он хорошо работает в государствах со стабильными рынками и налаженными рыночными механизмами. Применение его в странах, для которых характерна переходная экономическая модель, грозит существенными неточностями, поскольку адекватно просчитать многие риски для нахождения нормы дисконта в таких условиях очень трудно.
Формула коэффициента дисконтирования
Сущность коэффициента дисконтирования
Предприниматели, которые планируют совершенствовать бизнес и двигаться по направлению к финансовому благополучию компании предприятия, не должны пренебрегать понятием «коэффициент дисконтирования».
С точки зрения финансового анализа, формула коэффициент дисконтирования обозначает приведение будущих поступлений предприятия кстоимости настоящего времени.
Процесс приведения стоимости называют «дисконтированием», а ставку, используемую при этом, – ставкой дисконтирования.
Формула коэффициента дисконтирования применяется на сегодняшний день во многих экономических и финансовых областях. Коэффициент легко применим для определения эффективности бизнес-плана, прогнозирования успеха деятельности любой компании.
Формула коэффициента дисконтирования
Формула коэффициента дисконтирования требует определения стоимости будущих денежных потоков. Для этого сумму предполагаемых поступлений необходимо умножить на коэффициент дисконтирования.
Для того, что бы определить дисконт, используют соответствующую формулу:
Kд=1/ (1+i)N
Здесь i – ставка дисконтирования,
N – время действия проекта, в течение которого планируется получение прибыли.

Ставка дисконтирования
Ставку дисконтирования можно определить в качестве нормы дисконта, который представляет собой переменный показатель, зависящий от большого числа факторов. Ставка — процент, которым выражается доходность от вложенных средств.
На каждый индивидуальный случай существует своя процентная ставка. Например, в качестве процентной ставки может выступать:
- ставка рефинансирования,
- проценты по вкладу (доходность),
- уровень инфляции,
- процентная ставка по кредиту,
- предполагаемая доходность проектов и др.
В процессе вычислений результат всегда будет меньше 1, то есть коэффициент дисконтирования отражает стоимость одной единицы валюты из определенного промежутка времени, которая приводится на текущий день.
Ставка представляет собой объект интереса для инвесторов, поскольку с позиции доходности способ капиталовложения с более высокой нормой дисконта привлекает его больше, чем другой, обладающий аналогичными факторами риска.
Норма дисконта
Формула коэффициента дисконтирования предполагает расчет нормы дисконта, от которого зависит итоговая оценка доходности инвестиционных проектов.
Ставка при этом отражает уровень доходности вложения при учете соответствующего риска, в том числе затрат времени.
Норма дисконта может включать в себя следующие элементы:
- темп инфляции;
- показательуровня риска вложений;
- минимум доходности.
В процессе расчета нормы дисконта могут быть использованы разные ставки, выбор которых происходит в зависимости от ситуации.
Формула рсчета нормы дисконта выглядит следующим образом:
СД = БС + Р
Здесь СД – ставка дисконтирования,
БС – безрисковая ставка,
Р – риски.
К рискам относятся факторы, по причине которых вложение в проекты может быть небезопасным:
- неликвидность проекта,
- ошибка персонала,
- риски, которые характерны для определенной отрасли или государства.
Примеры решения задач
Дисконтирование
– процесс обратный начислению сложных
процентов; он позволяет оценить, что мы
потеряем, не вложив деньги ни в один
проект, в том числе, не поместив их на
депозит. Другими словами, дисконтирование
дает возможность судить о степени
обесценивания денег за n периодов.
Метод
дисконтирования – это метод приведения
денежной суммы будущего периода к
текущему моменту. С позиций текущего
момента будущая сумма (F)
всегда будет меньше настоящей (P),
поскольку знаменатель дроби меньше 1.
,
(1.31)
где
— коэффициент дисконтирования или индекс
приведения будущей суммы к текущему
моменту;
— ставка дисконта, принятая на уровне
среднего % ЦБ по вкладам.
Значения
множителя находятся в специальных
финансовых таблицах.
1.4.4. Оценка денежных потоков с неравными поступлениями
Денежные
потоки в рамках одного временного
периода могут быть распределены
неравномерно, то есть денежные поступления
или выплаты могут быть сконцентрированы
либо в начале периода (поток пренумерандо),
либо в конце периода (постнумерандо).
На практике большее распространение
получил поток постнумерандо. Именно
этот поток лежит в основе методик анализа
инвестиционных проектов. Отчасти это
можно объяснить тем, что подводить итоги
и оценивать финансовый результат принято
в конце отчетного года.
Оценка
денежного потока может выполняться с
позиций будущего (метод наращивания) и
настоящего (метод дисконтирования)
момента времени.
Оценка потока
постнумерандо
Наращенный
денежный поток для исходного потока
постнумерандо имеет вид:
;
…
;
(1.32)
Схему
наращения денежных потоков (С1,
С2…Сn) можно
представить следующим образом:
|
С1 |
|||||||
|
|
|||||||
|
0 |
|||||||
|
|
|||||||
|
Сn |
|||||||
|
Cn-1=Cn-1(1+r) |
|||||||
|
C3(1+r)n-3 |
|||||||
|
C2(1+r)n-2 |
|||||||
|
C1(1+r)n-1 |
Рис.
1.2. Схема наращения денежных потоков.
На С1, первое денежное поступление
начисляются сложные проценты за период
(n-1), и оно в конце первого
периода станет равным С1(1+r)n-1
и т.д. На последнее поступление Сn
% не начисляются.
Будущая стоимость исходного денежного
потока (С1, С2…Сn)
постнумерандо Fpst
может быть оценена как сумма
наращенного потока:
, (1.33)
где k – порядковый номер поступления
(или количество периодов начисления).
Приведенный денежный поток для исходного
потока постнумерандо согласно рис. 1.2
(1.34)
|
С1 |
|||||||
|
|
|||||||
|
0 |
|||||||
Рис.
1.3. Схема приведения денежных потоков.
Приведенная
стоимость денежного потока постнумерандо
PVpst
в общем случае рассчитывается по
формулам:
(1.35)
Пример.
Рассчитать приведенную стоимость
денежного потока постнумерандо 70, 120,
60, 90, если ставка дисконтирования r-12%.
|
Год |
Денежный поток, ден. ед. |
Коэффициент дисконтирования |
Приведенный поток (текущая стоимость), |
|
1 2 3 4 |
70 120 60 90 |
0,8929 0,7972 0,7118 0,6355 |
62,5 95,67 42,71 57,20 |
|
340 |
258,1 |
Оценка потока
пренумерандо.
Логика
оценки денежного потока в этом случае
аналогична предыдущей, разница в формулах
объясняется сдвигом поступлений к
началу соответствующих периодов. Схема
наращения денежного потока пренумерандо
будет выглядеть следующим образом.
(1.36)
Очевидно, что
(1.37)
|
C1 |
||||||
|
|
||||||
|
0 |
||||||
|
|
||||||
|
Сn(1+r) |
||||||
|
С3(1+r)n-2 |
||||||
|
С2(1+r)n-1 |
||||||
|
С1(1+r)n |
Рис.
1.4. Схема наращения потока пренумерандо
Схема
дисконтирования потока пренумерандо
может быть представлена следующим
образом:
|
С1 |
|||||||||
|
|
|||||||||
|
0 1 |
|||||||||
|
|
|||||||||
Рис.
1.5. Схема дисконтирования потока
пренумерандо.
В этом
случае приведенный поток пренумерандо
будет иметь вид:
,
(1.38)
а его
стоимость может быть рассчитана по
формуле:
или (1.39)
(1.40)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

Рассмотрим более детально данное понятие и способы определения его величины. Коэффициент является показателем, позволяющим определить количество денег, которое сможет получить инвестор через определенный период времени, учитывая потенциальные риски и временной фактор. Это предусматривает приведение денежных потоков в будущей перспективе к состоянию на текущий период, то есть на дату проведения расчетов.
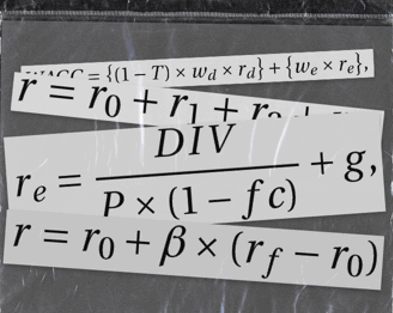
Это свидетельствует о том, что перед инвестированием у инвестора должны быть гарантии того, что в продолжении жизненного цикла инвестиционного проекта он не только не потерпит убытки за счет удешевления денег, но и сможет извлечь определенный доход.
Временной период, в течение которого проходит реализация проекта и она начинает приносить прибыль инвесторам, определяется предварительно. Чаще всего он устанавливается в соответствии с нормативными сроками эксплуатации оборудования, после завершения которых исчерпываются технические возможности процессов производства. Объективность расчетов обусловлена грамотным определением временных интервалов реализации проекта.

- оценить экономическую эффективность деятельности компании;
- рассчитать эффективность инвестпроекта;
- изучить альтернативы возможного инвестирования денег между различными направлениями и проектами, а также внутри одной компании, и выбрать самые перспективные направления инвестиционного развития;
- выполнить многосторонние вычисления;
- взять кредит в банке на инвестиционное развитие.
Коэффициент фактически определяет своего рода норматив издержек или поступления средств при инвестировании капитала в другой проект. Иначе говоря, данный показатель позволяет рассчитать величину процента, на который необходимо умножить планируемую прибыль с целью выхода на определенную сумму в отношении к текущему состоянию.
Как определить коэффициент дисконтирования
Разберем подробно, как вычислить данный показатель. Как правило, имеется в виду многоэтапный расчет, позволяющий определить перспективность и экономический эффект от реализации инвестпроекта. По этой причине коэффициент способствует приведению объема денежных потоков на N-м шаге к моменту приведения.
Для расчета коэффициента дисконтирования формула имеет следующий вид:
PV (приведенная стоимость) = FV (будущая стоимость) х 1/(1+R) n
Если выделить параметр приведения стоимости, получаем следующую формулу:
КД = 1/(1+R) х n
где R представляет собой определенный показатель нормы дисконта (ставка дисконтирования), а n – число шагов (временных интервалов от будущего момента до текущего в виде количества месяцев или лет).
Полученное значение всегда не превышает единицу. Он демонстрирует стоимость одной вложенной денежной единицы спустя какой-либо временной период. При этом условия должны соответствовать тем, которые были приняты для расчетов.
Основным элементом, необходимой составляющей для расчета коэффициента дисконтирования считается ставка дисконтирования. Для вычисления нормы дисконта предусмотрено много методов. Каждый из них базируется на разных принципах:
- различные модификации модели CAPM, определяющие стоимость капитальных активов компании;
- модель WACC, предусматривающая определение объема заемного капитала и собственных денежных средств;
- ROE, ROA и другие методики определения рентабельности капитала;
- кумулятивный метод расчета рисковых премий;
- экспертный (субъективный) метод, который базируется на аналитических прогнозах экспертов;
- модель Гордона, которая представляет собой дивидендный метод.
V = CF i+1 / R – g
Где V представляет собой окончательную стоимость на момент завершения прогнозного периода, CF i+1 – денежные потоки, полученные в течение 1-го года остаточного (постпрогнозного) периода.
R – это норма дисконта, g – темпы роста потока денег в долгосрочной перспективе.
За ставку дисконтирования могут быть приняты:
- темпы инфляции;
- стоимость долгосрочных депозитов;
- стоимость долгосрочных займов;
- величина ставки рефинансирования ЦБ РФ.
Инвестор сам определяет подходящий для него оценочный критерий, при этом сам несет риски, связанные с данным выбором.
При неправильном определении ставки дисконтирования или в случае, если она не учитывает главные риски, коэффициент будет рассчитан некорректно. Инвестор получит недостоверный прогноз, который повлечет за собой убытки.
Еще одним элементом формулы является жизненный цикл инвестиционного проекта. Он представляет собой число анализируемых временных интервалов, в продолжении которых инвестпроект будет способен к генерированию денежных потоков. Чем более достоверно определены эти составляющие, тем выше точность окончательного результата.
Примеры расчетов денежных потоков с применением коэффициента дисконтирования
Разберем примеры вычислений. Инвестор вложил в новый инвестпроект 800 000 руб. сроком на 6 лет. В соответствии с изученным бизнес-планом по прошествии этого периода инвестор сможет одним платежом получить 1 500 000 руб. Кумулятивно вычислена норма дисконта. Она составляет 12 процентов, причем процент ставки дисконтирования при расчетах учитывается, как 0,12.
Применяя вышеуказанную формулу, можно определить коэффициент дисконтирования:
КД = 1 / (1 + 0,12) х 6 = 0,5066

PV = FV * 1/(1+R) х n = 1 500 000 х 0,5066 = 759 900 руб.
На основании полученных результатов можно прийти к заключению, которое будет неблагоприятным для инвестора. С учетом данных условий он не только не получит прибыли. но и не сможет вернуть инвестированные средства.
Таким образом, инвестору лучше отказаться от такой идеи вложения средств. Существуют также следующие варианты (при наличии возможности):
- предложение о внесении изменений в главные условия инвестпроекта;
- сокращение срока реализации инвестиционного проекта;
- уменьшение ставки дисконтирования.
Допустим, в приведенном примере ставка дисконтирования уменьшена до 10 процентов. В данном случае коэффициент будет равен 0,5645, а приведенная стоимость денежного потока увеличится до 846 750 руб. Это поможет сделать инвестпроект доходным.
Аналогично сложится ситуация, если уменьшить период реализации проекта на один год. Даже с учетом предыдущей ставки дисконтирования коэффициент составит 0,5674, а стоимость приведенного денежного потока будет равна 851 100 руб.
Стоит заметить, что для вычисления коэффициента можно не использовать указанные выше формулы. Чтобы упростить процедуру расчетов существует и часто используется инвесторами таблица коэффициентов дисконтирования.
Она сформирована согласно стандартным принципам построения таблиц. Горизонтальная ось содержит процентные ставки, на вертикальной оси указываются периоды реализации инвестиционного проекта. Чтобы найти необходимое значение, находится ячейка пересечения подходящего срока и процентной ставки. Коэффициенты в таблице указаны с точностью до 10-тысячных. Наглядно это можно увидеть на скриншоте ниже.
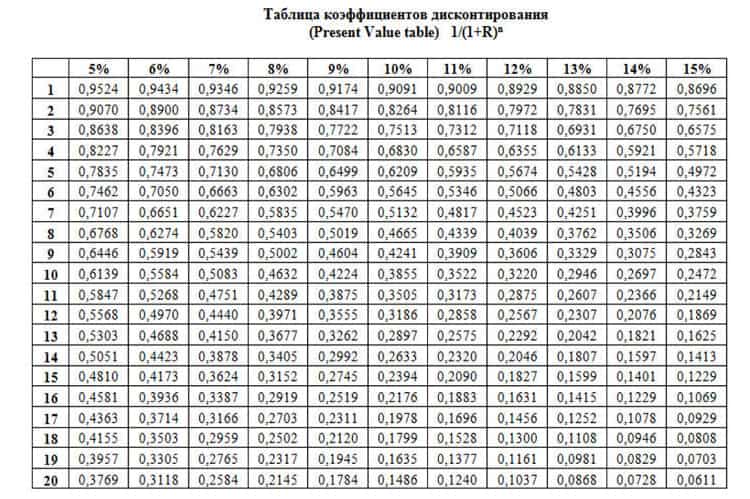
В указанном выше примере рассматривалась выплата средств единым платежом, который проводится по завершении инвестиционного проекта. Практический опыт показывает, что намного чаще предусматриваются ежегодные выплаты. В этом случае, чтобы расчеты были корректными, следует вычислять коэффициент в отдельности для каждого года.
Например, 1 500 000 руб. инвестор получит за шестилетний период реализации проекта при ставке дисконтирования, равной 10 процентов, в равных частях, в виде аннуитетных платежей по 250 000 руб. ежегодно.
Используя формулы ежегодных вычислений можно определять коэффициенты дисконтирования в отдельности для каждого временного интервала. Потом их можно суммировать.

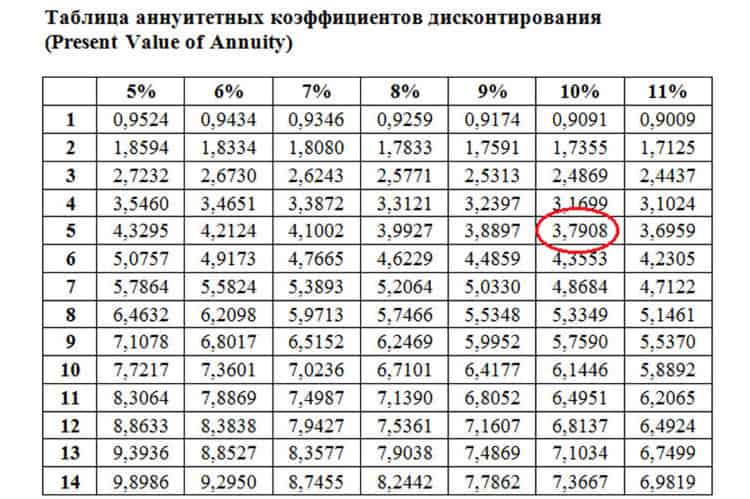
Особенности расчетов коэффициента, используемых на практике
В завершении рассматриваемой темы, следует остановиться на некоторых особенностях, которые связаны с вычислением стоимость приведенных потоков денег. У начинающих инвесторов часто возникает вопрос: как определить коэффициент дисконтирования при условии, если шаг задан в различных единицах. Есть ли отличия в формулах в данной ситуации.
Если интервал равен месяцу, фактор дисконтирования рассчитывается так:
1 / (1 + R) (Месяц – 1) / 12
Если интервал равен году, коэффициент рассчитывается так же, только в формулу вместо месяца подставляется год.
1 / (1 + R) (Год – 1) / 12
При расчете поквартального интервала учитывается показатель для каждого месяца, который равен последнему в каждом квартале. Другими словами, для 1-го, 2-го и 3-го месяца учитывается значение 3-го и так далее.
Одним из распространенных вопросов, интересующих инвесторов, является ситуация, при которой контролирующие инстанции выставляют требования проводить расчеты коэффициента вместо стандартной формулы, рассмотренной выше, по следующей:
КД = 1/(1+R) (n-0,5)
Данный подход к определению коэффициента носит название «модель среднегодового (среднепериодического) дисконтирования», которое производится по состоянию не на начало или конец интервала (чаще всего года), а на его середину.
Среднегодовое дисконтирование целесообразно при направлении постоянного и равномерного денежного потока. К примеру, это характерно для предприятий, осуществляющих деятельность в различных отраслях промышленности. Однако мнения экспертов о целесообразности такой модели расчетов зачастую расходятся.
За счет гибкости в применении коэффициент дисконтирования пользуется популярностью среди экономистов и финансовых аналитиков. Он позволяет определить перспективность и потенциальную прибыльность каждого инвестпроекта в определенном периоде времени. Стоит учесть, что данный финансовый инструмент имеет один весомый недостаток. Он является эффективным, если государство имеет стабильные финансовые рынки и отлично налаженные рыночные механизмы. Использовать его в государствах с переходной моделью экономики не рекомендуется в результате неточности и некорректности расчетов. Адекватно рассчитать риски для определения ставки дисконтирования в данной ситуации будет затруднительно.
Кроме приведенных выше расчетов, начинающим инвесторам важно руководствоваться методами фундаментального анализа, которые изучают такие факторы, как денежные потоки, оценку спроса и предложения, взаимосвязь финансовых рынков между собой и многие другие.
Важнейший этап на пути к собственному бизнесу – это разработка бизнес-плана. Будучи руководством к действию, направленному на достижение экономической выгоды, бизнес-план в обязательном порядке содержит статью расходов, в которую финансовые менеджеры рекомендуют включать ставку дисконтирования.
Но как показывает практика, многие начинающие предприниматели не только избегают использования этого параметра, но и не догадываются о его существовании.
Что такое коэффициент дисконтирования, как рассчитать этот показатель и чем объясняется необходимость его присутствия в бизнес-плане?
Содержание
- Понятие
- Расчет
- Ставка дисконтирования
- Пример расчета
- Таблица
- Преимущества и недостатки дисконта
Понятие
Предпринимателям, планирующим развивать бизнес и двигаться по направлению к финансовому благополучию предприятия, стоит освоить понятие «коэффициент дисконтирования».
Что это такое? На языке финансового анализа, таким термином обозначают приведение будущих поступлений фирмы к их стоимости в настоящий момент.
Сам процесс приведения в экономике называют «дисконтированием», а ставку, используемую для расчета показателя – ставкой дисконтирования.
Сегодня применение данному показателю нашли практически в любой сфере экономики и финансов. Его легко можно применить для определения эффективности бизнес-проекта, он способен предугадать финансовый успех конкретной организации.
При разработке строки затрат бизнес-плана сложно обойтись без коэффициента дисконтирования, так как он поможет рассчитать необходимые капиталовложения или выбрать альтернативный вариант, чтобы избежать лишних расходов.
Расчет
Чтобы определить стоимость денежных потоков в будущем, необходимо умножить сумму предполагаемых поступлений на коэффициент дисконтирования. Как найти этот показатель?
Для расчета дисконта применяют следующую формулу:
Kd=1/ (1+i)n;
Где n – время, в течение которого планируется получить прибыль.
Величина i обозначает ставку дисконтирования. Она также известна под названием «норма дисконта». Это переменный показатель, который зависит от множества факторов. Ставкой является процент, выражающий доходность от вкладываемых средств.
Для каждого индивидуального случая предназначена своя процентная ставка. Так, в качестве данной величины может быть использована ставка рефинансирования, процент доходности по вкладу, инфляция, кредитная процентная ставка, предполагаемая доходность проекта и прочее.
В ходе вычислений результат всегда оказывается ниже единицы. Коэффициент дисконтирования показывает, сколько стоит одна единица валюты из определенного периода времени, приведенная на текущую дату.
Ставка дисконтирования
В процессе вычисления коэффициента дисконтирования одной из самых важных задач является расчет нормы дисконта, так как от этого зависит итоговая оценка доходности инвестиционного проекта.
Сама по себе ставка является объектом интереса для инвестора, так как с точки зрения доходности способ капиталовложения с более высокой нормой дисконта должен привлекать его больше, нежели любой другой с аналогичными факторами риска.
Чтобы произвести дисконтирование, необходимо осуществлять расчет по данной формуле коэффициента.
Стоит учитывать и тот факт, что ставка отражает уровень доходности вложений с учетом определенных рисков, а также временных затрат. Что включает в себя норма дисконта:
- рост инфляции;
- показатель, отражающий уровень риска вложений;
- минимальную степень доходности, на которую в любом случае может рассчитывать инвестор.
Как уже было указано, для расчета нормы дисконта используются различные ставки, выбор которых зависит от заданной ситуации. Проценты по депозитам или уровень доходности от облигаций – это лишь основа, «безрисковая ставка» которая берется с поправкой на некоторые риски и временной фактор.
Формула расчета нормы дисконта:
Ставка дисконтирования=безрисковая ставка + риски
В качестве рисков принимаются различные факторы, под воздействием которых вложение денежных средств в конкретный проект становится небезопасным. В данный список можно отнести:
Риски неликвидности нового проекта:
- риски, характерные для какой-либо отрасли;
- ошибки персонала;
- проблемы, определяемые конкретно для данной страны.
Чем точнее определяют процентную ставку дисконта, тем больше шансов получить желаемую доходность от проекта.
Пример расчета
Для большей наглядности и лучшего понимания понятия «коэффициент дисконтирования», стоит привести пример расчета показателя по формуле.
Предположим, некий инвестор планирует получить от каких-либо вложений сумму в 100000 долларов через 5 лет. Чему равнозначна эта сумма в пересчете на сегодня?
Чтобы произвести дисконтирование, необходимо осуществлять расчет по формуле Kd=1/ (1+i)n. Если взять за ставку дисконтирование 10%, можно получить следующее значение: Kd=1(1+10%)5=0,6209. Это значит, что один доллар из предполагаемой суммы через пять лет, приведенный на текущую дату, равен 62,09 центам.
Следовательно, 100000 долларов через пять лет – это 62090 долларов сегодня при ставке 10%. Иными словами, 62090 долларов – дисконтированная стоимость суммы в 100000 долларов.
Таблица
Исходя из формулы расчета коэффициента, можно сделать вывод о зависимости его значения от количества периодов и ставки дисконтирования. Чтобы сэкономить время и не производить расчеты дисконта каждый раз, принято пользоваться так называемой таблицей коэффициентов дисконтирования.
Таблица приводит данные с точностью до десятитысячных.
Пользоваться ею достаточно просто – стоит лишь знать исходную ставку дисконтирования и предполагаемый период для расчета. Нужное значение дисконта можно найти на пересечении столбцов этих значений.
Принцип использования таблицы легко усвоить на примере. Предположим, у инвестора появляется необходимость выбора:
- Получить 12000 евро сегодня.
- Получить 15000 евро через 3 года.
Сделать правильный выбор поможет расчет дисконта по таблице. Для этого, необходимо выяснить, чему равна сумма в 15000 евро к получению через 3 года, приведенная на текущую дату. Чтобы произвести вычисления, придется выяснить средний процент по банковским валютным депозитам, оформленным на 3 летний срок.
Если предположить, что ставка по депозиту равна 10%, можно определить коэффициент дисконтирования:
| Период/ставка | 9% | 10% |
| 3 | 0,7722 | 0,7513 |
| 4 | 0,7084 | 0,6830 |
Итак, на пересечении столбцов «3» и «10%» находится показатель, равный 0,7513. Он означает, что 1 евро спустя 3 года равен 75,13 евроцентам сегодня при депозитной ставке в 10%. Далее следует составить элементарную пропорцию:
| Сегодня | Через 3 года |
| 0,7513 евро | 1 евро |
| Х | 15000 евро |
Х=0,7513*15000/1=11269,5 евро. Эта сумма является дисконтированной стоимостью суммы 15000 евро к получению через 3 года. То есть, 15000 евро, приведенные на текущую дату, дешевле суммы в 12000 евро, взятых сегодня. Соответственно, инвестору из задачи стоит воспользоваться первым предложением.
По аналогии с таблицей дисконта, можно пользоваться таблицей наращения. Она действует прямо противоположно – показывает номинальную стоимость текущих доходов в будущем периоде.
Преимущества и недостатки дисконта
Польза определения коэффициента дисконтирования очевидна: показатель переводит стоимость будущих денежных потоков в настоящий момент и помогает оценить степень рисков.
При этом коэффициент обладает и некоторыми минусами:
- сложность в прогнозировании относительно инвестиционных проектов;
- невозможность учета внешних факторов, таких, как неблагоприятные погодные условия.
Несмотря на выявленные недостатки, коэффициент дисконтирования является незаменимым способом для оценки привлекательности бизнес-идеи.