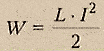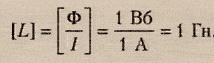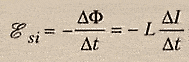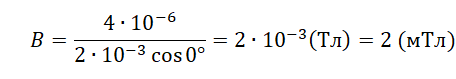Магнитный поток как найти угол - AvtoShod.ru - решение различных проблем

Φ — магнитный поток
B — магнитная индукция
S — площадь
α — угол

Найти

Известно, что:

Вычислить ‘Φ‘

Источник

Скачать материал

Сейчас обучается 110 человек из 46 регионов

Сейчас обучается 141 человек из 54 регионов

Сейчас обучается 20 человек из 14 регионов

Описание презентации по отдельным слайдам:

2 слайд

Вектор магнитной индукции

Там, где силовые линии гуще, индукция магнитного поля больше.

Там, где силовые линии реже, индукция магнитного поля меньше
В
В
В
В
3 слайд

Отличие магнитной индукции от магнитного потока
Вектор магнитной индукции В характеризует магнитное поле в каждой точке пространства, а магнитный поток – определенную область пространства
Магнитный поток определяется числом линий, пронизывающих контур)
4 слайд

Зависимость магнитного потока от площади S
Уменьшение площади контура при неизменной магнитной индукции магнитного поля приводит к уменьшению числа линий, пронизывающих контур и, следовательно, к уменьшению Ф.
При одинаковой магнитной индукции В, чем больше
площадь контура S, тем больше магнитный поток Ф, пронизывающего данный контур.
5 слайд

Зависимость магнитного потока от магнитной индукции В
При усилении магнитного поля количество силовых линий возрастает, следовательно, возрастает и магнитный поток.
При одинаковой площади контура S, чем больше магнитная индукция В, тем больше магнитный поток Ф, пронизывающего данный контур.
6 слайд

Зависимость магнитного потока от угла α
Поворот контура также приводит к изменению числа линий, пронизывающих замкнутый контур.
7 слайд

Зависимость магнитного потока от угла α
Если же плоскость контура параллельна линиям магнитной индукции, то поток сквозь него равен нулю: Ф = 0.
8 слайд

Зависимость магнитного потока от угла α
Если угол α = 0º
В этом случае линии В и нормали n к площадке параллельны.
Но В и площадка S перпендикулярны друг другу !!!
Тогда cos 0º =1 , магнитный поток принимает свое максимальное значение.

n
B
n
n
s
9 слайд

Зависимость магнитного потока от угла α
2) Если угол α= 90 º
В этом случае линии В и нормали n к площадке перпендикулярны
Но В и площадка S параллельны друг другу!!!
cos 90º =0 и магнитный поток будет минимальным. Ф=0

n
В
s
10 слайд

Способы изменения магнитного потока

1) Путем изменения площади контура S

2) Путем изменения величины магнитного поля В

3) Путем изменения угла α
11 слайд

Обозначение и формула магнитного потока
Ф — символ магнитного потока
Ф — скалярная величина.

Формула для расчета магнитного потока
Ф=В·S·cosα

В
f
α
n
s
12 слайд

Величины, входящие в формулу
Ф=В·S·cosα

n
В – магнитная индукция,
S – площадь контура,
ограничивающего площадку,
α – угол между направлением вектора индукции В и нормалью n
(перпендикуляром) к площадке

S
В
α
13 слайд

Определение магнитного потока
Произведение индукции магнитного поля, пронизывающей поперечное сечение контура, на площадь этого контура называется магнитным потоком
В
S
14 слайд

Вильгельм Эдуард Вебер
1804 – 1891 г.г
15 слайд

Единица измерения магнитного потока
Вб
1 Вб — магнитный поток, созданный магнитным полем с индукцией 1 Тл через поверхность площадью 1м2 , расположенную перпендикулярно вектору магнитной индукции.
S=1м2

В=1 Тл
16 слайд

Как надо ориентировать рамку в однородном магнитном поле, чтобы поток через рамку был равен нулю?
Б) параллельно линиям магнитной индукции
А) перпендикулярно линиям магнитной индукции
В) под любым углом к линиям магнитной индукции
16
Меняется ли магнитный поток при таком вращении контура, когда линии магнитной индукции то пронизывают его, то скользят по его поверхности?
17 слайд

Как изменится магнитный поток, пронизывающий контуры I и II, при их вращении вокруг указанных осей?
17
контур I
II
контур II
18 слайд

В) если магнит покоится относительно катушки?
Как изменяется магнитный поток, пронизывающий витки катушки…
А) при вдвигании магнита внутрь катушки?
Б) при выдвигании магнита из катушки?
18
19 слайд

19
Электрический ток, протекающий по виткам катушки К1, создает в пространстве вокруг нее магнитное поле. Как можно менять магнитный поток, пронизывающий катушку К2?
+
—
20 слайд

Решение задач
Задача №1
Контур с площадью
100 см2 находится в однородном магнитном поле с индукцией 2 Тл. Чему равен магнитный поток, пронизывающий контур, если плоскость контура и вектор индукции перпендикулярны ?
S=100 см2 0,01м2
В=2 Тл
α=0º
Ф — ?

Ф=В·S·cosα
Ф=0,02 Вб
21 слайд

Решение задач
Задача №2
Контур площадью 1 м2 находится в однородном магнитном поле с индукцией 0,5Тл, угол между вектором индукции и нормалью к поверхности контура 60º. Каков магнитный поток через контур?

S=1 м2
В=0,5 Тл
α=60º
Ф — ?

Ф=В·S·cosα
Ф=0,25 Вб
22 слайд

Решение задач
Задача 3
Проволочное кольцо радиусом 1 м ,
поворачивается на 1800 относительно вертикальной оси. Индукция магнитного поля равна 5 Тл и сразу перпендикулярна кольцу. Найдите изменение магнитного потока через кольцо в результате поворота
R=1 м2
В=5 Тл
α1 =0º
α2 =180º S=R2
ΔФ — ?

ΔФ=В·S·(cosα1- cosα2)
ΔФ=62,8 Вб
23 слайд

Домашнее задание
п 42, упр 39(все варианты)

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 267 631 материал в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

Другие материалы

30.01.2023
85
6

30.01.2023
79
1

30.01.2023
77
3

30.01.2023
73
1

30.01.2023
111
3

Вам будут интересны эти курсы:

Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»
Курс повышения квалификации «Формирование компетенций межкультурной коммуникации в условиях реализации ФГОС»
Курс повышения квалификации «Основы управления проектами в условиях реализации ФГОС»
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС педагогических направлений подготовки»
Курс профессиональной переподготовки «Организация маркетинга в туризме»
Курс повышения квалификации «ЕГЭ по физике: методика решения задач»
Курс профессиональной переподготовки «Управление ресурсами информационных технологий»
Курс повышения квалификации «Психодинамический подход в консультировании»
Курс профессиональной переподготовки «Организация маркетинговой деятельности»
Курс профессиональной переподготовки «Технический контроль и техническая подготовка сварочного процесса»

Источник

Магнитный поток

Автор:
Субботин Б.П.

На
картинке показано однородное магнитное
поле. Однородное означает одинаковое
во всех точках в данном объеме. В поле
помещена поверхность с площадью S. Линии
поля пересекают поверхность.

Определение
магнитного потока:

Магнитным
потоком Ф через поверхность S называют
количество линий вектора магнитной
индукции B, проходящих через поверхность
S.

Формула
магнитного потока:

Ф
= BS cos α

здесь
α — угол между направлением вектора
магнитной индукции B и нормалью к
поверхности S.

Из
формулы магнитного потока видно, что
максимальным магнитный поток будет при
cos α = 1, а это случится, когда вектор B
параллелен нормали к поверхности S.
Минимальным магнитный поток будет при
cos α = 0, это будет, когда вектор B
перпендикулярен нормали к поверхности
S, ведь в этом случае линии вектора B
будут скользить по поверхности S, не
пересекая её.

А
по определению магнитного потока
учитываются только те линии вектора
магнитной индукции, которые пересекают
данную поверхность.

Измеряется
магнитный поток в веберах (вольт-секундах):
1 вб = 1 в * с. Кроме того, для измерения
магнитного потока применяют максвелл:
1 вб = 10⁸ мкс.
Соответственно 1 мкс = 10^-8 вб.

Магнитный
поток является скалярной величиной.

ЭНЕРГИЯ
МАГНИТНОГО ПОЛЯ ТОКА

Вокруг
проводника с током существует магнитное
поле, которое обладает энергией.
Откуда
она берется? Источник тока, включенный
в эл.цепь, обладает запасом энергии.
В
момент замыкания эл.цепи источник тока
расходует часть своей энергии на
преодоление действия возникающей ЭДС
самоиндукции. Эта часть энергии,
называемая собственной энергией тока,
и идет на образование магнитного
поля.

Энергия магнитного поля
равна собственной
энергии тока.
Собственная
энергия тока численно равна работе,
которую должен совершить источник тока
для преодоления ЭДС самоиндукции, чтобы
создать ток в цепи.

Энергия
магнитного поля, созданного током, прямо
пропорциональна квадрату силы тока.
Куда
пропадает энергия магнитного поля после
прекращения тока? — выделяется ( при
размыкании цепи с достаточно большой
силой тока возможно возникновение искры
или дуги)

4.1. Закон электромагнитной индукции. Самоиндукция. Индуктивность

Основные
формулы

· Закон
электромагнитной индукции (закон
Фарадея):

,
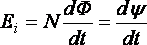
(39)

где – эдс индукции;–
полный магнитный поток (потокосцепление).

· Магнитный
поток, создаваемый током в контуре,

,
(40)

где –
индуктивность контура;–
сила тока.

· Закон
Фарадея применительно к самоиндукции

.
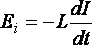
(41)

· Эдс индукции, возникающая при
вращении рамки с током в магнитном поле,

,
(42)

где –
индукция магнитного поля;–
площадь рамки;–
угловая скорость вращения.

· Индуктивность
соленоида

,
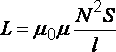
(43)

где –
магнитная постоянная;–
магнитная проницаемость вещества;–
число витков соленоида;–
площадь сечения витка;–
длина соленоида.

· Сила
тока при размыкании цепи

,
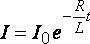
(44)

где –
установившаяся в цепи сила тока;–
индуктивность контура,–
сопротивление контура;–
время размыкания.

· Сила
тока при замыкании цепи

.
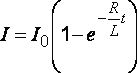
(45)

· Время
релаксации

.
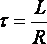
(46)

Примеры
решения задач

Пример
1.

Магнитное
поле изменяется по закону ,
где=
15 мТл,. В
магнитное поле помещен круговой
проводящий виток радиусом = 20
см под угломк
направлению поля (в начальный момент
времени). Найти эдс индукции, возникающую в
витке в момент времени=
5 с.

Решение

По
закону электромагнитной индукции возникающая в
витке эдс индукции ,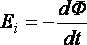
где–
магнитный поток, сцепленный в витке.

где –
площадь витка,;– угол
между направлением вектора магнитной
индукциии
нормалью к контуру:.

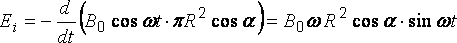
Подставим
числовые значения: =
15 мТл,,= 20
см = = 0,2 м,.

Вычисления
дают .

Пример
2

В
однородном магнитном поле с индукцией =
0,2 Тл расположена прямоугольная рамка,
подвижная сторона которой длиной= 0,2
м перемещается со скоростью=
25 м/с перпендикулярно линиям индукции
поля (рис. 42). Определить эдс индукции, возникающую в
контуре.

Решение

При
движении проводника АВ в магнитном
поле площадь рамки увеличивается,
следовательно, возрастает магнитный
поток сквозь рамку и возникает эдс индукции.

По
закону Фарадея ,
где,
тогда,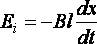
но,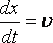
поэтому.

Так, .

Знак
«–» показывает, что эдс индукции
и индукционный ток направлены против
часовой стрелки.

САМОИНДУКЦИЯ

Каждый
проводник, по которому протекает эл.ток,
находится в собственном магнитном поле.

При
изменении силы тока в проводнике меняется
м.поле, т.е. изменяется магнитный поток,
создаваемый этим током. Изменение
магнитного потока ведет в возникновению
вихревого эл.поля и в цепи появляется
ЭДС индукции.

Это
явление называется самоиндукцией.Самоиндукция —
явление возникновения ЭДС индукции в
эл.цепи в результате изменения силы
тока.
Возникающая при этом ЭДС
называется ЭДС
самоиндукции

Проявление
явления самоиндукции

Замыкание
цепи

При
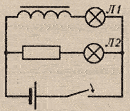
замыкании в эл.цепи нарастает ток, что
вызывает в катушке увеличение магнитного
потока, возникает вихревое эл.поле,
направленное против тока, т.е. в катушке
возникает ЭДС самоиндукции, препятствующая
нарастанию тока в цепи ( вихревое поле
тормозит электроны).
В результатеЛ1
загорается позже, чем
Л2.

Размыкание
цепи

При
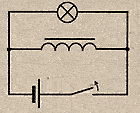
размыкании эл.цепи ток убывает, возникает
уменьшение м.потока в катушке, возникает
вихревое эл.поле, направленное как ток
( стремящееся сохранить прежнюю силу
тока) , т.е. в катушке возникает ЭДС
самоиндукции, поддерживающая ток в
цепи.
В результате Л при выключении ярко
вспыхивает.

Вывод

в
электротехнике явление самоиндукции
проявляется при замыкании цепи (эл.ток
нарастает постепенно) и при размыкании
цепи (эл.ток пропадает не сразу).

ИНДУКТИВНОСТЬ

От
чего зависит ЭДС самоиндукции?

Эл.ток
создает собственное магнитное поле .
Магнитный поток через контур пропорционален
индукции магнитного поля (Ф ~ B), индукция
пропорциональна силе тока в проводнике
(B
~ I), следовательно магнитный поток
пропорционален силе тока (Ф ~ I).
ЭДС
самоиндукции зависит от скорости
изменения силы тока в эл.цепи, от свойств
проводника
(размеров и формы) и от
относительной магнитной проницаемости
среды, в которой находится
проводник.
Физическая величина,
показывающая зависимость ЭДС самоиндукции
от размеров и формы проводника и от
среды, в которой находится проводник,
называется коэффициентом самоиндукции
или индуктивностью.

Индуктивность —
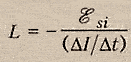
физ. величина, численно равная ЭДС
самоиндукции, возникающей в контуре
при изменении силы тока на 1Ампер за 1
секунду.
Также индуктивность можно
рассчитать по формуле:

где
Ф — магнитный поток через контур, I — сила
тока в контуре.

Единицы
измерения индуктивности в
системе СИ:

Индуктивность
катушки зависит от:
числа витков,
размеров и формы катушки и от относительной
магнитной проницаемости среды
(
возможен сердечник).

ЭДС
САМОИНДУКЦИИ

ЭДС
самоиндукции препятствует нарастанию
силы тока при включении цепи и убыванию
силы тока при размыкании цепи.

Для
характеристики намагниченности вещества
в магнитном поле используетсямагнитный
момент (Р_м). Он
численно равен механическому моменту,
испытываемому веществом в магнитном
поле с индукцией в 1 Тл.

Магнитный
момент единицы объема вещества
характеризует его намагниченность
— I,
определяется по формуле:

I= Р_м /V,
(2.4)

где V —
объем вещества.

Намагниченность
в системе СИ измеряется, как и напряженность,
в А/м,
величина векторная.

Магнитные
свойства веществ характеризуются объемной
магнитной восприимчивостью — c_о , величина
безразмерная.

Если
какое-либо тело поместить в магнитное
поле с индукцией В₀,
то происходит его намагничивание.
Вследствие этого тело создает свое
собственное магнитное поле с индукцией В^‘,
которое взаимодействует с намагничивающим
полем.

В
этом случае вектор индукции в среде (В)будет
слагаться из векторов:

В
= В₀ +
В^‘(знак
вектора опущен), (2.5)

где В^‘ —индукция
собственного магнитного поля
намагнитившегося вещества.

Индукция
собственного поля определяется магнитными
свойствами вещества, которые характеризуются
объемной магнитной восприимчивостью
— c_о ,
справедливо выражение:В^‘ = c_о В₀(2.6)

Разделим
на m₀выражение
(2.6):

В^‘/
m_о= c_о В₀/m₀

Получим: Н^‘= c_о Н₀ , (2.7)

но Н^‘определяет
намагниченность вещества I,
т.е. Н^‘ = I,
тогда из (2.7):

I
= c_о Н₀.
(2.8)

Таким
образом, если вещество находится во
внешнем магнитном поле с напряженностьюН₀,
то внутри него индукция определяется
выражением:

В=В₀ +
В^‘ =
m₀Н₀ +m₀Н^‘ =
m₀(Н₀ +
I) (2.9)

Последнее
выражение строго справедливо, когда
сердечник (вещество) находится полностью
во внешнем однородном магнитном поле
(замкнутый тор, бесконечно длинный
соленоид и т.д.).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

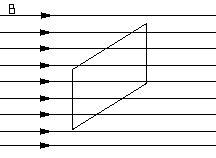
Вероятно, термин «поток» ассоциируется у вас с потоком воды. Если бы вы хотели описать этот поток количественно, то имели бы в виду определенное количество воды, протекающей через поперечное сечение в определенной точке. Такой поток может нести большое или малое количество воды в зависимости от скорости воды и площади этого поперечного сечения.

Магнитный поток — это физическая величина, тесно связанная с явлением электромагнитной индукции. Это сложная величина, довольно абстрактная. Но, как вы правильно догадались, его название берет свое начало в гидродинамике. Здесь, однако, нет потока материи через поверхность, есть только векторы магнитной индукции B, «пронзающие» поверхность и иногда «скользящие» по ней.

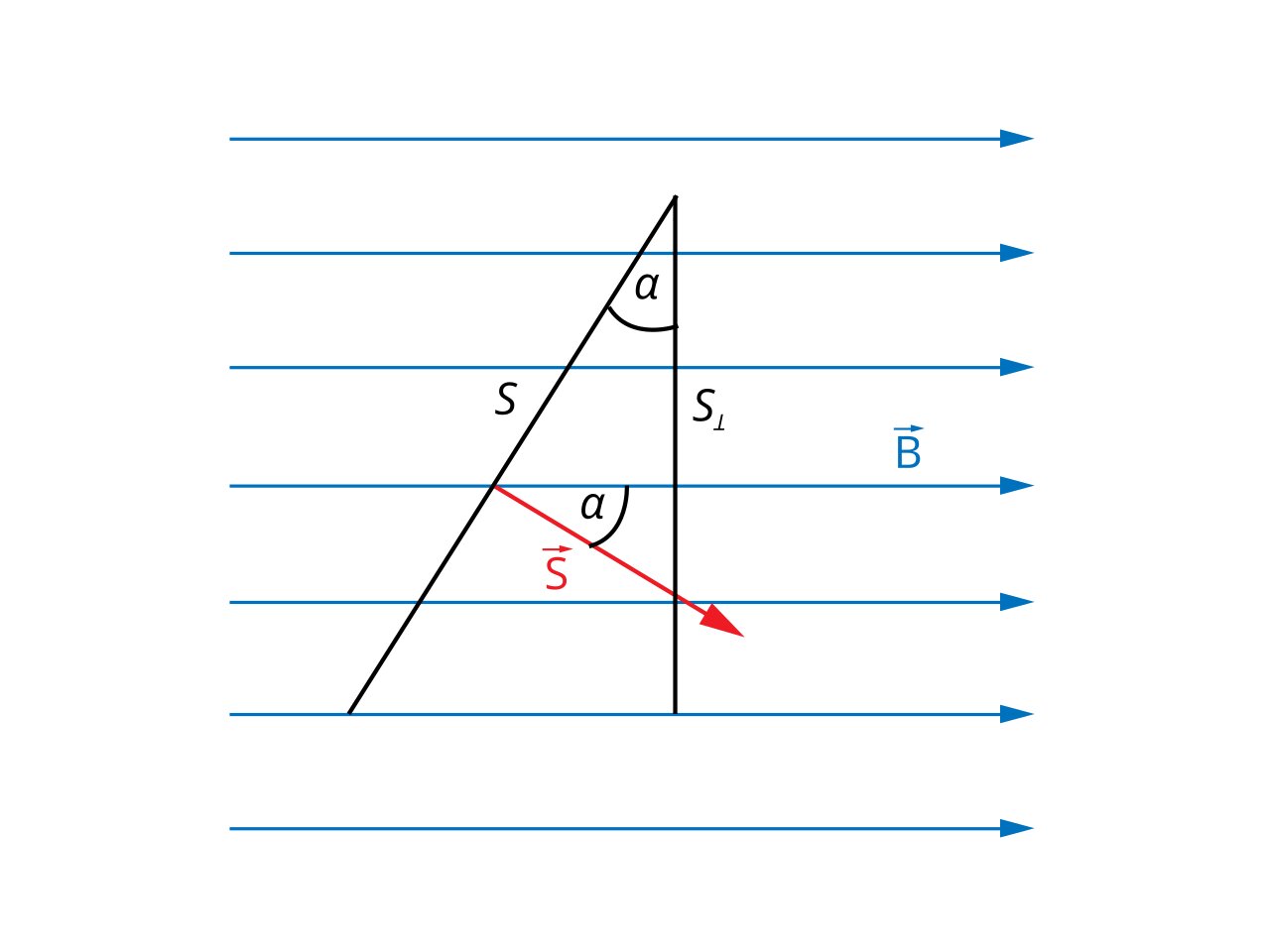
Представьте себе однородное магнитное поле, описываемое вектором магнитной индукции B. Мы помещаем плоскую поверхность с полем S в это поле совершенно произвольным образом, то есть под любым углом по отношению к вектору B (рис. 1). Теперь определим вектор B, перпендикулярный плоскости поверхности. Пусть длина этого вектора равна величине поверхности.

Рис. 1. Плоская поверхность в магнитном поле. Красным цветом обозначен вектор S, представляющий эту поверхность.

Потоком вектора магнитной индукции Ф_B через поверхность S называется скалярное произведение векторов B и S.

Итак можно дать следующее определение термину «магнитный поток»:

Магнитный поток — это поток вектора магнитной индукции B через некоторую поверхность. Для бесконечно малого участка равен произведению модуля | B | на площадь участка dS и косинус угла α между B и нормалью n к плоскости участка. Для поверхности конечных размеров находится как сумма (интеграл) по её малым фрагментам.

Википедия

Зависимости магнитного потока

Используя формулу, можно увидеть, что магнитный поток зависит от трех переменных: магнитного поля B, площади S и угла α.

Магнитный поток линейно зависит от B и S. Например, если увеличить площадь S, но оставить магнитное поле B и угол α прежними, то магнитный поток будет больше. Поэтому большая площадь означает большой поток, а маленькая площадь — маленький магнитный поток.

Если, с другой стороны, увеличить магнитное поле B, то магнитный поток также увеличится. Сильное магнитное поле приводит к большому потоку, слабое поле — к малому магнитному потоку.

В целом, чем больше магнитное поле B или площадь S, тем больше магнитный поток.

Ситуация с углом α немного сложнее. Представьте, что ваша поверхность перпендикулярна магнитному полю, тогда ваш угол α = 0^° . Здесь у вас самый большой магнитный поток. Если теперь шаг за шагом увеличивать угол, магнитный поток уменьшается. Когда вы достигаете α = 90^°, магнитный поток равен нулю, потому что магнитное поле параллельно поверхности. После этого он снова начинает увеличиваться.

Единица измерения и обозначение магнитного потока

Магнитное поле B имеет единицу Тесла (T), а площадь — единицу квадратный метр м² .

Поток является скалярной величиной и его единицей измерения является вебер (Вб): 1 Вб = 1 Т * м² , то есть [Ф] = Т * м² . Обозначается магнитный поток как Ф (символ формулы — греческая фи).

Примеры

Приведенные ниже примеры дадут вам лучшее понимание того, что представляет собой новая концепция и аналогия с потоком воды.

В случае, показанном на рис. 2, поток магнитного поля с магнитной индукцией B через поверхность S составляет: Ф_B = B * S и при этом его значение максимально, так как:

Рис. 2. Поверхность перпендикулярна силовым линиям магнитного поля. Векторы B и S параллельны

2. А в каком случае при ненулевой магнитной индукции Ф_B = 0 ?

Рис. 3. Поверхность параллельна силовым линиям магнитного поля. Векторы B и S перпендикулярны

Определение магнитного потока показывает, что это тот случай, когда:

потому что cos 90^° = 0.

На рис. 3 мы видим, как в этой ситуации располагается плоская поверхность относительно векторов магнитной индукции.

Обратите внимание, что Ф_B можно представить как произведение В и S_⟂, где S_⟂ = S * cos α. Аналогично, вы всегда можете рассчитать величину потока магнитного поля, умножив составляющую магнитной индукции, перпендикулярную поверхности, на величину площади поверхности (см. рис. 4а. и 4б.).

Рис. 4а. Поверхность S⊥ — это проекция поверхности S в направлении, параллельном линиям магнитного поля

Рис. 4б. Вектор B_⟂ — это проекция вектора B на направление вектора S

Как можно рассчитать поток магнитного поля, если поле неоднородно и/или поверхность искривлена? Мы делим поверхность, через которую мы должны вычислить поток, на такие маленькие участки, что можно считать, что они плоские и поле однородное. Все это для того, чтобы можно было применить определение потока. Поэтому мы вычисляем небольшие «потоки» и суммируем их. Описанная процедура называется вычислением поверхностного интеграла, который записывается в виде:

Вычислять такие интегралы совсем не обязательно, но полезно понимать смысл такой процедуры.

Источник

Английский физик и химик Майкл Фарадей считал, что если электрический ток может намагнитить кусок железа, то магнит тоже каким-то образом должен вызывать появление электрического тока. И он оказался прав. В 1831 году он открыл явление электромагнитной индукции.

Определение

Электромагнитная индукция — явление, заключающееся в возникновении электрического тока в проводящем контуре, который либо покоится в переменном во времени магнитной поле, либо движется в постоянном магнитном поле таким образом, что число линий магнитной индукции, пронизывающих контур, меняется.

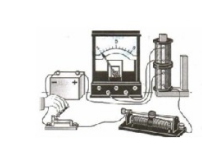
Опыты Фарадея

Сначала Фарадей открыл электромагнитную индукцию в неподвижных друг относительно друга проводниках пи замыкании и размыкании цепи. Он собрал установку, состоящую из источника тока, реостата, гальванометра, ключа и двух катушек. Одну катушку он соединил с реостатом, ключом и подключил к источнику питания. Вторую он подключил к гальванометру и устанавливал ее на тот же сердечник, что и первую. Всякий раз, как он замыкал или размыкал цепь, стрелка гальванометра отклонялась от нулевого значения шкалы.

Затем электромагнитная индукция была обнаружена при сближении и удалении катушек в замкнутой цепи. Если ученый перемещал одну катушку относительно второй, стрелка гальванометра также отклонялась.

Потом явление электромагнитной индукции было обнаружено при изменении силы тока в подключенной к источнику питания катушке с помощью реостата. Если сила тока уменьшалась или увеличивалась, стрелка гальванометра отклонялась от начального положения. Но она вставала на нулевое значение, если прекращать перемещение ползунка реостата (делать силу тока постоянной).

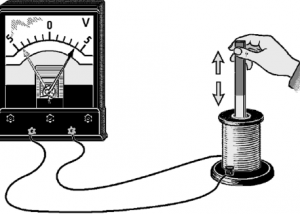
Ученый понимал, что магнит представляет собой совокупность маленьких токов, циркулирующих в молекулах. Поэтому он поставил следующий опыт.

Фарадей собрал установку, состоящую из катушки и подключенного к ней гальванометра. Затем он взял полосовой магнит и ввел его внутрь катушки. В этот момент стрелка амперметра отклонилась от нулевого значения. Если же ученый останавливал движение магнита внутри катушки, стрелка прибора возвращалась в исходное положение. При извлечении магнита из катушки стрелка амперметра отклонялась в противоположную сторону.

Все эти опыты позволили Фарадею уловить то общее, от чего зависит появление индукционного тока в катушках. В замкнутом проводящем контуре возникает ток при изменении числа линий магнитной индукции, пронизывающих поверхность, ограниченную этим контуром. При этом причина изменения числа линий магнитной индукции совершенно безразлична. Это может быть изменение числа линий магнитной индукции, пронизывающих поверхность неподвижного проводящего контура вследствие изменения силы тока в соседней катушке, и изменение числа линий индукции вследствие движения контура в неоднородном магнитном поле, густота линий которого меняется в пространстве.

Магнитный поток

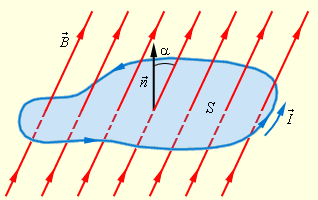
Вектор магнитной индукции →B характеризует магнитное поле в каждой точке пространства. Можно ввести еще одну величину, зависящую от значения вектора →B не в одной точке, а во всех точках поверхности, ограниченной плоским замкнутым контуром. Для этого рассмотрим плоский замкнутый проводник (контур) с площадью поверхности S, помещенный в однородное магнитное поле. Нормаль →n к плоскости проводника составляет угол α с направлением вектора магнитной индукции →B (см. рисунок).

Определение

Магнитным потоком, или потоком магнитной индукции через поверхность площадью S называют величину, равную произведению модуля вектора магнитной индукции →B на площадь S и косинус угла α между векторами →B и →n. Обозначается магнитный поток как Φ.

Φ=BScosα

Произведение Bcosα=Bn представляет собой проекцию вектора магнитной индукции на нормаль к плоскости контура. Поэтому:

Φ=BnS

Магнитный поток можно представить как величину, пропорциональную числу линий магнитной индукции, пронизывающих поверхность площадью S.

Единица измерения магнитного потока — вебер (Вб). Магнитный поток в 1 Вб создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м², расположенную перпендикулярно вектору магнитной индукции.

Пример №1. Линии индукции однородного магнитного поля пронизывают рамку площадью 0,5 м² под углом 30° к её поверхности, создавая магнитный поток, равный 0,2 Вб. Чему равен модуль вектора индукции магнитного поля?

Выразим модуль вектора магнитной индукции:

В=ΦScosα

Так как нам дан угол между поверхностью рамки и вектором магнитной индукции, угол между вектором магнитной индукцией и нормалью будет равен разности 90^о и угла поверхностью рамки и вектором магнитной индукции. Отсюда:

0,20,5cos(90°−30°)=0,20,5·0,5=0,8 (Тл)

Задание EF18180

Плоская рамка помещена в однородное магнитное поле, линии магнитной индукции которого перпендикулярны её плоскости. Если площадь рамки увеличить в 3 раза, а индукцию магнитного поля уменьшить в 3 раза, то магнитный поток через рамку

Ответ:

а) увеличится в 9 раз

б) не изменится

в) уменьшится в 3 раза

г) уменьшится в 9 раз

Алгоритм решения

1.Записать формулу, раскрывающую зависимость магнитным потоком, площадью рамки, помещенной в магнитное поле и индукции этого поля.

2.Установить, как изменится магнитной поток при изменении указанных в задаче величин.

Решение

Магнитный поток, пронизывающий площадь, ограниченную рамкой, определяется формулой:

Φ=BScosα

По условию задачи площадь рамки увеличивают в 3 раза, а индукцию магнитного поля уменьшают во столько же раз. Следовательно:

S1=3S

B1=B3

Следовательно:

Φ1=B1S1cosα=3S·B3cosα=BScosα=Φ

Следовательно, магнитный поток не изменится.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18285

Линии индукции однородного магнитного поля пронизывают рамку площадью 0,5 м² под углом 30° к её поверхности, создавая магнитный поток, равный 0,2 Вб. Чему равен модуль вектора индукции магнитного поля?

Ответ:

а) 0,2 Тл

б) 0,4 Тл

в) 0,8 Тл

г) 0,16 Тл

Алгоритм решения

1.Записать исходные данные.

2.Записать формулу для определения потока магнитной индукции.

3.Выразить искомую величину.

4.Подставить исходные данные и выполнить вычисления.

Решение

Запишем исходные данные:

• Магнитный поток, пронизывающий рамку: Φ = 0,2 Вб.

• Площадь рамки, находящейся в однородном магнитном поле: S = 0,5 м².

• Угол между вектором магнитной индукции и плоскостью, ограниченной контуром рамки: β = 30^о.

Запишем формулу для определения потока магнитной индукции:

Φ=BScosα

Так как в условиях задачи указан угол между вектором магнитной индукции и плоскостью рамки, то угол между нормалью и плоскостью рамки будет равен α=90°−β.

Выразим модуль вектора индукции магнитного поля:

B=ΦScos(90−β)=0,20,5·cos(90°−30°)=0,40,5=0,8 (Тл)

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Задание EF19000

Проволочная рамка площадью 2×10^–3м²вращается в однородном магнитном поле вокруг оси, перпендикулярной вектору магнитной индукции. Магнитный поток, пронизывающий площадь рамки, изменяется по закону Ф=4×10^–6cos10πt, где все величины выражены в СИ. Чему равен модуль магнитной индукции? Ответ выразите в мТл.

Алгоритм решения

1.Записать исходные данные.

2.Записать формулу для определения потока магнитной индукции.

3.Выразить искомую величину.

4.Подставить исходные данные и выполнить вычисления.

Решение

Запишем исходные данные:

• Магнитный поток, пронизывающий рамку: Φ = 4∙10^–6cos10πt Вб.

• Площадь рамки, находящейся в однородном магнитном поле: S = 2∙10^–3 м².

Запишем формулу для определения потока магнитной индукции:

Φ=BScosα

Выразим модуль вектора индукции магнитного поля:

B=ΦScosα

Так как рамка вращается в однородном магнитном поле, угол между нормалью, проведенной к ее плоскости, и вектором магнитной индукции постоянно меняется. Если мы примем этот угол за 0 градусов, то косинус этого угла будет равен 1. Тогда мы получим максимальное значение магнитного потока, пронизывающего рамку, и сможем вычислить модуль вектора магнитной индукции.

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 3.6k

Источник

Описание презентации по отдельным слайдам:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Материал подходит для УМК

Другие материалы

Вам будут интересны эти курсы:

Магнитный поток

4.1. Закон электромагнитной индукции. Самоиндукция. Индуктивность

Зависимости магнитного потока

Единица измерения и обозначение магнитного потока

Примеры

Опыты Фарадея

Магнитный поток

Не пропустите также: