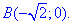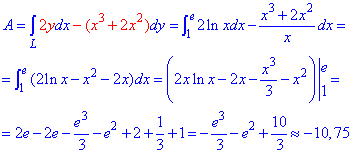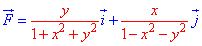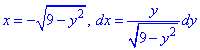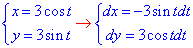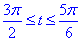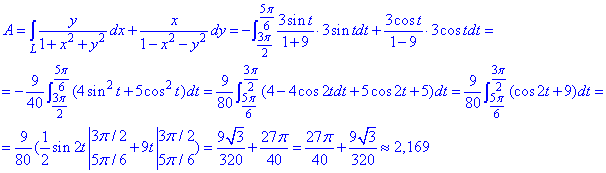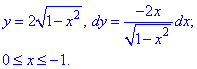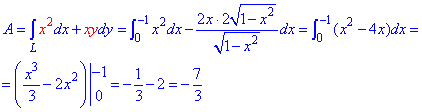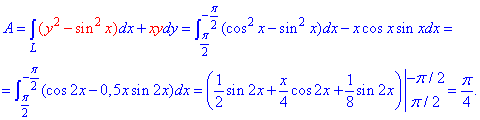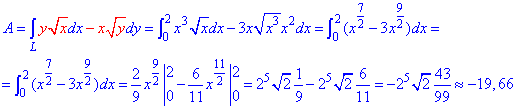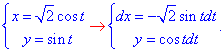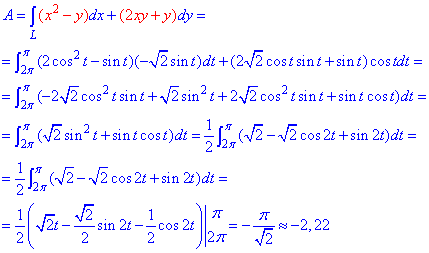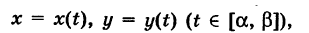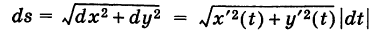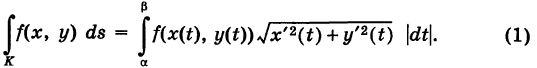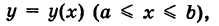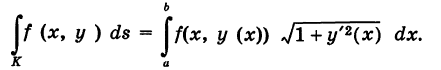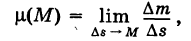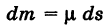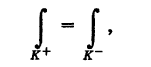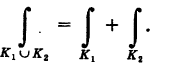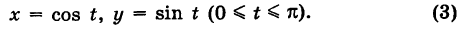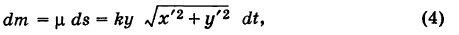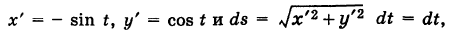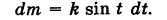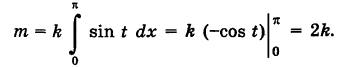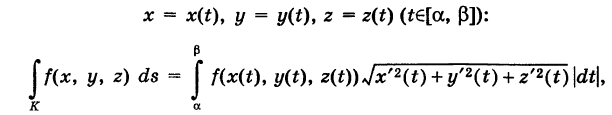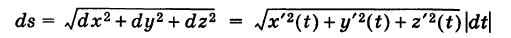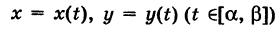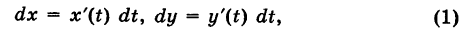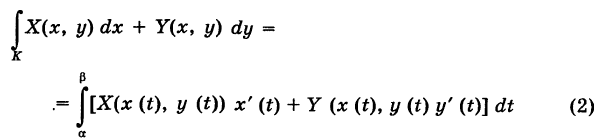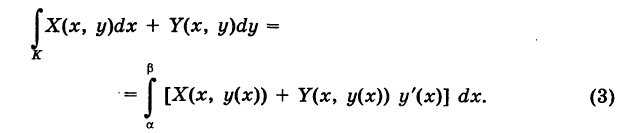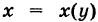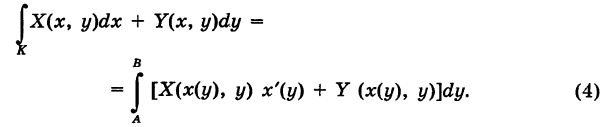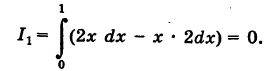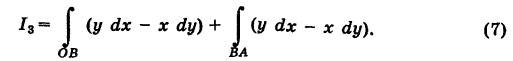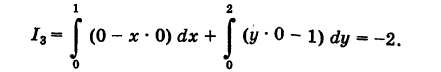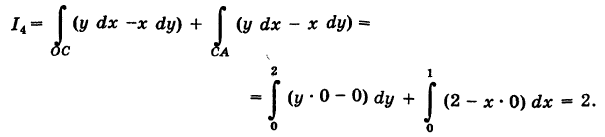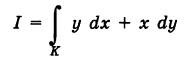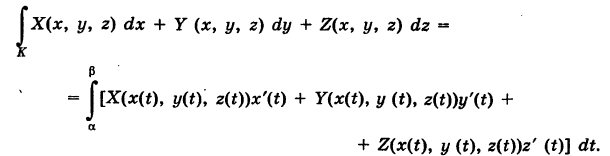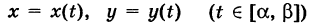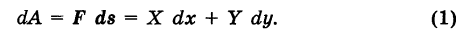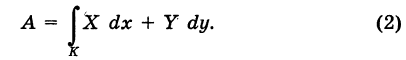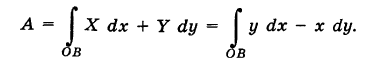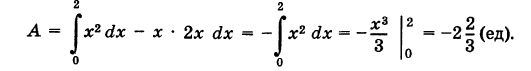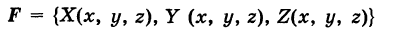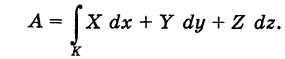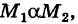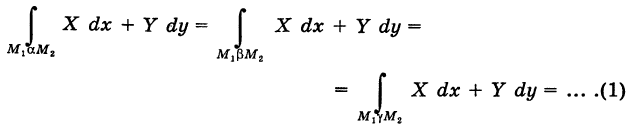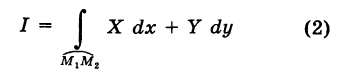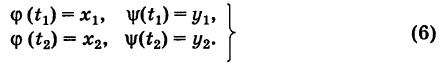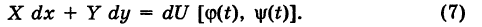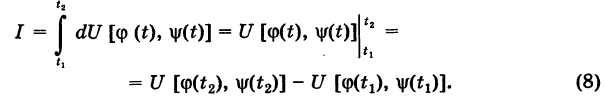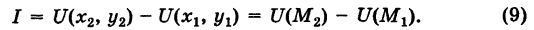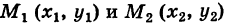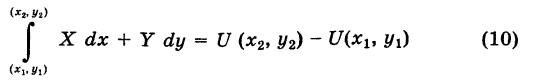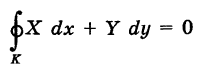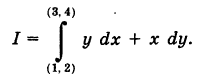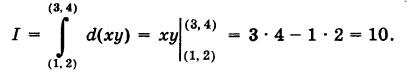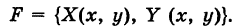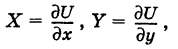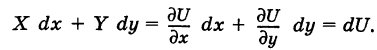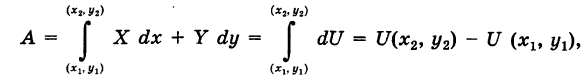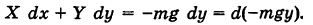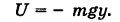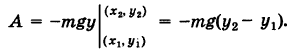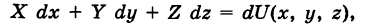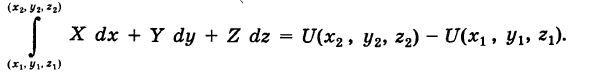Продолжаем предыдущий урок на тему «Применение криволинейных интегралов 2 рода».
Готовые ответы задач на работу силового поля помогут студентам выучить тему, и научат быстро находить нужные интегралы.
Пример 4.2 Найти работу силы F (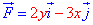
x2/4+y2/9=1 от точки A(- 2;0) к точке B(0;3).
Решение: Запишем уравнение заданного эллипса в параметрическом виде: x=2*cos(t), y=3*sin(t).
Наведем графически траекторию материальной точки вдоль эллипса.
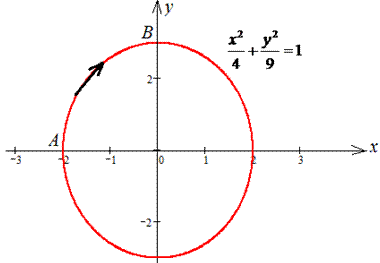
Тогда дифференциал переменных по параметру будет равен dx=-2*sin(t)dt, dy=3*cos(t)dt .
При этом пределы интегрирования ограничатся точками Pi и Pi/2.
Найдем работу силы F по кривой C через криволинейный интеграл ІІ рода : 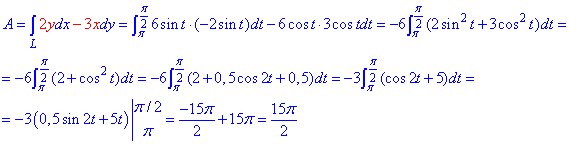
Пересмотрите внимательно формулы интегрирования синуса и косинуса, и понижения степени для таких функций.
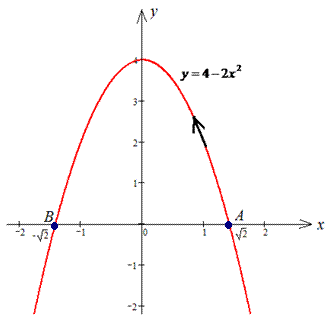
Пример 4.4 Найти работу силы 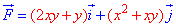
y=4-2x^2 от точки 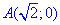
Решение: Построим траекторию движения материальной точки вдоль параболы L: y=4-2x2.
Вычисляем дифференциал дуги y=4-2x2, dy=-4x*dx и из условия выписиваем пределы интегрирования
Работа силы F находим с помощью криволинейного интеграла второго рода
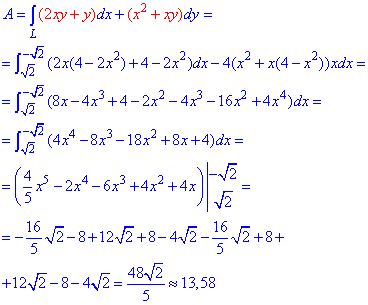
Интегрирование занимает не мало времени и при превращениях можно допустить ошибку, поэтому будьте внимательные в этих местах.
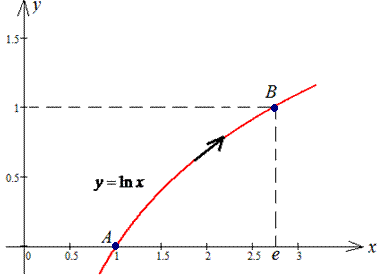
Пример 4.11 Найти работу силы 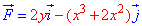
y=ln(x) от точки A(1;0) к точке B(e;1).
Решение: Траектория материальной точки вдоль логарифма имеет вид
Находим дифференциал логарифма y=ln (x), dy=dx/x.
Пределы интегрирования изменяются от единицы к экспоненте.
Работа силы F с помощью криволинейного интеграла ІІ рода примет значение:
Здесь для логарифма применили правило интегрирования частями (u*dv).
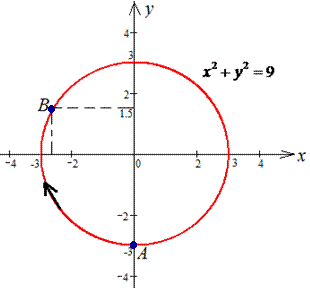
Пример 4.13 Найти работу силы F при перемещении вдоль кривой C:
x2+y2=9 от точки A (0;-3) к точке 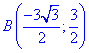
Решение: Построим траекторию движения материальной точки вдоль круга радиусом 3.
Чтобы не выражать две функции (верхняя и нижняя кривая круга) запишем зависимость x(y) и вычислим дифференциал дуги
При этом ордината изменяется от — 3 до 3/2.
Применяя криволинейный интеграл ІІ рода находим роботу силы F при перемещении вдоль круга:
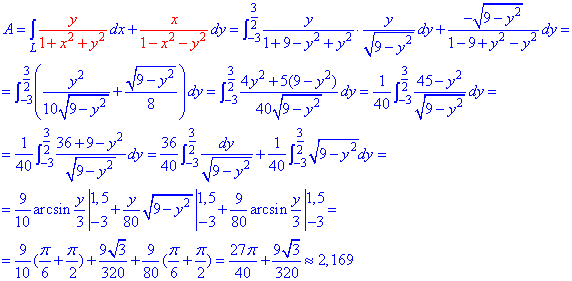
Бороться с корнями во время интегрирования непросто, о чем свидетельствует приведенные вычисления.
Намного проще вычислять интеграл при переходе к полярной системе координат.
Дальше наведем методику интегрирования:
ІІ — способ:
Параметризуэм заданный круг:
Учитывая, что во время движения от точки A(0;-3) к точке 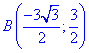
Вычисляем искомый криволинейный интеграл ІІ рода :
В плане вычислений второй метод более легкий, поэтому для круговых и эллиптических форм кривой при симметричном вхождении x, y в уравнение силы рекомендуем переходить к полярной системе координат.
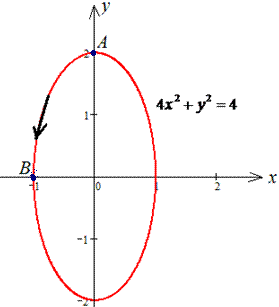
Пример 4.15 Найти работу силы 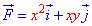
4x2+y2=4 от точки A(0;2) к точке B (-1;0).
Решение: Траектория движения материальной точки по эллипсу приведена ниже
Записываем верхнюю дугу эллипса и ее производную.
Пределы интегрирования изменяются от 0 к -1
Работа силы F через криволинейный интеграл второга рода выражается зависимостью:
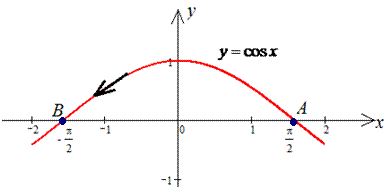
Пример 4.18 Найти работу силы 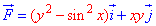
y=cos(x) от точки A(Pi/2;0) к точке B(-Pi/2;0).
Решение: Изобразим траекторию материальной точки вдоль косинуса
Построим дифференциал кривой y=cos(x), dy=-sin(x)*dx.
Он нужен для возведения криволинейного интегралу ІІ рода к определенному.
Находим работу силы F по перемещении вдоль контура интегрированием
Для понижения под интегралом степеней косинуса и синуса применили известные тригонометрические формулы.
Пример 4.21 Найти работу силы 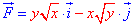
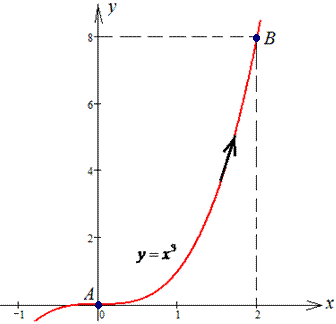
y=x3 от точки A(0;0) к точке B(2;8).
Решение: Построим траекторию материальной точки вдоль кривой y=x3.
Вычисляем дифференциал дуги dy=3x2dx.
Пределы интегрирования приведены на рисунку и в условии.
Работа силы F находим с помощью криволинейного интегралу ІІ рода:
Превращаем все к показательной форме и интегрируем.
Пример 4.23 Найти работу силы 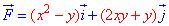
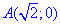
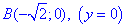
Решение: За инструкцией строим траекторию материальной точки вдоль эллипса: x2+2y2=2.
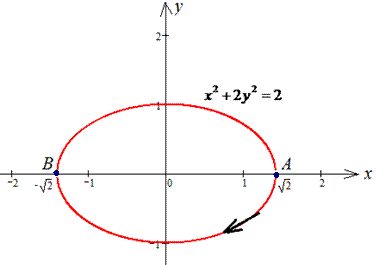
Для простоты вычислений криволинейного интеграла ІІ рода параметризуэм эллипс:
Учитывая, что от точки 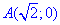
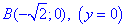
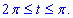
Понижаем степени и интегрируем.
Пример 4.24 Найти работу силы 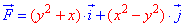
y=1-|x| от точки A(-1;0) к точке B(2;- 1).
Решение: Наведем траекторию материальной точки вдоль модуль функции.
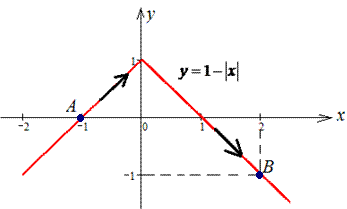
Как ни хотелось встретить задания с разбитием кривой на два интервала, однако одно Пример содержит такое условие. Разделим на две части: y=1+x, тогда пределы равны [-1;0] и дифференциал dy=dx;
На втором участке y=1-x имеем [0;2] и dy=-dx.
Вычисляем работу силы F, потраченную на перемещении точки вдоль модуль функции:
На этом ознакомление из такого сорта примерами завершено.
Больше готовых ответов из курса высшей математики ищите на страницах сайта.
Приложения криволинейных интегралов
Краткая теория
Длина дуги
Длину дуги
плоской или пространственной линии
определяют по формуле:
Масса дуги
Если
– линейная плотность вещества в точках дуги,
то массу
дуги
определяют по формуле:
Статистические моменты
Статистические
моменты
и
плоской дуги
относительно координатных осей
и
определяют по формулам:
Моменты инерции
Моменты
инерции
,
плоской дуги
относительно координатных осей
и
определяют по формулам:
Полярный момент инерции
Полярный
момент инерции
плоской дуги
относительно начала координат определяют по
формуле:
Площадь фигуры
Площадь
фигуры, расположенной в плоскости
и ограниченной замкнутой линией
, вычисляют по формуле:
Работа, приложенная к точке, при перемещении по дуге
Работу, совершаемую силой
приложенной в точке
при перемещении ее по дуге
, вычисляют по формуле:
Примеры решения задач
Задача 1
Найти
момент инерции относительно оси
четверти однородной окружности
, расположенной в первом
квадранте.
Решение
Окружность
однородна, следовательно
, следовательно искомый
момент инерции:
Для
удобства вычислений перейдем к параметрическим уравнениям окружности
Тогда:
Ответ:
Задача 2
Найти
массу дуги кривой
от точки
до
, если плотность в каждой точке
ее равна абсциссе точки;
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Плотность
дуги:
Искомая масса будет выражаться
криволинейным интегралом 1-го рода:
Производная:
Искомая масса:
Ответ:
.
Задача 3
Найти
массу дуги окружности
, лежащей в первой
четверти, если плотность в каждой ее точке равна абсциссе точки.
Решение
Плотность:
Искомая масса будет
выражаться криволинейным интегралом 1-го рода:
Параметрическое
уравнение окружности:
Окружность лежит в
первой четверти, поэтому
Ответ:
.
Задача 4
Вычислить
работу силы
при обходе точки ее приложения по границе
области
в положительном направлении, начиная от точки
.
Решение
Искомая
работа будет равна криволинейному интегралу 2-го рода:
Для
вычисления интеграла воспользуемся формулой Грина:
Ответ:
.
Задача 5
Вычислить
работу силового поля
при перемещении материальной точки вдоль пути
.
Решение
Искомая работа будет
выражаться криволинейным интегралом 2-го рода:
Параметр
:
Перейдем к
определенному интегралу:
Искомая работа:
Ответ:
Задача 6
Вычислить
работу силы
при перемещении материальной точки вдоль линии
от точки
до точки
.
Решение
Искомая работа будет
выражаться криволинейным интегралом 2-го рода:
Криволинейный
интеграл 2-го рода можно свести к определенному интегралу по следующей формуле:
Получаем:
Ответ:
Содержание:
Криволинейные интегралы
Криволинейный интеграл первого рода
Пусть К — некоторая гладкая (или кусочно-гладкая) плоская кривая
где t — параметр, а
— ее дифференциал дуги. Здесь если 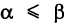
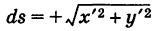
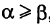
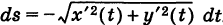
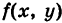
Если кривая 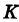
то, рассматривая х как параметр, получим
Допустим, что кривая К — материальная, т. е. имеет массу. Пусть 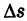
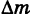
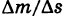
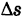
т. е предел средней плотности дуги при условии, что дуга 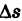
Если 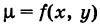
есть масса бесконечно малой дуги ds (элементарная масса) и интеграл
представляет собой массу линии (физический смысл криволинейного интеграла первого рода).
Криволинейный интеграл первого рода обладает следующими очевидными свойствами.
1) При изменении направления интегрирования криволинейный интеграл первого рода не изменяет своего значения (рис. 238), т. е.
где К+ — кривая К, пробегаемая в заданном направлении (например, при возрастании параметра t), а К-— кривая К, пробегаемая в противоположном направлении (соответственно при убывании t).
2) Если кривая интегрирования К с помощью некоторой точки разбита на части: 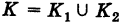
Пример:
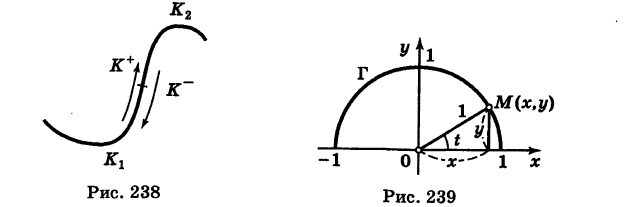
Найти массу полуокружности 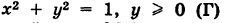
Решение:
Беря в качестве параметра t полярный угол (рис. 239), получаем параметрические уравнения полуокружности
Элементарная масса
где k — коэффициент пропорциональности. Так как
то из (4) имеем
Отсюда масса линии Г будет равна
Аналогично определяется криволинейный интеграл первого рода от функции f(x, у, z), взятый по кусочно-гладкой пространственной кривой К:
где
— дифференциал дуги пространственной кривой -К.
Криволинейный интеграл второго рода
Пусть
— гладкая (или кусочно-гладкая) кривая К с выбранным направлением (такую линию, для краткости, будем называть путем) и Х(х, у), Y (х, у) — пара функций, непрерывных на кривой К. Учитывая, что дифференциалы текущих координат х и у кривой К имеют вид
под криволинейным интегралом второго рода от пары функций X и Y, взятым по кривой К, понимается интеграл
(по традиции для выражения, стоящего слева, скобки не пишутся и предполагается, что интеграл 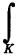
Если путь К задается уравнением 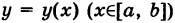
Аналогично, если K, задается уравнением 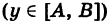
Криволинейный интеграл второго рода обладает следующими свойствами.
1) При изменении направления пути интегрирования криволинейный интеграл второго рода изменяет свой знак на обратный, т. е
Действительно, изменение направления пути интегрирования равносильно перестановке пределов интегрирования 
2) Если путь интегрирования К состоит из двух частей К = 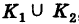
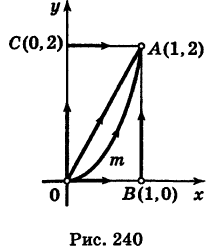
Пример:
Найти значения интеграла 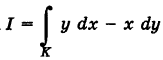
Решение:
1) Уравнение прямой OA есть у = 2х 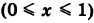
2) Уравнение параболы 
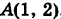
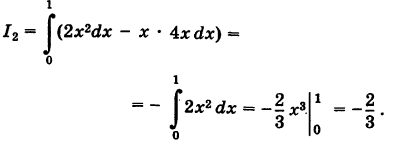
3) На основании свойства 2 имеем
Так как уравнение ОВ есть у = 0 
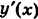
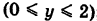
4) Аналогично,
Заметим, что здесь интеграл I при фиксированных концах пути интегрирования К зависит от вида этого пути.
Пример:
Найти
вдоль линий К, указанных в примере 1.
Воспользовавшись приведенными выше уравнениями линии К, последовательно имеем:
Таким образом, здесь интеграл I имеет одно и то же значение для различных путей, соединяющих точки О и А. Принципиальное различие примеров 1 и 2 будет разъяснено. Если
есть кусочно-гладкая пространственная кривая 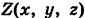
Физический смысл криволинейного интеграла второго рода
Пусть 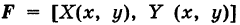
— путь К, пробегаемый точкой ее приложения (рис. 241); обозначим через 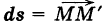
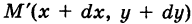
Интегрируя выражение (1) вдоль кривой К, получим работу силы
Выражение (2), очевидно, есть соответствующий криволинейный интеграл второго рода.
Итак, криволинейный интеграл второго рода представляет собой работу переменной силы вдоль пути интегрирования, проекциями которой на координатные оси являются соответствующие коэффициенты при дифференциалах переменных.
Пример:
Найти работу А переменной силы 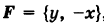
Решение:
Согласно формуле (2) имеем
Из уравнения (3) получаем dy = 2х dx, поэтому
Аналогично, работа пространственной силы
вдоль пути К: 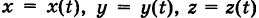
- Заказать решение задач по высшей математике
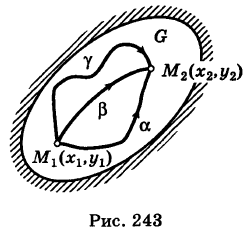
Условие независимости криволинейного интеграла второго рода от вида пути интегрирования
Пусть 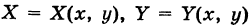
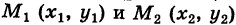
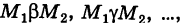
В таком случае говорят, что криволинейный интеграл второго рода
не зависит от вида пути интегрирования в данной области G.
Если выполняются условия (1), то для интеграла (2) нет необходимости указывать путь интегрирования, а достаточно отметить лишь его начальную точку 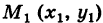
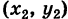
Справедлива следующая теорема:
Теорема: Если в области G подынтегральное выражение X dx + Y dy является полным дифференциалом некоторой функции U = U (х, у), т. е.
то криволинейный интеграл (2) не зависит от пути интегрирования в области G.
Доказательство: Пусть
— произвольный путь К в области G, соединяющий точки 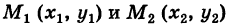
Из формулы (4) имеем
Отсюда получаем
Далее, используя соотношения (6), будем иметь
Таким образом, значение интеграла I одно и то же при любом выборе функций 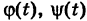
Следствие 1. Если выполнено соотношение (4), то в силу (9) имеем
(обобщенная формула Ньютона — Лейбница).
Следствие 2. Если подынтегральное выражение X dx + Y dy есть полный дифференциал и путь интегрирования К замкнутый, то
(кружок при интеграле обозначает интегрирование вдоль замкнутого пути).
Пример:
Найти
Решение:
Так как у dx + х dy = d (ху), то, независимо от вида пути, соединяющего точки 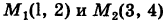
Работа потенциальной силы
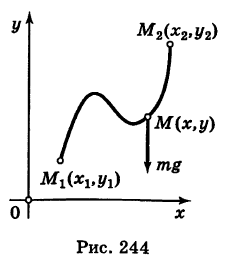
Теорема предыдущего параграфа имеет физическое содержание. Пусть в области G определено силовое поле
Примером силового поля может служить поле силы тяжести у поверхности Земли, где на любую материальную точку массы т действует сила mg (g — ускорение свободного падения). Более общим примером силового поля является гравитационное поле, создаваемое массой М. Здесь на материальную точку массы 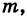
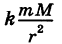
Если существует функция 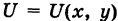
то говорят, что поле потенциальное (иначе, F — потенциальная сила), а функцию U называют потенциалом поля. В этом случае, очевидно,
Отсюда для работы А потенциальной силы F вдоль пути, соединяющего точки 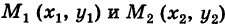
т. е. работа потенциальной силы не зависит от вида пути и равна разности потенциалов силы для конечной и начальной точек пути.
В частности, если путь замкнут, то работа А = 0.
Пример:
Найти работу А силы тяжести при перемещении в вертикальной плоскости Оху (вблизи поверхности Земли) точки массы т из положения 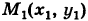
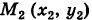
Решение:
Если ось Ох горизонтальна, а ось Оу вертикальна, то проекции силы тяжести, действующей на материальную точку массы т, равны X = 0, У = -mg. Имеем
Поэтому за потенциал поля силы тяжести можно принять
Отсюда работа силы тяжести, независимо от пути 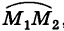
Замечание. Аналогичные результаты справедливы для криволинейного интеграла, взятого по пространственной кривой. В частности, если
то
- Двойные и тройные интегралы
- Делимость чисел в математике
- Обыкновенные дроби
- Отношения и пропорции
- Уравнения поверхности и линии в пространстве
- Общее уравнение плоскости
- Угол между плоскостями
- Понятие о производной вектор-функции
Работа
— это изменение формы движения,
рассматриваемое с его количественной
стороны. В общем смысле работа
— это процесс превращения одних форм
движения материи в другие и одновременно
количественная характеристика этого
процесса.
Механическая
работа —
процесс, в котором под действием сил
изменяется энергия системы, и одновременно
количественная мера этого изменения.
При совершении
работы всегда имеются сила, действующая
на материальную точку (систему, тело),
и вызванное данной силой перемещение.
При отсутствии хотя бы одного из этих
факторов работа не совершается.
Элементарная
работа
некоторой силы F,
действующей на материальную точку
(тело, систему), вызывающей элементарное
перемещение dr,
равна произведению силы на перемещение:
dA
= Fdr
= Fdrcos
= Frdr,
(7.1)
где
α
— угол между направлением перемещения
и направлением действующей силы.
Из (7.1) следует, что при
α
< π/2,
dA > 0 — работа положительная;
α
= π/2,
dA = 0 — работа не совершается;
α
> π/2,
dA < 0 — работа отрицательная;
α
= 0, dA = Fdr
— направление перемещения и направление
действующей силы совпадают.
В том случае, когда
величина тангенциальной составляющей
силы остаётся всё время неизменной, то
работа определяется соотношением
.
(7.2)
В
частности, это условие выполняется,
если тело движется прямолинейно, и
постоянная по величине сила
образует с направлением движения
постоянный угол.
Поэтому выражению (7.2) в данном случае
можно придать следующий вид:
.
(7.3)
Надо
отметить, что понятие работы в механике
существенно отличается от обыденного
представления о работе. Например, для
того, чтобы держать тяжелый груз, стоя
неподвижно, а тем более для того, чтобы
перенести этот груз по горизонтальному
пути, носильщик затрачивает определенные
усилия, т.е. «совершает работу».
Однако работа как механическая величина
в этих случаях равна нулю.
Вектор
силы на плоскости всегда можно разложить
на две составляющие — нормальную и
тангенциальную. Ясно, что только
тангенциальная составляющая силы
способна совершить работу. В случае,
когда величина проекции силы на
направление перемещения не остается
постоянной во времени, для вычисления
работы следует разбить путь S на
элементарные участки
,
взяв их столь малыми, что за время
прохождения телом такого участка можно
было бы считать силу постоянной. Тогда
на каждом элементарном участке путиS1работа
силы равна
.
(7.4)
А
работа на всем пути S может быть вычислена
как сумма элементарных работ:
.
(7.5)
В
общем случае, когда материальная точка
(тело, система), двигаясь по криволинейной
траектории, проходит путь конечной
длины, можно мысленно разбить этот путь
на бесконечно малые элементы, на каждом
из которых сила F
может считаться постоянной, а элементарная
работа может быть вычислена по формуле
(7.1). Сложив все эти элементарные работы
и перейти к пределу, устремив к нулю
длины всех элементарных перемещений,
а их число – к бесконечности, получим
. (7.6)
Выражение
(7.6) называют криволинейным интегралом
вектора F
вдоль траектории L.
Рис.7.1
Работу, определяемую
формулой (7.6), можно изобразить графически,
в координатах F — S,
площадью фигуры, что соответствует
нахождению криволинейного интеграла.
На рис.7.1 построен график F
как функции положения точки на траектории.
Из рисунка видно, что элементарная
работа
численно равна площади заштрихованной
полоски, а работана пути от точки 1 до точки 2 численно
равна площади фигуры, ограниченной
кривой F(S),
вертикальными прямыми 1 и 2 и осью OS.
Единица
измерения работы в СИ носит название
джоуль (Дж).
Найдем
работу, совершаемую при растяжении
пружины, подчиняющемуся закону Гука.
Сила, растягивающая пружину, равна по
величине и противоположна по направлению
упругой силе, т.е.
,
(7.7)
где
– удлинение пружины.
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #