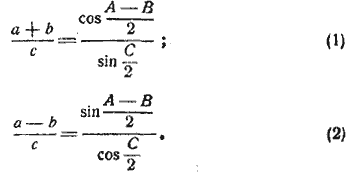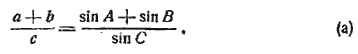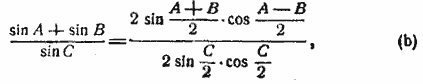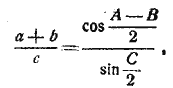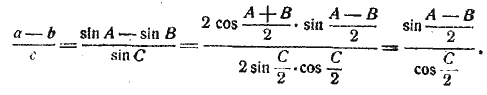Косоугольные треугольники способы решения (Таблица)
Обозначения: A, B, C — углы против сторон a, b, c

|
Даны |
Способы решения, формулы для определения остальных элементов |
|
сторона и два угла (а, А, В) |
 |
|
две стороны и угол между ними (a, b, С) |
1-й способ: 2-й способ: Углы А и В находятся из системы двух уравнений: |
|
две стороны и угол против одной из них (а, b, А) |

Если a ≥ b, то В < 90°, имеется одно решение. Если b sin А > a, то решение невозможно. Если b sin А = а, то имеется одно решение В = 90°. Если b sin А < а, то решений два: B1 и В2, причем В3 = 180° — B1; |
|
три стороны (а, Ь, с) |
1-й способ: 2-й способ: |
ВИДЕО УРОК
Условимся, как это принято, обозначать элементы
косоугольного треугольника с вершинами А, В, С следующими буквами
А,
В, С – внутренние углы треугольника;
a,
b, c – соответствующие
стороны, противоположные углам треугольника;
ha,
hb, hc –
высоты треугольника относительно сторон a, b и с;
ba,
bb, bc –
биссектрисы внутренних углов;
ma, mb,
mc – соответствующие медианы;
– полупериметр треугольника;
S – площадь треугольника;
R – радиус описанной окружности;
r – радиус вписанной окружности;
ra,
rb, rc –
радиусы вневписанных окружностей.
Основные теоремы и формулы о соотношениях между элементами треугольника.
Сума
внутренних углов.
Формулы половинных
углов.
Формула для высот треугольников.
Формулы для вычисления
биссектрис.
Формула для вычисления
медиан.
Формулы для вычисления
радиуса описанной окружности.
Формулы для вычисления
радиуса вписанной окружности.
Основные случаи решения косоугольных треугольников.
Основными случаями решения треугольников называются задачи на вычисление
элементов треугольника по трём его данным независимым основным элементам.
К основным элементам относят стороны и внутренние углы треугольника, причем
углы связаны между собой соотношением
А
+ В + С = π,
поэтому только два из них могут быть независимыми.
Решение косоугольного
треугольника по стороне и двум углам.
В треугольнике АВС даны:
сторона а и углы В и С. Найти угол А и стороны
b и с.
Если даны два угла треугольника, то третий определяем как
А
=180° – (В + С).
Неизвестные стороны b и с определяются по теореме синусов из пропорций:
Откуда получаем:
но
sin А = sin
[180° –
(В + С)] = sin (В + С),
а потому
ПРИМЕР:
Дано:
а = 400,
А = 36°40‘,
В = 79°50‘.
Найти b, с, С.
РЕШЕНИЕ:
1) С = 180° – (А + В),
С = 180° – (36°40‘ + 79°50‘) = 69°30‘.
В последнем случае при определении стороны с можно
было взять и такую пропорцию:
Но в эту пропорцию
введём только что найденную сторону b. Если при отыскании
b была допущена ошибка, то она отразится и на
величине с, несмотря на безошибочные вычисления при определении
последней.
ПРОВЕРКА:
Найдём угол
С через
найденные стороны b и с по
формуле:
Имеем:
Имеем совпадение с полученным ранее результатом.
Решение косоугольного
треугольника по двум сторонам и углу, противолежащему одной из них.
ПРИМЕР:
Пусть в треугольнике
АВС даны: стороны а, b и угол
А.
требуется найти сторону с и углы В и С.
РЕШЕНИЕ:
Угол В определяется
по теореме синусов. Имеем:
Откуда
Угол С находится из
соотношения
С = 180° – (А + В).
Из пропорции
находим с:
Для построения
треугольника по двум его данным сторонам
а и b и
углу А, противолежащему стороне а, можно поступить так: строим угол
А
и на одной из его сторон от точки А откладываем отрезок АС
= b. Затем строим окружность радиуса а с центром в точке С.
Если эта окружность не пересечёт второй стороны угла А,
то задача не имеет решения (случай I), если эта
окружность коснётся второй стороны угла, то задача имеет одно решение (случай II
– искомый
треугольник АСВ1), если эта окружность пересечёт вторую
сторону угла, то задача имеет два решения (случай III, треугольники АСВ2 и АСВ3) и, наконец, если окружность пересечёт
сторону угла лишь в одной точке, то задача имеет одно решение (случай
IV, АСВ4).
На чертеже
рассмотрен случай, когда
угол А – острый. На следующем чертеже
рассмотрен случай, когда этот угол тупой. В этом случае
задача или не имеет решения (I) или имеет только одно решение (II).
Пусть угол
А – острый. Тогда как следует из чертежа
в случае
а < b sin А
задача не имеет решения (I), в случае
а = b sin А
задача имеет одно решение (II), если
b ˃ а ˃
b sin А,
задача имеет два решения (III), наконец,
если а ≥ b,
задача имеет одно решение (IV).
Если угол
А – тупой, то в случае а ≤ b задача не имеет решения (I), а в случае а ˃ b – имеет и при том только одно решение (II).
ПРИМЕР:
Дано:
а = 242,
b = 767,
В = 36°53‘.
Найти с, А, С.
РЕШЕНИЕ:
Так как угол
В – острый и
b ˃ а, то задача имеет решение и, причём, только
одно.
(А – острый угол, так как а < b
и А < В).
2) С = 180° – (А + В),
С ≈180° – (10°55‘ + 36°53‘) = 132°12‘.
ПРОВЕРКА:
Вычислим по следующей формуле угол В.
Имеем совпадение с данным значением угла В.
ПРИМЕР:
Дано:
а = 400,
b = 500,
А = 40°.
Найти с, В, С.
РЕШЕНИЕ:
Так как угол
А – острый и
b ˃ а ˃ b sin А, то задача имеет два решения
Первое решение найдено. Второе решение найдём,
приняв В равным
180° – 53°28‘ = 126°32‘.
Угол С будет другой, а в
связи с этим изменится и сторона с. Обозначим эти новые значения соответственно через
В‘, С‘, с‘.
Имеем:
1) В‘ =
126°32‘.
2) С‘ = 180° – (А + В‘),
С‘ ≈180° – (40° + 126°32‘) = 13°28‘.
Следовательно, имеется два различных треугольника, у
которых
а = 400,
b = 500,
А = 40°,
один из них – остроугольный, другой – тупоугольный.
Построение треугольника при этих данных подтверждает полученные два ответа.
ПРИМЕР:
Дано:
а = 165,
b = 268,
А = 53°08‘.
Найти с, В, С.
РЕШЕНИЕ:
Имеем
b sin А ≈ 268 ∙ 0,8000 ˃ а =
165,
Следовательно, задача не имеет решений.
Формулы для определения угла
треугольника по двум его сторонам и углу между ними.
ТЕОРЕМА:
ДОКАЗАТЕЛЬСТВО:
Рассмотрим сначала
случай, когда угол С – острый.
Проведём из вершины В высоту
ВD = h.
Из прямоугольного
треугольника АВD получаем
соотношение
Из треугольника ВСD находим:
h = a sin C
и далее:
AD = AC – DC,
DC = a cos C.
Равенство
AD = AC – DC
теперь представится в таком виде:
AD = b – a cos C.
Выражение для h из равенства
h = a sin C
и AD из равенства
AD = b – a cos C
подставляем в
Получим:
В случае, когда
С – тупой,
получим:
Но
h = a sin (180° – C) = a sin C,
а
СD = a соs (180° – C) = –a соs C.
На основании
h = a sin C
и
СD = –a соs C
равенство
примет вид:
Аналогично доказывается и равенство
Выражения для
tg В и tg С
представляется в такой форме:
Решение косоугольного
треугольника по двум сторонам и углу между ними.
ПРИМЕР:
В треугольнике АВС дано: стороны а и b и угол С.
Найти сторону с и углы А и В.
РЕШЕНИЕ:
1-й способ. По теореме косинусов имеем:
c2 = a2 + b2
– 2ab cos C.
Откуда получим с.
Угол А находим
по теореме синусов. Имеем:
откуда
Точно так же из
пропорции
получим
Углы в рассмотренном
случае отыскиваем по теореме синусов. Угол, лежащий против большей стороны
треугольника, следует искать последним. Например, если а ˃ b, то угол
В – острый. Определив из
этот острый угол В, находим угол А:
А = 180° – (В + С).
Контролем может служить формула
2-й способ. Выражаем тангенс одного из искомых
углов, например tg A, через данные
a, b и С по
формуле:
Угол В находим из
соотношения:
B = 180° – (A + С).
Сторону с находим,
пользуясь теоремой синусов:
Первым способом
целесообразно пользоваться, если ищется только сторона, а вторым – если только
угол.
Каждый из этих
способов может быть использован для проверки решения другим способом.
ПРИМЕР:
Дано: а = 320, b = 400, С = 110°21‘.
Найти с, А и В.
РЕШЕНИЕ:
Первый способ.
1) По
теореме косинусов имеем:
c2 = a2 + b2
– 2ab cos C.
Откуда получим с:
c2 = 3202 + 4002
– 2 ∙ 320 ∙ 400 cos 110°21‘ =
3202 + 4002 – 2 ∙
320 ∙ 400 cos 69°39‘ ≈
102 400 + 256 000 ∙ 0,3478 ≈ 351 437.
с ≈
592,8.
В ≈ 39°15‘.
ПРОВЕРКА:
110°21‘ + 30°24‘ + 39°15‘ = 180°.
Второй способ.
В ≈ 39°15‘.
2) А =
180° – (В + С),
А ≈ 180° – (39°15‘ + 110°21‘) = 30°24‘.
Формулы для определения углов треугольника по трём его сторонам.
Возьмём треугольник АВС.
Впишем в него круг радиуса r.
Центр О этого круга
находится на пересечении биссектрис внутренних углов треугольника.
Пусть D, Е, F
точки, в которых
стороны треугольника касаются окружности.
Из геометрии известно, что отрезки двух касательных, проведённых из одной
точки к окружности, равны между собой. На этом основании можем заключить о
равенстве следующих отрезков, входящих в состав сторон треугольника:
AD
= AF = k,
BD
= BE = m,
CE
= CF = n.
Если проведём радиусы
OD,
OE, OF
в точки касания, то образуются шесть прямоугольных треугольников.
Из треугольника AOF имеем:
выразим r и k через стороны
треугольника a,
b, c. Из чертежа видно,
что
a
+ b + c = 2k + 2m + 2n.
Если периметр треугольника обозначим через
2p, то получим
2p = 2k + 2m
+ 2n,
откуда
p
= k + m + n.
Так как m
+ n = a, то из равенства
p
= k + m + n
получим, что
k
= p – a.
Из геометрии известно, что r круга, вписанного в треугольник, выражается
через полупериметр p и стороны его так:
На основании равенств
равенство
примет вид:
По аналогии получатся формулы
то есть во всяком треугольнике тангенс половины
одного из его углов равен квадратному корню из дроби, у которой числитель есть
произведение разностей между полупериметром треугольника и каждой из сторон,
образующих угол, а знаменатель – произведение полупериметра на разность между
полупериметром и стороной, противолежащей этому углу.
Так как A,
B, C – углы треугольника, то половины их A/2, B/2, C/2 – всегда углы острые. Поэтому
tg A/2, tg B/2, tg C/2
положительны.
Формулы для определения углов
треугольника по трём его сторонам с помощью теоремы косинусов.
Теорема косинусов
даёт такую зависимость между тремя сторонами треугольника и углом:
a2 = b2 + с2
– 2bс cos А.
Выразив из этого
равенства cos А, получим:
так же можно по аналогии написать выражения для
косинусов остальных углов:
Решение
косоугольного треугольника по трём сторонам.
В
треугольнике АВС
даны стороны а, b, с. Требуется найти углы
А, В и С треугольника.
Углы А, В и С треугольника
можно определить по формулам, выражающим
cos А, cos В, cos C
через стороны треугольника:
Или
же углы А, В и С определяются по
формулам, выражающим
tg
А/2, tg В/2, tg С/2.
через а, b, с:
ПРИМЕР:
Дано: а = 13, b = 18, с = 15.
Найти А, В и
С.
РЕШЕНИЕ:
Первый способ.
ПРОВЕРКА:
А + В + С =
45°16‘ + 79°40‘ + 55°4‘ = 180°.
Второй способ.
Имеем:
2р = 13 + 18 + 15 = 4,
р = 23,
р – а =10,
р – b = 5,
р – с = 8.
ПРОВЕРКА:
(р – а) + (р – b) + (р – с) =
раскроем скобки
р – а + р – b + р
– с =
сгруппируем и приведём подобные члены
3р – (а + b + с) =
Так как (а + b + с) это периметр Р = 2р, то получаем:
3р – 2р = р.
10 + 5 + 8 = 23.
Получились те же
значения углов, что и при решении первым способом.
Задания к уроку 16
- Задание 1
- Задание 2
- Задание 3
ДРУГИЕ УРОКИ
- Урок 1. Градусное измерение угловых величин
- Урок 2. Радианное измерение угловых величин
- Урок 3. Основные тригонометрические функции
- Урок 4. Натуральные тригонометрические таблицы
- Урок 5. Периодичность тригонометрических функций
- Урок 6. Область определения и область значения тригонометрических функций
- Урок 7. Знаки тригонометрических функций
- Урок 8. Чётность и нечётность тригонометрических функций
- Урок 9. Тригонометрические функции некоторых углов
- Урок 10. Построение угла по данному значению его тригонометрической функции
- Урок 11. Основные тригонометрические тождества
- Урок 12. Выражение всех тригонометрических функций через одну из них
- Урок 13. Решение прямоугольных и равнобедренных треугольников с помощью тригонометрических функций
- Урок 14. Теорема синусов
- Урок 15. Теорема косинусов
- Урок 17. Примеры решения задач по планиметрии с применением тригонометрии
- Урок 18. Решение практических задач с помощью тригонометрии
- Урок 19. Формулы приведения (1)
- Урок 20. Формулы приведения (2)
- Урок 21. Формулы сложения и вычитания аргументов тригонометрических функций
- Урок 22. Формулы двойных и тройных углов (аргументов)
- Урок 23. Формулы половинного аргумента
- Урок 24. Формулы преобразования суммы тригонометрических функций в произведение
- Урок 25. Графики функций y = sin x и y = cos x
- Урок 26. Графики функций y = tg x и y = ctg x
- Урок 27. Обратные тригонометрические функции
- Урок 28. Основные тождества обратных тригонометрических функций
- Урок 29. Выражение одной из аркфункций через другие
- Урок 30. Графики обратных тригонометрических функций
- Урок 31. Построение графиков тригонометрических функций методом геометрических преобразований
© 2023 Все права защищены
При использовании материалов данного сайта обязательно указывать ссылку на источник
- Формулы по алфавиту
- Карта сайта
О РЕШЕНИИ ТРЕУГОЛЬНИКОВ.
X. Косоугольные треугольники.
§ 97. Соотношения между элементами косоугольного треугольника.
Начнем с геометрического соотношения между углами треугольника:
А + В + С = 180°.
Заметим некоторые следствия из него.
а) Так как сумма значений А и В + С равна 180°, то синусы их равны, а косинусы различаются знаками; поэтому
sin (B + C) = sin A; cos (B+C)= — cos A; cos A = — cos {В + С).
Точно так же:
tg ( B+ C ) = — tg A.
б) Так как сумма значений и
равна 90°, то сходные функции их соответственно равны (§ 17); например:
sin = cos
; sin
= cos
и т. д.
в) Полезно запомнить еще следующие соотношения между угламя треугольника:
l) sin A + sin B + sin С = 4 cos • cos
• cos
2) tg A + tg B+ tg C = tg A • tg B • tg C;
3) ctg + ctg
+ ctg
= ctg
• ctg
• ctg
.
Вывод этих формул предоставляется учащемуся.
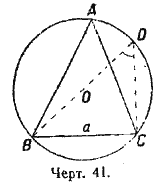
§ 98. Лемма. Во всяким треугольнике сторона равна диаметру описанного круга, умноженному на синус противолежащего угла.
Обозначая радиус описанного круга через R, докажем, например, что а = 2R • sin A, где угол А есть острый или тупой.
Доказательство. 1) Угол А острый (черт. 41). В oписанном круге из конца данной стороны проведем диаметр и соединим другие концы этой стороны и диаметра; получим прямоугольный треугольник. На чертеже 41 таким треугольником будет BDC; из него, на основании § 21, находим: BC = BD • sin D, или a = 2R• sin D; нo /
D = /
А1); следовательно, a = 2R• sin A.
1) Тот и другой измеряются половиной дуги ВС.
2) Угол А тупой. Сделаем такое же вспомогательное построение, как раньше. Из прямоугольного треугольника ВСЕ (черт. 42) найдем: a = 2R• sin E; но Е + А = 180°, следовательно sin E = sin A, поэтому a = 2R• sin A. Итак, вообще:
a = 2R• sin A; b = 2R• sin B; c = 2R• sin C.
§ 99. Теорема. Во всяком треугольнике стороны пропорциональны синусам противолежащих углов.
Требуется доказать, что:
a/sin A = b/sin B = c/sin C
Доказательство. По § 98 для всякого треугольника как остроугольного, так и тупоугольного имеем:
a = 2R• sin A; b = 2R• sin B; c = 2R• sin C.
Отсюда находим:
2R = a/sin A ; 2R = b/sin B ; 2R = c/sin C ,
следовательно:
a/sin A = b/sin B = c/sin C = 2R.
Таким образом, для одного и того же треугольника частное от деления стороны на синус противолежащего угла есть величина постоянная, равная диаметру описанного круга.
Из соотношения a/sin A = b/sin B = c/sin C , переставляя члены пропорции, получим:
a : b : c = sin A : sin B : sin С,
т. е. во всяком треугольнике стороны, относятся между собой, как синусы противолежащих углов.
Пример. Определить a : b : c, если А : В : С= 3 : 4 : 5.
Так как А + В + С =180°, то сначала разделим 180° в отношении 3 : 4 : 5; получим
А = 45°, B = 60° и С = 75°. Теперь по доказанному будем иметь:
a : b : c = sin 45° : sin 60° : sin 75°.
Подставляя сюда _ _
sin 45° = √2/2, sin 60° = √3/2 и sin 75° = cos 30°/2= 1/2
получим, освободясь от знаменателей:
a : b : c = √2 : √3 : .
§ 100. Теорема. Сумма двух сторон треугольника так относится к их разности, как тангенс полусуммы противолежащих углов относится к тангенсу полуразности тех же углов.
Доказательство. По §98 находим:
a + b = 2R {sin A + sin В) и а — b = 2R (sin A — sin В);
отсюда:
Применяя здесь ко второй части формулу (XVII) (§ 65), получим:
( a + b ) : (а — b ) = tg : tg
,
чем и выражается теорема.
§ 101. Формулы Мольвейде. Так называются следующие две пропорции, которые содержат отношения суммы и разности двух сторон треугольника к третьей стороне:
Доказательство. 1) По §98:
a + b = 2R (sin A + sin B) и c = 2R • sin C;
отсюда
Преобразуем вторую часть:
но sin = cos
, так как
+
== 90°. По сокращении же дроби (b) будет окончательно:
2) Таким же образом получим:
§ 102. Теорема. Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения их на косинус угла между ними.
Требуется доказать, что а2 = b2 + с2 — 2bс • соs A (одинаково и в случае острого и в случае тупого;
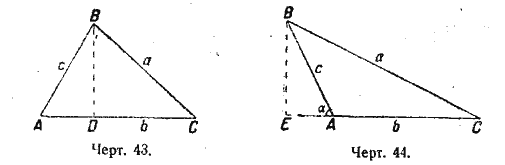
Доказательство. 1) Если угол А острый, то на основании теоремы геометрии о квадрате стороны, лежащей против острого угла, имеем (черт. 43):
а2 = b2 + с2 — 2b • AD,
но из прямоугольного треугольника ABD можно заменить AD через с • cos A; тогда получим:
а2 = b2 + с2 — 2bс • соs A.
2) Если угол A тупой, то применяем теорему о квадрате стороны против тупого угла треугольника (черт. 44). Получаем
а2 = b2 + с2 + 2b • AE.
Из треугольника ABC находим:
AE = с • соs α,
но так как
α = /
BAE = 180° — А,
то
cos α = cos (180° — А) = — cos A,
поэтому
АЕ = — с • cos A.
Подставляя это выражение в геометрическую формулу, получим:
а2 = b2 + с2 — 2bс • соs A,
т, е. то же самое, что и в первом случае.
Теоретический материал
Алгебра
Глава 12. Тригонометрические функции и треугольники
12.5. Решение косоугольных треугольников
Под косоугольными треугольниками понимают остроугольные и тупоугольные треугольники. Рассмотрим примеры решения таких треугольников на основании теорем синусов и косинусов.
Пример 1.
Дана сторона и два угла треугольника, например, ,
и
. Определить стороны
,
, угол
и площадь
.
Решение:
. По теореме синусов
,
откуда
.
Из пропорции
находим
.
Площадь треугольника
.
Пример 2.
Даны две стороны и угол между ними, например, ,
,
. Найти
,
,
,
.
Решение:
По теореме косинусов .
На основании этой же теоремы найдем и угол :
.
Наконец, .
Пример 3.
Даны две стороны и угол против одной из них, например ,
и
. Вычислить:
,
,
,
.
Решение:
По теореме синусов:
,
откуда
.
Определив , найдем
.
По теореме синусов:
,
откуда
.
Пример 4.
Даны три стороны треугольника ,
и
.
,
,
,
= ?
Решение:
Из теоремы косинусов находим углы:
и
,
а затем
и
.