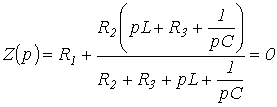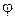Как в уравнение найти корень характеристического уравнения

Корни характеристического уравнения. Постоянная времени

Выражение
свободной составляющей
общего
решения х дифференциального уравнения
(2) определяется видом корней
характеристического уравнения (см.
табл. 3).

Таблица
3. Выражения свободных составляющих
общего решения

Вид корней характеристического уравнения	Выражение свободной составляющей
Корни вещественные и различные
Корни вещественные и
Пары комплексно-сопряженных корней

Необходимо
помнить, что, поскольку в линейной цепи
с течением времени свободная составляющая
затухает, вещественные части корней
характеристического уравнения не могут
быть положительными.

При
вещественных корнях
монотонно
затухает, и имеет местоапериодический
переходный процесс. Наличие пары
комплексно сопряженных корней
обусловливает появление затухающих
синусоидальных колебаний (колебательный
переходный процесс).

Поскольку
физически колебательный процесс связан
с периодическим обменом энергией между
магнитным полем катушки индуктивности
и электрическим полем конденсатора,
комплексно-сопряженные корни могут
иметь место только для цепей, содержащих
оба типа накопителей. Быстроту затухания
колебаний принято характеризовать
отношением

которое
называется декрементом колебания,
или натуральным логарифмом этого
отношения

называемым
логарифмическим декрементом колебания,где.

Важной
характеристикой при исследовании
переходных процессов является постоянная
времени t, определяемая для цепей первого
порядка, как:

где
р – корень характеристического уравнения.

Постоянную
времени можно интерпретировать как
временной интервал, в течение которого
свободная составляющая уменьшится в е
раз по сравнению со своим начальным
значением. Теоретически переходный
процесс длится бесконечно долго. Однако
на практике считается, что он заканчивается
при

Литература

Основы
теории цепей: Учеб. для вузов
/Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
С.В.Страхов. –5-е изд., перераб. –М.:
Энергоатомиздат, 1989. -528с.
Бессонов
Л.А.Теоретические основы электротехники:
Электрические цепи. Учеб. для студентов
электротехнических, энергетических и
приборостроительных специальностей
вузов. –7-е изд., перераб. и доп. –М.:
Высш. шк., 1978. –528с.
Теоретические
основы электротехники. Учеб. для
вузов. В трех т. Под общ. ред. К.М.Поливанова.
Т.1. К.М.Поливанов. Линейные электрические
цепи с сосредоточенными постоянными.
–М.: Энергия- 1972. –240с.

Контрольные вопросы

Чем
обусловлены переходные процессы?
Как
определяется порядок дифференциального
уравнения, описывающего переходный
процесс?
Для
каких цепей применим классический
метод расчета переходных процессов?
Доказать
законы коммутации:
и—
с энергетических позиций.
В
каких цепях и почему возможен колебательный
процесс?
Определить
величину токов
и
напряженийна
конденсаторе ина
катушке индуктивности в момент
коммутации в цепи на рис. 4, если.

Ответ:
;

Лекция n 25 Способы составления характеристического уравнения

Характеристическое
уравнение составляется для цепи после
коммутации. Оно может быть получено
следующими способами:

непосредственно
на основе дифференциального уравнения
вида (2) (см. лекцию №24), т.е. путем
исключения из системы уравнений,
описывающих электромагнитное состояние
цепи на основании первого и второго
законов Кирхгофа, всех неизвестных
величин, кроме одной, относительно
которой и записывается уравнение (2);
путем
использования выражения для входного
сопротивления цепи на синусоидальном
токе;
на
основе выражения главного определителя.

Согласно
первому способу в предыдущей лекции
было получено дифференциальное уравнение
относительно напряжения
на
конденсаторе для последовательной
R-L-C-цепи, на базе которого записывается
характеристическое уравнение.

Следует
отметить, что, поскольку линейная цепь
охвачена единым переходным процессом,
корни характеристического уравнения
являются общими для всех свободных
составляющих напряжений и токов ветвей
схемы, параметры которых входят в
характеристическое уравнение. Поэтому
по первому способу составления
характеристического уравнения в качестве
переменной, относительно которой оно
записывается, может быть выбрана любая.

Применение
второго и третьего способов составления
характеристического уравнения рассмотрим
на примере цепи рис. 1.

Составление
характеристического уравнения по методу
входного сопротивления заключается в
следующем:

записывается
входное сопротивление цепи на переменном
токе;

jw
заменяется на оператор р;

полученное
выражение
приравнивается
к нулю.

Уравнение

совпадает
с характеристическим.

Следует
подчеркнуть, что входное сопротивление
может быть записано относительно места
разрыва любой ветви схемы. При этом
активный двухполюсник заменяется
пассивным по аналогии с методом
эквивалентного генератора. Данный
способ составления характеристического
уравнения предполагает отсутствие в
схеме магнитосвязанных ветвей; при
наличии таковых необходимо осуществить
их предварительное развязывание.

Для
цепи на рис. 1 относительно зажимов
источника

Заменив
jw на р и приравняв полученное выражение
к нулю, запишем

или

(1)

При
составлении характеристического
уравнения на основе выражения главного
определителя число алгебраических
уравнений, на базе которых он записывается,
равно числу неизвестных свободных
составляющих токов. Алгебраизация
исходной системы интегро-дифференциальных
уравнений, составленных, например, на
основании законов Кирхгофа или по методу
контурных токов, осуществляется заменой
символов дифференцирования и интегрирования
соответственно на умножение и деление
на оператор р. Характеристическое
уравнение получается путем приравнивания
записанного определителя к нулю.
Поскольку выражение для главного
определителя не зависит от правых частей
системы неоднородных уравнений, его
составление можно производить на основе
системы уравнений, записанных для полных
токов.

Для
цепи на рис. 1 алгебраизованная система
уравнений на основе метода контурных
токов имеет вид

Отсюда
выражение для главного определителя
этой системы

Приравняв
D к нулю, получим результат, аналогичный
(1).

Соседние файлы в папке Лекции

Источник

Линейные однородные дифференциальные уравнения второго порядка имеют вид
y′′+ay′+by=0y» +ay^prime +by=0
На первом этапе решения составляется характеристическое уравнение

k2+ak+b=0k^2+ak+b=0

При решении этого уравнения могут получиться три варианта корней, в зависимости от которых общее решение будет иметь свой вид.

Корни характеристического уравнения действительные и различные

Корни характеристического уравнения k1k_1, k2k_2 действительные и различные.

В этом случае общее решение

y=C1ek1x+C2ek2xy=C_1 e^{k_1 x}+ C_2 e^{k_2 x}

Пример

y′′+3y′+2y=0y» +3y’ +2y=0

k2+3k+2=0k^2+3k+2=0

D=9−4⋅1⋅2=1D=9-4cdot 1cdot 2=1

k1=−3−12=−2;k2=−3+12=−1k_1=frac{-3-sqrt 1}{2}=-2; k_2=frac{-3+sqrt 1}{2}=-1

Тогда общее решение

y=C1e−2x+C2e−xy=C_1 e^{-2 x}+ C_2 e^{- x}

Корни характеристического уравнения действительные и кратные

В этом случае общее решение

y=ekx(C1+C2x)y= e^{kx}left(C_1+ C_2 xright)

Пример

y′′−4y′+4y=0y» -4y^prime +4y=0

k2−4k+4=0k^2-4k+4=0

D=16−4⋅1⋅4=0D=16-4cdot 1cdot 4=0

k1=k2=42=2k_1=k_2=frac{4}{2}=2

Тогда общее решение

y=e2x(C1+C2x)y=e^{2 x}left(C_1+ C_2 xright)

Корни характеристического уравнения комплексные

k=α±βik=alphapm beta i

В этом случае общее решение

y=eαx(C1cos⁡βx+C2sin⁡βx)y=e^{alpha x}left(C_1cos beta x+C_2sin beta xright)

Пример

y′′−2y′+17y=0y» -2y’ +17y=0

k2−2k+17=0k^2-2k+17=0

D=4−4⋅1⋅17=−64D=4-4cdot 1cdot 17=-64

k1=2−−642=1−8i;k2=2+−642=1+8ik_1=frac{2-sqrt -64}{2}=1-8i; k_2=frac{2+sqrt -64}{2}=1+8i

α=1;β=8alpha=1;beta=8

Тогда общее решение

y=ex(C1cos⁡8x+C2sin⁡8x)y=e^{x}left(C_1cos 8x+C_2sin 8xright)

Источник

Линейные однородные дифференциальные уравнения с постоянными коэффициентами

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Частный случай: уравнение второго порядка Пусть имеем линейное однородное дифференциальное уравнение второго порядка где р, Р2 — действительные числа. Чтобы найти общее решение этого уравнения, надо найти два его линейно независимых частных решения. Следуя Эйлеру, будем искать их в виде где тогда Подставляя эти выражения для у и ее производных в уравнение (1), получаем .

Так как , то должно выполняться равенство Следовательно, функция у = eAz будет решением уравнения (1), т. е. будет обращать его в тождество по х, если А будет удовлетворять алгебраическому уравнению Уравнение (3) называется характеристическим уравнением по отношению к уравнению (1), а его левая часть называется характеристическим много-членом.

Уравнение (3) есть квадратное уравнение. Обозначим его корни через А] и 1 они могут быть 1) действительными и разными; 2) комплексными; 3) действительными и равными. Рассмотрим каждый случай в отдельности. 1. Если корни Л|, Аг характеристического уравнения действительные и разные, то частными решениями уравнения (1) будут функции Эти решения линейно независимы (Aj Ф А2) и, следовательно, образуют фундаментальную систему решений уравнения.

Общее решение уравнения

Общее решение уравнения имеет вид — произвольные постоянные). Пример 1. Найти общее решение уравнения М Составляем характеристическое уравнение: Оно имеет корни Линейные однородные дифференциальные уравнения с постоянными коэффициентами Общий случай: уравнение произвольного порядка Физические приложения: уравнение колебаний Уравнения, приводящие к уравнениям с постоянными коэффициентами Линейные неоднородные дифференциальные уравнения Отсюда получаем искомое общее решение 2.

Пусть корни характеристического уравнения комплексные. Так как коэффициенты р], р2 характеристического уравнения действительные, комплексные корни входят попарно сопряженными. Положим, что Частные решения дифференциального уравнения (1) можно записать в виде Это комплекснозначные функции действительного аргумента х, а мы будем заниматься лишь действительными решениями.

С помощью формул Эйлера частные решения ij и у2 уравнения (1) можно представить в виде Воспользовавшисьтеоремой 4, получим, что частными решениями уравнения (1) будут также функции _ Эти решения линейно независимы, так как Решения образуют фундаментальную систему решений уравне-ния (1), общее решение которого в этом случае имеет вид или Пример 3.

Найти общее решение уравнения 4 Характеристическое уравнение имеет кратные корни Поэтому общее решение исходного дифференциального уравнения: Замечание. Пусть имеем линейное однородное дифференциальное уравнение (вообще, с переменными коэффициентами) Пусть — частное решение уравнения. Введем новую искомую функцию ti(x) соотношением (разрешимым относительно н(х) в тех интервалах, где yi(x) не обращается в нуль).

Из этого соотношения найдем производные от у : и подставим их в уравнение (5): Для функции и(х) получаем опять уравнение порядка п, но коэффициент при м(х) есть £(yil-Он тождественно равен нулю, так как yi (х) есть решение уравнения (5). Следовательно, в полученном уравнении порядок понизится, если ввести новую искомую функцию z(x) = и'(х).

Разделив, кроме того, все члены последнего уравнения на yi(x) Ф 0, приведем его к виду Итак, если известно частное решение уравнения (5), то задача интегрирования этого уравнения приводится к интегрированию линейного однородного уравнения порядка п — . Можно показать, что если известны два частных линейно независимых решения, то порядок уравнения может быть понижен на две единицы. Вообше, если известно г частных линейно независимых решений линейного однородного дифференциального уравнения, то порядок этого уравнения может быть понижен на г единиц. 6.2.

Физические приложения: уравнение колебаний Линейные дифференциальные уравнения с постоянными коэффициентами возникают в задачах о механических и электрических колебаниях. Рассмотрим уравнение свободных механических колебаний, причем независимой переменной будем считать время t: где у — отклонение колеблющейся точки от положения равновесия, rh — масса точки, h — коэффициент трения (считаем, что сила трения пропорциональна скорости), к > 0 — коэффициент упругости восстанавливающей силы (считаем, что эта сила пропорциональна отклонению).

Характеристическое уравнение

Характеристическое уравнение для (6) имеет корни Если трение достаточно велико, h2 > Атк, то эти корни действительные и отрицательные. Общее решение уравнения (6) в этом случае имеет вид Так как то из (7) заключаем, что при большом трен и и отклонение точки от положения равновесия с возрастанием t стремится к нулю, не совершая колебаний. Если трение мало, Атк, то характеристическое уравнение имеет комплексно сопряженные корни Общее решение уравнения (6) в этом случае определяется формулой или Отсюда видно, что в случае малого трения происходят затухающие колебания. Пусть теперь трение отсутствует, .

В этом случае характеристическое уравнение имеет чисто мнимые корни Решение уравне- ния (6) имеет вид . в этом случае происходят незатухающие гармонические колебания с частотой ш = и произвольными амплитудой А и начальной фазой 6. Задача. При каких 1) все решения уравнения стремятся к нулю при 2) каждое решение уравнения обращается в нуль на бесконечном множестве точек х? 6.3. Общий случай: уравнение произвольного порядка Рассмотрим теперь линейное однородное дифференциальное уравнение произвольного порядка п (п ^ 1) с постоянными коэффициентами ) гдерьрг,,Рп — действительные числа.

Общее решение дифференциального уравнения (8) находим так же, как и в случае уравнения второго порядка. Ищем решение в виде Подставляя вместо у величину еХх в уравнение (8), получаем , что приводит к характеристическому уравнению 2. Находим корни характеристического уравнения. 3. По характеру корней выписываем частные линейно независимые решения уравнения (8), руководствуясь тем, что: а) Каждому действительному однократному корню А характеристическою уравнения соответствует частное решение уравнения (8).

б) Каждой паре однократных комплексно сопряженных корней соответствуют два линейно независимых частных решения уравнения (8). в) Каждому действительному корню А кратности г соответствует г линейно независимых частных решений уравнения (8). Рассмотрим случай в) подробнее. Пусть число А есть корень кратности г характеристического уравнения . Функцию будем рассматривать как функцию двух аргументов: ж и А.

Возможно вам будут полезны данные страницы:

Она имеет непрерывные производные по а: и по А всех порядков, причем Поэтому частные производные функции по х и по А не зависят от порядка дифференцирования (операции дифференцирования функции у по х и по А перестановочны), так что Воспользовавшись этой перестановочностью, а также тем, что Если А есть г-кратный корень характеристического уравнения то стало быть, правые части (10) и (11) тождественно по х равны нулю: Это означает, что функции являются в этом случае решениями уравнения (8).

Легко проверить, что функции линейно независимы на любом интервале (a, b) изменения х. г) Приведенные в пункте в) рассуждения сохраняют силу и для комплексных корней.

Поэтому каждой паре комплексно сопряженных корней p кратности l отвечает 2/х частных решений уравнения 4. Число построенных таким образом частных решений уравнения (8) равно порядку п этого уравнения. Можно показать, что все эти решения линейно независимы в совокупности. Имея п линейно независимых частных решений 3/i(x), skfc). уп(я) уравнения (8), получаем общее решение этого уравнения, где произвольные постоянные. Прммер 4. Найти общее решение уравнения Составляем характеристическое уравнение: 2. Находим корни характеристического уравнения: 3.

По характеру корней выписываем частные линейно независимые решения дифференциального уравнения: 4. Общее решение дифференциального уравнения имеет вид Схема решения линейного дифференциального уравнения с постоянными коэффициентами Дифференциальное уравнение действительные числа). Характеристическое уравнение Корни характеристического уравнения Частные линейно независимые решения дифференциального уравнения Общее решение уравнения — произвольные постоянные). §7.

Уравнения, приводящие к уравнениям с постоянными коэффициентами Существуют линейные дифференциальные уравнения с переменными коэффициентами, которые с помощью замены переменных преобразуются в уравнения с постоянными коэффициентами. К их числу принадлежит уравнение Эйлера где pi.tp2, —tPn — постоянные числа.

Ограничимся рассмотрением уравнения Эйлера 2-го порядка (оно встречается в задачах математической физики): Линейные однородные дифференциальные уравнения с постоянными коэффициентами Общий случай: уравнение произвольного порядка Физические приложения: уравнение колебаний Уравнения, приводящие к уравнениям с постоянными коэффициентами Линейные неоднородные дифференциальные уравнения Положим Подставляя выражения для , получим дифференциальное уравнение с постоянными коэффициентами.

Последнее интегрируется обычным приемом: составляем характеристическое уравнение находим его корни и по характеру корней выписываем общее решение уравнения (2), после чего возвращаемся к старой переменной х. Пример. Найти общее решение уравнения Замена переменной х = приводит к уравнению характеристическое уравнение которого имеет корни Общее решение преобразованного уравнения равно Учитывая, что , для общего решения исходного уравнения получаем выражение Замечание 1.

Для преобразованного уравнения (2) в случае действительных и различных корней характеристического уравнения (3) частные решения имеют вид Поэтому можно сразу задаться этим видом частного решения. Подставляя в уравнение (1), получим для к уравнение ) совпадающее с (3). Каждому простому действительному корню уравнения (4) отвечает частное решение уравнения (1); двукратному корню отвечают два решения уравнения (1).

Паре комплексных сопряженных корней уравнения (4) будут соответствовать два решения уравнения (I). Замечание 2. Уравнение постоянные числа) подстановкой также приводится к уравнению с постоянными коэффициентами. §8. Линейные неоднородные дифференциальные уравнения Линейное неоднородное дифференциальное уравнение п-го порядка имеет вид Здесь заданные на некотором интервале (а, р) функции. Если ао(ж) Ф 0 на (а, то после деления на ац(х) получим уравнение.

Из теоремы 1 существования и единственности решения задачи Коши получаем: если на отрезке [а, 6] коэффициенты Рк(х) и правая часть /(х) уравнения (2) непрерывны, то это уравнение имеет единственное решение, удовлетворяющее условиям Уравнение (2) можно записать в виде где, как и выше, Теорема 12. Если у(х) есть решение неоднородного уравнения есть решение соответствующего однородного уравнения мПо условию, В силу линейности оператора £ имеем Это означает, что функция есть решение уравнения Теорема 13.

Если у(х) есть решение уравнения есть решение уравнения та функция есть решение уравнения По условию, используя линейность оператора £, получаем Последнее означает, что функция есть решение уравнения Теорема выражает так называемый принцип суперпозиции (наложения). Теорема 14. Если уравнение где все коэффициенты и функции действительные, имеет решение то действительная часть решения и(х) и его мнимая часть v(x) являются соответственно решениями уравнений.

По условию имеем Отсюда получаем: Теорема 15 (о структуре общего решения линейного неоднородного дифференциального уравнения). Общее решение в области — уравнения с непрерывными на отрезке коэффициентами , и правой частью f(x) равно сумме общего решения соответствующего однородного уравнения и какого-нибудь частного решения у(х) неоднородного уравнения, т. е. Надо доказать, что где произвольные постоянные, линейно независимые решения соответствующего однородного уравнения £[у] = 0, является общим решением неоднородного уравнения.

Будем исходить из определения общего решения и просто проверим, что семейство функций у(ж), определяемое формулой (4), удовлетворяет условиям 1) и 2), содержащимся в этом определении. В самом деле, функция у(х), определяемая формулой (4), является решением уравнения (2) при любых значениях постоянных, поскольку сумма какого-либо решения неоднородного уравнения и любого решения соответствующего однородного уравнения есть решение неоднородного уравнения.

Так как для уравнения (2) при х 6 [а, Ь] выполнены условия теоремы 1 существования и единственности решения задачи Коши, то остается показать, что подбором постоянных С, в (4) можно удовлетворить произвольно заданным начальным условиям где хо € (а,6), т.е. можно решить любую задачу Коши. Ограничимся случаем, когда п = 3.

Потребовав, чтобы решение (4) удовлетворяло начальным условиям (5), приходим к системе уравнений для отыскания Эта линейная по отношению к система трех уравнений с тремя неизвестными допускает единственное решение относительно з при произвольных правых частях, так как определитель этой системы есть определитель Вронского W(x$) для линейно независимой системы решений соответствующего однородного уравнения и, следовательно, отличен от нуля в любой точке ж € (а, Ь), в частности в точке ж = жо.

Значит, какова бы ни была тройка чисел

уо, Уо> Уо» найдется решение С?, С?, Cj системы (6) такое, что функция будет решением дифференциального уравнения (2), удовлетворяющим начальным условиям Линейные однородные дифференциальные уравнения с постоянными коэффициентами Общий случай: уравнение произвольного порядка Физические приложения: уравнение колебаний.

Уравнения, приводящие к уравнениям с постоянными коэффициентами Линейные неоднородные дифференциальные уравнения Из этой теоремы следует, что задача нахождения общего решения линейного неоднородного уравнения сводится к отысканию какого-либо частного решения этого неоднородного уравнения и общего решения соответствующего однородного уравнения. Интегрирование линейного неоднородного дифференциального уравнения методом вариации постоянных 155 Пример 1.

Найти общее решение уравнения М Нетрудно заметить, что функция является частным решением данного неоднородного уравнения. Чтобы найти общее решение этого уравнения, остается отыскать общее решение соответствующего однородного уравнения Это уравнение есть линейное однородное уравнение с постоянными коэффициентами. Характеристическое уравнение, соответствующее уравнению , есть корни его Поэтому общее решение уравнения (*) имеет вид . Общее решение исходного неоднородного уравнения:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

корней характеристического уравнения

Одним из косвенных показателей качества систем управления является степень удаленности корней характеристического уравнения замкнутой САУ от мнимой оси комплексной плоскости. Пусть ближайшие к мнимой оси комплексно-сопряженные корни устойчивой системы имеют значение

. (7.1)

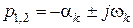
Расстояние (рис. 8.2) ближайших к мнимой оси комплексно-сопряженных корней называется степенью устойчивости системы.

Угол φ, образуемый лучами, проведенными из начала координат через эти корни, характеризует колебательность системы. Степенью колебательности системы (коэффициентом затухания колебаний) называют количественную характеристику, определяемую выражением

. (7.2)

Чтобы система обладала заданной колебательностью, все корни характеристического уравнения должны вписываться в угол 2φ (см. рис. 7.2). Для большинства систем управления допустимое перерегулирование не должно превышать (10…20)%, что соответствует m=0,2…0,5.

Рис. 7.2. Область расположения корней

с заданными показателями и

При корневых методах оценки качества системы, т. е. по расположению корней характеристического полинома, исходят из следующих соображений.

Решение однородного уравнения, характеризующего свободное движение системы, представляет собой сумму затухающих экспонент вида (6.2). Полагая, что качество САУ в основном определяется ближайшим к мнимой оси вещественным корнем или ближайшей к мнимой оси парой комплексно-сопряженных корней (доминирующих корней), можно записать

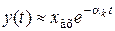
Полагая, что зона δ установления переходного процесса составляет (2…5)% от установившегося значения , можно найти требуемое соотношение степени устойчивости системы и времени регулирования t_р:

. (7.3)

Следовательно, задаваясь временем регулирования, можно рассчитать минимальное (по модулю) значение вещественных частей корней характеристического уравнения.

Аналогично можно связать степень колебательности m системы со степенью затухания колебаний. Пусть по условиям технологии требуется, чтобы каждая последующая амплитуда колебаний затухала в k раз по сравнению с предыдущей. Тогда

. (7.4)

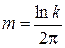
Пусть k=10, тогда в соответствие с (7.4) получим m=0,336 и

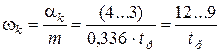
Таким образом, задаваясь временем регулирования и соотношением амплитуд колебаний k, можно определить допустимую область расположения корней на комплексной плоскости или решить обратную задачу расчета параметров и k переходного процесса по расположению доминирующих корней характеристического уравнения. Следует отметить, что данный подход дает приемлемую точность оценки качества регулирования, если действительные части остальных корней характеристического уравнения больше действительной части доминирующих корней, по крайней мере, в 5 раз [6].

Для построения в плоскости параметров областей, обеспечивающих требуемые показатели качества регулирования целесообразно использовать метод D-разбиения [6]. В качестве примера используем уравнение Вышнеградского, описывающего в параметрической форме характеристический полином 3-го порядка,

. (7.5)

где A и B – обобщенные параметры характеристического уравнения.

Подставим выражение для комплексного корня в (7.5). Тогда получим

Приравнивая нулю вещественную и мнимую части, получим

, (7.6)

Полагая в (7.6), получим границу области устойчивости системы в параметрической форме

(7.7)

— уравнение гиперболы Вышнеградского (кривая 1, рис. 7.3).

Рис. 7.3. Границы областей устойчивости,

колебательности и апериодичности на

Полагая в (7.6), получим границу области апериодичности системы в параметрической форме (кривые 2 и 3 на рис. 7.3)

Поскольку на кривой 1 ω ≠ 0, а на кривых 2 и 3 ω = 0, то области I и III являются областями комплексных, а область II – вещественных корней (см. рис. 7.3). Следовательно, если параметры A, B принадлежат области II, то переходные процессы имеют апериодический характер, причем, чем эти параметры больше, тем процессы более затянуты. Если параметры принадлежат области I, то переходные процессы имеют колебательный характер, причем, чем больше A и меньше B, тем выше колебательность. Область III является областью монотонности решения однородного дифференциального уравнения, соответствующего (7.5), а, следовательно, переходные процессы, имея колебательный характер, тем не менее, затухают монотонно (без перерегулирования).

Диаграмма Вышнеградского [19] помимо приведенных кривых содержит кривые равных вещественных частей комплексных корней (равной степени устойчивости), причем для двух случаев расположения корней, когда ближайшими к мнимой оси являются комплексные корни и, когда ближайшим к мнимой оси расположен вещественный корень (на рис. 7.3 эти кривые не показаны). В частности, на границе областей I и III (кривая 4) все три корня равно удалены от мнимой оси.

Требования повысить быстродействие и одновременно снизить перерегулирование в системе являются противоречивыми друг другу, что заставляет искать компромисс. В общем случае, с точки зрения переходного процесса наилучшей считается САУ, у которой все корни характеристического уравнения n-го порядка равны друг другу (на практике редко реализуется), т. е.

, i=1, 2, 3…n.

В этом случае перерегулирование не превышает 10%, а время нарастания регулирования является минимальным.

Если все корни являются вещественными, то система характеризуется отсутствием перерегулирования, т. е. апериодическими переходными процессами. Время регулирования будет тем меньше, чем меньше среднегеометрический корень или, иначе, чем ближе к мнимой оси расположен центр корней.

При анализе качества системы корневыми методами необходимо учитывать влияние нулей передаточной функции на переходный процесс.

Прежде всего, нужно проверить, насколько близки нули к полюсам.

Если нуль и полюс совпадают, то их нужно сократить, и они не будут влиять на качество системы. Порядок системы при этом, естественно, будет понижен.

Если полюсы и нули передаточной функции не совпадают, то полюсы определяют отдельные составляющие переходного процесса (апериодические и гармонические), а нули определяют удельный вес каждой из этих составляющих. Чем ближе нуль передаточной функции расположен к какому-либо полюсу, тем меньше его вклад в переходную характеристику составляющей, соответствующей данному полюсу.

7.2.2. Интегральные оценки качества

В основе интегральных оценок качества лежит предположение, что качество регулирования тем выше, чем меньше площадь между кривой переходного процесса и заданным значением регулируемой переменной. Интегральные оценки качества являются строгой математической формулировкой понятия качества системы, и их минимизация позволяет определить оптимальные параметры системы управления, т. е. решить задачу параметрического синтеза системы. Для этой цели применяются процедуры безусловной и условной оптимизации [2, 6, 10-12, 19-21].

Наибольшее применение для косвенной оценки качества САУ находят интегральные оценки вида [6, 11, 12, 19]:

; (7.8)

; (7.9)

; (7.10)

; (7.11)

, (7.12)

где — текущая ошибка регулирования, являющаяся функцией времени,

С – некоторый весовой коэффициент, характеризующий допустимую скорость изменения ошибки регулирования, а, следовательно, выходной координаты в переходном процессе.

В критерии (7.8) подынтегральное выражение линейно относительно ошибки регулирования и такая оценка применяется только для апериодического переходного процесса, когда ошибка имеет положительный знак.

Интегральная квадратичная оценка (ИКО) вида (7.9) применяется при колебательном характере переходных процессов, характеризующихся сменой знака ошибки регулирования. Интегральная квадратичная оценка (7.10) применяется в тех случаях, когда требуется учитывать ограничения энергии управления.

Широко используемым видом оценки качества является интеграл от модуля ошибки (ИМО) – (7.11), позволяющем учесть смену знака подынтегральной функции.

Чтобы уменьшить вклад начальной ошибки в интеграл (7.11) и учесть связанную с этим ошибку была предложена [6] оценка в виде интеграла от взвешенного модуля ошибки (ИВМО) в виде (7.12).

Рассмотрим пример. Пусть передаточная функция замкнутой системы 2-го порядка имеет вид:

, (7.13)

где — коэффициент затухания.

Нормированное значение собственной частоты принято . На рис. 7.4 приведены кривые, отражающие изменение двух из приведенных выше интегральных оценок системы (ИКО и ИВМО) в функции коэффициента затухания [6].

Рис. 7.4. Интегральные оценки

качества системы второго порядка

Как видим, оценка ИВМО по сравнению с ИКО имеет ярко выраженный минимум (хорошую избирательность), соответствующий = 0,707, что для данной системы 2-го порядка обеспечивает наиболее быстрое протекание переходного процесса с перерегулированием около 4,3%.

Рассмотрим еще один пример. Пусть передаточная функция замкнутой системы имеет достаточно общий вид нерекурсивного фильтра n-го порядка:

. (7.14)

Безусловная оптимизация систем первого-четвертого порядка (n=1…4), описываемых передаточными функциями (7.14), по критерию ИВМО дает оптимальные значения коэффициентов полиномов знаменателей этих передаточных функций, приведенные в табл. 7.1. Значения коэффициентов нормированы относительно собственной частоты колебаний .

На рис. 7.5 приведены кривые переходных процессов, соответствующих оптимальным по критерию ИВМО фильтрам первого-четвертого порядка.

Порядок системы	Полином знаменателя передаточной функции
n=1
n=2
n=3
n=4

Значения коэффициентов нормированы относительно собственной частоты колебаний . На рис. 7.5 приведены кривые переходных процессов, соответствующие оптимизации фильтров первого-четвертого порядка по критерию ИВМО.

Рис. 7.5. Переходные характеристики, соответствующие

оптимизации систем по ИВМО

Графики построены в зависимости от нормированного времени .

Кроме приведенных оценок для оптимизации систем управления применяются и другие интегральные критерии качества, в частности, лежащие в основе синтеза фильтров Баттерворта, широко применяемых при настройке контуров электромеханических систем управления.

8. Метод пространства состояний

Широкое распространение компьютеров и мощных систем программирования побуждает к исследованию САУ во временной области, а, следовательно, к непосредственному использованию описания динамических систем управления в форме обыкновенных дифференциальных уравнений без перехода к операторной форме. Кроме того, как уже отмечалось, векторно-матричные формы описания и исследования применимы не только к одномерным, линейным, стационарным САУ, но и к широкому классу многомерных, нелинейных и нестационарных САУ.

Чтобы получить пригодную для компьютерного синтеза и анализа модель САУ, необходимо представить ее в переменных состояния системы, используя далеко не единственный набор переменных. Следует отметить, что описание систем во временной области в векторно-матричной форме лежит в основе современной теории управления и оптимизации. В настоящей главе рассмотрены вопросы применения метода пространства состояния к непрерывным системам управления.

8.1. Векторно-матричное описание САУ

Состояние системы – это совокупность значений переменных системы (координат состояния), существенных с точки зрения решаемой задачи. В общем случае, в это число включают не только выходные и внутренние переменные САУ, но и задающие воздействия, и доминирующие возмущающие воздействия внешней среды. Чем полнее достоверной информации о состоянии системы в текущий момент времени, тем проще определить будущие значения всех ее переменных. Инженерно-технический персонал, разрабатывающий и эксплуатирующий технические системы управления, оперирует, как правило, с такими физическими переменными, которые могут быть измерены с помощью соответствующих датчиков. К таким физическим переменным САУ относят ускорение, скорость, перемещение, давление, расход, температуру, уровень и т. п. Координатами датчиков технологических координат САУ являются другие переменные — напряжение, ток, частота следования импульсов, двоичный код и т. п., что дает исследователю возможность выбора для синтеза и анализа необходимого набора координат состояния САУ.

Векторно-матричная модель многомерной, нелинейной, нестационарной САУ записывается в виде [6, 10, 11, 19]

, (8.1)

где X(t), U(t),F(t), Y(t) – соответственно векторы состояния, управления, возмущения и выходных (управляемых) координат системы,

– вектор первых производных координат состояния,

– нелинейные, нестационарные функции координат состояния, управления и возмущения системы.

В уравнении (8.1) вектор управления U(t) является, в общем случае, некоторой нелинейной нестационарной функцией задающих координат, координат состояния и возмущения САУ и призван обеспечить оптимальное управление системой. Описание многомерных, нелинейных, нестационарных САУ в форме (8.1) не позволяет, как правило, получить инженерное решение задачи структурно-параметрического синтеза оптимального управления U(t) или такое решение приводит к неоправданным затратам на реализацию (в техническом или экономическом аспектах). В большинстве случаев такие модели сводят к одномерным или многомерным линейным (линеаризованным) квазистационарным моделям, для которых имеются развитые методы и инженерные методики синтеза оптимального управления.

Линейную (линеаризованную) модель многомерной стационарной (квазистационарной) САУ представляют в виде системы обыкновенных дифференциальных уравнений первого порядка в форме Коши:

, (8.2)

Эту же систему дифференциальных уравнений можно представить в векторно-матричной форме [6, 11, 19]:

, (8.3)

где — векторы (векторы-столбцы) соответственно состояния и управления САУ,

, ;

— символ транспонирования (иногда для обозначения транспонирования применяют буквенный символ “т”);

— стационарные матрицы соответственно состояния и управления,

, .

В общем случае, на объект управления помимо управляющих воздействий действуют возмущающие воздействия. В этом случае векторно-матричную модель системы представляют в виде

, (8.4)

где — вектор-столбец возмущающих воздействий САУ, C – стационарная матрица возмущений,

Выходные (управляемые) переменные не всегда непосредственно принадлежат вектору состояния. В линейных САУ они линейно связаны с переменными состояния, управляющими и возмущающими переменными. В этом случае к уравнениям (8.3), (8.4) присоединяют алгебраические линейные уравнения

(8.5)

или , (8.6)

где — вектор выходных переменных САУ, ;

K, L, M – стационарные матрицы соответственно размерностей (r n), (r m), (r d).

Следует отметить, что приведенные уравнения (8.1)…(8.6) дают описание лишь объекта управления или разомкнутой системы, если вектор управления U(t) не является функцией координат состояния САУ. В замкнутых линейных САУ управление обычно формируют как линейную форму координат состояния и, в общем случае, возмущения САУ.

В качестве примера приведем векторно-матричное описание ранее рассматриваемого электродвигателя постоянного тока как объекта регулирования по цепи якоря. Пусть выходной (регулируемой) координатой является скорость вращения двигателя. Полагая, что напряжение возбуждения , а магнитный поток , математическую модель электродвигателя можно представить в виде:

. (8.7)

Воспользуемся векторно-матричной моделью линейных САУ в виде (8.4), (8.5). Зададимся векторами состояния, управления и возмущения в виде:

; ;

(8.8)

По уравнениям (8.7) найдем матрицы состояния, управления и возмущения:

; ; . (8.9)

Поскольку выходная переменная всего одна и ей является координата состояния , уравнение выхода преобразуется к скалярной форме

. (8.10)

По описанию системы в форме векторно-матричных уравнений (ВМУ) можно непосредственно получить эквивалентную передаточную функцию (ПФ) и, наоборот, зная ВМУ системы, можно получить ее ПФ. Для этого в системе MATLAB имеется две функции: функция tf и функция ss.

Пусть ВМУ системы имеет вид (8.3), (8.5). Применительно к системе MATLAB ВМУ записывают в виде

Для получения ВМУ в системе MATLAB необходимо определить функцию ss(A,B,C,D). Для преобразования ВМУ к ПФ системы необходимо записать:

sys_ss=ss(A,B,C,D); % Формирование ВМУ системы;

sys_tf=tf(sys_ss), % Преобразование ВМУ к ПФ системы.

Для обратного преобразования ПФ к ВМУ необходимо записать:

sys_tf=tf(num,den); % Формирование ПФ системы;

sys_ss=ss(sys_tf); Преобразование ПФ к ВМУ системы.

Рассмотрим пример. Пусть ПФ системы имеет вид

Тогда запишем скрипт преобразования ПФ к ВМУ и обратного преобразования ВМУ к ПФ:

sys_tf=tf(num,den); % Формирование ПФ системы;

sys_ss=ss(sys_tf); %Преобразование ПФ к ВМУ системы;

Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами

Ниже разберем способы, как решить линейные однородные и неоднородные дифференциальные уравнения порядка выше второго, имеющих постоянные коэффициенты. Подобные уравнения представлены записями y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 и y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) , в которых f 0 , f 1 , . . . , f n — 1 — являются действительными числами, а функция f ( x ) является непрерывной на интервале интегрирования X .

Оговоримся, что аналитическое решение подобных уравнений иногда неосуществимо, тогда используются приближенные методы. Но, конечно, некоторые случаи дают возможность определить общее решение.

Общее решение ЛОДУ и ЛДНУ

Мы зададим формулировку двух теорем, показывающих, какого вида общих решений ЛОДУ и ЛНДУ n -ого порядка следует искать.

Общим решением y 0 ЛОДУ y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 на интервале
X (коэффициенты f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) непрерывны на X ) будет линейная комбинация
n линейно независимых частных решений ЛОДУ y j , j = 1 , 2 , . . . , n , содержащая произвольные постоянные коэффициенты C j , j = 1 , 2 , . . . , n , то есть y 0 = ∑ j = 1 n C j · y j .

Общим решением y ЛНДУ y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) на интервале X (коэффициенты f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) непрерывны на X ) и функцией f ( x ) будет являться сумма y = y 0 + y

, где y 0 — общее решение соответствующего ЛОДУ y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 , а y

— некоторое частное решение исходного ЛНДУ.

Итак, общее решение линейного неоднородного дифференциального уравнения, содержащего постоянные коэффициенты y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) , нужно искать, как y = y 0 + y

— некоторое его частное решение, а y 0 = ∑ j = 1 n C j · y j – общее решение соответствующего однородного дифференциального уравнения y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 .

В первую очередь рассмотрим, как осуществлять нахождение y 0 = ∑ j = 1 n C j · y j — общее решение ЛОДУ n -ого порядка с постоянными коэффициентами, а потом научимся определять частное решение y

линейного неоднородного дифференциального уравнения n -ого порядка при постоянных коэффициентах.

Алгебраическое уравнение n -ого порядка k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 носит название характеристического уравнения линейного однородного дифференциального уравнения n -ого порядка, содержащего постоянные коэффициенты, записи y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 .

Возможно определить n частных линейно независимых решений y 1 , y 2 , . . . , y n исходного ЛОДУ, исходя из значений найденных n корней характеристического уравнения k 1 , k 2 , . . . , k n .

Методы решения ЛОДУ и ЛНДУ

Укажем все существующие варианты и приведем примеры на каждый.

Когда все решения k 1 , k 2 , . . . , k n характеристического уравнения k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 действительны и различны, линейно независимые частные решения будут выглядеть так:
y 1 = e k 1 · x , y 2 = e k 2 · x , . . . , y n = e k n · x . Общее же решение ЛОДУ n -ого порядка при постоянных коэффициентах запишем как: y 0 = C 1 · e k 1 · x + C 2 · e k 2 · x + . . . + C n · e k n · x .

Пример 1

Задано ЛОДУ третьего порядка, содержащее постоянные коэффициенты y ‘ ‘ ‘ — 3 y » — y ‘ + 3 y = 0 . Определите его общее решение.

Решение

Cоставим характеристическое уравнение и найдем его корни, разложив предварительно многочлен из левой части равенства на множители, используя метод группировки:
k 3 — 3 k 2 — k + 3 = 0 k 2 ( k — 3 ) — ( k — 3 ) = 0 ( k 2 — 1 ) ( k — 3 ) = 0 k 1 = — 1 , k 2 = 1 , k 3 = 3

Ответ: найденные корни являются действительными и различными, значит общее решение ЛОДУ третьего порядка с постоянными коэффициентами запишем как: y 0 = C 1 · e — x + C 2 e x + C 3 · e 3 x .

Когда решения характеристического уравнения являются действительными и одинаковыми ( k 1 = k 2 = . . . = k n = k 0 ) , линейно независимые частные решения линейного однородного дифференциального уравнения n -ого порядка с постоянными коэффициентами буду иметь вид: y 1 = e k 0 · x , y 2 = x · e k 0 · x , . . . , y n = x n — 1 · e k 0 · x .

Общее же решение ЛОДУ будет выглядеть так:
y 0 = C 1 · e k 0 · x + C 2 · e k 0 · x + . . . + C n · x n — 1 · e k 0 · x = = e k 0 · x · C 1 + C 2 · x + . . . + C n · x n — 1

Задано дифференциальное уравнение: y ( 4 ) — 8 k ( 3 ) + 24 y » — 32 y ‘ + 16 y = 0 . Необходимо определить его общее решение.

Решение

Составим характеристическое уравнение заданного ЛОДУ: k 4 — 8 k 3 + 24 k 2 — 32 k + 16 = 0 .

Преобразуем данное характеристическое уравнение, используя формулу бинома Ньютона, оно примет вид: k — 2 4 = 0 . Отсюда мы выделим его четырехкратный корень k 0 = 2 .

Ответ: общим решением заданного ЛОДУ станет: y 0 = e 2 x · C 1 + C 2 · x + C 3 · x 2 + C 4 · x 3

Когда решения характеристического уравнения линейного однородного дифференциального уравнения n -ого порядка при постоянных коэффициентах — различные комплексно сопряженные пары α 1 ± i · β 1 , α 2 ± i · β 2 , . . . , α m ± i · β m , n = 2 m , линейно независимые частные решения такого ЛОДУ будут иметь вид:
y 1 = e α 1 x · cos β 1 x , y 2 = e α 1 x · sin β 1 x , y 3 = e α 2 x · cos β 2 x , y 4 = e α 2 x · sin β 2 x , … y n — 1 = e α m x · cos β m x , y n = e α m x · sin β m x

Общее же решение запишем так:

y 0 = e α 1 x · C 1 · cos β 1 x + C 2 · sin β 1 x + + e α 2 x · C 3 · cos β 2 x + C 4 · sin β 2 x + . . . + + e α m x · C n — 1 · cos β m x + C n · sin β m x

Задано ЛОДУ четвертого порядка при постоянных коэффициентах y ( 4 ) — 6 y ( 3 ) + 14 y » — 6 y ‘ + 13 y = 0 . Необходимо его проинтегрировать.

Решение

Составим характеристическое уравнение заданного ЛОДУ: k 4 — 6 k 3 + 14 k 2 — 6 k + 13 = 0 . Осуществим преобразования и группировки:

k 4 — 6 k 3 + 14 k 2 — 6 k + 13 = 0 k 4 + k 2 — 6 k 3 + k + 13 k 2 + 1 = 0 k 2 + 1 k 2 — 6 k + 13 = 0

Из полученного результата несложно записать две пары комплексно сопряженных корней k 1 , 2 = ± i и k 3 , 4 = 3 ± 2 · i .

Ответ: общее решение заданного линейного однородного дифференциального уравнения n -ого порядка с постоянными коэффициентами запишется как:
y 0 = e 0 · C 1 · cos x + C 2 · sin x + e 3 x · C 3 · cos 2 x + C 4 · sin 2 x = = C 1 · cos x + C 2 · sin x + e 3 x · C 3 · cos 2 x + C 4 · sin 2 x

Когда решения характеристического уравнения — это совпадающие комплексно сопряженные пары α ± i · β , линейно независимыми частными решениями линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами будут записи:
y 1 = e α · x · cos β x , y 2 = e α · x · sin β x , y 3 = e α · x · x · cos β x , y 4 = e α · x · x · sin β x , … y n — 1 = e α · x · x m — 1 · cos β x , y n = e α · x · x m — 1 · sin β x

Общим решением ЛОДУ будет:

y 0 = e α · x · C 1 · cos β x + C 2 · sin β x + + e α · x · x · C 4 · cos β x + C 3 · sin β x + . . . + + e α · x · x m — 1 · C n — 1 · cos β x + C n · sin β x = = e α · x · cos β x · C 1 + C 3 · x + . . . + C n — 1 · x m — 1 + + e α · x · sin β x · C 2 + C 4 · x + . . . + C n · x m — 1

Задано линейное однородное дифференциальное уравнение с постоянными коэффициентами y ( 4 ) — 4 y ( 3 ) + 14 y » — 20 y ‘ + 25 y = 0 . Необходимо определить его общее решение.

Решение

Составим запись характеристического уравнения, заданного ЛОДУ, и определим его корни:

k 4 — 4 k 3 + 14 k 2 — 20 k + 25 = 0 k 4 — 4 k 3 + 4 k 2 + 10 k 2 — 20 k + 25 = 0 ( k 2 — 2 k ) 2 + 10 ( k 2 — 2 k ) + 25 = 0 ( k 2 — 2 k + 5 ) 2 = 0 D = — 2 2 — 4 · 1 · 5 = — 16 k 1 , 2 = k 3 , 4 = 2 ± — 16 2 = 1 ± 2 · i

Таким образом, решением характеристического уравнения будет двукратная комплексно сопряженная пара α ± β · i = 1 ± 2 · i .

Ответ: общее решение заданного ЛОДУ: y 0 = e x · cos 2 x · ( C 1 + C 3 · x ) + e x · sin 2 x · ( C 2 + C 4 · x )

Встречаются различные комбинации указанных случаев: некоторые корни характеристического уравнения ЛОДУ n -ого порядка с постоянными коэффициентами являются действительными и различными, некоторые — действительными и совпадающими, а какие-то — комплексно сопряженными парами или совпадающими комплексно сопряженными парами.

Пример 5

Задано дифференциальное уравнение y ( 5 ) — 9 y ( 4 ) + 41 ( 3 ) + 35 y » — 424 y ‘ + 492 y = 0 . Необходимо определить его общее решение.

Решение

Составим характеристическое уравнение заданного ЛОДУ: k 5 — 9 k 4 + 41 k 3 + 35 k 2 — 424 k + 492 = 0 .

Левая часть содержит многочлен, который возможно разложить на множители. В числе делителей свободного члена определяем двукратный корень k 1 = k 2 = 2 и корень k 3 = — 3 .

На основе схемы Горнера получим разложение: k 5 — 9 k 4 + 41 k 3 + 35 k 2 — 424 k + 492 = k + 3 k — 2 2 k 2 — 8 k + 41 .

Квадратное уравнение k 2 — 8 k + 41 = 0 дает нам оставшиеся корни k 4 , 5 = 4 ± 5 · i .

Ответ: общим решением заданного ЛОДУ с постоянными коэффициентами будет: y 0 = e 2 x · C 1 + C 2 x + C 3 · e — 3 x + e 4 x · C 4 · cos 5 x + C 5 · sin 5 x

Таким образом, мы рассмотрели основные случаи, когда возможно определить y 0 — общее решение ЛОДУ n -ого порядка с постоянными коэффициентами.

Следующее, что мы разберем – это ответ на вопрос, как решить линейное неоднородное дифференциальное уравнение n -ого порядка с постоянными коэффициентами записи y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) .

Общее решение в таком случае составляется как сумма общего решения соответствующего ЛОДУ и частного решения исходного ЛНДУ: y = y 0 + y

. Поскольку мы уже умеем определять y 0 , остается разобраться с нахождением y

, т.е. частного решения ЛНДУ порядка n с постоянными коэффициентами.

Приведем все способы нахождения y

согласно тому, какой вид имеет функция f ( x ) , находящаяся в правой части рассматриваемого ЛНДУ.

n -ой

f ( x ) = P n ( x )

= Q n ( x ) · x γ . Здесь Q n ( x ) является многочленом степени n , а r – указывает, сколько корней характеристического уравнения равно нулю.
Когда функция f ( x ) представлена в виде произведения многочлена степени n и экспоненты f ( x ) = P n ( x ) · e α · x , частным решением ЛНДУ второго порядка станет: y

= e α · x · Q n ( x ) · x γ . Здесь Q n ( x ) является многочленом n —ой степени, r указывает, сколько корней характеристического уравнения равно α .
Когда функция f ( x ) записана как f ( x ) = A 1 cos ( β x ) + B 1 sin ( β x ) , где А 1 и В 1 – числа, частным решением ЛНДУ станет запись y

= A cos β x + B sin β x · x γ . Здесь где А и В являются неопределенными коэффициентами, r – указывает, сколько комплексно сопряженных пар корней характеристического уравнения равно ± i β .
Когда f ( x ) = e α x · P n ( x ) sin β x + Q k x cos β x , то y

= e α x · L m x sin β x + N m x cos β x · x γ , где r – указывает, сколько комплексно сопряженных пар корней характеристического уравнения равно α ± i β , P n ( x ) , Q k ( x ) , L m ( x ) и N m ( x ) являются многочленами степени n , k , m и m соответственно, m = m a x ( n , k ) .

Коэффициенты, которые неизвестны, определяются из равенства y

( n — 1 ) + . . . + f 1 y

Подробности нахождения решений уравнений в каждом из указанных случаев можно изучить в статье линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами, поскольку схемы решения ЛНДУ степени выше второй полностью совпадают.

Когда функция f ( x ) имеет любой иной вид, общее решение ЛНДУ возможно определить, используя метод вариации произвольных постоянных. Его разберем подробнее.

Пусть нам заданы y j , j = 1 , 2 , . . . , n — n линейно независимые частные решения соответствующего ЛОДУ, тогда, используя различные вариации произвольных постоянных, общим решением ЛНДУ
n -ого порядка с постоянными коэффициентами будет запись: н = ∑ j = 1 n C j ( x ) · y j . В нахождении производных функций C j ( x ) , j = 1 , 2 , . . . , n поможет система уравнений:

∑ j = 1 n C j ‘ ( x ) · y j = 0 ∑ j = 1 n C j ‘ ( x ) · y ‘ j = 0 ∑ j = 1 n C j ‘ ( x ) · y » j = 0 … ∑ j = 1 n C j ‘ ( x ) · y j ( n — 2 ) = 0 ∑ j = 1 n C j ‘ ( x ) · y j ( n — 1 ) = 0

а собственно функции C j ( x ) , j = 1 , 2 , . . . , n найдем при последующем интегрировании.

Задано ЛНДУ с постоянными коэффициентами: y ‘ ‘ ‘ — 5 y » + 6 y ‘ = 2 x . Необходимо найти его общее решение.

Решение

Составим характеристическое уравнение: k 3 — 5 k 2 + 6 k = 0 . Корни данного уравнения: k 1 = 0 , k 2 = 2 и k 3 = 3 . Таким образом, общим решением ЛОДУ будет запись: y 0 = C 1 + C 2 · e 2 x + C 3 · e 3 x , а частные линейно независимые решения это: y 1 = 1 , y 2 = e 2 x , y 3 = e 3 x .

Варьируем произвольные постоянные: y = C 1 ( x ) + C 2 ( x ) · e 2 x + C 3 ( x ) · e 3 x .

Чтобы определить C 1 ( x ) , C 2 ( x ) и C 3 ( x ) , составим систему уравнений:

C ‘ 1 ( x ) · y 1 + C ‘ 2 ( x ) · y 2 + C ‘ 3 ( x ) · y 3 = 0 C ‘ 1 ( x ) · y ‘ 1 + C ‘ 2 ( x ) · y ‘ 2 + C ‘ 3 ( x ) · y ‘ 3 = 0 C ‘ 1 ( x ) · y » 1 + C ‘ 2 ( x ) · y » 2 + C ‘ 3 ( x ) · y » 3 = 2 x ⇔ C ‘ 1 ( x ) · 1 + C ‘ 2 x · e 2 x ‘ + C ‘ 3 ( x ) · y 3 = 0 C ‘ 1 ( x ) · 1 ‘ + C ‘ 2 x · e 2 x ‘ + C ‘ 3 ( x ) · e 3 x ‘ = 0 C ‘ 1 ( x ) · 1 ‘ ‘ + C ‘ 2 x · e 2 x ‘ ‘ + C ‘ 3 ( x ) · e 3 x ‘ ‘ = 2 x ⇔ C ‘ 1 ( x ) · 1 + C ‘ 2 x · e 2 x + C ‘ 3 ( x ) · e 3 x = 0 C ‘ 1 ( x ) · 0 + C ‘ 2 ( x ) · 2 e 2 x + C ‘ 3 ( x ) · 3 e 3 x = 0 C ‘ 1 ( x ) · 0 + C ‘ 2 ( x ) · 4 e 2 x + C ‘ 3 ( x ) · 9 e 3 x = 2 x

Решаем, используя метод Крамера:

∆ = 1 e 2 x e 3 x 0 2 e 2 x 3 e 3 x 0 4 e 2 x 9 e 3 x = 18 e 2 x · e 3 x — 12 e 2 x · e 3 x = 6 e 5 x ∆ C 1 ‘ ( x ) = 0 e 2 x e 3 x 0 2 e 2 x 3 e 3 x 2 x 4 e 2 x 9 e 3 x = e 5 x · 2 x ⇒ C ‘ 1 ( x ) = ∆ C 1 ‘ ( x ) ∆ = e 5 x · 2 x 6 e 5 x = 1 6 · 2 x ∆ C 2 ‘ ( x ) = 1 0 e 3 x 0 0 3 e 3 x 0 2 x 9 e 3 x = — 3 e x · 2 x ⇒ C ‘ 2 ( x ) = ∆ C 2 ‘ ( x ) ∆ = — 3 e 3 x · 2 x 6 e 5 x = — 1 2 · e — 2 x · 2 x ∆ C 3 ‘ ( x ) = 1 e 2 x 0 0 2 e 2 x 0 0 4 e 2 x 2 x = 2 e 2 x · 2 x ⇒ C ‘ 3 ( x ) = ∆ C 3 ‘ ( x ) ∆ = 2 e 2 x · 2 x 6 e 5 x = 1 3 · e — 3 x · 2 x

Интегрируем C ‘ 1 ( x ) = 1 6 · 2 x с помощью таблицы первообразных, а
C ‘ 2 ( x ) = — 1 2 · e — 2 x · 2 x и C ‘ 3 ( x ) = 1 3 · e — 3 x · 2 x при помощи метода интегрирования по частям, получим:
C 1 ( x ) = 1 6 · ∫ 2 x d x = 1 6 · 2 x ln 2 + C 4 C 2 ( x ) = — 1 2 · ∫ e — 2 x · 2 x d x = — 1 2 · e — 2 x · 2 x ln 2 — 2 + C 5 C 3 ( x ) = 1 3 · ∫ e — 3 x · 2 x d x = 1 3 · e — 3 x · 2 x ln 2 — 3 + C 6

Ответ: искомым общим решением заданного ЛОДУ с постоянными коэффициентами будет:

y = C 1 ( x ) + C 2 ( x ) · e 2 x + C 3 ( x ) · e 3 x = = 1 6 · 2 x ln 2 + C 4 + — 1 2 · e — 2 x · 2 x ln 2 — 2 + C 5 · e 2 x + + 1 3 · e — 3 x · 2 x ln 2 — 3 + C 6 · e 3 x

где C 4 , C 5 и C 6 – произвольные постоянные.

источники:

http://poisk-ru.ru/s49289t1.html

http://zaochnik.com/spravochnik/matematika/differentsialnye-uravnenija/linejnye-differentsialnye-uravnenija-vysshih-por-1/

Источник

From Wikipedia, the free encyclopedia

In mathematics, the characteristic equation (or auxiliary equation^[1]) is an algebraic equation of degree n upon which depends the solution of a given nth-order differential equation^[2] or difference equation.^[3]^[4] The characteristic equation can only be formed when the differential or difference equation is linear and homogeneous, and has constant coefficients.^[1] Such a differential equation, with y as the dependent variable, superscript (n) denoting n^th-derivative, and a_n, a_n − 1, …, a₁, a₀ as constants,

${displaystyle a_{n}y^{(n)}+a_{n-1}y^{(n-1)}+cdots +a_{1}y'+a_{0}y=0,}$

will have a characteristic equation of the form

$a_{n}r^{n} + a_{n-1}r^{n-1} + cdots + a_{1}r + a_{0} = 0$

whose solutions r₁, r₂, …, r_n are the roots from which the general solution can be formed.^[1]^[5]^[6] Analogously, a linear difference equation of the form

${displaystyle y_{t+n}=b_{1}y_{t+n-1}+cdots +b_{n}y_{t}}$

has characteristic equation

${displaystyle r^{n}-b_{1}r^{n-1}-cdots -b_{n}=0,}$

discussed in more detail at Linear recurrence with constant coefficients#Solution to homogeneous case.

The characteristic roots (roots of the characteristic equation) also provide qualitative information about the behavior of the variable whose evolution is described by the dynamic equation. For a differential equation parameterized on time, the variable’s evolution is stable if and only if the real part of each root is negative. For difference equations, there is stability if and only if the modulus of each root is less than 1. For both types of equation, persistent fluctuations occur if there is at least one pair of complex roots.

The method of integrating linear ordinary differential equations with constant coefficients was discovered by Leonhard Euler, who found that the solutions depended on an algebraic ‘characteristic’ equation.^[2] The qualities of the Euler’s characteristic equation were later considered in greater detail by French mathematicians Augustin-Louis Cauchy and Gaspard Monge.^[2]^[6]

Derivation[edit]

Starting with a linear homogeneous differential equation with constant coefficients a_n, a_n − 1, …, a₁, a₀,

${displaystyle a_{n}y^{(n)}+a_{n-1}y^{(n-1)}+cdots +a_{1}y^{prime }+a_{0}y=0,}$

it can be seen that if y(x) = e^rx, each term would be a constant multiple of e^rx. This results from the fact that the derivative of the exponential function e^rx is a multiple of itself. Therefore, y′ = re^rx, y″ = r²e^rx, and y⁽ⁿ⁾ = rⁿe^rx are all multiples. This suggests that certain values of r will allow multiples of e^rx to sum to zero, thus solving the homogeneous differential equation.^[5] In order to solve for r, one can substitute y = e^rx and its derivatives into the differential equation to get

${displaystyle a_{n}r^{n}e^{rx}+a_{n-1}r^{n-1}e^{rx}+cdots +a_{1}re^{rx}+a_{0}e^{rx}=0}$

Since e^rx can never equal zero, it can be divided out, giving the characteristic equation

${displaystyle a_{n}r^{n}+a_{n-1}r^{n-1}+cdots +a_{1}r+a_{0}=0.}$

By solving for the roots, r, in this characteristic equation, one can find the general solution to the differential equation.^[1]^[6] For example, if r has roots equal to 3, 11, and 40, then the general solution will be ${displaystyle y(x)=c_{1}e^{3x}+c_{2}e^{11x}+c_{3}e^{40x}}$ , where $c_{1}$ , $c_{2}$ , and $c_{3}$ are arbitrary constants which need to be determined by the boundary and/or initial conditions.

Formation of the general solution[edit]

Solving the characteristic equation for its roots, r₁, …, r_n, allows one to find the general solution of the differential equation. The roots may be real or complex, as well as distinct or repeated. If a characteristic equation has parts with distinct real roots, h repeated roots, or k complex roots corresponding to general solutions of y_D(x), y_R₁(x), …, y_{R_h}(x), and y_C₁(x), …, y_{C_k}(x), respectively, then the general solution to the differential equation is

${displaystyle y(x)=y_{mathrm {D} }(x)+y_{mathrm {R} _{1}}(x)+cdots +y_{mathrm {R} _{h}}(x)+y_{mathrm {C} _{1}}(x)+cdots +y_{mathrm {C} _{k}}(x)}$

Example[edit]

The linear homogeneous differential equation with constant coefficients

${displaystyle y^{(5)}+y^{(4)}-4y^{(3)}-16y''-20y'-12y=0}$

has the characteristic equation

${displaystyle r^{5}+r^{4}-4r^{3}-16r^{2}-20r-12=0}$

By factoring the characteristic equation into

${displaystyle (r-3)(r^{2}+2r+2)^{2}=0}$

one can see that the solutions for r are the distinct single root r₁ = 3 and the double complex roots r_2,3,4,5 = 1 ± i. This corresponds to the real-valued general solution

${displaystyle y(x)=c_{1}e^{3x}+e^{x}(c_{2}cos x+c_{3}sin x)+xe^{x}(c_{4}cos x+c_{5}sin x)}$

with constants c₁, …, c₅.

Distinct real roots[edit]

The superposition principle for linear homogeneous differential equations says that if u₁, …, u_n are n linearly independent solutions to a particular differential equation, then c₁u₁ + ⋯ + c_nu_n is also a solution for all values c₁, …, c_n.^[1]^[7] Therefore, if the characteristic equation has distinct real roots r₁, …, r_n, then a general solution will be of the form

${displaystyle y_{mathrm {D} }(x)=c_{1}e^{r_{1}x}+c_{2}e^{r_{2}x}+cdots +c_{n}e^{r_{n}x}}$

Repeated real roots[edit]

If the characteristic equation has a root r₁ that is repeated k times, then it is clear that y_p(x) = c₁e^r₁x is at least one solution.^[1] However, this solution lacks linearly independent solutions from the other k − 1 roots. Since r₁ has multiplicity k, the differential equation can be factored into^[1]

${displaystyle left({frac {d}{dx}}-r_{1}right)^{k}y=0.}$

The fact that y_p(x) = c₁e^r₁x is one solution allows one to presume that the general solution may be of the form y(x) = u(x)e^r₁x, where u(x) is a function to be determined. Substituting ue^r₁x gives

${displaystyle left({frac {d}{dx}}-r_{1}right)!ue^{r_{1}x}={frac {d}{dx}}left(ue^{r_{1}x}right)-r_{1}ue^{r_{1}x}={frac {d}{dx}}(u)e^{r_{1}x}+r_{1}ue^{r_{1}x}-r_{1}ue^{r_{1}x}={frac {d}{dx}}(u)e^{r_{1}x}}$

when k = 1. By applying this fact k times, it follows that

${displaystyle left({frac {d}{dx}}-r_{1}right)^{k}ue^{r_{1}x}={frac {d^{k}}{dx^{k}}}(u)e^{r_{1}x}=0.}$

By dividing out e^r₁x, it can be seen that

${displaystyle {frac {d^{k}}{dx^{k}}}(u)=u^{(k)}=0.}$

Therefore, the general case for u(x) is a polynomial of degree k − 1, so that u(x) = c₁ + c₂x + c₃x² + ⋯ + c_kx^k −1.^[6] Since y(x) = ue^r₁x, the part of the general solution corresponding to r₁ is

${displaystyle y_{mathrm {R} }(x)=e^{r_{1}x}!left(c_{1}+c_{2}x+cdots +c_{k}x^{k-1}right).}$

Complex roots[edit]

If a second-order differential equation has a characteristic equation with complex conjugate roots of the form r₁ = a + bi and r₂ = a − bi, then the general solution is accordingly y(x) = c₁e^{(a + bi )x} + c₂e^{(a − bi )x}. By Euler’s formula, which states that e^iθ = cos θ + i sin θ, this solution can be rewritten as follows:

${displaystyle {begin{aligned}y(x)&=c_{1}e^{(a+bi)x}+c_{2}e^{(a-bi)x}\&=c_{1}e^{ax}(cos bx+isin bx)+c_{2}e^{ax}(cos bx-isin bx)\&=left(c_{1}+c_{2}right)e^{ax}cos bx+i(c_{1}-c_{2})e^{ax}sin bxend{aligned}}}$

where c₁ and c₂ are constants that can be non-real and which depend on the initial conditions.^[6] (Indeed, since y(x) is real, c₁ − c₂ must be imaginary or zero and c₁ + c₂ must be real, in order for both terms after the last equals sign to be real.)

For example, if c₁ = c₂ = 1/2, then the particular solution y₁(x) = e^ax cos bx is formed. Similarly, if c₁ = 1/2i and c₂ = −1/2i, then the independent solution formed is y₂(x) = e^ax sin bx. Thus by the superposition principle for linear homogeneous differential equations, a second-order differential equation having complex roots r = a ± bi will result in the following general solution:

${displaystyle y_{mathrm {C} }(x)=e^{ax}(C_{1}cos bx+C_{2}sin bx)}$

This analysis also applies to the parts of the solutions of a higher-order differential equation whose characteristic equation involves non-real complex conjugate roots.

References[edit]

^ ^a ^b ^c ^d ^e ^f ^g Edwards, C. Henry; Penney, David E. (2008). «Chapter 3». Differential Equations: Computing and Modeling. David Calvis. Upper Saddle River, New Jersey: Pearson Education. pp. 156–170. ISBN 978-0-13-600438-7.
^ ^a ^b ^c Smith, David Eugene. «History of Modern Mathematics: Differential Equations». University of South Florida.
^ Baumol, William J. (1970). Economic Dynamics (3rd ed.). p. 172.
^ Chiang, Alpha (1984). Fundamental Methods of Mathematical Economics (3rd ed.). pp. 578, 600. ISBN 9780070107809.
^ ^a ^b Chu, Herman; Shah, Gaurav; Macall, Tom. «Linear Homogeneous Ordinary Differential Equations with Constant Coefficients». eFunda. Retrieved 1 March 2011.
^ ^a ^b ^c ^d ^e Cohen, Abraham (1906). An Elementary Treatise on Differential Equations. D. C. Heath and Company.
^ Dawkins, Paul. «Differential Equation Terminology». Paul’s Online Math Notes. Retrieved 2 March 2011.

Источник

(схема 47)

Линейным называется дифференциальное уравнение n-го порядка,
если оно 1-ой степени относительно искомой функции y(x) и ее производных , то есть имеет вид:

. (8.42)

Если коэффициент P₀(x) ≠ 1, то на
него можно поделить и после соответствующих переобозначений получить:

. (8.43)

Уравнение (8.43) называется уравнением с переменными
коэффициентами. Предположим, что в нем функции , непрерывны на интервале . Тогда для уравнения (8.43) на данном интервале имеет место задача Коши, сформулированная нами
ранее.

Примечание. Частным случаем (8.43) является линейное
дифференциальное уравнение 2-го порядка с переменными коэффициентами:

(8.44)

Если
в уравнении (8.43) f(x)≡0, то оно
называется однородным, если f(x) ≠ 0, то неоднородным.

Теорема 8.3 (о
структуре общего решения линейного неоднородного ДУ). Общее решение
линейного неоднородного дифференциального уравнения представляет собой сумму
общего решения соответствующего однородного и некоторого частного решения
неоднородного уравнения . Запишем коротко:

Однородное дифференциальное уравнение,
соответствующее неоднородному уравнению (8.43), имеет вид:

. (8.45)

Пусть в уравнении (8.45) функции. Тогда оно принимает вид:

(8.46)

и
называется линейным однородным дифференциальным
уравнением n-го порядка с постоянными коэффициентами, где –
функции, n раз дифференцируемые.

Рассмотрим решения уравнений (8.45) и (8.46).
Обозначим полную совокупность их линейно независимых решений через . Тогда, по свойству
решений однородного уравнения, их линейная комбинация также является решением
уравнения (8.45) и (8.46), то есть общее
решение может быть записано в виде:

, (8.47)

где
c_i– константы интегрирования.

Перейдем к конструированию функций . Какого они вида? Так как эти функции в уравнениях (8.45) и
(8.46) n раз дифференцируемы, то их конструкция при дифференцировании не
меняется. Это возможно в случае экспоненциального вида функций, то есть при

, (8.48)

где , . Отсюда, линейная комбинация функций (8.48):

(8.49)

– также
решение уравнений (8.45) и (8.46).

Рассмотрим одну из функций (8.48) – функцию y=e^λx как решение для уравнения (8.46) с постоянными
коэффициентами. Продифференцируем ее n раз:

По определению решения
дифференциального уравнения при подстановке y=e^λx
и ее производных в (8.46) имеем тождество: . После вынесения общего множителя e^λx получаем:.

Так как e^λx≠ 0, то (8.50)

–алгебраическое
уравнение n-ой степени относительно λ, называемое характеристическим уравнением для
уравнения (8.46). Известно, что уравнение n-ой степени имеет равно n корней как действительных, так и комплексных, с
учетом их кратности. Значит, характеристическое уравнение (8.50) дает нам n значений
числа λ, ранее обозначенных нами
через , которые при подстановке в (8.49) приводит нас к
окончательному виду общего решения линейного однородного дифференциального
уравнения (8.46) с постоянными коэффициентами.

Рассмотрим наиболее распространенный частный случай
уравнения (8.46) – его аналог 2-го порядка:

. (8.51)

Для данного уравнения характеристическое уравнение (8.50)
принимает вид:

. (8.52)

Уравнение (8.52) является квадратным относительно λ. В зависимости от дискриминанта D характеристического
уравнения рассматривают три случая, приведенных в таблице 8.1.

Таблица 8.1

Пример 8.17. Найти общее решение уравнений:

Решение.

а) Составляем характеристическое уравнение λ²+2λ–15 = 0. Корнями этого уравнения
будут λ₁= –5 и λ₂= 3. Тогда, применяя (8.53), получаем общее решение: y=C₁e
^–^5x+C₂e^3x.

б) Составляем характеристическое уравнение λ²–16λ+64 = 0.

Решая это уравнение,
получим λ₁= λ₂= 8. Так как корни равные, то, применяя (8.54), будем иметь:

в) Характеристическое уравнение λ²–4λ+13 = 0 имеет комплексные корни λ₁= 2+3i и λ₂= 2–3i. Положив в (8.55) α=2
и β=3, получим общее
решение: .

г) Характеристическое уравнение λ²+9 = 0 имеет корни λ_1;2= ±3i. Полагая в (8.55) α=0 и
β=3,
получим общее решение

Рассмотрим теперь линейное неоднородное дифференциальное
уравнение 2-го порядка с постоянными коэффициентами:

, (8.56)

являющееся частным случаем уравнения (8.44). Функция f(x) может представлять собой функцию специального вида.
Тогда общее решение уравнения находится с помощью следующей теоремы.

Теорема 8.4.
Пусть
задано линейное дифференциальное неоднородное уравнение второго порядка с
постоянными коэффициентами и правой частью специального вида

. (8.57)

1. Если не является корнем
характеристического уравнения соответствующего однородного уравнения, то частное
решение уравнения (8.57) имеет вид:

, (8.58)

где – многочлены общего
вида (с неопределенными коэффициентами).

2. Если – корень
характеристического уравнения кратности s, то частное решение уравнения (8.57) имеет вид:

, (8.59)

– многочлены общего
вида

Рассмотрим в
таблице 8.2 некоторые случаи составления частного решения линейного
неоднородного дифференциального уравнения (8.57) по специальному виду его правой
части.

Таблица 8.2

Пример 8.18. Найти общее решение уравнения .

Решение. Найдем общее решение соответствующего однородного ДУ: . Характеристическое
уравнение λ²+2λ+1 = 0 имеет корень λ₁= 1 кратности 2 (смотри таблицу 8.1). Значит, y_o_._o_.= c₁∙e^x+c₂∙x∙e^x.
Находим частное решение исходного уравнения. В нем правая часть x–4=(x–4)∙e^0∙^x есть
формула вида P₁(x)∙e^0∙^x,
причем α=0 не является
корнем характеристического уравнения: α ≠ λ. Поэтому согласно формуле (8.58), частное решение y_ч.н.
ищем в виде y_ч.н. = Q₁(x)∙e^0∙^x, т.е.
y_ч.н. = Ax+B, где A и B –
неопределенные коэффициенты. Тогда

. Подставив в исходное уравнение,
получим –2A+Ax+B = x–4
или Ax+(–2A+B) = x–4. Приравнивая коэффициенты при
одинаковых степенях x, получим систему уравнений:. Отсюда A=1, B= –2. Поэтому частное решение данного уравнения имеет вид
y_ч.н. = x–2. Следовательно, искомое общее решение уравнения

Пример 8.19. Решить уравнение .

Решение. Находим общее решение
y_o_._o_.
соответствующего однородного

уравнения . Характеристическое уравнение λ²–4λ+13 = 0 имеет корни λ₁= 2+3i, λ₂= 2–3i (смотри таблицу 8.1). Следовательно,.

Находим частное решение y_ч.н.. Правая часть неоднородного уравнения в нашем случае
имеет вид

. Так как не совпадают с корнями характеристического уравнения, то согласно формуле
(8.58), частное решение ищем в виде . Дифференцируем частное решение, получаем:. Подставляя y_ч.н. и его производные в исходное уравнение, получаем:

Отсюда, сравнивая коэффициенты при косинусе и синусе,
имеем . Следовательно, A=1, B= –3. Поэтому . И наконец, с учетом теоремы 8.3 получаем общее решение
заданного линейного неоднородного ДУ в виде:

Пример 8.20.
Найти
частное решение уравнения , удовлетворяющее
начальным условиям .

Решение. Находим общее решение
однородного уравнения. Характеристическое уравнение λ² – λ – 2 = 0 имеет два корня λ₁= –1 и λ₂= 2 (смотри таблицу 8.1); тогда y_o_._o_.= C₁∙e^–^x+C₂∙e²^x – общее решение
соответствующего однородного ДУ.

В правой части заданного уравнения имеется
показательная функция. Так как в данном случае α=2 совпадает с одним из
корней характеристического уравнения, то частное решение следует искать в виде функции Axe²^x. Таким образом, y_ч.н.= Axe²^x. Дифференцируя дважды это равенство, получим: . Подставим y_ч.н. и ее производные в левую часть заданного уравнения
и найдем коэффициент A: . Следовательно, частное решение y_ч.н.= 3xe²^x, общее решение

. (8.60)

Используя начальные условия, определим значения
произвольных постоянных C₁ и C₂. Дифференцируя общее
решение (8.60), получим:

Подставим в общее решение (8.60) значения x=0
и y=2,
будем иметь 2 = C₁+C₂. Подставим в выражение для значения x=0 и , будем иметь: 13 = –C₁+2C₂+3; 10 = –C₁+C₂. Из этих уравнений составим
систему, из которой находим: C₁= –2 и C₂=4. Таким образом, есть то частное
решение, которое удовлетворяет заданным начальным условиям

Теорема 8.5
(о наложении решений). Если правая часть
уравнения (8.56) представляет собой сумму двух функций: , а y₁_ч.н. и y₂_ч.н.– частные решения уравнений и соответственно, то
функция