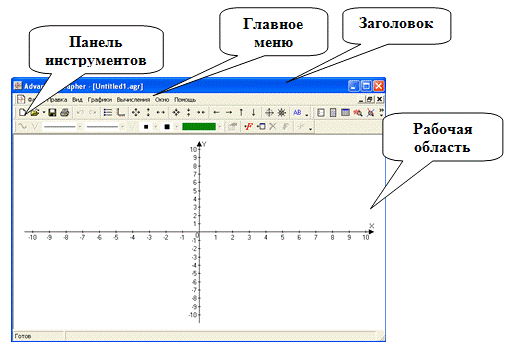
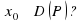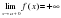Как найти уравнение асимптот и указать их на графике в advanced grapher
Как построить график функции?
С каждым днём всё больше и больше развиваются технологии и теперь уже неизбежно их внедрение в науку. В этой статье рассмотрим, как технологии внедряются в математику, и в особенности, остановимся на рисовании графиков с помощью специальной программы Advanced Grapher.
В начале хочу заметить, что также очень бурно развивается Интернет технологии, и сейчас легко можно нарисовать график функции одной переменной прямо на сайте, это очень удобно и быстро.
Но вернёмся к программе Advanced Grapher, с её помощью можно строить графики не только функций одной переменной, но и:
- параметрических функций,
- функций двух переменных,
- неравенств,
- функций в полярной системе координат,
- а также, графики заданные с помощью таблицы.
Версия 2.2 этой программы совершенно бесплатная для некоммерческих целей, поэтому мы можем легко ею пользоваться. Устанавливается она также очень просто, запускаем setup-файл, который скачали с Интернета, только не забываем указать, что программа для не коммерческих целей, а далее всё без изменений.
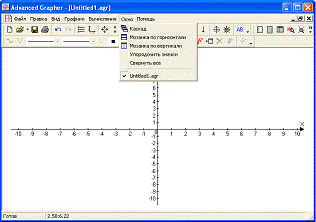
И так, сразу рассмотрим, как построить график функции. Нажимаем вкладку «Графики» в верхнем меню и выбираем пункт «Добавить график» (можно ещё просто нажать на кнопку «Добавить график», которая есть среди кнопок, что расположены под Главным меню или нажать правой клавишей мыши в окне «Список графиков» и выбрать пункт «Добавить график»).
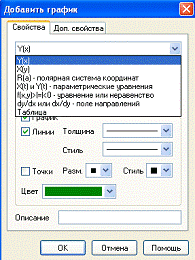
После чего, перед нами появится окно, где мы можем выбрать вид функции, то есть, как она будет задана (с одной переменной или двумя, или может с параметром и т.д.). Выбрав вид функции, вводим в поле «Формула» саму функцию. Также ещё можем выбрать толщину линии её стиль и цвет (это удобно, если на одном рисунке несколько разных графиков). Ещё можете заполнить поле «Описание» (это не обязательно), то есть дать имя своёму графику.
После того, как всё это сделали, нажимаем кнопку «ОК» и видим свой график. Сразу в правом окне «Список графиков» появится наш график, если надо изменить какие-то его свойства, то кликаем два раза по нему и вновь появится предыдущее окно, но уже с указанными свойствами этого графика и там всё можно изменить. Если надо удалить конкретный график, то ищем его в списке и нажимаем правой клавишей мыши и в появившемся списке выбираем пункт «Удалить». Или можно просто снять галочку, что стоит напротив этой функции, тогда график исчезнет, а если он опять понадобится, то поставить галочку снова.
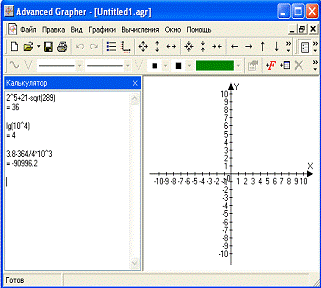
Кроме этого вы можете сделать много других полезных вычислений связанных с графиками, с ними вы можете ознакомиться во вкладке «Вычисления» главного меню. Там вы можете:
- Исследовать функцию, то есть найти нули и экстремумы функции;
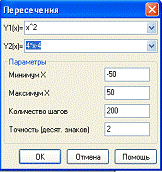
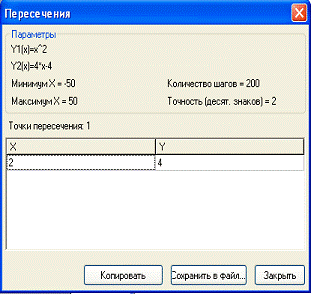
- Вычислить точки пересечения функций;
- Найти производную функции и нарисовать её график;
- Найти касательную или нормаль функции и нарисовать её график;
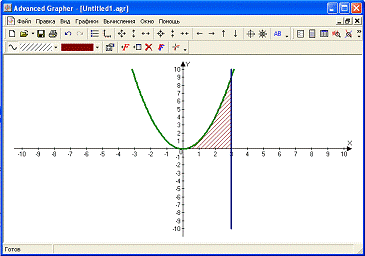
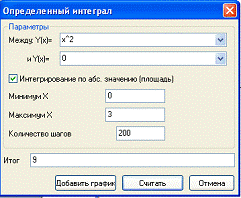
- А с помощью интегрирования, вычислить площадь фигуры, что расположена между функциями, и нарисовать её график.
Всё это делается очень просто, после того, как вы нарисовали график, вы выбираете соответствующий пункт в меню, потом в появившемся окне выбираете ту функцию (или функции) для которой вам надо найти вышеуказанные характеристики (или характеристику). Если это надо, то изменяете нужные параметры, и получаете результат. Там всё интуитивно понятно.
Часто бывает нужно, что бы на графике была сетка, для этого вы клацаете правой клавишей мыши по окну, с нарисованными графиками, и ставите галочки около пунктов «Вертикальные и Горизонтальные линии сетки». Там же вы можете поставить галочку напротив пункта «Легенда». Легенда – это список нарисованных графиков. Ещё там вы увидите пункт «Свойства документа», можете зайти и ознакомится с ними, если вам что-то понабиться, то измените там.
Ну и на конец, если вам надо увеличить или уменьшить масштаб по главных осях, вы можете пользоваться не только «Свойствами документа» (где можно указать числа максимума и минимума), но и соответствующими кнопками, что расположены под главным меню.
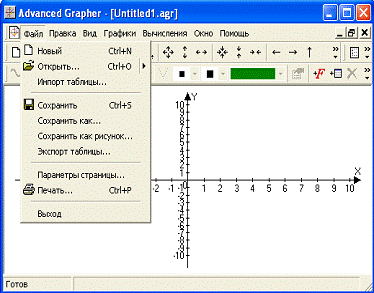
Для того, что бы сохранить ваш график в виде рисунка (после того, как всё нарисовали) выбираем вкладку «Файл» и там пункт «Сохранить как рисунок». Там выбираем формат и место, где сохранить этот рисунок (кнопка «Обзор»), после чего нажимаем «ОК».
Методическая разработка открытого занятия по математике Асимптоты графика функции.Нахождение асимптот.
Государственное образовательное учреждение
среднего профессионального образования
Луганской Народной Республики
«Луганский строительный колледж»
по дисциплине «Математика» на тему:
«Асимптоты графика функции. Нахождение асимптот»
по специальности 38.02.01 «Экономика и бухгалтерский учёт (по отраслям).
категории Еськова Л.В.
Познакомить студентов с определением асимптоты графика функции, видами асимптот и методами их нахождения, обобщить и систематизировать знания определения предела функции и закрепить умения нахождения пределов функции;
Развивать аналитическое мышление, умение проводить аналогии, сравнивать и обобщать;
Воспитывать аккуратность, графическую культуру, усидчивость и настойчивость в достижении результата.
Материально-техническое обеспечение и дидактические средства, ТСО: доска, ПК, мультимедийная установка , программное обеспечение ( Windows 7, Advanced Grapher ), раздаточный материал .
Высшая математика. (В 3-х томах) Бугров Я.С., Никольский С.М.Т.2. Дифференциальное и интегральное исчисление. М., Дрофа, 2004. – 512 с.
Высшая математика. (В 3-х томах) Бугров Я.С., Никольский С.М. Т.3. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. М., Дрофа, 2004. — 512 с.
Грибанов В.М., Крамарь Н.М., Швед О.П. Высшая математика. Курс лекций (часть I , II , III ).-Луганск: Изд-во ВНУ им. В.Даля, 2003.
Н.Д. Владыкина, А.И. Ермаков, С.С. Курчанова, Г.И. Хмеленко. – Луганск: изд. Восточноукр. Нац. ун-та им. В. Даля, 2002. — 100 стр. Методические указания по курсу высшей математики. Часть 1.
Роева Т.Г., Хроленко Н.Ф. Алгебра в таблицах, 10-11 класс: Учеб. пособие.- Х.: Издательская группа «Академия».
Приветствие. Сообщение темы и цели занятия.
Мотивация учебной деятельности.
Сегодня на занятии мы знакомимся с очень важным понятием математического анализа асимптотами графика функции. Вы уже умеете проводить исследование функции и построение графика с помощью производной, находить промежутка монотонности, экстремумы функции и промежутки выпуклости и вогнутости, точки перегиба. Но как ведет себя функция в точках разрыва, как построить ее график вблизи этих точек. Ответы на эти и другие вопросы мы должны узнать на этом занятии. Итак, запишите в тетради план занятия:
Асимптоты графика функции.
Использование программного обеспечения для построения асимптот.
Нахождение асимптот графиков функции.
2. Актуализация опорных знаний.
Так как нахождение асимптот напрямую связано с вычислением пределов функции, то давайте повторим основные правила нахождения пределов.
Как найти предел многочлена при
Как найти предел дробно — рациональной функции: при , если
Как избавиться от неопределенности или ?
Назовите первый замечательный предел.
Изложение нового материала.
При исследовании графика функции при или в окрестности точек разрыва второго рода, часто оказывается, что график функции сколько угодно близко приближается к некоторой прямой. Такие прямые называются асимптотами графика функции.
Если график функции имеет бесконечные ветви, то у графика функции возможно есть асимптоты. Асимптоты — это прямые, к которым неограниченно приближается кривая графика функции при стремлении аргумента функции к бесконечности (рис. 1). Прежде чем приступить к построению графика функции, нужно найти все вертикальные и наклонные (горизонтальные) асимптоты, если они существуют.
Определение Прямая L называется асимптотой графика функции , если расстояние d от переменной точки графика до прямой L стремится к нулю при удалении точки М по кривой в бесконечность.
Определение. Прямая называется асимптотой графика функции при , если .
Существует три вида асимптот: горизонтальные, вертикальные и наклонные.
Определение. Прямая называется вертикальной асимптотой графика функции , если хотя бы один из пределов (правый предел) или (левый предел) равняется или , т.е. (рис. 2).
Очевидно, прямая не может быть вертикальной асимптотой, если функция непрерывная в точке , потому что в этом случае . Итак, вертикальные асимптоты следует искать в точках разрыва функции или на концах ее области определения , если и — конечные числа.
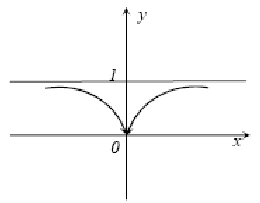
Определение. Прямая называется горизонтальной асимптотой графика функции , если существуют конечные пределы или (рис. 3).
Если конечен только один из пределов или , то функция имеет лишь одну правостороннюю или левостороннюю горизонтальную асимптоту. Если = =, то говорят просто о горизонтальной асимптоте. В том в случае, когда , то функция не имеет соответствующей горизонтальной асимптоты, но может иметь наклонную асимптоту.
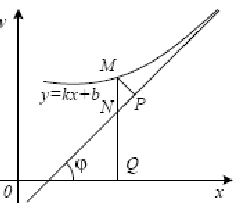
Определение . Прямая называется наклонной асимптотой графика функции , если функция определена при достаточно больших и существуют конечные пределы (рис. 4).
Если, хотя бы один из пределов не существует или равен бесконечности, то график исследуемой функции не имеет соответствующей наклонной асимптоты.
Использование программного обеспечения Advanced Grapher к построению асимптот графика функции.
Advanced Grapher является мощным программным графическим обеспечением. Вы можете использовать его для построения графиков функций, уравнений, неравенств и таблиц.
Программа также позволяет выполнять построение кривых, анализировать
функции, находить точки пересечения графиков с осями координат, касательные и нормали графиков и многое другое.
Вы можете указать цвет, стиль и ширину линий, стиль и размер точек, построение по линиям и (или) точкам, стиль затенения (для неровности) для каждого графика. Вы также можете изменить дополнительные свойства графиков в зависимости от типа графика, например, количество точек, построение интервалов, сортировка (для таблиц), и т.д. Программа имеет многоязычный интерфейс (рис. 5).
Нахождение асимптот графика функции.
Пример № 1. Найти вертикальные и горизонтальные асимптоты графика функции
Очевидно, что область определения функции . Вертикальные асимптоты ищем в точках разрыва функции. Таким образом, прямая может быть вертикальной асимптотой данной функции. Вычисляем границы
и Из этого вытекает, что прямая является вертикальной асимптотой графика исследуемой функции.
Найдем горизонтальную асимптоту . Вычисляем пределы,
используя правило Лопиталя. Получим
=. Поэтому, что = =, то график функции имеет только одну горизонтальную асимптоту. С помощью программы Advanced Grapher легко построить график функции и асимптоты (рис. 6)
Пример № 2. Найти асимптоты графика функции
Очевидно, что график функции не имеет ни вертикальных асимптота (нет точек разрыва), ни горизонтальных асимптот.
Найдем наклонную асимптоту. Вычисляем границы и , .
Таким образом, правая наклонная асимптота имеет вид . Очевидно, что левая наклонная асимптота будет иметь те же значения, что и правая, а это значит, что график исследуемой функции имеет одну наклонную асимптоту. Что и подтверждает построение в программе Advanced Grapher (рис.7).
Перейдем к практической части нашего занятия – решению примеров.
Закрепление изложенного материала.
Пример № 1. Найти асимптоты графика функции
Решение : Исследуем функцию сначала на наличие наклонной асимптоты. Найдем и пределы
Прямая является наклонной асимптотой графика функции при , а также прямая также является асимптотой графика функции при . Проверим наличие вертикальных асимптот.
Точка является точкой разрыва функции. Найдем предел
, он равен бесконечности, поэтому прямая (ось ) является вертикальной асимптотой.
Построение асимптот видим на рисунке (рис 8).
Пример № 2. Найти асимптоты графика функции .
Решение : Найдем пределы и
Подставляя найденные значения и в уравнение наклонной асимптоты, получим уравнение . Точка это точка разрыва функции. Найдём предел , поэтому прямая является вертикальной асимптотой.
График в программе Advanced Grapher наглядно демонстрирует построение асимптот (рис. 9).
Пример № 3. Найти асимптоты графика функции .
, подставляя значение , получим .
Подставляя найденные значения и в уравнение наклонной асимптоты, получим уравнение . Точка это точка разрыва функции.
Найдем предел , поэтому прямая является вертикальной асимптотой.
Построение асимптот видим на рисунке (рис.10).
Пример № 4. Найти асимптоты графика функции .
Решение : Найдем пределы Найдем Таким образом прямая является асимптотой графика данной функции при .
Аналогично прямая также является асимптотой графика данной функции при .
Пример № 5. Найти асимптоты графика функции .
Рассмотрим точки и . Это точки разрыва функции. Имеем . Поэтому прямые и являются вертикальными асимптотами графика данной функции (рис.12). Найдем предел , поэтому ось является горизонтальной асимптотой.
Подведение итогов. Домашнее задание.
Итак, сегодня мы ознакомились с определением асимптот графика функции, видами асимптот и способом их вычисления с помощью пределов. Рассмотрели некоторые примеры нахождения асимптота графика функции.
Проработать материал учебника Высшая математика. Бугров Я.С., Никольский С.М.Т.2 § 4.20, с. 212-215. Найти асимптоты графиков функции: 1). ; 2). .
Асимптоты графика функции. Нахождение асимптот.

Методическая разработка занятия дисциплине «Математика» на тему:
«Асимптоты графика функции. Нахождение асимптот» по специальности 38.02.01 «Экономика и бухгалтерский учёт (по отраслям) выполнена в соответствии с рабочей программой.
Организация-разработчик: ГОУ СПО ЛНР «Луганский строительный колледж».
Разработчик: Еськова Лариса Викторовна, преподаватель – методист высшей квалификационной категории.
Аннотация: данная методическая разработка помогает в доступной форме с использованием компьютерных технологий обучения ознакомить студентов с понятием асимптоты графика функции, видами асимптот и методами их нахождения. Использование графического редактора позволяет наглядно продемонстрировать правильность найденного решения или же найти допущенную ошибку.
Формы организации познавательной деятельности:
*метод коллективного взаимодействия;
*метод контроля и оценки
Просмотр содержимого документа
«Асимптоты графика функции. Нахождение асимптот.»
Государственное образовательное учреждение
среднего профессионального образования
Луганской Народной Республики
«Луганский строительный колледж»
занятия по дисциплине «Математика» на тему:
«Асимптоты графика функции. Нахождение асимптот»
специальностm 38.02.01 «Экономика и бухгалтерский учёт (по отраслям)».
категории Еськова Л.В.
Познакомить с определением асимптоты графика функции, видами асимптот и методами их нахождения, обобщить и систематизировать знания определения предела функции и закрепить умения нахождения пределов функции;
Развивать аналитическое мышление, умение проводить аналогии, сравнивать и обобщать;
Воспитывать аккуратность, графическую культуру, усидчивость и настойчивость в достижении результата.
Материально-техническое обеспечение и дидактические средства, ТСО: доска, ПК, мультимедийная установка, программное обеспечение (Windows 7, Advanced Grapher), раздаточный материал.
Бугров Я.С., Никольский С.М. Высшая математика. (В 3-х томах)Т.2. Дифференциальное и интегральное исчисление. М., Дрофа, 2004. – 512 с.
Бугров Я.С., Никольский С.М. Высшая математика. (В 3-х томах) Т.3. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного пер еменного. М., Дрофа, 2004. — 512 с.
Грибанов В.М., Крамарь Н.М., Швед О.П. Высшая математика. Курс лекций (часть I, II, III).-Луганск: Изд-во ВНУ им. В.Даля, 2003.
Н.Д. Владыкина, А.И. Ермаков, С.С. Курчанова, Г.И. Хмеленко. – Луганск: изд. Восточноукр. Нац. ун-та им. В. Даля, 2002. — 100 стр. Методические указания по курсу высшей математики. Часть 1.
Роева Т.Г., Хроленко Н.Ф. Алгебра в таблицах, 10-11 класс: Учеб. пособие.- Х.: Издательская группа «Академия».
Приветствие. Сообщение темы и цели занятия.
Мотивация учебной деятельности.
Сегодня на занятии мы знакомимся с очень важным понятием математического анализа асимптотами графика функции. Вы уже умеете проводить исследование функции и построение графика с помощью производной, находить промежутка монотонности, экстремумы функции и промежутки выпуклости и вогнутости, точки перегиба. Но как ведет себя функция в точках разрыва, как построить ее график вблизи этих точек. Ответы на эти и другие вопросы мы должны узнать на этом занятии. Итак запишите в тетради план занятия:
Асимптоты графика функции.
Использование программного обеспечения для построения асимптот.
Нахождение асимптот графиков функции.
2. Актуализация опорных знаний.
Так как нахождение асимптот напрямую связано с вычислением пределов функции, то давайте повторим основные правила нахождения пределов.
Как найти предел многочлена 
Как найти предел дробно — рациональной функции: 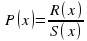
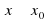
Как избавиться от неопределенности 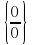
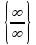
Назовите первый замечательный предел.
Изложение нового материала.
При исследовании графика функции при 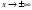
Если график функции 
Определение Прямая L называется асимптотой графика функции 
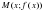
Определение. Прямая 

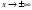
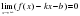
Существует три вида асимптот: горизонтальные, вертикальные и наклонные.
Вертикальная асимптота 
Определение. Прямая 



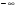
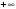
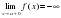
Очевидно, прямая 






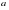
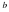
Горизонтальная асимптота 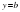
Определение. Прямая 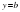


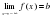
Если конечен только один из пределов 
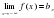


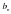
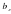
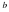
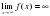
Наклонная асимптота
Определение. Прямая 

Если, хотя бы один из пределов не существует или равен бесконечности, то график исследуемой функции не имеет соответствующей наклонной асимптоты.
Использование программного обеспечения Advanced Grapher к построению асимптот графика функции.
Advanced Grapher является мощным программным графическим обеспечением. Вы можете использовать его для построения графиков функций, уравнений, неравенств и таблиц.
Программа также позволяет выполнять построение кривых, анализировать
http://infourok.ru/metodicheskaya-razrabotka-otkritogo-zanyatiya-po-matematike-asimptoti-grafika-funkciinahozhdenie-asimptot-1979499.html
http://kopilkaurokov.ru/matematika/uroki/asimptoty_ghrafika_funktsii_nakhozhdieniie_asimptot
ИСПОЛЬЗОВАНИЕ ПРОГРАММЫ Advanced Grapher НА УРОКАХ АЛГЕБРЫ В СТАРШИХ КЛАССАХ
П. Н. Ермолина,
МОУ – СОШ № 3 (г. Можайск Московской обл.)
e-mail: panermolini@mail.ru
В статье подробно рассказано, как используя программу Advanced Grapher можно строить графики алгебраических и тригонометрических функций в декартовой системе координат, исследовать функции, находить производную, первообразную, вычислять площади замкнутых фигур. Приведены примеры решения типичных задач на уроке алгебры в старших классах и показаны преимущества программы при исследованиях функции.
Ключевые слова: программа Advanced Grapher, графики, исследование функций.
Учитель, располагающий компьютером, имеет уникальную возможность сделать процесс обучения более наглядным и динамичным с помощью графической программы Advanced Grapher, которая обладает огромным количеством возможностей, в том числе, позволяет строить графики в полярной системе координат, а также линии, заданные параметрически, что упрощает работу ученика при построении графиков.
Рассмотрим особенности использования программы Advanced Grapher на уроке алгебры в старших классах.
Цели:
1. Закрепить умение строить графики в различных системах координат.
2. Закрепить знания школьного алгоритмического языка.
3. Закрепить математические знания по теме: “Исследования функции”.
4. Развивать внимательность, логику мышления.
Тип урока: интегрированный.
Задачи урока:
образовательные:
- усвоение учащимися понятий алгоритмического языка, математического языка, знание темы исследование функции;
- формирование у учащихся умений и навыков работы с программой Advanced Grapher;
- развивать умение считывать информацию и пользоваться ею;
развивающие:
- развитие познавательного интереса учащихся;
- развитие у учеников логического мышления, памяти, внимания;
- формирование информационной культуры учащихся;
воспитательные:
- воспитание трудолюбия;
- прививание учащимся навыков самостоятельной работы.
Ход урока
I. Учет знаний:
а) вспомнить ключевые слова из школьного алгоритмического языка:
— абсолютная величина: abs;
— корень: sqrt;
— запись тригонометрический функций: sin(x), cos(x) и т.д.;
— степень 2x, 2^x, sin2x – (sin(x))^2.
II. Работа в классе:
№ 1. Исследовать функцию y = (x2 – 1)/ x, построив её график [1].
РЕШЕНИЕ
Используя график построенной функции определим:
1. Область определения.
Область значений.
2. Монотонность функции (т.е. промежутки возрастания или убывания
функции).
3. Промежутки знакопостоянства:
а) f(x) > 0;
б) f(x) < 0.
4. Чётность или нечётность, т.е. f(-x) = f(x) — симметрично относительно
оси координат; f(-x) = — f(x) — симметрично относительно начала координат.
5. Нули функции (точки пересечения графика):
а) с осью Оx:
б) с осью Оy:
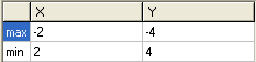
6. Точки экстремума: max y = [ ]; min y = [ ].
Каждый учитель и ученик знает, как однообразны и трудоёмки уроки исследования функций, как порой нелегко объяснить некоторые этапы исследования: особенности окрестности точки, в которых происходит перегиб; асимптоты графика и другие. Данная программа облегчает объяснение материала, а ученикам позволяет быстрее усвоить трудные места этого материала, поскольку дает возможность увеличить размеры графика, выполнить дополнительные построения, более детально и полно производить исследование функции.
Выполнение работы в программе Advanced Grapher
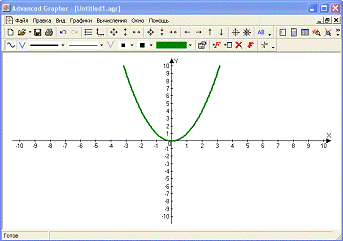
1) График→Добавить график→Свойства y(x)→(вносим формулу (x^2 – 1)/ x)) (рис. 1). Полученный график представлен на рис. 2.
Рис. 1
Рис. 2
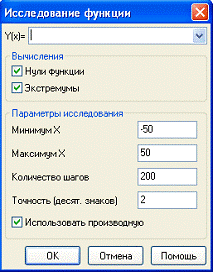
2) Вычисления→Исследования функции→(вносим функцию целиком) →Нули функции + экстремумы функции + min + max (+ использование производной) (рис. 3).
Рис.3
3) Результат исследования (по производной):
а) нули функции;
б) экстремумы (рис. 4).
Рис.4
4) Результат исследования без производной:
а) нули функции;
б) max;
в) min.
5) Вычисления→Пересечения→y(x1) = (x^2 – 1)/ x;
y(x2);
x = -1, y = 0.
x = 1, y = 0.
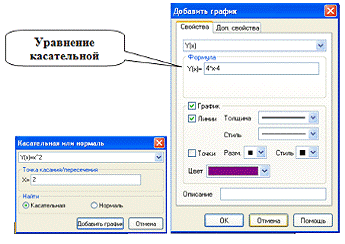
6) Касательная y(x) = (x^2 – 1)/ x, точка касания x = -1.
Касательная→Добавить график→Свойства→OK(формула).
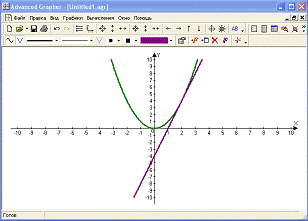
Результат решения показан на рис. 5.
Рис. 5
График любой функции можно построить и по точкам, т.е. по таблице.
Таблица значений→формула (x^2 – 1)/ x от -10 до 10 с шагом 1 →Вычисления функции→ формула (x^2 – 1)/ x→Считать.
Мы рассмотрели подробно пример решения №1, так же были исследованы и построены графики функций примеров №2 — №4.
№2. Построить график функции: y = ׀2x + 3׀ +3׀x-1׀ – ׀x+2׀.
№3. Построить график функции: y = 2x ·cosx.
(Графики→Наборы свойств→Тригонометрический набор
y(x) = 2^x * cos(x)) →OK→Получаем график.
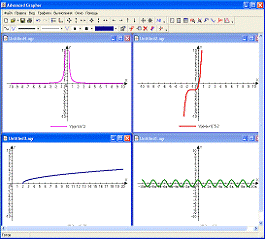
№4. Построить графики функций: (не на одном)
а) y = 1 + sinx; б) y = x + 2sinx; в) y = 1+ cos2x.
С помощью программы можно построить графики и в полярной системе координат, а также линии, заданные параметрически. Кроме того, она чертит графики и направления, которые задаются с помощью уравнений или неравенств, выполнение которых на уроках занимают большое количество времени. Рассмотрим результатат построения такого графика.
№5. В полярных координатах построить графики следующих функций
(выполнить построение последовательно на одном графике):
1) R(a) = 4sin4a; 2) x(t) = 8cost – 2cos4t и y(t) = 8sint – 2sin4t;
3) (x2 + y2)2 – 54(x2 — y2) = 0 – в декартовой системе координат [2] (рис 6).
Рис. 6
№6. Для самостоятельного выполнения. Построить график функции:
1) y = ׀ x2 – 5x+ 6 ׀, (y(x) = abs(x^2 – 5*x +6))
2) y = ׀ x2 – 5 ׀ x ׀ + 6 ׀, (y(x) = abs(x^2 – 5abs(x) +6)
3) y = ׀׀ x2 ׀ -5 ׀ x ׀ +6 ׀, (y(x) = abs(abs(x^2) – 5abs(x) +6)
III. Подведение итогов урока.
IV. Домашнее задание: записать алгоритм построения графиков задания № 6.
Литература
- Мордкович А.Г. Алгебра и начала анализа. 10-11 кл.(в двух частях). Ч.1: учебник для общеобразовательных учреждений. – М.: Мнемозина, 2005.
- Азевич А.И. Advanced Grapher на уроке и после него // Математика в школе. – 2001. — №6. – С. 69.
На уроке рассказывается, как используя программу Advanced Grapher можно строить графики алгебраических и тригонометрических функций в декартовой системе координат, исследовать функции, находить производную, первообразную, вычислять площади замкнутых фигур с применением знаний основ алгоритмизации. Приводятся примеры решения типичных задач на уроке алгебры в старших классах и показываются преимущества программы при исследованиях функции.
Учитель, располагающий компьютером, имеет уникальную возможность сделать процесс обучения более наглядным и динамичным с помощью графической программы Advanced Grapher. Программа строит графики в полярной системе координат, а также линии, заданные параметрически, что упрощает работу ученика при построении графиков.
Цели:
- Закрепить умение строить графики в различных системах координат
- Закрепить знания школьного алгоритмического языка
- Закрепить математические знания по теме «Исследования функции»
- Развивать внимательность, логику мышления
Тип урока: интегрированный.
Задачи урока:
образовательные:
- усвоение учащимися понятий алгоритмического языка, математического языка, знание темы исследование функции;
- формирование у учащихся умений и навыков работы с программой Advanced Grapher;
- развивать умение считывать информацию и пользоваться ею.
развивающие:
- развитие познавательного интереса учащихся;
- развитие у учеников логического мышления, памяти, внимания;
- формирование информационной культуры учащихся.
воспитательные:
- воспитание трудолюбия;
- прививание учащимся навыков самостоятельной работы.
Ход урока
I. Учет знаний
а) вспомнить ключевые слова из школьного алгоритмического языка:
— абсолютная величина: abs;
— корень: sqrt;
— запись тригонометрический функций: sin(x), cos(x) и т.д.;
— степень 2x, 2^x, sin2x— (sin(x))^2.
II. Работа в классе
№ 1. Исследовать функцию y = (x2 — 1)/ x, построив её график [1].
РЕШЕНИЕ
Используя график построенной функции определим:
1. Область определения.
Область значений.
2. Монотонность функции (т.е. промежутки возрастания или убывания функции)
3. Промежутки знакопостоянства:
а) f(x) > 0
б) f(x) < 0
4. Чётность или нечётность, т.е. f(-x) = f(x) — симметрично относительно оси координат f(-x) = — f(x) — симметрично относительно начала координат
5. Нули функции (точки пересечения графика):
а) с осью Оx:
б) с осью Оy:
6. Точки экстремума:
Каждый учитель и ученик знает, как однообразны и трудоёмки уроки исследования функций, как порой нелегко объяснить некоторые этапы исследования: особенности окрестности точки, в которых происходит перегиб; асимптоты графика и другие. Данная программа облегчает объяснение материала, а ученикам позволяет быстрее усвоить трудные места этого материала, поскольку дает возможность увеличить размеры графика, выполнить дополнительные построения, более детально и полно производить исследование функции.
Выполнение работы:
Вводим на алгоритмическом языке функцию:
y = (x^2 — 1)/ x
(График → Добавить график → Cвойства y(x) → (вносим формулу (x^2 — 1)/ x) (рис. 1). Полученный график представлен на рис. 2.
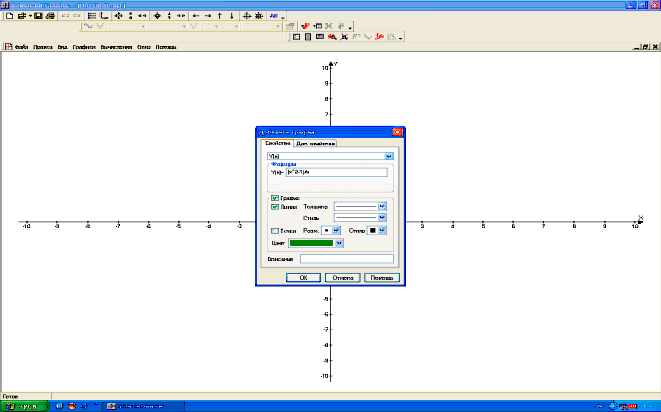
Рис. 1
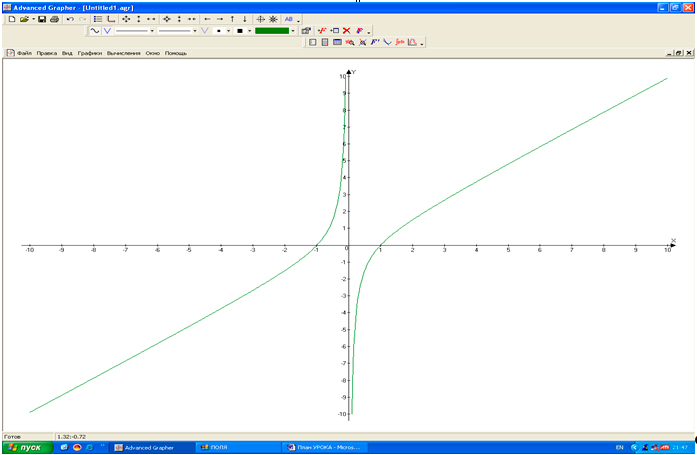
2) Вычисления → Исследования функции → (вносим функцию целиком) → Нули функции + экстремумы функции + min + max (+ использование производной). 3) Результат исследования (по производной):
а) нули функции;
б) экстремумы (рис. 4).
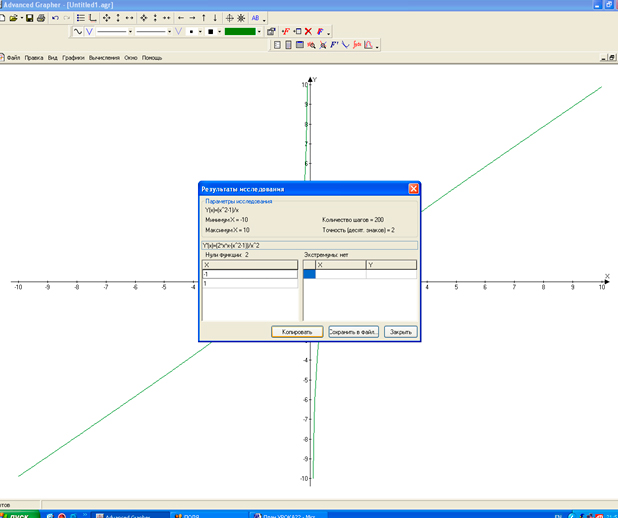
Рис. 4
4) Результат исследования без производной:
а) нули функции;
б) max;
в) min.
5) Вычисления → Пересечения → y(x1) = (x^2 — 1)/ x (рис. 5)
y(x2);
x = -1, y = 0.
x = 1, y = 0.
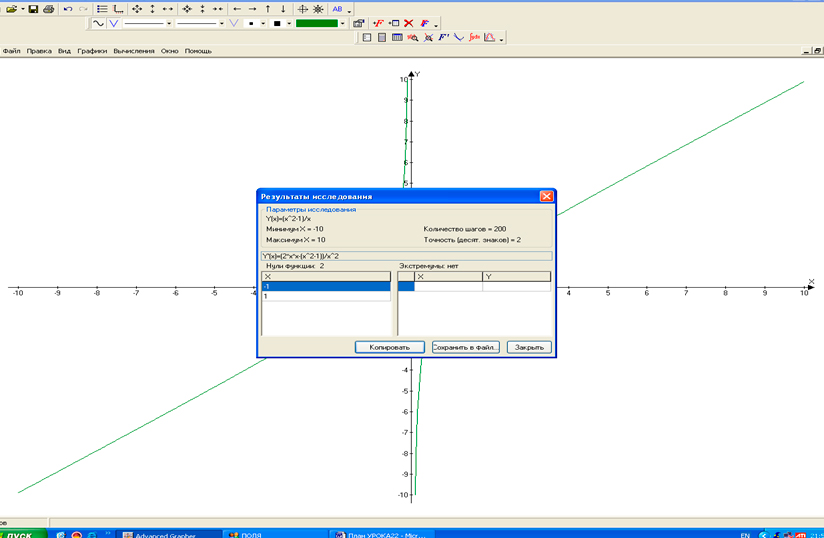
Рис. 5
6) Касательная y(x) = (x^2 — 1)/ x, точка касания x = -1.
Касательная → Добавить график → Свойства → OK (формула)
Результат решения показан на рис. 6.
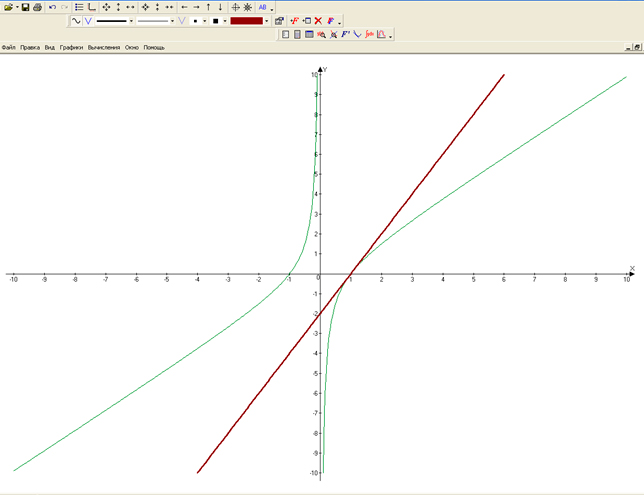
Рис. 6
График любой функции можно построить и по точкам, т.е. по таблице.
Таблица значений → формула (x^2 — 1)/ x от -10 до 10 с шагом 1.
→ Вычисления функции → формула (x^2 — 1)/ x → Считать.
Мы рассмотрели подробно пример решения №1, так же были исследованы и построены графики функций примеров №2 — №4.
№2. Построить график функции: y = ׀ 2x + 3׀ + 3׀x-1׀ — ׀x+2׀
№3. Построить график функции: y = 2x ·cosx.
(Графики → Наборы свойств → Тригонометрический набор)
(y(x) = 2^x * cos(x)) → OK → Получаем график
(Вид → Панели инструментов → Стандартная)
№4. Построить график функции: (не на одном)
а) y = 1 + sinx;
б) y = x + 2sinx;
в) y = 1+ cos2x.
С помощью программы можно построить графики и в полярной системе координат, а также линии, заданные параметрически. Кроме того, она чертит графики и направления, которые задаются с помощью уравнений или неравенств, выполнение которых на уроках занимают большое количество времени. Рассмотрим пример построения такого графика.
№5. В полярных координатах построить графики следующих функций (выполнить построение последовательно на одном графике):
1) R(a) = 4sin4a;
2) x(t) = 8cost — 2cos4t и y(t) = 8sint — 2sin4t;
3) (x2 + y2)2 — 54(x2 — y2) = 0 — в декартовой системе координат [2].
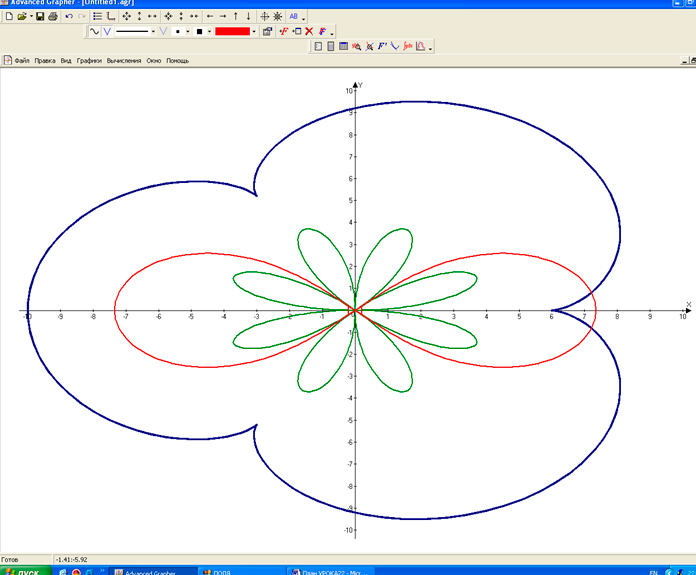
Рис. 7
№6. Для самостоятельного выполнения. Построить график функции:
1) y = ׀ x2 — 5x+ 6 ׀, (y(x) = abs(x^2 — 5*x +6))
2) y = ׀ x2 — 5 ׀ x ׀ + 6 ׀, (y(x) = abs(x^2 — 5abs(x) +6)
3) y = ׀׀ x2׀ -5 ׀ x ׀ +6 ׀, (y(x) = abs(abs(x^2) — 5abs(x) +6)
III. Подведение итогов урока
IV. Домашнее задание
Записать алгоритм построения графиков задания № 6.
Литература
- Мордкович А.Г. Алгебра и начала анализа. 10-11 кл. (в двух частях). Ч.1: учебник для общеобразовательных учреждений. — М.: Мнемозина, 2005.
- Азевич А.И. Advanced Grapher на уроке и после него // Математика в школе. — 2001. — №6. — С. 69.
- Босова Л.Л., Босова А.Ю. Информатика и ИКТ (в двух частях). Ч. 1: учебник для общеобразовательных учреждений. — М.: Бином, 2012.
Применение программы Advanced Grapher в курсе высшей математики в вузах, в качестве виртуальной моделирующей среды
Содержание
Введение
. Общая характеристика программы Advanced Grapher
. Возможности программы Advanced Grapher и ее описание
. Применение графической программы Advanced Grapher
.1 Решение систем уравнений и неравенств
.2 Теория пределов. Дифференцирование функций одной
переменной
.3 Исследование функций с помощью производной
3.4 Интегральное исчисление функций одной переменной
3.5 Ряды
.6 Аналитическая геометрия на плоскости
.7 Теория вероятностей и математическая статистика
4. Графики некоторых из замечательных кривых
Заключение
Литература
Приложение
Введение
Изучение высшей математики можно спланировать с широким привлечением
информационных технологий. Информационные технологии следует применять как на
лекциях, так и на практических занятиях. Лекции можно проводить с помощью
мультимедийной системы и компьютера, заранее подготовив слайды с изложением
основного текста лекции, а также используя некоторые компьютерные программы или
электронные учебные издания.
Трудности, возникающие при изучении тем: исследование и построение
графиков функций, решение уравнений и неравенств графическим способом,
исследование функций с помощью производной, нахождение первообразной функции и
площади криволинейной трапеции, требуют новых подходов в организации учебного
процесса. Использование на занятиях информационно-коммуникационных технологий,
в частности графической программы Advanced Grapher, позволяет с успехом решать
эти задачи.
Данная работа
посвящена применению графопостроителя Advanced Grapher, мощной и простой в использовании
программе для построения графиков и их анализа. Приведены примеры применения
программы Advanced Grapher в курсе высшей математики в вузах, в качестве
виртуальной моделирующей среды. Реализация этих предложений внесла бы
определенный вклад в дело подготовки студентов к интенсивному использованию
математических методов в своей практической и научной деятельности, к
применению современных программных средств и информационных технологий для
инженерных расчетов и графических построений. В работе перечислены конкретные
области применения.
В приложении приведен список полезных программ для студентов,
использование которых в значительной мере упростить изучение конкретных
областей математики.
. Общая характеристика программы Advanced Grapher
Advanced Grapher мощная и простая в использовании программа для
построения графиков и их анализа. Поддерживает построение графиков функций вида
Y(x), X(y), в полярных координатах, заданных параметрическими уравнениями,
графиков таблиц, неявных функций (уравнений) и неравенств. До 100 графиков в
одном окне. Вычислительные возможности: регрессионный анализ, нахождение нулей
и экстремумов функций, точек пересечения графиков, нахождение производных,
уравнений касательных и нормалей, численное интегрирование. Большое количество
параметров графиков и координатной плоскости. Имеет возможности печати,
сохранения и копирования графиков в виде рисунков, многодокументный
настраиваемый интерфейс. Поддерживает русский интерфейс.
Программа Advanced Grapher позволяет не только строить разнообразные
графики на плоскости, но и проводить исследование функций, находить приближенно
корни алгебраического уравнения и точки экстремума функции одной переменной,
получать аналитическое выражение для производной, выполнять численное интегрирование,
графически решать неравенства, осуществлять регрессионный анализ и т.д.
Начиная работу с программой, надо выбрать готовый шаблон с системой
координат или создать новый, используя кнопку Свойства документа на панели
инструментов. Изменить систему координат и ее настройки можно в любой момент
работы с данным чертежом. Одновременно на чертеже можно изобразить до 100
геометрических объектов (это могут быть графики функций, заданных явно или
неявно в декартовых координатах, параметрически, в полярных координатах, так
называемые графики таблиц, а также заштрихованные области, лежащие между двумя
графиками функций или являющиеся множествами решений системы неравенств).
Построенные объекты фиксируются в Списке функций в левой части окна программы. Если
убрать галочку в Списке функций против некоторых объектов, то эти объекты
исчезнут (временно) с плоскости чертежа (это удобно для объяснения учебного
материала).
Можно вычислить значения любой функции вида y=f(x) в отдельной точке с помощью кнопки
Вычисление функций или же вычислить значения такой функции с некоторым шагом с
помощью кнопки Таблица значений. Можно также нажать кнопку Добавить график
таблицы и заполнить таблицу значений x и y тем или иным способом,
затем по таблице построить график функции (в виде ломаной, ломаной с узлами,
отдельных точек, сглаженной кривой). Программа Advanced Grapher позволяет также
выделить и увеличить нужную прямоугольную область на построенном чертеже
(используется кнопка Выбрать интервал на панели инструментов), эту операцию
можно повторить несколько раз. С помощью кнопки Трассировка можно вывести
значение функции в дискретном наборе точек данного графика, а с помощью кнопки
Добавить метку можно делать надписи, установив указатель в место надписи.
Оставаясь в рамках функциональных возможностей программы Advanced
Grapher, сравним ее, например, с универсальными пакетами MATHCAD, MATLAB и MAPLE. Безусловно, что легче освоить и
удобнее использовать в повседневной практике программу Advanced Grapher, чем
эти пакеты. В то же время изучение хотя бы одного из этих математических
пакетов желательно.
.
Возможности программы Advanced Grapher и ее описание
Программа Advanced
Grapher обладает современными графическими
характеристиками. Вы можете свободно добавлять, перемещать, копировать графики
и изменять их расположение на графическом листе. Внешний вид программы:
Рисунок 1
· Функции:
Advanced Grapher позволяет
использовать следующие функции: sin —
синус cos — косинус tan — тангенс cot — котангенс atan — арктангенс asin — арксинус acos — арккосинус abs — абсолютная величина (модуль) sqrt — корень ln — натуральный логарифм lg — логарифм по основанию 10 exp — экспанента int — целая часть числа round — округленное значение frac — дробная часть числа sinh — гиперболический синус cosh — гиперболический косинус tanh — гиперболический тангенс coth — гиперболический котангенс random — счетчик случайных чисел (пример, random(x)=rnd*x, rnd -случайная величина, 0<=rnd<1)
and, or,xor, not-логические
функции
При использовании функций необходимо использовать синтаксис <Имя
функции>(<Аргумент>). Примеры: sin(x+2); ln(ln(1/x)); sin(x)^3.
· Очередность выполнения операций:
1. Функции 2. ^ — возведение в степень 3. *,/ — умножение и деление 4.
+,- — сложение и вычатание 5. >=,=,<=,<,>,<> — операции
отношения 6. and, or,xor, not — логические операции.
Функции имеют наивысший приоритет; and, or и xor — наименьший. Пример: not 1+2 and 0 = (not
(1+2)) and 0 = 0
Дополнительная информация Можно пропускать знак умножения. Примеры: xy,
(x+1)(5y+x), xx, xsin(x).
· Постоянные (константы):
Advanced Grapher опознает
число p. Если Вы хотите использовать
константу e (основание натурального логарифма), введите exp(1).
· Переменные:
Программа позволяет использовать одну или несколько переменных, например:
x,X; y,Y; a, A или t,T (в зависимости от поставленной задачи).
· Операции импорта и экспорта данных
Advanced Grapher позволяет
ввод и вывод информации из других программ и файлов. Вы можете импортировать и
экспортировать следующую информацию:
— графические рисунки. Advanced Grapher позволяет: 1. Копировать графические рисунки в
формате EMF или BMP в другие документы (с помощью команд главного меню:
Правка Копировать как рисунок). Копировать в формате EMF особенно важно, если вам необходимо экспортировать
графики в документы Microsoft Word. 2. Сохранять графические рисунки в
формате EMF или BMP (с помощью команд главного меню: Файл Сохранить как).
Когда вы копируете или сохраняете графики как рисунки, вы можете устанавливать
коэффициент масштабирования. Это особенно важно, если вы хотите печатать
графические рисунки из Advanced Grapher в других
программах.
— Табличнаяинформация.Выможете: 1. Импортировать таблицы из
текстовых файлов (с помощью команд главного меню: Файл Импорттаблицы). 2.
экспортировать таблицы в текстовые файлы (с помощью команд главного меню: Файл
Экспорт таблицы). Вы можете также копировать/вырезать/вставлять таблицы, когда
вы работаете с графиками в рабочем окне программы.
Печать графических рисунков осуществляется с помощью команд главного
меню: Файл Печать.
Рисунок 2
· Дополнительные свойства:
· При создании нескольких графиков на одном графическом листе,
вы можете использовать разные цвета и тип линий, записывать легенду (формулу
графика функции) и вносить дополнительные записи в рабочую область выбранным
(размером и цветом) шрифтом.
· Функция может быть задана:
— в декартовой системе координат Y(X), X(Y);
— в полярной системе координат R(a);
— в параметрической системе координат X(t), Y(t).
Рисунок 3
· Для решения уравнений или неравенств используется команда F(x,y)>|=|<0
· Программа позволяет производить вычисления с помощью команды
калькулятор.
Рисунок 4
·
Программа позволяет вычислять производную, строить ее график, находить нули
функции и экстремумы;
Рисунок 5
· Advanced Grapher используется для построения касательной (нормали) к
графику функции в точке и нахождения уравнения касательной;
Рисунок 6
Рисунок 7
После построения касательной, можно найти точку пересечения касательной с
графиком функции:
Рисунок 9
Рисунок 10
· Advanced Grapher позволяет находить площадь криволинейной трапеции и
интеграл.
Рисунок 11
· Advanced Grapher позволяет решать иррациональные, показательные,
логарифмические (используются функции натурального и логарифмического
логарифмов) уравнения и неравенства;
Рисунок 12
· Удобный интерфейс позволяет строить несколько графиков в
одной рабочей области, располагая графические листы различным способом:
Рисунок 13
Рисунок 14
3. Применение графической программы Advanced Grapher
.1 Решение системы уравнений и неравенств
Пусть надо решить графически систему из двух неравенств: 2x+y2>0, 2x<=y.
Первый способ. Можно решить систему, последовательно строя область
решений для каждого неравенства и взять затем пересечение этих областей. Для
этого сначала нажать кнопку Добавить функцию, выбрать в диалоговом окне вместо Y(x) опцию «f(x,y)<|=|>0 уравнение или неравенство», ввести в поле
Формула одно из неравенств, выбрать способ штриховки и цвет области решений
неравенства; аналогично для второго неравенства, но штриховку взять другую. При
этом граничную линию 2x=y придется строить отдельно. В
результате построений наглядно будет видна область решений системы неравенств.
Второй способ (с помощью оператора логического умножения and). Надо
нажать кнопку Добавить функцию, в диалоговом окне выбрать вместо Y(x) опцию «f(x,y)<|=|>0 уравнение или неравенство», ввести в поле
Формула выражение вида (2x+y^2>0)and(2x<=y) и выбрать >0 вместо =0. В результате получится
область решений системы (см. рис. 15). Но при этом граничная линия 2x=y не отобразится. Ее для наглядности надо построить отдельно
как обычно, причем на вкладке Дополнительные свойства надо указать пределы
изменения переменных.
Аналогичные построения выполняются и для других систем из уравнений и
неравенств.
.2 Теория пределов. Дифференцирование функций одной переменной
Перечислим те действия в программе Advanced Grapher, которые можно
использовать в учебном процессе по дисциплине «Математика» в вузе. После знака
\ здесь и далее указаны соответствующие конкретные области применения.
Рис.
15. Решение системы неравенств с помощью логического умножения.
.
Построение графиков функций, заданных явно уравнениями y=f(x)
или x=f(y), заданных неявно уравнением f(x,y)=0,
заданных параметрическими уравнениями или уравнением в полярных координатах.
Трассировка графиков функций. Построение (в виде ломаной, ломаной с узлами,
отдельных точек, сглаженной кривой) графиков функций, заданных таблицей
значений. \ Наглядное представление о способах задания функции и виде их
графиков.
.
Построение графиков функций y=f(x) и составление для них таблицы значений (с помощью
кнопки Таблица значений). Построение графиков функций y=f(x),
заданных несколькими формулами (в закладке Дополнительные свойства при нажатии
кнопки Добавить график указывать интервалы изменения переменной для каждой
формулы). \ Исследование области определения функции. Свойства основных
элементарных функций. Преобразования графиков.
.
Построение графиков функций y=f(x), трассировка графиков, составление для них таблицы
значений, близких к данной точке x0(с
помощью кнопки Таблица значений). Увеличение окрестности исследуемой точки
графика с помощью кнопки Выбрать интервал (повторить несколько раз). \ Предел
функции. Вычислительный эксперимент, связанный с понятием предела функции.
.
Построение графиков функций y=sinx и y=x в окрестности точки x=0, трассировка
графиков, увеличение окрестности точки O(0,0) с помощью
кнопки Выбрать интервал (повторить несколько раз). Аналогично для функций tgx, arcsinx,
arctgx, ln(1+x) и т.д. \ Эквивалентные бесконечно малые.
.
Построение последовательности точек на оси Ox (нажать кнопку Добавить график
таблицы, заполнить столбцы с клавиатуры или использовать команду Заполнить).
Построение в виде отдельных точек графиков функций y=f(n)
при натуральных n (с помощью кнопки Добавить график таблицы), трассировка
графиков. Составление для таких функций таблицы значений при больших n (с
помощью кнопки Таблица значений). \ Понятие последовательности. Вычисление
предела последовательности.
.
Построение графика функции y=sinx/x и составление таблицы значений этой функции при x,
близких к нулю. Составление таблицы значений последовательности (1+1/n)n при
больших n. \ Вычислительный эксперимент, связанный с первым и вторым замечательным
пределом.
.
Составление таблицы значений отношения приращения функции к приращению
аргумента, когда приращение аргумента близко к нулю (с помощью кнопки Таблица
значений). \ Вычислительный эксперимент, связанный с понятием производной в
точке.
.
Построение касательных и нормалей к графику функции y=f(x)(с
помощью кнопки Касательная или нормаль). Увеличение окрестности исследуемой
точки графика с помощью кнопки Выбрать интервал (повторить несколько раз). \
Геометрический смысл производной. Вычислительный эксперимент, связанный с
понятием касательной и дифференциала.
.
Вычисление первой и второй производной, а также их значений в отдельных точках
(с помощью кнопок Производная и Таблица значений). \ Правила дифференцирования
функций. Производные высших порядков.
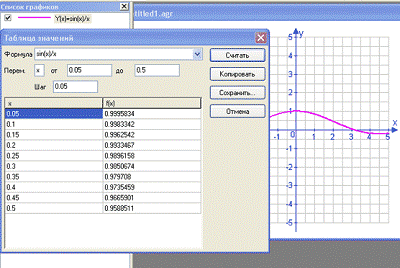
Построим,
например, график функции y=sinx/x (см. рис. 2). Нажмем кнопку Таблица значений и для
построенной функции вычислим ее значения при с шагом
0.05.
Рис.
16. Изучение первого замечательного предела.
.3
Исследование функций с помощью производной
.
Построение графиков функций y=f(x), трассировка графиков. Вычисление производных (с
помощью кнопки Производная) и построение графиков производных. \ Исследование
функции на монотонность и экстремумы по виду графика и исследование поведения
ее производной.
.
Построение графиков функций y=f(x), и отыскание точек экстремума с помощью команды
Экстремумы в диалоговом окне кнопки Исследование функции. Вычисление
производной функции y=f(x), с помощью кнопки Производная и отыскание нулей
производной с помощью команды Нули функции в диалоговом окне кнопки
Исследование функции. \ Исследование функций на монотонность и экстремумы с
помощью производной.
.
Построение графиков функций y=f(x), и их касательных (с помощью кнопки Касательная или
нормаль) в некоторых точках, трассировка графиков. \ Исследование функций на
выпуклость и вогнутость, точки перегиба с помощью касательных.
.
Вычисление второй производной функции y=f(x),
(с помощью кнопки Производная) и отыскание нулей второй производной (с помощью
кнопки Исследование функции). \ Исследование функций на выпуклость,
вогнутость, точки перегиба с помощью второй производной.
.
Построение графиков функций y=f(x),и их наклонных и вертикальных асимптот, трассировка
графиков. Увеличение исследуемых частей графика с помощью кнопки Выбрать
интервал (повторить несколько раз). \ Асимптоты кривых. Полное исследование
функций и построение их графиков.
.
Построение графика функции y=f(x),, отыскание точек пересечения графика с осью абсцисс
(с помощью кнопки Исследование функции или кнопки Пересечения). Построение двух
графиков функций и отыскание точек их пересечения (с помощью кнопки
Пересечения). Дополнительные построения для отыскания нескольких первых
приближений к корню уравнения вида f(x)=0 методом
хорд или методом касательных. \ Приближенное решение уравнений вида f(x)=0
методом хорд или методом касательных. Отыскание (точное или приближенное)
корней многочленов и нулей функций вида y=f(x).
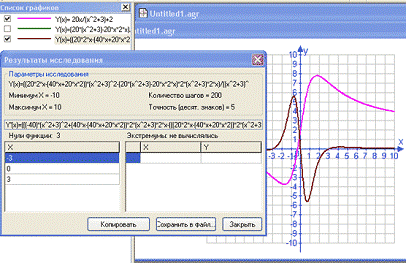
Для
примера построим график функции на
промежутке от -10 до 10 (см. рис. 17). Исследуем ее на выпуклость и вогнутость.
Нажмем кнопку Производная и построим график первой производной, получив также
ее аналитическое выражение. Если в Списке функций выделить первую производную,
и еще раз нажать кнопку Производная, то можно построить график второй
производной от исходной функции и получить ее аналитическое выражение (замечу,
что вид выражений для производных в программе Advanced Grapher не очень
удобен). Теперь нажмем кнопку Исследование функции и в появившемся диалоговом
окне в поле Y(x) выберем нужную из трех построенных функций (вторую
производную). Найдем нули второй производной (на указанном промежутке), это -3,
0, 3. Знаки второй производной в соответствующих интервалах определяем по ее
графику. Делаем окончательный вывод о промежутках выпуклости и вогнутости
данной функции и наличии точек перегиба. С помощью кнопки Трассировка находим
координаты точек перегиба, это (-3,-3), (0,2), (3,7). Или же нажмем кнопку
Таблица значений, выберем в диалоговом окне нужную функцию из построенных
функций и вычислим ее значения от -3 до 3 с шагом 3.
Рис.
17. Построение графика функции и отыскание нулей ее второй производной.
Особое место в алгебре и началах анализа занимает тема: «Исследование и
построение графика функции с помощью производной». Графическая программа
Advanced Grapher делает изучение этой сложной темы понятным и интересным.
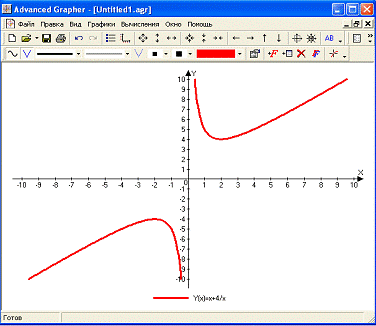
Построим график функции у=х+4/х и исследуем его с помощью универсальной
схемы:
. область определения функции D(f);
. область значения функции E(f);
. четность (нечетность) функции;
4. горизонтальная, вертикальная асимптота;
. нули функции;
. промежутки знакопостоянства;
. стационарные и критические точки;
8. промежутки монотонности;
9. экстремумы функции;
. наибольшее и наименьшее значения функции
Рис. 18. График функции у=х+4/х
1. D(y)=(-∞;0) U (0;∞);
2. E(y)=( -∞;-4) U (4; ∞);
3. Функция
нечетная, т.к. симметрична относительно начала координат ( f(-x) =
-x+ = -(x+
) = f(-x) );
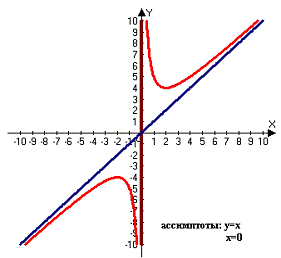
. Вертикальная
асимптота:
Рисунок 19
5. Нули функции:
6. Промежутки знакопостоянства: y>0, при xє(0; ∞);
y<0,
при xє(-∞;0).
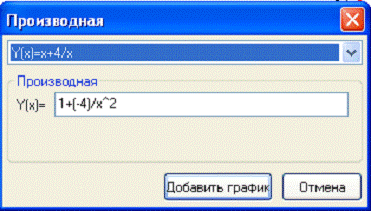
7. Стационарные и критические точки: -2;0;2.
Рис. 21. Нахождение производной
8. Промежутки монотонности:
функция возрастает (-∞;-2) U (2;∞);
функция убывает (-2;0) U (0;2).
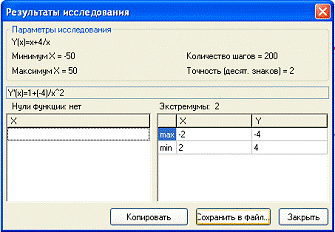
9. Экстремумы функции:
Рисунок 22
10. Наименьшее
значение на интервале x>0 функция y= x + принимает в точке x=2, f(2)=4;
Наибольшее
значение на интервале x<0 функция y= x + принимает в точке x=-2, f(-2)=-4.
.4 Интегральное исчисление функций одной переменной
1.
Составление таблицы значений последовательности интегральных
сумм функции y=f(x) (с помощью кнопки Добавить график таблицы или
Таблица значений). \ Вычислительный эксперимент, связанный с понятием
определенного интеграла.
.
Вычисление определенного интеграла от функции y=f(x) по
данному отрезку (с помощью кнопки Интегрирование). \ Определенный интеграл.
Приближенное вычисление определенного интеграла по формулам прямоугольников,
трапеций, парабол.
.
Построение криволинейной трапеции, ограниченной на данном отрезке сверху и
снизу двумя графиками функций вида y=f(x) (с
помощью кнопки Интегрирование). Вычисление определенного интеграла от разности
этих функций (с помощью кнопки Интегрирование). \ Геометрический смысл
определенного интеграла. Вычисление площади криволинейной трапеции.
.
Построение области, ограниченной несколькими линиями. Построение криволинейного
сектора в полярных координатах. Вычисление определенного интеграла (с помощью
кнопки Интегрирование). \ Вычисление площади плоской пластинки в декартовых или
полярных координатах с помощью определенного интеграла.
.
Построение кривой на плоскости, заданной параметрическими уравнениями, явным
уравнением y=f(x) или уравнением в полярных координатах. Вычисление
определенного интеграла (с помощью кнопки Интегрирование). \ Вычисление длины
дуги кривой, заданной параметрическими уравнениями, явным уравнением или y=f(x)
уравнением в полярных координатах.
.
Вычисление определенного интеграла с переменным верхним пределом от функции y=f(x),
не интегрируемой в элементарных функциях, и составление таблицы значений
первообразной (с помощью кнопок Интегрирование и Добавить график таблицы).
Построение графика первообразной по таблице ее значений. \ Свойства некоторых
специальных функций.
.
Построение графика функции вида y=f(x), трассировка графика. Составление таблицы значений F(x)-F(a)
для приращения ее первообразной (с помощью кнопки Добавить график таблицы или
кнопки Таблица значений функции). \ Вычислительный эксперимент, связанный с
понятием несобственного интеграла по бесконечному промежутку или от
неограниченной функции.
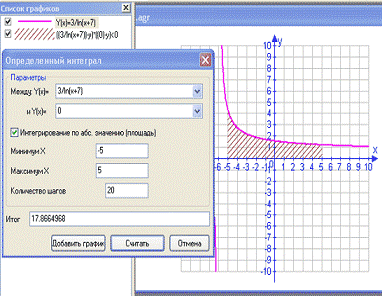
Рассмотрим
для примера интеграл 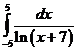
график подынтегральной функции на промежутке от -10 до 10 (см. рис. 23). Нажмем
кнопку Интегрирование и в диалоговом окне выберем параметры: между какими из
построенных функций следует заштриховать криволинейную трапецию, а также укажем
промежуток интегрирования. Выполним сначала действие Добавить график, появится
заштрихованная область. Затем еще раз нажмем кнопку Интегрирование, но теперь
выполним действие Считать, появится итог — приближенное значение данного
интеграла.
Рис.
23. Построение криволинейной трапеции и вычисление определенного интеграла.
3.5
Ряды
.
Составление таблицы значений последовательности {Sn}
частичных сумм ряда при больших n (с помощью кнопки Добавить график таблицы или
Таблица значений). \ Вычислительный эксперимент, связанный с понятием
сходимости ряда.
.
Построение графика функции y=f(x) и ее многочленов Тейлора в окрестности данной точки.
Составление таблицы для остатка ряда Тейлора. \ Разложение функций в ряд
Тейлора. Применение рядов Тейлора в приближенных вычислениях.
.
Вычисление коэффициентов ряда Тейлора данной функции двумя способами. (Первый
способ: найти с помощью кнопки Производная аналитические выражения для
производных первого, второго и т.д. порядков от данной функции и вычислить
значения этих производных в точке x0 с помощью кнопки Таблица значений. Второй способ:
вычислить с помощью кнопки Вычисление функций значения в точке x0 первой, второй и т.д. производных, найденных обычным
путем.). \ Составление ряда Тейлора. Разложение функций в ряд Тейлора.
.
Построение графика функции sinx и ее многочленов Тейлора в окрестности точки x=0.
Увеличение окрестности точки O(0,0) с помощью кнопки Выбрать интервал (повторить
несколько раз). Аналогично для cosx, ex, ln(1+x), ln(1-x). \ Разложение в ряд Маклорена элементарных функций.
.
Вычисление коэффициентов Эйлера-Фурье (вычисление определенных интегралов с
помощью кнопки Интегрирование). Построение графика функции и частичных сумм ее
ряда Фурье на данном промежутке. \ Составление рядов Фурье. Разложение функций
в ряд Фурье.
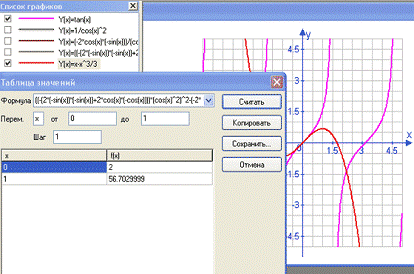
Для
примера построим график функции y=tgx и найдем несколько первых членов ее разложения в ряд
Маклорена (см. рис. 24). С помощью программы Advanced Grapher удается найти
аналитически только первую, вторую и третью производные способом, описанным
ранее (четвертую производную в данном случае найти нельзя, так как получается
слишком длинное выражение). Вычислим значения найденных производных в точке x=0 с
помощью кнопки Трассировка или кнопки Таблица значений. Составим многочлен
Тейлора третьей степени и построим его. Используя кнопку Выбрать интервал,
можно увидеть, насколько этот многочлен близок к функции y=tgx в
окрестности точки x=0.
Рис.
24. Приближение функции ее многочленом Тейлора.
.6
Аналитическая геометрия на плоскости
.
Задание и настройка подходящей декартовой или полярной системы координат на
плоскости (кнопка Свойства документа). Построение кривых на плоскости, заданных
явно уравнениями y=f(x) или x=f(y), заданных неявно уравнением f(x,y)=0,
заданных параметрическими уравнениями или уравнением в полярных координатах. \
Полярная система координат. Способы задания кривых на плоскости.
.
Построение прямых на плоскости, заданных уравнением с угловым коэффициентом,
общим уравнением (как график неявной функции f(x,y)=0),
параметрическими уравнениями, уравнением в полярных координатах, а также
вертикальных прямых. \ Решение задач с использованием прямых на плоскости.
.
Построение кривых второго порядка, заданных каноническими или неканоническими
уравнениями (как функций, заданных неявно уравнением ). Построение осей
эллипса, асимптот гиперболы, оси параболы, фокусов. \ Кривые второго порядка.
.
Построение двух прямых на плоскости, отыскание точки пересечения двух прямых (с
помощью кнопки Пересечения). \ Графическое решение системы из двух линейных
уравнений с двумя неизвестными.
.
Построение области решений системы линейных неравенств с двумя переменными
(двумя способами, описанными выше). \ Графическое решение системы линейных
неравенств с двумя переменными.
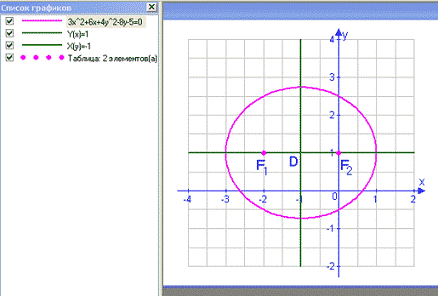
Построим,
например, кривую второго порядка, заданную уравнением
x2+6x+4y2-8y-5=0
По
чертежу определяем, что это эллипс. Для уточнения его параметров приведем
уравнение к каноническому виду:
Следовательно,
центр эллипса находится в точке D (-1;1), оси эллипса параллельны координатным
осям, и их тоже можно построить. Фокусы находятся в точках F1(-2;1) и F2(0;1) для их построения используем кнопку Добавить график
таблицы.
Рис.
25. Построение кривой второго порядка.
.7
Теория вероятностей и математическая статистика
.
Построение многоугольника распределения дискретной случайной величины в виде
ломаной с узлами (с помощью кнопки Добавить график таблицы). \ Дискретные
случайные величины.
.
Построение графика функции распределения, нахождение ее производной, т.е.
плотности распределения, с помощью кнопки Производная. Построение графика
плотности распределения y=f(x). Вычисление определенного интеграла от плотности (с
помощью кнопки Интегрирование). \ Функция распределения и плотность
распределения непрерывной случайной величины. Вычисление вероятности попадания
непрерывной случайной величины в интервал.
.
Построение графика плотности распределения y=f(x).
Построение фигуры под кривой распределения (с помощью кнопки Интегрирование).
Вычисление математического ожидания и дисперсии непрерывной случайной величины
(с помощью кнопки Интегрирование). \ Числовые характеристики непрерывных
случайных величин.
.
Построение графиков плотности нормального распределения при разных значениях
параметров. Вычисление определенного интеграла от плотности нормального
распределения (с помощью кнопки Интегрирование). \ Нормально распределенная
случайная величина, вычисление вероятности ее попадания в интервал.
.
Составление таблицы значений для функции Лапласа или приведенной функции
Лапласа (с помощью кнопки Интегрирование) и построение по этой таблице графика
(с помощью кнопки Добавить график таблицы). \ Свойства функции Лапласа и
приведенной функции Лапласа.
.
Внесение в таблицу значений случайной величины x1,x2,…,xN, полученных последовательно в результате проведения N
опытов, и нахождение оценок числовых характеристик случайной величины (использовать
кнопку Добавить график таблицы и команду info в появляющемся диалоговом окне).
Аналогично для значений (x1,y1),(x2,y2),…,(xN,yN) системы двух случайных величин. \ Точечные оценки
числовых характеристик случайной величины и системы двух случайных величин.
.
Внесение в таблицу имеющихся экспериментальных значений двух зависимых
случайных величин X и Y (использовать кнопку Добавить график таблицы).
Нахождение (с помощью кнопки Регрессионный анализ) уравнения регрессии и
построение линии регрессии вида Y=f(X)(можно выбрать линейную, квадратичную или иную
зависимость между случайными величинами, а также лучшую). \ Линия регрессии.
Регрессионный анализ.
.
Генерация случайных чисел (нажать кнопку Вычисление функций, ввести в поле
Формула функцию random (1) и вычислять ее значение при x=0). \
Статистическое моделирование случайных событий и случайных величин.
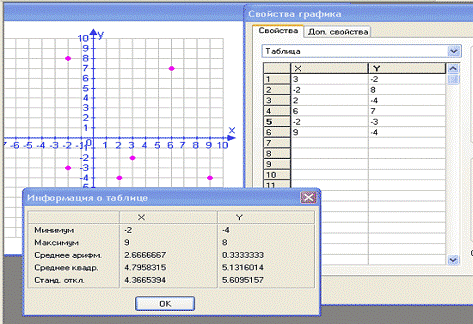
Пусть,
например, даны координаты точек попадания в прямоугольную мишень при 6
выстрелах, т.е. выборка значений системы случайных величин (X,Y) в
1-ом, 2-ом, … , 6-ом опытах. Нажмем кнопку Добавить график таблицы и заполним
ее (см. рис.7). Построим соответствующий график в виде отдельных точек
плоскости. Нажмем кнопку info в диалоговом окне этой таблицы. Получим значение
выборочного среднего (в графе Среднее аримф.) и значение несмещенного
выборочного среднего квадратического отклонения (в графе Станд. откл.) для
случайных величин X и Y.
Рис.
26. Точечные оценки числовых характеристик случайных величин.
4.
Графики некоторых из замечательных кривых
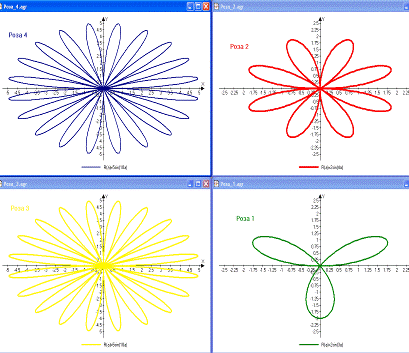
Рис. 27. Розы.
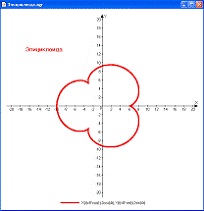
Рис. 28. Циклоида. Рис. 29. Эпициклоида.
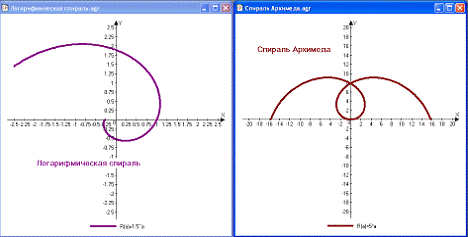
Рис. 30. Логарифмическая спираль. Рис. 31. Спираль Архимеда.
Заключение
Мы рассмотрели некоторые примеры того, как изучение различных разделов
математики может сопровождаться графическими иллюстрациями, вычислительными
экспериментами, таблицами, расчетами, выполненными с помощью программы Advanced
Grapher.
Трудности, возникающие при изучении тем: исследование и построение
графиков функций, решение уравнений и неравенств графическим способом,
исследование функций с помощью производной, нахождение первообразной функции и
площади криволинейной трапеции, требуют новых подходов в организации учебного
процесса. Использование графической программы Advanced Grapher, позволяет с
успехом решать эти задачи. Это будет способствовать тому, чтобы студенты
успешно применяли математические методы при изучении различных специальных
дисциплин, а после окончания вуза — в своей практической и научной
деятельности.
Очевидным является целесообразность использования программы Advanced
Grapher на лекциях, практических и лабораторных занятиях по математике, а также
при разработке тем студенческих научных и курсовых работ.Grapher является
достаточно мощной и в то же время простой в использовании программой. Его
освоение преподавателями и студентами не требует больших усилия и знания языков
программирования.
программа advanced grapher геометрия
1.
Азевич А.И. Advanced Grapher на уроке и после него // Математика в школе. —
2001. — N 6. — С. 65-69.
2. Андреева,
Босова, Фалина. Математические основы информатики. Уч. пособие.2005 год.
3. Кудрявцев
Л.Д. «Курс математического анализа Том 1». Высшая школа.1981.
4. В.И.
Кан. Математический анализ. Часть 1. Мультимедиа курс. Томский государственный
университет. — Институт дистанционного образования, 2002.
5. А.А.
Грешилов, И.В. Дубограй. Вычисление пределов функций. Техника
дифференцирования. Исследование функций и построение графиков. Компьютерный
курс. Учебное пособие. — М.: «Логос», 2004.
6. А.А.
Грешилов, Т.И. Белова. Аналитическая геометрия. Векторная алгебра. Кривые
второго порядка. Компьютерный курс. Учебное пособие. — М.: «Логос», 2004.
Приложение
ПОЛЕЗНЫЕ ПРОГРАММЫ ДЛЯ СТУДЕНТОВ- мощный графический пакет для обработки
и анализа двумерных и трехмерных данных; один из продуктов MathSoft. —
программа для построения графиков функций (обычных и параметрических) с
расширенными возможностями. Дифференцирование любого порядка (с упрощением).
Построение касательных к графику. Простой и понятный интерфейс с подробной
документацией и примерами работы.- программа предназначена для наглядного
представления геометрических объектов, описываемых параметрически задаваемыми
поверхностями, таких как сфера, тор, лента Мёбиуса и прочие. Для описания
объектов используется Паскаль-подобный язык с поддержкой всех стандартных
математических функций языка Паскаль и нескольких дополнительных. Полученный
объект отображается в векторной форме с использованием оригинального алгоритма
растеризации векторов, позволяющим получить плавное и естественное изображение
даже на низком разрешении монитора и не требующим никакой аппаратной поддержки.
Возможен экспорт изображения в BMP файл. В комплект программы входит около 50
примеров различной тематики и направлений. — система работы с символьными и
численными выражениями, включающая дифференцирование, интегрирование,
разложение в ряд, преобразования Лапласа, обыкновенные дифференциальные
уравнения, системы линейных уравнений, многочлены, множества, списки, векторы,
матрицы и тензоры. Maxima производит численные расчеты высокой точности,
используя точные дроби, целые числа и числа с плавающей точкой произвольной
точности. Система позволяет строить графики функций и статистических данных в
двух и трех измерениях. — калькулятор периметров, площадей, объемов и других
характеристик (боковые поверхности, высоты, эксцентриситеты) различных
геометрических фигур на плоскости и в пространстве. Фигуры снабжены поясняющими
иллюстрациями и поделены на категории — цилиндрические, призматические,
конические, сферические, многогранные…- Программа для решения уравнений и построения
графиков произвольных математических функций. Позволяет с заданной погрешностью
найти корень практически любого уравнения в пределах своей функциональности (т.
е. оперируя доступными пользователю функциями). Другими словами, если корень
существует, и лежит в области допустимых значений (настраивается), программа
его найдет. Также работает и как обычный строковый калькулятор с поддержкой
большого числа функций. Function — программа предназначена для школьников
старших классов и студентов. Она проста в освоении, нетребовательна к ресурсам
компьютера и работает сравнительно быстро. Основные функции программы:
Вычисление выражений любой сложности с использованием основных
математических функций. Любая степень вложенности скобок.
Вычисление последовательностей, числовых и степенных рядов за счет
специальных переменных: n — натуральное возрастающее число, a — значение
результата последнего вычисления.
Построение графиков функций вида y = f(x). Максимальная точность
построения: 0.00001 на пиксель экрана. Функции могут быть заданы в виде обычной
зависимости f(x) и в виде последовательности или ряда. Например функция y =
exp(x) может быть представлена степенным рядом y = a+x^n/fact(n).
Последующая работа с графиками: перемещение, увеличение и уменьшение
масштаба, возможность увеличить выбранную область графика, отображение по
центру и т.д. А также функция сохранения графика в bmp-файле.
Анализ функций: вычисление значения функции и ее производной в заданной
точке, нахождение определенного интеграла.
Выражение или функцию можно сохранить для последующей работы.
Microsoft Student
Graphing Calculator — калькулятор для студентов с
возможностью построения графиков и решения уравнений. Pro — представляет собой
универсальное средство обработки математических и статистических функций,
построения графиков этих функций, а также инструмент разработки
узкоспециализированных математических программ и средств визуализации
графических данных. Считается стандартом де факто во многих научных
лабораториях.
Математика+ от AV v.1.2 — программа позволяет строить, исследовать и
печатать двухмерные и трехмерные графики одним щелчком мыши, а также
производить расчеты в любой системе счисления, используя встроенный
двухпанельный калькулятор с сохранением истории расчетов. Программа имеет очень
интуитивный дружелюбный интерфейс и подробную справку.
Опубликовано в Видеоуроки, Программы для решения математики
Как и обещал продолжаю тему «Программы, которые помогают решать математику!!!». И сегодня расскажу о программе Advanced Grapher, с помощью которой легко можно построить график практически любой функции.
Посмотрев эти видеоуроки вы узнаете как можно легко построить график:
- обычной функции;
- функции в полярной системе координат;
- заданный параметрическим уравнением;
- касательной или нормали;
- неравенства;
- производной;
- любой части плоскости;
- и многое другое.
Также вы можете скачать программу для построения графиков Advanced Grapher нажав по ссылке: скачать Advanced Grapher.
Или можете просто посмотреть видео-уроки по данной теме ниже:
Видеоурок часть 1:
Видеоурок часть 2:
Материалы по теме:
- Как найти производную с помощью Mathcad???
- Сейчас, чтобы приблизить часть графика функции, вам надо просто её выделить!
- Решай уравнения только ПРАВИЛЬНО, не допуская ошибок!!!
- Программы, которые помогают решать математику!!!
Загрузка…
Комментарии
-
Андрей
Здравствуйте! На смартфон с windows phonе 7.5 эта программа встанет?
on 12.02.2012 Ответить
-
Попробуйте или почитайте на их официальном сайте!
on 13.02.2012 Ответить
-
Александра
Как построить векторную диаграмму комплексного числа?
on 02.05.2012 Ответить
-
Татьяна
Как построить уравнение окружности?
on 24.01.2013 Ответить
-
Ввести данное уравнение в программу! 🙂
on 24.01.2013 Ответить
-
Андрей
Пожалуйста подскажите,как по этому выражению 2.82sin(314t+30) построить график??? Очень срочно надо!!!
on 03.04.2013 Ответить
-
Как вариант вместо t написать x!
on 03.04.2013 Ответить
-
Кирилл
Как построить траекторию движения точки на графике?
on 31.05.2013 Ответить
-
А какая должна быть траектория?
on 31.05.2013 Ответить
-
Алексей
как построить график системы из двух нелинейных уравнений? не выражая одно через другое?
on 16.11.2013 Ответить
-
График строить на бумаге или с помощью данной программы? Пишите конкретные примеры.
P.S. График системы, это будут точки пересечения графиков уравнений данной системы.on 17.11.2013 Ответить
-
Сергей
Как с помощью программы построить график функции Кубического корня. Как записать значения?
on 22.01.2015 Ответить
-
Например, можно попробовать записать так: «x^(1/3)»
on 27.01.2015 Ответить
-
анна
-
Переходите по ссылке, что в статье или ищите в Интернете
on 07.02.2017 Ответить