Как составить закон распределения двумерной случайной величины - AvtoShod.ru

Двумерной называют случайную величину

, возможные значения
которой есть пары чисел

. Составляющие

, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку

на плоскости

либо как случайный вектор

Дискретной называют двумерную величину, составляющие которой дискретны.

Закон распределения дискретной двумерной СВ.
Безусловные и условные законы распределения составляющих

Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.

Закон
распределения дискретной двумерной случайной величины может быть задан:

а) в
виде таблицы с двойными входом, содержащей возможные значения и их вероятности;

б) аналитически, например в виде функции распределения.

Зная
закон распределения двумерной дискретной случайной величины, можно найти законы
каждой из составляющих. В общем случае, для того чтобы найти вероятность

, надо просуммировать
вероятности столбца

. Аналогично сложив
вероятности строки

получим вероятность

Пусть
составляющие

дискретны и имеют соответственно следующие
возможные значения:

;

Условным распределением составляющей

при

(j сохраняет одно и то же
значение при всех возможных значениях

) называют совокупность
условных вероятностей:

Аналогично
определяется условное распределение

Условные
вероятности составляющих

вычисляют соответственно по формулам:

Для
контроля вычислений целесообразно убедиться, что сумма вероятностей условного
распределения равна единице.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Ковариация (корреляционный момент)

Ковариация двух случайных величин характеризует степень зависимости случайных величин, так
и их рассеяние вокруг точки

Ковариацию
(корреляционный момент) можно найти по формуле:

Свойства ковариации

Свойство 1.

Ковариация двух независимых случайных величин равна нулю.

Свойство 2.

Ковариация двух случайных величин равна математическому ожиданию их
произведение математических ожиданий.

Свойство 3.

Ковариация двухмерной случайной величины по абсолютной случайной величине не
превосходит среднеквадратических отклонений своих компонентов.

Коэффициент корреляции

Коэффициент корреляции – отношение ковариации двухмерной случайной
величины к произведению среднеквадратических отклонений.

Формула коэффициента корреляции:

Две
случайные величины

называют коррелированными, если их коэффициент
корреляции отличен от нуля.

называют некоррелированными величинами, если
их коэффициент корреляции равен нулю

Свойства коэффициента корреляции

Свойство 1.

Коэффициент корреляции двух независимых случайных величин равен нулю. Отметим,
что обратное утверждение неверно.

Свойство 2.

Коэффициент корреляции двух случайных величин не превосходит по абсолютной
величине единицы.

Свойство 3.

Коэффициент корреляции двух случайных величин равен по модулю единице тогда и
только тогда, когда между величинами существует линейная функциональная
зависимость.

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Линейная регрессия

Рассмотрим
двумерную случайную величину

, где

– зависимые случайные величины. Представим
одну из величины как функцию другой. Ограничимся приближенным представлением
величины

в виде линейной функции величины

где

– параметры, подлежащие определению. Это можно
сделать различными способами и наиболее употребительный из них – метод
наименьших квадратов.

Линейная
средняя квадратическая регрессия

на

имеет вид:

Коэффициент

называют
коэффициентом регрессии

на

, а прямую

называют
прямой среднеквадратической регрессии

на

Аналогично
можно получить прямую среднеквадратической регрессии

на

Смежные темы решебника:

Двумерная непрерывная случайная величина
Линейный выборочный коэффициент корреляции
Парная линейная регрессия и метод наименьших квадратов

Задача 1

Закон
распределения дискретной двумерной случайной величины (X,Y) задан таблицей.

Требуется:

—
определить одномерные законы распределения случайных величин X и Y;

— найти
условные плотности распределения вероятностей величин;

—
вычислить математические ожидания m_x и m_y;

—
вычислить дисперсии σ_x и σ_y;

—
вычислить ковариацию μ_xy;

—
вычислить коэффициент корреляции r_xy.

xy	3	5	8	10	12
-1	0.04	0.04	0.03	0.03	0.01
1	0.04	0.07	0.06	0.05	0.03
3	0.05	0.08	0.09	0.08	0.05
6	0.03	0.04	0.04	0.06	0.08

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 2

Задана
дискретная двумерная случайная величина (X,Y).

а) найти
безусловные законы распределения составляющих; б) построить регрессию случайной
величины Y на X; в) построить регрессию случайной величины X на Y; г) найти коэффициент ковариации; д) найти
коэффициент корреляции.

Y	X
1	2	3	4	5
30	0.05	0.03	0.02	0.01	0.01
40	0.03	0.02	0.02	0.04	0.01
50	0.05	0.03	0.02	0.02	0.01
70	0.1	0.03	0.04	0.03	0.01
90	0.1	0.04	0.01	0.07	0.2

Задача 3

Двумерная случайная величина (X,Y) задана
таблицей распределения. Найти законы распределения X и Y, условные
законы, регрессию и линейную регрессию Y на X.

x y	1	2	3
1.5	0.03	0.02	0.02
2.9	0.06	0.13	0.03
4.1	0.4	0.07	0.02
5.6	0.15	0.06	0.01

Задача 4

Двумерная
случайная величина (X,Y) распределена по закону

XY	1	2
-3	0,1	0,2
0	0,2	0,3
-3	0	0,2

Найти
законы распределения случайных величины X и Y, условный закон
распределения Y при X=0 и вычислить ковариацию.
Исследовать зависимость случайной величины X и Y.

Задача 5

Случайные
величины ξ и η имеют следующий совместный закон распределения:

P(ξ=1,η=1)=0.14

P(ξ=1,η=2)=0.18

P(ξ=1,η=3)=0.16

P(ξ=2,η=1)=0.11

P(ξ=2,η=2)=0.2

P(ξ=2,η=3)=0.21

1)
Выписать одномерные законы распределения случайных величин ξ и η, вычислить
математические ожидания Mξ, Mη и дисперсии Dξ, Dη.

2) Найти
ковариацию cov(ξ,η) и коэффициент корреляции ρ(ξ,η).

3)
Выяснить, зависимы или нет события {η=1} и {ξ≥η}

4)
Составить условный закон распределения случайной величины γ=(ξ|η≥2) и найти Mγ и
Dγ.

Задача 6

Дан закон
распределения двумерной случайной величины (ξ,η):

	ξ=-1	ξ=0	ξ=2
η=1	0,1	0,1	0,1
η=2	0,1	0,2	0,1
η=3	0,1	0,1	0,1

1) Выписать одномерные законы
распределения случайных величин ξ и η, вычислить математические ожидания M_ξ,
M_η и дисперсии D_ξ, D_η

2) Найти ковариацию cov(ξ,η) и
коэффициент корреляции ρ(ξ,η).

3) Являются ли случайные события |ξ>0|
и |η> ξ | зависимыми?

4) Составить условный закон
распределения случайной величины γ=(ξ|η>0) и найти M_γ и D_γ.

Задача 7

Дано
распределение случайного вектора (X,Y). Найти ковариацию X и Y.

XY	1	2	4
-2	0,25	0	0,25
1	0	0,25	0
3	0	0,25	0

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 8

Случайные
приращения цен акций двух компаний за день имеют совместное распределение,
заданное таблицей. Найти ковариацию этих случайных величин.

YX	-1	1
-1	0,4	0,1
1	0,2	0,3

Задача 9

Найдите
ковариацию Cov(X,Y) для случайного дискретного вектора (X,Y),
распределенного по закону:

	X=-3	X=0	X=1
Y=-2	0,3	?	0,1
Y=1	0,1	0,1	0,2

Задача 10

Совместный
закон распределения пары

задан таблицей:

xh	-1	0	1
-1	1/12	1/4	1/6
1	1/4	1/12	1/6

Найти
закон распределения вероятностей случайной величины xh и вычислить cov(2x-3h,x+2h).
Исследовать вопрос о зависимости случайных величин x и h.

Задача 11

Составить двумерный закон распределения случайной
величины (X,Y), если известны законы независимых составляющих. Чему равен коэффициент
корреляции r_xy?

X	20	25	30	35
P	0.1	0.1	0.4	0.4

Задача 12

Задано
распределение вероятностей дискретной двумерной случайной величины (X,Y):

XY	0	1	2
-1	?	0,1	0,2
1	0,1	0,2	0,3

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 13

Совместное
распределение двух дискретных случайных величин ξ и η задано таблицей:

ξη	-1	1	2
0	1/7	2/7	1/7
1	1/7	1/7	1/7

Вычислить
ковариацию cov(ξ-η,η+5ξ). Зависимы ли ξ и η?

Задача 14

Рассчитать
коэффициенты ковариации и корреляции на основе заданного закона распределения
двумерной случайной величины и сделать выводы о тесноте связи между X и Y.

XY	2,3	2,9	3,1	3,4
0,2	0,15	0,15	0	0
2,8	0	0,25	0,05	0,01
3,3	0	0,09	0,2	0,1

Задача 15

Задан
закон распределения случайного вектора (ξ,η). Найдите ковариацию (ξ,η)
и коэффициент корреляции случайных величин.

xy	1	4
-10	0,1	0,2
0	0,3	0,1
20	0,2	0,1

Задача 16

Для
случайных величин, совместное распределение которых задано таблицей
распределения. Найти:

а) законы
распределения ее компонент и их числовые характеристики;

b) условные законы распределения СВ X при условии Y=b и СВ Y при
условии X=a, где a и b – наименьшие значения X и Y.

с)
ковариацию и коэффициент корреляции случайных величин X и Y;

d) составить матрицу ковариаций и матрицу корреляций;

e) вероятность попадания в область, ограниченную линиями y=16-x² и y=0.

f) установить, являются ли случайные величины X и Y зависимыми;
коррелированными.

XY	-1	0	1	2
-1	0	1/6	0	1/12
0	1/18	1/9	1/12	1/9
2	1/6	0	1/9	1/9

Задача 17

Совместный
закон распределения случайных величин X и Y задан таблицей:

XY	0	1	3
0	0,15	0,05	0,3
-1	0	0,15	0,1
-2	0,15	0	0,1

Найдите:

а) закон
распределения случайной величины X и закон распределения
случайной величины Y;

б) EX, EY, DX, DY, cov(2X+3Y, X-Y), а
также математическое ожидание и дисперсию случайной величины V=6X-8Y+3.

Задача 18

Известен
закон распределения двумерной случайной величины (X,Y).

а) найти
законы распределения составляющих и их числовые характеристики (M[X],D[X],M[Y],D[Y]);

б)
составить условные законы распределения составляющих и вычислить
соответствующие мат. ожидания;

в)
построить поле распределения и линию регрессии Y по X и X по Y;

г)
вычислить корреляционный момент (коэффициент ковариации) μ_xy и
коэффициент корреляции r_xy.

	5	20	35
100	—	—	0.05
115	—	0.2	0.15
130	0.15	0.35	—
145	0.1	—	—-

Источник

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Пусть дана двумерная случайная величина $(X,Y)$.

Определение 1

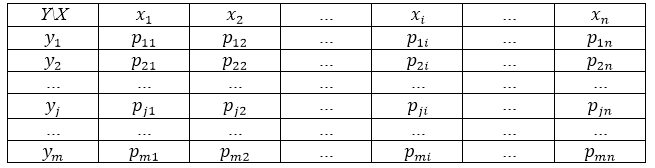
Законом распределения двумерной случайной величины $(X,Y)$ — называется множество возможных пар чисел $(x_i, y_j)$ (где $x_i epsilon X, y_j epsilon Y$) и их вероятностей $p_{ij}$.

Чаще всего закон распределения двумерной случайной величины записывается в виде таблицы (Таблица 1).

Рисунок 1. Закон распределения двумерной случайной величины.

Вспомним теперь теорему о сложении вероятностей независимых событий.

Вероятность суммы конечного числа независимых событий ${ A}_1$, ${ A}_2$, … ,$ { A}_n$ вычисляется по формуле:

[Pleft(sumlimits^n_{i=1}{{ A}_n}right)=sumlimits^n_{i=1}{P({ A}_n)}]

Пользуясь этой формулой можно получить законы распределения для каждой компоненты двумерной случайной величины, то есть:

Отсюда будет следовать, что сумма всех вероятностей двумерной системы имеет следующий вид:

Рассмотрим подробно (поэтапно) задачу, связанную с понятием закона распределения двумерной случайной величины.

Пример 1

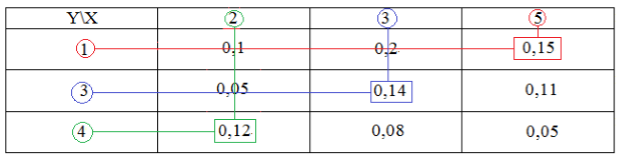
Закон распределения двумерной случайной величины задан следующей таблицей:

Рисунок 2.

Найти законы распределения случайных величин $X, Y$, $X+Y$ и проверить в каждом случае выполнение равенства полной суммы вероятностей единице.

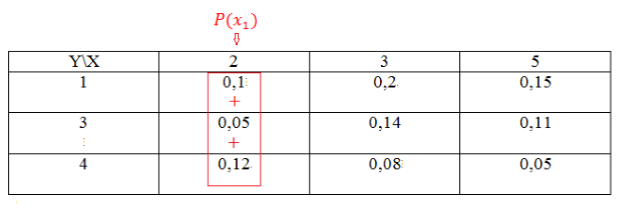
Найдем сначала распределение случайной величины $X$. Случайная величина $X$ может принимать значения $x_1=2,$ $x_2=3$, $x_3=5$. Для нахождения распределения будем пользоваться теоремой 1.

Найдем вначале сумму вероятностей $x_1$ следующим образом:

Рисунок 3.

[Pleft(x_1right)=0,1+0,05+0,12=0,27]

Аналогично найдем $Pleft(x_2right)$ и $Pleft(x_3right)$:

[Pleft(x_2right)=0,2+0,14+0,08=0,42] [Pleft(x_3right)=0,15+0,11+0,05=0,31]

Значит, закон распределения величины $X$ имеет следующий вид:

Рисунок 4.

Проверим выполнение равенства полной суммы вероятностей:

[0,27+0,42+0,31=1-верно.]

Найдем теперь распределение случайной величины $Y$. Случайная величина $Y$ может принимать значения $x_1=1,$ $x_2=3$, $x_3=4$. Для нахождения распределения будем пользоваться теоремой 1.

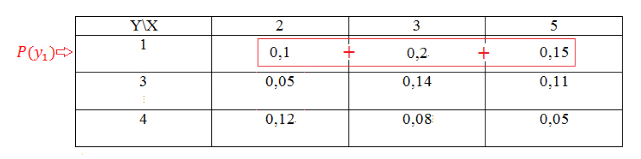
Найдем вначале сумму вероятностей $y_1$ следующим образом:

Рисунок 5.

[Pleft(y_1right)=0,1+0,2+0,15=0,45]

Аналогично найдем $Pleft(y_2right)$ и $Pleft(y_3right)$:

[Pleft(y_2right)=0,05+0,14+0,11=0,3] [Pleft(y_3right)=0,12+0,08+0,05=0,25]

Значит, закон распределения величины $X$ имеет следующий вид:

Рисунок 6.

Проверим выполнение равенства полной суммы вероятностей:

[0,45+0,3+0,25=1-верно.]

Осталось найти закон распределения случайной величины $X+Y$.

Обозначим её для удобства через $Z$: $Z=X+Y$.

Вначале найдем, какие значения может принимать данная величина. Для этого будем попарно складывать значения величин $X$ и $Y$. Получим следующие значения: 3, 4, 6, 5, 6, 8, 6, 7, 9. Теперь, отбрасывая совпавшие величины, получим, что случайная величина $X+Y$ может принимать значения $z_1=3, z_2=4, z_3=5, z_4=6, z_5=7, z_6=8, z_7=9. $

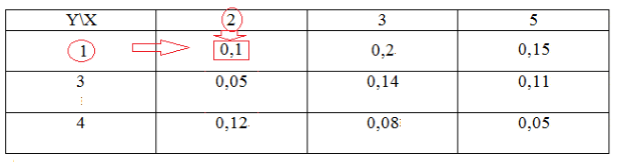
Найдем для начала $P(z_1)$. Так как значение $z_1$ единично, то оно находится следующим образом:

Рисунок 7.

[Pleft(z_1right)=0,1]

Аналогично находятся се вероятности, кроме $P(z_4)$:

[Pleft(z_2right)=0,2, Pleft(z_3right)=0,05, Pleft(z_5right)=0,08, Pleft(z_6right)=0,11, Pleft(z_7right)=0,05]

Найдем теперь $P(z_4)$ следующим образом:

Рисунок 8.

[Pleft(z_4right)=0,12+0,14+0,15=0,41]

Значит, закон распределения величины $Z$ имеет следующий вид:

Рисунок 9.

Проверим выполнение равенства полной суммы вероятностей:

[0,1+0,2+0,05+0,41+0,08+0,11+0,05=1-верно.]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Глава 6

Двумерная случайная величина

В главе рассматривается новый вопрос о зависимости между случайными величинами.

6.1Двумерная случайная величина, ее функция распределения

Определение. Двумерной случайной величиной называется упорядоченная пара (X, Y )

одномерных случайных величин X и Y . При этом предполагаются определенными вероятности произведения событий X < x и Y < y для любых вещественных x, y. Одномерные случайные величины X, Y называются компонентами двумерной случайной величины

(X, Y ).

Двумерную случайную величину называют также случайным двумерным вектором, случайной двумерной точкой, системой двух случайных величин.

Примеры реальных двумерных случайных величин.

1.Два размера детали в массовом производстве.

2.Величина сигнала в управляющем устройстве в два момента времени.

3.Абсцисса и ордината точки попадания сигнала.

4.Количество бракованных деталей в двух выборках из партии изделий.

Определение. Функцией распределения FXY (x, y) двумерной случайной величины

(X, Y ) называется вероятность произведения двух событий X < x, Y < y, определенная для любых вещественных x, y:

FXY (x, y) = P (X < x, Y < y).

Здесь произведение событий под знаком вероятности обозначено через запятую. Функцию FXY (x, y) будем называть двумерной функцией распределения. Свойства двумерной функции распределения.

1.FXY (−∞, y) = 0; FXY (x, −∞) = 0, так как X < −∞ и Y < −∞ — невозможные события и произведение невозможного события с любым другим событием есть также невозможное событие.

2. FXY (+∞, +∞) = 1, так как оба события X < +∞, Y < +∞ являются достоверными.

3. FXY (x, +∞) = FX (x); FXY (+∞, y) = FY (y), так как Y < +∞ — достоверное событие,

его произведение с событием X < x есть событие X < x; FXY (x, +∞) = P (X < x, Y < +∞) =

4.FXY (x, y) не убывает по каждому из своих аргументов при фиксированном другом аргументе.

Замечание. Для того, чтобы из двумерной функции распределения получить законы распределения компонентов, достаточно устремить один из аргументов к +∞.

Обратное неверно, т.е. из одномерных функций распределения компонент в общем случае нельзя получить функцию распределения двумерной случайной величины. Таким образом, двумерная функция распределения несет существенно больше информации, чем две одномерные функции распределения компонент X и Y . Рассматривая случайные величины X, Y порознь, а не в системе, нельзя получить сведения о их зависимости.

Будем различать дискретные и непрерывные двумерные случайные величины.

6.2Дискретная двумерная случайная величина, ее таблица распределения

Определение. Двумерная случайная величина называется дискретной, если множество ее значений (x, y) — конечное или счетное.

Примеры реальных дискретных случайных величин.

1.(X, Y ), где X — число деталей, изготовленных за смену на первом станке, Y — на втором.

2.(X, Y ), где X — число клиентов, поступивших за время T в первую систему массового обслуживания, Y — во вторую.

Закон распределения вероятностей двумерной дискретной случайной величины (X, Y ) можно задать формулой

P (X = xi, Y = yk) = pik (i = 1, . . . , m; k = 1, . . . , n).

Это вероятности совмещения событий X = xi, Y = yk. Так как события, означающие одновременное выполнение равенств X = xi, Y = yk (1, . . . , m; k = 1, . . . , n) являются попарно несовместными и образуют полную группу, то

pik = 1.

i=1 k=1

В случае конечности чисел m и n закон распределения дискретной двумерной случайной величины можно оформить в виде таблицы распределения:

XY	y1	y2	…	yn
x1	p11	p12	…	p1n
…	…	…	…	…
xm	pm1	pm2	…	pmn

Формулы согласованности для дискретной случайной величины имеют вид:

	n
pi• =	Xk
pik,
	=1
	m
p•k =	Xi
pik.
	=1

Здесь

pi• = P (X = xi), i = 1, . . . , m; p•k = P (Y = yk), k = 1, . . . , n

— одномерные законы распределения компонент случайной величины. Формулы согласованности позволяют из закона распределения двумерной случайной величины получить одномерные законы распределения ее компонент, которые, таким образом, не произвольные, а согласованы друг с другом.

Функция распределения дискретной двумерной случайной величины по аналогии с одномерным случаем может быть записана в виде

<x y <y

Здесь суммирование распространяется на те значения i и k, для которых xi < x, yk < y. Пример. Задана таблица распределения дискретной двумерной случайной величины.

Требуется найти одномерные законы распределения компонент.

XY		y1	y2		y3	pi•
x1		1			1		1	7

	12	6		3		12

x2		1			1		1		5
6		6		12	12

p•k		1			1		5	1
4		3		12

Применим формулы согласованности. Согласно этим формулам суммы вероятностей pik по строкам таблицы дают pi•, а по столбцам — p•k. Эти суммы записаны в дополнительном столбце справа и в дополнительной строке внизу.


					1		1		1		7			1		1	1			5
p1• =			+				+			=		; p2• =		+		+		=			;
12	6	3	12	6	6	12	12
	1			1		1					1		1	1			1			1		5
p•1 =			+			=			; p•2 =		+		=	; p•3	=		+		=		.
12	6	4	6	6	3	3	12	12

6.3Непрерывная двумерная случайная величина. Плотность вероятности

Определение. Двумерная случайная величина называется непрерывной, если существует неотрицательная функция fXY (x, y), называемая двумерной плотностью вероятности, такая, что вероятность попадания случайной величины (X, Y ) в область D равна двойному интегралу от плотности по области D:

P ((X, Y ) D) = fXY (x, y)dxdy.

Из приведенной формулы следует выражение для функции распределения двумерной непрерывной случайной величины:

x	y
FXY (x, y) = P (−∞ < X < x, −∞ < Y < y) = Z	Z	fXY (x, y)dxdy.

−∞ −∞

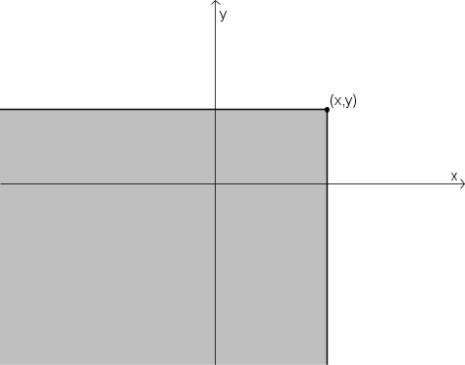
Это есть вероятность попадания случайной точки (X, Y ) в «юго-западный»квадрант с вершиной в точке (x, y).

Рис. 6.1: «Юго-западный» квадрант с вершиной в точке (x, y)

Из формулы, определяющей связь между двумерной плотностью вероятности и функцией распределения следует, что FXY (x, y) непрерывна на всей плоскости xOy.

Свойства двумерной плотности вероятности.

1. Определена на всей плоскости xOy.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Закон распределения дискретной двумерной СВ. Безусловные и условные законы распределения составляющих

Ковариация (корреляционный момент)

Свойства ковариации

Коэффициент корреляции

Свойства коэффициента корреляции

Линейная регрессия

Двумерная случайная величина

6.1Двумерная случайная величина, ее функция распределения

6.2Дискретная двумерная случайная величина, ее таблица распределения

6.3Непрерывная двумерная случайная величина. Плотность вероятности

Не пропустите также:

Закон распределения дискретной двумерной СВ.
Безусловные и условные законы распределения составляющих