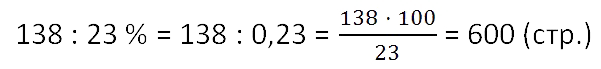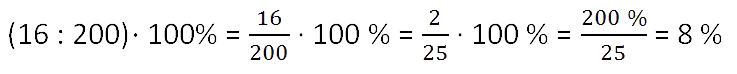Чек-лист «Решение задач на проценты»
|
1 тип. Нахождение процента от числа |
2 тип. Нахождение числа по его процентам |
3 тип. Нахождение процентного отношения двух |
||
|
Чтобы найти процент от числа, |
Чтобы найти число по его процентам, |
Чтобы найти процентное отношение двух |
||
|
Подсказки: — известно — — |
Подсказки: — известно — — |
Подсказки: — известны — — — в краткой записи условия: числа (или величины) записываются |
||
|
Пример 1. В книге 60 страниц, Артём Решение:
Прочитал — ? стр., 30 % 30 % = 60 : 100 Ответ: Артём прочитал 18 страниц. |
Пример 2. Денис прочитал Решение: Прочитал 45 % или 180 стр. Всего страниц в книге — ? (100 %) 45 % = 180 : 45 Ответ: в книге 400 страниц. |
Пример 3. Фрекен Бок Решение: Испекла – 250 пирожков Съел – 10 пирожков, ? %. 10 : 250 Ответ: 4 %. |
||
|
Алгоритм решения задачи на проценты.
1. 2. 3. 4. 5. |
На чтение 4 мин. Просмотров 17.8k.
Обновлено 29.08.2021
В этой статье вы узнаете, что такое процент, как решать задачи на проценты. Примеры, а также вашему вниманию предлагаю инфографику, которую вы можете скачать и распечатать для наглядного представления данной темы. Изучать тему начинают в 5 классе, поэтому все объяснения адаптированы для детей 11-12 лет.
Содержание
- Что такое процент
- Видео урок на решение задач с процентами в 5 классе
- Как перевести процент в десятичную дробь
- Как найти процент от числа
- Решить задачу можно двумя способами.
- Нахождение числа по его процентам
- Решение
- Найти процентное отношение чисел
- Наглядное пособие по процентам распечатать
Что такое процент
За 1 процент принято считать сотую долю от любой величины. Следовательно, 100% — это есть вся величина.
Например, если путник прошел весь путь 5 км, то 5 км — это 100%.
1% пути вычисляем 5 км : 100% = 0,05 км
Маша прочитала всю книгу в 120 листов. 120 листов — 100%. 1% 120 : 100 = 1,2%
Видео урок на решение задач с процентами в 5 классе
Как перевести процент в десятичную дробь
Соответственно, если мы будем оперировать понятием целого, то сделана вся работа будет равно 1, а если понятием проценты — сделана на 100%.
Например, студент напечатал весь реферат на 100 листах. Получается, что выполнения вся работа. Это равно единице (понятие «Целое»), или 100% реферата (понятие «Процент»).
1 страница реферата занимает глава «Введение». Значит, 1% реферата (сотая часть) приходится на введение. 1 страница — это 1/100 реферата, что можно выразить в десятичной дроби, как 0,01.
2 страницы реферата — это 2%, или 0,02 всей печатной работы.
Чтобы перевести проценты в десятичную дробь, нужно число процента разделить на 100.
Примеры перевода процентов в десятичную дробь:
50% = 50: 100 = 0,5
18% = 18 : 100 = 0,18
1% = 1 : 100 = 0,01
120% = 120 : 100 = 1,2
2000% = 2000 : 100 = 20
Если вся величина 100%, то откуда может берется понятие 120%, 200% и даже 500% ?
Это легко понять на следующих примерах:
Путешественник проделал путь 100 км в первый день пути на велосипеде. (проехал 100%)
На следующий день он проехал расстояние в 120 км. (120%, т.к. на следующий день он проехал на 20% больше).
Как найти процент от числа
Когда нам известно значение всей величины и проценты, то мы можем найти числовое значение, которое приходится на проценты.
Иван написал сочинение на 8 листах. 25% он написал утром. Сколько листов сочинения Иван написал за утро?
Решить задачу можно двумя способами.
1 способ.
Найдем вначале сколько листов приходится на 1%. Вспомним, что 1 процент — это сотая часть.
1) 8 : 100 = 0,08 листа — 1% сочинения.
теперь узнаем сколько листов приходится на 25%:
2) 0,08 x 25 = 2 листа — это 25%
2 способ
Его проще запомнить. Сначала нужно перевести процент в десятичную дробь.
1) 25% = 0,25
0,25 — часть от целого нужно найти, чтобы узнать количество листов. Вся работа — единица (1).
Найдем 0,25 от 8.
2) 8 x 0,25 = 2 л.
Смотрите другой пример на графике ниже
Нахождение числа по его процентам
Следующая ситуация, с которой школьникам 5 класса будут регулярно сталкиваться в задачах на проценты, — это нахождение величины, когда известно какой процент, она составляет.
Пример.
Мама потратила в магазина на продукты 120 рублей. Это 40% от всей суммы, которую мама потратила на покупки. Сколько денег истратила мама в магазине?
Решение
Так же, как и в первом варианте, эту задачу можно решить тремя способами.
1 способ
Мы можем посчитать сколько денег составляет 1% от всей покупки:
1) 120 : 40 = 3 рубля приходится на 1%
Теперь посчитаем 100% (сумму всей покупки)
2) 3 x 100 = 300 рублей составляет 100% (истратила мама на покупки).
2 способ
Переведем проценты в десятичную дробь
1) 40% = 40 : 100 = 0,4
Чтобы найти сколько это составляет процентов, нужно величину, составляющую долю от целого, разделить на процент, выраженный десятичной дробью:
2) 120 : 0,4 = 300 рублей — вся затраченная сумма.
3 способ
Подойдет для тех, кто знаком с пропорцией.
120 рублей — это 40%
x рублей — это 100%
Отсюда получаем пропорцию:
Другая задача разобрана на рисунке с диаграммой ниже:
Найти процентное отношение чисел
Еще один тип задач на проценты подразумевает выражение отношения величин в процентах.
Задача.
В классе 30 учеников. Мальчиков — 12. Какой процент составляют мальчики?
Решение
1 способ
Найдем, какая часть класса приходится на мальчиков:
1) 12 : 30 = 0,4
Выразим найденное в процентах:
2) 0,4 x 100 = 40%
2 способ
Можно решить составлением пропорции
30 учеников — это весь класс и составляет 100%, 12 мальчиков — это X %
Бонусом еще одна задача:
Наглядное пособие по процентам распечатать
Вы можете распечатать данное учебное пособие, чтобы наглядно видеть, как решать задачи на проценты. Если ежедневно обращаться к данной шпаргалке, то материал запомнится сам собою.
Скачать шпаргалку здесь >>>
Задача 1
Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?
- Решение
- 1) 76 : 100 = 0,76 (кг) 1% от массы человека;
- 2) 0,76 * 70 = 53,2(кг).
- Ответ: масса воды 53,2 кг.
Задача 2
Металлический конструктор состоит из 300 деталей. 12% этих деталей гайки. Сколько гаек в металлическом конструкторе?
- Решение
- 1) 300 : 100 = 3(детали) 1% всех деталей конструктора;
- 2) 3 * 12 = 36 (гаек).
- Ответ: в конструкторе 36 гаек.
Задача 3
В грушах сладких сортов содержится сахара 15% от их массы. Сколько кг сахара будет содержаться в 6 кг груш?
- Решение
- 1) 6 : 100 = 0,06 (кг) 1% от шести килограмм;
- 2) 0,06 * 15 = 0,9 (кг).
- Ответ: в шести кг груш будет содержаться 0,9 кг сахара.
Задача 4
В классе 30 человек, из них девочек – 18. Сколько процентов мальчиков в классе?
- Решение
- 1) 30 : 100 = 0,3 — 1% процент всех детей класса;
- 2) 30 – 18 = 12 – мальчиков в классе;
- 3) 12 : 0,3 = 40%.
- Ответ: в классе учится 40% мальчиков.
Задача 5
Если высушить свежие груши, то их масса уменьшится на 80%. Сколько понадобится свежих груш для приготовления 8 кг сушеных?
- Решение
- 1) 100 – 80 = 20% — составляет масса сухих груш относительно свежих;
- 2) 8 : 20 = 0,4 (кг) 1% свежих груш для приготовления 8 кг сушеных;
- 3) 0,4 * 100 = 40 (кг).
- Ответ: понадобится 40 кг свежих груш.
Задача 6
1% процент книги, которую читал Сережа, составляет 4 страницы. Сколько страниц осталось прочитать Сереже, если он уже прочитал 30%?
- Решение
- 1) 30 * 4 = 120 (стр.) прочитал Сережа;
- 2) 4 * 100 = 400 (стр.) все страницы книги;
- 3) 400 – 120 = 280 (стр.).
- Ответ: Сереже осталось прочесть 280 страниц.
Задача 7
Количество сливок, получаемых из молока, равно 21%. Сколько сливок получиться, если использовать 48 литров молока?
- Решение
- 1) 48 : 100 = 0,48 (л) 1% от 48 литров;
- 2) 0,48 * 21 = 10,08 (л).
- Ответ: сливок получится 10,08 литров.
Задача 8
Периметр прямоугольника равен 80 см. 60% этого периметра – сумма длин прямоугольника. Чему равна ширина прямоугольника?
- Решение
- 1) 80 : 100 = 0,8 (см) 1% от периметра прямоугольника;
- 2) 100 – 60 = 40% — часть суммы ширин в периметре;
- 3) 0,8 * 40 = 32 (см);
- 4) 32 : 2 = 16 (см).
- Ответ: ширина прямоугольника равна 16 см.
Задача 9
Одна из сторон треугольника равна 15 см, длина второй равна 80% первой, а длина третей – 150% второй. Чему равен периметр этого треугольника?
- Решение
- 1) 12 : 100 = 0,15 (см) 1% от длины первой стороны;
- 2) 0,15 * 80 = 12 (см) длина второй стороны;
- 3) 12 : 100 = 0,12 (см) 1% от длины второй стороны;
- 4) 0,12 * 150 = 18 см (см) длина третьей стороны.
- 5) 12 + 15 + 18 = 45 (см).
- Ответ: периметр треугольника равен 45 см.
Задача 10
На приготовление ужина у мамы ушло 2 часа. Для приготовления мясных блюд понадобилось 40% времени, десерт занял 20%, все остальное время было затрачено на приготовление салатов. Сколько времени понадобилось маме для приготовления каждого из блюд?
- Решение
- 1) 40 + 20 = 60% времени ушло у мамы на приготовление мясных блюд и десерта;
- 2) 100 – 60 = 40% времени заняло приготовление салатов;
- 2 часа = 120 мин.
- 3) 120 : 100 = 1,2 (мин) 1% от 2 часов;
- 4) 40 * 1,2 = 48 (мин);
- 5) 20 * 1,2 = 24 (мин).
- Ответ: на приготовление салатов 48 мин, на приготовление мясных блюд 48 минут, на приготовление десерта 24 минуты.
Задача 11
В течении месяца Саша играл с папой в шахматы. За это время было сыграно 25 партий, из которых 80% выиграл папа. Сколько партий в шахматы выиграл за месяц Саша?
- Решение
- 1) 100 – 80 = 20% партий выиграл Саша;
- 2) 25 : 100 = 0,25 – 1% процент от всех партий;
- 3) 20 * 0,25 = 5 (партий).
- Ответ: Саша выиграл 5 партий.
Задача 12
У Лены в аквариуме 8 меченосцев, что составляет 40% всех ее рыбок. Сколько всего рыбок у Лены в аквариуме?
- Решение
- 1) 8 : 40 = 0,2 — 1% от всех рыбок;
- 2) 0,2 * 100 = 20 (рыбок).
- Ответ: всего у Лены 20 рыбок в аквариуме.
Задача 13
За зиму медведь Вини Пух съел 16 горшочков меда. Сколько горшочков меда заготовил Вини Пух, если у него осталось 20% всех его запасов?
- Решение
- 1) 100 – 20 = 80% — меда съел за зиму Вини Пух;
- 2) 16 : 80 = 0,2 (меда) 1% от всего меда;
- 3) 0,2 * 100 = 20.
- Ответ: на зиму Вини Пух заготовил 20 горшочков меда.
Задача 14
Грибы теряют при сушке 75% своей массы. Сколько понадобится свежих грибов для приготовления 4 кг сушеных?
- Решение
- 1) 100 – 75 = 25% масса сушеных грибов от массы свежих;
- 2) 4 : 25 = 0,16 1% от массы свежих грибов;
- 3) 0,16 * 100 = 16 (кг).
- Ответ : понадобится 16 кг свежих грибов.
Задача 15
На олимпиаде школьная команда набрала 72 очка. Сколько очков можно набрать на олимпиаде, если набранные командой очки составляют 80% из всех возможных?
- Решение
- 1) 72 : 80 = 0,9(очков) 1% от всех возможных очков;
- 2) 0,9 * 100 = 90 (очков).
- Ответ: на олимпиаде можно набрать 90 очков.
Предлагаю Вашему вниманию небольшой список типовых задач на проценты —5 класс. Материал ориентирован на способных учеников, в работе с которыми репетитор по математике имеет, как правило, достаточную свободу в плане соответствия программным и возрастным стандартам. Часть задач является базовыми только для 6 класса (по учебнику Виленкина), но вполне могут быть рассмотрены уже в 5 классе. Данный материал был подготовлен мной специально для занятия с Артемом — учеником Курчатовской школы.
Задачи по математике 5 класс / проценты
1) Билет на концерт стоит 2400 рублей, а стоимость билета в кино составляет 20% от стоимости билета на концерт. Сколько стоит билет в кино?
2) Маша потратила в магазине 45% своих денег. Найдите потраченную сумму денег, если у нее всего было 800 рублей.
3) Бегун пробежал 600м, что составляет 40% всей его намеченной дистанции. Найдите длину дистанции.
4) В младших классах учится 200 учеников, что составляет 40% учеников старших классов. Сколько учеников учится в школе?
5) В книге 3 главы. Число страниц в первой главе составляет 30% всей книги, число страниц второй главы – 45% книги, а в третьей 50 страниц. Сколько страниц в книге?
6) В магазин привезли арбузы. В первый день продали 25% всех арбузов, во второй 55% арбузов, а остальные 60кг арбузов в третий день. Сколько всего килограммов арбузов привезли в магазин?
7) Цена на товар увеличилась на 20%. Найдите новую цену, если старая составляла 400рублей.

9) Цена на ботинки выросла на 30%. Сколько стоят ботинки теперь, если раньше они стоили 3100руб?
10) 31 декабря елка подешевела на 40%. Найдите новую стоимость елки, если до 31 числа она стоила 2100рублей.
11) После увеличения цена на мобильный телефон на 10% он стал стоить 6600 руб. Определите первоначальную цену телефона.
12) После снижения цены на товар на 30% он стал стоить 4200рублей. Найдите его первоначальную цену.
13) Банкомат берет 3% от положенной в него суммы денег. Сколько денег положить в банкомат, чтобы на счету оказалось 776 рублей?
14) Банкомат берет комиссию в 2% от внесенной суммы денег. Сколько денег необходимо опустить в банкомат, чтобы на счет пришло 196рублей?
15) После снижения цены на 15% товар стал стоить 255 рублей. Найдите начальную его цену.
16) После увеличения стоимости брюк на 5% они стали стоить 2310руб. Какова была их начальная стоимость?
17) Банкомат берет комиссию в 4% от внесенной суммы денег. Сколько рублей нужно опустить в банкомат, чтобы после вычитания из этой суммы комиссии на счету оказалось 288 рублей?
18) В школе 800 учеников. Из низ 120 человек приняли учатие в лыжной гонке. сколько процентов всех учеников школы приняло участие в гонке?
19) Витя пошел в магазин, взяв с собой 400 рублей. Он купил тетрадь за 24 рубля. Сколько процентов всех денег он потратил?
20) Школьники решили посадить на субботнике 200 деревьев. В первый час работы было посажено 54 дерева. Сколько % всех деревьев они успели посадить за это время?
21) Цена на товар увеличилась на 25%. На сколько % ее теперь надо снизить, чтобы вернуть начальную цену?
22) В саду росли яблоки и груши. Если сорвать 50% всех яблок и 25% всех груш, то и тех и других окажется поровну. Сколько растет в саду яблок и сколько груш, если их всего 360 штук?
23) Карлсон с Малышом поедали вкусные плюшки. Малыш съел только 20% своих плюшек, а Карлсон слопал все свои. Во сколько раз больше имелось плюшек у Карлсона, чем у Малыша, если на пару они съели 80% всех имевшихся у них плюшек?
Скачать задачи на проценты 5 класс
Указание репетиторам по математике: Все номера подобраны с учетом специфики программного изучения математики в 5 классе (по учебнику Виленкина) и предполагают решения без использования десятичных дробей и необходимости умножать (делить) на обыкновенные дроби. Для 5 класса задачи под номерами 21 и 22 являются близкими к олимпиадными и должны включатся репетитором по математике в план урока только при наличии определенных способностей ученика. Никаких иксов и отношений в этих номерах!!! Так бы они решились в 6 классе. Ученику 5 класса необходимо сделать рисунок и показать доли целого объекта. Чаще сопровождайте задачи рисунками и, конечно же, следите за точностью и лаконичностью своих объяснений.
Список содержит достаточное количество упражнений как для решения совместно с репетитором, так и для домашнего закрепления. Я постарался подобрать несколько задач на каждый их типовой вариант.
Вдогонку от репетитора: Стоит отметить, что подборки дополнительных задач на проценты в современной школьной дидактике и учебных интернет проектах часто не имеют четкого ориентира на работу с конкретным возрастом, классом или программой, что сильно усложняет репетитору по математике подготовку к уроку. Мешанина — наиболее точное слово для описания характера составления таких материалов. Задача часто включается в учебный список уже только потому, что в ее тексте присутствует знак «%». А ведь школьники в 5 классе еще не имеют полного представления о дробях и не могут работать с % в сложных сравнениях (у Маши на 10% больше денег, чем у Вити), требующих соответствующего выражения величин через переменные, понять дробные/десятичные проценты, а также взрослые решения с применением пропорций и уравнений. Во многих рассмотренных мной подборках отсутствовала полноценная дидактическая поддержка закрепления пройденного (следующая задача часто не похожа на предыдущую). Поэтому я уже давно пользуюсь своими разработками. Материалы на урок я стараюсь составлять так, чтобы в них полностью отсутствовали перечисленные выше недостатки (за исключением закрепеления понимания отдельных усложненных/олимпиадных задач). Приходите заниматься.
Колпаков А.Н. Репетитор по математике. Москва. Автор подборки задач.
Метки:
Дидактика репетитора,
Проценты,
Текстовые задачи
Рассмотрим три основных типа задач на проценты.
Нахождение процента от числа
Запомните!
Чтобы найти процент от числа, нужно число умножить на процент.
Разбор примера
Предприятие изготовило за квартал 500 насосов, из которых
60% имели высшую категорию качества. Сколько насосов высшей категории качества
изготовило предприятие?
Решение:
Найдем 60% от 500 (общее количество насосов).
60 % = 0,6
500 · 0,6 = 300 насосов высшей категории качества.
Ответ: 300 насосов высшей категории качества.
Нахождение числа по его проценту
Запомните!
Чтобы найти число по его проценту, нужно его известную часть разделить на то,
сколько процентов она составляет от числа.
Так как задачи «процент по числу» и «число по его проценту» очень похожи и часто
не сразу понятно какой тип задачи перед нами, старайтесь внимательно читать
текст. Если вам встречаются слова «который», «что составляет» и «который составляет»,
скорее всего перед вами задача «число по его проценту».
Разбор примера
Ученик прочитал 138 страниц, что составляет 23%
числа всех страниц в книге. Сколько страниц в книге?
Решение:
Итак, нам неизвестно сколько всего страниц в книге. Но мы знаем, что часть, которую
прочитал ученик (138 страниц) составляет 23% от общего количества
страниц в книге.
Так как 138 стр. — это всего лишь часть, само количество
страниц, естественно, будет больше 138. Это поможет нам при проверке.
Проверка: 600 > 138 (это означает, что 138 является частью 600).
Ответ: 600 (стр.) — общее количество страниц в книге.
Сколько процентов одно число составляет от другого
Запомните!
Чтобы найти, сколько процентов одно число составляет от другого, нужно ту часть, о которой спрашивается,
разделить на общее количество и умножить на 100%.
Разбор примера
Из 200 арбузов 16 оказались незрелыми.
Сколько процентов всех арбузов составили незрелый арбузы?
Решение:
О чем спрашивают? О незрелых арбузах. Значит, 16
делим на общее количество арбузов и умножаем на 100%.
Ответ: 8% — составляют незрелые арбузы от всех арбузов.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
8 апреля 2023 в 0:03
Надежда Горскова
Профиль
Благодарили: 0
Сообщений: 1
Надежда Горскова
Профиль
Благодарили: 0
Сообщений: 1
Благодарю.
0
Спасибо
Ответить
9 января 2020 в 14:39
Владислав Кругомов
Профиль
Благодарили: 0
Сообщений: 1
Владислав Кругомов
Профиль
Благодарили: 0
Сообщений: 1
Масса сплава меди и серебра равна 7,2 кг.Масса серебра состовляет 80% массы меди. Сколько килограммов меди в сплаве?
Можно пожалуйста решения не уравнением!
0
Спасибо
Ответить
11 января 2020 в 18:02
Ответ для Владислав Кругомов
Иван Войт
Профиль
Благодарили: 0
Сообщений: 2
Иван Войт
Профиль
Благодарили: 0
Сообщений: 2
Т.к. серебро — 0.8 (80%) от меди, а медь — 1 (100%), то их сумма =1,8. Т.к. 1.8 (180%) это 7.2 кг, то (7.2/1.8)= 4 (кг) — это медь, а серебро = 3,2 (7,2-4 или 4*0.8 (80%))
Ответ: серебро — 3,2 кг, медь -4 кг
0
Спасибо
Ответить
11 января 2020 в 18:02
Ответ для Владислав Кругомов
Иван Войт
Профиль
Благодарили: 0
Сообщений: 2
Иван Войт
Профиль
Благодарили: 0
Сообщений: 2
Т.к. серебро — 0.8 (80%) от меди, а медь — 1 (100%), то их сумма =1,8. Т.к. 1.8 (180%) это 7.2 кг, то (7.2/1.8)= 4 (кг) — это медь, а серебро = 3,2 (7,2-4 или 4*0.8 (80%))
Ответ: серебро — 3,2 кг, медь -4 кг
0
Спасибо
Ответить
4 сентября 2016 в 9:48
София Ниязова
Профиль
Благодарили: 0
Сообщений: 1
София Ниязова
Профиль
Благодарили: 0
Сообщений: 1
40% числа 15 и 9,5% числа 280… Если знаете как решать это напишите прошу вас!
0
Спасибо
Ответить
4 сентября 2016 в 16:15
Ответ для София Ниязова
Юлия Анарметова
Профиль
Благодарили: 0
Сообщений: 11
Юлия Анарметова
Профиль
Благодарили: 0
Сообщений: 11
1. (40 · 15): 100=6
2.(9.5 · 280) :100=26.6
0
Спасибо
Ответить
10 мая 2016 в 23:58
Илья Московец
Профиль
Благодарили: 0
Сообщений: 1
Илья Московец
Профиль
Благодарили: 0
Сообщений: 1
У Первого человека было 50 рублей, у второго тоже 50 рублей вместе у них 100 рублей. это 100%. Первый человек добавил 25 рублей всего стало 125 рублей. Вопрос: в процентах как это поменялось? и как вы считаете?
0
Спасибо
Ответить
11 мая 2016 в 19:13
Ответ для Илья Московец
Дмитрий Захаров
Профиль
Благодарили: 0
Сообщений: 3
Дмитрий Захаров
Профиль
Благодарили: 0
Сообщений: 3
либо 1% стал меньше, либо стало 125 %
0
Спасибо
Ответить
22 сентября 2016 в 11:42
Ответ для Илья Московец
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Чтобы расчитать изменение в процентах, нужно понять относительно чего изменения? Если относительно первоначальной суммы, то увеличилось на 25%. Если относительно количества денег у каждого из людей, то у первого увеличилось на 50% от вервоначальной суммы.
1
Спасибо
Ответить
12 апреля 2016 в 15:41
Денис Захарченко
Профиль
Благодарили: 0
Сообщений: 1
Денис Захарченко
Профиль
Благодарили: 0
Сообщений: 1
Ёмкость с водой на 1000л имеет 3 одинаковых трубы снизу, ведущие в 3 бочки, на каждой трубе кран, 1-й открыт на 100%, второй и третий на 30%, на сколько литров наполниться каждая из бочек?
0
Спасибо
Ответить
13 апреля 2016 в 7:51
Ответ для Денис Захарченко
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Спасибо за интересную задачу. Тянет на олимпиадную, на правильность не претендую, но логика вроде верная.
Т.к. трубы в равных условиях, то вытекает вода из них одно и тоже время. Обозначим это время за Х. Скорость, с которой вытекает из первый трубы, возьмём условно за 1. А из двух оставшихся за 0,3. Тогда количество воды вытекающей из первой трубы будет равно 1 · Х, а из двух оставшихся 0,3 · Х. Т.к. известно, что всего в ёмкости 1000 литров, составим уравнение и решим:
1 · x+0,3 · x+0,3 · x=1000
1,6 · x=1000
x=625
Проверка:
625+0,3 · 625+0,3 · 625=625+187,5+187,5=1000
1000=1000
Вытекло в 1ую бочку: х =625
Вытекло во 2ую бочку: 0,3 · х=187,5
Вытекло в 3ю бочку: 0,3 · х=187,5
Ответ: 625л;187,5л; 187,5л.
Если будет возможность, прошу предоставить правильный ответ.
Заранее благодарен!
0
Спасибо
Ответить
1 октября 2015 в 17:39
Дима Дима
Профиль
Благодарили: 0
Сообщений: 1
Дима Дима
Профиль
Благодарили: 0
Сообщений: 1
масса сушёных груш состовляет 20% массы свежих.Сколько кг сушёных груш получится из 100кг;350кг;25кг свежих? Сколько процентов массы свежих груш теряется при сушке?
0
Спасибо
Ответить
1 июля 2016 в 17:06
Ответ для Дима Дима
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Для вычисления процента от числа необходимо умножить на количество процентов и разделить на 100. Следовательно 20: 100 = .
100 · =100: 5 = 20 (кг).
Аналогично с остальными примерами:
350 : 5 = 70 (кг)
25: 5 = 5 (кг)
Масса свежей груши 100%. масса сушеной груши 20%. Значит груша теряет 100%-20%=80% своей массы при высыхании.
Ответ: 20 кг, 70 кг, 5 кг, 80%.
0
Спасибо
Ответить
11 мая 2015 в 23:20
Эдуард Селивоненко
Профиль
Благодарили: 0
Сообщений: 1
Эдуард Селивоненко
Профиль
Благодарили: 0
Сообщений: 1
в цветочном магазине 35%гвоздик -крассные, и их 105 штук ,25%-белых, а остольные розавые. вапрос сколько белых и сколько розавых?
0
Спасибо
Ответить
17 апреля 2016 в 16:18
Ответ для Эдуард Селивоненко
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
В этом разделе подробно описан вопрос про проценты: http://math-prosto.ru/index.php?page=pages/percent/percent1.php
Решение:
35% это 0,35
Обозначим общее количество гвоздик за Х, тогда
0,35 · x=105
x=300 — всего в магазине 300 гвоздик.
Найдём количество белых:
300 · 0,25 = 75 — белых гвоздик в магазине.
Найдём количество розовых:
Для этого из общего количества гвозик отнимаем количество красных и белых:
300 — 75 — 105 = 120 — розовых гвоздик.
Ответ: 75 белых и 120 розовых гвоздик было в магазине.
0
Спасибо
Ответить
19 апреля 2015 в 14:16
Маша Галлямова
Профиль
Благодарили: 0
Сообщений: 2
Маша Галлямова
Профиль
Благодарили: 0
Сообщений: 2
Цену на товар сначала снизили на 20%, а затем увеличили на 20%. Больше или меньше станет цена на товар относительно его первоначальной стоимости и на сколько процентов?
0
Спасибо
Ответить
20 апреля 2015 в 21:49
Ответ для Маша Галлямова
Константин Лебедев
Профиль
Благодарили: 0
Сообщений: 1
Константин Лебедев
Профиль
Благодарили: 0
Сообщений: 1
Пусть х цена товара. Снижение на 20% равносилно умножению цены на 0.8=1-20/100, следовательно цена стала равна х*0.8. Затем увеличили на 20% это означает, что новую цену умножили 1.2. В итоге получили окончательно новую цену х*0.8*1.2 =х*0.96. Таким образом первоначальная цена стала меньше т.к. умножилась на величину меньшую единицы. Так же видно, что цена уменьшилась на 4%. Видно и то, что от порядка выполнения операций снижения, а потом увеличения цены на одно и тоже число процентов, или наоборот повышения а потом снижения, окончательная цена будет меньше первоночальной и приводит к снижению цены. В общем виде обозначим число процентов pb пусть а=р/100, тогда новая цена будет равна х*(1-а)(1+а)=x*(1-а^2). Мы доказали что цена уменьшается на а^2*100%.
0
Спасибо
Ответить
16 апреля 2015 в 15:17
Лёня Стародубцев
Профиль
Благодарили: 0
Сообщений: 1
Лёня Стародубцев
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
14 апреля 2016 в 11:32
Ответ для Лёня Стародубцев
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
В статье подробно описано, как это делается: http://math-prosto.ru/index.php?page=pages/percent/percent1.php
А именно: «Чтобы перевести проценты в дробь, нужно убрать знак % и разделить число на 100.»
33
%= %
Переведём проценты в дробь:
: 100=
60 · =20
Ответ: 20
0
Спасибо
Ответить