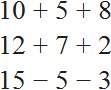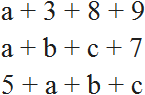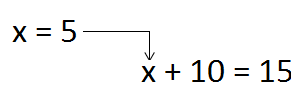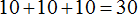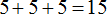Выражение — это любое сочетание чисел, букв и знаков операций. Можно сказать, что вся математика состоит из выражений.
Выражения бывают двух видов: числовые и буквенные.
Числовые выражения состоят из чисел и знаков математических операций. Например, следующие выражения являются числовыми:
Буквенные выражения помимо чисел и знаков операций содержат ещё и буквы. Например, следующие выражения являются буквенными:
Буквы, которые содержатся в буквенных выражениях, называются переменными. Запомните это раз и навсегда! Спросите любого школьника что такое переменная — этот вопрос поставит его в ступор, несмотря на то что он будет решать сложные задачи по математике, не зная что это такое. А между тем, переменная это фундаментальное понятие, без понимания которого математику невозможно изучать.
Под словом «изучать» мы подразумеваем самостоятельное чтение соответствующей литературы и способность понимать, что там написано. А то вроде и знаешь математику на четвёрку, задачи решаешь, но не можешь понять, что написано в лекциях и книгах. Каждому знакомо такое чувство, особенно студентам.
Поскольку понятие переменной очень важно, остановимся на нём подробнее. Посмотрите внимательно на слово «переменная». Ничего не напоминает? Слово «переменная» происходит от слов «меняться», «изменить», «изменить своё значение». Переменная в математике всегда выражена какой-то буквой. Например, запишем следующее выражение:
a + 5
Это буквенное выражение. Здесь одна переменная a. Поскольку она является переменной, значит может изменить свое значение в любой момент времени. Изменить значение может любой: вы, учитель, ваш товарищ, кто угодно. Например, давайте изменим значение этой переменной. Присвоим ей значение 5. Для этого запишем саму переменную, затем поставим знак равенства и запишем 5
a = 5
Что случится в результате этого? Значение переменной a, то есть 5 отправится в главное выражение a + 5, и подставится вместо a.
В результате имеем: 5 + 5 = 10
Конечно, мы рассмотрели простейшее выражение. На практике встречаются более сложные выражения, в которых присутствуют дроби, степени, корни и скобки. Выглядит это устрашающе. На самом деле ничего страшного. Главное понять сам принцип.
В учебниках часто встречаются задания следующего содержания: найдите значение выражения x + 10, при x = 5. Такие задания как раз и требуют, чтобы вместо переменной подставили её значение. Давайте выполним это задание. Значение переменной x равно 5. Подставляем эту пятёрку в исходное выражение x + 10 и получаем 5 + 10 = 15.
Переменная это своего рода контейнер, где хранится значение. Переменные удобны тем, что они позволяют, не приводя примеров доказывать теоремы, записывать различные формулы и законы.
Вспомним второй урок «Основные операции». Чтобы понять сложение, мы привели пример 5 + 2 = 7 и сказали, что числа 5 и 2 являются слагаемыми, а число 7 — суммой. Но можно было понять эту тему и без примера, если бы мы воспользовались буквенным выражением. Обозначили бы слагаемые любыми буквами, например a и b, а сумму обозначили бы как с.
Тогда у нас получилось бы выражение с тремя переменными a + b = c, и можно было сказать, что a и b — это слагаемые, c — сумма.
И далее имея выражение a + b = c, можно пользоваться им, подставляя вместо переменных a и b любые числа. А переменная c будет получать своё значение автоматически, в зависимости от того какие числа будут подставлены вместо a и b
В качестве практики можете выполнить следующее задание. Дано выражение a + b = c. Найдите его значение, если a = 10, b = 6. Переменная c получит своё значение автоматически. Ответ запишите следующим образом: при a = 10 и b = 6, переменная c равна такому-то числу.
Решение:
a + b = c
10 + 6 = 16
Ответ: при a = 10 и b = 6, переменная c равна 16.
Значение выражения
Фраза «выполнить действие» означает выполнить одну из операций действия.
В учебниках младших классов часто можно встретить задания такого содержания: выполнить действия, и далее приводятся примеры, которые нужно решить. Когда перед нами подобное задание, мы сразу должны понимать, что от нас требуют решить пример. В народе это звучит как «решить пример«, но более правильно надо говорить «найти значение выражения». Решить пример и найти значение выражения это фактически одно и то же.
Например, если дано выражение 10 + 6, и от нас требуют найти значение этого выражения, это означает что нам нужно решить данный пример. Поставить знак равенства = и записать ответ:
10 + 6 = 16
Сумма 16, которая получилась в результате и называется значением выражения 10 + 6.
Значение выражения — это результат выполнения действий, содержащихся в выражении.
Рассмотрим еще примеры:
- 16 это значение выражения 4 × 4, поскольку 4 × 4 = 16
- 20 это значение выражения 10 + 10, поскольку 10 + 10 = 20
- 5 это значение выражения 10 ÷ 2, поскольку 10 ÷ 2 = 5
Задания для самостоятельного решения
Задание 1. Найдите значение выражения 5 + x при x = 4
Задание 2. Найдите значение выражения a + 3 при a = 7
Задание 3. Найдите значение выражения a + a + a при a = 10
Задание 4. Найдите значение выражения a + b при a = 10 и b = 20
Задание 5. Найдите значение выражения b + b + b при b = 5
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

На чтение 3 мин. Просмотров 21.7k.
При решении примеров и уравнений нужно четко отличать — что такое числовые выражение, а что такое буквенные выражения. Поэтому сегодня пройдем эту тему и посмотрим видео. Итак, выучите правила.
Правила математики о числовых и буквенных выражениях
Числовое выражение — это такое выражение, которое составлено из чисел и имеет знаки «+», «-», а также знаки умножения или деления. В числовом выражении могут также быть и скобки.
Число, которое получается в результате выполнения математических операций, входящих в это числовое выражение, называется значением числового выражения.
Буквенные выражения — это выражения, содержащие латинские буквы, а также знаки математических операций сложения, вычитания, умножения и деления или скобки (при необходимости).
Числа, которые заменяют букву, называются значениями этой буквы.
Чтобы запомнить правила, давайте обратимся к примерам. Примеры — самый простой наглядный способ запомнить утверждения, приведенные выше.
Посмотрите видео:
Примеры числовых выражений
— в левой части этого равенства стоит числовое выражение, а в правой части — значение числового выражения.
— в левой части равенства — числовое выражение, а в правой части — значение числового выражения.
Посмотрите еще примеры числовых выражений:
Примеры буквенных выражений
Примеры буквенных выражений:
Буквенных выражений может быть множество. Для буквенных выражений каждая буква — это определенное число. Или множество разных чисел.
Когда применяются буквенные выражения
Буквенные выражения применяются тогда, когда нам надо, например, ввести формулу для нахождения той или иной величины. Например, вы знаете — что периметр прямоугольника, это сумма всех его сторон. Для периметра в общем виде можно записать буквенное выражение:
, где
— ширина прямоугольника, а
— его длина.
В правой части вы увидели буквенное выражение, значениями букв и
— будут числа — значения ширины и длины прямоугольника.
Математические выражения
Математическое выражение — это выражение, содержащее и числовое и буквенное выражение, а также их произведение, сумму, разность или деление.
То есть, например
— это математическое выражение.
Число перед буквой в математическом выражении — это коэффициент, означающий, что это число умножается на букву, которая может иметь переменное значение.
Буквенные, числовые и математические выражения — необходимо различать, чтобы понимать условия задачи, например, вас могут попросить упростить математическое выражение или попросить найти значение числового выражения. Поэтому необходимо знать — что это такое.
Если вам все понятно — выполните тест «Числовые и буквенные выражения».
- Главная
- Справочники
- Справочник по математике для начальной школы
- Числовые и буквенные выражения
Числовые выражения
В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.
Числовое выражение – это запись , состоящая из чисел и знаков действий между ними.
Например, 44 + 32
Значение выражения — это результат выполненных действий.
Например, в записи 44 + 32 = 76, значение выражения — это 76.
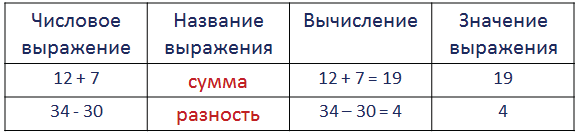
Чтение числовых выражений
12 + 9 — сумма
49 — 20 — разность
34 — (8 + 21) — из 34 вычесть сумму чисел 8 и 21
13 + (26 — 
Решение числовых выражений
45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13
Сравнение значений числовых выражений
Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.
Давай сравним значения двух выражений: 14 — 6 и 18 — 9.
Для этого найдем значения каждого из них:
14 — 6 = 8
18 — 9 = 9
8 < 9, значит,
14 — 6 < 18 — 9
Буквенные выражения
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.
В этих выражениях буквы могут обозначать различные числа. Число, которым заменяют букву, называют значением.
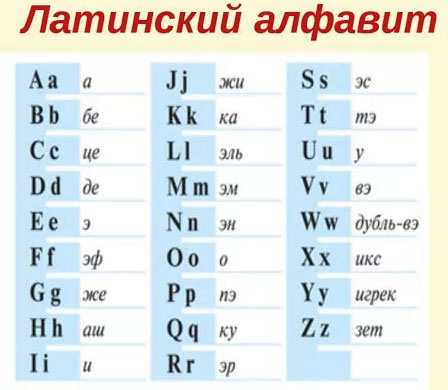
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.
Чаще всего используются буквы:
a, b, c, d, x, y, k, m, n
Алгоритм решения буквенного выражения
Алгоритм — значит, порядок, план выполнения команд.
1. Прочитать буквенное выражение
2. Записать буквенное выражение
3. Подставить значение неизвестного в выражении
4. Вычислить результат
Например, 28 – с
Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с
Подставим вместо неизвестного «с» число 4.
У нас получается выражение: 28 – 4
Вычисляем результат:
28 – 4 = 24
Переменные
Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства
c = 2, x = 3
Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:
2 + 3 + 2
Теперь мы можем найти значение этого выражения:
с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7
Советуем посмотреть:
Уравнения
Правило встречается в следующих упражнениях:
1 класс
Страница 8. Урок 5,
Петерсон, Учебник, часть 2
Страница 10. Урок 6,
Петерсон, Учебник, часть 2
Страница 11. Урок 6,
Петерсон, Учебник, часть 2
Страница 43. Урок 22,
Петерсон, Учебник, часть 2
Страница 49. Урок 25,
Петерсон, Учебник, часть 2
Страница 31. Урок 16,
Петерсон, Учебник, часть 3
Страница 35. Урок 18,
Петерсон, Учебник, часть 3
Страница 43. Урок 22,
Петерсон, Учебник, часть 3
Страница 44. Урок 23,
Петерсон, Учебник, часть 3
Страница 88. Урок 35,
Петерсон, Учебник, часть 3
2 класс
Страница 53,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 56,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 78,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 48. ПР 4. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 15,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 12. Урок 4,
Петерсон, Учебник, часть 3
Страница 15. Урок 5,
Петерсон, Учебник, часть 3
Страница 55. Урок 19,
Петерсон, Учебник, часть 3
Страница 75. Урок 28,
Петерсон, Учебник, часть 3
Страница 99. Повторение,
Петерсон, Учебник, часть 3
3 класс
Страница 104,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 3,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 13,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 29,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 7. Урок 3,
Петерсон, Учебник, часть 2
Страница 49. Урок 20,
Петерсон, Учебник, часть 2
Страница 53. Урок 21,
Петерсон, Учебник, часть 2
Страница 81. Урок 35,
Петерсон, Учебник, часть 2
Страница 82. Урок 35,
Петерсон, Учебник, часть 2
Страница 86. Урок 37,
Петерсон, Учебник, часть 2
4 класс
Страница 13,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 21,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 22,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 33,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 54,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 62,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 14,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 47,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 5. Урок 2,
Петерсон, Учебник, часть 1
5 класс
Задание 1291,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1841,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1845,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 260,
Мерзляк, Полонский, Якир, Учебник
Номер 292,
Мерзляк, Полонский, Якир, Учебник
Номер 432,
Мерзляк, Полонский, Якир, Учебник
Номер 544,
Мерзляк, Полонский, Якир, Учебник
Номер 1127,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 6,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 315,
Мерзляк, Полонский, Якир, Учебник
Номер 331,
Мерзляк, Полонский, Якир, Учебник
Номер 400,
Мерзляк, Полонский, Якир, Учебник
Номер 401,
Мерзляк, Полонский, Якир, Учебник
Номер 1063,
Мерзляк, Полонский, Якир, Учебник
Номер 1097,
Мерзляк, Полонский, Якир, Учебник
Номер 1099,
Мерзляк, Полонский, Якир, Учебник
Номер 1106,
Мерзляк, Полонский, Якир, Учебник
Задание 597,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1110,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 259,
Мерзляк, Полонский, Якир, Учебник
Номер 315,
Мерзляк, Полонский, Якир, Учебник
Номер 316,
Мерзляк, Полонский, Якир, Учебник
Номер 480,
Мерзляк, Полонский, Якир, Учебник
Номер 906,
Мерзляк, Полонский, Якир, Учебник
Номер 1071,
Мерзляк, Полонский, Якир, Учебник
Номер 1139,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 46,
Мерзляк, Полонский, Якир, Учебник
Номер 47,
Мерзляк, Полонский, Якир, Учебник
Номер 229,
Мерзляк, Полонский, Якир, Учебник
Номер 391,
Мерзляк, Полонский, Якир, Учебник
Номер 392,
Мерзляк, Полонский, Якир, Учебник
Чтобы составить задачу, которая приведёт к этим выражениям, например, с двумя неизвестными, нужно сначала поиграться с числами.
Берём две машины. Одна движется со скоростью 60 км/час, а вторая на 20 быстрее 80 км/час. У этих скоростей оптимальный общий множитель 48. Увеличиваем его в 10 раз получится 480 км.
Первой машине потребуется 8 часов, для преодоления этого расстояния, а второй 6 на 2 часа меньше. 480 км — это известное расстояние. Неизвестные величины — это скорость и время.
Напускаем туману. Определяемся, что скорость 1-й машины на 20 км/час меньше второй машины. Но вторая выехала на 2 часа позже и догнала первую на расстоянии 480 км. Задача готова. Нужно хитро задать вопрос. Например: Через какое время 2-я машина будет на расстоянии в 100 км от первой после из встречи.
Чтобы решить такую задачу потребуется составлять выражение. Принимать за «х» скорость первой или второй машины до встречи. За «у» время первой или второй машины также до встречи. Или обходиться одним «х», а можно и просто обойтись числами. Но это не для составителя. Составитель оперирует известными ему числами, а «решала» составляет выражения.
Конечно это интересно. Составить хитрую математическую задачку, и чтобы её не быстро решили. А выдёргивать с интернета любой может. Я составляю сама. Бывает до взрыва мозга, а не такую легкотню, как написала выше. Например вот эта: про курагу, чернослив и инжир.
Числовое выражение – это выражение, состоящее из чисел и знаков действий, а также скобок.
Пример №1. В каждом из этих выражений содержатся числа, между которыми есть знаки действий, а также бывают скобки. Это и есть числовые выражения.
- 256 : 2 + 315×5
- (181 – 19)×6 – 121:11
- 13,5 + 16 – 11
- 122 – 14×8,5
Если выполнить по порядку все действия, которые есть в числовом выражении, то получится определенное число, которое называют значением числового выражения. Порядок действий в числовых выражениях определяется правилами.
Важно!
Действия сложение и вычитание принято называть действиями первой ступени, а умножение и деление – действиями второй ступени. Возведение в степень – это действие третьей ступени.
Порядок действий в выражении, не содержащем скобки
Порядок действий без скобок
- При наличии действий одной ступени их выполняют по порядку слева направо.
- При наличии действий разных ступеней – выполнение начинается с высшей ступени (то есть с третьей).
Пример №2.
890 – 567 + 2340 – 124
в данном выражении действия одной ступени (сложение и вычитание), поэтому выполняем их по порядку слева направо:
- 890 – 567 = 323
- 323 + 2340=2663
- 2663 – 124=2539
Пример №3.
1260:20×3,7:10
в этом выражении также действия одной ступени (умножение и деление), поэтому выполняем их по порядку слева направо:
- 1260:20=63
- 63 3,7=233,1
- 233,1:10=23,31
Пример №4.
560:2 + 162 – 3×76,2
здесь присутствуют действия всех ступеней. Поэтому начинаем выполнять их с наивысшей ступени – возведения в степень. Затем слева направо выполняем деление и умножение, а затем слева направо – сложение и вычитание:
- 162=256
- 560:2=280
- 3 76,2=228,6
- 280+256=536
- 536 – 228,6=307,4
Порядок действий в выражении, содержащем скобки
Порядок действий со скобками
Если числовое выражение содержит скобки, то выполняют сначала действия в скобках, следуя правилу, а затем – действия за скобками.
Пример №5.
(3245 + 67,92:2)×3 + (126×2 – 321:3) – 125
здесь числовое выражение содержит скобки, поэтому действия выполняем в скобках слева (деление, затем сложение), затем в скобках справа (умножение, деление, вычитание):
- 67,92:2=33,96
- 3245+33,96=3278,96
- 126×2=252
- 321:3=107
- 252-107=145
Теперь выполняем действия за скобками слева направо (умножение, сложение, вычитание):
- 3278,96×3=9836,88
- 9836,88+145=9981,88
- 9981,88 – 125=9856,88
Буквенные выражения. Числовое значение буквенного выражения.
Какие выражения называют буквенными?
Выражения, содержащие не только числа и знаки действий, но и буквы, называют буквенными. Буквы также можно называть «переменная». Обращаем внимание на то, что знак «умножить» между числом и буквой не пишется.
Пример №6. Примеры буквенных выражений:
- 5х + 6у
- 18 + a + b
- 12с – 11
- m + n
- (x + n) – 11m
Числовое значение буквенного выражения
Числовое значение буквенного выражения – это значение числового выражения, полученного при подстановке конкретных значений переменной в данное выражение.
Пример №7. Найдем значение выражения с + х при с=23, х=0,17. Для этого подставим вместо с и х их данные числовые значения и получим числовое выражение 23 + 0,17. Теперь вычислим результат и получим 23,17. Таким образом, числовое значение буквенного выражения с + х равно 23,17.
Пример №8. Найдем значение выражения 11х +(с – d) при х=10, c=178, d=121. Для этого подставляем вместо каждой переменной соответствующие числовые значения и получим числовое выражение 11×10 + (178 – 121). Выполнив действия, получим ответ 167. Это и есть числовое значение буквенного выражения.
Заметим, что и числовые и буквенные выражения можно называть еще как алгебраические выражения.
Задание OM2001
Найти значение выражения 41a – 11b + 15, если 4a−9b+39a−4b+3=5
Для начала преобразуем нашу дробь, которая дана по условию. Применим правило пропорции, умножив на 5 знаменатель данной дроби:
4a−9b+39a−4b+3=5
5(9а – 4b + 3)=4a – 9b+3
Раскроем скобки и перенесем слагаемые с буквами а и b влево, а свободные члены вправо (не забывая изменять при переносе знаки на противоположные):
45a – 20b +15 =4a – 9b+3
45a – 20b – 4a + 9b=3 – 15
Приведем подобные слагаемые:
41a – 11b = – 12
Выпишем выражение, значение которого надо найти: 41a – 11b + 15 и заменим в нем 41a – 11b на число -12, полученное при упрощении нашей дроби:
41a – 11b + 15= – 12 + 15=3. Видим, что значение нашего выражения получилось равным 3.Ответ: 3
pазбирался: Даниил Романович | обсудить разбор
Задание OM1301o
Найдите значение выражения: (x + 5)2 — x (x- 10) при x = — 1/20
В данном случае необходимо сначала упростить выражение, для этого раскроем скобки:
(x + 5)2 – x (x – 10) = x2 + 2 • 5 • x + 25 – x2 + 10x
Затем приведем подобные слагаемые:
x2 + 2 • 5 • x + 25 – x2 + 10x = 20 x + 25
Далее подставим x из условия:
20 x + 25 = 20 • (-1/20) + 25 = – 1 + 25 = 24
Ответ: 24
pазбирался: Даниил Романович | обсудить разбор
Задание OM0703o
На координатной прямо отмечены числа a и b:
Какое из приведенных утверждений для этих чисел неверно:
- ab²<0
- a — b > 0
- a + b < 0
- ab < 0
Для удобства решения необходимо оценить данные нам числа. Из координатной прямой видно, что a > 0, так как расположено справа от ноля, а b < 0, так как расположено слева. К тому же, b значительно более удалено от ноля, а значит больше по модулю.
Для удобства, исходя из вышеизложенных рассуждений, примем a = 1, а b = -2.
Теперь подставим значения в данные неравенства:
- ab²<0
1 • (-2)² = 4 > 0
Значит, утверждение неверно.
- a — b > 0
1 — (-2) = 3 > 0
Утверждение верно.
- a + b < 0
1 + (-2) = -1 < 0
Утверждение верно.
- ab < 0
1 • (-2) = -2 < 0
Утверждение верно.
Следовательно, правильный ответ первый.
Ответ: ab²<0
pазбирался: Даниил Романович | обсудить разбор
Алла Василевская | Просмотров: 6.2k