Инфоурок
›
Математика
›Презентации›ЕГЭ, ОГЭ 2015.Как составить свой тренировочный вариант с сайта «Решу ЕГЭ» с решением
Скачать материал

Скачать материал


- Сейчас обучается 75 человек из 34 регионов


- Сейчас обучается 26 человек из 17 регионов


- Сейчас обучается 30 человек из 12 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Составление своего тренировочного варианта ЕГЭ с сайта «РЕШУ ЕГЭ»
Инструкцию составила Волкова Н.В.
МБОУ СОШ № 37
Г. Смоленск -
-
-
-
-
-
-
-
-
Краткое описание документа:
В презентации показано как составить вариант ЕГЭ по всем школьным предметам, и сообщив №варианта учащимся, учащиеся выполняют его, а система проверит этот вариант и пришлёт вам результат!Останется только поставить оценки
Инструкция по составлению своего варианта ЕГЭ:
1.Зарегистрируйтесь на сайте «Решу ЕГЭ».
2.Щёлкнете левой кнопкой мыши 1 раз по названию своего предмета
3.ЛКМ «Каталог» и запишите номера какие вы хотите видеть в будущей работе.
4.На главной странице левой кнопкой мыши (ЛКМ)1 раз нажать «Учителю)(панель слева).
5.ЛКМ «Создать тест из подобранных заданий»
6.Лкм «Создать пустую контрольную работу».
7.Навести курсор на заголовок и написать его.
8.Написать инструкцию
9.Сохранить заголовок и инструкцию.
10.Написать в окошко «Добавить» выбранный номер», если надо и ещё аналогично набрать номера в окошечке, предварительно удаляя прежний номер.(номер варианта сообщить учащимся)
11.Зайти на страницу «учителю»,
12.ЛКМ нажать вариант
13.ЛКМ «ВЕРСИЯ ДЛЯ ПЕЧАТИ».
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 263 017 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 11.02.2015
- 2238
- 21
Рейтинг:
4 из 5
- 11.02.2015
- 7713
- 78
- 11.02.2015
- 1291
- 0
- 11.02.2015
- 858
- 1
- 11.02.2015
- 1271
- 1
- 11.02.2015
- 1519
- 1
- 11.02.2015
- 695
- 0
-
Настоящий материал опубликован пользователем Волкова Нина Владимировна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 8 лет и 4 месяца
- Подписчики: 0
- Всего просмотров: 51601
-
Всего материалов:
15
ЕГЭ по математике профильного уровня — один из самых сложных экзаменов. Планируете сдавать его, но не знаете, с чего начать? Этот экзамен не покажется вам таким трудным, если вы узнаете про него побольше и грамотно подготовитесь. В этой статье обсудим, что нужно знать про ЕГЭ по математике 2023, из каких разделов он состоит и как к нему подготовиться.
В этой статье:
Какие темы важно знать для ЕГЭ по математике 2023?План успешной подготовки к ЕГЭ по математике 2023Как решать часть с кратким ответомЗадания с развернутым ответом: немного статистикиОсобенности уровней ЕГЭ по математикеСтруктура ЕГЭ по математике 2023Разделы ЕГЭ по математикеКакие задания входят в ЕГЭ по математике?
До ЕГЭ все меньше времени, и 11-классники уже на финишной прямой. Усилить подготовку и написать на максимальный балл поможет «ЕГЭ-гонка» 🏁 На экспресс-марафоне вы повторите ключевые разделы предмета, прорешаете множество заданий и попробуете симуляцию экзамена, а также узнаете все секреты ЕГЭ-2023 от преподавателей, написавших работу в досрочный период. Записывайтесь на марафон и придите первыми в гонке ЕГЭ!
Какие темы важно знать для ЕГЭ по математике 2023?
В математике, как и в любом предмете, есть опорные темы. Если вы их выучите, будет легче справиться с экзаменом.
Формулы тригонометрии
Очень важно знать формулы тригонометрии и уметь применять их. Хорошая новость: в справочных материалах можно найти несколько тригонометрических формул.
Но формул гораздо больше. Я советую не зубрить их, а научиться выводить: приходить к формулам шаг за шагом, опираясь на тождества. Кстати, мы учим выводить формулы на курсах подготовки к ЕГЭ: это полезно, чтобы оказаться на экзамене во всеоружии и ничего не перепутать.
Квадратные уравнения
Эти уравнения мы учимся решать еще в 7 классе. Они встречаются в ЕГЭ по математике постоянно: и как самостоятельные задания, и внутри более сложных уравнений или неравенств. Квадратные уравнения могут встретиться в математических моделях № 9 и № 15, в задачах на геометрию и стереометрию, в задании № 17 с параметром.
Самое главное — хорошо знать универсальные методы решения. Первый — через формулу дискриминанта, второй — через теорему Виета, которая может сэкономить время на экзамене.
Треугольники
Эта замечательная тема, которую проходят в 7 классе — основа основ всей геометрии. Она нужна и для решения стереометрии, и для простейших планиметрических задач. Еще треугольники необходимы, чтобы освоить огромное количество теорем. Выучите все, что с ними связано! Особое внимание обратите на прямоугольные треугольники, которые встречаются чаще остальных — тогда геометрические задачи сразу станут проще.
Проценты
Самая нелюбимая тема моих учеников после тригонометрии, которую необходимо хорошо знать. Проценты нужны для реальной математики — это № 9 (с кратким ответом) и № 15 (с развернутым ответом). Понимание этой темы может принести вам 3 первичных балла.
План успешной подготовки к ЕГЭ по математике 2023
Если вы хотите получить больше 80 баллов на ЕГЭ, нужно идеально решать часть с кратким ответом, а также справляться с большинством заданий с развернутым ответом.
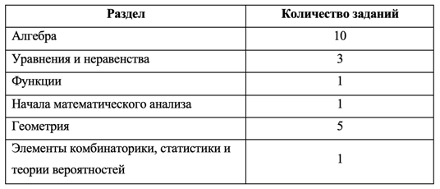
Чтобы постепенно прорабатывать материал, воспользуйтесь кодификатором. В нем обратите внимание на таблицу 2, а именно на блоки:
- Алгебра
- Уравнения и неравенства
- Элементы комбинаторики, статистики и теории вероятностей
- Функции
- Начала математического анализа
- Геометрия
Ориентируйтесь на указанную последовательность, но геометрию изучайте параллельно с остальными блоками — на нее нужно больше времени.
Самое главное — ни в коем случае не ограничивайтесь теорией. Ее у вас не спросят на экзамене, а вот задания решать придется. Поэтому тренируйте практические навыки: актуальные задания вы сможете найти в открытом банке заданий на сайте ФИПИ или в нашем тренажере «Решутест».
Как решать часть с кратким ответом
Ни в коем случае не пренебрегайте частью с кратким ответом! Иначе будет обидно: например, вы наберете за экономическую задачу № 15 полные 2 балла, но потеряете их в двух заданиях первой части. Это актуально для всех ЕГЭ: подробнее о том, как идеально справляться с первой частью экзамена, читайте здесь.
Еще одно заблуждение: «часть с кратким ответом простая, к ней можно не готовиться». Даже в первой части иногда встречаются такие задания, которые ученики даже не решают, потому что не готовились к ним.
Как я уже говорила, часть с кратким ответом содержит 11 заданий. Начинать подготовку необходимо именно с заданий базового уровня сложности, потому что это та основа, на которую потом накладывается более сложная теория.
Что касается задач повышенного уровня сложности, то среди каждого номера есть лайфхаки, например, в этой статье я уже рассказывала про № 11, в котором нужно работать с производной.
Задания с развернутым ответом: немного статистики
Многие думают, что эта часть ЕГЭ по математике очень сложная. Поэтому ребята, которые не рассчитывают на высокие баллы, даже не приступают к ней. И очень зря! С помощью этих заданий можно заработать дополнительные баллы и побороться за высокое место в рейтинге.
Сейчас будет немного статистики. В среднем около 35% учеников получают полные 2 балла за решение № 12, а вот неравенство № 14 дается хуже, только около 12% с ним справляются на полный балл. Геометрия даётся ещё хуже: стереометрию № 13 полностью решают 2% выпускников, планиметрию (№ 16) менее 5%. А вот с экономической задачей (№ 15) справляются около 20%, а это целых 2 балла! Что касается № 17 и 18, то они даются ещё хуже, но на то они и самые сложные, хотя 1 балл за № 18 по статистике получают около 25% сдающих — там нужно просто привести пример.
Особенности уровней ЕГЭ по математике
В 2015 году ЕГЭ по математике разделили на базовый и профильный уровни. Это упростило жизнь выпускникам, которые не планируют поступать на специальности, связанные с математикой. Если ЕГЭ по математике нужен только для получения аттестата, можно сдать его облегченную версию, оставив время и силы для профильных экзаменов.
Базовый уровень ЕГЭ по математике
Как устроен базовый ЕГЭ по математике? Экзамен идет 180 минут, он состоит из 21 задания, за каждое из которых можно получить 1 балл. Этот экзамен единственный, который переводится не в 100-бальную систему, а в оценки.
В ЕГЭ по математике базового уровня 6 тематических блоков:
Также обратите внимание, что базовый ЕГЭ по математике не поменялся с точки зрения наполнения, изменился лишь порядок заданий. Вот что пишут ФИПИ:
Подробнее про базовый ЕГЭ по математике, включая разбор всех заданий, читайте здесь, а мы перейдём к профильному.
Профильный уровень ЕГЭ по математике
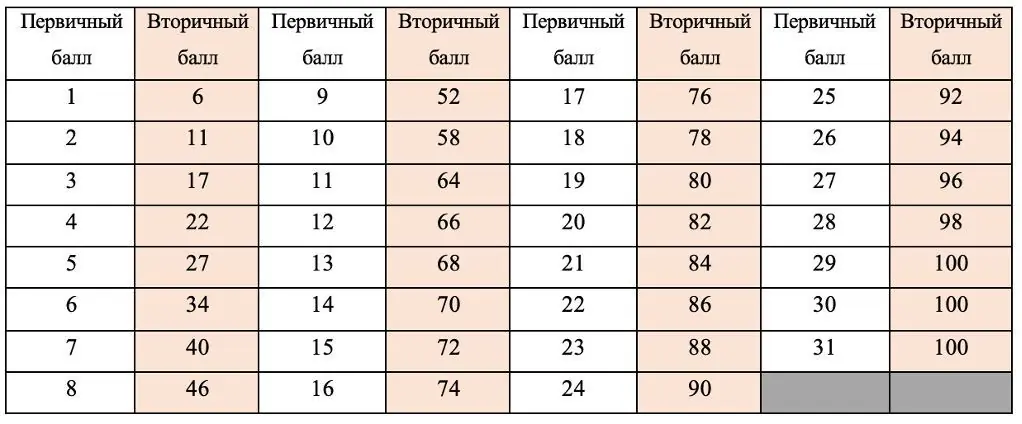
Данный экзамен, как и остальные ЕГЭ, переводится в 100-бальную систему:
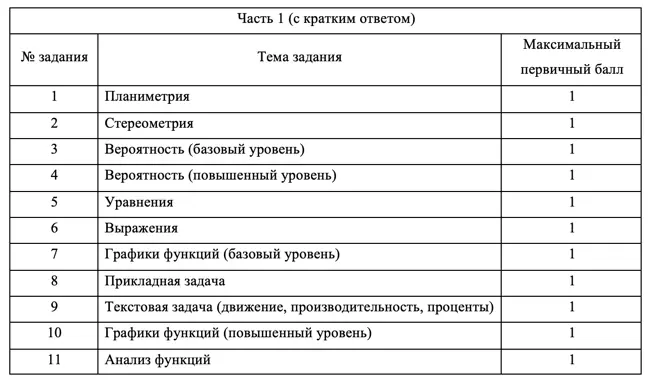
Экзамен состоит из двух частей: Часть 1 с кратким ответом, а Часть 2 — с развернутым. Длится он 235 минут. Всего есть 18 заданий, которые разделены на 3 блока: алгебра, геометрия и реальная математика. Максимальное количество первичных баллов — 31.
Структура ЕГЭ по математике 2023
Часть 1:
- Приносит 11 баллов, то есть 35% всего экзамена
- 11 заданий с кратким ответом
Часть 2:
- Приносит 20 баллов, то есть 65% всего экзамена
- 7 заданий с развернутым ответом
Внимание! Вся нумерация заданий в статье соответствует ЕГЭ 2023 года.
В заданиях с кратким ответом нужно лишь записать верное число в бланк. Заданий с развернутым ответом 7, в них нужно подробно расписать решение, которое должно соответствовать критериям оценивания.
ЕГЭ — стандартизированный экзамен, поэтому каждое задание всегда соответствует определенной теме.
Обратите внимание, что по сравнению с 2022 годом, в части 1 изменился только порядок заданий. Сами сотрудники ФИПИ говорят следующее:
Задания с кратким ответом принесут вам до 11 первичных баллов (64 вторичных). Если не понимаете, что это за баллы и откуда они берутся, почитайте эту статью. Самая популярная цель на ЕГЭ по математике — набрать 80 баллов, для этого раньше было необходимо 19 первичных баллов. Ранее многие ученики пользовались рабочей стратегией — решить всю часть с кратким ответом, а также № 12, 14 и 15. Если хорошо разбирались в геометрии, выбирали № 13 и 16 — или использовали их как запасные задания. Сейчас стратегия должна быть другая, так как № 13 (стереометрия) стал стоить дороже — 3 балла вместо 2, а № 15 (экономическая задача) — подешевел с 3 баллов до 2. Изменилась также шкала перевода баллов, поэтому подумайте, какими заданиями вы сможете набрать необходимое количество первичных баллов.
Разделы ЕГЭ по математике
- Алгебра и начала анализа — 8 заданий, 13 первичных баллов
- Геометрия — 4 задания, 8 первичных баллов
- Реальная математика — 6 заданий, 10 первичных баллов
Какие задания входят в ЕГЭ по математике?
Здесь вам на помощь приходят документы с официального сайта ФИПИ: кодификатор, демоверсия и спецификация.
- Кодификатор — это краткий перечень всех блоков и тем, которые включены в экзамен.
Сейчас кодификатор общий для обоих уровней экзамена, как базового, так и профильного. Он снова представляет собой единый документ, так что не запутаетесь.
- Демоверсия — типовой вариант ЕГЭ. Он показывает уровень экзамена и ориентировочную сложность заданий.
- Спецификация — это документ, описывающий структуру экзамена и разбалловку.
Подготовка к ЕГЭ по математике
Из каких частей состоит ЕГЭ по математике в 2023 году
Математика — один из двух обязательных предметов на ЕГЭ. Но, в отличие от русского языка, эта дисциплина предлагает 2 уровня сложности: профильный и базовый. Какий именно вариант выбрать, зависит от вашей цели. Если вуз, в который вы хотите поступить, требует профильного уровня, нужно сдавать его. Обычно это касается технических специальностей.
Для получения аттестата выпускникам школ хватит и базового. Но финальное решение за вами. Если вы хотите сдать профильный вариант, просто чтобы проверить свои знания и уровень подготовки, — дерзайте!
Структура базового уровня ЕГЭ по математике
Базовый уровень проверяет основные знания школьника по математике. Такой экзамен не делится на части: в него входит только 21 задание с кратким ответом. Ответом может быть целое число, десятичная дробь или ряд цифр. По уровням сложности задания экзамена тоже не делятся — все задачи в нем базового уровня. Чтобы выполнить такую работу, ученику дают 180 минут.
Структура профильного уровня ЕГЭ по математике
Варианты профильного уровня проверяют основные и углубленные знания школьника. В 2023 году ЕГЭ состоит из 2 частей:
-
1-я часть: 11 задач с кратким ответом;
-
2-я часть: 7 задач с развернутым ответом.
В первой части ответом может быть целое число, десятичная дробь или ряд цифр. Во второй части — полное обоснованное решение и ответ. Чтобы выполнить задания экзамена, школьнику дают 235 минут.
Задачи ЕГЭ по математике профильного варианта делятся на категории по уровням сложности. В таблице ниже можно увидеть, как именно.
| Базовый | 6 |
| Повышенный | 10 |
| Высокий | 2 |
| Всего | 18 |
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Как сдать ЕГЭ по математике: разбор сложных задач
Экзамен по математике не зря считают одним из самых трудных. Даже в заданиях базового варианта можно легко ошибиться по невнимательности. Что уж говорить о действительно сложных задачах с полным решением, где много «подводных камней»? Чтобы вы знали, как подготовиться к ЕГЭ по профильной математике, мы разобрали несколько из них.
Задание 16
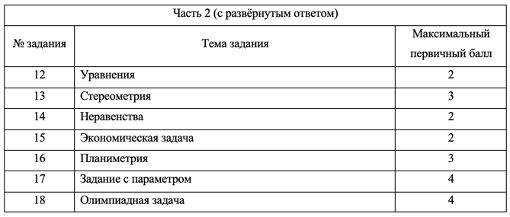
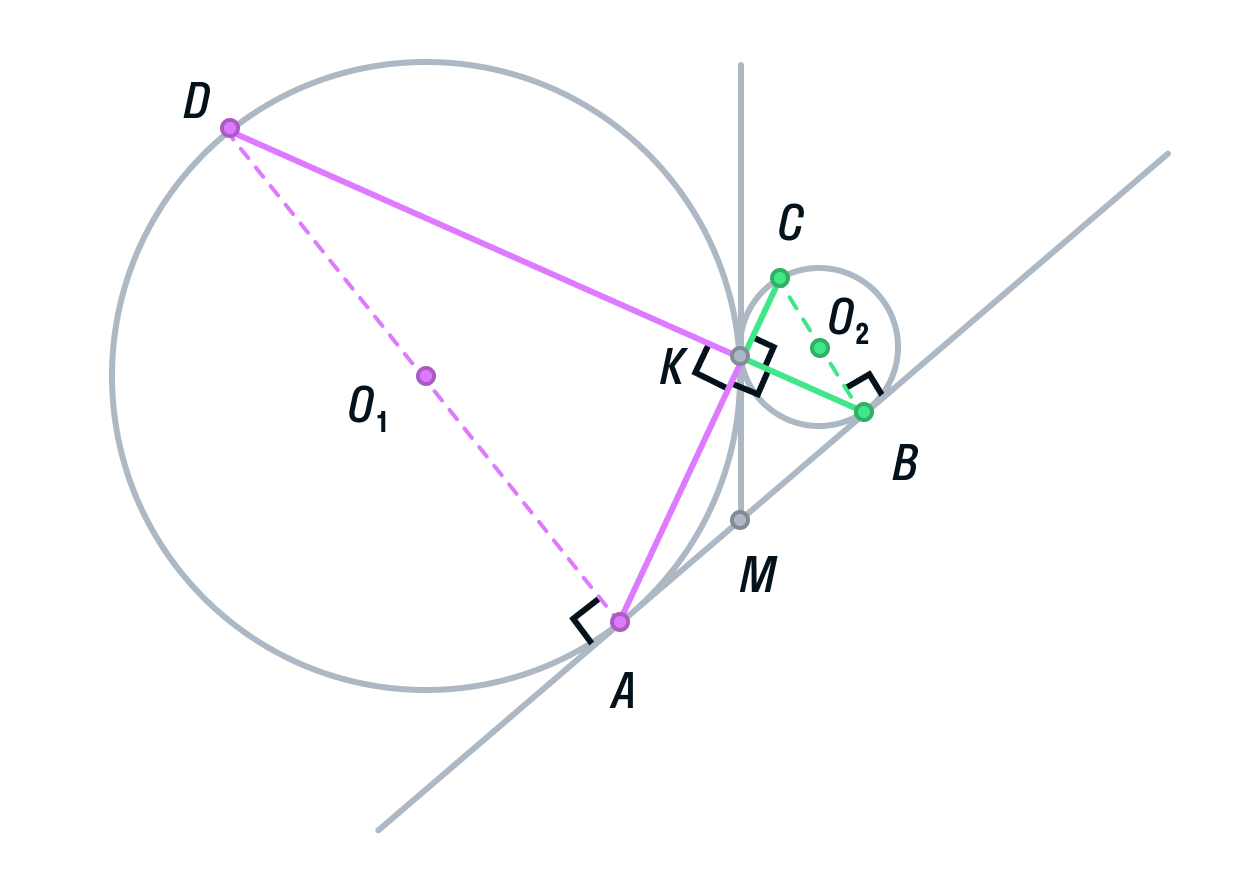
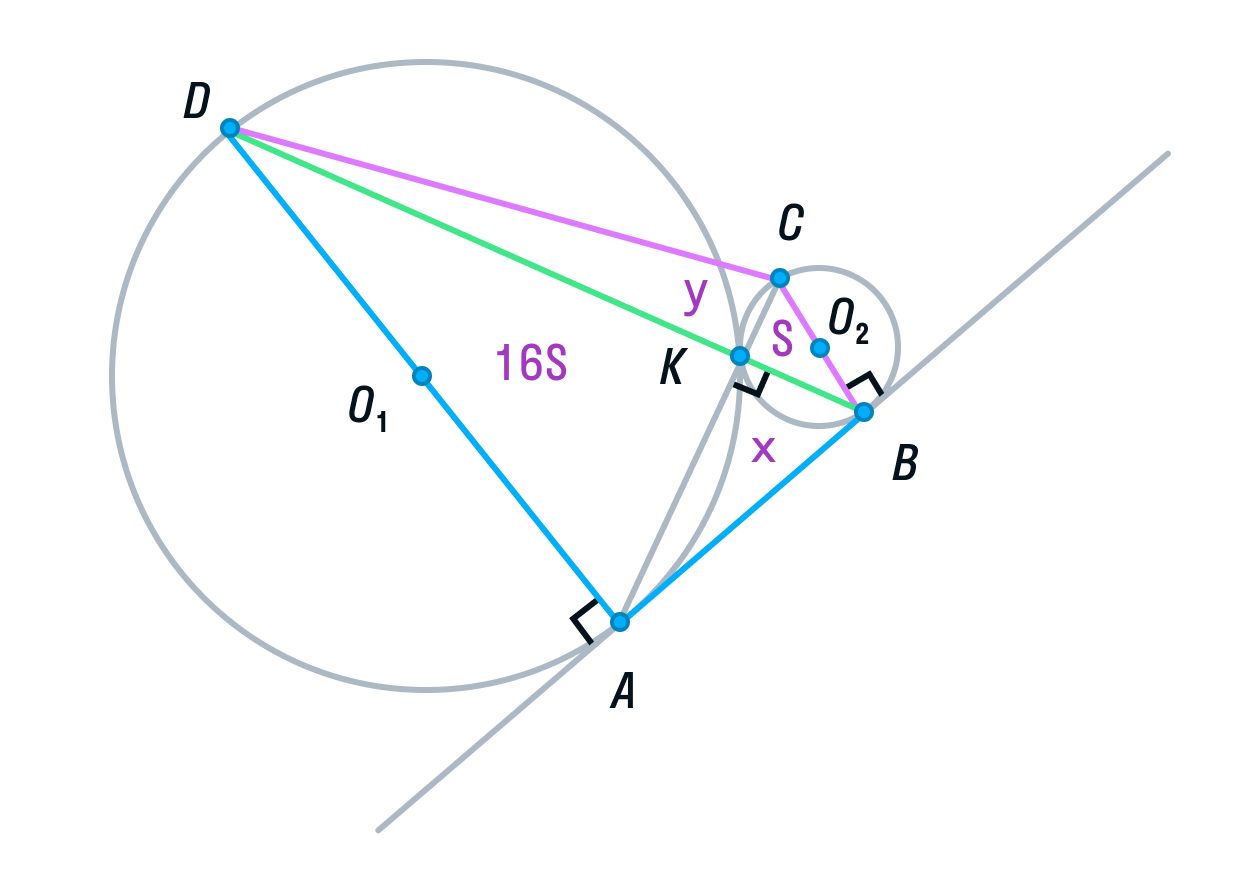
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Совет
Для этого задания советуем повторить темы:
-
Касательные к окружности и их свойства.
-
Свойства вписанных углов.
-
Взаимное расположение окружностей.
-
Свойства прямоугольного треугольника.
-
Признаки и свойства параллельных прямых.
-
Подобные треугольники, площади подобных фигур.
-
Свойство площадей (в частности: отношение площадей треугольников с одинаковой стороной).
-
Трапеция, её свойства. Площадь трапеции.
-
Теорема Пифагора.
Проследите, чтобы они были в вашем плане подготовки к профилю ЕГЭ по математике.
Решение
а) Выполним построение.
-
Окружности с центрами О1 и О2 соответственно касаются друг друга в одной точке К.
-
Прямая АВ касается обеих окружностей в точках А и В соответственно.
-
Прямые АК и ВК пересекают окружности в точках С и D соответственно
-
Пусть общая касательная окружностей в точке К, пересекает прямую АВ в точке М.
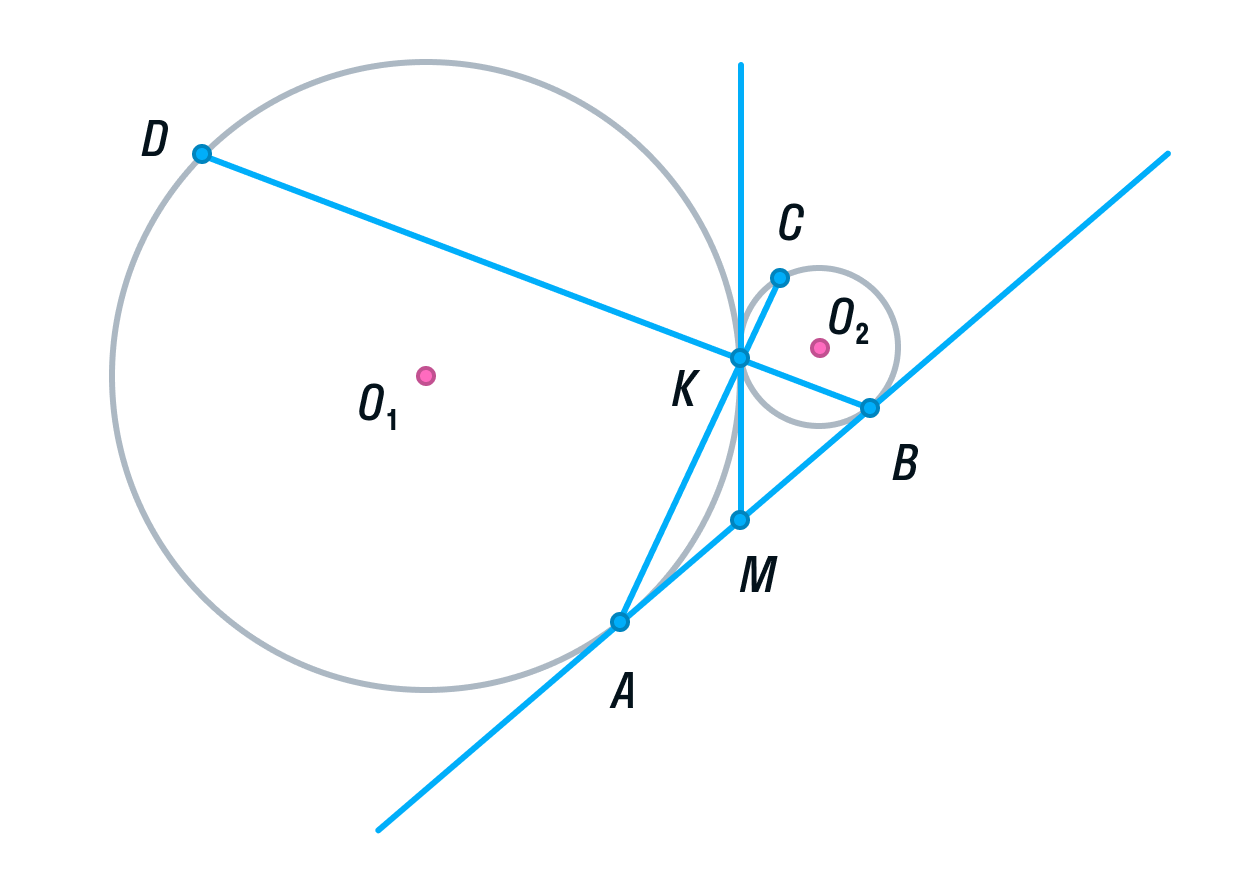
Тогда по свойству касательных, проведенных из одной точки, AM = KM и KM = BM.
-
Рассмотрим треугольник АВК. Его медиана АМ равна половине стороны, которую она разбивает. Следовательно, делаем вывод, что треугольник АВК прямоугольный, а угол К = 90°.
-
Вписанный угол AKD является смежным углом АКВ, а значит, он тоже 90° как прямой. Следовательно, угол AKD опирается на диаметр AD. Значит, AD ⊥ AB, так как радиус, а в данном случае диаметр, перпендикулярен касательной в точке касания.
-
Аналогично рассмотрев угол ВКС, получим, что BC⊥ AB.
-
Прямые AD и ВС перпендикулярны третьей прямой АВ, следовательно, прямые AD и BC параллельны. Ч. т. д.
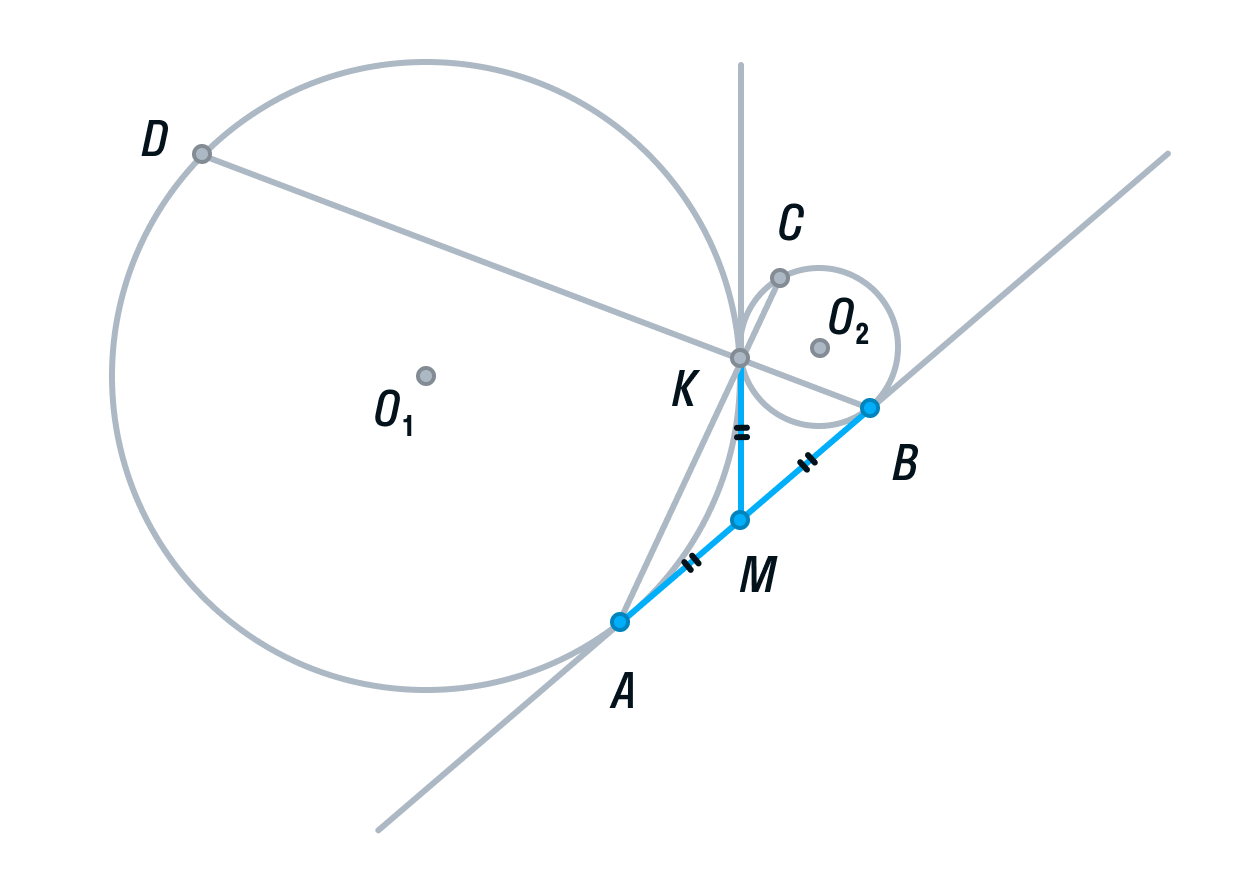
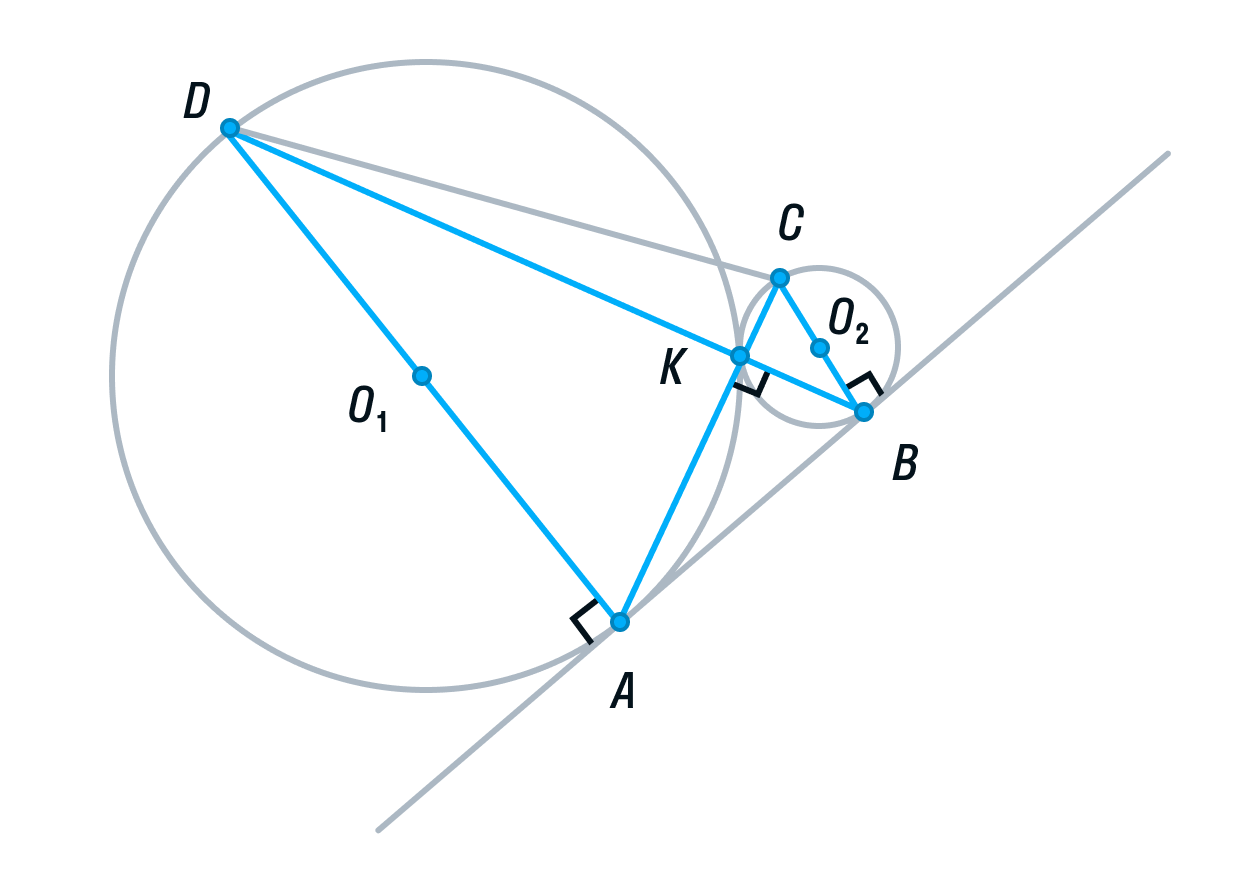
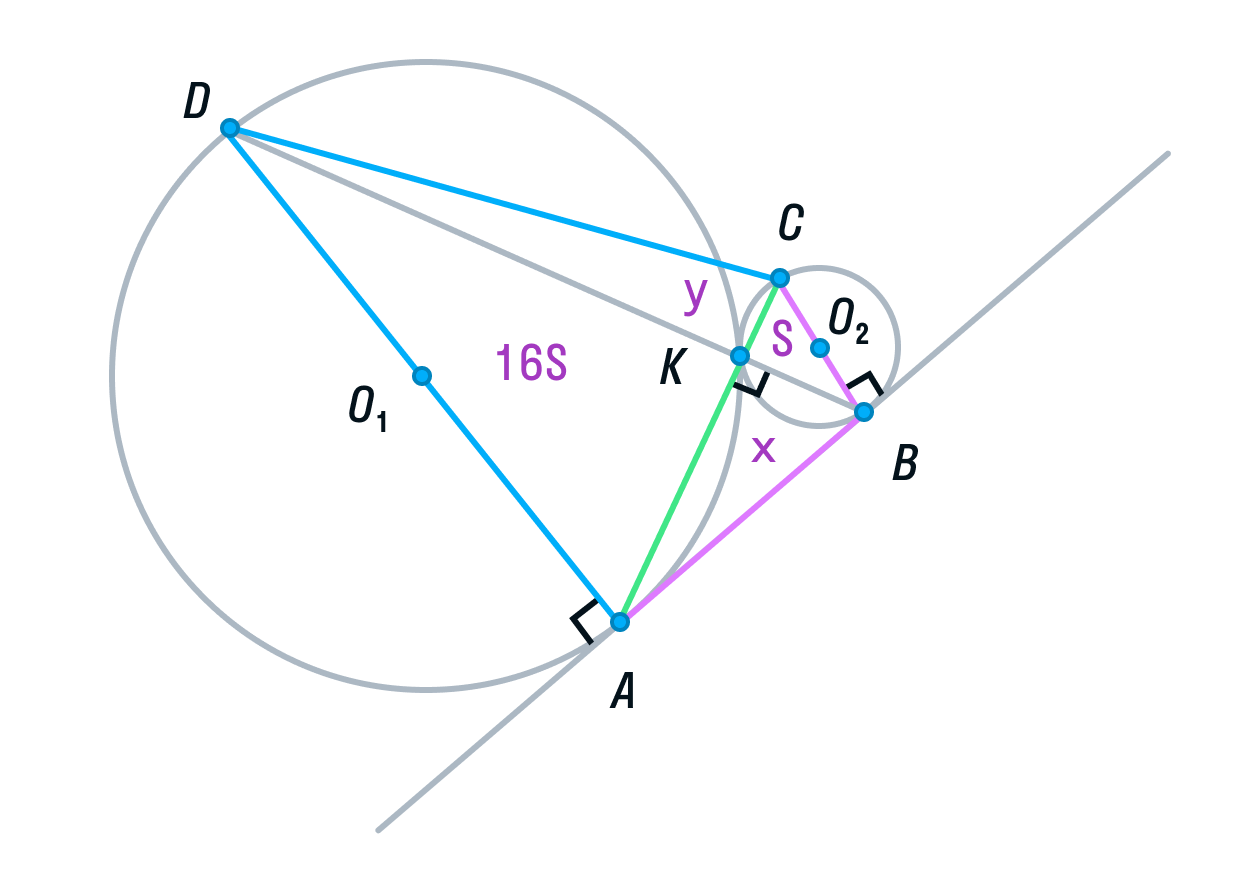
б) Пусть радиус первой окружности равен 4, а радиус второй окружности равен 1. Тогда АD = 8, ВС = 2.
-
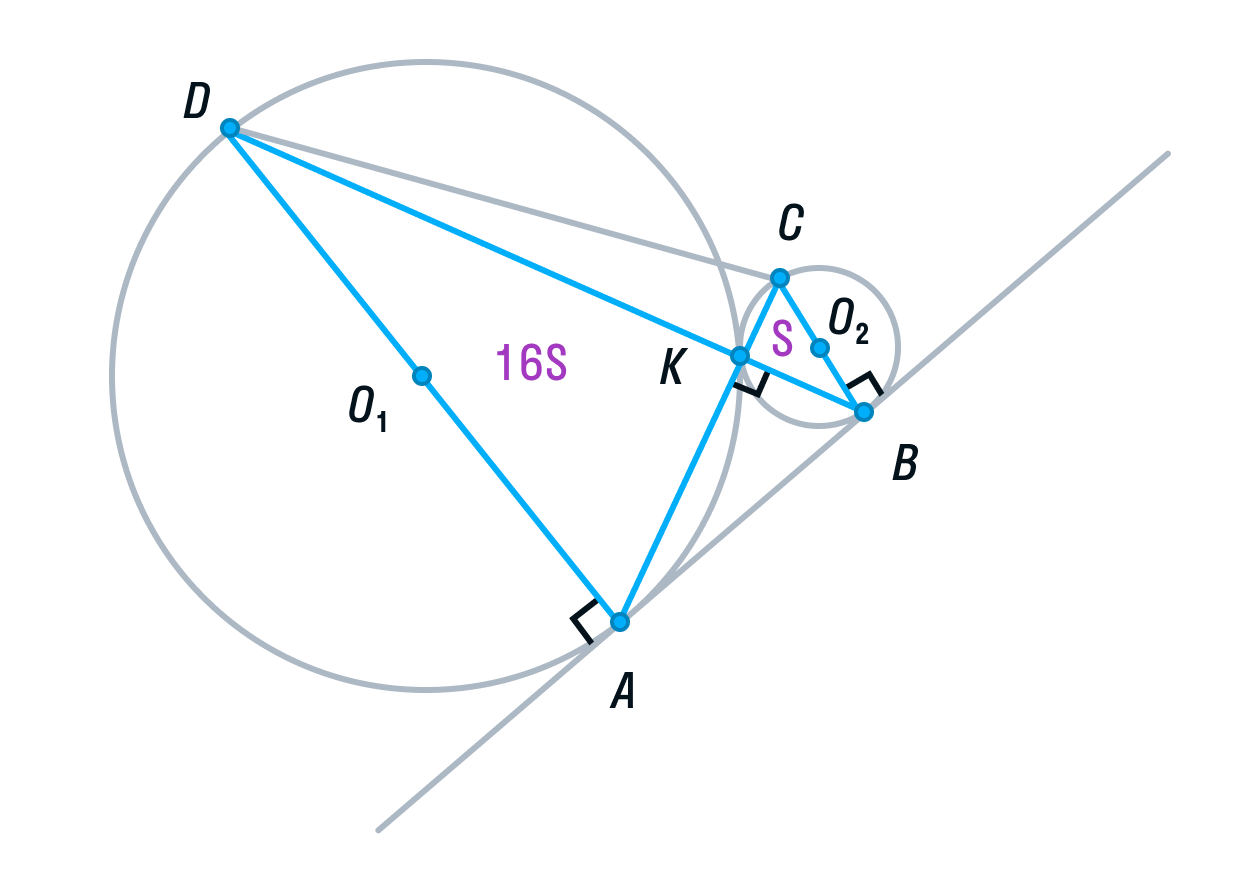
Рассмотрим треугольники ADK и СВК. Они подобны, т. к. имеют два равных угла (К – вертикальный, С и А — накрест лежащие). Из подобия треугольников следует, что их площади относятся как коэффициент подобия в квадрате:
-
Обозначим площадь треугольника СВК за S, тогда площадь треугольника ADK будет равна 16S.
-
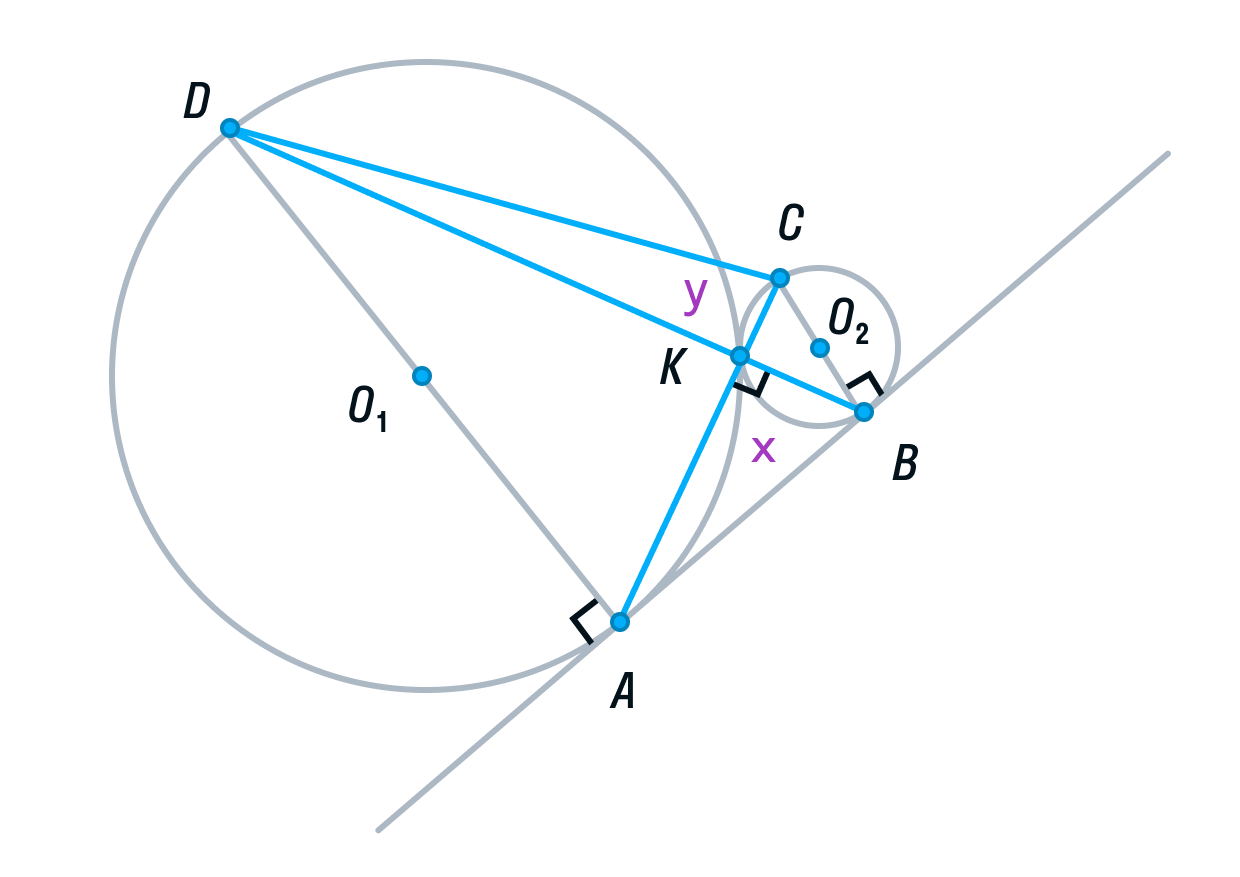
Пусть площади треугольников АВК и CDK будут равны х и у соответственно.
-
Вспомним свойство, связывающее высоты треугольников с общим основанием и получим следующие равенства: DB — общая сторона треугольников ADB и СDB, следовательно:
(равно 4 из подобия треугольников ADK и СВК, см. выше),
-
Аналогично, AC — общая сторона треугольников ADС и ABC, следовательно,
(равно 4 из подобия треугольников ADK и СВК, см. выше),
-
Решим полученную систему уравнений:
-
Из первого уравнения
подставим во второе и найдем y.
следовательно,
подставим во второе и найдем y.
-
Площадь ABCD равна 16S + 4S + 4S + S = 25S.
-
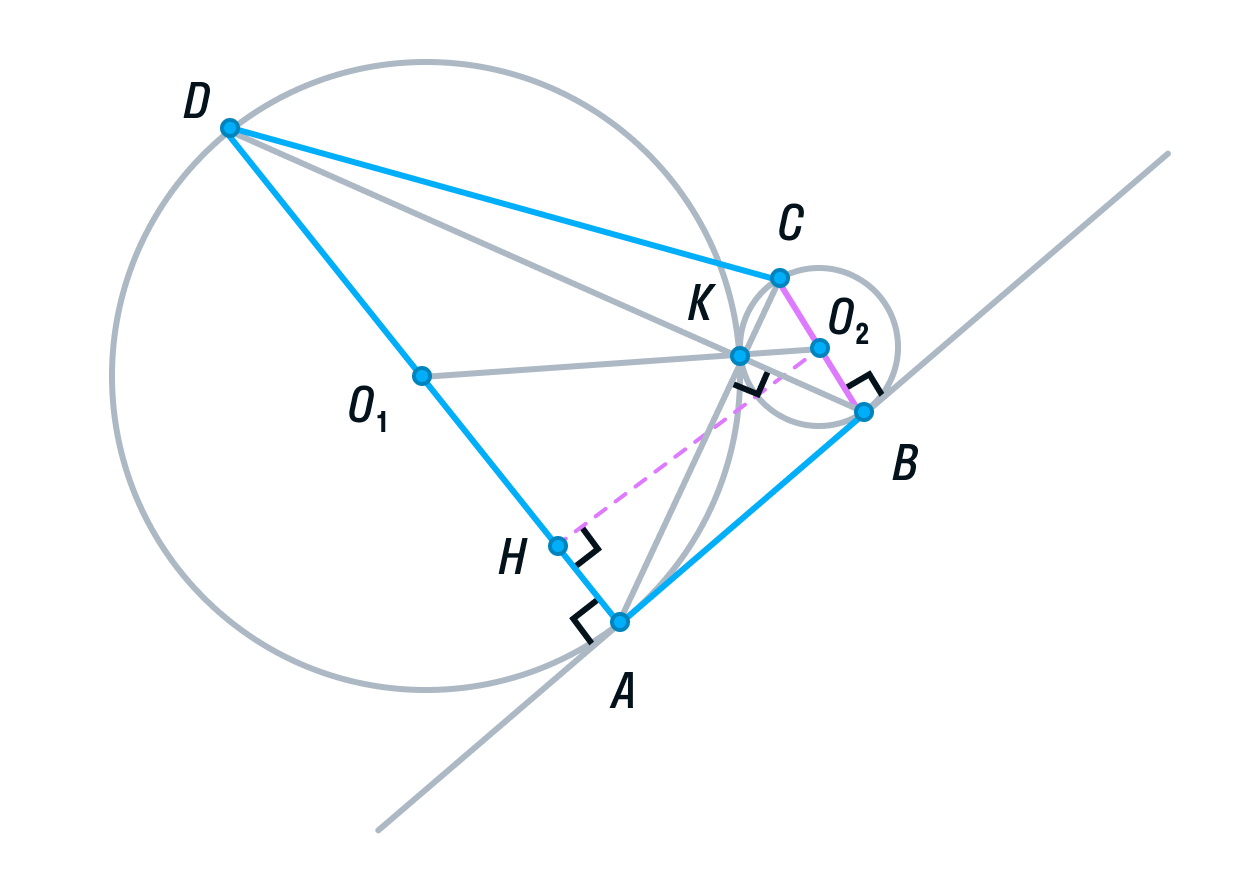
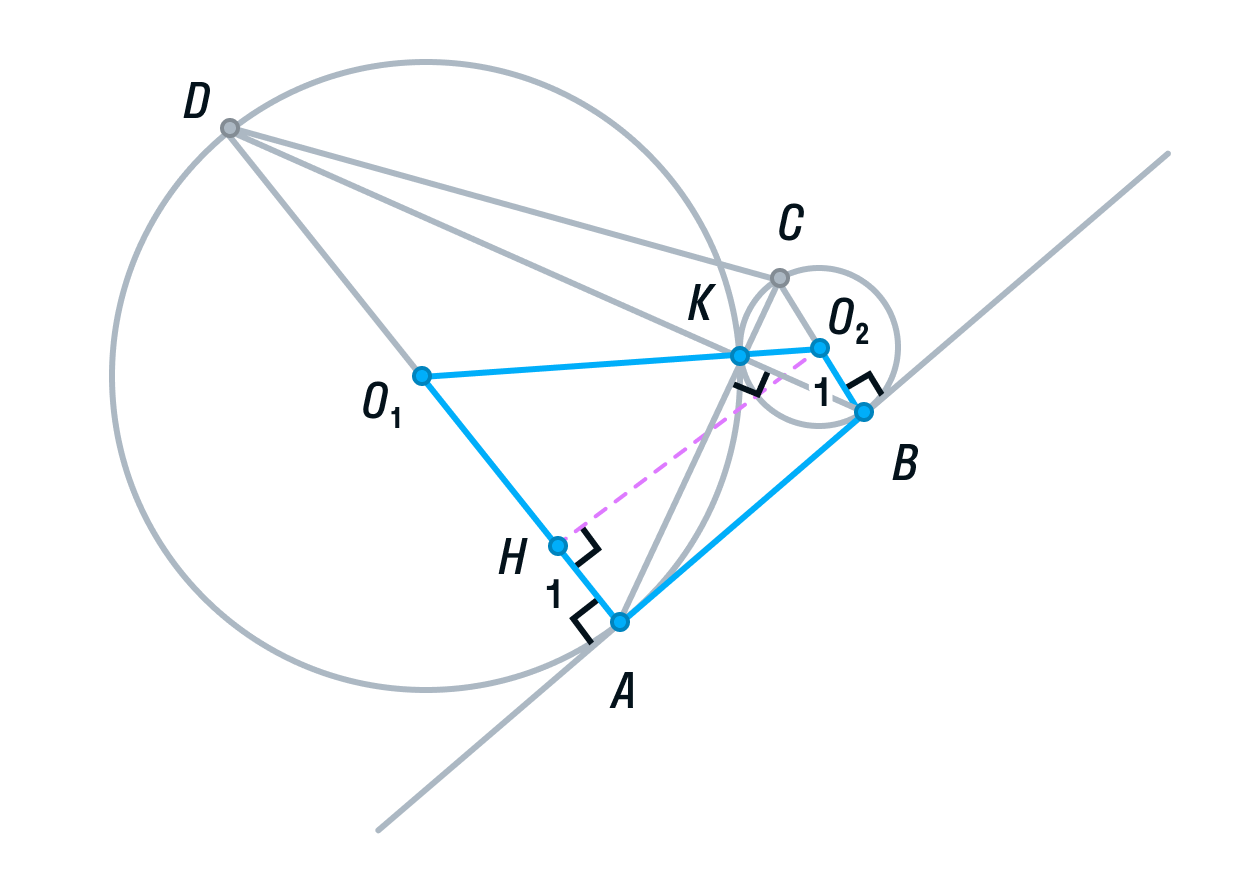
Заметим, что ABCD — прямоугольная трапеция (AD||BC, AB — перпендикулярна основаниям). Для вычисления ее площади нужно полусумму оснований умножить на высоту.
-
Для того, чтобы найти высоту, рассмотрим меньшую трапецию AO1O2B.
Ее основания равны 1 и 4, так как О2В и О1А — радиусы. O1O2 = 5, так как О2К и О1К — радиусы. О2H — высота трапеции AO1O2B.
-
По теореме Пифагора найдём О2H:
-
Вычислим площадь трапеции ABCD:
-
С другой стороны мы нашли
Отсюда S = 0,8.
-
Площадь треугольника АКВ = 4S, следовательно,
Ответ: 3,2.
Задание 18
В школах № 1 и № 2 учащиеся писали тест. В каждой школе тест писали по крайней мере 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешел из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе № 1 уменьшиться в 10 раз?
б) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 7?
в) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
Совет
Чтобы справиться с этой задачей, нужно повторить темы:
-
Понятие натурального и целого числа.
-
Среднее арифметическое.
-
Делимость чисел.
-
Процент. Нахождение процента от числа, уменьшение числа на заданный процент.
-
Составление и решение линейных уравнений.
Добавьте их в ваш план подготовки к ЕГЭ по математике, если собираетесь сдавать профиль.
Решение:
а)
-
Допустим, что в школе № 1 писали тест 2 учащихся, один из них набрал 1 балл, а второй набрал Х баллов и перешёл в другую школу. Тогда средний балл в школе был равен (1 + Х) : 2 = 10, а стал равен 1, т. е. уменьшился в 10 раз.
-
Решим уравнение и получим Х = 19 — натуральное число. Следовательно, наше предположение верно.
-
Или мы можем предположить другой вариант: что один учащийся набрал 2 балла. Тогда средний балл изначально равняется 20, а после ухода второго станет 2, т. е. изменится в 10 раз.
-
Решим уравнение (2 + Х) : 2 = 20, отсюда Х = 38 — натуральное число, что тоже удовлетворяет условию задачи.
Ответ: средний балл в школе № 1 мог уменьшиться в 10 раз.
б)
-
Пусть в школе № 2 писали тест m учащихся, n — сумма баллов m учащихся, средний балл равнялся B, а перешедший в неё учащийся набрал u баллов.
-
Умножим обе части полученного уравнения на 10, получим:
-
По условию B = 7, тогда получим, что 10u кратно 10, а
не делится на 10, так как ни один из множителей не делится на 10. Это противоречие.
Ответ: Первоначальный средний балл в школе № 2 не мог равняться 7.
в)
-
Пусть в школе № 1 средний балл равнялся A, общее количество баллов — p, количество писавших работу — (9 – m).
(из пункта б).
Следовательно,
-
Попробуем найти средний балл в школе № 2 методом подбора. Пусть:
В = 1, тогда:
кратно 10, а
не делится на 10.
В = 2, тогда:
пусть u = 1, тогда m = 4:
— не является целым числом.
u = 2 не может быть, т. к. m ≥ 1
В = 3, тогда:
кратно 10, а
не делится на 10.
В = 4, тогда:
Чтобы m было натуральным числом u должно быть четным, u = 2, тогда m = 4, что невозможно (доказали при В = 2).
u = 4, тогда m меньше 0, что невозможно т. к. m ≥ 1.
В = 5, тогда:
пусть u = 1, тогда m = 7, что невозможно (доказали в пункте б);
пусть u = 2, тогда m = 5:
— не является целым числом;
пусть u = 3, тогда m = 3:
-
Этот случай реализуется, например, в школе № 2 при m = 3, B = 5. Предположим, что каждый ученик набрал по 5 баллов. Тогда в школе № 1 писали 9 – m = 9 – 3 = 6 учащихся, 3 из них набрали по 1 баллу, а 3 – по 3 балла, тогда средний балл:
-
Переход из школы № 1 в школу № 2 совершил ученик с 3 баллами, тогда
средний балл в школе № 1 стал равен:что на 10% меньше от первоначального значения.
-
Тогда средний балл в школе № 2 стал равен:
что на 10% меньше от первоначального значения.
Ответ: наименьшее значение первоначального среднего балла в школе № 2 равно 5.
Ответ: а) да; б) нет; в) 5.
Как выставляют баллы за ЕГЭ по математике
С базовым уровнем сложности все просто: за каждый правильный ответ вашего варианта вы получаете по 1 первичному баллу. То же самое касается и первой части профиля: задания 1–11 тоже оценивают в 1 балл.
Как вы помните, во 2-й части профильного варианта нужны и решение, и ответ. Здесь задания оценивают по нескольким критериям. Они сложнее, но и баллов за них можно получить больше. Давайте же разберемся, как выставляют баллы во второй части профиля. Это поможет вам подготовиться к заданиям ЕГЭ по математике как самостоятельно, так и с учителем.
| Задание № 12 | Баллы |
|---|---|
| В обоих пунктах есть обоснованные ответы | 2 |
| Есть обоснованный ответ только в пункте а или есть неверный ответ из-за ошибки в вычислениях, но шаги в решениях обоих пунктов верные |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 13 | Баллы |
|---|---|
| Верно доказан пункт а, в пункте б есть обоснованный ответ | 3 |
| Есть только обоснованный ответ в пункте б или верно доказан пункт а, в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ |
2 |
| Есть только верное доказательство пункта а, или в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ, или есть обоснованный ответ в пункте в, который получен с помощью пункта а, но сам пункт а не выполнен |
1 |
| Все остальные случаи. | 0 |
| Максимальный балл | 3 |
| Задание № 14 | Баллы |
|---|---|
| Есть обоснованный ответ | 2 |
| Ответ обоснован, но он отличается от верного исключением точек –12 и/или 0 или шаги решения верные, но из-за ошибки в вычислениях получен неверный ответ |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 15 | Баллы |
|---|---|
| Есть обоснованный ответ | 2 |
| Ученик верно построил математическую модель | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 2 |
| Задание № 16 | Баллы |
|---|---|
| Верно доказан пункт а, в пункте б есть обоснованный ответ | 3 |
| Есть только обоснованный ответ в пункте б иЛИ Верно доказан пункт а, в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ |
2 |
| Есть только верное доказательство пункта а, или в пункте б шаги решения верные, но из-за ошибки в вычислении получен неверный ответ, или есть обоснованный ответ в пункте в, который получен с помощью пункта а, но сам пункт а не выполнен |
1 |
| Все остальные случаи | 0 |
| Максимальный балл | 3 |
| Задание № 17 | Баллы |
|---|---|
| Есть обоснованный ответ | 4 |
| Рассуждения и значения параметра верные, но в ответе есть 1–2 неверных значения или решение недостаточно обосновано | 3 |
| Есть верное рассуждение и хотя бы одно правильное значение | 2 |
| Задача сведена к исследованию взаимного расположения 3 окружностей или двух квадратных уравнений с параметром | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 4 |
| Задание № 18 | Баллы |
|---|---|
| Есть обоснованный ответ в пунктах а, б, в | 4 |
| Есть обоснованный ответ в пункте в и есть обоснованный ответ в пунктах а или б | 3 |
| Есть обоснованный ответ в пунктах а и б или есть обоснованный ответ в пункте в. |
2 |
| Есть обоснованный ответ в пунктах а или б | 1 |
| Все остальные случаи | 0 |
| Максимальный балл | 4 |
Узнать больше о структуре экзамена, вариантах и критериях, по которым оценивают работы, можно на официальном сайте ФИПИ, в разделе «Демоверсии, спецификации, кодификаторы». Там же вы найдете методические указания для подготовки.
Сколько баллов нужно набрать, чтобы получить 3, 4 и 5
Теперь, когда мы разобрали критерии, можно посчитать, сколько баллов нужно набрать на конкретную оценку. В этом нам помогут таблицы ниже. Заодно разберемся, как первичные баллы переводятся в тестовые — финальные.
| Шкала перевода баллов в базовой математике | |
|---|---|
| Первичные баллы | Оценка |
| <7 | 2 |
| 7–11 | 3 |
| 12–16 | 4 |
| 17–21 | 5 |
| Максимальный балл | 4 |
Обратите внимание: с 2008 года официально баллы ЕГЭ не переводят в привычные нам оценки по пятибальной системе. Но если вам хочется это сделать, можно примерно оценить работу по таблице ниже.
| Шкала перевода баллов в профильной математике (неофициальная) | ||
|---|---|---|
| Первичные баллы | Тестовые баллы | Оценка |
| <5 | <27 | 2 |
| 5–8 | 27–49 | 3 |
| 8–20 | 50–67 | 4 |
| 21–31 | 68–100 | 5 |
6 советов от эксперта, как готовиться к ЕГЭ по математике
Мы занимаемся подготовкой учеников к экзамену каждый год и понимаем, насколько это важно и волнительно. Вам предстоит ответственная работа, от которой многое зависит. Чтобы облегчить ее, мы собрали несколько советов, которые помогут вам как можно лучше подготовиться к ЕГЭ по математике:
-
Осознанно выберите уровень сложности и поставьте цель в баллах.
-
Составьте план подготовки к ЕГЭ по математике: больше времени уделяйте темам, которые у вас «западают». Чтобы выявить их, ученики Skysmart проходят тест на бесплатном уроке.
-
Узнайте все о ЕГЭ: сколько времени длится экзамен, из каких частей состоит, по каким темам будут задания, сколько вариантов, какие дадут справочные материалы и т. д.
-
Составьте сбалансированное расписание для подготовки и следите, чтобы в нем было достаточно времени для отдыха.
-
Много практикуйтесь: решайте варианты из Открытого банка заданий ЕГЭ и сдавайте тестовые экзамены.
-
Систематически консультируйтесь и занимайтесь с наставником, который часто имеет дело с подготовкой к ЕГЭ — преподавателем в школе или репетитором.
Все пункты в этом списке важны для тех, кто хочет набрать 80–100 баллов, но последний — особенно. Преподаватель расскажет о том, что представляет из себя ЕГЭ, и тогда на реальном экзамене не будет неприятных сюрпризов.
На курсах подготовки к ЕГЭ по математике в Skysmart учителя помогают школьникам разобраться в КИМах и прорешать каждый тип задач. Ученики заранее знакомятся с частыми ошибками, что помогает избегать их в работе и сохранять баллы. А еще мы учим готовиться морально, чтобы не допустить ошибок из-за паники и невнимательности. Начните подготовку к ЕГЭ по математике с нуля вместе со Skysmart: первый урок — бесплатно!
✍
Тема 2 (Математика, 6 класс). Признаки делимости (7 типов заданий)
-
2.1 Даны числа: 5125; 1622; 9330; 1616; 5495; 2352; 4115; 9920; 9820. Выпишите те из них, которые:
а) не кратны 2
б) делятся на 5
в) делятся на 10.
[Ответ: а) 5125; 5495; 4115; б) 5125; 9330; 5495; 4115; 9920; 9820; в) 9330; 9920; 9820.][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
-
2.2 Даны числа: 1017; 4455; 5454; 4815; 819; 729; 3825; 6018; 5352. Выпишите те из них, которые:
а) делятся на 3 и являются чётными
б) кратны 9, но не кратны 2.
[Ответ: а) 5454; 6018; 5352; б) 1017; 4455; 4815; 819; 729; 3825.][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
-
2.5 На четырех карточках записаны цифры 5, 9, 0, 2.
Какие четырехзначные числа, кратные 5, можно выложить из этих карточек? Выпишите все возможные варианты.
[Ответ: 2095; 2590; 2905; 2950; 5290; 5920; 9025; 9205; 9250; 9520.][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
-
2.6 Замените звёздочку в записи числа 474*, чтобы получилось число, кратное:
а) 2; б) 3; в) 5; г) 9; д) 10.
К каждому случаю укажите все возможные решения.
[Ответ: а) 4740; 4742; 4744; 4746; 4748; б) 4740; 4743; 4746; 4749; в) 4740; 4745; г) 4743; д) 4740.][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
✍
Тема 4 (Математика, 6 класс). Основное свойство дроби. Сокращение дробей (14 типов заданий)
-
4.4 Среди приведенных равенств укажите верные: 1)
frac{10}{11} = frac{80}{88}
2)
frac{1}{4} = frac{2}{9}
3)
frac{4}{5} = frac{36}{45}
4)
frac{3}{4} = frac{6}{11}
5)
frac{4}{11} = frac{12}{33}
6)
frac{3}{5} = frac{24}{43}
[Ответ: 135]
[просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
-
4.8 Сократите дробь frac{24}{228}.
[Ответ: frac{2}{19}][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. Добавьте три задания в карточку (или количество, кратное трём), чтобы ученики смогли рассмотреть все возможные случаи, и чтобы сложность заданий для всех была одинаковой.
Вы можете добавлять до 9 таких заданий.
-
4.10 Представьте число 0.544 в виде обыкновенной несократимой дроби.
[Ответ: frac{68}{125}][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. Добавьте чётное количество заданий в карточку, чтобы ученики смогли рассмотреть все возможные случаи, и чтобы сложность заданий для всех была одинаковой.
-
4.14 Приведите дроби frac{1}{2} и frac{2}{3} к наименьшему общему знаменателю
[Ответ: frac{3}{6} и frac{4}{6}][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. Добавьте чётное количество заданий в карточку, чтобы сложность заданий для всех была одинаковой.
✍
Тема 5 (Математика, 6 класс). Сложение, вычитание, умножение, деление обыкновенных дробей (20 типов заданий)
-
5.2 Вычислите, предварительно сократив дроби: frac{23}{46} + frac{51}{63}
[Ответ: frac{55}{42}=1 frac{13}{42}][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. Добавьте чётное количество заданий в карточку, чтобы сложность заданий для всех была одинаковой.
-
5.3 Выполните действия: frac{27}{28} + frac{1}{3} + frac{3}{4}
[Ответ: frac{43}{21}=2 frac{1}{21}][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. Добавьте чётное количество заданий в карточку, чтобы сложность заданий для всех была одинаковой.
-
5.4 Выполните действия, предварительно сократив дроби: frac{10}{20} + frac{99}{121} + frac{12}{72}
[Ответ: frac{49}{33}=1 frac{16}{33}][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. Добавьте чётное количество заданий в карточку, чтобы сложность заданий для всех была одинаковой.
Сложение и вычитание обыкновенных дробей и смешанных чисел
✍
Тема 7 (Алгебра, 7 класс). Задачи из ОГЭ/ЕГЭ, решаемые с помощью линейных уравнений (8 типов заданий)
-
7.1 Вася и Оля выполняют одинаковый тест. Вася отвечает за час на 15 вопросов теста, а Оля — на 25. Они одновременно начали отвечать на вопросы теста, и Вася закончил свой тест позже Оли на 48 минут. Сколько вопросов содержит тест?
[Ответ: 30][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
-
7.8 Рыболов в 5:00 на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 3 часа ловил рыбу и вернулся обратно в 23:00 того же дня. На какое расстояние от пристани он отдалился, если скорость течения реки равна 4 км/ч, а собственная скорость лодки 6 км/ч?
[Ответ: 25][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Задачи на совместную работу
Задачи на движение по воде
✍
Тема 13 (Геометрия, 7 класс). Точка, прямая, отрезок, луч, угол. Смежные углы (3 типа заданий)
-
13.1 Начертите прямую c и отметьте на ней точки T, O, S и M так, чтобы точка S лежала между точками T и O, а точка M — между точками O и S.
[Ответ: —][просмотреть похожие]
[сообщить об ошибке]
[✖ видеоразбор отсутствует] -
13.2 Луч TF делит угол STH на два угла. Найдите угол STF,
если angle STH = 166^{circ}, angle HTF = 24^{circ}.
[Ответ: 142^{circ}][просмотреть похожие]
[сообщить об ошибке]
[✖ видеоразбор отсутствует] -
13.3 а) Сопоставьте буквенные обозначения углов с их градусными мерами (для выполнения задания пользоваться транспортиром нет необходимости);
б) выпишите все пары смежных углов на рисунке.
Углы:
А) ∠PRC
Б) ∠ZRP
В) ∠ZRC
Г) ∠ZRF
Д) ∠CRF
Е) ∠PRFГрадусные меры:
1) 90o
2) 19o
3) 71o
4) 109o
5) 180oВ таблицу занесите номера градусных мер, соответствующие буквам
Буквы (углы): А Б В Г Д Е Цифры
от 1 до 5:[Ответ: а) 543211; б) ∠PRF и ∠CRF, а также ∠PRZ и ∠CRZ]
[просмотреть похожие]
[сообщить об ошибке]
[✖ видеоразбор отсутствует]
✍
Тема 14 (Геометрия, 7 класс). Признаки равенства треугольников (3 типа заданий)
-
14.1 На рисунке ниже изображены треугольники NZB и MAX. Известно, что NB=MX, ZB=AX, и ∠ZBN = ∠AXM.
а) отметьте равенство указанных элементов на рисунке;
б) докажите, что ΔNZB = ΔMAX.
[Ответ: 1) NB=MX (по условию),
2)ZB=AX (по условию),
3) ∠ZBN = ∠AXM (по условию)
Значит, ΔNZB = ΔMAX по I признаку.][просмотреть похожие]
[сообщить об ошибке]
[✖ видеоразбор отсутствует] -
14.2 На рисунке ниже изображены треугольники RKN и EHO. Известно, что KN=HO, ∠RKN = ∠EHO, ∠KNR = ∠HOE.
а) отметьте равенство указанных элементов на рисунке;
б) докажите, что ΔRKN = ΔEHO.
[Ответ: 1) KN=HO (по условию),
2) ∠RKN = ∠EHO (по условию),
3) ∠KNR = ∠HOE (по условию).
Значит, ΔRKN = ΔEHO по II признаку.][просмотреть похожие]
[сообщить об ошибке]
[✖ видеоразбор отсутствует] -
14.3 На рисунке ниже изображены треугольники CZF и EHA. Известно, что CZ=EH, ZF=HA, CF=EA.
а) отметьте равенство указанных элементов на рисунке;
б) докажите, что ΔCZF = ΔEHA.
[Ответ: 1) CZ=EH (по условию),
2) ZF=HA (по условию),
3) CF=EA (по условию).
Значит, ΔCZF = ΔEHA по III признаку.][просмотреть похожие]
[сообщить об ошибке]
[✖ видеоразбор отсутствует]
✍
Тема 23 (Алгебра, 8 класс). Решение задач с помощью рациональных уравнений. Задачи из ОГЭ/ЕГЭ (21 тип заданий)
-
23.1 На изготовление 288 деталей ученик тратит на 8 часов больше, чем мастер на изготовление 800 таких же деталей. Известно, что ученик за час делает на 14 деталей меньше, чем мастер. Сколько деталей в час делает ученик?
[Ответ: 6][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. Эти задачи идентичны задачам из следующего номера, но здесь дискриминант квадратного уравнения, составляемого в процессе решения, НЕ выходит за пределы таблицы квадратов чисел от 1 до 100.
-
23.2 На изготовление 384 деталей ученик тратит на 6 часов больше, чем мастер на изготовление 840 таких же деталей. Известно, что ученик за час делает на 12 деталей меньше, чем мастер. Сколько деталей в час делает ученик?
[Ответ: 8][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. Эти задачи идентичны задачам из предыдущего номера, но здесь дискриминант квадратного уравнения, составляемого в процессе решения, ВЫХОДИТ за пределы таблицы квадратов чисел от 1 до 100.
-
23.3 Двое рабочих, работая вместе, могут выполнить работу за 56 часов. За сколько часов, работая отдельно, выполнит эту работу первый рабочий, если он за 2 часа выполняет такую же часть работы, какую второй – за 14 часов?
[Ответ: 64][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
-
23.4 Заказ на 160 деталей первый рабочий выполняет на 6 часов быстрее, чем второй.
Сколько деталей за час изготавливает первый рабочий, если известно, что он за час изготавливает на 6 деталей больше второго?
[Ответ: 16][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
-
23.5 Первая труба пропускает на 8 литров воды в минуту меньше, чем вторая.
Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 180 литров она заполняет
на 8 минут быстрее, чем первая труба?
[Ответ: 18][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
-
23.6 Первая труба пропускает на 18 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 135 литров она заполняет на 18 минут дольше, чем вторая труба заполняет резервуар объемом 567 литров?
[Ответ: 3][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. Эти задачи идентичны задачам из следующего номера, но здесь дискриминант квадратного уравнения, составляемого в процессе решения, НЕ выходит за пределы таблицы квадратов чисел от 1 до 100.
-
23.7 Первая труба пропускает на 9 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 96 литров она заполняет на 14 минут дольше, чем вторая труба заполняет резервуар объемом 130 литров?
[Ответ: 4][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. Эти задачи идентичны задачам из предыдущего номера, но здесь дискриминант квадратного уравнения, составляемого в процессе решения, ВЫХОДИТ за пределы таблицы квадратов чисел от 1 до 100.
-
23.8 Плиточники планируют уложить 248 м2 плитки. Если они будут укладывать на 23 м2 в день больше, чем запланировали,
то закончат работу на 23 дня раньше. Сколько квадратных метров плитки в день планируют укладывать плиточники?
[Ответ: 8][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
-
23.9 Два промышленных фильтра, работая одновременно, очищают цистерну воды за 20 минут.
Определите, за сколько минут второй фильтр очистит цистерну воды, работая отдельно, если известно,
что он сделает это на 9 минут быстрее, чем первый.
[Ответ: 36][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
-
23.10 При двух одновременно работающих принтерах расход бумаги составляет 1 пачку за 12 минут.
Определите, за сколько минут израсходует пачку бумаги первый принтер, если известно,
что он сделает это на 32 минуты быстрее, чем второй.
[Ответ: 16][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
-
23.12 Катер прошёл от одной пристани до другой, расстояние между которыми по реке равно 54 км,
сделал стоянку на 2 ч 58 мин и вернулся обратно через 14frac{29}{30} ч после начала поездки.
Найдите скорость течения реки, если известно, что скорость катера в стоячей воде равна 12 км/ч. Ответ дайте в км/ч.
[Ответ: 6][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
-
23.13 Расстояние между пристанями А и В равно 32 км. Из А в В по течению реки отправился плот,
а через 5 часов вслед за ним отправилась яхта, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А.
К этому времени плот прошел 44 км.
Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 4 км/ч. Ответ дайте в км/ч.
[Ответ: 12][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
-
23.14 Пристани A и B расположены на реке, скорость течения которой на этом участке равна 6 км/ч.
Лодка проходит туда и обратно без остановок со средней скоростью 9 км/ч. Найдите собственную скорость лодки.
[Ответ: 12][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. Вы можете добавлять в карточку не более 1 такого задания
-
23.15 Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь.
Второй проехал первую половину пути со скоростью 21 км/ч, а вторую половину пути – со скоростью,
на 14 км/ч большей скорости первого, в результате чего прибыл в пункт B одновременно с первым автомобилем.
Найдите скорость первого автомобиля. Ответ дайте в км/ч.
[Ответ: 28][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. Вы можете добавлять в карточку до 5 таких заданий. Если Вы делаете чередующиеся карточки, настоятельно рекомендуем не добавлять более одной-двух задач этого типа во избежание дублей в карточках!
-
23.16 Из пункта A в пункт B, расстояние между которыми 170 км, одновременно выехали автомобилист и велосипедист.
Известно, что за час автомобилист проезжает на 68 км больше, чем велосипедист.
Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 8 ч позже автомобилиста. Ответ дайте в км/ч.
[Ответ: 17][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
-
23.17 Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 126 км.
На следующий день он отправился обратно в A со скоростью на 5 км/ч больше прежней. По дороге он сделал остановку на 5 ч.
В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B.
Найдите скорость велосипедиста на пути из B в A. Ответ дайте в км/ч.
[Ответ: 14][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. Если Вы делаете чередующиеся карточки, настоятельно рекомендуем не добавлять более одной-двух задач этого типа во избежание дублей в карточках!
-
23.18 Два велосипедиста одновременно отправились в 63-километровый пробег.
Первый ехал со скоростью, на 2 км/ч большей, чем скорость второго, и прибыл к финишу на 2 ч раньше второго.
Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
[Ответ: 7][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. Если Вы делаете чередующиеся карточки, настоятельно рекомендуем не добавлять более одной-двух задач этого типа во избежание дублей в карточках!
-
23.19 Из городов A и B навстречу друг другу выехали мотоциклист и велосипедист.
Мотоциклист приехал в B на 0.5 ч раньше, чем велосипедист приехал в A, а встретились они через 1 ч 52 мин после выезда.
Сколько часов затратил на путь из B в A велосипедист?
[Ответ: 4][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
-
23.20 Товарный поезд каждую минуту проезжает на 200 метров меньше, чем скорый,
и на путь в 832 км тратит времени на 3 ч больше, чем скорый.
Найдите скорость товарного поезда. Ответ дайте в км/ч.
[Ответ: 52][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. Дискриминант квадратного уравнения, составляемого в процессе решения, может выходить за пределы таблицы квадратов чисел от 1 до 100.
-
23.21 Два гонщика участвуют в «Безумных гонках». Им предстоит проехать 80 кругов по кольцевой трассе протяжённостью 6 км.
Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 48 минут.
Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 12 минут?
Ответ дайте в км/ч.
[Ответ: 120][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. Если Вы делаете чередующиеся карточки, настоятельно рекомендуем не добавлять более одной-двух задач этого типа во избежание дублей в карточках!
Задачи из ОГЭ/ЕГЭ на совместную работу
Задачи из ОГЭ/ЕГЭ на движение по воде
Задачи из ОГЭ/ЕГЭ на движение по прямой
✍
Тема 24 (Геометрия, 8 класс). Четырехугольники (10 типов заданий)
-
24.1 На рисунке изображён четырехугольник DMTN. Укажите:
а) вершины четырехугольника;
б) стороны четырехугольника;
в) углы четырехугольника
г) соседние вершины;
д) противолежащие вершины;
е) соседние стороны;
ж) противолежащие стороны;
з) соседние углы;
и) противолежащие углы.[Ответ: а) D, M, T, N; б) DM, MT, TN, DN;
в) ∠D, ∠M, ∠T, ∠N ; г) D и M; M и T; T и N; D и N;
д) D и T; M и N; е) DM и MT; MT и TN; TN и DN; DM и DN;
ж) DM и TN; MT и DN; з) ∠D и ∠M; ∠M и ∠T; ∠T и ∠N; ∠D и ∠N;
и) ∠D и ∠T; ∠M и ∠N.][просмотреть похожие]
[сообщить об ошибке]
[✖ видеоразбор отсутствует] -
24.2 Три угла выпуклого четырехугольника равны 28^{circ},
57^{circ}, 99^{circ}. Чему равен четвертый угол?
[Ответ: 176o][просмотреть похожие]
[сообщить об ошибке]
[✖ видеоразбор отсутствует] -
24.3 Периметр параллелограмма равен 104 см. Найдите его стороны, если одна из них на 26 см меньше другой.
[Ответ: 13 см и 39 см][просмотреть похожие]
[сообщить об ошибке]
[✖ видеоразбор отсутствует] -
24.4 Периметр параллелограмма равен 176 см. Найдите его стороны, если одна из них больше другой в 7 раз.
[Ответ: 11 см и 77 см][просмотреть похожие]
[сообщить об ошибке]
[✖ видеоразбор отсутствует] -
24.5 В прямоугольнике EDFR точка B является
точкой пересечения диагоналей. ∠FBR = 122°. Найдите ∠DBF и ∠DEF.
[Ответ: ∠DBF = 58°; ∠DEF = 29°][просмотреть похожие]
[сообщить об ошибке]
[✖ видеоразбор отсутствует] -
24.6 В прямоугольнике XTOP точка F является точкой пересечения диагоналей.
∠XPT = 30°, TP = 72 см. Найдите углы и периметр треугольника XFT.
[Ответ: все углы по 60°; P=108 см][просмотреть похожие]
[сообщить об ошибке]
[✖ видеоразбор отсутствует] -
24.8 Диагонали ромба CMTS пересекаются в точке A. Найдите углы треугольника CAM, если ∠MTS = 52°.
[Ответ: ∠C = 26°; ∠M = 64°; ∠A = 90°][просмотреть похожие]
[сообщить об ошибке]
[✖ видеоразбор отсутствует] -
24.9 В равнобокой трапеции большее основание равно 99 см, меньшее — 14 см, а периметр трапеции равен 207 см. Найдите боковую сторону.
[Ответ: 47][просмотреть похожие]
[сообщить об ошибке]
[✖ видеоразбор отсутствует] -
24.10 Длины оснований трапеции отличаются на 49 см. Найдите основания, если боковые стороны равны 78 см и 100 см,
а периметр составляет 381 см.
[Ответ: 126 см и 77 см][просмотреть похожие]
[сообщить об ошибке]
[✖ видеоразбор отсутствует]
✍
Тема 26 (ЕГЭ). Задание 9, функции. Новинка 2022 года (35 типов заданий)
-
26.7 На рисунке изображён график функции y=ax^2+bx+c, где числа a, b и c — целые. Найдите f(0).
[Ответ: -29][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание. -
26.9 На рисунке изображён график функции f(x)=frac{k}{x}+a. Найдите, при каком значении x значение функции равно -2.75.
[Ответ: -1.6][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание. -
26.11 На рисунке изображён график функции f(x)=frac{k}{x+a}. Найдите значение x, при котором f(x) = -0.4.
[Ответ: 11.5][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание. -
26.15 На рисунке изображён график функции f(x)=b+log_ax. Найдите значение x, при котором f(x)=6.
[Ответ: 27][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание. -
26.17 На рисунке изображён график функции f(x)=log_a(x+b). Найдите значение x, при котором f(x)=-4.
[Ответ: 20][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание. -
26.19 На рисунке изображён график функции f(x) = a^x+b. Найдите значение x, при котором f(x) = 63.
[Ответ: 6][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание. -
26.21 На рисунке изображён график функции f(x) = a^{x+b}. Найдите значение x, при котором f(x) = 125.
[Ответ: 5][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание. -
26.23 На рисунке изображён график функции f(x) = ksqrt{x}. Найдите значение x, при котором f(x)=-6.9.
[Ответ: 5.29][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание. -
26.24 На рисунке изображены графики функций f(x)=7x-29 и g(x)=ax^2+bx+c, которые пересекаются в точках A и B. Найдите абсциссу точки B.
[Ответ: -3][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание. -
26.25 На рисунке изображены графики функций f(x)=-7x-20 и g(x)=ax^2+bx+c, которые пересекаются в точках A и B. Найдите ординату точки B.
[Ответ: -48][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание. -
26.26 На рисунке изображены графики функций f(x)=frac{k}{x} и g(x)=ax+b, которые пересекаются в точках A и B. Найдите абсциссу точки B.
[Ответ: -0.2][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание. -
26.27 На рисунке изображены графики функций f(x)=frac{k}{x} и g(x)=ax+b, которые пересекаются в точках A и B. Найдите ординату точки B.
[Ответ: 24][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание. -
26.28 На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
[Ответ: 4.6][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание. -
26.29 На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
[Ответ: 2.25][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание. -
26.30 На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.
[Ответ: 22.6][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание. -
26.31 На рисунке изображены графики двух линейных функций. Найдите ординату точки пересечения графиков.
[Ответ: -14.16][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание. -
26.32 На рисунке изображены графики функций f(x) = 3x^2+31x+80 и g(x) = ax^2+bx+c, которые пересекаются в точках A и B. Найдите абсциссу точки B.
[Ответ: -8.5][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание. -
26.33 На рисунке изображены графики функций f(x) = 3x^2+30x+74 и g(x) = ax^2+bx+c, которые пересекаются в точках A и B. Найдите ординату точки B.
[Ответ: 47][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание. -
26.34 На рисунке изображены графики функций f(x)=asqrt{x} и g(x)=kx+b, которые пересекаются в точке A. Найдите абсциссу точки A.
[Ответ: 9][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание. -
26.35 На рисунке изображены графики функций f(x)=asqrt{x} и g(x)=kx+b, которые пересекаются в точке A. Найдите ординату точки A.
[Ответ: -0.6][просмотреть похожие]
[сообщить об ошибке]
[смотреть видеоразбор]
Примечание для учителя. При создании карточек с очень большим количеством изображений могут возникнуть проблемы.
Узнайте, что это за проблемы и как их избежать — смотрите видеопримечание.
✍
Глава I. Параллельность прямых и плоскостей
ⓘ Здесь Вы можете скачать трехмерные чертежи к задачам из учебника Атанасяна Л.С. «Геометрия 10-11» в формате GeoGebra.
Рекомендуем ознакомиться с инструкцией по работе с готовыми моделями, прежде чем приступать к скачиванию и демонстрации.
§ 1. Параллельность прямых, прямой и плоскости. Задачи 16 — 33
§ 2. Взаимное расположение прямых в пространстве. Угол между двумя прямыми. Задачи 34 — 47
§ 3. Параллельность плоскостей. Задачи 48 — 65
§ 4. Тетраэдр и параллелепипед. Задачи 66 — 87
Дополнительные задачи 88 — 115
Рисунки к Главе I, §4, п. 14 «Построение сечений»
✍
Глава II. Перпендикулярность прямых и плоскостей
ⓘ Здесь Вы можете скачать трехмерные чертежи к задачам из учебника Атанасяна Л.С. «Геометрия 10-11» в формате GeoGebra.
Рекомендуем ознакомиться с инструкцией по работе с готовыми моделями, прежде чем приступать к скачиванию и демонстрации.
§ 1. Перпендикулярность прямой и плоскости. Задачи 116 — 137
§ 2. Перпендикуляр и наклонные. Угол между прямой и плоскостью. Задачи 138 — 165
§ 3. Двугранный угол. Перпендикулярность плоскостей. Задачи 166 — 173
24 августа вышла демоверсия ЕГЭ 2023 по профильной математике. Для тех, кто пока не готов вникать в тему основательно, успокоительный спойлер: почти ничего не изменилось, принципиально новых заданий нет. Всё в порядке.
А для тех, кто давно был на низком старте и ждал разбор демо ЕГЭ, математик Эйджей провёл стрим с решением заданий из демоверсии ЕГЭ 2023 по профильной математике. В этой статье собраны резюме по заданиям экзамена, которые составители ЕГЭ представили в демоверсии.
https://youtu.be/RFQwP8DW8sA
Что изменилось в ЕГЭ 2023 по профильной математике
По сути, никаких критически важных изменений в демоверсии ЕГЭ 2023 нет, о чём составители написали прямо: «Изменения в содержании КИМ отсутствуют». Но есть момент: все задания из первой части, кроме 11, изменили свои номера.
Будем искать позитивные моменты: если в 2022 году вы не смогли запомнить номера заданий в тесте — ничего страшного, запомните новые в 2023 году.
Главное, что новых заданий не появилось.
Важный момент в самостоятельной подготовке к ЕГЭ по профильной математике — выбор качественных сборников задач. Делимся лучшими ресурсами для повторения теории и отработки практики.
1, 2 задания
В демоверсии ЕГЭ 2023 по профильной математике всё начинается с простой геометрии и стереометрии. Составители хотят, чтобы геометрические задачи научились решать как можно больше ребят, поэтому поместили эти задания вперёд как одни из самых простых, чтобы поднять решаемость.






3, 4 задания
Задания 3–4 посвящены теории вероятности.
Задание 3 — обычная задача наподобие задачи из ОГЭ, а задание 4 — задача про монеты и проценты из КИМа 2022 года.




5, 6 задания
После вероятностей составители ЕГЭ 2023 по профильной математике решили поставить уравнения и выражения. Уравнения ожидаются не супер лёгкие, но вполне решаемые: будут корни, логарифмы и степени. В выражениях в демоверсии ЕГЭ встретилась тригонометрия и степени.






7 задание
Ура, 7 задание осталось на своём месте: это задание с графиком и производными. Почему-то его не объединили в общий блок с 11 заданием, тоже посвящённым производным.

Далее в разборе демоверсии ЕГЭ 2023 по профильной математике выпускников ждут две задачи.
8 задание
8 задача на подстановку: нужно подставить в формулу известные числа и вычислить какую-либо величину. Ничего сложного, главное внимательность.
9 задание
Ещё одна текстовая задача. Здесь могут встретиться темы «Движение по прямой», «Движение по окружности», «Движение по реке» и «Сплавы, смеси, растворы». Такие задачи считаются не самыми простыми. Вместе с Эйджеем разберём этот номер в Телеграме.



10 задание
10 задание в демо ЕГЭ 2023 — «новое старое задание». Этот тип заданий с графиком впервые появился в 2022 году, и в КИМ 2023 попал без изменений. Возможно, стоит ждать усложнения этого задания.
11 задание
Традиционное задание с производными и точками минимума и максимума, которое почему-то не объединили в блок с другим заданием на производные.
Итак, обобщим всё, что мы узнали про первую часть демоверсии ЕГЭ по математике: в 2023 году в экзамене не появились ни вектора, ни комплексные числа. Можно немного расслабиться! Осталось выучить новую нумерацию, и всё будет хорошо.
Нумерация второй части в демоверсии ЕГЭ 2023 осталась без изменений, и это радует: не придётся переучивать номера и переживать. Посмотрим, что приготовили составители в этом году.
12 задание
Традиционно в разборе демоверсии ЕГЭ 2023 по профильной математике в 12 задании выпускников ждёт тригонометрическое уравнение.
13 задание
В 13 задании осталась стереометрия: в демоверсии представлена треугольная призма.
14 задание
В 14 задании всё по плану, там остались неравенства с логарифмами, ничего нового.
Это задание вместе с 12-ым составляет «джентльменский набор» из второй части — их под силу решить каждому, и этому нужно обязательно научиться, чтобы набрать 70+ баллов за ЕГЭ по профильной математике.
15 задание
15 задание также считается вполне решаемым. В демоверсии это экономическая задача про человека, который взял кредит в банке и рассчитывает выплаты и проценты.
16 задание
В задании 16 демоверсии ЕГЭ 2023 представлена планиметрическая задача про две окружности.
17 задание
Задача на параметр. Как показывает практика прошлых лет, параметр — самое решаемое задание из сложных заданий ЕГЭ.

18 задание
Задача на целые числа. Из трёх пунктов, А и Б решить может каждый, если хорошо подготовиться.
Чтобы получить 80+ баллов по профильной математике, нужно без ошибок решить первую часть и выполнить 12, 14, 15 и 18аб задания. А планиметрия, стереометрия, параметр и 18 задание полностью помогут получить заветную сотку. Как повысить свои шансы на успешную сдачу ЕГЭ по математике, рассказали в нашей статье.
Мы разобрали демоверсию ЕГЭ 2023 по математике, и теперь вы знаете, что приготовили для вас составители экзамена. Можно смело начинать подготовку! Эйджей уже составил план занятий и ждёт вас на курсе «Основа». Это возможность разобраться во всех темах и набить руку в решении заданий в компании единомышленников и с личным наставником.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!












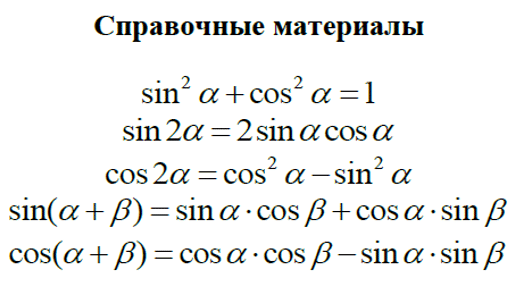




 смотреть видеоразбор]
смотреть видеоразбор]

























