Уравнение высоты треугольника
Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:
Примеры решений по аналитической геометрии на плоскости
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.
Решения задач о треугольнике онлайн
Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.
Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.
Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.
Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.
Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.
Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.
Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, — 4)$, $В(3, 0)$ и $С(0, 6)$.
Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.
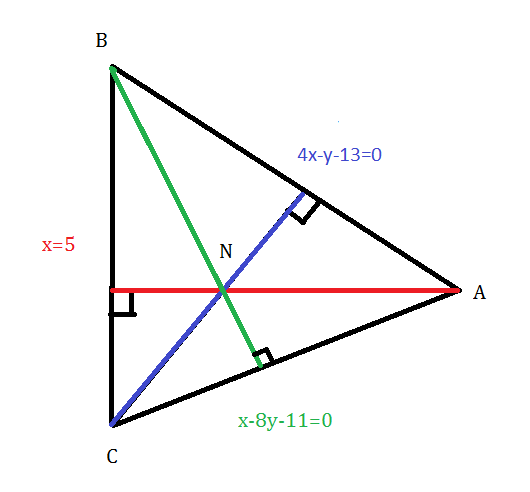
Задача 17886 Даны две вершины A(3; -1), B(5; 7).
Условие
Даны две вершины A(3; -1), B(5; 7) треугольника ABC и точка N(4; -1) пересечения его высот. Составить уравнения сторон этого треугольника.
Решение
Уравнение прямой АВ составим как уравнение прямой, проходящей через две точки:
(х-x_(A))/(x_(B)-x_(A))=(y-y_(A))/(y_(B)-y_(A))
Составим уравнение прямой AN
A(3; –1),N(4; –1)
Так как вторые координаты одинаковые, то значит прямая AN характеризуется тем свойством, что на ней расположены точки, у которых вторая координата равны -1.
Уравнение такой прямой имеет вид:
у=-1
Прямая ВС перпендикулярна прямой АN, значит уравнение этой прямой имеет вид
х=с ( с- константа)
Значит прямая ВС характеризуется тем свойством,что на ней расположены точки, у которых первая координата одинаковая.
Так как у точки В первая координата 5, то значит с=5
х=5 — уравнение прямой ВС.
Уравнение прямой ВN — уравнение прямой, проходящей через две точки:
(х-x_(B))/(x_(N)-x_(B))=(y-y_(B))/(y_(N)-y_(B))
(х-5)/(4-5)=(y-7)/(-1-7)
-8*(x-5)=-1*(y-7)
8x+y-47=0 — уравнение прямой BN.
Прямая АС перпендикулярна BN и проходит через точку А.
Если прямые у=k1x+b1 и y=k2x+b2 перпендикулярны, то
k1*k2=-1
y=(1/8)x+b — уравнение прямых, перпендикулярных BN.
Чтобы выделить из них прямую AC, подставим координаты точки А и найдем b.
y=(1/8)x-(11/8) или умножим на 8
8у=х-11
х-8у-11=0 — уравнение прямой АС
О т в е т.
4х-у-13=0 — уравнение прямой АВ
х-8у-11=0 — уравнение прямой АС
х=5 — уравнение прямой ВС
http://www.matburo.ru/ex_ag.php?p1=agtr
http://reshimvse.com/zadacha.php?id=17886
Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Пример.
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
Решение:
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:
|
0 / 0 / 0 Регистрация: 22.09.2015 Сообщений: 36 |
|
|
1 |
|
Составить уравнения высот треугольника, если известны уравнения его сторон01.12.2015, 22:28. Показов 12217. Ответов 9
составить уравнения высот треугольника, если известны уравнения его сторон: 2x-y+3=0 , x+5y-7=0 , 3x-2y+6=0
0 |
|
Диссидент 27483 / 17170 / 3784 Регистрация: 24.12.2010 Сообщений: 38,683 |
|
|
01.12.2015, 22:42 |
2 |
|
Для начала найди треугольничьи вершины. А дальше вместе будем думать…
0 |
|
1130 / 789 / 232 Регистрация: 12.04.2010 Сообщений: 2,012 |
|
|
02.12.2015, 21:58 |
3 |
|
уравнение стороны: 2x-y+3=0 Уравнение перпендикулярной прямой x + 2y + c = 0. Теперь надо найти константу c.
0 |
|
Диссидент 27483 / 17170 / 3784 Регистрация: 24.12.2010 Сообщений: 38,683 |
|
|
02.12.2015, 22:29 |
4 |
|
надо найти константу c. Да с радостью! Но для этого надо бы знать вершину! А ТС, как царь Кащей, чахнет над своей вершиной, и секретов никому не рассказывает. Наверное, она ему нужней чем нам. Добавлено через 1 минуту Добавлено через 17 минут Не по теме: Мог ошибиться в арифметике…Слабое это место у меня… Но ждать, когда нам ТС предоставит свои вершины — нет уж, увольте!
1 |
|
1130 / 789 / 232 Регистрация: 12.04.2010 Сообщений: 2,012 |
|
|
02.12.2015, 23:35 |
5 |
|
Решение Байт с использованием других терминов. Три прямые проходят через одну точку. Система 2x — y = -3, x + 5y = 7 , 2x + 3y = d имеет решение.
Уравнение пучка прямых, образованных первыми двумя сторонами 3 строка [2, 3, d]- линейная комбинация 1 и 2 строк. Равна
По условию перпендикулярности 3-й стороне То есть определитель
1 |
|
Диссидент 27483 / 17170 / 3784 Регистрация: 24.12.2010 Сообщений: 38,683 |
|
|
03.12.2015, 00:12 |
6 |
|
с использованием других терминов. Все правильно и совершенно замечательно! Что подчеркивает ловкость и избыточность науки «Аналитическая Геометрия». Это лабиринт. Но его своеобразие в том, что выход всегда есть. Вопрос лишь в том, сколько штреков нам придется проползти, и сколько матриц построить по дороге. Лично я люблю линейные методы решения, хотя бы потому, что не люблю редактор формул. Я в нем себя чувствую, как штопальщица, вдевающая нитку в иголку. И одновременно — иголкой, в которую вдевают нитку, и ниткой, которую вдевают иголку.
0 |
|
0 / 0 / 0 Регистрация: 22.09.2015 Сообщений: 36 |
|
|
03.12.2015, 11:51 [ТС] |
7 |
|
прошу прощения, но я ничего из этой писанины не понял
0 |
|
1130 / 789 / 232 Регистрация: 12.04.2010 Сообщений: 2,012 |
|
|
03.12.2015, 12:37 |
8 |
|
я ничего из этой писанины не понял Okas43, можно конкретнее? Что например, непонятно? Понятно ли условие задачи?
0 |
|
1130 / 789 / 232 Регистрация: 12.04.2010 Сообщений: 2,012 |
|
|
03.12.2015, 22:32 |
9 |
|
Еще вариант решения — графический. (Нарисуем прямые, построим высоты. По чертежу найдём уравнения.) Миниатюры
0 |
|
1742 / 662 / 87 Регистрация: 01.10.2012 Сообщений: 3,279 |
|
|
04.12.2015, 09:54 |
10 |
|
прошу прощения, но я ничего из этой писанины не понял , можно пожалуйста чисто решение, чтоб записать в контрольную Дано Найдем ур-е высоты опущенной из точки B на прямую АС 1) Находим координаты точки B решая систему линейных ур-й (раскрываете определители «крестиком») Отсюда получили bx и by 2) Ур-е прямой перпендикулярной AC: Подставляя в него найденные bx и by находим c. Готово. Для остальных высот — аналогично
0 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
04.12.2015, 09:54 |
|
Помогаю со студенческими работами здесь Найти координаты третьей вершины треугольника и составить уравнения его сторон Найти координаты всех вершин параллелограмма, если известны координаты одной вершины и уравнения двух его сторон
Составить уравнения сторон треугольника, зная две его вершины и точку пересечения медиан M (требуется проверка) Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 10 |
Ответ:
2х+3у-7=0
Пошаговое объяснение:
1) Нужно найти координаты вершины А. Очевидно, что она лежит на пересечении прямых АВ и АС, т.е. у этой точки значения у и х будут принадлежать области значений и определения обеих функций. Другими словами, нам нужно решить систему их уравнений.
Из уравнения АВ: у=2х-3,
подставляем в уравнение АС: х+5·(2х-3)-7=0
х+10х-15-7=0
11х=22
х=2
у=2·2-3=1
Итого, имеем координаты вершины А(2;1).
2) Нужно составить общее уравнение прямой а, проходящей через точку А и перпендикулярную прямой ВС.
Так как прямая а перпендикулярна прямой ВС, то направляющий вектор прямой а есть нормальный вектор заданной прямой 3x-2y+13=0, то есть, направляющий вектор прямой а имеет координаты (3;-2).
Теперь мы можем записать каноническое уравнение прямой а на плоскости, так как знаем координаты точки А, через которую проходит прямая а, и координаты направляющего вектора прямой а:
=
. <em>(Здесь в числителях задействованы координаты точки А, в знаменателях — координаты напрявляющего вектора) </em>
От полученного канонического уравнения прямой a перейдем к общему уравнению прямой:
=
⇒ -2·(х-2)=3·(у-1) ⇒ 2х+3у-7=0.
Ответ: уравнение высоты, проведенной через вершину A 2х+3у-7=0
Тема: записать уравнение высоты (Прочитано 4284 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Дано:( 2x+3y-6=0 (AB) )
( x+2y-5=0 (AC) )
угол ( B=frac{pi}{4} )
записать уравнение высоты из точки А на сторону BC
нашла A(-3;4)
а дальше не соображу
Анастасия
А как условие полностью звучит?
Зная уравнение двух сторон треугольника АВС ( 2x+3y-6=0 (AB) )
( x+2y-5=0 (AC) ) и внутренний угол при вершине В, равный ( frac{pi}{4} ) , записать уравнение высоты, опущенной из вершины А на сторону ВС.
Анастасия
Т.е. в задании конкретно указано, какие стороны задают уравнения:
Т.е. в задании конкретно указано, какие стороны задают уравнения:
ну все что дано я написала, я думаю сторону BC найти через этот угол и k стороны AB?
Анастасия
ну все что дано я написала
В задании так и сказано, что сторона АВ задается уравнением 2х+3у-6=0?
ну все что дано я написала
В задании так и сказано, что сторона АВ задается уравнением 2х+3у-6=0?
Да, а что Вас смущает??? я так думаю прежде чем найти сторону CB по коэф-ам, надо найти точку С, я не могу выразить ее, так то же по идее ее как то можно найти зная сторону AC и точку А, только я не сообра жу как это сделать
Анастасия
Анастасия
ну все что дано я написала
В задании так и сказано, что сторона АВ задается уравнением 2х+3у-6=0?
Да, а что Вас смущает???
Уравнением задается прямая, вот это и смущает.
Мне бы хотелось увидеть чертеж.
По сути имеется две прямые, которые пересекаются в точке ( A ), на прямой (в ваших обозначениях ( AB )) произволным образом берется точка ( B ) и проводится третья прямая ( l ), которая составляет угол ( frac{pi}{4} ) с вышеуказанной прямой. А найти нужно уравнение прямой, которая перпендикулярна ( l ). Вы согласны?
Поэтому точку С так как вы хотите найти не получится.
В принципе, задача с прямыми на плоскости.
Алгоритм нахождения подскажу после чертежа, если сами не догадаетесь.)
Чтобы правильно задать вопрос, нужно знать большую часть ответа. (с)
Формулы пишите в LaTex.
у меня нет чертежа. я ее решила еще вчера через пучек прямых в точке А, в принципе как вы и описали у меня вот такой ответ получился ( x-4y+7=0 ), не знаю только правильно ли.
« Последнее редактирование: 05 Ноября 2010, 21:16:10 от bocha86 »
Анастасия
у меня нет чертежа. я ее решила еще вчера через пучек прямых в точке А, в принципе как вы и описали у меня вот такой ответ получился ( x-4y+7=0 ), на знаю только правильно ли.
Замечательно. Если хотите, чтоб проверили, выкладывайте решение.
кстати а все таки можно точку С найти, зная уравнение стороны АС и точку А, просто я не смогла, а то бы другим путем стала решать?…
Уравнение прямой на которой лежит сторона ( AC ) у вас и так дано, точку ( A ) найти проще простого, только что это вам даст, я не пойму.
Координаты точки ( C ) зависят от того, как вы возьмете точку ( B ) на прямой ( 2x+3y-6=0 ), то есть таких точек по существу множество.
Чтобы правильно задать вопрос, нужно знать большую часть ответа. (с)
Формулы пишите в LaTex.
Замечательно. Если хотите, чтоб проверили, выкладывайте решение.
Уравнение прямой на которой лежит сторона ( AC ) у вас и так дано, точку ( A ) найти проще простого, только что это вам даст, я не пойму.
Координаты точки ( C ) зависят от того, как вы возьмете точку ( B ) на прямой ( 2x+3y-6=0 ), то есть таких точек по существу множество.
ну да я поняла, что точку А даже не стоило находить
сейчас выложу свое решение
Анастасия
( x+2y-5+lambda(2x+3y-6)=0 )
привела к виду ( ({1+2lambda})_{x}+({2+3lambda})_{y}+({-5-6lambda})=0 )
нашла угловой коэф. стороны BC
( tgfrac{pi}{4}=left|frac{k2-k1}{1+k1k2}right|=left|frac{k+frac{2}{3}}{1-frac{2}{3}k}right|=1
Rightarrow k=frac{1}{5} )
так как высота ( perp ) стороне ВС, то ее угл.коэф.=( -5 )
( frac{1}{5}frac{(1+2lambda)}{(2+3lambda )}=-5 )
( lambda=-frac{3}{5} )
( ({1+2lambda})_{x}+({2+3lambda})_{y}+({-5-6lambda})=0rightarrow
({1-frac{6}{5}})_{x}+({2-frac{9}{5}})_{y}+({-5+frac{18}{5})}=0 )
( ({-frac{1}{5}})_{x}+({frac{1}{5}})_{y}-(frac{7}{5})=0 *(-5)rightarrow x-y+7=0 )
даже свою ошибку нашла
Анастасия
( x+2y-5+lambda(2x+3y-6)=0 )
привела к виду ( ({1+2lambda})x+({2+3lambda})y+({-5-6lambda})=0 )
до этих пор все понятно.
нашла угловой коэф. стороны BC
( tgfrac{pi}{4}=left|frac{k_2-k_1}{1+k_1k_2}right|=left|frac{k+frac{2}{3}}{1-frac{2}{3}k}right|=1
k=frac{1}{5} )
а это не понимаю..
так как высота ( perp ) стороне ВС, то ее угл.коэф.=( -5 )
( frac{1}{5}frac{(1+2lambda)}{(2+3lambda )}=-5 )
При пендикулярности произведение угловых коэффициентов равно минус пяти??
А из вашего уравнения ( lambda=-frac{51}{77} ) получается.
Чтобы правильно задать вопрос, нужно знать большую часть ответа. (с)
Формулы пишите в LaTex.
нашла угловой коэф. стороны BC
( tgfrac{pi}{4}=left|frac{k_2-k_1}{1+k_1k_2}right|=left|frac{k+frac{2}{3}}{1-frac{2}{3}k}right|=1 )
( k=frac{1}{5} )
ну зная коэф.прямой AB и чему равен угол В, мы можем наити коэф. прямой СВ, что я и сделала
так как высота ( perp ) стороне ВС, то ее угл.коэф.=( -5 )
( frac{1}{5}frac{(1+2lambda)}{(2+3lambda )}=-5 )
ну если к1=1/5, то перпенд.=-1/к, или я что то не то поняла, по крайней мере у меня так в учебнике написано, вот и получилось -5.
« Последнее редактирование: 06 Ноября 2010, 00:27:14 от tig81 »
Анастасия





 , можно пожалуйста чисто решение, чтоб записать в контрольную
, можно пожалуйста чисто решение, чтоб записать в контрольную Составить уравнения высот треугольника
Составить уравнения высот треугольника


