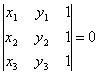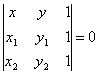Как составить уравнение двух сторон параллелограмма и его диагонали
Даны уравнения двух сторон параллелограмма 8х+3у+1=0, 2х+у-1=0 и уравнение одной из его диагоналей 3х+2у+3=0. Определить координаты вершин этого параллелограмма.
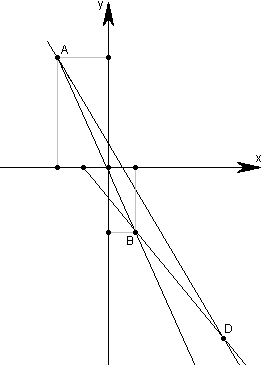
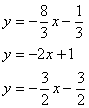
Для нахождения точки А приравняем эти два уравнения:
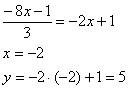
Мы видим, что уравнение 3х+2у+3=0 задает диагональ BD . Поэтому, приравняв сначала 1 и 3, а затем 2 и 3 уравнения, найдем соответственно точки D и В.
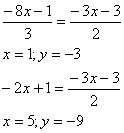
Как известно в параллелограмме противоположные стороны параллельны, то есть коэффициенты k при х равны. Поэтому для сторон ВС и CD остаются неизвестными только свободные члены d . Найдем их, подставив в уравнения прямых их известные точки D и В соответственно:
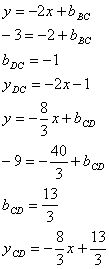
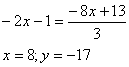
Как составить уравнение двух сторон параллелограмма и его диагонали
Даны уравнения двух сторон параллелограмма x + 2y + 1 = 0 (AB), 2x + y — 3 = 0 (AD) и точка пересечения его диагоналей N(1, 2). Найти уравнения двух других сторон этого параллелограмма.
При решении, замечая, что данные стороны параллелограмма не параллельны, будем следовать такому плану:
1) Найдем координаты точки A пересечения данных сторон.
2) Зная координаты точек A и N, найдем координаты точки C, что мы легко сможем сделать по формуле определения координат середины отрезка.
3) Через найденную точку C проведем сначала прямую, параллельную AD, а потом прямую, параллельную AB.
4) Определим координаты точки A, как точки пересечения прямых AB и AD, и получим, что
5) Формулы для определения координат середины отрезка в данном случае запишутся так:
По этим формулам получим
Итак, точка .
6) Через точку C проведем прямую, параллельную AD, и получим, что уравнение стороны BC будет таким:
Задача 36074 Помогите, пожалуйста, решить. Даны.
Условие
Помогите, пожалуйста, решить. Даны уравнения двух смежных сторон параллелограмма х+у+5=0 и х-4у=0. Составить уравнения двух других сторон, если известна точка пересечения его диагоналей Р(2;-2).
Решение
Найдем точку пересечения смежных сторон
4y+y+5=0
5y=-5
y=-1
x=-4
А(-1;-4)
Р-середина диагонали АС
Значит, можем найти координаты точки С
Две другие стороны параллельны данным
Запишем данные уравнения в виде уравнений с угловым коэффициентом
x+y+5=0⇒y=-x-5
k=-1
Значит уравнение параллельной стороны имеет вид
y=-x+b
Для нахождения b подставляем координаты точки С:
8=-5+b
b=13
y=-x+13
[b]x+y-13=0[/b]
x-4y=0 ⇒ y=(1/4)x
Значит уравнение параллельной стороны имеет вид
y=y=(1/4)x+b
Для нахождения b подставляем координаты точки С:
8=(1/4)*(5)+b
b=8-(5/4)=27/4
http://www.pm298.ru/reshenie/ljg83.php
http://reshimvse.com/zadacha.php?id=36074
Как составлять уравнение двух сторон параллелограмма
Даны уравнения двух сторон параллелограмма x + 2y + 1 = 0 (AB), 2x + y — 3 = 0 (AD) и точка пересечения его диагоналей N(1, 2). Найти уравнения двух других сторон этого параллелограмма.
При решении, замечая, что данные стороны параллелограмма не параллельны, будем следовать такому плану:
1) Найдем координаты точки A пересечения данных сторон.
2) Зная координаты точек A и N, найдем координаты точки C, что мы легко сможем сделать по формуле определения координат середины отрезка.
3) Через найденную точку C проведем сначала прямую, параллельную AD, а потом прямую, параллельную AB.
4) Определим координаты точки A, как точки пересечения прямых AB и AD, и получим, что
5) Формулы для определения координат середины отрезка в данном случае запишутся так:
По этим формулам получим
Итак, точка .
6) Через точку C проведем прямую, параллельную AD, и получим, что уравнение стороны BC будет таким:
Как составлять уравнение двух сторон параллелограмма
Даны уравнения двух сторон параллелограмма 8х+3у+1=0, 2х+у-1=0 и уравнение одной из его диагоналей 3х+2у+3=0. Определить координаты вершин этого параллелограмма.

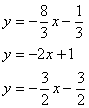
Для нахождения точки А приравняем эти два уравнения:
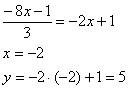
Мы видим, что уравнение 3х+2у+3=0 задает диагональ BD . Поэтому, приравняв сначала 1 и 3, а затем 2 и 3 уравнения, найдем соответственно точки D и В.
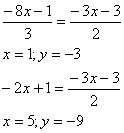
Как известно в параллелограмме противоположные стороны параллельны, то есть коэффициенты k при х равны. Поэтому для сторон ВС и CD остаются неизвестными только свободные члены d . Найдем их, подставив в уравнения прямых их известные точки D и В соответственно:
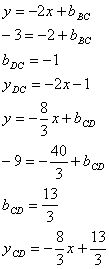
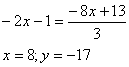
8.1.3. Свойство углов и сторон параллелограмма
Задача 1. Один из углов параллелограмма равен 65°. Найти остальные углы параллелограмма.
∠C =∠A = 65° как противоположные углы параллелограмма.
∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма.
∠В = 180° — ∠А = 180° — 65° = 115°.
∠D =∠B = 115° как противолежащие углы параллелограмма.
Ответ: ∠А =∠С = 65°; ∠В =∠D = 115°.
Задача 2. Сумма двух углов параллелограмма равна 220°. Найти углы параллелограмма.

∠А +∠В = 180° как углы, прилежащие к одной стороне параллелограмма, поэтому ∠А = 180° — ∠В = 180° — 110° = 70°. Тогда ∠C =∠A = 70°.
Ответ: ∠А =∠С = 70°; ∠В =∠D = 110°.
Задача 3. Один из углов параллелограмма в 3 раза больше другого. Найти углы параллелограмма.
Пусть ∠А =х. Тогда ∠В = 3х. Зная, что сумма углов параллелограмма, прилежащих к одной его стороне равна 180°, составим уравнение.
х = 180 : 4;
Получаем: ∠А =х = 45°, а ∠В = 3х = 3 ∙ 45° = 135°.
Противолежащие углы параллелограмма равны, следовательно,
∠А =∠С = 45°; ∠В =∠D = 135°.
Ответ: ∠А =∠С = 45°; ∠В =∠D = 135°.
Задача 4. Докажите, что если у четырехугольника две стороны параллельны и равны, то этот четырехугольник – параллелограмм.
Проведем диагональ BD и рассмотрим Δ ADB и Δ CBD.
AD = BC по условию. Сторона BD – общая. ∠1 = ∠2 как внутренние накрест лежащие при параллельных (по условию) прямых AD и BC и секущей BD. Следовательно, Δ ADB = Δ CBD по двум сторонам и углу между ними (1-й признак равенства треугольников). В равных треугольниках соответственные углы равны, значит, ∠3 =∠4. А эти углы являются внутренними накрест лежащими при прямых AB и CD и секущей BD. Отсюда следует параллельность прямых AB и CD. Таким образом, в данном четырехугольнике ABCD противолежащие стороны попарно параллельны, следовательно, по определению ABCD – параллелограмм, что и требовалось доказать.
Задача 5. Две стороны параллелограмма относятся как 2 : 5, а периметр равен 3,5 м. Найти стороны параллелограмма.
Периметр параллелограмма PABCD= 2 ∙ (AB + AD).
Обозначим одну часть через х. тогда AB = 2x, AD = 5x метров. Зная, что периметр параллелограмма равен 3,5 м, составим уравнение:
2 ∙ (2x + 5x) = 3,5;
2 ∙ 7x = 3,5;
x = 3,5 : 14;
Одна часть составляет 0,25 м. Тогда AB = 2 ∙ 0,25 = 0,5 м; AD = 5 ∙ 0,25 = 1,25 м.
Периметр параллелограмма PABCD= 2 ∙ (AB + AD) = 2 ∙ (0,25 + 1,25) = 2 ∙ 1,75 = 3,5 (м).
Так как противоположные стороны параллелограмма равны, то CD = AB = 0,25 м; BC = AD = 1,25 м.
источники:
http://methmath.ru/zadatcha9.html
http://mathematics-repetition.com/8-1-3-svoystvo-uglov-i-storon-parallelogramma/

Задача: Даны 2 смежные вершины паралелограмма А(-2.6), В(2,8). Диагонали пересекаются в точке М(2,2). Найти координаты 2 других вершин С и D и записать уравнения сторон в общем виде.
Мое решение: (-2+xC)/2=2 xC=6
(6+yC)/2=2 yC=2
C(6,2)
(2+xD)/2=2 xD=2
(8+yD)/2=2 yD=-4
D(2,-4)
Запишем уравнения сторон, используя формулу (x-x1)/(x2-x1)=(y-y1)/(y2-y1)
Уравнение для стороны BD
(x-2)/(2-2)=(y-8)/(-4-8)
y=8 НЕПРАВИЛЬНО?
Для АD
(x+2)/(2+2)=(y-6)/(-4-6)
5x +2y-2=0 ТУТ ВРОДЕ ВСЕ НОРМАЛЬНО
Для СD
(x-6)/(2-6)=(y+2)/(-4+2)
x-2y-8=0 НЕПРАВИЛЬНО?
Чертила этот паралелограмм, проверяла уравнения прямых, подставляя значения — 1 и 3 уравнения не правильные получаются.
Прошу, помогите разобраться чайнику!
210
-3), M5(3; -1), M6(-2; 1) лежат
на прямой
P2, P3, P4, P5 расположены
на прямой
числам 4; 0; 2; -2; -6. Определить ординаты этих точек.
Q2, Q3, Q4, Q5 расположены
на прямой
числам 1; 0; 2; -1, 3. Определить абсциссы этих точек.
пересечения прямой
осями и построить эту прямую на чертеже.
пересечения двух прямых
треугольника АВС даны соответственно
уравнениями
координаты его вершин.
сторон параллелограмма
его диагоналей
Определить координаты вершин
этого параллелограмма.
треугольника лежат на прямых
треугольника S=8, две его вершины суть точки А(1; -2),
В(2; 3), а третья вершина С лежит на прямой
треугольника S=1,5, две его вершины суть точки А(2;
-3), В(3; -2), центр масс этого треугольника лежит на
прямой
Определить координаты третьей
вершины С.
уравнение прямой и построить прямую на чертеже,
зная ее угловой коэффициент k и отрезок b,
отсекаемый ею на оси Oy:
коэффициент k и отрезок b, отсекаемый на оси Oy, для
каждой из прямых:
прямой:
данной прямой;
данной прямой.
проходящей через точку М0(2; 1):
прямой;
данной прямой.
сторон прямоугольника
А(2; -3). Составить уравнения двух других сторон
этого прямоугольника.
сторон прямоугольника
его диагоналей
Найти вершины прямоугольника.
точке Р(-5; 13) относительно прямой
симметричную точке Р(-5; 13) относительно прямой
следующих случаев составить уравнение прямой,
параллельной двум данным прямым и проходящей
посередине между ними:
коэффициент k прямой, проходящей через две данные
точки:
-5), M2(3; 2);
уравнения прямых, проходящих через вершины
треугольника A(5; -4), B(-1; 3), C(-3; -2) параллельно
противоположным сторонам.
сторон треугольника M1(2; 1), M2(5;
3), M3(3; -4). Составить
уравнение его сторон.
Q(-1; 0). Составить уравнение прямой, проходящей
через точку Q перпендикулярно к отрезку
уравнение прямой, если точка P(2; 3) служит
основанием перпендикуляра, опущенного из начала
координат на эту прямую.
треугольника M1(2; 1), M2(-1; -1),
M3(3; 2). Составить уравнения
его высот.
треугольника даны уравнениями
высот.
треугольника A(1; -1), B(-2; 1), C(3; 5). Составить
уравнение перпендикуляра, опущенного из вершины
А на медиану, проведенную из вершины В.
треугольника A(2; -2), B(3; -5), C(5; 7). Составить
уравнение перпендикуляра, опущенного из вершины
С на биссектрису внутреннего угла при вершине А.
уравнения сторон и медиан треугольника с
вершинами A(3; 2), B(5; -2), C(1; 0).
прямая. Определить точки пересечения этой прямой
с осями координат.
Доказать,
что условие, при котором три точки M1(x1,
y1), M2(x2, y2), M3(x3,
y3) лежат на одной прямой,
может быть записано в следующем виде:
Доказать,
что уравнение прямой, проходящей через две
данные точки M1(x1, y1),
M2(x2, y2), может
быть записано в следующем виде:
последовательные вершины выпуклого
четырехугольника A(-3; 1), B(3; 9), C(7; 6), D(-2; -6).
Определить точку пересечения его диагоналей.
вершины A(-3; -1), B(2; 2) параллелограмма ABCD и точка Q(3;
0) пересечения его диагоналей. Составить
уравнения сторон этого параллелограмма.
сторон прямоугольника
диагонали
сторон и второй диагонали этого прямоугольника.
треугольника A(1; -2), B(5; 4), C(-2; 0). Составить
уравнения биссектрис его внутреннего и внешнего
углов при вершине А.
уравнение прямой, проходящей через точку P(3; 5) на
одинаковых расстояниях от точек A(-7; 3) и B(11; -15).
точки P(-8; 12) на прямую, проходящую через точки A(2;
-3), B(-5; 1).
-9) относительно прямой,
проходящей через точки А(3; -4), B(-1; -2).
найти такую точку P, чтобы сумма ее расстояний до
точек M(1; 2), N(3; 4) была наименьшей.
найти такую точку P, чтобы сумма ее расстояний до
точек M(-3; 2), N(2; 5) была наибольшей.
расстояний которой до точек A(-7; 1), B(-5; 5) была бы
наименьшей.
расстояний которой до точек A(4; 1), B(0; 4) была бы
наибольшей.
проходящей через точку M0(2; 1) под углом 450 к данной прямой.
является вершиной квадрата, диагональ которого
лежит на прямой
уравнения сторон и второй диагонали этого
квадрата.
противоположные вершины квадрата A(-1; 3), C(6; 2).
Составить уравнения его сторон.
центром квадрата, одна из сторон которого лежит
на прямой
прямых, на которых лежат остальные стороны этого
квадрата.
Ox направлен луч света. Известно, что
до оси Ox, луч от нее отразился. Составить
уравнения прямых, на которых лежат падающий и
отраженный лучи.
по прямой
Составить уравнение прямой, на которой лежит
отраженный луч.
сторон треугольника
равнобедренный. Решить задачу при помощи
сравнения углов треугольника.
уравнение прямой, проходящей через точку M1(x1; y1) параллельно
прямой
уравнение прямой, проходящей через точку М1(2: -3) параллельно
прямой:
условие перпендикулярности прямых
в следующем виде:
из следующих пар прямых перпендикулярны. Решить
задачу, не вычисляя угловых коэффициентов данных
прямых.
Доказать,
что формула для определения угла между
прямыми ,
может
быть записана в следующей форме:
задачу, не вычисляя угловых коэффициентов данных
прямых.
треугольника M1(-10; 2), M2(6; 4);
его высоты пересекаются в точке
N(5; 2). Определить координаты третьей вершины M3.
-1), B(5; 7) треугольника ABC и точка N(4; -1) пересечения
его высот. Составить уравнения сторон этого
треугольника.
даны: уравнение стороны АВ:
высот АМ:
других сторон и третьей высоты этого
треугольника.
уравнения сторон треугольника АВС, если даны
одна из его вершина А(1; 3) и уравнения двух медиан
уравнения сторон треугольника, сли даны одна из
его вершин B(-4; -5) и уравнения двух высот
уравнения сторон треугольника, зная одну из его
вершин A(4; -1) и уравнения двух биссектрис
уравнения сторон треугольника, зная одну из его
вершин B(2; 6), а также уравнения высоты
биссектрисы
уравнения сторон треугольника, зная одну его
вершину B(2; -1), а также уравнения высоты
различных вершин.
уравнения сторон треугольника, зная одну его
вершину C(4; -1), а также уравнения высоты
одной вершины.
уравнения сторон треугольника, зная одну его
вершину B(2; -7), а также уравнения высоты
различных вершин.
уравнения сторон треугольника, зная одну его
вершину C(4; 3), а также уравнения биссектрисы
одной вершины.
уравнения сторон треугольника, зная одну его
вершину A(3; -1), а также уравнения биссектрисы
различных вершин.
уравнение прямой, которая проходит черезначало
координат и вместе с прямыми
треугольник с площадью, равной 1,5.
проходящих через точку P(3; 0), найти такую, отрезок
которой, заключенный между прямыми
пополам.
проведены всевозможные прямые. Доказать, что
отрезок каждой из них, заключенный между прямыми
в точке Р пополам.
проведены всевозможные прямые. Доказать, что
среди них нет прямой, отрезок которой,
заключенный между прямыми
пополам.
уравнение прямой, проходящей через начало
координат, зная, что длина ее отрезка,
заключенного между прямыми
уравнение прямой, проходящей через точку С(-5; 4),
зная, что длина ее отрезка, заключенного между
прямыми
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
|||
|
у меня мозг взрывается, помогите 6-ой день сижу мучаюсь Прямые 3х — 4у + 17 = 0 и 4х – у – 12 = 0 являются сторонами параллелограмма, а точка Р (2; 7 ) – точкой пересечения его диагоналей. Составить уравнения двух других сторон параллелограмма. Сделать чертеж.
|
||
| Вернуться к началу |
|
||
|
berKotiK |
|
||
|
а как первое действие сделать?
|
|||
| Вернуться к началу |
|
||
|
berKotiK |
Заголовок сообщения: Re: Составить уравнения двух других сторон параллелограмма
|
|
1) находим точку А- точку пересечения двух сторон, заданных уравнением 3х — 4у + 17 = 0 и 4х – у – 12 = 0 . Для этого решаем систему этих уравнений. Точку А нашли — А(5;8). C(-1;6)
|
|
| Вернуться к началу |
|
|
Alexdemath |
|
||
|
venjar писал(а): 1. Найдите координаты точки В (одна из вершин параллелограмма)- пересечения данных прямых. berKotiK писал(а): а как первое действие сделать? Решите систему [math]begin{cases}3x-4y+17=0,\ 4x-y-12=0.end{cases}[/math]
|
|||
| Вернуться к началу |
|
||
|
berKotiK |
Заголовок сообщения: Re: Составить уравнения двух других сторон параллелограмма
|
|
Alexdemath писал(а): venjar писал(а): 1. Найдите координаты точки В (одна из вершин параллелограмма)- пересечения данных прямых. berKotiK писал(а): а как первое действие сделать? Решите систему [math]begin{cases}3x-4y+17=0,\ 4x-y-12=0.end{cases}[/math] Решил получилось А (5,8)
|
|
| Вернуться к началу |
|
|
berKotiK |
Заголовок сообщения: Re: Составить уравнения двух других сторон параллелограмма
|
|
Analitik писал(а): berKotiK мне уже писали тоже самое.. я не понимаю как записать их.. пробывал разбирать аналогичный пример.. не получается… тогавт я совсем.. объясните как пожалуйста
|
|
| Вернуться к началу |
|
|
berKotiK |
Заголовок сообщения: Re: Составить уравнения двух других сторон параллелограмма
|
|
Analitik писал(а): berKotiK Вы знаете как выглядит уравнение прямой, которая проходит через точку параллельно заданному вектору?! static.php?p=uravneniya-pryamoi-kollinyearno-vektoru ]Уравнение_прямой[/url] я заочник, и закончил колледж! лекций не было, с вышкой первый раз сам разбираюсь поэтому ничего не понимаю! за этим обратился к вам на форум! Сидя дома не много поймёшь!
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Составить уравнения двух других сторон параллелограмма
в форуме Аналитическая геометрия и Векторная алгебра |
uhr |
2 |
786 |
29 окт 2015, 15:52 |
|
Написать уравнения 2-х других сторон параллелограмма
в форуме Аналитическая геометрия и Векторная алгебра |
Oleg95 |
7 |
682 |
13 янв 2015, 09:25 |
|
Уравнения сторон параллелограмма
в форуме Аналитическая геометрия и Векторная алгебра |
av 5566 |
4 |
1303 |
25 июн 2017, 17:31 |
|
Даны уравнения сторон параллелограмма
в форуме Аналитическая геометрия и Векторная алгебра |
vader2010 |
4 |
738 |
08 ноя 2015, 19:04 |
|
Найти уравнения сторон параллелограмма
в форуме Аналитическая геометрия и Векторная алгебра |
lanvandance |
3 |
495 |
05 ноя 2018, 18:17 |
|
уравнения двух сторон прямоугольника
в форуме Аналитическая геометрия и Векторная алгебра |
Okay |
1 |
694 |
11 ноя 2013, 17:26 |
|
Даны уравнения двух сторон
в форуме Аналитическая геометрия и Векторная алгебра |
VadimPlokhikh |
7 |
1862 |
31 янв 2014, 00:15 |
|
Составить уравнения сторон
в форуме Аналитическая геометрия и Векторная алгебра |
helpmeplzzz |
1 |
399 |
11 янв 2015, 19:02 |
|
Даны уравнения двух сторон треугольника
в форуме Аналитическая геометрия и Векторная алгебра |
Nino |
8 |
1040 |
07 ноя 2013, 07:59 |
|
Составить уравнения сторон треугольника
в форуме Аналитическая геометрия и Векторная алгебра |
PsiX |
1 |
1277 |
24 окт 2015, 23:12 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 4 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |