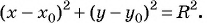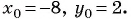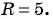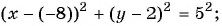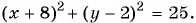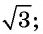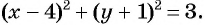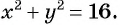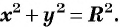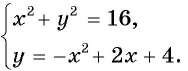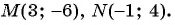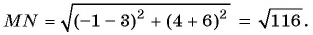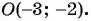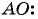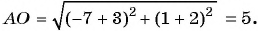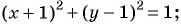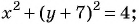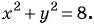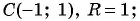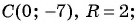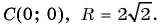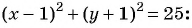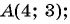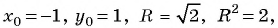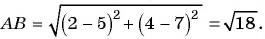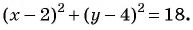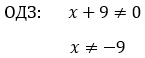Решение уравнений с дробями
О чем эта статья:
5 класс, 6 класс, 7 класс
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:
На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
Что еще важно учитывать при решении
- если значение переменной обращает знаменатель в 0, значит это неверное значение;
- делить и умножать уравнение на 0 нельзя.
Универсальный алгоритм решения
Определить область допустимых значений.
Найти общий знаменатель.
Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.
Раскрыть скобки, если нужно и привести подобные слагаемые.
Решить полученное уравнение.
Сравнить полученные корни с областью допустимых значений.
Записать ответ, который прошел проверку.
Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Решим обычное уравнение.
Пример 2. Найти корень уравнения
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Переведем новый множитель в числитель..
Сократим левую часть на (х+2), а правую на 2.
Пример 3. Решить дробное уравнение:
-
Найти общий знаменатель:
Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
Выполним возможные преобразования. Получилось квадратное уравнение:
Решим полученное квадратное уравнение:
Получили два возможных корня:
Если x = −3, то знаменатель равен нулю:
Если x = 3 — знаменатель тоже равен нулю.
Дробно-рациональные уравнения
Что такое дробно-рациональные уравнения
Дробно-рациональными уравнениями называют такие выражения, которые представляется возможным записать, как:
при P ( x ) и Q ( x ) в виде выражений, содержащих переменную.
Таким образом, дробно-рациональные уравнения обязательно содержат как минимум одну дробь с переменной в знаменателе с любым модулем.
9 x 2 — 1 3 x = 0
1 2 x + x x + 1 = 1 2
6 x + 1 = x 2 — 5 x x + 1
Уравнения, которые не являются дробно-рациональными:
Как решаются дробно-рациональные уравнения
В процессе решения дробно-рациональных уравнений обязательным действием является определение области допустимых значений. Найденные корни следует проверить на допустимость, чтобы исключить посторонние решения.
Алгоритм действий при стандартном способе решения:
- Выписать и определить ОДЗ.
- Найти общий знаменатель для дробей.
- Умножить каждый из членов выражения на полученный общий параметр (знаменатель), сократить дроби, которые получились в результате, чтобы исключить знаменатели.
- Записать уравнение со скобками.
- Раскрыть скобки для приведения подобных слагаемых.
- Найти корни полученного уравнения.
- Выполним проверку корней в соответствии с ОДЗ.
- Записать ответ.
Пример 1
Разберем предложенный алгоритм на практическом примере. Предположим, что имеется дробно-рациональное уравнение, которое требуется решить:
x x — 2 — 7 x + 2 = 8 x 2 — 4
Начать следует с области допустимых значений:
x 2 — 4 ≠ 0 ⇔ x ≠ ± 2
Воспользуемся правилом сокращенного умножения:
x 2 — 4 = ( x — 2 ) ( x + 2 )
В результате общим знаменателем дробей является:
Выполним умножение каждого из членов выражения на общий знаменатель:
x x — 2 — 7 x + 2 = 8 x 2 — 4
x ( x — 2 ) ( x + 2 ) x — 2 — 7 ( x — 2 ) ( x + 2 ) x + 2 = 8 ( x — 2 ) ( x + 2 ) ( x — 2 ) ( x + 2 )
После сокращения избавимся от скобок и приведем подобные слагаемые:
x ( x + 2 ) — 7 ( x — 2 ) = 8
x 2 + 2 x — 7 x + 14 = 8
Осталось решить квадратное уравнение:
Согласно ОДЗ, первый корень является лишним, так как не удовлетворяет условию, по которому корень не равен 2. Тогда в ответе можно записать:
Примеры задач с ответами для 9 класса
Требуется решить дробно-рациональное уравнение:
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
x x + 2 + x + 1 x + 5 — 7 — x x 2 + 7 x + 10 = 0
Определим область допустимых значений:
О Д З : x + 2 ≠ 0 ⇔ x ≠ — 2
x 2 + 7 x + 10 ≠ 0
D = 49 — 4 · 10 = 9
x 1 ≠ — 7 + 3 2 = — 2
x 2 ≠ — 7 — 3 2 = — 5
Квадратный трехчлен x 2 + 7 x + 10 следует разложить на множители, руководствуясь формулой:
a x 2 + b x + c = a ( x — x 1 ) ( x — x 2 )
x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0
Заметим, что общим знаменателем для дробей является: ( x + 2 ) ( x + 5 ) . Умножим на этот знаменатель уравнение:
x x + 2 + x + 1 x + 5 — 7 — x ( x + 2 ) ( x + 5 ) = 0
Сократим дроби, избавимся от скобок, приведем подобные слагаемые:
x ( x + 2 ) ( x + 5 ) x + 2 + ( x + 1 ) ( x + 2 ) ( x + 5 ) x + 5 —
— ( 7 — x ) ( x + 2 ) ( x + 5 ) ( x + 2 ) ( x + 5 ) = 0
x ( x + 5 ) + ( x + 1 ) ( x + 2 ) — 7 + x = 0
x 2 + 5 x + x 2 + 3 x + 2 — 7 + x = 0
2 x 2 + 9 x — 5 = 0
Потребуется решить квадратное уравнение:
2 x 2 + 9 x — 5 = 0
Первый корень не удовлетворяет условиям ОДЗ, поэтому в ответ нужно записать только второй корень.
Дано дробно-рациональное уравнение, корни которого требуется найти:
4 x — 2 — 3 x + 4 = 1
В первую очередь следует переместить все слагаемые влево и привести дроби к минимальному единому знаменателю:
4 ( x + 4 ) x — 2 — 3 ( x — 2 ) x + 4 — 1 ( x — 2 ) ( x + 4 ) = 0
4 ( x + 4 ) — 3 ( x — 2 ) — ( x — 2 ) ( x + 4 ) ( x — 2 ) ( x + 4 ) = 0
4 x + 16 — 3 x + 6 — ( x 2 + 4 x — 2 x — 8 ) ( x — 2 ) ( x + 4 ) = 0
x + 22 — x 2 — 4 x + 2 x + 8 ( x — 2 ) ( x + 4 ) = 0
Заметим, что получилось нулевое значение для дроби. Известно, что дробь может равняться нулю, если в числителе нуль, а знаменатель не равен нулю. На основании этого можно составить систему:
— x 2 — x + 30 ( x — 2 ) ( x + 4 ) = 0 ⇔ — x 2 — x + 30 = 0 ( x — 2 ) ( x + 4 ) ≠ 0
Следует определить такие значения для переменной, при которых в дроби знаменатель будет обращаться в нуль. Такие значения необходимо удалить из ОДЗ:
( x — 2 ) ( x + 4 ) ≠ 0
Далее можно определить значения для переменных, которые при подстановке в уравнение обращают числитель в нуль:
— x 2 — x + 30 = 0 _ _ _ · ( — 1 )
Получилось квадратное уравнение, которое можно решить:
Сравнив корни с условиями области допустимых значений, можно сделать вывод, что оба корня являются решениями данного уравнения.
Нужно решить дробно-рациональное уравнение:
x + 2 x 2 — 2 x — x x — 2 = 3 x
На первом шаге следует перенести все слагаемые в одну сторону и привести дроби к минимальному единому знаменателю:
x + 2 1 x ( x — 2 ) — x x x — 2 — 3 ( x — 2 ) x = 0
x + 2 — x 2 — 3 ( x — 2 ) x ( x — 2 ) = 0
x + 2 — x 2 — 3 x + 6 x ( x — 2 ) = 0
— x 2 — 2 x + 8 x ( x — 2 ) = 0 ⇔ — x 2 — 2 x + 8 = 0 x ( x — 2 ) ≠ 0
Перечисленные значения переменной обращают знаменатель в нуль. По этой причине их необходимо удалить из области допустимых значений.
— x 2 — 2 x + 8 = 0 _ _ _ · ( — 1 )
Корни квадратного уравнения:
x 1 = — 4 ; x 2 = 2
Заметим, что второй корень не соответствует ОДЗ. Таким образом, в ответе остается только первый корень.
Найти корни уравнения:
x 2 — x — 6 x — 3 = x + 2
Согласно стандартному алгоритму решения дробно-рациональных уравнений, выполним перенос всех слагаемых в одну сторону. Далее необходимо привести к дроби к наименьшему общему знаменателю:
x 2 — x — 6 1 x — 3 — x ( x — 3 ) — 2 ( x — 3 ) = 0
x 2 — x — 6 — x ( x — 3 ) — 2 ( x — 3 ) x — 3 = 0
x 2 — x — 6 — x 2 + 3 x — 2 x + 6 x — 3 = 0
0 x x — 3 = 0 ⇔ 0 x = 0 x — 3 ≠ 0
Такое значение переменной, при котором знаменатель становится равным нулю, нужно исключить из области допустимых значений:
Заметим, что это частный случай линейного уравнения, которое обладает бесконечным множеством корней. При подстановке какого-либо числа на место переменной х в любом случае числовое равенство будет справедливым. Единственным недопустимым значением для х в данном задании является число 3, которое не входит в ОДЗ.
Ответ: х — любое число, за исключением 3.
Требуется вычислить корни дробно-рационального уравнения:
5 x — 2 — 3 x + 2 = 20 x 2 — 4
На первом этапе необходимо выполнить перенос всех слагаемых влево, привести дроби к минимальному единому знаменателю:
5 ( x + 2 ) x — 2 — 3 ( x — 2 ) x + 2 — 20 1 ( x — 2 ) ( x + 2 ) = 0
5 ( x + 2 ) — 3 ( x — 2 ) — 20 ( x — 2 ) ( x + 2 ) = 0
5 x + 10 — 3 x + 6 — 20 ( x — 2 ) ( x + 2 ) = 0
2 x — 4 ( x — 2 ) ( x + 2 ) = 0 ⇔ 2 x — 4 = 0 ( x — 2 ) ( x + 2 ) ≠ 0
( x — 2 ) ( x + 2 ) ≠ 0
Данные значения переменной х являются недопустимыми, так как в этом случае теряется смысл дроби в связи с тем, что знаменатель принимает нулевое значение.
Заметим, что 2 не входит в область допустимых значений. В связи с этим, можно заключить, что у уравнения отсутствуют корни.
Ответ: корни отсутствуют
Нужно найти корни уравнения:
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 )
Начнем с определения ОДЗ:
— 5 ≠ 0 x ≠ 0 x ( x — 5 ) ≠ 0 x ≠ 5 x ≠ 0
При умножении обеих частей уравнения на единый знаменатель всех дробей и сокращении аналогичных выражений, которые записаны в числителе и знаменателе, получим:
x — 3 x — 5 + 1 x = x + 5 x ( x — 5 ) · x ( x — 5 )
( x — 3 ) x ( x — 5 ) x — 5 + x ( x — 5 ) x = ( x + 5 ) x ( x — 5 ) x ( x — 5 )
( x — 3 ) x + x = x + 5
Прибегая к арифметическим преобразованиям, можно записать уравнение в упрощенной форме:
x 2 — 3 x + x — 5 = x + 5 → x 2 — 2 x — 5 — x — 5 = 0 → x 2 — 3 x — 10 = 0
Для дальнейших действий следует определить, к какому виду относится полученное уравнение. В нашем случае уравнение является квадратным с коэффициентом при x 2 , который равен 1. Таким образом, целесообразно воспользоваться теоремой Виета:
x 1 · x 2 = — 10 x 1 + x 2 = 3
В этом случае подходящими являются числа: -2 и 5.
Второе значение не соответствует области допустимых значений.
Решение целых и дробно рациональных уравнений
Давайте познакомимся с рациональными и дробными рациональными уравнениями, дадим их определение, приведем примеры, а также разберем наиболее распространенные типы задач.
Рациональное уравнение: определение и примеры
Знакомство с рациональными выражениями начинается в 8 классе школы. В это время на уроках алгебры учащиеся все чаще начинают встречать задания с уравнениями, которые содержат рациональные выражения в своих записях. Давайте освежим в памяти, что это такое.
Рациональное уравнение – это такое уравнение, в обеих частях которого содержатся рациональные выражения.
В различных пособиях можно встретить еще одну формулировку.
Рациональное уравнение – это такое уравнение, запись левой части которого содержит рациональное выражение, а правая – нуль.
Определения, которые мы привели для рациональных уравнений, являются равнозначными, так как говорят об одно и том же. Подтверждает правильность наших слов тот факт, что для любых рациональных выражений P и Q уравнения P = Q и P − Q = 0 будут равносильными выражениями.
А теперь обратимся к примерам.
x = 1 , 2 · x − 12 · x 2 · y · z 3 = 0 , x x 2 + 3 · x — 1 = 2 + 2 7 · x — a · ( x + 2 ) , 1 2 + 3 4 — 12 x — 1 = 3 .
Рациональные уравнения точно также, как и уравнения других видов, могут содержать любое количество переменных от 1 до нескольких. Для начала мы рассмотрим простые примеры, в которых уравнения будут содержать только одну переменную. А затем начнем постепенно усложнять задачу.
Рациональные уравнения делятся на две большие группы: целые и дробные. Посмотрим, какие уравнения будут относиться к каждой из групп.
Рациональное уравнение будет являться целым в том случае, если в записи левой и правой его частей содержатся целые рациональные выражения.
Рациональное уравнение будет являться дробным в том случае, если одна или обе его части содержат дробь.
Дробно рациональные уравнения в обязательном порядке содержат деление на переменную или же переменная имеется в знаменателе. В записи целых уравнений такого деления нет.
3 · x + 2 = 0 и ( x + y ) · ( 3 · x 2 − 1 ) + x = − y + 0 , 5 – целые рациональные уравнения. Здесь обе части уравнения представлены целыми выражениями.
1 x — 1 = x 3 и x : ( 5 · x 3 + y 2 ) = 3 : ( x − 1 ) : 5 – это дробно рациональные уравнения.
К числу целых рациональных уравнений можно отнести линейные и квадратные уравнения.
Решение целых уравнений
Решение таких уравнений обычно сводится к преобразованию их в равносильные алгебраические уравнения. Достичь этого можно путем проведения равносильных преобразований уравнений в соответствии со следующим алгоритмом:
- сначала получим ноль в правой части уравнения, для этого на необходимо перенести выражение, которое находится в правой части уравнения, в его левую часть и поменять знак;
- затем преобразуем выражение в левой части уравнения в многочлен стандартного вида.
Мы должны получить алгебраическое уравнение. Это уравнение будет равносильным по отношению к исходному уравнению. Легкие случаи позволяют нам для решения задачи свести целое уравнение с линейному или квадратному. В общем случае мы решаем алгебраическое уравнение степени n .
Необходимо найти корни целого уравнения 3 · ( x + 1 ) · ( x − 3 ) = x · ( 2 · x − 1 ) − 3 .
Решение
Проведем преобразование исходного выражения с целью получить равносильное ему алгебраическое уравнение. Для этого произведем перенос выражения, содержащегося в правой части уравнения, в левую часть и заменим знак на противоположный. В итоге получим: 3 · ( x + 1 ) · ( x − 3 ) − x · ( 2 · x − 1 ) + 3 = 0 .
Теперь проведем преобразование выражения, которое находится в левой части в многочлен стандартного вида и произведем необходимые действия с этим многочленом:
3 · ( x + 1 ) · ( x − 3 ) − x · ( 2 · x − 1 ) + 3 = ( 3 · x + 3 ) · ( x − 3 ) − 2 · x 2 + x + 3 = = 3 · x 2 − 9 · x + 3 · x − 9 − 2 · x 2 + x + 3 = x 2 − 5 · x − 6
У нас получилось свести решение исходного уравнения к решению квадратного уравнения вида x 2 − 5 · x − 6 = 0 . Дискриминант этого уравнения положительный: D = ( − 5 ) 2 − 4 · 1 · ( − 6 ) = 25 + 24 = 49 . Это значит, действительных корней будет два. Найдем их, воспользовавшись формулой корней квадратного уравнения:
x = — — 5 ± 49 2 · 1 ,
x 1 = 5 + 7 2 или x 2 = 5 — 7 2 ,
x 1 = 6 или x 2 = — 1
Проверим верность корней уравнения, которые мы нашли в ходе решения. Для этого числа, которые мы получили, подставим в исходное уравнение: 3 · ( 6 + 1 ) · ( 6 − 3 ) = 6 · ( 2 · 6 − 1 ) − 3 и 3 · ( − 1 + 1 ) · ( − 1 − 3 ) = ( − 1 ) · ( 2 · ( − 1 ) − 1 ) − 3 . В первом случае 63 = 63 , во втором 0 = 0 . Корни x = 6 и x = − 1 действительно являются корнями уравнения, данного в условии примера.
Ответ: 6 , − 1 .
Давайте разберем, что значит «степень целого уравнения». С этим термином мы будем часто встречаться в тех случаях, когда нам надо будет представить целое уравнение в виде алгебраического. Дадим определение понятию.
Степень целого уравнения – это степень алгебраического уравнения, равносильного исходному целому уравнению.
Если посмотреть на уравнения из примера, приведенного выше, можно установить: степень данного целого уравнения вторая.
Если бы наш курс ограничивался решением уравнений второй степени, то рассмотрение темы на этом можно было бы закончить. Но все не так просто. Решение уравнений третьей степени сопряжено с трудностями. А для уравнений выше четвертой степени и вовсе не существует общих формул корней. В связи с этим решение целых уравнений третьей, четвертой и других степеней требует от нас применения целого ряда других приемов и методов.
Чаще прочих используется подход к решению целых рациональных уравнений, который основан на методе разложения на множители. Алгоритм действий в этом случае следующий:
- переносим выражение из правой части в левую с тем, чтобы в правой части записи остался нуль;
- представляем выражение в левой части как произведение множителей, а затем переходим к совокупности нескольких более простых уравнений.
Пример 4
Найдите решение уравнения ( x 2 − 1 ) · ( x 2 − 10 · x + 13 ) = 2 · x · ( x 2 − 10 · x + 13 ) .
Решение
Переносим выражение из правой части записи в левую с противоположным знаком: ( x 2 − 1 ) · ( x 2 − 10 · x + 13 ) − 2 · x · ( x 2 − 10 · x + 13 ) = 0 . Преобразование левой части в многочлен стандартного вида нецелесообразно в связи с тем, что это даст нам алгебраическое уравнение четвертой степени: x 4 − 12 · x 3 + 32 · x 2 − 16 · x − 13 = 0 . Легкость преобразования не оправдывает всех сложностей с решением такого уравнения.
Намного проще пойти другим путем: вынесем за скобки общий множитель x 2 − 10 · x + 13 . Так мы придем к уравнению вида ( x 2 − 10 · x + 13 ) · ( x 2 − 2 · x − 1 ) = 0 . Теперь заменим полученное уравнение совокупностью двух квадратных уравнений x 2 − 10 · x + 13 = 0 и x 2 − 2 · x − 1 = 0 и найдем их корни через дискриминант: 5 + 2 · 3 , 5 — 2 · 3 , 1 + 2 , 1 — 2 .
Ответ: 5 + 2 · 3 , 5 — 2 · 3 , 1 + 2 , 1 — 2 .
Точно также мы можем использовать метод введения новой переменной. Этот метод позволяет нам переходить к равносильным уравнениям со степенями ниже, чем были степени в исходном целом уравнении.
Есть ли корни у уравнения ( x 2 + 3 · x + 1 ) 2 + 10 = − 2 · ( x 2 + 3 · x − 4 ) ?
Решение
Если мы сейчас попробуем свести целое рациональное уравнение к алгебраическому, то получим уравнение 4 степени, которое не имеет рациональных корней. Потому нам будет проще пойти другим путем: ввести новую переменную у, которая заменит в уравнении выражение x 2 + 3 · x .
Теперь мы будем работать с целым уравнением ( y + 1 ) 2 + 10 = − 2 · ( y − 4 ) . Перенесем правую часть уравнения в левую с противоположным знаком и проведем необходимые преобразования. Получим: y 2 + 4 · y + 3 = 0 . Найдем корни квадратного уравнения: y = − 1 и y = − 3 .
Теперь проведем обратную замену. Получим два уравнения x 2 + 3 · x = − 1 и x 2 + 3 · x = − 3 . Перепишем их как x 2 + 3 · x + 1 = 0 и x 2 + 3 · x + 3 = 0 . Используем формулу корней квадратного уравнения для того, чтобы найти корни первого уравнения из полученных: — 3 ± 5 2 . Дискриминант второго уравнения отрицательный. Это значит, что действительных корней у второго уравнения нет.
Ответ: — 3 ± 5 2
Целые уравнения высоких степеней попадаются в задачах достаточно часто. Пугаться их не нужно. Нужно быть готовым применить нестандартный метод их решения, в том числе и ряд искусственных преобразований.
Решение дробно рациональных уравнений
Начнем рассмотрение этой подтемы мы с алгоритма решения дробно рациональных уравнений вида p ( x ) q ( x ) = 0 , где p ( x ) и q ( x ) – целые рациональные выражения. Решение остальных дробно рациональных уравнений всегда можно свести к решению уравнений указанного вида.
В основу наиболее употребимого метода решения уравнений p ( x ) q ( x ) = 0 положено следующее утверждение: числовая дробь u v , где v – это число, которое отлично от нуля, равна нулю только в тех случаях, когда числитель дроби равен нулю. Следуя логике приведенного утверждения мы можем утверждать, что решение уравнения p ( x ) q ( x ) = 0 может быть сведено в выполнению двух условий: p ( x ) = 0 и q ( x ) ≠ 0 . На этом построен алгоритм решения дробных рациональных уравнений вида p ( x ) q ( x ) = 0 :
- находим решение целого рационального уравнения p ( x ) = 0 ;
- проверяем, выполняется ли для корней, найденных в ходе решения, условие q ( x ) ≠ 0 .
Если это условие выполняется, то найденный корень является корнем исходного уравнения. Если нет, то корень не является решением задачи.
Найдем корни уравнения 3 · x — 2 5 · x 2 — 2 = 0 .
Решение
Мы имеем дело с дробным рациональным уравнением вида p ( x ) q ( x ) = 0 , в котором p ( x ) = 3 · x − 2 , q ( x ) = 5 · x 2 − 2 = 0 . Приступим к решению линейного уравнения 3 · x − 2 = 0 . Корнем этого уравнения будет x = 2 3 .
Проведем проверку найденного корня, удовлетворяет ли он условию 5 · x 2 − 2 ≠ 0 . Для этого подставим числовое значение в выражение. Получим: 5 · 2 3 2 — 2 = 5 · 4 9 — 2 = 20 9 — 2 = 2 9 ≠ 0 .
Условие выполняется. Это значит, что x = 2 3 является корнем исходного уравнения.
Ответ: 2 3 .
Есть еще один вариант решения дробных рациональных уравнений p ( x ) q ( x ) = 0 . Вспомним, что это уравнение равносильно целому уравнению p ( x ) = 0 на области допустимых значений переменной x исходного уравнения. Это позволяет нам использовать следующий алгоритм в решении уравнений p ( x ) q ( x ) = 0 :
- решаем уравнение p ( x ) = 0 ;
- находим область допустимых значений переменной x ;
- берем корни, которые лежат в области допустимых значений переменной x , в качестве искомых корней исходного дробного рационального уравнения.
Пример 7
Решите уравнение x 2 — 2 · x — 11 x 2 + 3 · x = 0 .
Решение
Для начала решим квадратное уравнение x 2 − 2 · x − 11 = 0 . Для вычисления его корней мы используем формулу корней для четного второго коэффициента. Получаем D 1 = ( − 1 ) 2 − 1 · ( − 11 ) = 12 , и x = 1 ± 2 3 .
Теперь мы можем найти ОДЗ переменной x для исходного уравнения. Это все числа, для которых x 2 + 3 · x ≠ 0 . Это то же самое, что x · ( x + 3 ) ≠ 0 , откуда x ≠ 0 , x ≠ − 3 .
Теперь проверим, входят ли полученные на первом этапе решения корни x = 1 ± 2 3 в область допустимых значений переменной x . Мы видим, что входят. Это значит, что исходное дробное рациональное уравнение имеет два корня x = 1 ± 2 3 .
Ответ: x = 1 ± 2 3
Второй описанный метод решения проще первого в случаях, когда легко находится область допустимых значений переменной x , а корни уравнения p ( x ) = 0 иррациональные. Например, 7 ± 4 · 26 9 . Корни могут быть и рациональными, но с большим числителем или знаменателем. Например, 127 1101 и − 31 59 . Это позволяет сэкономить время на проведении проверки условия q ( x ) ≠ 0 : намного проще исключить корни, которые не подходят, по ОДЗ.
В тех случаях, когда корни уравнения p ( x ) = 0 целые, целесообразнее использовать первый из описанных алгоритмов решения уравнений вида p ( x ) q ( x ) = 0 . Быстрее сразу находить корни целого уравнения p ( x ) = 0 , после чего проверять, выполняется ли для них условие q ( x ) ≠ 0 , а не находить ОДЗ, после чего решать уравнение p ( x ) = 0 на этой ОДЗ. Это связано с тем, что в таких случаях сделать проверку обычно проще, чем найти ОДЗ.
Найдите корни уравнения ( 2 · x — 1 ) · ( x — 6 ) · ( x 2 — 5 · x + 14 ) · ( x + 1 ) x 5 — 15 · x 4 + 57 · x 3 — 13 · x 2 + 26 · x + 112 = 0 .
Решение
Начнем с рассмотрения целого уравнения ( 2 · x − 1 ) · ( x − 6 ) · ( x 2 − 5 · x + 14 ) · ( x + 1 ) = 0 и нахождения его корней. Для этого применим метод решения уравнений через разложение на множители. Получается, что исходное уравнение равносильно совокупности четырех уравнений 2 · x − 1 = 0 , x − 6 = 0 , x 2 − 5 · x + 14 = 0 , x + 1 = 0 , из которых три линейных и одно квадратное. Находим корни: из первого уравнения x = 1 2 , из второго – x = 6 , из третьего – x = 7 , x = − 2 , из четвертого – x = − 1 .
Проведем проверку полученных корней. Определить ОДЗ в данном случае нам сложно, так как для этого придется провести решение алгебраического уравнения пятой степени. Проще будет проверить условие, по которому знаменатель дроби, которая находится в левой части уравнения, не должен обращаться в нуль.
По очереди подставим корни на место переменной х в выражение x 5 − 15 · x 4 + 57 · x 3 − 13 · x 2 + 26 · x + 112 и вычислим его значение:
1 2 5 − 15 · 1 2 4 + 57 · 1 2 3 − 13 · 1 2 2 + 26 · 1 2 + 112 = = 1 32 − 15 16 + 57 8 − 13 4 + 13 + 112 = 122 + 1 32 ≠ 0 ;
6 5 − 15 · 6 4 + 57 · 6 3 − 13 · 6 2 + 26 · 6 + 112 = 448 ≠ 0 ;
7 5 − 15 · 7 4 + 57 · 7 3 − 13 · 7 2 + 26 · 7 + 112 = 0 ;
( − 2 ) 5 − 15 · ( − 2 ) 4 + 57 · ( − 2 ) 3 − 13 · ( − 2 ) 2 + 26 · ( − 2 ) + 112 = − 720 ≠ 0 ;
( − 1 ) 5 − 15 · ( − 1 ) 4 + 57 · ( − 1 ) 3 − 13 · ( − 1 ) 2 + 26 · ( − 1 ) + 112 = 0 .
Проведенная проверка позволяет нам установить, что корнями исходного дробного рацинального уравнения являются 1 2 , 6 и − 2 .
Ответ: 1 2 , 6 , — 2
Найдите корни дробного рационального уравнения 5 · x 2 — 7 · x — 1 · x — 2 x 2 + 5 · x — 14 = 0 .
Решение
Начнем работу с уравнением ( 5 · x 2 − 7 · x − 1 ) · ( x − 2 ) = 0 . Найдем его корни. Нам проще представить это уравнение как совокупность квадратного и линейного уравнений 5 · x 2 − 7 · x − 1 = 0 и x − 2 = 0 .
Используем формулу корней квадратного уравнения для поиска корней. Получаем из первого уравнения два корня x = 7 ± 69 10 , а из второго x = 2 .
Подставлять значение корней в исходное уравнение для проверки условий нам будет достаточно сложно. Проще будет определить ОДЗ переменной x . В данном случае ОДЗ переменной x – это все числа, кроме тех, для которых выполняется условие x 2 + 5 · x − 14 = 0 . Получаем: x ∈ — ∞ , — 7 ∪ — 7 , 2 ∪ 2 , + ∞ .
Теперь проверим, принадлежат ли найденные нами корни к области допустимых значений переменной x .
Корни x = 7 ± 69 10 — принадлежат, поэтому, они являются корнями исходного уравнения, а x = 2 – не принадлежит, поэтому, это посторонний корень.
Ответ: x = 7 ± 69 10 .
Разберем отдельно случаи, когда в числителе дробного рационального уравнения вида p ( x ) q ( x ) = 0 находится число. В таких случаях, если в числителе находится число, отличное от нуля, то уравнение не будет иметь корней. Если это число будет равно нулю, то корнем уравнения будет любое число из ОДЗ.
Решите дробное рациональное уравнение — 3 , 2 x 3 + 27 = 0 .
Решение
Данное уравнение не будет иметь корней, так как в числителе дроби из левой части уравнения находится отличное от нуля число. Это значит, что ни при каких значениях x значение приведенной в условии задачи дроби не будет равняться нулю.
Ответ: нет корней.
Решите уравнение 0 x 4 + 5 · x 3 = 0 .
Решение
Так как в числителе дроби находится нуль, решением уравнения будет любое значение x из ОДЗ переменной x .
Теперь определим ОДЗ. Оно будет включать все значения x , при которых x 4 + 5 · x 3 ≠ 0 . Решениями уравнения x 4 + 5 · x 3 = 0 являются 0 и − 5 , так как, это уравнение равносильно уравнению x 3 · ( x + 5 ) = 0 , а оно в свою очередь равносильно совокупности двух уравнений x 3 = 0 и x + 5 = 0 , откуда и видны эти корни. Мы приходим к тому, что искомой областью допустимых значений являются любые x , кроме x = 0 и x = − 5 .
Получается, что дробное рациональное уравнение 0 x 4 + 5 · x 3 = 0 имеет бесконечное множество решений, которыми являются любые числа кроме нуля и — 5 .
Ответ: — ∞ , — 5 ∪ ( — 5 , 0 ∪ 0 , + ∞
Теперь поговорим о дробных рациональных уравнениях произвольного вида и методах их решения. Их можно записать как r ( x ) = s ( x ) , где r ( x ) и s ( x ) – рациональные выражения, причем хотя бы одно из них дробное. Решение таких уравнений сводится к решению уравнений вида p ( x ) q ( x ) = 0 .
Мы уже знаем, что мы можем получить равносильное уравнение при переносе выражения из правой части уравнения в левое с противоположным знаком. Это значит, что уравнение r ( x ) = s ( x ) равносильно уравнение r ( x ) − s ( x ) = 0 . Также мы уже разобрали способы преобразования рационального выражения в рациональную дробь. Благодаря этому мы без труда можем преобразовать уравнение r ( x ) − s ( x ) = 0 в тождественную ему рациональную дробь вида p ( x ) q ( x ) .
Так мы переходим от исходного дробного рационального уравнения r ( x ) = s ( x ) к уравнению вида p ( x ) q ( x ) = 0 , решать которые мы уже научились.
Следует учитывать, что при проведении переходов от r ( x ) − s ( x ) = 0 к p ( x ) q ( x ) = 0 , а затем к p ( x ) = 0 мы можем не учесть расширения области допустимых значений переменной x .
Вполне реальна ситуация, когда исходное уравнение r ( x ) = s ( x ) и уравнение p ( x ) = 0 в результате преобразований перестанут быть равносильными. Тогда решение уравнения p ( x ) = 0 может дать нам корни, которые будут посторонними для r ( x ) = s ( x ) . В связи с этим в каждом случае необходимо проводить проверку любым из описанных выше способов.
Чтобы облегчить вам работу по изучению темы, мы обобщили всю информацию в алгритм решения дробного рационального уравнения вида r ( x ) = s ( x ) :
- переносим выражение из правой части с противоположным знаком и получаем справа нуль;
- преобразуем исходное выражение в рациональную дробь p ( x ) q ( x ) , последовательно выполняя действия с дробями и многочленами;
- решаем уравнение p ( x ) = 0 ;
- выявляем посторонние корни путем проверки их принадлежности ОДЗ или методом подстановки в исходное уравнение.
Визуально цепочка действий будет выглядеть следующим образом:
r ( x ) = s ( x ) → r ( x ) — s ( x ) = 0 → p ( x ) q ( x ) = 0 → p ( x ) = 0 → о т с е и в а н и е п о с т о р о н н и х к о р н е й
Решите дробное рациональное уравнение x x + 1 = 1 x + 1 .
Решение
Перейдем к уравнению x x + 1 — 1 x + 1 = 0 . Преобразуем дробное рациональное выражение в левой части уравнения к виду p ( x ) q ( x ) .
Для этого нам придется привести рациональные дроби к общему знаменателю и упростить выражение:
x x + 1 — 1 x — 1 = x · x — 1 · ( x + 1 ) — 1 · x · ( x + 1 ) x · ( x + 1 ) = = x 2 — x — 1 — x 2 — x x · ( x + 1 ) = — 2 · x — 1 x · ( x + 1 )
Для того, чтобы найти корни уравнения — 2 · x — 1 x · ( x + 1 ) = 0 , нам необходимо решить уравнение − 2 · x − 1 = 0 . Получаем один корень x = — 1 2 .
Нам осталось выполнить проверку любым из методов. Рассмотрим их оба.
Подставим полученное значение в исходное уравнение. Получим — 1 2 — 1 2 + 1 = 1 — 1 2 + 1 . Мы пришли к верному числовому равенству − 1 = − 1 . Это значит, что x = − 1 2 является корнем исходного уравнения.
Теперь проведем проверку через ОДЗ. Определим область допустимых значений переменной x . Это будет все множество чисел, за исключением − 1 и 0 (при x = − 1 и x = 0 обращаются в нуль знаменатели дробей). Полученный нами корень x = − 1 2 принадлежит ОДЗ. Это значит, что он является корнем исходного уравнения.
Ответ: − 1 2 .
Найдите корни уравнения x 1 x + 3 — 1 x = — 2 3 · x .
Решение
Мы имеем дело с дробным рациональным уравнением. Следовательно, будем действовать по алгоритму.
Перенесем выражение из правой части в левую с противоположным знаком: x 1 x + 3 — 1 x + 2 3 · x = 0
Проведем необходимые преобразования: x 1 x + 3 — 1 x + 2 3 · x = x 3 + 2 · x 3 = 3 · x 3 = x .
Приходим к уравнению x = 0 . Корень этого уравнения – нуль.
Проверим, не является ли этот корень посторонним для исходного уравнения. Подставим значение в исходное уравнение: 0 1 0 + 3 — 1 0 = — 2 3 · 0 . Как видите, полученное уравнение не имеет смысла. Это значит, что 0 – это посторонний корень, а исходное дробное рациональное уравнение корней не имеет.
Ответ: нет корней.
Если мы не включили в алгоритм другие равносильные преобразования, то это вовсе не значит, что ими нельзя пользоваться. Алгоритм универсален, но он создан для того, чтобы помогать, а не ограничивать.
Решите уравнение 7 + 1 3 + 1 2 + 1 5 — x 2 = 7 7 24
Решение
Проще всего будет решить приведенное дробное рациональное уравнение согласно алгоритму. Но есть и другой путь. Рассмотрим его.
Отнимем от правой и левой частей 7 , получаем: 1 3 + 1 2 + 1 5 — x 2 = 7 24 .
Отсюда можно заключить, что выражение в знаменателе левой части должно быть равно числу, обратному числу из правой части, то есть, 3 + 1 2 + 1 5 — x 2 = 24 7 .
Вычтем из обеих частей 3 : 1 2 + 1 5 — x 2 = 3 7 . По аналогии 2 + 1 5 — x 2 = 7 3 , откуда 1 5 — x 2 = 1 3 , и дальше 5 — x 2 = 3 , x 2 = 2 , x = ± 2
Проведем проверку для того, чтобы установить, являются ли найденные корни корнями исходного уравнения.
http://wika.tutoronline.ru/algebra/class/9/drobnoraczionalnye-uravneniya
http://zaochnik.com/spravochnik/matematika/systems/reshenie-tselyh-i-drobno-ratsionalnyh-uravnenij/
Дробно-рациональные уравнения — это уравнения c одной переменной.
Содержание:
Определение дробно-рационального уравнения
Определение дробно-рационального уравнения:
Например, уравнения
являются дробно-рациональными.
Рассмотрим дробно-рациональное уравнение 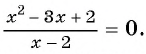
Рациональная дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю.
Таким образом, получим:
Ответ: 1.
Вернемся к уравнению 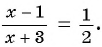
1) Перенесем все слагаемые из правой части уравнения в левую:
2) Преобразуем левую часть уравнения к рациональной дроби:
3) Применим условие равенства дроби нулю:
Ответ: 5.
Что нужно для решения дробно-рационального уравнения
Чтобы решить дробно-рациональное уравнение, нужно:
- Перенести все слагаемые из правой части уравнения в левую.
- Преобразовать левую часть уравнения к рациональной дроби.
- Применить условие равенства дроби нулю.
- Записать ответ.
Рассмотрим задачу: В дроби числитель на 2 больше знаменателя. Если числитель этой дроби уменьшить на 3, а знаменатель увеличить на 3, то новая дробь будет равна 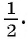
Решение:
Обозначим знаменатель первоначальной дроби через х, тогда ее числитель равен
Если числитель дроби уменьшить на 3, то получится числитель новой дроби: 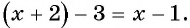
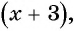
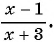
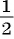
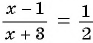
Решение многих задач приводит к уравнениям, у которых в левой или правой (или в той и другой) частях записаны дробные рациональные выражения. Такие уравнения называют дробно-рациональными уравнениями.
Пример №1
Решите уравнение
Решение:
(1)
(2)
(3)
(4) Ответ:
Пример №2
Решите уравнение
Решение:
(1)
(2)
(3)
(4) Ответ:
Пример №3
Решите уравнение
Решение:
(1)
(2)
(3)
(4) Ответ: -2; 6.
Пример №4
Решите уравнение
Решение:
Выполним замену переменной 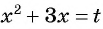
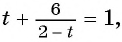
Подставим найденные значения 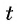
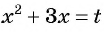
Ответ:
Дробно-рациональные уравнения используются как математические модели для решения задач, описывающих реальные ситуации.
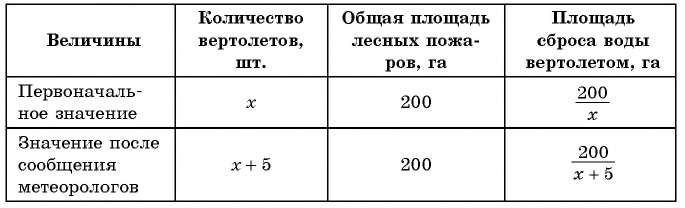
Например, рассмотрим задачу. На тушение лесных пожаров площадью 200 га отправлено несколько вертолетов с водосливными устройствами. По информации метеорологов предполагается усиление ветра, поэтому было выделено еще 5 вертолетов, в связи с чем площадь для сброса воды каждым вертолетом уменьшилась на 20 га. Сколько вертолетов участвовало в тушении пожаров первоначально?
Решение:
(1) Выясним, о каких величинах и зависимостях между ними в задаче идет речь. В задаче речь идет о площади лесных пожаров и количестве вертолетов для тушения пожаров.
(2) Выясним, какие значения, величин и зависимости между ними, известны. Известна зависимость между количеством вертолетов и площадью для сброса воды.
(3) Выясним, какие значения величин и зависимости между ними не известны. Неизвестно, сколько потребовалось вертолетов.
(4) Обозначим неизвестное значение одной величины через х, а остальные выразим через х и зависимости между величинами. Обозначим через 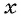
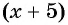
(5) Используя зависимости между известными и неизвестными значениями величин, составим уравнение (математическую модель задачи) и решим его.
По условию задачи 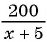
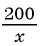
(6) Запишем ответ в соответствии со смыслом задачи. Поскольку 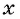
Ответ: 5 вертолетов.
Многие задачи, описывающие реальные процессы, имеют одну и ту же математическую модель. К таким относятся, например, задачи на движение, работу и т. п.
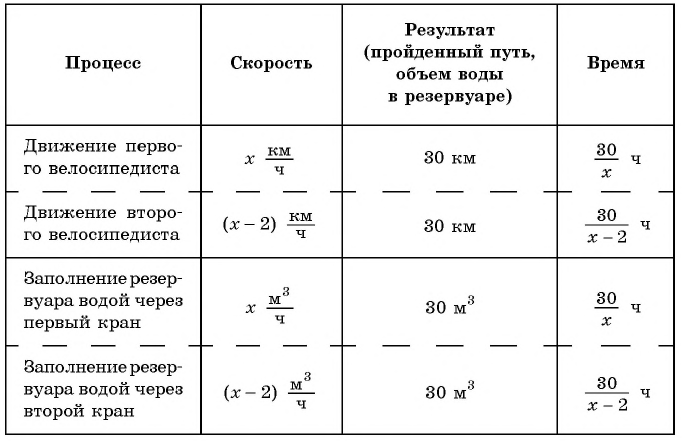
Рассмотрим две задачи:
Задача 1. Два велосипедиста выехали одновременно из поселка 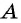
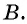
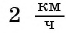
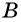
Задача 2. Для заполнения водой резервуара объемом 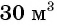
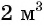
В обеих задачах речь идет о процессах: в первой — о процессе движения, во второй — о процессе заполнения резервуара водой.
Составим таблицу зависимостей между величинами.
Поскольку первый велосипедист прибыл в поселок на 0,5 ч раньше второго, а один кран заполняет резервуар на 0,5 ч быстрее другого, то уравнение 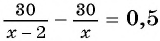
Решим полученное уравнение:
По условию каждой задачи подходит число 12.
Ответ задачи 1: скорость первого велосипедиста 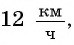
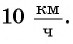
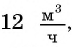
Пример №5
Является ли дробно-рациональным уравнение:
а)
б)
в)
г)
Решение:
Уравнение а) не является дробно-рациональным, так как его левая и правая части — целые рациональные выражения. Уравнения б)—г) являются дробно-рациональными, так как левые части этих уравнений — дробно-рациональные выражения.
Пример №6
Решите уравнение, используя условие равенства дроби нулю:
а)
б)
в)
г)
Решение:
а)
Ответ: 6.
б)
Ответ: -6.
в)
Ответ: 0; 6.
г)
Ответ: нет корней.
Пример №7
Какие из уравнений:
а)
б)
в)
г) 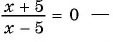
Решение:
а)
б)
в)
г)
Ответ: уравнения а), в), г) имеют один и тот же корень (уравнения равносильны).
Пример №8
Решите уравнение:
а)
б)
Решение:
а) (1)
(2)
(3)
(4) Ответ: 1; 2.
б)
Разложим на множители квадратный трехчлен в знаменателе первой дроби и получим:
Ответ: 2,5.
Пример №9
Найдите нули функции
Решение:
Так как нули функции — это значения аргумента, при которых значение функции равно нулю, то для решения задачи нужно решить уравнение
Используем условие равенства дроби нулю:
Ответ: 0; 3.
Пример №10
Найдите корни уравнения
Решение:
Выполним замену переменной в данном уравнении: 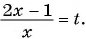
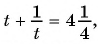
Решим его:
Выполним подстановку найденных значений переменной 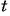
Ответ:
Моделирование реальных процессов с помощью дробно-рациональных уравнении
Задача:
Катер прошел 15 км по течению реки и 4 км по озеру, затратив на весь путь 1 ч. Чему равна скорость катера при движении по озеру, если скорость течения реки 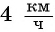
Решение:
В задаче идет речь о процессах движения катера по реке и по озеру. Составим таблицу зависимостей между величинами.
Так как по условию задачи на весь путь затрачен 1 ч, то составим уравнение: 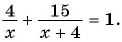
По условию подходит число 16.
Ответ: 16
Системы нелинейных уравнений для решения дробно-рациональных уравнений
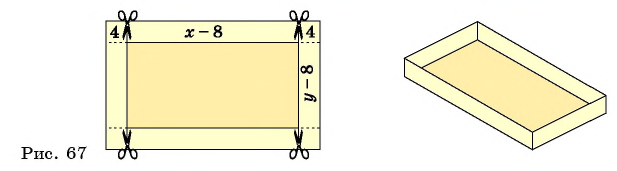
Рассмотрим задачу. Из листа картона прямоугольной формы нужно изготовить коробку без крышки, сделав надрезы в углах длиной 4 см (рис. 67). Найдите длину и ширину листа, зная, что его периметр равен 60 см, а объем коробки должен быть равен
Решение:
Обозначим длину и ширину листа соответственно 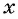
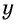
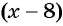

По условию задачи периметр листа прямоугольной формы равен 60 см, а объем коробки равен 160 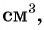
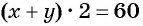
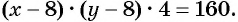
Полученная система уравнений содержит нелинейное рациональное уравнение 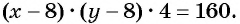
Способ подстановки
Решим полученную в задаче систему уравнений способом подстановки:
Из первого уравнения системы выразим переменную 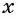
Заменим во втором уравнении переменную 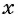
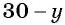
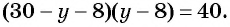
Найденные значения 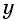
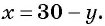
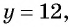
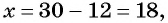
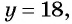
Решениями системы уравнений являются пары чисел 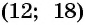
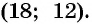
Чтобы решить систему уравнений способом подстановки, нужно:
- Из одного уравнения системы выразить одну из переменных.
- Заменить в другом уравнении эту переменную на ее выражение.
- Решить полученное уравнение.
- Найденные значения одной переменной подставить в выражение для другой переменной и найти значение другой переменной.
- В виде упорядоченных пар чисел записать ответ.
Решите систему уравнений
Решение:
(1) Из второго уравнения системы выразим переменную
(2) Заменим в первом уравнении переменную 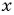
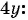
(3) Решим уравнение 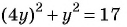
(4) Найденные значения 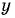
Если 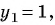
Если 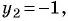
(5) Ответ: (4; 1), (-4; -1).
Способ сложения
Чтобы решить систему уравнений способом сложения, нужно:
- Одно из уравнений системы оставить без изменения, а другое заменить суммой уравнений системы.
- Из полученного уравнения (суммы) найти значения одной из переменных.
- Подставить эти значения переменной в оставленное без изменения уравнение системы и найти значения другой переменной.
- Записать ответ.
Решите систему уравнений
Решение:
(1)
(2)
(3) При 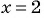
При 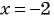
(4) Ответ: (2;1), (2;-1), (-2;1), (-2;-1).
- Заказать решение задач по высшей математике
Графический метод решения систем нелинейных уравнений
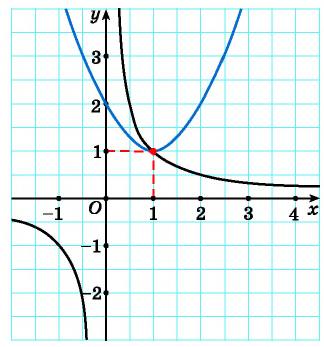
Решим систему уравнений 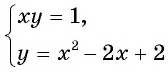
Первое уравнение системы равносильно уравнению 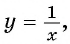
Графиком второго уравнения системы 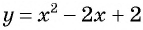
Единственная точка пересечения гиперболы 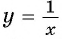
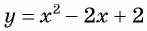
Рис. 68
Поскольку графический метод решения систем уравнений не является точным, то полученный результат необходимо проверить.
Подставим пару чисел (1; 1) в каждое из уравнений системы 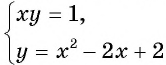
В рассмотренной системе решением оказалась пара целых чисел, которую легко было найти с помощью построенных графиков. В других случаях найти точные значения переменных по графику может оказаться затруднительно. Но, как правило, с помощью графического метода можно определить число решений системы уравнений.
Например, определим число решений системы уравнений 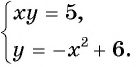
Рис. 69
Моделирование реальных процессов с помощью систем нелинейных уравнений
Системы нелинейных уравнений также являются математическими моделями при решении задач.
Задача:
Лечебными травами было решено засеять прямоугольный участок площадью 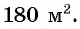
Решение:
В задаче речь идет о длине и ширине прямоугольного участка и его площади.
Если одну сторону участка обозначить через 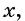
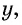
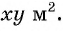
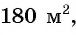
После уменьшения размеров участка площадь станет равной 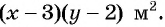
Объединим оба уравнения в систему
Получили математическую модель задачи в виде системы нелинейных уравнений. Решим ее, используя способ подстановки.
Условию задачи удовлетворяют найденные решения системы: стороны участка равны либо 15 м и 12 м, либо 18 м и 10 м.
Ответ: 15 м, 12 м или 18 м, 10 м.
Пример №11
Решите систему уравнений:
а)
б)
Решение:
а) Решим систему способом подстановки:
Ответ: (3; 0), (0; 3).
б) Применим способ сложения. Умножим первое уравнение на 2, сложим со вторым и получим:
Ответ:
Пример №12
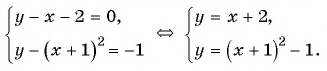
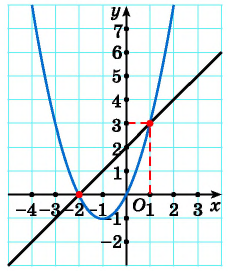
Решите графически систему уравнений
Решение:
Построим графики уравнений системы
График первого уравнения — прямая, проходящая через точки (-2; 0), (1; 3). График второго уравнения — парабола с вершиной в точке (-1; -1), пересекающая ось абсцисс в точках (-2; 0) и (0; 0), проходящая через точку (1; 3).
Прямая пересекается с параболой в точках с координатами (-2; 0), (1; 3). С помощью проверки убеждаемся, что пары чисел (-2; 0) и (1; 3) являются решениями данной системы.
Ответ: (-2; 0), (1; 3).
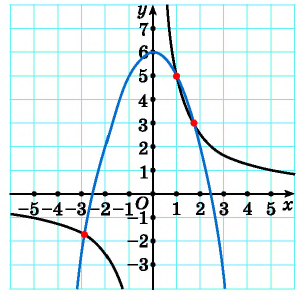
Пример №13
Сколько решений имеет система уравнений
Решение:
Построим в одной системе координат графики уравнений системы. Графиком первого уравнения системы является гипербола, проходящая через точки (-1; 4), (-4; 1). График второго уравнения — парабола с вершиной в точке (-4; 0), пересекающая ось ординат в точке (0; 16).
На рисунке видны только две точки пересечения графиков. Но, учитывая то, что парабола пересекает ось ординат, а гипербола не пересекает, делаем вывод, что графики пересекаются еще в одной точке. Таким образом, графики пересекаются в трех точках, а, значит, система имеет три решения.
Пример №14
Решите систему уравнений
Решение:
Решим систему методом замены переменных. Введем новые переменные: 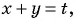
Тогда система примет вид
Решим ее способом подстановки:
Подставим 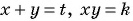
Решив каждую из двух систем совокупности способом подстановки, получим следующие решения исходной системы уравнений: (-5; 1); (1; -5); (4; 1); (1; 4).
Ответ: (-5; 1); (1; -5); (4; 1); (1; 4).
Задача:
Сумма квадратов цифр двузначного числа равна 13. Если из этого числа вычесть 9, то получится число, записанное теми же цифрами, но в обратном порядке. Найдите данное число.
Решение:
Обозначим цифру десятков данного числа через 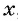
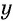
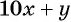
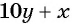
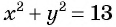
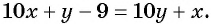
По условию задачи подходит только
Ответ: 32.
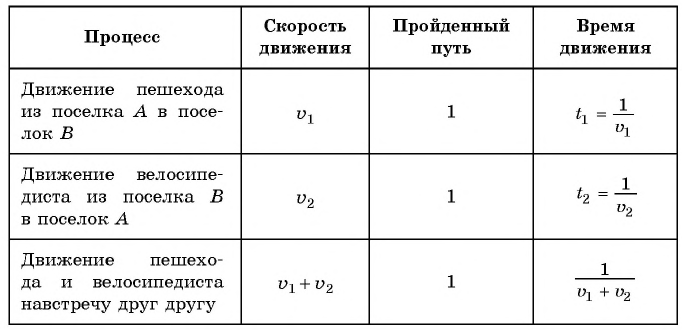
Задача:
Из поселка 
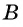
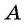
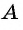
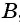
Решение:
Составим таблицу зависимостей между величинами.
По условию задачи велосипедист проделал бы тот же путь на 4 ч быстрее пешехода, поэтому получим уравнение
При движении навстречу друг другу пешеход и велосипедист встретились через 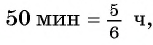
Составим и решим систему уравнений:
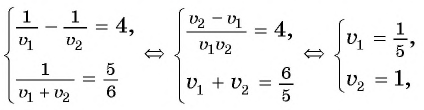
Ответ: 5 ч.
Задача:
Две бригады, работая вместе, ремонтировали дорогу в течение б дней, а затем одна вторая бригада закончила ремонт за 10 дней. За сколько дней могла бы отремонтировать дорогу одна первая бригада, если она может выполнить эту работу на б дней быстрее, чем одна вторая?
Решение:
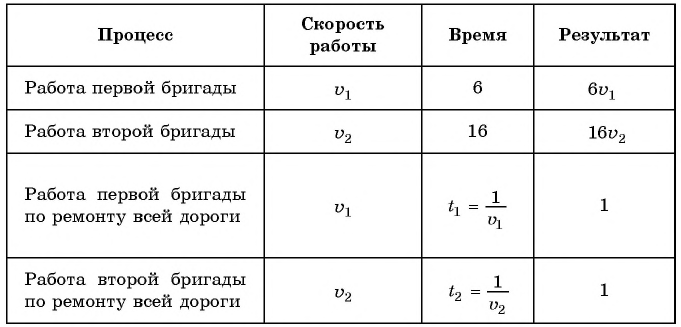
Составим таблицу зависимостей между величинами.
Обозначим объем всей работы через 1, тогда получим уравнение
Зная, что одна первая бригада может выполнить эту работу на б дней быстрее, чем одна вторая, составим уравнение
Составим и решим систему уравнений:
Ответ: 18 ч.
Формула длины отрезка с заданными координатами его концов. Уравнение окружности
Для применения графического метода решения систем необходимо знать графики различных уравнений. Многие из них вам уже знакомы. Это, например, прямая, гипербола, парабола.
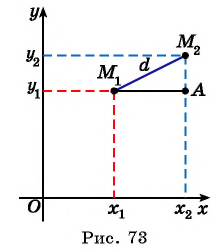
Расширим возможности использования графического метода решения систем нелинейных уравнений и выведем уравнение окружности с центром в заданной точке с заданным радиусом. Для этого сначала выведем формулу для вычисления длины отрезка с заданными координатами его концов, т. е. для вычисления расстояния между двумя точками, заданными своими координатами.
Рассмотрим точки 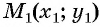
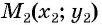
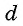
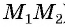
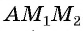
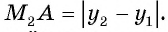
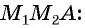
Получили формулу длины отрезка с заданными координатами его концов, или формулу расстояния между двумя точками с координатами
Пример №15
Найдите расстояние между точками А(-1; 3) и В(2; 5).
Решение:
Подставим координаты точек А(-1; 3) и В(2; 5) в формулу расстояния между двумя точками 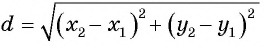
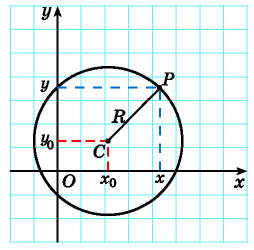
Рассмотрим окружность на координатной плоскости. Окружность — это множество точек плоскости, расстояние от каждой из которых до одной данной точки (центра окружности) является величиной постоянной, равной радиусу окружности
По формуле расстояния между двумя точками найдем расстояние от данной точки 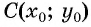
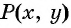
Рис. 74
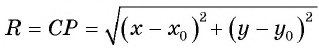
Таким образом, если точка принадлежит окружности с центром 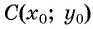
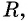
Уравнение 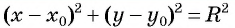
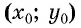
Если координаты точки удовлетворяют уравнению 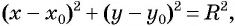
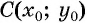
Покажем, что если точка 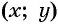
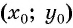
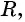
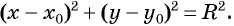
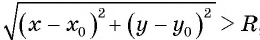
т. е.
Чтобы составить уравнение окружности, нужно:
- Определить координаты центра окружности
- Определить радиус окружности
- Подставить найденные значения
и
в уравнение окружности
Составьте уравнение окружности с центром в точке (-8; 2) и радиусом 5.
Решение:
(1)
(2)
(3)
Пример №16
Составьте уравнение окружности:
а) с центром в точке (4; -1) и радиусом
б) с центром в точке (0; 0) и радиусом 4.
Решение:
а) Подставим координаты центра окружности 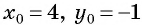
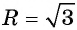
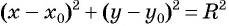
б) Координаты центра окружности: 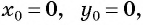
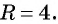
Если центром окружности радиуса 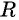
Пример №17
Определите количество решений системы уравнений
Решение:
Рис. 75
Построим графики уравнений системы. Первое уравнение — это уравнение окружности с центром в начале координат и радиусом, равным 4. Графиком второго уравнения является парабола с вершиной в точке (1; 5), пересекающая ось ординат в точке (0; 4).
Построенные графики пересекаются в четырех точках (рис. 75). Значит, данная система уравнений имеет 4 решения.
Ответ: 4 решения.
Пример №18
Найдите длину отрезка 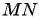
Решение:
По формуле длины отрезка 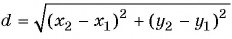
Пример №19
Найдите длину диагонали прямоугольника, если заданы его вершина 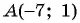
Решение:
Найдем длину отрезка
Длина отрезка 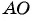
Пример №20
Определите координаты центра и радиус окружности:
а)
б)
в)
Решение:
а)
б)
в)
Пример №21
Какие из данных точек лежат на окружности
а)
б)
в)
г)
Решение:
Подставим координаты точек в уравнение окружности:
а) 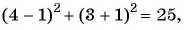
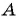
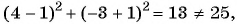
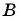
в) 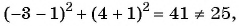
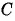
г) 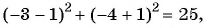
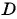
Пример №22
Запишите уравнение окружности с центром в точке (-1; 1) и радиусом
Решение:
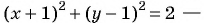
Пример №23
Запишите уравнение окружности с центром в точке 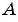
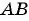
Решение:
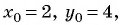
Уравнение окружности
Пример №24
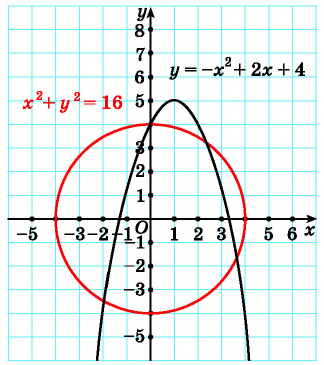
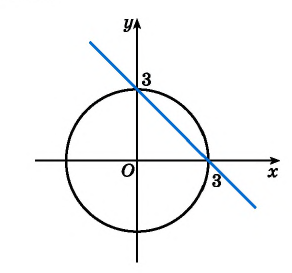
Решите систему уравнений 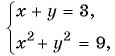
Решение:
График первого уравнения — прямая, проходящая через точки (3; 0), (0; 3). График второго уравнения — окружность с центром в начале координат и радиусом, равным 3.
Координаты точек пересечения (3; 0), (0; 3) — решения системы.
- Дробно-рациональные неравенства
- Прогрессии в математике — арифметическая, геометрическая
- Единичная окружность — в тригонометрии
- Определение синуса и косинуса произвольного угла
- Рациональная дробь
- Функция в математике
- Наибольшее и наименьшее значения функции
- Раскрытие неопределенностей
Методы решения уравнений, содержащих дроби
В этой статье я расскажу методики решения рациональных уравнений, содержащих дроби.
Что такое рациональное уравнение? Это уравнение, которое содержит в себе такие действия как сложение, вычитание, умножение, деление, возведение в степень с целым показателем. Извлечение корня — это недопустимое действие для рационального уравнения. Корень делает уравнение иррациональным, как, собственно, и дробный показатель степени.
В свою очередь рациональные уравнения делятся на два вида: целые рациональные и дробные рациональные.
К целым рациональным уравнениям относятся линейные и квадратные уравнения. Рассмотрим пример:
Это уравнение является…попробуешь угадать?…линейным. Его можно запросто увидеть, если деление на 2 и на 6 заменить умножением на 1/2 и 1/6 соответственно. Но оно все-таки содержит в себе знаменатель, поэтому мы его и рассматриваем в данной статье.
К дробным рациональным уравнениям относятся уравнения, которые содержат икс в знаменателе. Например, это уравнение дробное рациональное:
Методика решения приведенных примеров, в принципе, одинакова. Разница состоит в том, что в дробных рациональных уравнениях знаменатель не должен равняться нулю, поэтому при их решении оговаривают ограничения для икса. По-научному говорят, что находят область допустимых значений (ОДЗ).
Но давайте начнем с простого.
Целое рациональное уравнение.
Сначала решим целое рациональное уравнение.
Если ты в уравнении видишь дроби, то надо от них избавится, ведь уравнение без дробей решается намного приятнее)
В этом уравнении находим общий знаменатель. Он равен 6. Это значит, что обе части уравнения надо умножить на 6 (одинокий икс тоже).
Обычно этот шаг пропускают и переходят к следующему, но я его все равно распишу:
Числители и знаменатели сокращаются и получается элементарное уравнение:
Приводим подобные слагаемые:
Чтобы найди икс надо -10 разделить на 10 (произведение делим на известный множитель). Получаем ответ:
Готово!
Дробное рациональное уравнение.
Теперь решим дробное рациональное уравнение.
Я уже писала о том, что в дробных рациональных уравнениях знаменатели не должны равняться нулю. Знаменатель второй дроби нас устраивает, ведь 3 не равно 0) А вот знаменатель первой дроби требует от нас, чтобы мы нашли ОДЗ.
А дальше по накатанной: надо обе части уравнения умножить на общий знаменатель. Общим знаменателем будет выражение 3(х + 9).
Снова распишу подробно, но если ты шаришь, то следующую запись можешь не писать.
В первой дроби сокращаем (х + 9), а во второй — тройки. Получаем такое уравнение:
Здесь можно раскрыть скобки, потом перенести известные в одну сторону, а неизвестные — в другую… Но делать я этого не стану, а просто обе части уравнения разделю на -2. А еще поменяю местами левую и правую части уравнения, чтобы привести его к привычному виду.
Чтобы найти неизвестное слагаемое надо из суммы вычесть известное слагаемое, т.е. из -9 вычесть 9.
Ответ таков:
Сравниваем с ОДЗ… Всё отлично. Корень уравнения подходит.
Альтернативный метод решения уравнения с дробями.
Но нельзя пройти мимо другого метода решения данного уравнения: с помощью пропорции. Помнишь, как она раскрывается? Правильно, крест-накрест. И не надо искать общий знаменатель)
Перемножаем….и о чудо! Получаем уравнение, которое мы уже решали!
Дальнейшее решение расписывать не буду, оно есть выше.
Такой способ решения уравнений хорош, когда в уравнении имеются две дроби.
В завершении решу еще одно уравнение предложенными выше способами.
Только ты решаешь какой способ выбрать.
Твой персональный препод Васильева Анна)


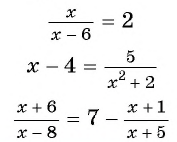
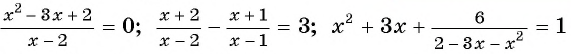
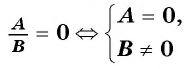
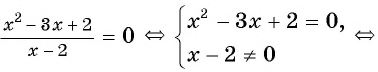
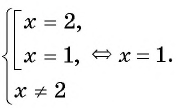
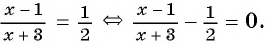
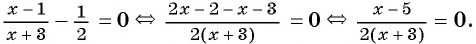
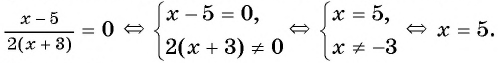
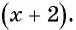
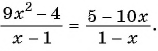
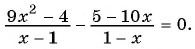
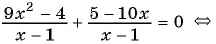
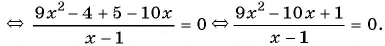
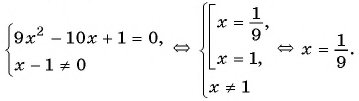
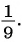
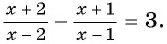
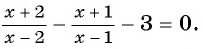
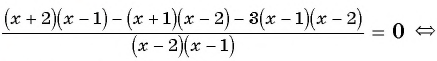
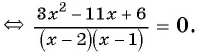
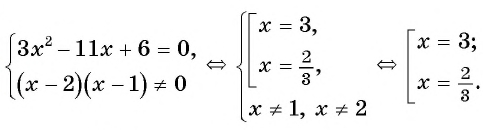
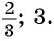
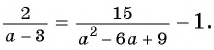
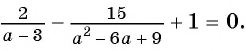
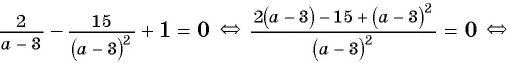
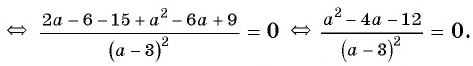
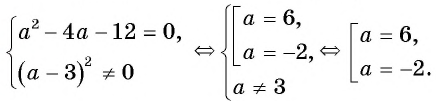
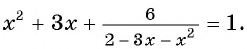
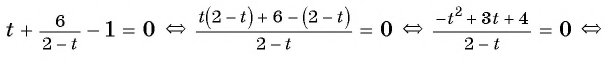
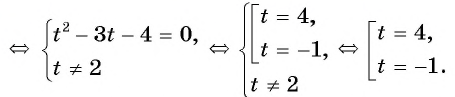
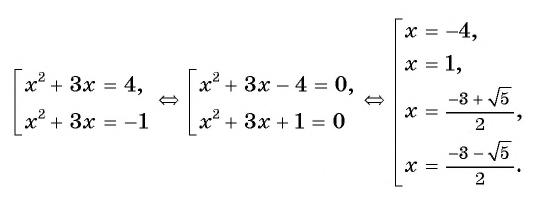

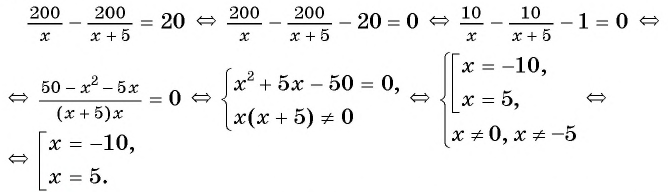
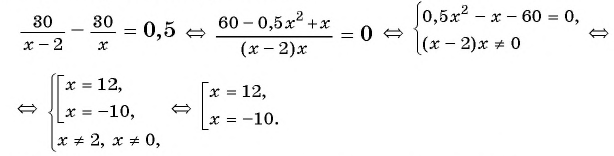
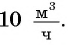
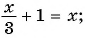
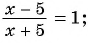
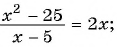
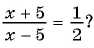
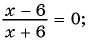
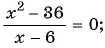
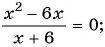
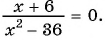
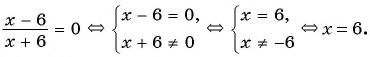
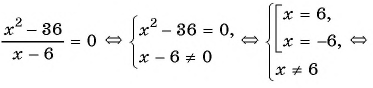
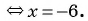
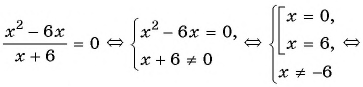
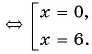
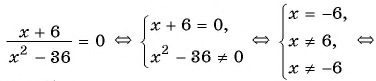
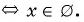
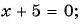
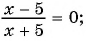
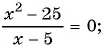
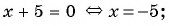
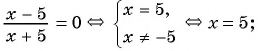
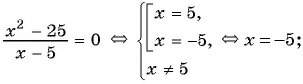
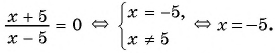
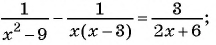
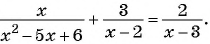
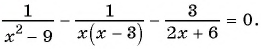
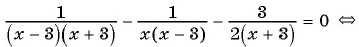
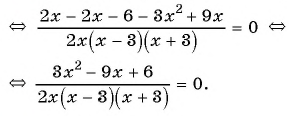
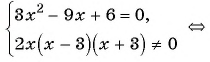
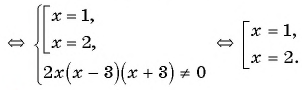
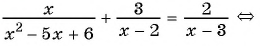
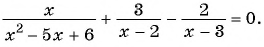
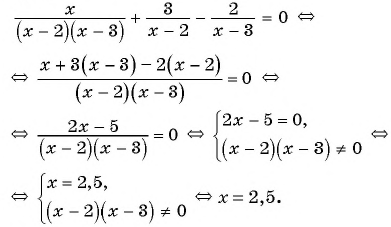
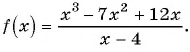
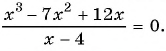
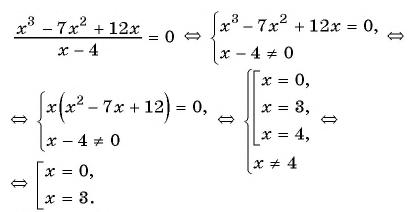
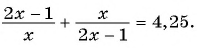
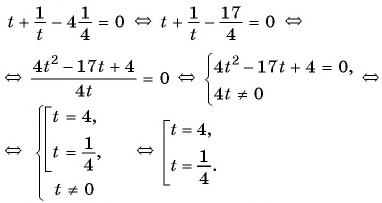
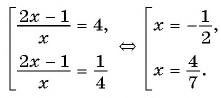
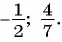

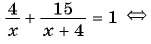
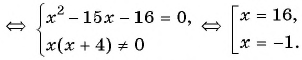
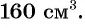
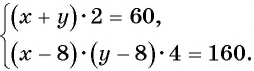
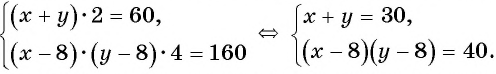
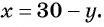
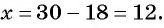
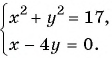
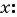
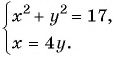
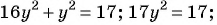
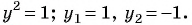
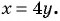
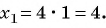
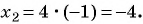
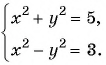
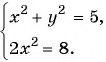
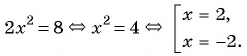
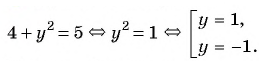
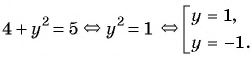
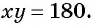
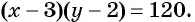
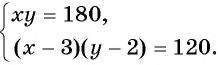
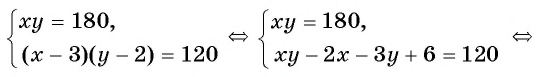
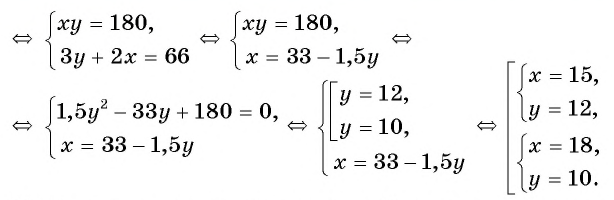
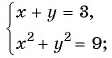
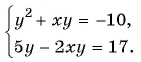
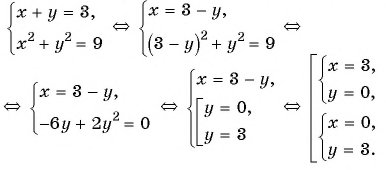
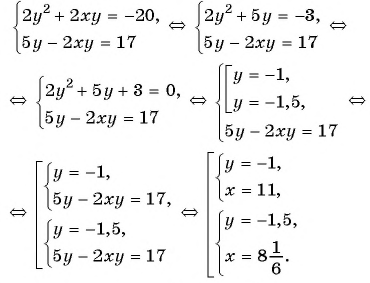
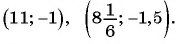
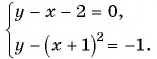
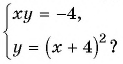
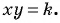
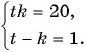
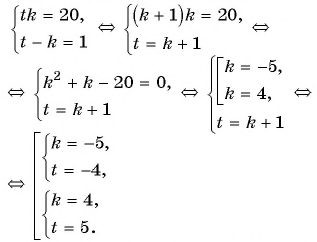
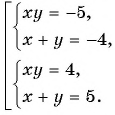
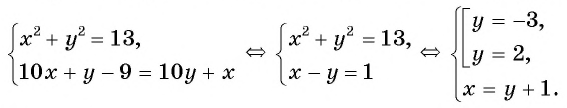
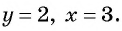
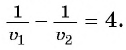
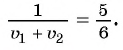
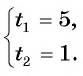
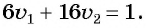
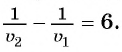
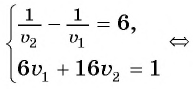
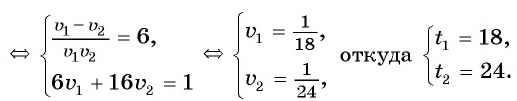
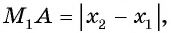
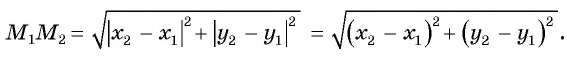
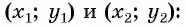
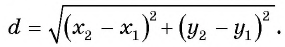
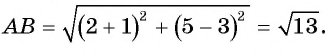
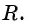
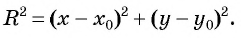
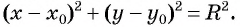
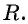
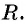
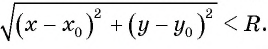
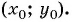
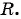
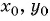 и
и 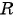 в уравнение окружности
в уравнение окружности