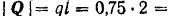Если
линии действия всех сил данной системы
расположены в одной плоскости и
параллельны между собой, то такая система
называется плоской
системой параллельных сил. Плоская
система параллельных сил является
частным случаем произвольной плоской
системы сил. Поэтому к плоской системе
параллельных сил можно применить условия
равновесия произвольной плоской системы
сил (см. § 4.6):
;
;
.
(1)
М
можем направить ось
перпендикулярно
к силам плоской системы параллельных
сил, а ось
параллельно
им (рисунок 64). Тогда проекция каждой из
сил на ось
будет
равна нулю и первое из равенств (1)
обратится в тождество вида
независимо от того, уравновешиваются
данные силы или нет. В результате для
плоской системы параллельных сил
останутся только два условия равновесия:
;
,
(2)
или
;
,
так
как проекция каждой силы на ось
равна
модулю этой силы, взятой с соответствующим
знаком
.
Таким
образом, для
равновесия плоской системы параллельных
сил необходимо и достаточно, чтобы
алгебраическая сумма всех этих сил
равнялась нулю и чтобы алгебраическая
сумма их моментов относительно
произвольной точки, взятой в плоскости
действия этой системы, также равнялась
нулю.
Другая форма
условий равновесия для плоской
параллельной системы сил, получающаяся
из равенств (5, § 22), имеет вид
;
(3)
где
точки А
и В
не должны лежать на примой, параллельной
данным силам.
Следовательно,
для
равновесия плоской системы параллельных
сил необходимо и достаточно, чтобы
алгебраические суммы моментов всех
этих сил относительно каждой из двух
произвольных точек А и В, взятых в
плоскости действия это системы, но не
лежащих на прямой, параллельной данным
силам, были равны нулю.
При
решении задач этой главы следует иметь
в виду все те общие указания, которые
были сделаны в §
2.7.
4.8 Указания к решению задач
Еще раз подчеркнем,
что приступая к решению задач, относящихся
к равновесию несвободного твердого
тела под действием произвольной плоской
системы сил, нужно:
1) выбрать тело,
равновесия которого следует рассмотреть
в данной задаче;
2) освободить от
связей выбранное тело и заменить их
действие силами реакции;
3) изобразить в
виде векторов все действующие на
выбранное тело (рассматриваемое как
свободное) заданные силы и силы реакций
от брошенных связей;
4) выбрать систему
осей декартовых координат;
5) составить
уравнения равновесия произвольной
плоской системы сил, в которые, корме
активных сил, войдут и реакции связей,
и решить их.
Так как тело,
равновесие которого рассматривают в
данной задаче, находится в покое, то все
приложенные к нему силы, включая и
реакции отброшенных связей, должны
удовлетворять условиям равновесия,
полученным в § 4.6 и 4.7. При этом нужно
применять ту из форм этих условий,
которая приводит к более простой системе
уравнений (наиболее простой будет та
система уравнений, в каждое из которых
входит по одному неизвестному).
Для
получения более простых уравнений
равновесия нужно: а) составляя
уравнения проекций, направлять одну
координатную ось перпендикулярно к
линии действия одной, а если возможно,
и двух неизвестных сил;
при
этом проекция силы на эту ось обратится
в нуль, а на ось, ей параллельную, сила
спроектируется в натуральную величину,
что облегчит решение задачи; б) составляя
уравнение моментов, выбрать центр
моментов в такой точке (если она есть),
через которую проходят линии действия
двух неизвестных сил;
тогда
в уравнение моментов всех сил войдет
только одна неизвестная сила. При
вычислении момента тоя или иной силы
можно брать момент самой силы или сумму
моментов составляющих ее сил (для этого
необходимо силу разложить на две
составляющие и воспользоваться теоремой
Вариньона) в зависимости oт
того, где проще определяются плечи сил.
Если
из уравнений равновесия найдены реакции
связей, а необходимо было найти давления,
оказываемые телом на те или иные плоскости
(поверхности), то необходимо учесть,
что, согласно аксиоме IV,
давления равны реакциям по модулю, но
направлены в противоположные им стороны.
Решение
многих задач статики сводится к
определению реакций опор, с помощью
которых закрепляются балки или мостовые
фермы. При этом, кроме балок, имеющих
две опоры (имеется в виду подвижная
шарнирная опора и неподвижная шарнирная
опора, которые уже были рассмотрены в
§ 3), встречается так называемая
балка-консоль.
Балка-консоль имеет один свободный
конец, а другой заделан (защемлен) в
стену или в какую-либо массивную часть
конструкции, препятствующая повороту
и смещению этого конца в любом направлении
(рисунок 65, а).
В такой неподвижной защемленной опоре,
как правило, в результате действия
активных сил
,
,
,
…,возникает
сила реакции и пара, момент которой
называется реактивным моментом (рисунок
65,в).
В
самом деле, на заделанный конец
балки-консоли со сторон опорных плоскостей
ab,
bc
и
cd
(рисунок 65, б)
действует система распределенных сил
реакций, которая может быть приведена
к одной равнодействующей реакции
,
модуль, направление и точка приложения
которой неизвестны. Перенесем эту силупараллельно самой себе в точкуА
пересечения оси балки с плоскостью
стены ab.
При этом сила
будет эквивалентна силе
,
приложенной в точкеА,
и присоединенной паре с неизвестным
реактивным моментом
(рисунок 65,в).
Силу
можно изобразить ее соответствующими
и
.
Таким образом, для нахождения реакции
неподвижной защемленной опоры надо
определить три неизвестных в
,
и
.
Найдем теперь эти величины.
Поскольку
на рассматриваемую балку-консоль
наряду с произвольной плоской системой
активных сил
,
,
…,
и
сил реакций
и
действует лежащая в той же плоскости
пара с реактивным моментом,
то
при составлении уравнений равновесия
в уравнения проекций пара не войдет,
так как сумма проекций сил пары на любую
ось, очевидно, равна нулю. В уравнении
же моментов к моментам сил алгебраически
прибавится реактивный момент
пары,
так как сумма моментов сил пары
относительно любого центра равна моменту
пары (§ 14). Таким образом, уравнения
равновесия при действии на балку-консоль
указанной системы сил и пары будут
;
;
.
Отсюда
;
;
.
Из первых двух
формул найдем модуль силы реакции:
.
В частных случаях
нагружения консоли в заделке может
возникнуть только сила реакции или
пара. Возможен также случай, когда
действующие
на консоль активные силы взаимно
уравновешиваются,
не вызывая в заделке
ни реакции, ни реактивного момента
(например,
когда балка-консоль нагружена
двумя противоположными парами
с
одинаковыми моментами).
Задача
11.
На
балку с защемленным концом действует
на участке CD
равномерно
распределенная нагрузка интенсивностью
т/м,
в точке В
действует
сила
т под углом
к балке, кроме того, на балку действует
пара сил с моментомт·м.
Определить
реакции заделки. Размеры указаны на
рисунке 66, а.
Решение.
Балка АВ
является
тем телом, равновесие которого мы должны
рассмотреть. К ней приложена сосредоточенная
сила
,
пара
сил с моментом т
и
силы, равномерно распределенные вдоль
отрезка CD
балки
АВ.
Эта
плоская система равномерно распределенных
сил характеризуется ее интенсивностью
q,
т.
е. величиной силы, приходящейся на
единицу длины нагруженного отрезка. В
рассматриваемом случае интенсивность
является величиной постоянной. При
статических расчетах эту систему сил
можно заменить равнодействующей
,
т. е. сосредоточенной силой. По модулю
эта равнодействующая равна
т.
При
этом сила
приложена
в середине О
отрезка
CD.
Заметим, что
сосредоточенной силой называют такую
силу, которая приложена к телу в
какой-нибудь одной его точке. Понятие
о сосредоточенной силе является условным,
так как практически приложить силу к
телу в одной точке нельзя. Силы, которые
в теоретической механике рассматриваются
как сосредоточенные, представляют собой
по существу равнодействующие некоторых
систем распределенных сил. В инженерных
расчетах часто приходится встречаться
с нагрузками, распределенными вдоль
данной поверхности по тому или иному
закону.
Связью,
наложенной на балку АВ,
является жесткая заделка А.
Применяя принцип освобождаемости от
связей к балке АВ,
заменим действие этой заделки на балку
силами реакций
и
иреактивным
моментом
(рисунок 66, б).
Рассмотрим теперь равновесие балки АВ
как сдвоенного твердого тела, на которое
действуют заданные силы
,
и
пара сил с моментом m,а
также неизвестные силы реакций
и
и пара сил в заделке с моментом
.
Для составления уравнений равновесия
этой произвольной плоской системы сил
выбираем оси координат, как показано
на рисунке 66, б,
и принимаем за центр моментов точку А.
Составим уравнение
равновесия произвольной плоской системы
сил в форме
;
;
.
В рассматриваемом
случае будем иметь
;
(1)
;
(2)
.
(3)
Из уравнения (1)
находим
т.
Из уравнения (2)
получаем
т.
Наконец, из уравнения
(3) находим
т·м.
Задача
12. Однородный
стержень АВ
весом
кГ
в точке А
закреплен
шарнирно, а в точке С
свободно опирается на опору С.
На стержень АВ
действует
пара сил с моментом
кг·м,
а
к
концу его В
привязана
веревка, перекинутая через блок D,
на
конце которой висит груз весом
кГ.
Определить
реакцию шарнира А
и
опоры С, если
см,
см,
а
угол
(Рисунок 67,а).
Р
Телом, равновесие которого в этой задаче
рассматривается, является стерженьАВ.
К
нему
приложена пара сил с известным моментом
т
и
две активные силы: в точке В
наклонная
сила
,
равная по модулю весу груза, т. е.Т
= Р (неподвижный
блок D,
не
изменяя модуля силы
,
изменяет
только ее направление), и на середине
Е
стержня
— вертикальная сила
(его собственный вес).
Связями,
наложенными на стержень АВ,
являются
шарнир А
и
опора С.
Так как стержень АВ
свободно
опирается на опору С, то реакция
этой опоры направлена перпендикулярно
к стержню. Неизвестную по направлению
и по модулю реакцию
шарнира
А
представляем
двумя составляющими
и
,
направленными
в положительные стороны двух координатных
осей Ах
и
Ау.
При
этом ось Ах
направим
вдоль стержня АВ,
а
ось Ау
– перпендикулярно к нему. Отбросим
связи и заменим их действие на стержень
АВ
реакциями
,
и
(рисунок
67, б).
Рассмотрим теперь равновесие стержня
АВ
как
свободного
твердого тела, на которое действуют
активные силы
и
и силы реакции
,
и
,
а
также пара сил с заданным моментом т.
За
центр моментов удобно взять точку А,
так как
через
нее проходят линии действия двух
неизвестных сил
и
.
Составим уравнения
равновесия произвольной плоской системы
сил в форме
;
;
.
Для этого
алгебраически сложим проекции всех сил
на каждую координатную ось, а также
моменты этих сил относительно центра
моментов и приравняем к нулю эти суммы:
;
(1)
;
(2)
.
(3)
Из уравнения (1)
находим
кГ.
Из уравнения (3)
получаем
кГ.
Из уравнения (2)
находим
кГ.
Знак
«минус» при
показывает, что сила реакции
имеет направление, противоположное
показанному на чертеже.
Задача
13.
Между опорами двухконсольной горизонтальной
балки CD
(рисунок
68, а)
приложена пара
,
к левой
консоли – равномерно распределенная
нагрузка интенсивностью q,
а
в точке D
правой
консоли – вертикальная нагрузка
т, Определить реакции опор, если
т,
т/м,
м.
Р
Двухконсольная балкаCD
является
тем телом, равновесие которого мы должны
рассмотреть. К ней приложена пара сил
с моментомт=Ра
и
две активные силы: в точке D
сила
и
на
середине левой консоли сила
,
являющаяся
равнодействующей равномерно распределенной
нагрузки (смотри задачу 11). Следовательно,
все приложенные к балке CD
активные
силы являются вертикальными, так как
пару сил
,
не изменяя ее действия на балку, можно
повернуть в плоскости рисунка так, чтобы
составляющие парусилы
и
были вертикальны.
Связями,
наложенными на балку CD,
являются
подвижная шарнирная опора В
и
неподвижная шарнирная опора А.
Отбросим
эти связи и заменим их действие на балку
CD
силами
реакций. Реакция
подвижной шарнирной опорыВ
нормальна
к плоскости опоры (рисунок 68, б).
Так как все действующие на балку CD
активные
силы вертикальны, то реакция
неподвижной шарнирной опорыА
также
вертикальна. Рассмотрим теперь равновесие
двухконсольной балки CD
как
свободного твердого тела, на которое
действует указанная плоская система
параллельных сил (рисунок 68, б).
Для составления уравнений равновесия
этой системы сил в форме
;
последовательно
примем за центр моментов точки А
и
В.
При
этом уравнения моментов будут содержать
только одно неизвестное.
Итак, в данном
случае будем иметь
;
(1)

(2)
Решая порознь
уравнения (1) и (2), найдем
т;
т.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Уравнения равновесия плоской системы параллельных сил
Так как параллельное расположение сил на плоскости является частным случаем их произвольного на ней расположения, то к такой системе также могут быть применены установленные в предыдущем параграфе три уравнения равновесия плоской системы сил:
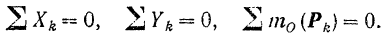
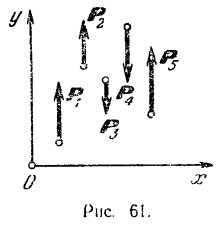
Пользуясь тем, что оси проекций можно располагать в плоскости действия сил как угодно, проведем ось 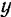
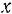
Проекция каждой из сил на ось 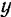
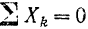
Так как все данные силы параллельны оси 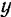
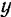
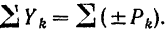
Для простоты будем в дальнейшем обозначать эту сумму просто
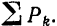
Таким образом, уравнения равновесия для плоской системы параллельных сил принимают вид
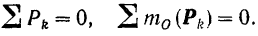
Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы порознь равнялись нулю алгебраическая сумма всех сил и сумма алгебраических величин моментов всех сил относительно любой точки, лежащей в плоскости действия сил.
Вспоминая сказанное на стр. 83 о третьей возможной форме уравнении равновесия плоской системы сил (уравнения (28)), уравнениям равновесия плоской системы параллельных сил можно придать другую форму.
Направим ось 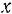
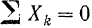
обращается о тождество и отпадает.
Остаются два уравнения
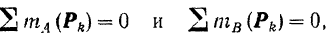
причем центры 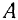
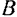
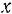
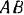
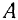
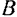
Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы порознь равнялись нулю суммы алгебраических величин моментов всех сил относительно каждой из двух произвольно выбранных, но не лежащих на прямой, параллельной данным силам, точек плоскости:
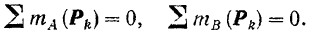
Пример задачи:
На двухконсольную горизонтальную балку действует пара сил с моментом 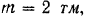
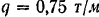
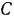
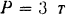
Решение:
Для определения реакций опор заменим распределенную нагрузку, действующую на участке балки длиной 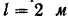
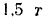
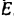
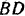
Реакция 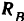
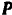
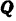
Составляем уравнения (30) равновесия балки. Так как (стр. 74) сумма алгебраических величии моментов сил пары относительно любого центра равна моменту пары и данная пара вращает плоскость чертежа по часовой стрелке, то
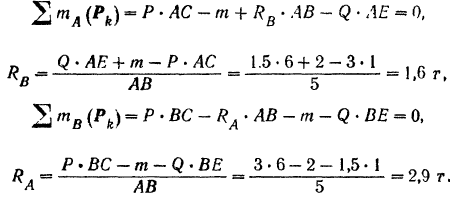
Полученный результат можно проверить. Так как балка находится в равновесии, то уравнение
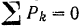
должно обращаться при подстановке в него значений приложенных к балке сил в тождество. Действительно,
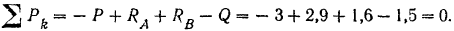
Силы пары в это уравнение мы не подставляем, так как алгебраическая сумма их всегда равна нулю.
Пример задачи:
Балка заложена в стену на глубину 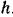
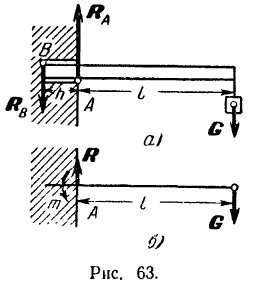
Решение:
Как видно из рис. 63, а, приложенная к балке сила 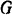
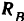
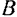
Составляя уравнения (30) равновесия для плоской системы параллельных сил, будем иметь:
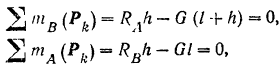
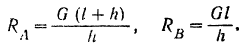
Найденным реакциям стены в месте заделки можно придать и другую (рис. 63,6), часто применяемую форму, о которой было сказано выше (стр. 85). Так как
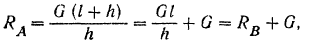
то реакцию 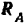
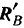
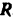
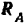
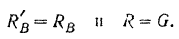
Силы 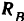
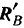
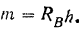
Этот момент, как видно из уравнения (II), равен но абсолютной величине моменту активной силы 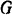
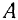
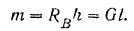
Он уравновешивает вращательный эффект приложенной к балке активной силы, т. е. препятствует вращению балки. Как видно из предыдущего равенства 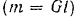
Реакция 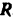
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
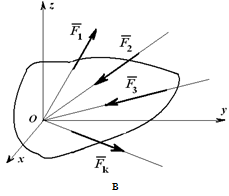
Рассмотрим условия равновесия произвольной плоской и пространственной систем сил, включая три основные формы и частные случаи равновесия для систем параллельных и сходящихся сил:
Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.
Если система уравновешена, то получаем условия равновесия: R=0, MO=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:
∑xi =0, ∑Mix=0;
∑yi =0, ∑Miy=0; (1.20)
∑zi =0, ∑Miz=0.
Формы условий равновесия
Первая форма
Для плоской системы сил (например, в плоскости Oxy) из этих уравнений получаются только три:
∑xi=0;
∑yi=0; (1.21)
∑MO=0,
причем оси и точка O, относительно которой пишется уравнение моментов, выбираются произвольно. Это первая форма уравнений равновесия.
Вторая форма
Уравнения равновесия могут быть записаны иначе:
∑xi =0;
∑MA=0; (1.22)
∑MB=0.
Это вторая форма уравнений равновесия, причем ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B.
Третья форма
∑MA=0;
∑MB=0; (1.23)
∑MC=0.
Это третья форма уравнений равновесия, причем точки A, B и C не должны лежать на одной прямой.
Предпочтительность написания форм уравнений равновесия зависит от конкретных условий задачи и навыков решающего.
Другие условия равновесия
При действии на тело плоской системы параллельных сил одно из уравнений исчезает и остаются два уравнения (рисунок 1.26, а):
∑xi =0;
∑MO=0. (1.24)
Рисунок 1.26
Для пространственной системы параллельных сил (рисунок 1.26, б) могут быть записаны три уравнения равновесия:
∑zi =0;
∑Mix=0; (1.25)
∑Miy=0.
Для системы сходящихся сил (линии действия которых пересекаются в одной точке) можно написать три уравнения для пространственной системы:
∑xi =0;
∑yi =0; (1.26)
∑zi =0
и два уравнения для плоской системы:
∑xi =0;
∑yi =0. (1.27)
В каждом из вышеприведенных случаев число неизвестных, находимых при решении уравнений, соответствует числу записанных уравнений равновесия.
Примеры решения задач >
Равновесие системы сходящихся сил >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Уравнение равновесия плоской системы сил
Условия равновесия плоской системы сил. Для равновесия плоской системы сил необходимо и достаточно, чтобы главный вектор 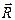
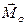
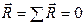
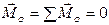
В векторной форме условие (7.8) применять для решения задач неудобно. Спроектировав уравнение (7.8) на оси координат, получим вместе с (7.9) три следующих скалярных равенства:
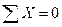

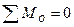
Систему (7.10) называют первой формой уравнений равновесия произвольной плоской системы сил, которая формулируется так: для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на каждую координатную ось (х, у) и алгебраическая сумма моментов этих сил относительно любой точки О, лежащей в плоскости действия сил, равнялись нулю.
Вторая форма уравнений равновесияформулируется так: для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы моментов всех сил относительно двух произвольных точек А и В и алгебраическая сумма проекций всех сил на какую-либо ось х или у, не перпендикулярную прямой АВ, равнялись нулю, т. е.
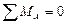
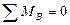
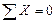
или 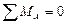
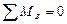
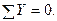
Условие неперпендикулярности сил и прямой АВ также обязательно. В противном случае, одно из уравнений системы (7.11) или (7.12) не является независимым.
Третья форма уравнений равновесияформулируется так: для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы моментов всех сил относительно трех произвольных точек А, В и С, не лежащих на одной прямой, равнялись нулю, т. е.
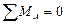
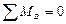
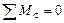
Если бы точки А, В и С лежали на одной прямой, то одно из уравнений не являлось бы независимым (его можно было получить из двух других путем тождественных преобразований). Решение задачи было бы равносильно решению системы двух уравнений с тремя неизвестными, что невыполнимо.
Все три формы уравнений равновесия совершенно равноправны. Отметим, что независимо от вида уравнений равновесия для плоской системы произвольно расположенных сил статика позволяет составить только три уравнения.
Условия равновесия плоской системы параллельных сил.Если силы перпендикулярны какой-либо оси х, то уравнение 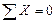
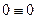
Первая форма. Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы алгебраическая сумма всех сил и алгебраическая сумма моментов всех сил относительно произвольной точки О равнялись нулю, т. е.
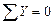
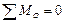
Вторая форма. Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы алгебраические суммы моментов всех сил относительно двух произвольных точек А и В равнялись нулю, т.е.
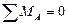
iSopromat.ru
Рассмотрим условия равновесия произвольной плоской и пространственной систем сил, включая три основные формы и частные случаи равновесия для систем параллельных и сходящихся сил:
Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.
Если система уравновешена, то получаем условия равновесия: R=0, MO=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:
Формы условий равновесия
Первая форма
Для плоской системы сил (например, в плоскости Oxy) из этих уравнений получаются только три:
причем оси и точка O, относительно которой пишется уравнение моментов, выбираются произвольно. Это первая форма уравнений равновесия.
Вторая форма
Уравнения равновесия могут быть записаны иначе:
Это вторая форма уравнений равновесия, причем ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B.
Третья форма
Это третья форма уравнений равновесия, причем точки A, B и C не должны лежать на одной прямой.
Предпочтительность написания форм уравнений равновесия зависит от конкретных условий задачи и навыков решающего.
Другие условия равновесия
При действии на тело плоской системы параллельных сил одно из уравнений исчезает и остаются два уравнения (рисунок 1.26, а):
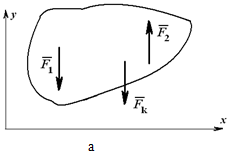
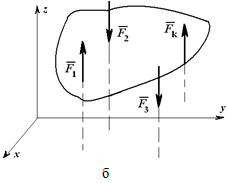
Для пространственной системы параллельных сил (рисунок 1.26, б) могут быть записаны три уравнения равновесия:
Для системы сходящихся сил (линии действия которых пересекаются в одной точке) можно написать три уравнения для пространственной системы:
и два уравнения для плоской системы:
В каждом из вышеприведенных случаев число неизвестных, находимых при решении уравнений, соответствует числу записанных уравнений равновесия.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Три формы равновесия произвольной плоской системы сил.
1. Произвольная плоская система сил находится в равновесии, если алгебраические суммы проекций всех сил на оси х и у равны нулю, а также равна нулю сумма моментов всех сил относительно любой точки.
2.Произвольная плоская система сил находится в равновесии, если алгебраические суммы проекций всех сил на одну из осей х или у равна нулю, а также, если равны нулю алгебраические суммы моментов всех сил относительно любых двух точек.
3.Произвольная плоская система сил находится в равновесии, если алгебраические суммы моментов всех сил относительно любых трех точек, не лежащих на одной прямой.
Пространственная система сил.
Пространственная система сил – это система сил, как угодно расположенных в пространстве.
Суммой трех сил, сходящихся в одной точке является сила по величине и направлению, совпадающая с диагональю параллелепипеда, построенного на заданных силах.
Момент силы относительно оси равен произведению модуля силы на кратчайшее расстояние от выбранной оси до линии действия силы.
Момент может равняться нулю, если:
1. Сила лежит на выбранной оси.
2.Сила пересекает выбранную ось.
3.Сила параллельна оси.
При приведении пространственной системы сил к точке, её можно заменять на эквивалентную систему с главным вектором и главным моментом.
Главный вектор – это геометрическая сумма всех сил системы.
Главный момент – это сумма моментов, компенсирующих пар.
Пространственная система сил находится в равновесии, если алгебраические суммы проекций всех сил на оси x, y, z равны нулю, а также равны нулю моменты всех сил относительно этих же осей.
Кинематика.
Кинематика изучает виды движения.
Плоско – параллельное движение.
Плоско – параллельное движение – это такое движение, при котором фигура полученная пересечением данного тела с выбранной плоскостью остается параллельной самой себе за все время движения.
При плоско – параллельном движении всегда существует точка, абсолютная скорость которой в данный момент времени равна нулю. Каждый последующий момент – это будет другая точка.
ДИНАМИКА.
Динамика изучает виды движения тела в зависимости от приложенных сил.
1. всякая изолированная точка находится в состоянии относительного покоя, или равномерного прямолинейного движения до тех пор, пока приложенные силы не выведут её из этого состояния.
2. Ускорение тела прямопропорциональных действующей на тело силе.
3. Если на тело действует система сил, то его ускорение будет складываться из тех ускорений, которые бы тело получало от каждой силы в отдельности.
4. Всякому действию есть есть равное по величине и противоположно направлению противодействие.
Центр тяжести – это точка приложения силы тяжести, при повороте тела центр тяжести не меняет своего положения.
Сила инерции.
Сила инерции – всегда направлена в противоположную сторону ускорению и приложена к связи.
При равномерном движении, т.е. когда а=0 сила инерции равна нулю.
При криволинейном движении раскладывается на две составляющие: на нормальную силу и на касательную.
Метод кинематики: условно прикладывают к телу силу инерции можно считать, что внешние силы реакции связей и сила инерции образуют уравновешенную систему сил. F+R+Pu=0
Сила трения.
Трение делится на два вида: трение скольжения и трение качения.
Законы трения скольжения:
1. Сила трения прямопропорциональной нормальной реакции опоры и направлена вдоль соприкасающихся поверхностей в противоположную сторону движению.
2.Коэффициент трения покоя всегда больше коэффициента трения движения.
3. Коэффициент трения скольжения зависит от материала и физически – механических свойств трущихся поверхностей.
Условие самоторможения.
Трение приводит к снижению срока службы деталей к их износу и нагреву. Для того, чтобы этого избежать необходимо вести смазку. Повысить качество обработки поверхности деталей. В трущихся местах применять другие материалы.
4. По возможности заменить трение скольжения трением качения.
Основные понятия сопротивления материалов.
Сопротивление материалов – это наука, изучающая методы расчета конструкций на прочность, жесткость и устойчивость.
Прочность – это способность конструкции выдерживать заданную нагрузку в течение срока службы без разрушения и появления остаточных деформаций.
Жесткость – это способность конструкции сохранять первоначальную форму упругого равновесия.
Устойчивость – это способность конструкции сохранять первоначальную форму упругого равновесия.
Все тела разделены на 3 группы:
1.Брус – это тело, один из размеров которого (длина) во много раз больше двух других.
2. Оболочка – это тело, один из размеров которого (толщина) во много раз больше двух других.
3. Массив – это тела, все размеры которого равны.
Классификация нагрузок:
1.По характеру действия:
2. По способу приложения:
Метод сечения.
Мысленно разрезаем нагруженный силами груз, для того, чтобы определить внутренние силовые факторы, для этого отбрасываем одну часть груза. Заменяем межмолекулярную систему сил эквивалентной системой с главным вектором и главным моментом. При разложении главного вектора и главного момента по осям x, y, z. устанавливаем вид деформации.
Внутри сечения бруса может возникать внутри силовых факторов, если возникает сила N (продольная сила), то брус растянут или сжат.
Если возникает Мк (крутящий момент) то деформация кручения, сила Q (поперечная сила) то деформация сдвига среза или изгиба. Если возникает Мих и Миz (изгибающий момент) то деформация изгиба.
Метод сечения позволяет определить напряжение в сечении груза.
Напряжение – это величина, показывающая, сколько нагрузки приходится на единицу площади сечения.
Эпюра – это график изменения продольных сил , напряжений, удлинений, крутящих моментов и т. д.
Растяжение (сжатие) – это такой вид деформации, при котором в поперечном сечении бруса возникает только продольная сила.
Правила знаков для нагрузки.
Если нагрузка направлена от сечения бруса, то продольная сила будет равна ей со знаком «плюс», если нагрузка направлена к сечению, то продольная сила будет со знаком «минус».
В пределах упругих деформаций нормальное напряжение прямо – пропорционально продольным деформациям.
Е – модуль Юнка, коэффициент, который характеризует жесткость материала при напряжениях, зависит от материала, образца из справочных таблиц.
Нормальное напряжение измеряется в Паскалях.
Расчет на прочность. Np≥[N] -Условие прочности при растяжении – сжатии.
Np – расчетный коэффициент запаса прочности.
[n] – допустимый коэффициент запаса прочности.
бmax – расчет максимального напряжения.
Кручение.
Кручение – такой вид деформации, при котором в поперечном сечении бруса возникает только один внутренний силовой фактор – крутящий момент. Кручению повергаются валы, оси. И пружины. При решении задач строятся эпюры крутящих моментов.
Правило знаков для крутящих моментов: Если вращающий момент поворачивает вал со стороны сечения по ходу часовой стрелки, то крутящий будет ему равен со знаком +, против – со знаком -.
http://megapredmet.ru/1-48289.html
- Подробности
- Категория: Теоретическая механика.Часть 1. — от СЗТУ
Теоретическая механика
Раздел первый. Статика.
Глава 5. Условия и уравнения равновесия систем сил.
§ 4. Уравнения равновесия плоской системы параллельных сил

Материалы
- Естествознание
- Физика
- Математика
- Химия
- Биология
- Экология
- Обществознание
- Обществознание — как наука
- Иностранные языки
- История
- Психология и педагогика
- Русский язык и литература
- Культурология
- Экономика
- Менеджмент
- Логистика
- Статистика
- Философия
- Бухгалтерский учет
- Технические науки
- Черчение и инженерная графика
- Материаловедение
- Сварка
- Электротехника и электроника
- АСУТП и КИПИА
- Технологии
- Теоретическая механика и сопромат
- САПР
- Метрология, стандартизация и сертификация
- Геодезия и маркшейдерия
- Программирование и сеть
- Информатика
- Языки программирования
- Алгоритмы и структуры данных
- СУБД
- Web разработки и технологии
- Архитектура ЭВМ и основы ОС
- Системное администрирование
- Создание программ и приложений
- Создание сайтов
- Тестирование ПО
- Теория информации и кодирования
- Функциональное и логическое программирование
- Программы
- Редакторы и компиляторы
- Офисные программы
- Работа с аудио видео
- Работа с компьютерной графикой и анимацией
- Автоматизация бизнеса
- Прочие
- Музыка
- Природное земледелие
- Рисование и живопись
Популярное
-
Spotlight 5: Student’s book. Workbook. Test booklet. Class CDs / Английский язык 5 класс -
Spotlight 6: Student’s book. Teacher’s book. Workbook. Test booklet. Class CDs / Английский язык 6 класс -
Spotlight 7: Student’s book. Workbook. Test booklet. Class CDs / Английский язык 7 класс -
Spotlight 4: Student’s book. Workbook. Test booklet. Class CDs / Английский язык 4 класс -
Spotlight 3: Student’s book. Workbook. Test booklet. Class CDs / Английский язык 3 класс